rRNA and Poly-β-Hydroxybutyrate Dynamics in Bioreactors Subjected to Feast and Famine Cycles

Abstract

Feast and famine cycles are common in activated sludge wastewater treatment systems, and they select for bacteria that accumulate storage compounds, such as poly-β-hydroxybutyrate (PHB). Previous studies have shown that variations in influent substrate concentrations force bacteria to accumulate high levels of rRNA compared to the levels in bacteria grown in chemostats. Therefore, it can be hypothesized that bacteria accumulate more rRNA when they are subjected to feast and famine cycles. However, PHB-accumulating bacteria can form biomass (grow) throughout a feast and famine cycle and thus have a lower peak biomass formation rate during the cycle. Consequently, PHB-accumulating bacteria may accumulate less rRNA when they are subjected to feast and famine cycles than bacteria that are not capable of PHB accumulation. These hypotheses were tested with Wautersia eutropha H16 (wild type) and W. eutropha PHB-4 (a mutant not capable of accumulating PHB) grown in chemostat and semibatch reactors. For both strains, the cellular RNA level was higher when the organism was grown in semibatch reactors than when it was grown in chemostats, and the specific biomass formation rates during the feast phase were linearly related to the cellular RNA levels for cultures. Although the two strains exhibited maximum uptake rates when they were grown in semibatch reactors, the wild-type strain responded much more rapidly to the addition of fresh medium than the mutant responded. Furthermore, the chemostat-grown mutant culture was unable to exhibit maximum substrate uptake rates when it was subjected to pulse-wise addition of fresh medium. These data show that the ability to accumulate PHB does not prevent bacteria from accumulating high levels of rRNA when they are subjected to feast and famine cycles. Our results also demonstrate that the ability to accumulate PHB makes the bacteria more responsive to sudden increases in substrate concentrations, which explains their ecological advantage.

rRNA-targeted hybridization techniques, such as fluorescence in situ hybridization and oligonucleotide membrane hybridization, are increasingly used to study microbial population diversity and dynamics in wastewater treatment systems (34). Although the temporal trends determined by these two techniques often agree with each other, their evaluations of population abundance may differ considerably. For example, Oerther and coworkers (19) reported that the Acinetobacter spp. population accounted for up to 43% of the total rRNA, while this population accounted for only up to 4.4% of the total number of cells in a municipal activated sludge system, suggesting that the cellular rRNA levels for this population were relatively high. In a related study, an opposite trend was found for the Gordonia spp. population in the same activated sludge treatment system (20). Some of the discrepancies can probably be explained by variation in the regulation of rRNA between species. However, the reactor conditions, specific metabolic functions, and ecological interactions may also contribute to modulation of the cellular rRNA level. The primary goal of this study was to investigate the effects of some of these factors on the dynamics of the rRNA pool.

Because of the positive correlation between growth rates and rRNA levels (3, 7, 13), it is widely believed that the results obtained with rRNA-targeted hybridization techniques depend on both the abundance and the activity of microorganisms present in the biomass. In the case of an activated sludge wastewater treatment system, the average growth rate of the biomass is controlled by the solids retention time (SRT) imposed on the biomass by operation of the reactor. Therefore, the average growth rate is the same for all microbial groups present in a properly functioning activated sludge reactor at steady state. Consequently, it should be possible to calibrate the specific rRNA level of a population with laboratory chemostat studies and to extrapolate to activated sludge reactors based on the operational SRT. In contrast to the biomass in a laboratory-scale chemostat reactor, the biomass in most full-scale activated sludge wastewater treatment plants is subjected to temporally varying substrate concentrations due the plug flow or relatively limited mixing characteristics of the reactor or due to operation as a sequencing batch reactor. Such conditions lead to what is often described in the activated sludge literature as feast and famine cycles (2, 5, 31), which are defined as the intermittent presence of electron donors in the bulk liquid (feast period) and the absence of electron donors near the outlet of the reactor (famine period). Limited information concerning the effect of rapidly changing substrate concentrations on the dynamics of the rRNA pool is available. In the few studies in which this question was examined, the workers observed that bacterial cells growing in continuously fed reactors accumulated more RNA when the feeding rate was varied cyclically than when the feeding rate was kept constant (22, 26). Although these studies were performed with relatively high dilution rates compared to the SRTs found in activated sludge systems, it is possible that bacteria growing in activated sludge systems accumulate more rRNA than the amount that would be expected if only the SRT was considered a measure of the growth rate. Thus, to properly interpret microbial population abundance and dynamics, there is a need to ascertain the effect of the feast and famine cycles typically found in activated sludge treatment systems on the rRNA level observed in bacterial cells.

In addition to the mixing characteristics of bioreactors, other factors can affect the dynamics of the rRNA pool of microorganisms growing in activated sludge treatment systems. For example, the ability to modulate the growth rate by coutilization of several substrates (14) or the up-regulation of production of rRNA to counteract the presence of inhibitors of ribosome assembly (17) can potentially alter the size of the rRNA pool compared with the size that would be expected based on the SRT. In the current study, we focused on yet another factor, the capacity to uncouple the uptake of substrate and the formation of new biomass by accumulation of storage compounds, such as poly-β-hydroxybutyrate (PHB). Determining the ability to accumulate storage compounds has been shown to be important for understanding the growth dynamics of activated sludge systems (2, 10, 31). Bacteria capable of accumulating storage compounds seem to rapidly take up substrate during the feast period and to use the substrate taken up that exceeds the capacity of new biomass production to synthesize storage compounds (8, 29, 31). During the famine period, they use the stored compounds to form new biomass and to meet maintenance requirements. It seems logical to hypothesize that bacteria that are not capable of accumulating storage compounds produce new biomass only during the feast period. Consequently, one could hypothesize that the impact of feast and famine cycles on the dynamics of the rRNA pool would be greatly reduced in bacteria that are capable of accumulating storage compounds.

The effects of feast and famine cycles and of storage metabolism on the dynamics of the rRNA pool were studied using two strains of Wautersia eutropha (formerly Ralstonia eutropha), a wild-type strain and a mutant that is not capable of accumulating PHB. The two strains were each grown in a chemostat and in a semibatch reactor (pulse fed every 3 h). The metabolic responses of the four cultures to pulse-wise addition of substrate were assayed to determine the impact of the ability to store PHB and the impact of the size of the rRNA pool on the metabolic response.

MATERIALS AND METHODS

Bacterial strains.

Two strains of W. eutropha were obtained from the Deutsche Sammlung von Mikroorganismen und Zellkulturen GmbH. W. eutropha strain H16 [= DSM 428; referred to below as the PHB(+) strain] is a wild-type strain. W. eutropha strain PHB-4 [= DMS 541; referred to below as the PHB(−) strain] is a mutant of strain H16 that cannot accumulate PHB (25) because of a deletion mutation in the phbC gene, which codes for the PHB synthase enzyme (work by Hein et al. [11] confirmed this mutation).

Culture conditions.

Microorganisms were cultured either in flasks or in reactors. The growth medium for the flask cultures contained (23) Na₂HPO₄ · 7H₂O (7.9 g/liter), KH₂PO₄ (1.5 g/liter), NH₄Cl (0.3 g/liter), MgSO₄ · 7H₂O (0.1 g/liter), CH₃COONa · 7H₂O (1.36 g/liter), and a trace element solution (33) (2 ml/liter). The flasks were incubated at 30°C and agitated on a shaking table at 300 rpm.

Each reactor consisted of a 3-liter chamber (Applikon, Schiedam, The Netherlands) with a 2-liter working volume and was equipped with three baffles and a central six-blade turbine rotating at 800 rpm. The reactors were fed medium containing (23) K₂HPO₄ (0.8g/liter), KH₂PO₄ (0.3 g/liter), NH₄Cl (0.8 g/liter), MgSO₄ · 7H₂O (0.2 g/liter), CH₃COONa · 7H₂O (5.45 g/liter), silicone antifoaming agent (0.1 ml/liter; BDH, Poole, Dorset, England), and a trace element solution (33) (2 ml/liter).

Two reactor configurations were used: chemostat and semibatch. The same dilution rate (1 volume per day, corresponding to a hydraulic retention time of 24 h) was used for both configurations. For the semibatch reactor, one-eighth of the reactor volume (250 ml) was withdrawn (in approximately 3 min) every 3 h, and the reactor was refilled (in approximately 2 min) with 250 ml of fresh medium. The reactors were aerated with air so that the oxygen concentration was at least 75% of saturation for the chemostat and at least 50% of saturation for the semibatch reactor during the steady-state period (see below). The pH was controlled at 7.5 in both reactors by using solutions of 1 M HCl and 1 M NaOH. The influent line of the chemostat was equipped with an aerated flow breaker to minimize discontinuity in feed addition. Finally, the maximum liquid level in the reactors was controlled by a level controller (18), while the minimum level in the semibatch reactor was adjusted by adjusting the height of the withdrawing tube.

Experimental approach and analytical techniques.

Each reactor was monitored by measuring the dissolved oxygen (DO) concentration continuously and by measuring the optical density at 420 nm (OD₄₂₀) and observing the culture with a phase-contrast microscope daily. Periodically, the purity of the culture was assessed by serial dilution plating on nutrient agar. At the same time, the biomass dry weight was determined by filtration through a 0.22-μm filter and drying the preparation to a constant weight in a microwave. We assumed that a reactor was at steady state when the DO concentration and the biomass level were constant (chemostat) or exhibited the same profiles for each cycle (semibatch reactor).

After steady state was reached, reactor operation was stopped, and each culture was tested by performing a pulse experiment equivalent to one cycle of the semibatch reactor (i.e., one-eighth of the reactor medium was replaced with new medium, and the culture was monitored for 180 min). During these experiments, 13 samples were obtained and were rapidly processed as follows. A portion of each sample was immediately filtered through a 0.22-μm filter and stored at −80°C to allow later analysis of acetate, soluble organic carbon (SOC), ammonium, nitrate, and nitrite contents; subsamples were immediately stored at −80°C for analysis of total organic carbon (TOC), protein, and RNA contents. In addition, a few drops of formaldehyde were added to subsamples kept for PHB analysis, which were stored at −80°C and freeze dried. Finally, the OD₄₂₀ was determined, and the oxygen uptake rate (OUR) was determined by respirometry using a Jenway (Dunmow, Essex, England) model 9300 DO meter equipped with data acquisition software.

TOC and SOC concentrations were determined by determining the difference between the total and inorganic carbon concentrations using a Dohrman (Tekmar-Dohrmann, Cincinnati, OH) model DC-190 TOC analyzer. The particulate organic carbon (POC) concentration was determined by subtracting the SOC concentration from the TOC concentration. Acetate was measured by gas chromatography by direct column injection (injector temperature, −80°C), using an HP-INNOWAX (cross-linked polyethylene glycol) capillary column (Agilent Technology, Amstelveen, The Netherlands) and a flame ionization detector (temperature, 200°C). The carrier gas was helium, and the following program was used: 60°C for 3 min, increase at a rate of 5°C/min, and 150°C for 5 min (6). The ammonium concentration was determined spectrophotometrically at 623 nm by using the phenate method (standard method 4500-NH₃.F) (1). The nitrite concentration was determined at 540 nm by using the colorimetric standard method (standard method 4500-NO₂⁻.B) (1). PHB was quantified as described by Smolders and coworkers (27) by first extracting the PHB from a freeze-dried cell pellet using a solution of concentrated HCl, isopropanol, and dichloromethane (1:4:5, vol/vol/vol) and then heating the preparation at 100°C for 2 h. The resulting organic phase was extracted with water, dried with Na₂SO₄, and analyzed by gas chromatography using a STABILWAX capillary column (Restek, Bellefonte, PA) at 200°C and a flame ionization detector (temperature, 240°C) with helium as the carrier gas. Benzoic acid was used as an internal standard, and the results were expressed as the mass proportion of the dried pellet (f_PHB,MASS) (equation 1).

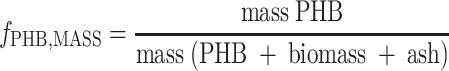(1)

The elemental composition of the biomass (C, H, N, and S) was determined by combustion in a partial oxygen atmosphere at 1,020°C with a Carbo Erba (Milan, Italy) model EA1108 elemental analyzer used according to the manufacturer's instructions. The mass proportion of atomic oxygen in the biomass was determined by subtracting from 1 the ash content and the mass proportions of the other elements. Protein concentrations were determined using the Bio-Rad (Hercules, CA) DC protein assay according to the manufacturer's instructions. RNA concentrations were determined by isolating RNA using the Trizol reagent as recommended by the manufacturer in conjunction with repeated pipetting with a 1-ml tip for cell disruption (Gibco BRL, Invitrogen, Carlsbad, CA) and measuring the absorbance at 260 nm (A₂₆₀); the conversion factor used was 40 mg · liter⁻¹ A₂₆₀⁻¹. All analyses were performed with duplicate samples.

Calculations.

The biomass was defined as the fraction of carbon that was structurally or enzymatically active in bacterial metabolism. Therefore, the highly variable PHB pool was not part of the biomass. The formula CH_1.5O_0.5 was assumed for PHB (formula weight of PHB [FW_PHB], 21.5 g mol⁻¹), and the formula for the biomass was determined to be CH_1.97O_0.54N_0.24 with a ash content of 7.3% (total formula weight of biomass with ash [FW_H+ASH], 28.0 g mol⁻¹). The carbon concentrations for PHB (X_PHB) (equation 2) and biomass (X_H) (equation 3) were calculated by converting the PHB mass ratio (f_PHB,MASS) to a carbon molar ratio using the formula weight of PHB and the total biomass and multiplying by the molar concentration of particulate carbon ([g POC liter⁻¹]/[12 g mol⁻¹]).

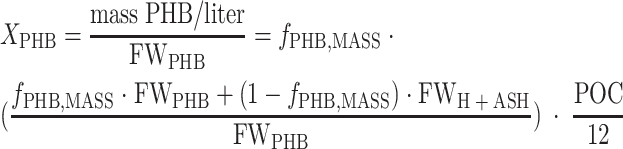(2)

(3)

where the average formula weight of the suspended particles is obtained as follows: f_PHB,MASS · FW_PHB + (1 − f_PHB,MASS) · FW_H+ASH. Finally, note that the carbon fraction of PHB (f_PHB) was defined as X_PHB/X_H to allow comparison with other studies.

The continuous OUR profile of each semibatch reactor was calculated from the online DO measurements using equation 4. The oxygen rate transfer rate coefficient (k_La) was determined by minimizing the sum of squared differences between the calculated OUR and the OUR measured by respirometry.

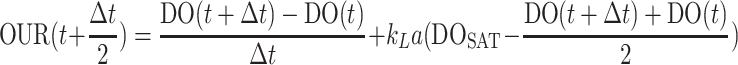(4)

where t is initial time of measurement, Δt is time between measurements, DO is the DO concentration, DO_SAT is the saturation DO concentration, and DO(t) and DO(t + Δt) are the two consecutive DO measurements.

The conversion rates and the standard errors for acetate, ammonium, and PHB during the feast phase of the pulse experiments were determined by linear regression of concentrations versus time, assuming zero-order rates with respect to the concentrations of reactants. The conversion rates were reconciled to the elemental mass and degree-of-reduction balances (i.e., mass and electron balances were performed) to allow calculation of the biomass formation rate and to test for gross measurement errors or errors in the description of the overall reaction (data consistency). These calculations were performed by the technique of van der Heijden and coworkers (30), using the Macrobal software (12).

For the analysis of the famine phase, it was not possible to assume that the rates were zero order with respect to the concentrations of the reactants. In addition, the sampling frequency was much less than that during the feast phase. Consequently, the analysis had to be adapted to each culture. The analysis of the PHB(+) cultures started by describing the degradation rate for the PHB fraction (f_PHB) by nonlinear regression of the PHB fraction over time, computed using the NLIN procedure of SAS/STAT (24). Although several equation were tested, the best fit was obtained with equation 5:

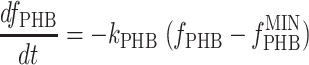(5)

where k_PHB is the first-order PHB degradation rate constant and 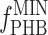is the minimum PHB fraction of the active biomass (29). After fitting, the PHB degradation rate at 110 min after the addition of acetate (approximately halfway through the famine phase) was estimated using equation 5. Based on the measured OUR at 110 min and the estimated PHB degradation rate, the rate of biomass formation was calculated based on mass and degree-of-reduction balances. For the PHB(−) cultures, it was assumed that the biomass degradation rate was balanced with the OUR.

Although the rate of change of the biomass concentration could be calculated from other conversion rates using the elemental mass and degree-of-reduction balances, an insufficient number of independent conversion rates was determined to allow a test for data consistency. Instead, the data were tested for consistency with the metabolic model (see below).

Metabolic model.

A metabolic model was used in this study to analyze the stoichiometry of the biological reactions. This model has been described elsewhere (29) and was based on seven intracellular reactions describing (i) acetate uptake, (ii) PHB formation, (iii) PHB degradation, (iv) biomass monomer formation, (v) biomass monomer polymerization, (vi) acetyl-coenzyme A (acetyl-CoA) catabolism, and (vii) oxidative phosphorylation. The model assumed that 0.267 mol of CO₂ was produced during the formation of 1 mol of biomass carbon monomers from acetyl-CoA (9), while the same reaction required 0.66 mol of ATP (28). The model further assumed that 1.5 mol of ATP was used to polymerize 1 mol of biomass monomers (32). Assuming that (i) the internal pools remained at steady state and (ii) PHB was not formed and degraded at the same time, the model yielded two linear stoichiometric equations (29), one for the feast phase (equation 6) and one for the famine phase (equation 7):

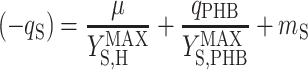(6)

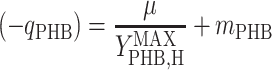(7)

where q_S is specific acetate conversion rate, μ is the specific biomass formation rate, q_PHB is the specific PHB conversion rate, 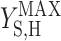, , 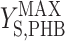and 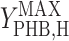are the maximum yield coefficients for biomass from acetate, for PHB from acetate, and for biomass from PHB, respectively, and m_S and m_PHB are the maintenance coefficients for growth on acetate and on PHB, respectively. The yield and maintenance coefficients are further defined as follows:

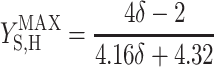(8)

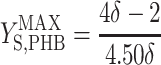(9)

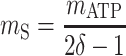(10)

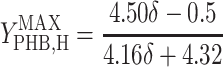(11)

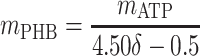(12)

Thus, there are only two unknown model parameters: the efficiency of the oxidative phosphorylation (phosphate-to-oxygen ratio [ATP produced/NADH oxidized]) (δ) and the amount of ATP required for maintenance (m_ATP). The stoichiometric equation for the feast phase (equation 6) can be used to analyze the PHB(−) cultures by considering q_PHB = 0. However, the stoichiometric equation for the famine phase (equation 7) cannot be used for the PHB(−) strain. By assuming that the amount of ATP required for maintenance was derived mainly from oxidative phosphorylation, the following stoichiometric equation was used to describe the famine phase of the mutant strain:

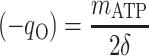(13)

where q_O is the specific oxygen conversion rate. Equations 6, 7, and 13 can be rewritten so that the measured rates are linear functions of δ and m_ATP.

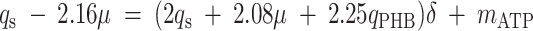(14)

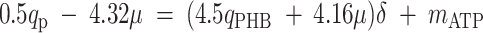(15)

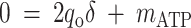(16)

where q_s, q_PHB, and q_p are the same as defined before. Assuming that δ and m_ATP are the same for the two strains and remain constant for the two culture conditions, the four pulse experiments provide eight combinations of metabolic rates (four for the feast phase and four for the famine phase), these rates can be used to determine the two unknown model parameters (δ and m_ATP) by linear regression of the right terms versus the left terms of the equations. In order to take into account the error associated with the two sides of the equations, major axis regression (16) was implemented in a Microsoft Excel worksheet to evaluate the values of δ and m_ATP. Finally, the regression approach also provides a test for the assumption that there is constant stoichiometry among strains and culture conditions, as strong departures from linearity would suggest that the stoichiometry is not constant.

RESULTS

General observations.

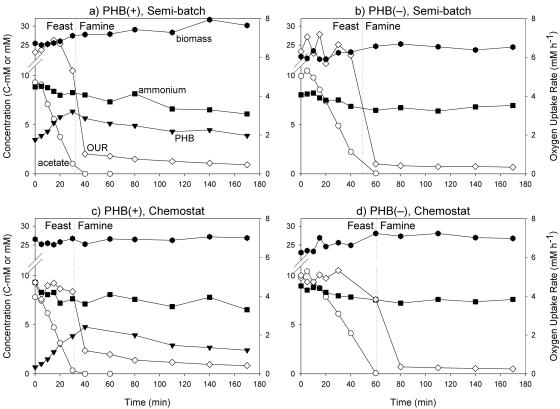
The chemostat and semibatch reactors were operated until steady state was reached in terms of the DO and biomass concentration profiles (approximately 2 weeks). Once steady state was reached, the reactor operation was stopped and pulse experiments equivalent to one cycle of the semibatch reactors were performed. The concentration profiles for acetate, ammonium, PHB, and biomass and the OUR profile are shown in Fig. 1. A clear change in the behavior of the cultures occurred when acetate disappeared. In the presence of acetate (feast phase), PHB accumulated in the PHB(+) cultures and the OUR was high for all cultures. PHB was not detected in the PHB(−) mutant cultures. In the absence of acetate (famine phase), the OUR was low but substantially above zero, PHB was degraded in the PHB(+) cultures, and the level of biomass slowly decreased in the PHB(−) cultures.

FIG. 1.

Concentrations of acetate (mmol C/liter) (○), PHB (mmol C/liter) (▾), ammonium (mmol/liter) (▪), and biomass (mmol C/liter) ( ) (left axis) and oxygen uptake rates (mmol/liter · h) (⋄) (right axis) during a pulse experiment. (a) PHB(+) in a semibatch reactor. (b) PHB(−) in a semibatch reactor. (c) PHB(+) in a chemostat reactor. (d) PHB(−) in a chemostat reactor. Note that the left y axes are broken between 12 and 21 mM.

In addition to the data shown in Fig. 1, SOC, nitrite, and nitrate concentrations were determined. Nitrate was never detected, while the maximum nitrite concentration measured was 11 μM. Because of these low levels, it was assumed that heterotrophic nitrification was not significant in these cultures. The level of SOC was measured (data not shown) in order to determine if the cultures excreted soluble organic compounds. The depletion of SOC corresponded to acetate uptake, suggesting that no compounds were excreted during the feast phase. For the PHB(+) cultures, the level of SOC remained stable during the famine phase. However, the level of SOC increased by approximately 0.5 mM in the PHB(−) cultures during the famine phase, suggesting that soluble metabolites were released.

Feast phase.

The rates of acetate, oxygen, and ammonium uptake and PHB formation were determined from measured concentrations. Although the biomass concentration clearly increased during the feast phase (Fig. 1), it was not possible to accurately determine the rate of biomass formation from these data or from the protein concentrations because the error for each measurement (approximately ±8% or ±2 mM C with respect to the biomass concentration) was large compared to the observed increase [approximately 3 mM C for the PHB(+) cultures and 6 mM C for the PHB(−) cultures]. Thus, the elemental mass and degree-of-reduction balances were used (i) to calculate the biomass formation rates, (ii) to reconcile the measured rates with the balances (Table 1), and (iii) to determine if the reconciled rates were different from the measured rates. The reconciled rates were not found to be significantly different from the measured rates (P > 0.25) (Table 1).

TABLE 1.

Test conditions, characteristic times, specific conversion rates, and macromolecular compositions of the biomass during the feast phase

Parameter	PHB(+)		PHB(−)
	Semibatch	Chemostat	Semibatch	Chemostat
Culture conditions
Initial acetate concn (mmol C liter−1)	10.04	9.72	10.25	10.75
Biomass concn (mmol C liter−1)	25.87 ± 0.43a	25.83 ± 0.28	22.43 ± 0.48	25.59 ± 0.69
Characteristic time
Lag time (min)	1.28 (NS)b	−2.68 (NS)	8.42 (S)c	5.17 (S)
End of feast phase (min)	32.54	31.16	49.18	60.84
Specific conversion rates
Acetate (mol C [mol C · h]−1)	−0.749 ± 0.029d	−0.668 ± 0.013	−0.673 ± 0.016	−0.452 ± 0.015
Oxygen (mol [mol C · h]−1)	−0.235 ± 0.028	−0.174 ± 0.008	−0.288 ± 0.011	−0.195 ± 0.006
PHB (mol C [mol C · h]−1)	0.236 ± 0.028	0.273 ± 0.021	NAe	NA
Biomass (mol C [mol C · h]−1)	0.238 ± 0.045	0.179 ± 0.026	0.37 ± 0.014	0.247 ± 0.012
h-statisticsf	0.22	0.45	0.27	0.12
P (h, 2)g	0.97	0.80	0.87	0.94
Macromolecular composition
Proteins (%, wt/wt)	59.6 ± 1.3h	64.7 ± 0.6	69.9 ± 1.1	69.7 ± 1.4
RNA (%, wt/wt)	1.54 ± 0.05h	0.89 ± 0.03	3.03 ± 0.15	1.43 ± 0.14

^aBiomass concentration (average ± standard error) during the feast period corrected for biomass increase (n = 6 to 8).

^bNS, not significantly different from 0 (P > 0.05).

^cS, significantly different from 0 (P < 0.05).

^dRates (average ± standard error) were first determined by linear regression and then adjusted by data reconciliation (30).

^eNA, not applicable.

^fh-statistics indicate the degree of consistency within the raw data and the elemental mass and degree-of-reduction balances (0 for a perfect balance). Ammonium measurements were included in the test, but the results are not shown.

^gProbability of the h-statistics (no difference between the measured and balanced rates) from a χ² distribution with 2 degrees of freedom (30).

^hComposition (average ± standard error) during the feast phase (n = 6 to 8).

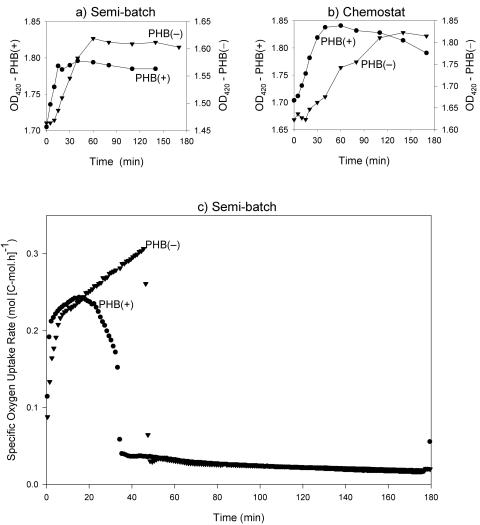
It was also noticed that the time required to reach the end of the feast phase (i.e., the time of acetate disappearance) varied widely between cultures, from 31 to 61 min (Table 1). Differences in biomass and specific acetate uptake rates partially explained these observations. In addition, a significant delay in the response of the PHB(−) cultures to the addition of fresh medium was observed based on the acetate concentrations (Fig. 1), the OD₄₂₀ measurements (Fig. 2a and b), and the OURs calculated from the DO curves for the semibatch reactor cultures (Fig. 2c). From the regression line for the acetate concentration over time, the lags were determined to be 5.17 and 8.42 min for the chemostat and semibatch cultures, respectively.

FIG. 2.

Optical density at 420 nm for semibatch reactors (a) and chemostat reactors (b) and specific OUR (c) calculated from the dissolved oxygen concentration for the semibatch reactors. •, PHB(+) cultures; ▾, PHB(−) cultures.

RNA and protein levels.

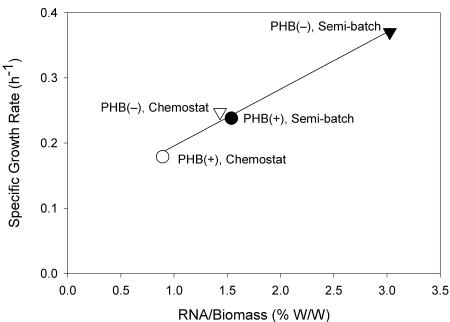
The measured values for the RNA and protein concentrations were too variable to detect any trend in the pulse experiments. However, the average levels were significantly different in the various cultures. The PHB(−) cultures were found to contain higher levels of protein and RNA than the PHB(+) cultures contained (Table 1). In addition, the levels of RNA were also higher for the cultures grown in the semibatch reactors than for the cultures grown in the chemostat reactors (Table 1). In agreement with expectations, the specific biomass formation rate during the feast phase correlated well with the average level of RNA per unit of biomass (Fig. 3).

FIG. 3.

Specific growth rate during the feast phase as a function of the level of RNA in the biomass. ○ and •, PHB(+) cultures; ▿ and ▾, PHB(−) cultures; solid symbols, semibatch reactor; open symbols, chemostat reactor.

Famine phase.

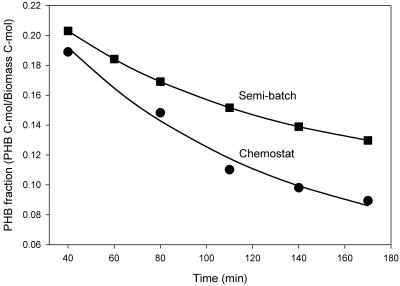
Slight differences in the behaviors of the cultures were observed during the famine phase. The PHB(+) cultures degraded PHB during the famine phase and produced new biomass by incorporating ammonium (Fig. 1a and c). The specific PHB degradation rate was satisfactorily described by equation 5. After fitting (Fig. 4), the first-order rate constant (k_PHB) was 6.42 h⁻¹ for both cultures. However, the minimum PHB fractions were 0.106 mol C (mol C)⁻¹ and 0.051 mol C (mol C)⁻¹ for the semibatch culture and the chemostat culture, respectively. Thus, the specific PHB degradation rate at 110 min after the addition of fresh medium (approximately halfway through the famine phase) was calculated to be 0.0297 mol C (mol C · h)⁻¹ in the semibatch reactor. Based on this value and the measured OUR, the specific biomass formation rate was determined to be 0.0103 h⁻¹. Correspondingly, the specific PHB degradation rate for the chemostat culture was 0.0398 mol C (mol C · h)⁻¹, and the specific biomass formation rate was 0.0254 h⁻¹.

FIG. 4.

Degradation of PHB in the PHB(+) cultures during the famine phase for the semibatch reactor (▪) and the chemostat reactor (•). The lines indicate the fit obtained with equation 5.

In the PHB(−) cultures, the biomass decreased slowly during the famine phase at specific rates of 0.019 h⁻¹ and 0.023 h⁻¹ for the semibatch and chemostat reactors, respectively. These decreases were accompanied by (i) oxygen consumption, (ii) release of ammonium (Fig. 1b and d), and (iii) release of SOC (data not shown). The trends for biomass decrease, release of ammonium, and release of SOC were not significant when they were tested independently. However, together they possibly described a physiological response in which some portion of the biomass was degraded to supply the excreted ammonium and carbon and the reducing equivalent that sustained the OUR.

Growth stoichiometry and metabolic model parameters.

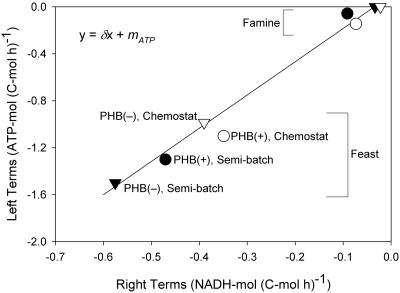
The constancy of growth stoichiometry between cultures was tested by use of a metabolic model. The rates determined during the feast phase and during the famine phase were introduced into the linearized model equations (equations 14, 15, and 16), and the values for δ and m_ATP were determined by major axis regression (Fig. 5). The values for δ and m_ATP were found to be 2.88 ± 0.17 mol ATP · mol NADH ⁻¹ and 0.100 ± 0.042 mol ATP (mol C · h)⁻¹, respectively. The regression line satisfactorily described the data, suggesting that the metabolic model parameters for all cultures were similar (i.e., there was constant growth stoichiometry across cultures). Finally, the results shown in Fig. 5 suggest that the measured famine conversion rates were accurate and consistent with the elemental and degree-of-reduction balances if it was assumed that δ and m_ATP are constant.

FIG. 5.

Major axis regression to determine the parameters of the metabolic model using equations 14, 15, and 16. The terms on the left of the equations were plotted on the y axis, while the multipliers of δ (terms on the right of the equations) were plotted on the x axis. For the regression line: δ = 2.88 ± 0.17 mol ATP (mol NADH)⁻¹, m_ATP = 0.100 ± 0.042 mol ATP (mol C · h)⁻¹), R² = 0.98. ○ and •, PHB(+) cultures; ▿ and ▾, PHB(−) cultures; solid symbols, semibatch reactor; open symbols, chemostat reactor.

DISCUSSION

RNA level.

The primary goal of this study was to determine the effects of (i) a reactor configuration that leads to feast and famine cycles and (ii) the ability to accumulate PHB on the amount of rRNA found in bacterial cells. Marked differences in cellular RNA and protein levels were observed for the same strain grown in different reactors (Table 1). Both strains accumulated more RNA when they were grown in semibatch reactors than when they were grown in chemostats. Since approximately 80 to 85% of RNA is rRNA (3), RNA measurements can be used to evaluate the size of the rRNA pool. Consequently, the results confirmed that the capacity to produce PHB did not stop the cells from increasing the size of the rRNA pool when they were exposed to feast and famine cycles. Since the size of the entire protein synthesis system is typically correlated with the cellular concentration of rRNA (3), the protein synthesis capacity was likely increased. However, the RNA level in the PHB(+) strain was only 73% higher when the strain was grown in the semibatch reactor than when it was grown in the chemostat. This contrasts with the results for the PHB(−) strain, which had a cellular RNA level that was 111% higher when the organism was grown in the semibatch reactor. Comparable to these observations was the higher level of RNA in the mutant cultures than in the wild-type cultures grown in homologous reactors (Table 1). Together, these observations suggest that regulation of rRNA is altered in the mutant. However, more work is necessary to ascertain the physiological foundation for this altered regulation.

The observed differences in RNA levels between cultures have direct implications for the interpretation of quantitative data for bacterial populations in activated sludge obtained by rRNA-targeted molecular techniques. The data show that reactor configurations and specific metabolic organizations affect the observed rRNA level for a given population, which may explain the wide range of cellular rRNA levels obtained for various populations in activated sludge (19, 20).

Conversion rates and growth stoichiometry.

Two important differences between cultures were observed for the conversion rates during the feast phase (Table 1): (i) the biomass formation rate of each culture was different and (ii) the acetate uptake rate of the chemostat-grown PHB(−) culture was approximately 33% lower than the rates for the other cultures. In general terms, these differences could be explained by differences in metabolic efficiency (biomass and PHB yields) or by differences in the kinetic abilities of the cellular systems. The possibility that the metabolic efficiencies of the cultures were different was tested using the metabolic model (equations 14, 15, and 16). Figure 5 shows that the metabolic efficiencies for cultures were similar as the combined conversion rates closely followed the expected linear relationship. Consequently, the differences in the conversion rates were more likely due to differences in the maximum instantaneous rates of limiting metabolic reactions.

The differences in the biomass formation rates were found to correlate well with the RNA levels (Fig. 3). Since most RNA is rRNA (3), measuring the total RNA also provides a measure of the level of ribosomes in cells. Therefore, it seems that the maximum instantaneous biomass formation rate during the feast phase is related to the level of ribosomes, which makes the pool of ribosomes likely to be limiting during this period. This is consistent with the near-maximal efficiency of ribosome activity immediately after a nutritional shift-up (4, 15), although bacterial cells typically accumulate more ribosomes than necessary to meet the protein synthesis need under balanced growth conditions (15).

The situation with the acetate uptake rate can be analyzed as follows. Based on the maximum growth rate of both strains (0.381 ± 0.007 h⁻¹, determined in four independent batch experiments [data not shown]) and the stoichiometric coefficients determined with the metabolic model (Table 2), a maximum acetate uptake rate for these cultures of 0.673 ± 0.057 mol C (mol C · h)⁻¹ was calculated (equation 6) (q_PHB = 0). This maximum acetate uptake rate is close to the uptake rates observed during the feast period for the two PHB(+) cultures and the semibatch reactor-grown PHB(−) culture (Table 1). Thus, it appears that the acetate uptake pathway was fully induced in these cultures. This result is in agreement with the results of other studies that found no relationship between the steady-state growth rates of cultures and the acetate uptake rates after pulse-wise addition of substrate (21, 29). It is also likely that the acetate uptake pathway was fully induced in the chemostat-grown PHB(−) culture despite the lower measured acetate uptake rate. In the case of this culture, it is possible that the limitation of biomass formation (see above) may have restricted the turnover of acetyl-CoA, which in turn restricted the uptake of acetate because acetate must be charged on free CoA to be metabolized (36). This scenario is consistent with the results of a study of Escherichia coli that reported that there was a restriction in the acetate uptake rate due to a reduced acetyl-CoA turnover rate when there was nutritional shift-up (35). In this context, the PHB synthesis pathway may act as an acetyl-CoA sink to sustain high acetate uptake rates.

TABLE 2.

Maximum yields and maintenance coefficients corresponding to the values for δ and m_ATP obtained

Model parameter	Units	Value (avg ± SE)
YS,HMAX	mol C (mol C)−1	0.584 ± 0.049
YS,PHBMAX	mol C (mol C)−1	0.735 ± 0.068
YPHB,HMAX	mol C (mol C)−1	0.764 ± 0.057
ms	mol C (mol C · h)−1	0.0209 ± 0.0089
mPHB	mol C (mol C · h)−1	0.0080 ± 0.0034

Implication for the ecology of PHB metabolism.

It has been documented that microorganisms capable of accumulating PHB are selected for in activated sludge systems (10, 29, 31). It is useful to quantify the cost and benefit of accumulating PHB in order to understand the ecological importance of this metabolic pathway. In the metabolic model framework used in this paper, the cost of using PHB storage in terms of biomass yield (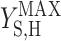versus  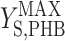× 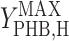) was quantified previously (2). In the current study, it was found that producing biomass from acetate via PHB reduced the biomass yield by 4%. Based on previously published data for δ, the cost was determined to range from 4% to 10% (2). The data presented in this paper made it possible to quantify the benefit of accumulating PHB in feast and famine cycles for the conditions tested.

It was found that the PHB(+) cultures and the semibatch reactor-grown PHB(−) culture had similar specific acetate uptake rates (Table 1) close to the maximum rates based on the maximum growth rate and yield. Therefore, the advantage of accumulating PHB does not seem to be the ability to develop a higher specific substrate uptake rate. However, only the rate for the chemostat-grown PHB(−) culture was unable to reach the maximum acetate uptake rate, indicating that repeated exposure to feast and famine cycles was necessary to develop this metabolic capacity. Thus, it seems that the ability of PHB-accumulating organisms to take up acetate is less sensitive to growth history. It is possible to quantify this benefit by realizing that the chemostat-grown PHB(−) culture took up only 50% of the available acetate in the time that it took the PHB(+) cultures to take up all the acetate, a percentage much higher than the 10% yield cost of PHB metabolism. If these results are extended to the ecology of activated sludge systems, they suggest that in an activated sludge system incoming populations that cannot accumulate PHB are not able to effectively compete upon introduction into the system. Therefore, the chance of becoming established is reduced.

Another competitive advantage of the PHB-accumulating bacteria may be their capacity to take up substrate faster after a period of famine. In the current experiments, a lag before the onset of acetate uptake at the beginning of the feast phase was observed for both PHB(−) cultures. As the length of the acetate uptake period was found to be between 30 and 35 min, a 5-min lag corresponds to uptake of an amount of acetate that is between 14% and 17% of the total amount of acetate available. This proportion of acetate is also greater than the yield cost of producing PHB (maximum, 10%).

In summary, it appears that the main advantage of bacteria that are capable of accumulating PHB and growing in activated sludge systems is their metabolic responsiveness. Accumulating a certain level of PHB allows the cells to take up acetate at the maximum uptake rate without delay and irrespective of the growth history. In the current experiments, these kinetic advantages corresponded to acetate uptake that was 14 to 50% greater than that in cultures that were not capable of accumulating PHB, values that are much higher than the metabolic cost of PHB storage.