An Expectation-Maximization–Likelihood-Ratio Test for Handling Missing Data

Abstract

The mapping of quantitative trait loci (QTL) is an important research question in animal and human studies. Missing data are common in such study settings, and ignoring such missing data may result in biased estimates of the genotypic effect and thus may eventually lead to errant results and incorrect inferences. In this article, we developed an expectation-maximization (EM)–likelihood-ratio test (LRT) in QTL mapping. Simulation studies based on two different types of phylogenetic models revealed that the EM-LRT, a statistical technique that uses EM-based parameter estimates in the presence of missing data, offers a greater statistical power compared with the ordinary analysis-of-variance (ANOVA)-based test, which discards incomplete data. We applied both the EM-LRT and the ANOVA-based test in a real data set collected from F₂ intercross studies of inbred mouse strains. It was found that the EM-LRT makes an optimal use of the observed data and its advantages over the ANOVA F-test are more pronounced when more missing data are present. The EM-LRT method may have important implications in QTL mapping in experimental crosses.

ANIMAL models and their corresponding genomes are highly useful for mapping traits that may apply to human diseases (Knoblauch and Lindpaintner 1999). Since genes are conserved throughout evolution, the identification of “evolutionary homologs” in animals is well appreciated in helping to find their counterparts in humans.

There are two primary methods for quantitative trait locus (QTL) mapping: (a) the single-marker method and (b) the interval-mapping method. The single-marker method is a traditional method for detecting the association between individual genetic markers and the quantitative trait of interest (Luo et al. 2000). The analysis-of-variance (ANOVA) represents the typical method applied in this kind of analysis. The interval-mapping method uses information provided by multiple linked markers to probabilistically assess potential QTL at chromosomal locations between such markers. In the interval-mapping approach developed by Lander and Botstein (1989), evidence for a putative QTL is summarized by a LOD (log of odds) score that exceeds a predefined threshold at a given chromosomal position.

The presence of missing data in studies usually lowers both the power of QTL mapping and the precision of parameter estimation, because the sample size for the incomplete data is less than it would be if the data were complete. In previous literature, the treatment of such a missing data problem is not adequate. Two simple methods have been most widely applied. One is simply to use the incomplete data by deleting all data records with any values missing, and it is called “listwise deletion.” A second approach is called “pairwise deletion,” which deletes those data records if either the phenotypic data or the genotypic data at the marker of interest are missing. In this article, we propose an expectation-maximization (EM)–likelihood-ratio test (LRT) to incorporate the flanking markers' information in the presence of missing marker data in the single-marker analysis. The LRT is derived from the maximum likelihood calculated using the EM algorithm based on all the observed data.

In the following section, we first introduce the mathematical model and notations, and then we derive the EM algorithm for maximum-likelihood estimation. Afterward, we describe the EM-LRT (or the EM-based Student's t-test) and the standard ANOVA-based tests (F-test and pairwise t-test). Then, we assess the validity of the EM-LRT at various sample sizes and various proportions of missing data, compare the performances of the proposed EM-based tests over the ANOVA-based tests through simulations, and evaluate whether or not it represents a more effective test for real data sets. Finally, we provide a summarization and some further discussions.

We have implemented the algorithm described in this article in the freely available statistical software R (Ihaka and Gentleman 1996). The code is available from the authors upon request.

MATERIALS AND METHODS

Model settings and notations:

Let us denote the genotypes at the trait marker locus A (the hypothesized QTL for the trait) as AA, Aa, and aa, the genotypes at its left-side flanking marker locus B as BB, Bb, bb, and the genotypes at its right-side flanking marker locus C as CC, Cc, and cc (note that we consider here only the biallelic markers, such as the simple sequence length polymorphisms). Let Y denote the phenotype value; let X₁, X₂, and X₃ denote the respective genotype values at the loci A, B, and C, where X₁ = 1, 2, and 3 denotes the three respective genotypes, AA, Aa, and aa, X₂ = 1, 2, and 3 denotes the three respective genotypes, BB, Bb, and bb, and X₃ = 1, 2, and 3 denotes the three respective genotypes, CC, Cc, and cc. Let μ_i denote E(Y|X₁ = i), where i = 1, 2, and 3. Then, what we test here is H₀: μ₁ = μ₂ = μ₃ (locus A is not a QTL for Y), vs. H_a: μ₁, μ₂, and μ₃ are not all equal (locus A is a QTL for Y).

This hypothesis test includes the test for both dominant and additive effects of the hypothesized QTL—locus A.

In practice, the genotype measure X₁ at locus A may be missing for some animals. The usual approaches for missing data such as listwise deletion and pairwise deletion would simply exclude such animals from the ANOVA-based tests, resulting in a lower power to detect the QTL. Here, we propose an EM-based approach utilizing information of incomplete data, rather than discarding it. When there are missing data at locus A, the approach makes use of genotype data not only at locus A, but also at its two most closely linked markers, loci B and C. For the three linked markers, A, B, and C, there are a total of 27 possible genotype combinations {X₁ = j, X₂ = k, X₃ = l}, where j, k, l = 1, 2, or 3. We denote the probabilities for the occurrence of each combination as p_j,k,l = Pr(X₁ = j, X₂ = k, X₃ = l).

By assuming a standard ANOVA model relating the phenotype Y to the genotype X₁, we have

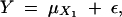1

where ε ∼ N(0, σ²) and X₁ can take one of the three possible genotype values of 1, 2, or 3 defined above. The complete data set in this case is {(Y_i, X_1,i, X_2,i, X_3,i), i = 1, … , n} for a sample size of n.

The log-likelihood of the complete data is 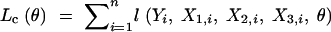, where

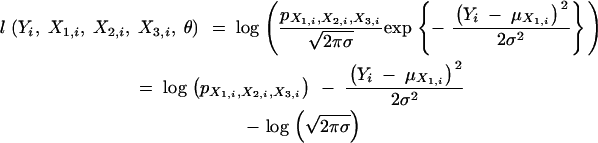and θ = (μ₁, μ₂, μ₃, σ², p_1,1,1, p_1,1,2, p_1,1,3, p_1,2,1, p_1,2,2, p_1,2,3, p_1,3,1, p_1,3,2, p_1,3,3, p_2,1,1, p_2,1,2, p_2,1,3, p_2,2,1, p_2,2,2, p_2,2,3, p_2,3,1, p_2,3,2, p_2,3,3, p_3,1,1, p_3,1,2, p_3,1,3, p_3,2,1, p_3,2,2, p_3,2,3, p_3,3,1, p_3,3,2, p_3,3,3). When there are missing data,

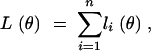2

where l_iθ is defined as follows. First, if the phenotype Y_i and the three genetic markers X_1,i, X_2,i, X_3,i are all observed for the ith animal, obviously,

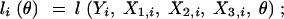3

second, if the phenotypeY_i is observed but some genetic markers are missing for the ith animal, then

4

and third, if the phenotypeY_i is missing for the ith animal,

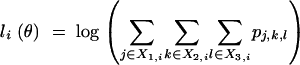5

Here and in the following, the notation of summation ∑_j∈X1,i denotes the summation over all possible values of X_1,i. For example, if X_1,i is observed to be 2, then the summation contains only one case (i.e., j = 2); on the other hand, if X_1,i is missing, then the summation is taken over all three possible values j = 1, 2, and 3.

We propose estimating the parameters by maximizing the log-likelihood Lθ as defined in Equations 2–5 above and using the corresponding LRT in hypothesis tests.

Direct maximization of Lθ is difficult, as we can see in the complicated equations [(2)–(5)] shown above. The EM algorithm (Dempster et al. 1977; Little and Rubin 1987) is an appropriate method for computing the maximum-likelihood estimator θ̂ when missing data are present. In the following, we first derive formulas for the EM algorithm to maximize the log-likelihood Lθ. Then, we deduce the LRT using the EM estimations and compare its performance with the ordinary ANOVA-based tests.

EM algorithm:

We now derive the formulas of the EM algorithm for this problem following standard notations (McLachlan and Krishnan 1997).

We start with an initial estimate θ⁰ (which can be either the ANOVA estimate or any other reasonable estimate). At the (m + 1)th iteration, we update the current estimate θ^m by completing the E-step and the M-step as follows.

E-step:

Compute 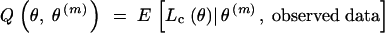. The computation is simplified to

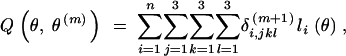6

where 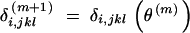denotes the Pr(X_1,i = j, X_2,i = k, X_3,i = l|observed data and θ^m). It can be computed according to the following formula: If Y_i is observed,

7

if Y_i is missing,

8

Here φ{j ∈ X_1,i, k ∈ X_2,i, l ∈ X_3,i} is the indicator function whether (j, k, l) is a possible value for (X_1,i, X_2,i, X_3,i).

M-step:

Update the parameter estimate to the value 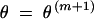that maximizes Qθ, θ^m. The maximization over θ becomes rather simple if we further write out the expression

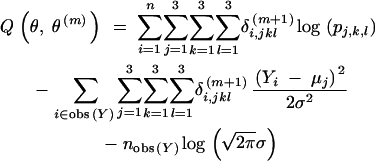Here, obs(Y) denotes the set of i's where Y_i is observed, and n_obs(Y) = |obs(Y)|.

The maximization of the above expression is very similar to a linear model and we find explicitly the following updating formula:

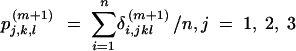9

10

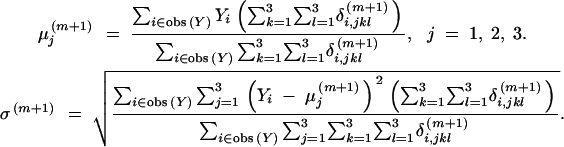11

The E-step and M-step are then iterated until the estimate θ^m converges to an estimated value, θ̂.

Hypothesis testing:

To check whether locus A is a QTL for the trait of interest, Y, statistically we test the hypothesis H₀: μ₁ = μ₂ = μ₃ (locus A is not a QTL for Y) vs. H_a: μ₁, μ₂, and μ₃ are not all equal (locus A is a QTL for Y). Here we first describe the ordinary ANOVA for single-marker analysis, which is the standard approach in the present literature (Rubattu et al. 1996; Vallejo et al. 1998; Poyan Mehr et al. 2003; Zhao and Meng 2003). When missing data are present, the ordinary ANOVA excludes all the data records with missing information on X₁ or Y, and a subset of observations is left {(Y_i, X_1,i), i = 1, … , n*}, (n* ≤ n). The ordinary ANOVA then estimates the mean phenotype given the genotype data,

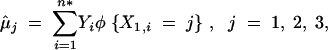where φ is an indicator function. The variance is estimated by

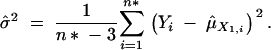Then, an F-test is constructed by comparing σ̂² with the between-group variance, σ̂²_b,

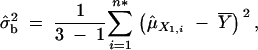where 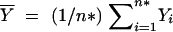. Therefore, the F-test statistic is constructed as

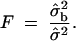12

The F-test would reject H₀ if F > F_α;2,n*−3, where F_α;2,n*−3 is the (1 − α)100th percentile of an F-distribution with d.f. = 2 and (n* − 3).

The ANOVA can also use the pairwise t-tests to examine the phenotypic difference between two particular genotypes. This pairwise t-test is used to evaluate H₀: μ_j = μ_m vs. H_a: μ_j ≠ μ_m for pairs of genotypes j and m (e.g., j = 1 and m = 2, or j = 1 and m = 3, or j = 2 and m = 3). The T-statistic is calculated as

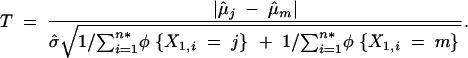13

The t-test would reject H₀ (therefore declare a phenotypic difference between genotypes j and m) when T > t_α/2;n*−3, where t_α/2;n*−3 is the (1 − α/2)100th percentile of a t-distribution with d.f. = (n* − 3).

As pointed out above, the power of the ordinary ANOVA is not optimal because it does not use information for those data records with either phenotype or genotype marker data missing. In the previous section, we proposed using the EM algorithm to incorporate information from the flanking loci (i.e., B and C) in the parameter estimation. Here we describe how to use these EM-based parameter estimates to develop a statistical test that replaces the corresponding F-test (or the pairwise t-test when applicable) in the ordinary ANOVA.

Basically, the F-test in the ordinary ANOVA is replaced by the LRT in the EM approach as follows: (a) use the EM algorithm of (6)–(11) to find the parameter estimate θ̂, and then compute the log-likelihood Lθ̂ according to (1); (b) fit the parameters again under H₀ (by the EM algorithm with formulas described in the next paragraph) to yield an estimate θ̂₀, and compute the log-likelihood Lθ̂₀; and (c) compute the likelihood-ratio statistic (LRS),

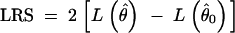14

The LRT will reject H₀ if LRS > χ²_α, where χ²_α is the (1 − α)100th percentile of the χ²-distribution with d.f. = 1.

The calculation of the LRS according to Equation 14 requires the calculations of both the maximum log-likelihood Lθ̂ under H_a and the maximum log-likelihood Lθ̂₀ under H₀. We have provided in the previous section EM formulas for fitting θ̂ in Equations 7–11. Here we describe EM formulas for fitting the parameters θ̂₀ under H₀. The EM algorithm under H₀ is simpler because μ₁ = μ₂ = μ₃ = μ. Therefore, we would estimate μ by the overall sample mean under H₀. Correspondingly, the variance is estimated by the sample variance. That is, we can get the estimates without going through any iterations:

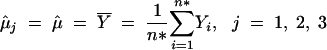10′

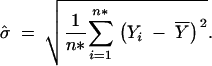11′

Thus, for estimating p_j,k,l's, we need to iterate only between the E-step,

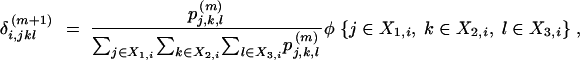8′

and the M-step,

9′

The estimate θ̂₀ consists of μ̂_j in (10′), σ̂ in (11′), and p̂_j,k,l's that are the values of (9′) at convergence. Then θ̂₀ is plugged into Equation 1 to calculate Lθ̂₀, which is then used to compute the LRS in (14).

The pairwise t-test in the ordinary ANOVA is replaced by a corresponding adjusted t-test in the EM approach. Since μ̂_j − μ̂_m = ∑_i∈obs(Y)Y_i∑_k,l(δ_i,jkl/∑_i∈obs(Y)∑_k,lδ_i,jkl − δ_i,mkl/∑_i∈obs(Y)∑_k,lδ_i,mkl), the variance of μ̂_j − μ̂_m is approximately ∑_i∈obs(Y)[∑_k,l(δ_i,jkl/∑_i∈obs(Y)∑_k,lδ_i,jkl − δ_i,mkl/∑_i∈obs(Y)∑_k,lδ_i,mkl)]²σ̂². The adjusted t-test statistic, T, for testing the pair of genotypes j and m is

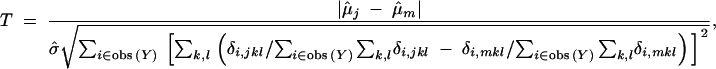15

where μ̂_j, μ̂_m, and σ̂ are from the EM estimate, θ̂. The t-test would reject H₀ when T > t_α/2;n−30, where t_α/2;n−30 is the (1 − α/2)100th percentile of a t-distribution with d.f. = (n − 30).

As the proportion of missing data increases, but is kept below the upper limit such that the type I error is not inflated, we would expect the EM-LRT to perform better than the ANOVA-based test in the single-marker analysis.

Comparison with the interval-mapping method:

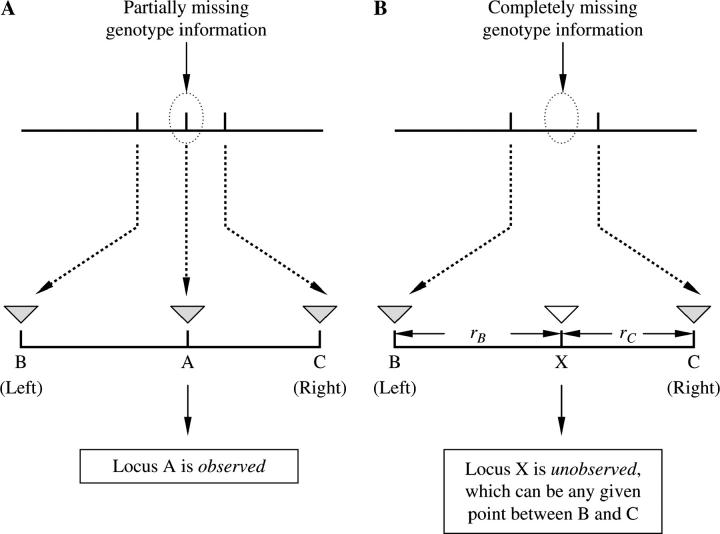
The proposed EM-LRT above uses the genotype information at flanking marker loci to allow more efficient QTL detection at the trait locus when there are missing genotype or phenotype data. The idea of using genotype information at flanking marker loci for capturing information of incomplete data is similar to the idea adopted by the interval-mapping method (Lander and Botstein 1989). The interval-mapping method also uses the EM algorithm to incorporate flanking markers' genotype information for inferring the association (expressed as a LOD score) of the phenotypic trait with genetic variation at any given point between the two flanking markers, but there is a significant difference between our method and the interval-mapping method. First, the main strategy is different. Our method is exactly a single-marker test when no data are missing, and it uses information of the flanking markers only when data are missing at the marker of interest; in contrast, the interval-mapping method intends to “screen” any given point, locus X, in the interval bracketed by two linked markers, assuming (a) genotypic variation at such theoretical point exists and (b) its recombination rates from the two flanking markers are correctly specified. Therefore, the trait locus X is a putative locus and is totally unobserved, and the interval-mapping method uses recombination rates, r_B and r_C, to compute the conditional probabilities 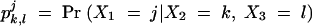, thus reducing the number of parameters to 2. However, such reduction of the number of parameters is valid only if the underlying assumptions regarding the recombination rates (i.e., r_B and r_C in Figure 1) hold. Our proposed EM-LRT, on the other hand, makes no assumptions on the recombination rates (i.e., r_B and r_C), but instead it computes p^j_k,l through p_j,k,l = Pr(X₁ = j, X₂ = k, X₃ = l), only if there are some incomplete phenotype data or genotype data at locus A (Figure 1). For convenience of mathematical derivation, we have written our formula in terms of p_j,k,l. Hence our EM-LRT involves 27 p_j,k,l's and we did not reduce them to two parameters, r_B and r_C, which are used in interval-mapping methods. However, the trade-off is that our EM-LRT is more generic with no model assumptions on the specification of recombination rates: for example, for very tightly linked markers, it has been shown that the rate of recombination is no longer a monotone function of the physical distance (Thompson et al. 1988), and the assumption of the interval-mapping method would appear to be overly strong. Under such circumstances, when there are missing data, our EM-LRT is still valid. We therefore consider our EM-LRT as a complimentary method for the interval-mapping method, particularly when markers are very densely spaced (<1 cM).

Figure 1.—

A schematic illustrating (a) EM-LRT and (b) the interval-mapping method. The shaded inverted triangles indicate observed markers, the open inverted triangle indicates the putative locus.

RESULTS

Assessment of the validity of EM-LRT in finite samples:

EM-LRT is a valid test asymptotically; however, its validity for finite sample sizes needs to be carefully checked. We used extensive simulations to assess the validity of the EM-LRT for various sample sizes under various proportions of missing data.

We simulated a data set of n animals with the phenotype measurement (Y_i) and three genetic markers (X_1,i, X_2,i, X_3,i) for each animal i: {(Y_i, X_1,i, X_2,i, X_3,i)}, where i = 1, … , n. The phenotype Y for each animal was generated according to the linear model: Equation 1, with parameters μ₁ = μ₂ = μ₃ = 100 and σ = 10. We assigned p_j,k,l to be proportional to (4 − j) + (4 − k) + (4 − l). [We initially intended to simulate p_j,k,l proportional to j + k + l. However, as j = 1 denotes the homozygous wild-type genotype, it should have higher probability than j = 3. Hence, we used the transformations (4 − j) to flip the probabilities.] We then randomly dropped phenotype observations at the trait marker locus A according to a missing probability.

For each data set, we first fitted the EM estimates θ̂ through iterations of Equations 6–11. The iteration started with the initial estimates:

The iteration would stop when a convergence criterion of 10⁻⁴ relative change was met. Next, we fitted the EM estimates θ̂₀ again under H₀ through Equations 8′–11′. Then θ̂ and θ̂₀ were used in computing the LRS in (14).

We repeatedly ran the simulation 1000 times. For each simulated data set, we computed the EM-LRT (14) and recorded their values. The empirical type I error of EM-LRT was calculated as the proportions of the 1000 data sets where H₀ was rejected at the significance level α = 0.05.

We simulated for n = 50, 100, 200, 500, and 1000, respectively. For each sample size of n, we increased the missing probability from 10% upward, until the type I error exceeds the nominal significance level α = 0.05 significantly (that is, it exceeds by two standard deviations, 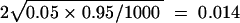). Table 1 shows the type I error for EM-LRT for various sample sizes.

TABLE 1.

The empirical type I error of EM-LRT over 1000 simulations

	Proportion of missing genotype
Sample size (n)	10%	20%	30%	40%	50%	60%	70%
50	0.059	0.068	—	—	—	—	—
100	0.043	0.055	0.072	—	—	—	—
200	0.046	0.055	0.061	0.060	0.060	0.086	—
500	0.054	0.055	0.049	0.048	0.052	0.058	0.088
1000	0.060	0.048	0.056	0.051	0.048	0.046	0.081

Note that the type I error calculations were made only at those proportions of missing data when the EM-LRT remains valid or when the type I error starts to be inflated.

As shown in Table 1, for a small sample size (n = 50), the EM-LRT is valid for up to 10% missing observations. When n = 100, the EM-LRT is valid when as much as 20% data were missing. When n = 200, the EM-LRT can tolerate up to 50% missing data. These simulations showed that we have to be careful in applying the EM-LRT. For a small sample (e.g., n = 40), which is often encountered in real-world experiments, the type I error rates were 0.060 and 0.077 for 10 and 20% missing, respectively. Thus, for n = 40 (see the real example in III shown below), we can still use EM-LRT if 10% or fewer observations are missing. When there are ≥200 animals, we can use the tests with up to half of all observations missing.

To evaluate the accuracy of parameter estimates, we calculated the coefficient of variability (CV) for each model parameter estimate. CV is conventionally defined as 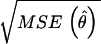/θ, where MSE(θ̂) denotes the mean squared error of the estimate for parameter θ over 1000 simulation runs. Table 2 shows the average CV for estimates of p_j,k,l's, μ_j's, and σ². (It turned out the CVs for estimates of p_j,k,l's were rather similar and thus we presented only their average values.)

TABLE 2.

The average CVs for the parameter estimates of EM-LRT over 1000 simulations

		Proportion of missing genotype
Sample size (n)	Parameters of interest	10%	20%	30%	40%	50%	60%	70%
50	pj,k,l	0.767	0.812	—	—	—	—	—
50	μj	0.023	0.025	—	—	—	—	—
50	σ2	0.106	0.110	—	—	—	—	—
100	pj,k,l	0.536	0.571	0.603	—	—	—	—
100	μj	0.018	0.019	0.020	—	—	—	—
100	σ2	0.071	0.073	0.074	—	—	—	—
200	pj,k,l	0.386	0.402	0.423	0.453	0.487	0.541	—
200	μj	0.013	0.013	0.014	0.015	0.016	0.019	—
200	σ2	0.051	0.051	0.052	0.053	0.053	0.055	—
500	pj,k,l	0.241	0.253	0.267	0.285	0.306	0.336	0.387
500	μj	0.008	0.008	0.009	0.009	0.010	0.011	0.014
500	σ2	0.032	0.031	0.031	0.032	0.032	0.033	0.033
1000	pj,k,l	0.172	0.180	0.188	0.198	0.216	0.239	0.269
1000	μj	0.006	0.006	0.006	0.007	0.007	0.008	0.009
1000	σ2	0.021	0.023	0.022	0.022	0.023	0.023	0.023

Note that the average CVs for the parameter estimates were calculated only at those proportions of missing data when the EM-LRT remains valid or when the type I error starts to be inflated.

It can be seen that the ancillary parameters p_j,k,l were estimated less accurately compared to the estimates of the main parameters μ_j and σ² across the board. However, because p_j,k,l's are parameters that are used only in the adjustment of the impacts of the missing data on the main parameters, the main parameters of interest (i.e., μ_j's and σ²) were not much affected by the accuracies of the estimates of p_j,k,l's. All parameters were estimated more accurately when the sample size n became larger. As a result, the EM-LRT is a valid test for increasingly greater missing proportions as n becomes larger.

Power comparison of EM-LRT with ANOVA-based tests:

To compare the power of EM-LRT with that of the ANOVA-based test, we conducted simulation studies using two types of phylogenetic models.

Simulation models:

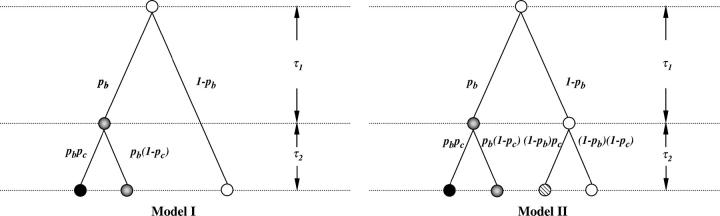
In the simulations performed, genetic markers were generated according to two phylogenetic models (Figure 2). Let A, B, and C denote the wild-type alleles and a, b, c their corresponding mutant alleles for the three loci, A, B, and C, respectively. We assume that the A → a event has arisen before either B → b or C → c occurred, and B → b or C → c events occurred only on the aBC haplotype. In model I, the B → b took place first on the ancestral haplotype aBC, followed by the mutation of locus C on the haplotype abC, resulting in four distinctive haplotypes: ABC, aBC, abC, and abc. In model II, the mutation at locus B took place first on the ancestral haplotype aBC, followed by the mutation of locus C on the haplotypes bearing either the wild-type allele (i.e., aBC) or the mutant allele (i.e., abC) at locus B, resulting in five distinctive haplotypes: ABC, aBC, abC, aBc, and abc.

Figure 2.—

Two phylogenetic models for three linked loci (i.e., A, B, and C) residing on the same chromosome, all starting from an ancestral haplotype aBC, which arose from its founder haplotype, ABC (i.e., A → a is the most ancestral event, and B → b or C → c took place only on the aBC haplotype). In model I, the B → b event took place first on the ancestral haplotype ABC, followed by the the C → c event occurring on the AbC haplotype only, resulting in four distinct haplotypes. In model II, the mutation at locus B took place first on the ancestral haplotype ABC, followed by the mutation of locus C on the haplotypes bearing either the wild-type allele (i.e., ABC) or the mutant allele (i.e., AbC) at locus B, resulting in five distinctive haplotypes. Open circles, aBC; shaded circles, AbC; hatched circles, aBc; solid circles, abC.

In model I, we assume that C → c occurred only on the abC haplotype, as shown in Figure 2. Let p_a denote the proportion of the “a” allele in the population, p_b denote the probability of the B → b event conditional on the A → a event, and p_c denote the probability of the C → c event conditional on the B → b event. Two variants of model I were considered:

• model IA: the genotype measures X₁, X₂, and X₃ refer to loci A, B, and C, respectively (e.g., genotype “aaBbCC” corresponds to X₁ = 3, X₂ = 2, X₃ = 1);

• model IB: the genotype measures X₁, X₂, and X₃ refer to loci B, A, and C, respectively (e.g., genotype aaBbCC now corresponds to X₁ = 2, X₂ = 3, X₃ = 1).

In model II, we considered the case where B → b and C → c events were independent (see Figure 2); without loss of generality, we assume that B → b occurred before C → c. Under this model, p_a and p_b were defined similarly as we defined in model I, but p_c is defined as the probability of the C → c event conditional on the A → a event.

In our simulations, we considered the following parameter settings for p_a, p_b, and p_c: p_b = p_c = 0.8, and p_a of values 0.1, 0.2, and 0.4. For example, p_a = 0.2 would mean that the a allele is present in 20% of the population, and hence ∼32% of the animals have the genotype Aa and 4% have the genotype aa.

Simulation and fitting procedures:

For these models, we simulated for n = 200: {(Y_i, X_1,i, X_2,i, X_3,i)}, where i = 1, … , n. The phenotype Y for each animal is again generated according to the linear model—Equation 1, with parameters μ₁ = 100 − Δ, μ₂ = 100, μ₃ = 100 + Δ, and σ = 10. Here we randomly dropped values from each variable with a probability, p_m. We conducted simulations under two scenarios: (a) p_m = 10% and (b) p_m = 20%. Note that in our simulations used for assessing the validity of EM-LRT in finite samples, the missing proportion refers to the missing probability of X₁. Here, p_m refers to the missing probability of all variables, Y, X₁, X₂, and X₃. The validity of the EM-LRT for the simulation used here was verified by checking the values of the empirical type I error rates (i.e., when Δ = 0).

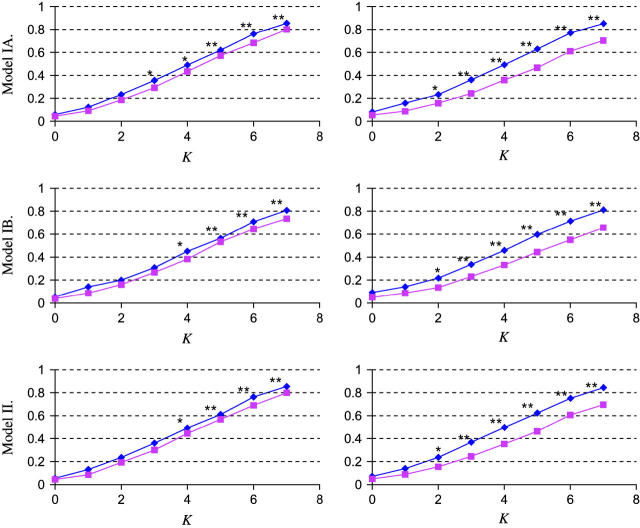
For each model setting, we repeatedly ran the simulation 1000 times. For each simulated data set, we computed the EM-LRT (14) and ANOVA F-test (12) statistics and recorded their values. The empirical powers of the EM-LRT and F-test were calculated as the proportions of data sets where H₀ was rejected at the significance level α = 0.05. Figures 3 and 4 display the empirical powers from the 1000 simulation runs for p_a = 0.2 and 0.4, respectively. The statistical powers were calculated and compared for all three models (IA, IB, and II), for various values of Δ and for different missing probabilities (10 and 20% on the left-hand and right-hand sides, respectively for Figures 3–5). The simulated Δ values were defined as Kσ/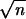, where K = 0, 1, 2, … For the simulation runs with p_a = 0.1 (Figure 5), we replaced the comparison between EM-LRT (14) and ANOVA F-test (12) with the comparison between the EM-adjusted t-test (15) and the ANOVA t-test (13) for the following reason: when the minor allele (a) frequency is low (p_a = 0.1), it would be expected that only ∼1% of animals would carry the aa genotype. Since a total of 200 animals were in each simulation, there were on average <2 animals with the aa genotype in most simulated data sets. In many simulation runs, there was not a single observation in the aa genotype group. Therefore, in this case, the phenotypic comparison is needed only between the pair of genotypes AA and Aa, with respective mean values denoted as μ₁ and μ₂. It was thus more appropriate to compare the power of the EM-adjusted t-test (15) with that of the ordinary ANOVA t-test (13).

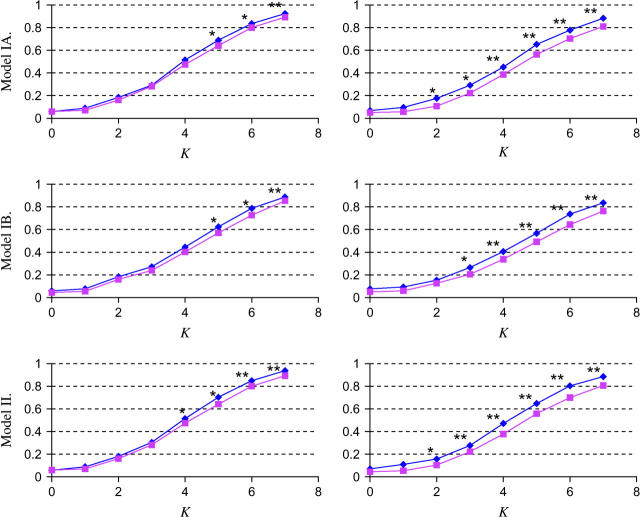
Figure 3.—

Power estimation and comparison of the EM-LRT and ANOVA F-test when P(A → a) = 20%. The points plotted indicate the empirical proportion of tests (by use of a nominal level α = 0.05) that rejected the H₀ among 1000 simulated data sets. K = Δ/σ/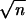. Plots on the left correspond to cases with 10% missing data. Plots on the right correspond to cases with 20% missing data. * indicates cases where P < 0.05, and ** indicates cases where P < 0.005. Here “P” refers to the P-value of Wilcoxon rank-sum tests comparing the power difference between the EM-LRT and the F-test. Solid diamonds denote the power of the EM-LRT; solid squares denote the power of the ANOVA F-test.

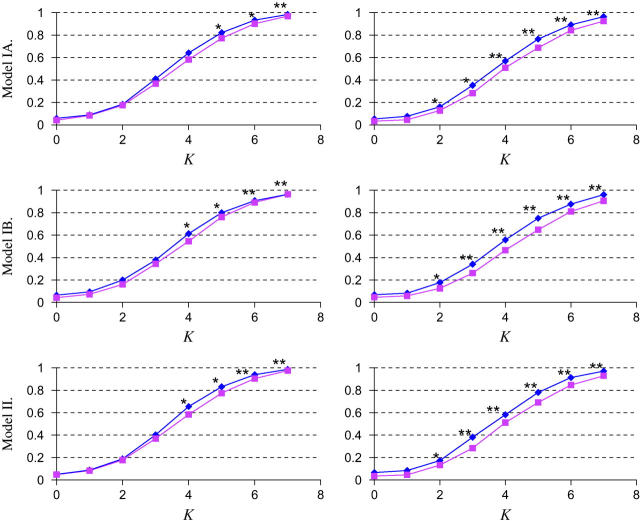
Figure 4.—

Power estimation and comparison of the EM-LRT and ANOVA F-test when P(A → a) = 40%. The points plotted indicate the empirical proportion of tests (by use of a nominal level α = 0.05) that rejected the H₀ among 1000 simulated data sets. K = Δ/σ/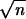. Plots on the left correspond to cases with 10% missing data. Plots on the right correspond to cases with 20% missing data. * indicates those cases where P < 0.05, and ** indicates those cases where P < 0.005. Here “P” refers to the P-value of Wilcoxon rank-sum tests comparing the power difference between the EM-LRT and the F-test. Solid diamonds denote the power of the EM-LRT; solid squares denote the power of the ANOVA F-test.

Figure 5.—

Power estimation and comparison of the EM-adjusted t-test and the ordinary t-test when P(A → a) = 10%. The points plotted indicate the empirical proportion of tests (by use of a nominal level α = 0.05) that rejected the H₀ among 1000 simulated data sets. K = Δ/(σ/n). Plots on the left correspond to cases with 10% missing data. Plots on the right correspond to cases with 20% missing data. * indicates those cases where P < 0.05, and ** indicates those cases where P < 0.005. Here “P” refers to the P-value of Wilcoxon rank-sum tests comparing the power difference between the EM-adjusted t-test and the ordinary t-test. Solid diamonds denote the power of the EM-adjusted t-test; solid squares denote the power of the ordinary t-test.

Power comparisons:

For a hypothesis test, a type I error occurs if H₀ is rejected when it is true. If H₀ holds, a correct test should have a type I error rate ≤ α. The H₀ in this case was represented by Δ = 0 (or equivalently, K = 0) or the left-most case in Figures 3–5. It can be seen that in those cases the empirical type I error rates for both the EM-LRT and the ANOVA F-test were close to α = 0.05, confirming that they were both valid tests.

The power of a test is defined as one minus the type II error. Among valid tests with correct type I error rates, it is clear that a test with a higher power is preferred. It can be seen from Figures 3 and 4 that the empirical powers of EM-LRT were higher than the empirical powers of the F-test. Due to simulation variations, however, a higher empirical power does not necessarily mean the real power is higher. To see whether the difference in power is statistically significant, we conducted a pairwise nonparametric test (the Wilcoxon rank-sum test) on the 1000 pairs of P-values for EM-LRTs and F-tests. The cases where the powers of EM-LRTs are statistically significantly higher are indicated by asterisks in the figures.

As illustrated in Figures 3 and 4, when p_m = 10%, the power of the EM-LRT was significantly higher than that of F-test when K > 3 for models IA, IB, and II. And when p_m = 20%, the EM-LRT started to outperform the F-test when K = 2. Not surprisingly, the power improvement of EM-LRT over the F-tests became more significant when more data were missing.

The comparison results shown in Figure 5 were similar to those of Figures 3 and 4: when 10% of data were missing, the EM-adjusted t-test started to significantly outperform the ordinary ANOVA t-test for K = 3 or 4; when 20% of data were missing, the better performance started when K = 2.

Application to a real data set in experimental crosses:

As an illustration, we applied the proposed method to a real data set based on an F₂ intercross study. This data set, based on a previously published report (Rosen and Williams 2001), consisted of a total of 36 mice from an F₂ intercross between a strain with low brain weight (A/J) and a strain with high brain weight (BXD5). Brain volume, striatal volume, striatal neuron number, striatal neuron number residual, striatal volume residual, and brain weight were measured using standard procedures. We studied a total of 13 microsatellite markers—9 markers on chromosome 10 (D10Mit106, D10Mit3, D10Mit194, D10Mit61, D10Mit186, D10Mit266, D10Mit233, D10Mit179, and D10Mit180), and 4 markers on chromosome 18 (D18Mit20, D18Mit120, D18Mit122, and D18Mit184). The map locations of the loci studied were obtained from Ensembl (http://www.ensembl.org/Mus_musculus/).

The P-values of both the ANOVA F-test and EM-LRT are displayed in Tables 2 and 3.

TABLE 3.

TheP-values of the ANOVAF-test for associations between the phenotypes and genetic markers for the mouse data

	Phenotype
Genetic marker	Brain volume	Striatal volume	Striatal neuron no.	Striatal neuron no. residual	Striatal volume residual	Brain weight
D10Mit106	0.1506	0.0055	0.2186	0.8832	0.0441	0.0240
D10Mit3	0.2361	0.0781	0.4253	0.4546	0.0568	0.0261
D10Mit194	0.4302	0.0135	0.4712	0.3219	0.1759	0.0229
D10Mit61	0.0555	0.0020	0.2007	0.1048	0.2857	0.0118
D10Mit186	0.0062	0.0004	0.0225	0.0062	0.2073	0.0037
D10Mit266	0.0640	0.0029	0.1382	0.2667	0.0754	0.0438
D10Mit233	0.0749	0.0032	0.1314	0.2031	0.0553	0.0290
D10Mit179	0.1523	0.0463	0.4410	0.5620	0.4758	0.1031
D10Mit180	0.1185	0.0521	0.5966	0.6470	0.7244	0.0697
D18Mit20	0.2476	0.0955	0.1081	0.0837	0.3491	0.0012
D18Mit120	0.5902	0.3389	0.9843	0.4053	0.2581	0.0037
D18Mit122	0.2092	0.2850	0.4006	0.2872	0.8266	0.0208
D18Mit184	0.6908	0.4677	0.2811	0.1631	0.8803	0.0904

P-values <0.01 are in italics.

Since few missing observations were present in the data, the differences in P-values were very small between the ANOVA F-tests (Table 3) and the EM-LRT (Table 4). Both methods showed that D10Mit186 affects most phenotypes in the study. Also, two markers on chromosome 18, D18Mit20 and D18Mit120, significantly affect brain weight.

TABLE 4.

TheP-values of EM-LRT for associations between the phenotypes and genetic markers for the mouse data

	Phenotype
Genetic marker	Brain volume	Striatal volume	Striatal neuron no.	Striatal neuron no. residual	Striatal volume residual	Brain weight
D10Mit106	0.1268	0.0035	0.1904	0.8733	0.0332	0.0171
D10Mit3	0.2057	0.0568	0.3822	0.5158	0.077	0.0232
D10Mit194	0.3488	0.0101	0.5458	0.3501	0.2025	0.0123
D10Mit61	0.0426	0.0012	0.1735	0.0854	0.2549	0.0079
D10Mit186	0.0039	0.0002	0.0160	0.0039	0.1796	0.0022
D10Mit266	0.0391	0.0012	0.1067	0.2279	0.0492	0.0261
D10Mit233	0.0536	0.0016	0.1003	0.1952	0.0339	0.0197
D10Mit179	0.1284	0.0350	0.4093	0.5334	0.4448	0.0838
D10Mit180	0.1284	0.0350	0.4093	0.5334	0.4448	0.0838
D18Mit20	0.4458	0.1223	0.2379	0.1652	0.3077	0.0010
D18Mit120	0.5360	0.3015	0.9819	0.3581	0.1829	0.0017
D18Mit122	0.2882	0.2364	0.4726	0.3259	0.8005	0.0125
D18Mit184	0.8812	0.2694	0.4598	0.1603	0.9425	0.0281

P-values <0.01 are in italics.

To illustrate the effects of missing genotype observations, we randomly dropped 10% of the genotype observations at the interested locus and recalculated the P-values of the ANOVA and EM-LRT. Table 5 presents the P-values of the ANOVA F-test and EM-LRT for all phenotypes of interest with and without the dropped D10Mit186 genotype data. Similarly, Table 6 presents the P-values of the ANOVA F-test and EM-LRT for brain weight with and without the dropped D18Mit20 and D18Mit120 genotype data.

TABLE 5.

TheP-values of the ANOVAF-test and the EM-LRT for associations between the phenotypes and genetic markerD10Mit186 for the mouse data with various proportions of missing genotype data

		Proportion of missing D10Mit186 genotype
Phenotype	Estimation method	0%	10%
Brain volume	ANOVA F-test	0.0062	0.0014
EM-LRT	0.0039	0.0032
Striatal volume	ANOVA F-test	0.0003	0.0180
EM-LRT	0.0002	0.0001
Striatal neuron no.	ANOVA F-test	0.0225	0.0231
EM-LRT	0.0159	0.0165
Striatal neuron no.	ANOVA F-test	0.0062	0.0107
Residual	EM-LRT	0.0039	0.0039
Striatal volume	ANOVA F-test	0.2072	0.3731
Residual	EM-LRT	0.1796	0.1664
Brain weight	ANOVA F-test	0.0036	0.0004
	EM-LRT	0.0022	0.0014

P-values <0.01 are in italics.

TABLE 6.

TheP-values of the ANOVAF-test and the EM-LRT for association between brain weight and genetic markersD18Mit20 andD18Mit120 for the mouse data with various proportions of missing genotype data

		Proportion of missing genotype
Genetic marker	Estimation method	0%	10%
D18Mit20	ANOVA F-test	0.0011	0.0166
EM-LRT	0.0010	0.0030
D18Mit120	ANOVA F-test	0.0037	0.0261
	EM-LRT	0.0017	0.0011

P-values <0.01 are in italics.

As we can see from these tables, P-values for the ANOVA F-tests were more sensitive to the dropped phenotype data than were those for the EM-LRT. For example, in Table 6, the ANOVA tests are no longer able to detect the association at the α = 0.01 level with brain weight when 10% of genotype observations at the interested locus were dropped while the EM-LRT can still detect the association under the same condition. On the other hand, as shown in Table 5, the effect of dropping 10% D10Mit186 genotype data is less pronounced. The results produced by ANOVA tests led to the same conclusions on the associations of the D10Mit186 genotype with all the phenotypes except the striatal neuron number residual. The ANOVA test was not able to detect the association between the D10Mit186 genotype and the striatal neuron number residual when 10% of data were missing while the EM-LRT could still detect the association. By and large, we see that the EM-LRT improves the statistical power over the case when all missing data were excluded.

DISCUSSION

In this article, we presented an EM-LRT using flanking markers information in single-marker analysis to utilize information contained in incomplete data. By using both simulated and real data sets, we demonstrated that EM-LRT utilizing incomplete data is a valid test for finite samples with moderate proportions of missing values and is a more powerful test compared to ordinary ANOVA-based tests that discarded all missing data from the analysis.

Missing information on either genotype or phenotype can obscure the true genetic effect (Sen and Churchill 2001). To reduce the proportion of missing data, the best solution is to repeat the experiment, but it can be costly and time-consuming. The EM algorithm is a standard maximum-likelihood estimation method for handling missing data (Dempster et al. 1977). In the present context, the method fractionally assigns (E-step) the incomplete data to their theoretically possible values on the basis of the current estimates of the parameters and then revises the parameter estimates to maximize (the M-step) the likelihood on the basis of the pseudo-complete data. This two-step, alternating iteration procedure is repeated until convergence can be reached. Statistical theory guarantees that the observed data likelihood increases to a maximum via the algorithm, and thus the EM-LRT can be performed validly (Dempster et al. 1977). Likelihood methods with the EM algorithm allow the recovery of much of the lost information and make statistically efficient use of the data. In the simulated data sets, the EM-LRT outperforms the ANOVA-based tests at various marker allele frequencies, and the differences in statistical power became increasingly more pronounced with an increasing portion of missing data or an increasing value of Δ (Figures 3–5). In the real data set example on inbred mouse strains, we found that with 10% missing data the significant associations of D18Mit20 and D18Mit120 with brain weight could still be detected by EM-LRT, but not by ANOVA-based tests. Taken together, we argue that the EM-LRT is an attractive statistical method that can utilize information from incomplete data.

The EM-LRT is a valid test asymptotically (i.e., a large n). For finite samples, our simulations indicated that, for n = 100, the method can tolerate up to 20% missing genotype data; for n = 200, the method can tolerate up to 50% missing genotype data. Thus, there is another potential application of the proposed EM-LRT for a combined analysis of different studies. For example, suppose in study I (with a sample size of n₁) that we already collected phenotype data and genotype data on D10Mit61 and D10Mit266, and later we decide to study other nearby genetic markers, say D10Mit186 as well as D10Mit61 and D10Mit266 in a new, independent study, study II (with a sample size of n₂). We might combine study I with study II by treating the D10Mit186 genotype data as missing in study I, and then the EM-LRT can be used to detect the association between the phenotype of interest and D10Mit186 by merging studies I and II together (with a sample size of n₁ + n₂). When we use this approach to combine different studies, we have to pay particular attention to the assumption of “missing at random.” That is, the genotype missing probability is not related to the phenotype value. This can be ensured by checking that the animals in different studies come from exactly the same genetic backgrounds (e.g., common F₀ parents) under the same experimental and breeding conditions. The tests developed in this article can be applied to the combined (studies I and II altogether) data provided that each of the new markers selected is independent from study I. In other words, the new genetic marker is not selected because the flanking markers already showed associations with the phenotype in study I. If the new genetic marker is selected because of an association observed in regard to the flanking markers in study I, then a sequential design is needed. How to adjust our tests for the sequential design is an interesting research topic that deserves further investigation.