Capturing Intervention Effects Over Time: Reanalysis of a Critical Time Intervention for Homeless Mentally Ill Men

Abstract

Objectives. We analyzed whether a method for identifying latent trajectories—latent class growth analysis (LCGA)—was useful for understanding outcomes for individuals subject to an intervention.

Methods. We used LCGA to reanalyze data from a published study of mentally ill homeless men in a critical time intervention (CTI) program. In that study, 96 men leaving a shelter’s onsite psychiatric program were randomly assigned to experimental and control groups. The former received CTI services and the latter usual services. Each individual’s housing circumstances were observed for 18 months after program initiation. Our outcome measure was monthly homelessness: a person was considered homeless in a month if he was homeless for even 1 night that month.

Results. Four latent classes were found among the control group, but just 3 among the experimental group. Control, but not experimental, group individuals showed a small class of chronically homeless men. The size of the never-homeless class was 19 percentage points larger for the experimental than for the control group. J- and inverted-U-shaped patterns were also found among both groups, but with important differences in timing of patterns.

Conclusions. Our results reveal effects not apparent in the original analysis, suggesting that latent class growth models improve intervention evaluation.

Intervention research commonly estimates an impact of a particular intervention over a specified follow-up time period to identify average differences between intervention and control groups. However, intervention research into homelessness does not typically differentiate temporal patterns, i.e., patterns in sequencing, duration, or timing of the intervention’s impact among individuals. Ignoring such information might obscure or incorrectly estimate intervention effects. We analyzed the utility of latent class growth analysis (LCGA)1^,2 for differentiating such temporal patterns by reanalyzing data from a randomized critical time intervention (CTI) trial that was designed to prevent recurrent homelessness among men with mental disorders. The previous analysis3 used an 18-month observation period to identify several temporal effects: the intervention group averaged 61 fewer nights homeless; it had half the number of homeless episodes; and its differences from the control group in the probability of extended homelessness grew over time. Our study carries the analysis further by demonstrating how LCGA can identify different, latent, temporal patterns among individuals resulting from the intervention. By using more of the temporal information in the data and by allowing individuals to vary simultaneously from themselves over time and from each other at each time point, our analysis portrays a more nuanced dynamic of temporal change than the prior analysis. As a result, it better specifies how subgroups, characterized by different dynamics, were differentially affected by CTI. In so doing, our analysis suggests the general utility of latent trajectory analysis for intervention research.

BACKGROUND

Time in Homeless Intervention Research

Intervention research usually focuses on estimating impacts of interventions over time without differentiating patterns among individuals. Most commonly, studies estimate differences between test and control or comparison groups in means, proportions, and standard deviations at 2 or more postintervention time points.4^–11 Point-in-time measures, however, collapse temporality, and taking several such measures at a few postintervention time points (e.g., at 6, 12, and 18 months) may produce too small a sample of the universe of time points to characterize program impacts. Further, we do not know if the chosen time points are the right ones to be sampled. Choices seem to be driven by weak theoretical expectations and strong emphases on culturally accepted time points for a 12-month calendar. More sophisticated but less common approaches have used time series analysis to estimate change in a cross-sectionally measured outcome of interest12; random-effects models to evaluate change over the postintervention time period13; or, as in the CTI analysis, survival analysis to construct probability curves of postintervention responses.3 These approaches offer great advances in estimating impact over time, but, like point-in-time analyses, they allow only 1 curve each to be found for test and control groups. They assume, in effect, that variation around the relevant statistic is random. These “single-curve” approaches do not differentiate subgroups of individuals within the test and control groups on the basis of shared responses on the outcome of interest. (Subgroup analyses are possible, of course, but subgroup membership is defined by shared gender, ethnicity, education, and so forth, rather than by similarities on the outcome of interest.)

Efforts to differentiate such subgroups have created taxonomies based on individuals’ sharing similar values on the outcome of interest (alone or combined with other traits) over the entire postintervention time period.3^,14^,15 One approach has been to aggregate or average data for each individual over the postintervention period and create cutpoints to form subgroups. Total nights homeless, number of homeless episodes, and the average duration of these episodes are common measures in this approach. Cutpoints for a measure, or some combination of measures, are then subjectively created, generating subgroups. Commonly, a taxonomy of transient, episodic, and chronic homeless people is developed.14^,16^–18 Aggregating data, however, fails to show the impact of the intervention on the ordering and timing of the outcome of interest. It does not distinguish, for example, someone who was homeless during the first 3 months of follow-up from someone who was homeless during any other 3-month period. Thus, aggregation does not use available temporal information that helps us better specify an intervention’s impact. Further, cutpoints are commonly not derived from theory or data but are created with arbitrary decision rules. This risks producing subgroups that are not very meaningful for assessing the theory and practice of an intervention and may generate significant within-subgroup heterogeneity, making it harder to find effects. Last, because these taxonomies collapse time, they fail to achieve what the “single-curve” studies accomplish: an analysis of intervention impact on the postintervention temporal trajectory. These taxonomies succeed, however, where the single-curve approach does not: differentiating subgroups of individuals over follow-up.

Critical Time Intervention Study

The CTI analysis used both approaches to assess program impact on recurrent homelessness among mentally ill men. Survival curves were constructed for experimental and control groups to elucidate differences in homeless trends over the follow-up period. This period of 540 days was divided into 18 periods of 30 days (a “month”), and the probability of a major homeless episode (> 30 days) starting in a month for those housed at the beginning of that month was calculated. Cumulative survival probabilities were then calculated, 1 each for the experimental and control groups. The former declined from a 100% to an 80% chance of retaining housing at the 18th month; the latter from 100% to 50%. The study focused on the finding that the difference between the 2 curves grew over time. This contrasts with previous clinical trials of community mental health interventions, in which the intervention’s effects had faded after the intervention period.

The CTI authors also created a taxonomy of homelessness to evaluate experimental/control group differences. Four subgroups were arbitrarily defined for the entire sample on the basis of the total number of nights individuals were homeless over the follow-up period: extended (> 54 nights homeless), intermediate (30–54 nights homeless), transient (1–29 nights homeless), and never (0 nights homeless). The fourth subgroup was not part of the analysis. To test for CTI impact, the study compared the distributions of experimental and control subjects across subgroups. The major reported finding was that extended homelessness among the experimental group was half of that among the control group (21% vs 40%, respectively); no differences were found for other subgroups.

The taxonomic analysis of this study showed that homelessness varied across individuals; survival analysis showed that homelessness changed over time for the population. Taken together, these suggest that individuals differed in their temporal patterns of homelessness. By identifying 1 curve for each group, survival analysis implies that such differences were random, even though taxonomic analysis suggests they were not. By collapsing time, taxonomic analysis leaves open the possibility that individuals’ homelessness did not change over time, even as survival analysis suggests they did. To determine whether individuals differed in their patterns of homelessness, we need to simultaneously examine individual change over time and variation among individuals at each time point.

Temporal-Based Approach

Latent class growth analysis attempts to do both. It allows us to identify subgroups of individuals who have similar postintervention trajectories, that is, who share similarities in the timing, duration, and sequencing of the outcome of interest over the follow-up period. It does this by combining the reasoning of both the taxonomic and single-curve approaches. Like the taxonomic approach (but in contrast to single-curve analyses), LCGA assumes that heterogeneity across individuals in the follow-up period is derived from a mixture of distributions in the population representing different underlying subgroups, rather than that heterogeneity is random. Thus, as with the taxonomic approach, LCGA leaves us with latent classes of individuals sharing similar temporal qualities. Like single-curve analyses (but in contrast to taxonomy formation), LCGA uses information on individuals at each measured postintervention time point to identify trajectory patterns and uses statistical reasoning rather than subjective judgments to arrive at results. Thus, as with survival, time series, and growth curve analyses, LCGA leaves us with statistically defined trajectories of behavior over the follow-up period. In the end, we have, for both experimental and control groups, subgroups of individual trajectory patterns, thereby producing a more exact understanding of the nature of the intervention’s impact than single-curve or taxonomy approaches. LCGA thus helps us understand the impact of a program more deeply by framing outcomes in terms of the actual biographies of individual people (e.g., 1 group of people improves while another remains unchanged) rather than as a set of relations among variables.19^,20

We carried out our study by reanalyzing data from the well-known CTI evaluation previously identifed.3 We chose this study because (1) it was well designed and well executed, with validated measures and tight program and study procedures; (2) it followed up over a relatively long time period; and thus (3) it was able to employ analyses representing both single-curve and taxonomy approaches to assess intervention impact. Findings from each approach can be usefully compared with the results from the latent trajectory approach. In particular, because the initial CTI findings were strong, that study provides a more robust test for the ability of the latent trajectory approach to find further impacts. Additionally, CTI is thought to be a potentially valuable new approach for enhancing continuity of care and thereby reducing the risk of homelessness and other adverse outcomes among mentally ill persons after discharge from shelters, hospitals, and other institutions. The CTI model has now been applied and evaluated with diverse populations (e.g., persons being discharged from inpatient psychiatric treatment, homeless mothers with children leaving shelters, homeless veterans treated by specialized outreach teams) and was recently cited as a model program by the President’s New Freedom Commission on Mental Health.21 Demonstrating the utility of trajectory analysis in this context, then, would be particularly helpful for furthering continuing research on an important policy initiative.

METHODS

Study Design

The CTI study was a random-assignment study assessing the impact on recurrent homelessness of providing particular services when mentally ill homeless people are transitioning from shelters to housing in the community. For the experimental group, the intervention consisted of helping strengthen these people’s ties to services, family, and friends and providing them with practical and emotional support after they left the shelter. Each person was assigned a CTI worker to implement a plan transferring care from the shelter to the community and to work with the person in the community for 9 months after shelter discharge. After this time, the experimental group received “usual services,” as did the control group throughout the 18-month postshelter period. Usual services involved referrals to mental health and rehabilitation programs of generally high quality, as well as other referrals as needed (e.g., medical care, substance abuse treatment).

The sample was male residents discharged to housing in the community from an onsite, New York City shelter psychiatric program. All the men had severe mental illness, such as schizophrenia or other psychotic disorders. Ninety-six of the 102 discharged from the program over a 2-year period participated in the intervention and study. They were randomly assigned to receive either CTI or usual services after post–psychiatric program housing placement. After the men left the shelter, data were collected at 30-day intervals over the 18-month period through structured surveys by trained interviewers who were blinded to experimental or control status of the study participants. At initial data collection and at each 30-day assessment, housing data were collected, with high test-retest reliability (κ = 0.93). The baseline interview collected demographic data (age, education, race/ethnicity), lifetime histories of mental health and alcohol and drug abuse, and information on current psychiatric diagnoses and symptoms. Table 1 ▶ shows baseline characteristics of the sample for the experimental and control groups. There were no statistically significant differences between groups at P≤ .05.

TABLE 1—

Demographic Characteristics and Diagnoses of Mentally Ill Men in the Experimental and Control Groups

	Experimental Group, No. (%) (n = 48)	Control Group, No. (%) (n = 48)
Age, y
< 35	18 (38)	20 (42)
≥ 35	30 (62)	28 (58)
Race/ethnicity
African American	38 (79)	33 (69)
Other	10 (21)	15 (31)
Education
< High school	26 (54)	31 (65)
≥ High school	22 (46)	17 (35)
Lifetime homelessness, y
≤1	7 (15)	14 (29)
> 1	41 (85)	34 (71)
Psychiatric hospitalizations, No.
< 5	28 (58)	33 (69)
≥5	20 (42)	15 (31)
Psychiatric diagnosisa
Schizophrenia	32 (67)	33 (69)
Other	16 (33)	15 (31)
Cocaine dependencea
No	21 (44)	30 (62)
Yes	27 (56)	18 (38)
Alcohol dependencea
No	20 (42)	24 (50)
Yes	28 (58)	24 (50)

Source. Susser et al.3

^aLifetime diagnosis.

Outcome

Our outcome measure consists of trajectories of homelessness over the observation period, divided into 18 months of 30 days each. A person was considered homeless within any 30-day period if he resided in a shelter, on the street, or in any other public place for just 1 night during that period. The intervention was thus held to a high standard: preventing a single night of homelessness in a given month. Less stringent criteria (≤ 5, ≤ 10, and ≤ 15 nights homeless) produced essentially similar results, albeit with lower statistical power. This threshold approximates that used to construct the CTI taxonomy: at least 1 night homeless over the follow-up period placed an individual in 1 of the 3 homeless subgroups. It is a lower threshold than that used in the survival analysis, in which individuals were counted homeless for a 30-day period if they began that period homeless and were or remained homeless for at least 30 days.

Analytic Approach

We first reanalyzed CTI data to replicate descriptive statistics reported in the original article. We then analyzed the data using LCGA modeling. This approach assumes that a population is composed of a mixture of subgroups with distinctive patterns of behavior over time; in this case, patterns in the sequence, duration, and timing of homelessness. Membership in a subgroup, however, is unobserved; only the mixture of subgroups is observed. Consequently, it is not possible to directly estimate each subgroup’s size and pattern of exposure to homelessness over time. Rather, subgroup membership is inferred from the data. In LCGA modeling, this heterogeneity is captured by an unobserved (latent) categorical variable, and observed outcomes at each time point—in this case, homeless status each month—serve as indicators of the latent class variable. Because subgroup membership is unobserved, the proportion of cases in each class is unknown and must be estimated by the model, as must the conditional item probabilities for each class. LCGA works by estimating the form of the relation linking individual-level behavior to some temporal measure (age, calendar time, and so forth). Trajectories result from maximum likelihood estimation of the probability of observing each individual’s sequence of measurements. Resulting model coefficients determine trajectory shape and are allowed to vary across subgroups, making it possible to find more than 1 subgroup in the population. Trajectories and subgroup membership are estimated simultaneously by maximum likelihood estimation using the expectation–maximization (EM) algorithm. These models and some applications are described by Muthén et al.1^,22^–25 and by Nagin and Land2^,26 (for critiques, see Bauer and Curran27).

We used Mplus version 3.1228 to estimate models and to calculate the 3 statistics used to evaluate performance of alternative models: Bayesian information criterion (BIC), Lo-Mendell-Rubin likelihood ratio test (LMR LRT), and entropy. BIC29 rewards more parsimonious models (fewer latent classes) that more accurately reproduce the data and takes into account the number of parameters used in model estimation. Models with smaller BIC values represent improvement over models with larger values. LMR LRT30 adjusts the conventional likelihood ratio test for k versus k−1 classes for violating regularity conditions to evaluate the proper number of classes.31 Entropy shows how well separated the subgroups produced by a model are by calculating how homogeneous (different from 1.0) are the average posterior probabilities for each class given the number of cases and classes.32 Thus, an entropy value of 1.0 (the upper limit) indicates that all individuals in each class have a 100% chance of being in the class to which they were assigned, that is, classes are completely distinct. A value of 0.0 (the lower limit) indicates that classes are not at all distinct.

We first assessed trajectories for control subjects,22 because they represent the counterfactual condition of having received only usual services. Results for experimental subjects were then modeled. In both cases, we compared models fitting 2, 3, 4, and 5 trajectory classes. Consistent with prior analysis of this randomized intervention, we report results without having controlled for baseline covariates.

RESULTS

Table 2 ▶ reports model performance statistics for individuals in the control and experimental group. The upper part of the table shows that a 4-class model provides the best fit for the control group. The reduction in BIC from the 3-class model is substantial (50.6); the LMR LRT statistic suggests a significant improvement in fit (evaluated at the .05 significance level); and the entropy value is excellent (0.999). Adding a fifth class does not contribute appreciably to BIC and does not improve the LMR LRT or entropy.

TABLE 2—

Fit Indices for Latent Class Growth Analysis Models

	Fit Indices
No. of Classes	BIC	LMR LRT P	Entropy
Control group
2	575.487	.0001	1.000
3	502.893	.0326	0.999
4	452.260	.0330	0.999
5	451.790	.0632	0.995
Experimental group
2	380.569	.0665	0.992
3	327.784	.0003	0.998
4	326.964	.0444	0.971
5	315.635	.0170	0.960

Note. BIC = Bayesian information criterion; LMR LRT = Lo-Mendel-Rubin likelihood ratio test.

The lower part of Table 2 ▶ suggests that 3 classes are sufficient to characterize trajectories present among the experimental group. The reduction in BIC from the 2-class model is large (52.8), the LMR LRT is significant at P≤ .05, and the entropy is very high (0.998). Although the LMR LRT also indicates good fit for 4- and 5-class solutions, these additional classes do not strongly reduce the BIC and result in poorer entropy values. Taken together, these results suggest that the experimental group is most parsimoniously characterized by 3 trajectory classes. Thus, strikingly, only 3 classes are needed to account for the heterogeneity within the CTI group, whereas 4 classes are needed for controls.

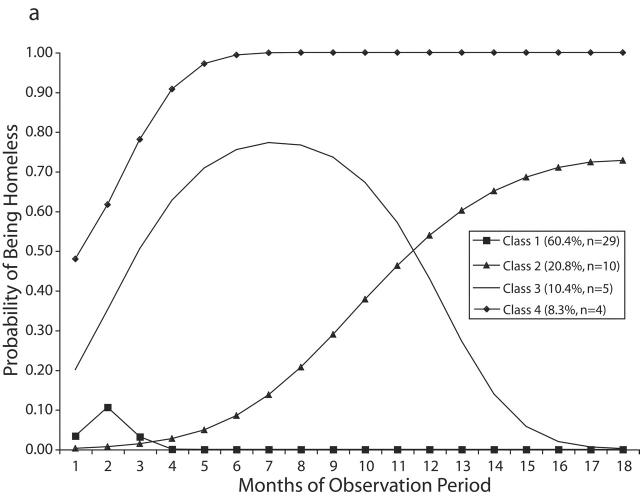
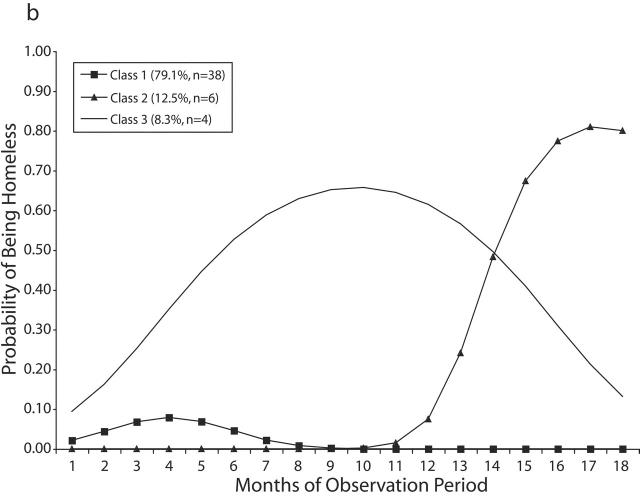
For the selected models, Figure 1 ▶ reports the size and nature of the classes for control and experimental groups. It shows that 3 of the classes are similar in nature for both groups, but that class 4 in the control group does not exist in the experimental group. Although this trajectory does not contain many men, it is an important subgroup: those with a high probability of becoming homeless quickly after discharge and remaining chronically homeless throughout the observation period.

FIGURE 1—

Class trajectories for selected models for (a) the control group and (b) the experimental group.

Further, the largest trajectory class within both groups (class 1) is those unlikely to be homeless at any point during the observation period. In particular, a larger portion of experimental (79.1%) than control (60.4%) subjects were in this class, indicating that for certain individuals, CTI had an immediate and enduring impact in preventing subsequent homelessness.

Figure 1 ▶ also portrays a small class of experimental subjects (class 2; 12.5%) who became increasingly homeless just after critical time services were ended around the ninth month. A similar pattern of increasing probability of homelessness exists for more control subjects (20.8%), but their movement into homelessness occurred earlier and was more linear than the J-shaped pattern found for the experimental group.

Finally, both control and experimental groups contain small subgroups with an inverted U-shaped pattern (class 3). An increasing probability of homelessness was followed by a gradual decline reaching almost zero by the end of the observation period. The decline began somewhat later among the experimental group, however, and specifically around the time when CTI services ended.

DISCUSSION

Some of these results reiterate findings from the prior analysis. This suggests that our findings are not simply artifacts of the method. But other findings go beyond the prior analysis, deepening our understanding of CTI by both conflicting with and expanding on prior CTI findings.

Reiterative Results

The prior and current analyses both indicate that a large majority of men in the study had very low probabilities of becoming homeless over the observation period. That men receiving CTI were more heavily represented in this subgroup compared with the control group suggests that CTI was more effective than usual services in preventing enduring homelessness.

Also like the prior analysis, the current findings suggest that intervention effects may last beyond the 9 months of active service provision. The current analysis, however, specifies 2 different ways that such success may be achieved: the excess of CTI subjects not becoming homeless at all and the absence of chronically homeless among the experimental group.

Deepening Results

In their survival analysis, Susser et al.3 found a monotonic decline in the probability of housing retention among both experimental and control groups and an increasing difference between these groups in that probability. By contrast, our results suggest that multiple subgroups exist within both experimental and control groups.

Further, these subgroups are different from those suggested by the taxonomy analysis in Susser et al.3 Specifically, the CTI group did not have a class of persistently homeless persons and had a class whose increasing homelessness was reversed. Only among the control group did homelessness become chronic. These differences suggest that the program had stronger effects than initially found: CTI kept people out of chronic homelessness and dramatically improved housing chances for a subgroup prone to chronic homelessness during the early months of the intervention.

In addition, the subgroup that only avoided homelessness through continuing CTI services (class 2) contrasts with the implication of the prior study that CTI effects persisted past the program period for all experimental subjects. Rather, this finding uncovers a group of individuals who may need a booster intervention33 or greater continuity of service (e.g., referral to long-term follow-up by an assertive community treatment team). However, compared with the second control group class, which struggled against homelessness through usual services but failed earlier and at higher rates, this CTI class showed the effectiveness of CTI for the subgroup that seems service dependent.

Limitations

The initial CTI study identified several data limitations, which the reader can consult for details.3 Most important for our analysis is that the number of cases is relatively small. This is offset somewhat by the large number of follow-up periods and completeness of follow-up data. That the models fit well and that entropy values are high increases our confidence in the findings. Nevertheless, modest sample size has meant that several subgroups contain few individuals. The results should thus be read more as demonstrating the utility of our analytic approach than as definitively assessing the impact of CTI.

Our model evaluation should also be qualified. Reduction in BIC from k classes to k+1 classes is the most commonly used index for assessing competing models, but no consensus exists on how large a reduction must be to indicate significant change. Raftery34 suggested reductions of at least 10 points, and BIC works quite well with small sample sizes. More research is needed, however, for a stronger consensus regarding BIC in this framework. Following Muthén and Muthén,28 we also used LMR LRT to assess competing models, but the validity of testing nonnested models with this method is debatable,35 and more research is necessary to better understand its utility in this context.

More research is needed, as well, on criteria for establishing adequate statistical power. The sample size required to detect intervention effects in mixture models depends on several factors: the distribution of the variables, a balanced or unbalanced data set, the number of model parameters and of observation waves, and the location in trajectories of intervention effects. The Monte Carlo methods used by Mplus can help the researcher determine the power and sample size for a study design.36

Implications

The LCGA approach may be applied to a broad range of studies with longitudinal data, including randomized, quasi-experimental, and nonexperimental designs. We focus on 3 implications for intervention research. The first is that we can examine covariate effects on trajectory subgroup formation and on change in trajectory subgroup membership. Covariate effects are estimated simultaneously with maximum likelihood estimation of latent classes and may be measured at baseline or throughout the course of the observation period. The second is that information on trajectory group membership and its predictors should allow service programs to develop—and researchers to evaluate—interventions better tailored to specific trajectory subgroups and not assume a universal intervention for everyone in a particular population. Alternatively, subgroups not responding to a universal intervention could receive targeted or booster interventions to improve impacts; following the methods of TenHave et al.,37 randomized assignments could be incorporated at this stage to evaluate the impact of these added interventions. The third implication is the utility of collecting more precise temporal data. Our analysis makes clear the usefulness of knowing exactly when individuals enter and leave a particular state (such as homelessness) and not simply the number of times and durations of such states. Incorporating such data collection into intervention studies should become essential to evaluation research.