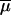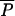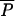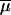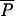Bayesian Analysis of an Admixture Model With Mutations and Arbitrarily Linked Markers

Abstract

We introduce here a Bayesian analysis of a classical admixture model in which all parameters are simultaneously estimated. Our approach follows the approximate Bayesian computation (ABC) framework, relying on massive simulations and a rejection-regression algorithm. Although computationally intensive, this approach can easily deal with complex mutation models and partially linked loci, and it can be thoroughly validated without much additional computation cost. Compared to a recent maximum-likelihood (ML) method, the ABC approach leads to similarly accurate estimates of admixture proportions in the case of recent admixture events, but it is found superior when the admixture is more ancient. All other parameters of the admixture model such as the divergence time between parental populations, the admixture time, and the population sizes are also well estimated, unlike the ML method. The use of partially linked markers does not introduce any particular bias in the estimation of admixture, but ML confidence intervals are found too narrow if linkage is not specifically accounted for. The application of our method to an artificially admixed domestic bee population from northwest Italy suggests that the admixture occurred in the last 10–40 generations and that the parental Apis mellifera and A. ligustica populations were completely separated since the last glacial maximum.

HYBRID populations have been central to theories on adaptation and speciation (Barton 2001), and their study has encountered a new interest since it was shown that they could be ideal in detecting disease genes (Chakraborty and Weiss 1988). The assessment of the degree of admixture of a given population has traditionally relied on the comparison of allele frequencies between two potential parental populations and a putative hybrid population (Roberts and Hiorns 1965; Chakraborty and Weiss 1988; Long 1991). Recently, these methods have been improved by incorporating information on the molecular diversity present in the admixed and in parental populations (Bertorelle and Excoffier 1998; Dupanloup and Bertorelle 2001) or by explicitly taking into account the genetic drift of allele frequencies since the admixture event (Chikhi et al. 2001; Wang 2003). However, the accuracy of the estimation of the contribution of the parental populations to the hybrid depends highly on the extent of differentiation between parental populations (Bertorelle and Excoffier 1998) and the time elapsed since the admixture event (Chikhi et al. 2001; Choisy et al. 2004). No single method was found to date superior to others in all circumstances (Choisy et al. 2004). Recent likelihood-based methods, including Bayesian (Chikhi et al. 2001) and maximum-likelihood (Wang 2003) approaches, are computationally intensive but have been shown to produce estimates with smaller variances across independent replicates or simulations, especially when the estimate was based on a small number of loci (Wang 2003; Choisy et al. 2004). A promising alternative to these methods has been the development of an approach using nongenetic information to more precisely define the contribution of sampled populations to the hybrid (Gaggiotti et al. 2002, 2004). Finally, recognizing that a major drawback of all these former approaches is to require an explicit definition of the source populations, some recent methods have attempted to identify admixed individuals without requiring the source parental populations to be defined (Pritchard et al. 2000; Dawson and Belkhir 2001; Anderson and Thompson 2002; Falush et al. 2003), but their statistical power remains to be assessed.

As stated previously, a common problem with most of the previous methods is their inability to explicitly handle mutations (but see Bertorelle and Excoffier 1998; Dupanloup et al. 2004), whereas this is likely to be particularly important when the admixture event is ancient. While ML methods have the potential to provide accurate estimations of demographic and mutational parameters, the calculation of likelihoods under models of nonrecent hybridization events for which mutations have to be taken into account at both independent and partially linked markers remains problematic. A powerful Bayesian alternative to likelihood computation for parameter estimation has been introduced recently (Fu and Li 1997; Tavaré et al. 1997; Pritchard et al. 1999; Estoup et al. 2001), dubbed as approximate Bayesian computation (ABC; Beaumont et al. 2002; Marjoram et al. 2003). This approach does not require the computation of likelihoods, but simply relies on the comparison of summary statistics computed on observed data with those computed on data simulated under a model for which the parameters of interest are known (Beaumont et al. 2002; Marjoram et al. 2003). Although the ABC method relies on summary statistics and thus does not use all available data, it has been shown to provide very accurate results in the analysis of relatively simple evolutionary scenarios where full maximum-likelihood methods were available (Beaumont et al. 2002; Marjoram et al. 2003). Hence, by construction, ABC methods have the potential to consider models of any complexity, provided only that data can be simulated under the model. Recent applications of the latest developments of ABC methods (Beaumont et al. 2002) illustrate their potential for the analysis of complex demographic scenarios (Estoup and Clegg 2003; Estoup et al. 2004). Recent coalescent-based packages (e.g., Hudson 2002; Laval and Excoffier 2004) provide an efficient tool for simulating genetic data under complex scenarios (including introgression or hybridization scenarios) and have the potential to generate data for independent or partially linked markers. Such versatile simulation packages make it possible, even for biologists unfamiliar with simulation algorithms, to perform parameter estimation under the ABC framework and consider various evolutionary scenarios.

In this article, we apply the ABC method to the estimation of all the parameters of an explicit admixture model (Figure 1) defined previously (Bertorelle and Excoffier 1998; Wang 2003) and described in methods. We use the SIMCOAL2 coalescent simulation program (Laval and Excoffier 2004) to generate a large number of microsatellite data sets for random values of the admixture model parameters, on which several summary statistics are evaluated. These simulated summary statistics are used for parameter estimation in a series of test data sets, which allows us to validate our approach and to compare its performance with a previously published maximum-likelihood (ML) method (Wang 2003). The method is then applied to the case of an admixed population of honeybees from northwestern Italy.

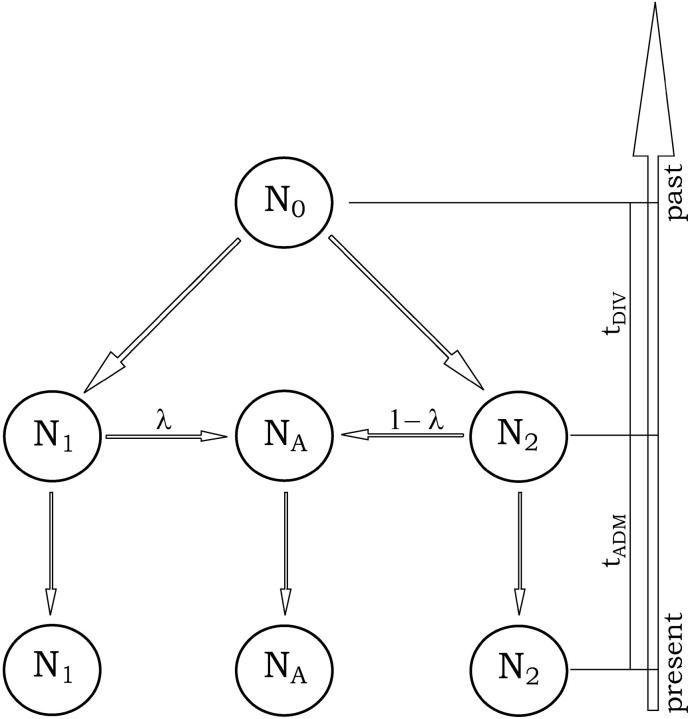
Figure 1.—

Admixture model considered in this study. A hybrid population is created t_ADM generations ago from a mixture of two parental populations that diverged t_DIV generations before admixture time. Except for the admixture event itself, all populations are genetically isolated. The demographic model is characterized by seven parameters, which are the effective number of genes in the ancestral (N₀), parental (N₁ and N₂), and admixed (N_A) populations; the times of admixture (t_ADM) and divergence (t_DIV); as well as the admixture proportion (λ) taken as the relative contribution of parental population 1 to the admixed population.

METHODS

The demographic model:

To compare the behavior and performances of our approach with previous methods, we used a classical admixture scenario described in Figure 1 and similar to that used in previous studies (e.g., Long 1991; Bertorelle and Excoffier 1998; Wang 2003; Choisy et al. 2004).

The genetic model:

Unlike almost all methods considering that gene frequencies evolve only through genetic drift, our approach also takes mutations into account (as in Bertorelle and Excoffier 1998). This involves the choice of a mutation model and of its parameters. We restricted our study to microsatellite markers for which we used a multistep mutation model, sometimes called generalized stepwise mutation (GSM) model (Zhivotovsky et al. 1997; Estoup et al. 2002), requiring two parameters per locus: the mutation rate (μ_i) and the coefficient (P_i) of the geometric distribution of the length by which a new mutant allele differs from its ancestor. However, these two series of parameters are considered as nuisance parameters, and we will pay attention only to their average values across loci: 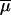and .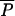

Data thus consist here of multilocus genotypes of n individuals sampled from each of the three populations.

The ABC approach:

The rationale and the full description of the ABC method are given in Beaumont et al. (2002). In short, the approach involves three successive steps detailed in Figure 2. The first step (simulation step) consists of simulating many (typically 1 million) multilocus data sets with characteristics similar to the observed data set (same number of samples, same number of individuals per sample, same number of loci), using parameter values randomly drawn from some prior distributions (as defined in Table 1). The second step consists of comparing the simulated data set to an observed data set, by mean of a series of summary statistics, retaining the simulations that are arbitrarily close to the observations, and rejecting the other simulations. Finally, the third step is the estimation of the parameters by performing a multiple and locally weighted linear regression on the summary statistics associated with the retained simulations. The set of simulations retained for parameter estimation was selected by strictly following Beaumont et al. (2002), by computing a Euclidean distance (δ) between simulated and observed summary statistics and retaining the 1000 simulations having the smallest δ distance (being closest) to the test data set.

Figure 2.—

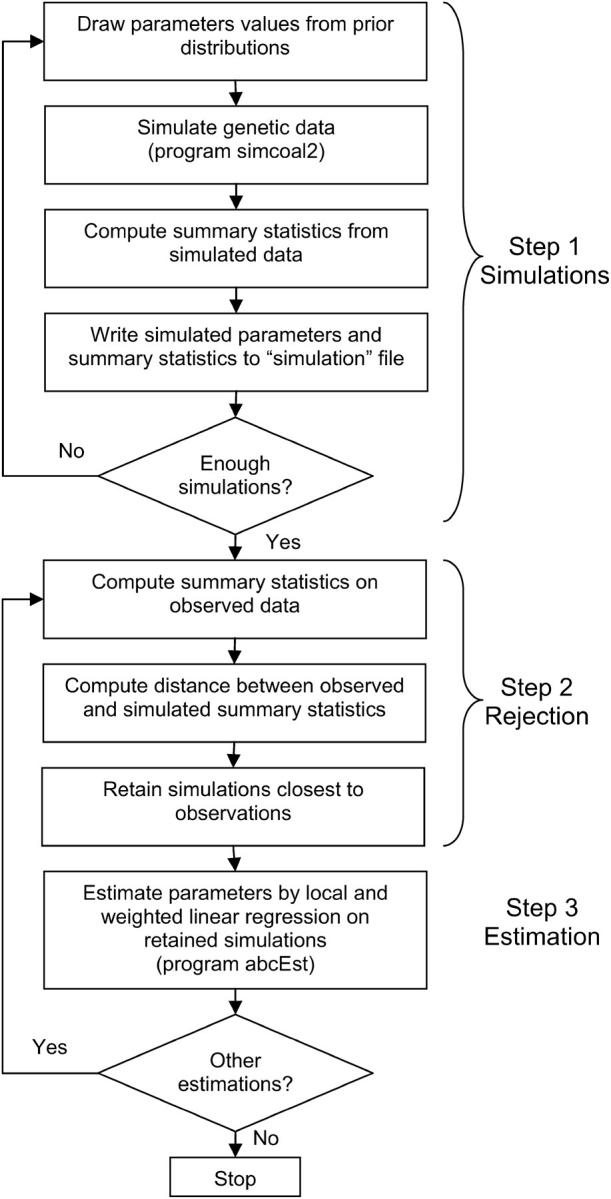
Synopsis of the ABC parameter estimation approach. Step 1 usually includes a loop over hundreds of thousands to millions of simulations. It is the most time-consuming task, generally involving several days of computations. In contrast, the computations in steps 2 and 3 usually take seconds or minutes. To validate the ABC approach, steps 2 and 3 can be repeated hundreds of times on pseudo-observed data generated by step 1-type simulations based on fixed predefined parameter values.

TABLE 1.

Prior distributions of simulated parameters

				Quantiles
Parameters	Distribution	Mean	Mode	5%	50%	95%
N0, N1, N2, NA	Log Uniform[100, 40,000]	6,690	100	135	1,993	29,676
λ	Uniform[0, 1]	0.500	IR	0.05	0.500	0.950
tADM	Log Uniform[1, 1,000]	143	1	1.4	30.8	704
tDIV	Log Uniform[100, 100,000]	14,540	100	141	3,170	70,942
	Log Uniform[10−4, 5 × 10−3]	1.3 × 10−3	10−4	1.2 × 10−4	7.1 × 10−4	4.1 × 10−3
μi	Gamma(2, 2/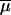)	1.3 × 10−3	1.7 × 10−4	5.6 × 10−5	5.5 × 10−4	4.9 × 10−3
	Uniform[0, 0.5]	0.250	IR	0.025	0.250	0.475
Pi	Beta(a, b)*	0.250	IR	0.023	0.250	0.482

N₀, N₁, N₂, and N_A, effective population size (number of gene copies) in ancestral (N₀), parental (N₁ and N₂), and admixed (N_A) populations, respectively; λ, contribution of parental population 1 to the admixed population; t_ADM, time since admixture; t_DIV, divergence time between parental populations before admixture; 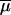and μ_i, average and individual-locus mutation rates, respectively; 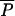and P_i, average and individual-locus parameters of the geometric distribution of the GSM, respectively; *Prior distribution for P_i is as follows: if 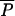≥ 0.001 then P = Beta(a, b) with a = 0.5 + 199 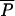and b = a(1 − 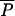)/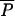; otherwise P = 0. IR, irrelevant.

The SIMCOAL2 program (Laval and Excoffier 2004), freely available on http://cmpg.unibe.ch/software/simcoal2, has been used to generate microsatellite data sets in the first step, and a new program (abcEst) has been developed for parameter estimation (step 3 in Figure 2). The program abcEst (Windows or Linux version) is available from L. Excoffier upon request. Compared to the published version of the SIMCOAL2 program, two enhancements were added: the implementation of the generalized stepwise mutation model and the possibility of having different mutation rates at different loci. Microsatellite allele size constraints were included in our simulations by imposing reflecting boundaries at the edge of an allele size range of 30 continuous allelic states (Feldman et al. 1997; Pollock et al. 1998). This range is consistent with empirical data on repeat numbers at microsatellites in various species (e.g., Garza et al. 1995; Goldstein and Pollock 1997; Estoup et al. 2000).

Regarding mutation modeling, we draw for each simulation an average mutation rate across loci 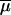from a log Uniform distribution, and individual locus mutation rates are then drawn from a Gamma distribution with mean equal to 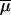. A similar procedure is also used for the average and individual locus coefficients of the geometric distribution of step lengths 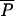and P_i (see Table 1 for details). Note that we have chosen to implement this hierarchy of parameters and did not draw locus-specific parameters μ_i and P_i from unique distributions, since the average parameters 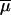and 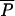would have been virtually identical across simulations of a large number of loci and equal to the mean of the priors. Their estimation would thus have been meaningless. Note also that we have chosen a relatively broad prior for 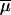compared to previous studies (e.g., Wilson and Balding 1998), such as to cover a wide range of possible mutation rates (see Table 1).

In addition to the 9 basic parameters of the admixture model (the admixture proportion λ, the four effective population sizes, the time of divergence t_DIV, the time of admixture t_ADM counted in generations, and the mutational parameters 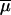and 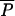), 11 composite parameters were computed and recorded. They correspond, respectively, to the times of divergence and admixture scaled by the population sizes (t/N_i, with t = t_ADM or t_DIV, and i = 0, 1, 2, or A), to the population sizes scaled by the mutation rate (θ_i = 2N_iμ, with i = 0, 1, 2, and A), and to the times of divergence and admixture scaled by the mutation rate (τ = 2tμ, with t = t_ADM or t_DIV). The estimation procedure was thus carried out separately on the 9 basic parameters as well as on the 11 composite parameters.

Summary statistics:

The following 15 summary statistics were computed on all the simulated microsatellite data sets: the average number of alleles over loci for each of the two parental and the admixed population samples, the average heterozygosity over loci and average modified M statistics (Garza and Williamson 2001) over loci for the same three samples, the (δμ)² genetic distance (Goldstein et al. 1995) between the two parental population samples, the measure of differentiation F_ST (Weir and Cockerham 1984) between all three pairs of population samples, the average extent of linkage disequilibrium D′ between independent markers in the admixed population, and the m_Y admixture coefficient estimator (Bertorelle and Excoffier 1998). The formula of the modified M statistics is 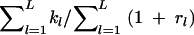, where k_l is the number of alleles at the lth locus, r_l is the difference in number of repeats between the largest and the smallest allele at locus l (i.e., the range of allele sizes), and L is the number of loci. Compared to its original definition (Garza and Williamson 2001), it just avoids a division by zero when a gene sample is fixed for a single allele. Note that the summary statistics were chosen such as to capture different features of the data, both at the within- and at the between-population level. This choice is partially arbitrary, since there is currently no objective way to define an optimal set of statistics (Beaumont et al. 2002), but we have tried to use statistics thought to be informative for some of the parameters of our model. For instance, one would expect heterozygosity to be informative for the estimation of population size, but it should also depend on the admixture proportion in the hybrid population. Also, pairwise F_ST's are expected to bring information about divergence times between parental populations and about admixture proportions. The m_Y admixture coefficient should obviously bring information on admixture proportion, while D′ in the admixed population should decay with admixture time, but also depend on the absolute sizes of the populations (drift). However, we did not attempt here to define an optimal set of statistics or to study the effect of removing or adding summary statistics, which could be the subject of a later study.

Simulated data sets:

A first series of 10⁶ data sets was simulated and consisted of 50 diploid individuals (100 genes) typed at 50 independent microsatellite loci. This large data set was fractioned into subsets to study the effect of sample size and number of loci on parameter estimation, and thus data sets consisting of 5, 10, 20, and 50 loci studied in samples of 20 and 100 genes were obtained. A second series of 10⁶ data sets, consisting of 50 diploid individuals typed at a mixture of 20 independent and partially linked loci, was simulated. The 20 loci consisted of two unlinked groups of 10 partially linked loci. Each group of 10 partially linked loci was itself divided into two subsets of 5 completely linked loci (genetic distance of 0 cM), 1 cM distant from each other. The 190 pairs of loci thus fell into three linkage categories: unlinked (100 pairs of loci), partially linked at 1 cM (50), and totally linked (40). The coefficient of linkage disequilibrium D′ was computed separately in the three categories of markers, thus adding two summary statistics to these simulated data sets with recombination. Note that our choice of three categories of linkage is somewhat arbitrary. While the “completely linked” and independent sets of markers are easy to justify and are commonly found in many data sets, the spacing of 1 cM was chosen such as to have a different amount of loss of potential disequilibrium created by the admixture process over the time periods studied below. Indeed, one would expect that markers 1 cM apart would lose ∼5, 63.4, and 98.2% of the original disequilibrium caused by the admixture after 5, 100, and 400 generations, respectively, thus allowing one to potentially use linkage disequilibrium (LD) to estimate admixture time.

Performance evaluation and test data sets:

The performances of our ABC approach were evaluated in a series of samples having fixed values of the admixture model. For each combination of parameters, the SIMCOAL2 program was used to generate 100 data sets, on which summary statistics were computed and then used as pseudo-observed summary statistics. The same data set was also used as input to a recent ML method (Wang 2003) denoted hereafter WANG03. The latter method has been chosen for a comparison with our approach, because it has been shown to produce good estimates of admixture coefficients, and because it estimates other parameters of the admixture model that can be also compared with those of our ABC method. Moreover, compared to the method of Chikhi et al. (2001), Wang's ML method was notably faster, allowing us to get 100 estimates for fixed simulated parameter values in a reasonable amount of time.

It is worth noting that while the simulation of 1 million data sets and the computation of their associated summary statistics for our ABC approach is time consuming (∼12 hr on 15 computer nodes), the ABC estimation of the parameters on a given test data set takes only seconds to minutes, so that the evaluation of the performance of our estimation procedure can be easily achieved without much additional computing cost. This evaluation was thus performed in seven situations. Due to the huge amount of computations needed for the comparisons presented here, a few parameters were fixed across the simulations. The population sizes (numbers of genes) were set to 300, the average mutation rate to 0.0005 (reviewed in Ellegren 2004), and the geometric coefficients P to 0.3 (e.g., Estoup et al. 2002). The first situation modeled a recent admixture (t_ADM = 5 generations, i.e., t_ADM/N_e = 0.0167), an ancient divergence (t_DIV = 5000 generations, i.e., t_DIV/N_i = 16.7), and an admixture proportion of 0.3. This situation was used to evaluate the effects of different numbers of loci and of different sample sizes (Table 2). The other six situations were chosen to evaluate the effects of increasing the time of admixture for two different admixture proportions and of having partially linked markers. The performance of our ABC method and of WANG03 was characterized by the relative bias (average difference between the estimate and the true value divided by the true value), the relative root mean square error (RMSE—square root of the mean square error divided by the true value), the 95% coverage (proportion of times in which the true value is within the equal-tailed 95% confidence or credible interval around the estimate), and the factor 2 (proportion of times in which the estimated value is in an interval bounded by values equal to 50 and 200% that of the true value). All measurements of bias, RMSE, and factor 2 were computed by taking the mode of the posterior distribution as a point estimate. The factor 2 parameter is intuitively appealing and brings qualitatively different information than the 95% coverage. It indeed tells users how often the estimator is arbitrarily close (factor 2 here) to the true value, while the inclusion of the true value within a confidence interval does not imply that the estimated parameter is “close” to its true value, as this depends on the width of this interval. All measures of performance were estimated over 100 simulated test data sets. Note that 100 replicates may not be enough to get very accurate estimates of relative RMSEs, so that the numbers for this measure should be considered as indicative only.

TABLE 2.

Effect of the number of independent loci on the estimation of the admixture rate λ by the ABC and Wang's (2003) methods

		ABC
100,000 simulations				1,000,000 simulations				WANG03
Sample size	No. of loci	Bias	RMSE	Coverage 95%	Factor 2	Bias	RMSE	Coverage 95%	Factor 2	Bias	RMSE	Coverage 95%	Factor 2
20	5	−0.057	0.232	0.99	0.98	−0.029	0.228	0.99	0.99	0.003	0.212	0.95	0.98
10	−0.055	0.181	1.00	0.99	−0.046	0.171	1.00	1.00	0.016	0.157	0.89	1.00
20	−0.044	0.125	1.00	1.00	−0.054	0.118	0.99	1.00	−0.010	0.114	0.93	1.00
50	−0.012	0.071	1.00	1.00	−0.010	0.074	0.99	1.00	0.003	0.074	0.93	1.00
100	5	−0.089	0.175	1.00	1.00	−0.078	0.162	1.00	1.00	−0.026	0.134	0.89	1.00
10	−0.051	0.125	1.00	1.00	−0.043	0.112	1.00	1.00	−0.009	0.091	0.86	1.00
20	−0.035	0.091	1.00	1.00	−0.025	0.079	0.99	1.00	−0.009	0.070	0.87	1.00
	50	−0.003	0.058	1.00	1.00	−0.010	0.042	0.99	1.00	−0.004	0.039	0.89	1.00

Simulated conditions are independent loci. λ = 0.3, t_ADM = 5, t_DIV = 5000, N₀ = N₁ = N₂ = 300. Bias and root mean square error (RMSE) are expressed in relative units. Coverage 95% represents the number of times among 100 that the true value of λ (0.3) lies within the estimated 95% confidence interval. Factor 2 represents the number of times that the true value of λ lies within an interval limited by 50 and 200% of the estimated λ value.

RESULTS

Recent admixture events:

The performance of the ABC method on the recovery of admixture proportions λ for different numbers of loci and different samples sizes is reported in Table 2 and compared to the ML method of Wang (2003). This comparison is based on a scenario that can be considered as advantageous for admixture estimation, because it involves a small admixture time (5 generations) and a long divergence time (5000 generations) relative to the population size (300 genes). In that case, when ABC estimation is performed on 1 million simulated samples, its performance is very similar to Wang's ML method, as attested by the relative RMSE, especially when the number of loci is high (20 or more). As expected, estimations obtained with 1 million simulations are more accurate than those obtained with 100,000 simulations. However, the latter are already quite good with virtually identical negative relative bias and only slightly larger relative RMSE. Note, however, that the same trend is visible in Figure 3, where we report the posterior distributions obtained from the analysis of a single (randomly chosen) case from 10⁶ or 10⁵ simulations. While the modes of the distributions (taken as a point estimate) obtained from the analysis of 10⁶ or 10⁵ simulations are very similar, the distributions obtained from 10⁶ simulations are usually narrower and would lead to smaller credible intervals. We note here that the ABC method generally produces a small negative bias consisting of underestimating the contribution of the source population contributing the least to the admixed population, but that this bias becomes negligible with a larger number of loci.

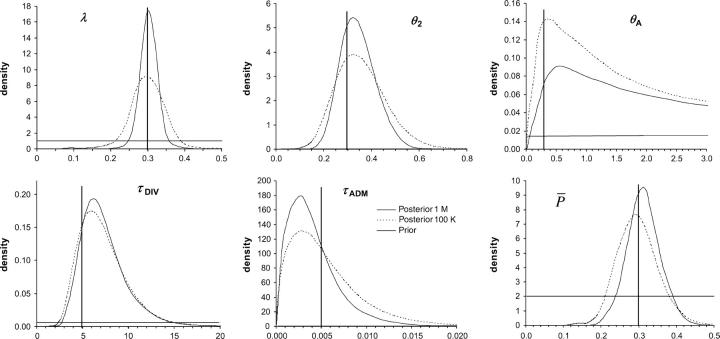
Figure 3.—

Posterior distributions of some parameters of the admixture model. We contrast here posterior distributions obtained from an analysis performed on a set of 1 million (solid line) or 100,000 (dashed line) simulated summary statistics. In both cases, the estimation and the posterior distribution were obtained by a local weighted regression (Beaumont et al. 2002) on the 1000 simulations closest to the test data set. True parameter values are shown as vertical boldface lines: N = 300 for all population sizes; admixture rate, λ = 0.3; divergence time between populations, t_DIV = 5000 generations; admixture time, t_ADM = 5; mutation rate, 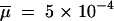; and parameter of the geometric distribution of mutation steps, 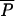= 0.3. Note that the posterior distributions shown here are the output of a single (randomly chosen) analysis, and that they are not averaged over 100 replicates as reported in Tables 2–4.

The ABC and Wang's ML methods are found consistent as their accuracy increases with larger samples sizes and larger numbers of loci. They both produce estimates that are almost always closer than a factor 2 from the true value. The only notable difference between the two methods is in the coverage of the 95% confidence intervals around the estimated values: the ABC method tends to produce conservative (too broad) intervals, while Wang's ML method gives too narrow intervals with larger samples where the true value is found only in <90% of the cases.

Old admixture events:

In Table 3, we report the effect of older admixture times on the estimation of the admixture rate for 20 independent or 20 partially linked loci. While the ABC and Wang's ML methods have very similar performance for short admixture time, the ABC method produces more accurate results when the admixture event occurred >100 generations ago, as shown by much smaller relative RMSE values, higher factor 2 scores, and much better coverage properties for the ABC than for the ML method. For both unlinked and partially linked loci, it is important to note that the coverage of the ABC 95% confidence intervals is always very good. On the other hand, confidence intervals provided by the ML method become poorer with longer admixture time for unlinked loci and are already much too low in the case of a recent admixture studied with partially linked loci. The latter effect is certainly due to the fact that the ML method assumes that the loci are unlinked. As a consequence, loci that are correlated provide similar information and tend to generate thinner distributions because they overestimate the amount of information in the data. This is not the case for the ABC method since we explicitly model the correlation between partially linked markers in our simulations.

TABLE 3.

Effect of admixture time and partial linkage on the estimation of the admixture rate λ by the ABC and Wang's (2003) methods

		ABC				WANG03
	tADM	Bias	RMSE	Coverage 95%	Factor 2	Bias	RMSE	Coverage 95%	Factor 2
20 unlinked loci
λ = 0.1	5	−0.107	0.193	1.00	0.99	−0.015	0.126	0.90	1.00
100	0.029	0.575	0.91	0.80	−0.470	0.643	0.52	0.16
400	0.574	0.875	0.99	0.71	0.568	2.294	0.23	0.13
λ = 0.3	5	−0.025	0.079	0.99	1.00	−0.009	0.070	0.87	1.00
100	−0.045	0.253	0.94	0.97	−0.123	0.412	0.52	0.84
400	−0.032	0.384	0.99	0.92	0.348	1.078	0.12	0.43
20 partially linked loci
λ = 0.1	5	−0.060	0.311	0.97	0.94	−0.031	0.323	0.38	0.95
100	0.326	1.013	0.85	0.55	−0.077	1.059	0.37	0.37
400	0.970	1.314	0.98	0.54	0.351	2.218	0.13	0.05
λ = 0.3	5	−0.050	0.194	0.93	1.00	−0.013	0.172	0.33	1.00
100	−0.040	0.436	0.89	0.83	−0.049	0.570	0.32	0.69
	400	0.161	0.554	0.99	0.84	0.359	1.244	0.04	0.25

Simulated conditions are 10⁶ simulations; sample size, 100 genes. λ = 0.3, t_DIV = 5000, N₀ = N₁ = N₂ = N_A = 300.

While 20 independent loci provide accurate estimation of admixture rates, there is a serious drop in the quality of the ABC estimates based on partially linked markers, especially for very unequal contribution of the parental population to the admixed population (i.e., λ = 0.1). The decrease in ABC accuracy between linked and unlinked loci is especially marked for older admixture events. Curiously, the ML method is less affected than the ABC method by partial linkage, in the sense that its performance evaluated by the relative bias and RMSE does not degrade much when partially linked markers are used instead of independent markers. However, although the ABC method somewhat suffers from the use of nonindependent loci, its relative RMSE remains two to three times lower than that obtained from the ML method for the oldest admixture times (400 generations).

Estimation of divergence and admixture times:

Wang's ML method provides estimates of composite parameters such as divergence and admixture times scaled by population sizes; we report in Table 4 the corresponding parameters obtained from the ABC method. Because this ML method assumes that no mutation occurred since the divergence of the two parental populations, and thus that genetic differences between populations are due to a pure drift process, it leads to grossly underestimated divergence and admixture times and presents poor coverage property, even for recent admixtures. By contrast, the divergence time scaled by parental population size N₂ (t_DIV/N₂) is only slightly overestimated with the ABC method from both linked and unlinked markers, with good coverage and factor 2 scores. The admixture time scaled by parental population size N₂ (t_ADM/N₂) is very well estimated by the ABC method when it is relatively ancient and is underestimated only by 12 and 48% on average when it is recent (five generations) for unlinked and linked markers, respectively. This parameter is also, to a lesser extent, well estimated by the ML method when admixture is recent. However, it is increasingly underestimated for older admixture times, resulting in a virtual absence of coverage by the ML confidence intervals for admixture times ≥100 generations. Finally, the admixture time scaled by the admixed population size N_A (t_ADM/N_A) is only relatively well estimated by the ML method for recent admixtures. Its estimation follows a more complex pattern for the ABC method. The bias is large and negative for recent admixture events, and it becomes positive and associated with a large RMSE for t_ADM = 100; for older admixture times (t_ADM = 400), the bias becomes very low and the relative RMSE drops considerably. This pattern is probably due to the poor estimation of the admixed population size N_A for short admixture times, since small or large population sizes will not create very contrasting patterns of diversity in a few generations, while they should lead to more contrasted patterns for longer evolutionary periods such as a few hundred generations.

TABLE 4.

Effect of admixture time and partial linkage on the estimation of various composite parameters by the ABC and Wang's (2003) methods

		ABC				WANG03
Parameters	tADM	Bias	RMSE	Coverage 95%	Factor 2	Bias	RMSE	Coverage 95%	Factor 2
tDIV/N2
Unlinked loci	5	0.134	0.427	0.99	0.97	−0.976	0.976	0.00	0.00
100	0.226	0.633	0.96	0.85	−0.982	0.982	0.00	0.00
400	0.232	0.636	1.00	0.83	−0.978	0.978	0.00	0.00
Linked loci	5	0.343	0.727	0.97	0.84	−0.975	0.975	0.00	0.00
100	0.315	0.673	0.98	0.89	−0.980	0.980	0.00	0.00
400	0.226	0.636	0.99	0.80	−0.978	0.978	0.00	0.00
tADM /N2
Unlinked loci	5	−0.122	0.534	0.97	0.73	−0.720	0.759	0.20	0.19
100	0.007	0.581	0.99	0.79	−0.841	0.849	0.00	0.00
400	0.039	0.460	0.97	0.88	−0.969	0.970	0.00	0.00
Linked loci	5	−0.478	0.556	0.98	0.45	−0.690	0.734	0.22	0.23
100	−0.019	0.561	0.97	0.69	−0.883	0.889	0.00	0.00
400	−0.048	0.536	0.98	0.78	−0.964	0.965	0.00	0.00
tADM /NA
Unlinked loci	5	−0.531	0.575	0.85	0.37	−0.625	0.639	0.02	0.19
100	0.101	1.489	1.00	0.68	−0.764	0.766	0.00	0.00
400	0.014	0.337	0.98	0.96	−0.904	0.904	0.00	0.00
Linked loci	5	−0.565	0.740	0.83	0.27	−0.773	0.798	0.05	0.09
100	0.059	1.148	1.00	0.65	−0.773	0.776	0.00	0.00
	400	0.018	0.442	1.00	0.88	−0.911	0.912	0.00	0.00

Simulated conditions are 10⁶ simulations, 20 loci, sample size 100 genes, λ = 0.3, t_DIV = 5000, N₀ = N₁ = N₂ = N_A = 300.

ABC estimation of mutation-scaled parameters:

In Table 5, we present results on the estimation of composite parameters depending on mutations. These parameters are computed only in the ABC method so that comparison with Wang's ML method is not possible. The scaled divergence time τ_DIV is relatively well estimated for short admixture time (17% of positive bias) and its relative RMSE is only slightly increased with longer admixture times, resulting in a small drop (96–89%) for the factor 2 score. The scaled admixture time τ_ADM is increasingly better estimated with older admixture events, in keeping with results obtained for the scale parameter t_ADM/N₂. The relatively poor recovery of this parameter for recent admixture is also visible in Figure 3, where the posterior distribution of τ_ADM is not centered at all around the true value in that case. The scaled population sizes θ_A and θ₂ (θ₁ is not shown in Table 5, but follows the same pattern as θ₂) are very well estimated even for old admixture times, while the scaled size of the admixed population (θ_A) is better estimated with increasing admixture times. For t_ADM = 400, θ_A estimation shows virtually no relative bias (−0.4%), a relative RMSE (31%) becoming very similar to that of θ₂ (26%), and an excellent factor 2 score (98%). The relatively flat posterior distribution of θ_A for recent admixtures (five generations) underlines the absence of information in the data for such recent events (Figure 3). On the other hand, the mean parameter of the geometric distribution of the GSM model 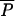is well estimated with 20 loci and does not seem much affected by the age of admixture. Finally, we note that the coverage of the 95% confidence intervals is very good for all parameters and tends to be too conservative except for .

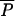TABLE 5.

Effect of admixture time on the estimation of various composite parameters depending on the mutation rate, as well as the admixed population size (N_A) by the ABC method

		ABC
Parameters	tADM	Bias	RMSE	Coverage 95%	Factor 2
τDIV= 2μ tDIV	5	0.170	0.437	1.00	0.96
100	0.128	0.447	1.00	0.96
400	0.231	0.575	1.00	0.89
τADM= 2μ tADM	5	−0.158	0.439	0.97	0.85
100	−0.034	0.429	0.99	0.80
400	−0.016	0.412	0.97	0.89
θ2 = 2N2μ	5	0.069	0.248	1.00	1.00
100	−0.025	0.272	0.98	0.97
400	0.032	0.257	0.98	0.98
θA = 2NAμ	5	2.666	3.425	1.00	0.24
100	−0.147	0.477	1.00	0.82
400	−0.004	0.307	0.99	0.98
	5	−0.024	0.210	0.97	0.98
100	−0.019	0.239	0.95	0.95
400	−0.052	0.246	0.95	0.95
NA	5	5.594	6.230	0.99	0.01
100	0.675	0.924	1.00	0.75
	400	0.090	0.315	1.00	0.99

Application to a honeybee data set:

This honeybee data set has been previously described and analyzed in Choisy et al. (2004). The population under study is located in Courmayeur at the extreme north of the Aosta valley (northwestern Italy) and represented by a sample of 33 worker bees (one per colony). It is considered an artificially admixed population between two different subspecies of Apis mellifera, the West-European black honeybee (A. m. mellifera) and the Italian yellow honeybee (A. m. ligustica). The two parental populations are represented in the analysis by a sample of A. m. mellifera from the sanctuary of Ouessant (French Brittany, n = 49) and a sample of A. m. ligustica from Forli (Emilia-Romania, n = 19), an area of intensive queen rearing for exportation. All sampled honeybees were characterized at eight microsatellite loci, and the admixture coefficient of the Courmayeur sample has already been estimated by six different methods (see Choisy et al. 2004 for more details). Such estimates of the proportion of A. m. mellifera genes in the Courmayeur genetic pool ranged from 0.195 to 0.371 (Choisy et al. 2004). Table 6 shows that our ABC estimate (0.259) is well within this range, as is Wang's ML estimate (0.287). These two methods also agree in their estimates of the time of admixture, which is ∼0.01–0.02 in units of N. Considering that effective population sizes (in number of gene copies) in European honeybee subspecies are of the order of 1000–2000 [Estoup et al.'s (1995) Table 4], this implies a rather recent admixture of 10–40 generations, corresponding to 20–80 years (using an average generation time of 2 years for the queens). This is in good agreement with the development of the Italian queen selling industry in Europe in the middle of the twentieth century. As expected from our previous simulations (Table 4), the two methods provide very different estimates of the time of divergence of the two parental populations scaled by effective population sizes. Wang's ML estimates are ∼0.15–0.25, whereas the ABC estimates reach 7.2–8.3. A. m. ligustica and A. m. mellifera have long been considered as two very distinct subspecies of honeybees. At the end of the 1980s (e.g., Ruttner 1988), the current theory based on paleogeography and morphometry was that the Quaternary ice ages were responsible for the separation of the two subspecies, so the divergence time was estimated at ∼50,000 years before present (BP). However, mitochondrial studies showed that these two subspecies belonged to two highly divergent lineages having probably diverged ∼1 million years ago (Garnery et al. 1992). Quite recently, Franck et al. (2000) showed that the subspecies ligustica had actually a hybrid origin using a much larger sample of colonies, and that its genetic pool was a mixture of two lineages: the M lineage constituted mainly by the mellifera subspecies and the C lineage encompassing the South-European subspecies carnica and cecropia, as well as the Asian caucasica. According to Franck et al. (2000), the admixture might have taken place any time after the Riss period (in the last 130,000 years), and it is probably rather ancient. The estimated divergence time could thus not correspond to the separation of the C and M lineages, but rather to the time when the admixed ligustica and the mellifera subspecies were last separated. If we admit the timing given by Franck et al. (2000), a sensible estimate would be some time during the last ice age (which at maximum occurred 22,000–14,000 years BP), when honeybee populations were restricted to southern Mediterranean refuges (namely the Iberian and Italian peninsulas, respectively). Taking population sizes as above, we get divergence time estimate intervals of 150–500 years with Wang's ML estimates and 14,400–33,200 years with our ABC approach. Wang's ML estimates for the time of divergence of the two subspecies hence appear clearly underestimated, while the ABC method gives estimates much more compatible with our current knowledge of the evolutionary history of European honeybee populations.

TABLE 6.

Estimated parameters of the admixture model for the Courmayeur honeybee sample

	ABC		WANG03
Parameters	Mode	95% CI	Mode	95% CI
λ	0.26	0.11–0.38	0.29	0.15–0.40
Parameters scaled by population sizes
tDIV/N1	8.25	3.11–97.39	0.25	0.15–0.38
tDIV/N2	7.17	2.00–64.56	0.15	0.076–0.242
tADM/N1	0.018	0.0003–0.071	0.0053	<0.0005–0.019
tADM/N2	0.007	0.0002–0.044	0.0176	<0.0005–0.035
tADM/NA	0.027	0.0003–0.062	0.0170	0.009–0.025
Parameters scaled by the mutation rate
θ0	2.27	0.04–12.34
θ1	0.73	0.29–1.62
θ2	1.15	0.57–2.50
θA	0.61	0.02–6.06
τDIV	8.76	2.20–74.67
τADM	0.001	0.0002–0.053
Parameters of the mutation model
	1.85 × 10−4	3.9 × 10−5–8.8 × 10−4
	0.45	0.32–0.51

Simulated conditions are 10⁶ simulations, prior distributions are as in Table 1. CI, credibility interval.

The ABC approach also allows the estimation of several other parameters not estimated by Wang's ML method (Table 6), such as the mutation scaled population sizes (θ's) and the times of divergence τ_DIV or admixture τ_ADM. Using the mode of the posterior distribution of the average mutation rate (1.85 × 10⁻⁴), we obtain an estimate of 23,665 generations (47,330 years) for the divergence time and 26 generations (52 years) for the time of admixture. Both values are in excellent agreement with those mentioned above and with other studies (Ruttner 1988; Franck et al 2000). The average geometric coefficient 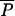of the GSM mutation model is very high (0.446) and very close to the upper bound of our prior distribution (Table 1). This extreme value implies a surprisingly large proportion of mutations leading to non-single-step mutations (precisely 0.446; Estoup et al. 2002). This probably results from the fact that this data set does not fit well to the modeled scenario. More specifically, the potential hybrid nature of one parental population (ligustica) may have widened the distribution of allele lengths in the corresponding sample, forcing the analysis to increase the average length of the mutation steps to cope with this widened allelic distribution.

DISCUSSION

This study shows that the ABC framework allows a fine analysis of an admixture model, providing very satisfactory estimates of admixture rate (λ), mutation-scaled parental population sizes (θ₁ and θ₂), and divergence time τ_DIV, as well as those of the mutation model. Estimates of scaled ancestral population size (θ₀) are usually poor, and those of the admixed population size (θ_A) are good only when the admixture time is large. The mutation-scaled admixture time (τ_ADM) is itself very well estimated when the admixture event is relatively old (100 or more generations), while it leads to reasonable point estimates but large credible intervals when it is very recent. Unscaled parameters, such as raw population sizes and raw divergence and admixture times, were usually not estimated as well as the scaled parameters (results not shown), as they do not have independent and contrasting effects on genetic diversity. However, it is worth noting that the size of the admixed population N_A was very well estimated in the case of old admixture events (i.e., 400 generations). As shown in Table 5, the relative bias on N_A is indeed <10% when the admixture time is 400 generations, while it was ∼560% for an admixture event only 5 generations old. This result suggests that the absolute size of old admixed populations could be well estimated under our framework. This is probably because our method implicitly attempts to reconstruct the genetic composition of the admixed population at the time of admixture, which puts us into a framework very similar to a temporal spacing of samples, which is the ideal situation for estimating population sizes independently from mutation rates (e.g., Williamson and Slatkin 1999; Anderson et al. 2000; Berthier et al. 2002).

Compared to Wang's ML method, our ABC approach shows comparable performance for the estimation of the admixture coefficient when admixture is recent, but leads to increasingly better relative results when the admixture time is older. We attribute this better performance to the specific handling of mutations, which cannot be neglected when admixture time is ancient. However, to estimate admixture coefficients, methods based on a pure drift process are not handicapped by mutations having occurred before the admixture, as they merely result in larger diversity in parental populations. Drift-based (like current likelihood-based) methods seem also to better deal with short divergence time between parental populations (e.g., 200 generations instead of 5000) than does our ABC procedure when the admixture is recent (results not shown). However, this advantage is valid only for recent admixtures (e.g., <50 generations). Another advantage of the present ABC approach is its ability to correctly estimate other parameters of the admixture model, such as divergence and admixture times. These parameters are often as important as the admixture coefficient itself. The better performance of our approach is probably linked to the fact that we are using information not specifically handled by Wang's ML method, such as information on patterns of LD and mutations, as well as range of allele size. Moreover, our ABC approach allows us to explicitly include information on partial linkage between markers, so that, in contrast to Wang's ML method, accurate confidence intervals are also obtained in this case.

While the admixture model analyzed here (with a hybrid population and two isolated parental populations at mutation-drift equilibrium) corresponds to the standard model assumed by most methods of estimation of admixture coefficients (e.g., Long 1991; Bertorelle and Excoffier 1998; Wang 2003; Choisy et al. 2004), real models of admixture may be much more complex. They may indeed involve: (i) more than two source populations (Dupanloup and Bertorelle 2001); (ii) some regular (and thus not instantaneous) admixture events over relatively long periods (reviewed in Chakraborty 1986); (iii) subdivided source populations, so that the actual parental population is only partially sampled; and (iv) parental population(s) that are not at mutation-drift equilibrium, due to population size fluctuations or introgression event(s) in a more or less recent past. The ABC approach has the potential to assess the effect of such deviations from the standard admixture model on parameter estimations since the ratio of acceptance under two alternative models approximates the Bayes factor (e.g., Estoup et al. 2004; Pritchard et al. 1999). Such quantitative model comparisons could be particularly useful in the present evolutionary context to assess the likelihood of different deviations from the standard admixture model and hence learn more about the admixture process that produced the observed data set and potentially consider more realistic models for parameter estimation.

A general feature of the ABC methods that should be underlined here is their ability to assess their performance at almost no extra computation cost. Other estimation methods generally require a validation step, which includes the time-consuming analysis of independently produced simulated data sets (e.g., Choisy et al. 2004), whereas this is intrinsic in the ABC approach (cf. Figure 2). As a matter of fact, the same ABC process used to build the reference table can be derived to produce test data sets with known values of parameters. The same rejection and regression steps can then be applied to these data sets to produce estimates of parameters that can be compared to their known true values. It is therefore relatively quick and easy to evaluate the performance of the method for any subset of the parameter space under a given model. The applicability of the ABC method to particular cases should, however, depend on available computer power, as a few days of computing time are necessary to obtain a large number of simulated summary statistics from which the estimation procedure proceeds (e.g., 10⁶ iterations). However, reasonable point estimates can be obtained using much fewer simulations and hence shorter computation times (e.g., 10⁵ iterations). It seems reasonable to anticipate that progress in simulation algorithms and higher computing power will be available in future years, promoting the ABC method as the method of choice for analyzing complex evolutionary scenarios and, more specifically in the context of the present study, for old admixture models in which mutation cannot be neglected or when nonindependent markers are available.