Persistence and Loss of Meiotic Recombination Hotspots

Abstract

The contradiction between the long-term persistence of the chromosomal hotspots that initiate meiotic recombination and the self-destructive mechanism by which they act strongly suggests that our understanding of recombination is incomplete. This “hotspot paradox” has been reinforced by the finding that biased gene conversion also removes active hotspots from human sperm. To investigate the requirements for hotspot persistence, we developed a detailed computer simulation model of their activity and its evolutionary consequences. With this model, unopposed hotspot activity could drive strong hotspots from 50% representation to extinction within 70 generations. Although the crossing over that hotspots cause can increase population fitness, this benefit was always too small to slow the loss of hotspots. Hotspots could not be maintained by plausible rates of de novo mutation, nor by crossover interference, which alters the frequency and/or spacing of crossovers. Competition among hotspots for activity-limiting factors also did not prevent their extinction, although the rate of hotspot loss was slowed. Key factors were the probability that the initiating hotspot allele is destroyed and the nonmeiotic contributions hotspots make to fitness. Experimental investigation of these deserves high priority, because until the paradox is resolved all components of the mechanism are open to doubt.

SEXUAL recombination is one of the main forces shaping eukaryote evolution, but implicit in its mechanism is a serious paradox. The mechanism, called double-strand break repair, was first proposed for fungi in 1983 (Szostak et al. 1983). It has become increasingly well understood and well supported in a wide variety of organisms, and double-strand DNA breaks (DSBs) are now thought to be the primary initiators of meiotic recombination in eukaryotes (Keeney 2001; Petes 2001). DSBs usually occur at chromosomal sites called recombination hotspots, whose evolutionary persistence is at the heart of the paradox. DSBs appear to frequently cause destruction of the DNA sequence specifying the hotspot and replacement of this sequence by the sequence of its homolog (Nicolas et al. 1989; Kauppi et al. 2004). Over many generations this self-destructive mechanism is expected to cause all active hotspot alleles to be replaced by alleles incapable of initiating DSBs (Boulton et al. 1997). The paradox is that this has not happened.

Recombination hotspots are defined as short segments (usually <1 kb) with a much higher probability of undergoing a meiotic DSB than surrounding sequences. Each chromosome typically has many such hotspots; for example, 177 were identified in a genome-wide screen of the 16 yeast chromosomes (Gerton et al. 2000). Only a fraction of the available hotspots initiate recombination in any single meiosis, and not all of these initiation events lead to crossing over; usually most resolve as simple patches of gene conversion or heteroduplex DNA (Bowring and Catcheside 1996; Jeffreys and May 2004).

The crossing over that hotspots cause plays two important roles in meiosis, one physical and one genetic. First, it creates covalent bonds between homologous chromosomes and thus physically connects the homologs at meiosis. In most organisms such connections are required for accurate chromosome alignment on the metaphase plate and segregation into the haploid daughter cells (Zickler and Kleckner 1999; Walker and Hawley 2000; Petronczki et al. 2003). Second, these new connections create new combinations of alleles on each chromosome, greatly increasing the diversification of haplotypes that is thought to be meiosis's primary function.

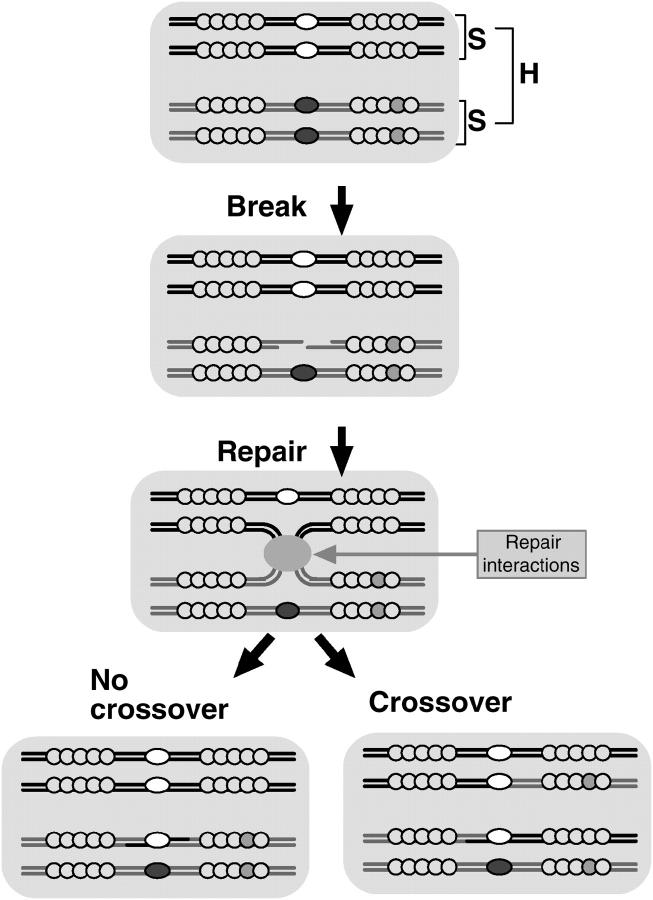
The double-strand break repair (DSBR) model for DSB-initiated meiotic recombination is illustrated in Figure 1 (Szostak et al. 1983) and described in the Figure 1 legend. It differs from an earlier model of recombination (Holliday 1964) in its asymmetry—DNA is cut and degraded at the initiation site in only one of the interacting homologs—and this asymmetry is the source of the paradox. The asymmetry of the DSBR model was necessitated by the asymmetric gene conversion seen in crosses between strains of ascomycete fungi containing more-active and less-active alleles at one of their hotspots. Such crosses consistently produce an excess of spores containing the less-active hotspot allele and its neighbors. The conversion bias of some hotspots (ratio of asci with 3:1 segregation to those with 1:3 segregation) can be 10-fold or higher (Gutz 1971; Nag and Kurst 1997). The DSBR model accounts for this bias by having recombination initiated by a single chromatid whose DNA is cut and partially degraded, rather than by nicks in both partners.

Figure 1.—

The DSBR mechanism of crossing over and the genetic structure of the chromosomes in the model. Clusters of shaded circles, gene clusters determining viability (light-shaded circles, wild type; dark-shaded circles, mutant); solid ovals, active hotspot alleles; open ovals, inactive hotspot alleles. S, sister chromatids; H, homologous chromosomes. Recombination is initiated by a meiosis-specific DSB at the site of an active hotspot allele, with sequence degradation at the 5′ ends extending a variable distance into the flanking DNA. The free 3′ ends created by the degradation then trigger gap repair by base pairing with complementary sequences of one of the two homologous chromatids; strands of this chromatid act as templates for resynthesis of the degraded strands. This creates two Holliday junctions, where the strands of the chromatids have switched partners. Depending on how these junctions are resolved, the sequences flanking the recombination site will be either in their original relationships or recombined by a crossover.

As implied by these genetic studies, recombination hotspots are heritable. The primary determinant of the locations of recombination-initiating DSBs is the DNA sequence at and around the break sites (Ponticelli et al. 1988; de Massy and Nicolas 1993; Nicolas 1998; Jeffreys and Neumann 2002), and a hotspot locus can be defined genetically as a site of allelic difference that causes local differences in recombination initiation frequency. No consistent hotspot consensus sequence has been identified, although some patterns have emerged. For example, in Schizosaccharomyces pombe many hotspots are members of a family of sequences related to the cAMP response element (Fox et al. 2000), and in Saccharomyces cerevisiae many belong to a CoHR family (Blumental-Perry et al. 2000). In most organisms, however, the feature unifying all hotspots appears to be not a specific sequence but the ability of various sequences to cause a relatively “open” local chromatin structure that exposes DNA to the meiosis-specific nuclease SPO11 (Ohta et al. 1999; Fox et al. 2000; Lichten 2001). Different hotspots often have intrinsically different levels of DSB activity, reflecting not only their differing sequences but also their interactions with various DNA-binding proteins encoded at other loci (Kon et al. 1997; Mizuno et al. 2001). In yeast, recombination hotspots often coincide with promoters of transcriptionally active genes (Nicolas 1998).

Although most studies of the inheritance of hotspots have used hotspot variants discovered in lab cultures or created by mutagenesis, hotspot loci are known to be polymorphic in natural populations (Catcheside 1975; Guillon and de Massy 2002; Carrington and Cullen 2004). Furthermore, biased conversion in hotspot heterozygotes has also been detected in human and mouse meioses (Jeffreys and Neumann 2002; Yauk et al. 2003). As predicted by the DSBR model, the less-active hotspot allele preferentially replaces the more-active one.

The break-and-repair mechanism provides an elegant explanation for the link between biased gene conversion and crossing over but has the drawback of making the long-term maintenance of crossing over problematic due to the biased conversion of the initiation sites (Nicolas et al. 1989). At any hotspot polymorphic for alleles with different DSB activities, recombination will usually be initiated by the more-active allele, causing its preferential conversion to the less-active allele. Because hotspot alleles with reduced activity are expected to inevitably arise by mutation of active alleles, every hotspot should eventually become subject to this process. Thus, over repeated generations, less-active hotspot alleles are expected to replace more-active alleles, and inactive ones to eventually arise and replace all active ones. Hotspot loss is a very strong prediction of all versions of the DSBR model (because it is so consistently observed in crosses), but it is contradicted by the observed abundance of hotspots.

Can the benefits of recombination select for active hotspots strongly enough to overcome their occasional loss by conversion (Nicolas et al. 1989; McKee 1996)? Although such benefits are often assumed to be very large, the forces creating these benefits are subtle and complex, and the benefits themselves are often weak (Barton and Charlesworth 1998; Burt 2000; Otto and Barton 2001). The problem is not that recombination cannot create highly adaptive novel combinations of alleles, but that its probability of doing so is low, sometimes lower than its probability of doing harm.

A previous model examining the loss of active hotspots (Boulton et al. 1997) found that recombination of deleterious mutations did not provide benefits large enough to prevent the rapid loss of an active hotspot allele or even to slow its rate of loss. The model, however, assumed an infinitely large population, whereas many of the benefits of genetic recombination are thought to derive from the stochastic nature of events in small populations (Otto and Barton 2001). The model also considered only chromosomes with a single hotspot and hence could not address the effects of interactions among multiple hotspots, known to be important in real chromosomes. Archetti (2003) pointed out that the paradox would disappear if active hotspot alleles spread by preferentially converting their inactive homologs (a model that might be called “proselytizing DNA”). However, the evidence he cited for such trans-acting effects is far weaker than the evidence for self-conversion of active alleles.

The conflict between the evolutionary persistence of hotspots and the instability intrinsic to their mode of action implies a deep flaw in our understanding of the mechanism of meiotic recombination. The paradox is not simply due to an error in current models of recombination, but rather arises directly from the experimental evidence that highly active hotspot alleles convert themselves to their less-active homologs. To clarify the issues and to provide guidance for molecular and genetic investigations into the mechanisms, we have created a computer model that simulates the range of forces acting on hotspots. The simplest simulations we report followed Szostack's mechanism for DSBR, but various permutations allowed many features of more recent models to be investigated. This analysis has identified the molecular features of recombination that are key to resolving the hotspot paradox.

MATERIALS AND METHODS

Population of haploid gametes:

The life cycle starts with a population of N haploid gametes (usually N = 1000) each containing a single chromosome with 1 or 10 hotspot loci. We consider two hotspot allele types, active and inactive, each of which may arise from the other by mutation at rates μ_B and μ_F, respectively.

Each hotspot locus is flanked by clusters of genes affecting viability (2 or 11 clusters for chromosomes with 1 or 10 hotspots, respectively; see Figure 2). Because there is no within-cluster recombination, the number of viability genes in each cluster is not specified and each cluster is treated as a single viability locus. Each viability locus can accumulate multiple mutations, each arising with probability μ_v; there are no back mutations. Mutation rates are per allele and per generation.

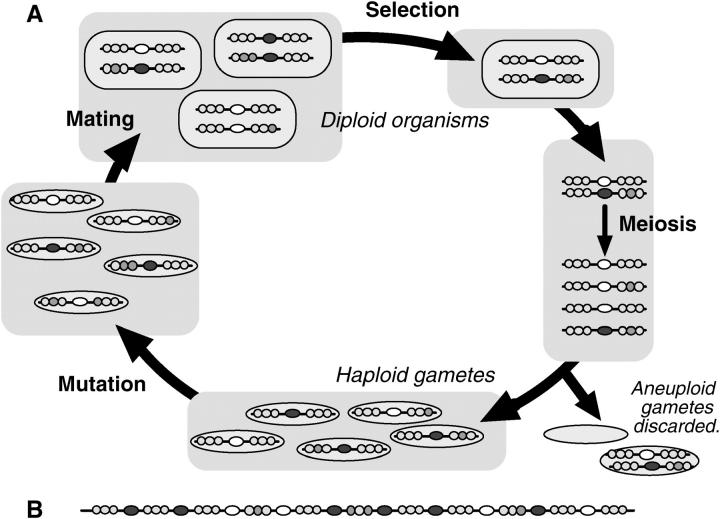
Figure 2.—

Components of the simulation model. Symbols are as in Figure 1. (A) The simulated life cycle for chromosomes with one hotspot. (B) A chromosome with 10 hotspots and 11 viability gene clusters. See materials and methods for details.

Mating:

Gametes are paired randomly forming N/2 diploid individuals.

Selection:

In most simulations fitness depends only on the number of viability mutations according to the multiplicative fitness function W = (1 − s)^m, where s is the selection coefficient and m is the number of mutations summed over all viability loci in the diploid genome. In some simulations the hotspot loci also directly affected fitness, with each inactive allele adding to the effective number of viability mutations in the genome.

The fitness of each individual in the diploid population affects only its probability of being chosen to produce gametes for the next generation. Some meioses may fail to produce euploid gametes (see Segregation below), so >N/4 meioses may be needed to produce the N gametes that regenerate the population in the next generation. Thus the model chooses individuals one at a time to undergo meiosis until N euploid gametes have been obtained. Highly fit individuals may contribute more than one meiosis while less fit individuals may contribute none.

Meiosis:

The molecular events of meiosis are explicitly specified in the model: DNA replication, DNA breakage at randomly chosen active hotspot alleles, template pairing, conversion of broken hotspot alleles during repair, crossing over, and chromosome segregation. (Figure 1).

Premeiotic DNA replication:

The homologous chromosomes of the chosen individual first replicate, each producing two identical sister chromatids.

Initiation by DNA breakage:

Each active hotspot allele may then undergo a DSB with probability P_DSB (usually P_DSB = 0.1 or 0.01). In simulations using multiple hotspot loci this probability can be changed to P^′_DSB by competition with active hotspots elsewhere in the chromosome as follows. Under local competition 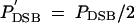if one of the adjacent hotspot loci has an active allele, and 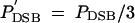if both adjacent loci are active. Under global competition, 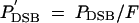, where F is the frequency of active alleles on the entire chromosome. Sequence degradation at the DSB destroys both strands of the hotspot allele with probability P_C. The model does not explicitly consider cases where only one strand of the hotspot DNA is destroyed.

The distributions of DSBs among the active hotspots are random, with the constraint that no more than two DSBs are allowed among the four chromatids at a single hotspot locus. This ensures that each DSB has an unbroken nonsister chromatid to pair with. To prevent this limit from biasing the locations of breaks, the order in which the chromatid breaks are assigned is randomized along the chromosome in each meiosis.

Recombinational repair and conversion:

Broken chromatids are next repaired by copying information from the homologous position on an unbroken nonsister chromatid (the repair template). If both of these chromatids are unbroken, one is chosen at random. If the hotspot allele has been destroyed and the template carries an inactive allele, this inactive allele replaces the active allele of the broken chromatid.

Crossovers:

• Mechanism A: The resolution of each repair interaction will, with probability P_X, produce a crossover between the flanking viability loci of the participating chromatids. Otherwise the chromatids retain the parental configuration. Strong interference is approximated by allowing each chromatid to participate in only a single crossover (otherwise five were allowed); excess repair interactions beyond the limit always separate without crossing over.

• Mechanism B (used only for “counting” interference): The DSBs in each meiosis are numbered sequentially from 1, 2, 3, 4, or 5 (initial value chosen randomly). Every fifth DSB becomes a crossover; the rest retain the parental configuration.

Segregation:

Completion of meiosis produces four gametes. If the meiosis has at least one crossover, segregation is Mendelian, and each gamete receives a single chromatid. If there are no crossovers, with probability P_A the chromatids will become four aneuploid and inviable gametes, which are discarded. If P_A = 0, meioses produce haploid gametes even without a crossover. All haploid gametes are placed in the gamete pool of the next generation. Diploids from the parent population continue to be chosen for meiosis until the total number of gametes equals N.

Equilibria and confidence limits:

Nonequilibrium confidence limits (e.g., for the data in Figures 3 and 4) are standard deviations of the final values unless otherwise specified. Because simulations with balanced forces of conversion and selection reached equilibrium very slowly, each simulation for Table 2 was continued until apparent equilibrium was reached (determined by inspection). The equilibrium values in Table 2 are the means of two such equilibria, each averaged over the subsequent 100 generations of equilibrium. Because genetic drift often caused polymorphic populations to exhibit substantial fluctuations in hotspot frequency even at equilibrium, the equilibrium hotspot frequencies in Figures 5 and 6 were determined as follows. After initial estimation of equilibrium frequencies by inspection of graphed data, two simulations were initiated, one with active hotspot alleles initially present at a frequency well above the approximate equilibrium and another with them at a frequency well below it. As these simulations proceeded, each generation at which the hotspot frequencies of the two populations intersected was used as an estimate of the true equilibrium. The error bars indicate the standard deviations of these estimates.

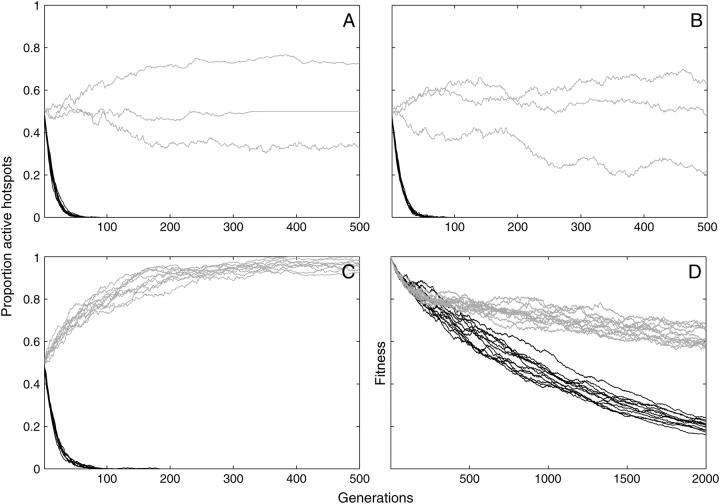
Figure 3.—

Results for chromosomes with one hotspot locus. Simulations in A, B, and C had μ_F = μ_B = 0 and were initiated with 50% active hotspot alleles with P_DSB = 0.1. (A) μ_v = 0, s = 0, P_A = 0. Bottom 10 lines (n = 10), full conversion (P_C = 1); shaded top lines (n = 10, three typical simulations shown), no conversion (P_C = 0). (B) μ_v = 0.01, s = 0.01, P_A = 0. Solid bottom lines (n = 10), P_C = 1; shaded top lines (n = 10, three typical simulations shown), P_C = 0. (C) μ_v = 0, s = 0, P_A = 0.5. Solid bottom lines (n = 10), P_C = 1; shaded top lines (n = 10), P_C = 0. (D) μ_v = 0.01, s = 0.01, P_DSB = 0.1, P_C = 1, P_A = 0.5, μ_F = μ_B.

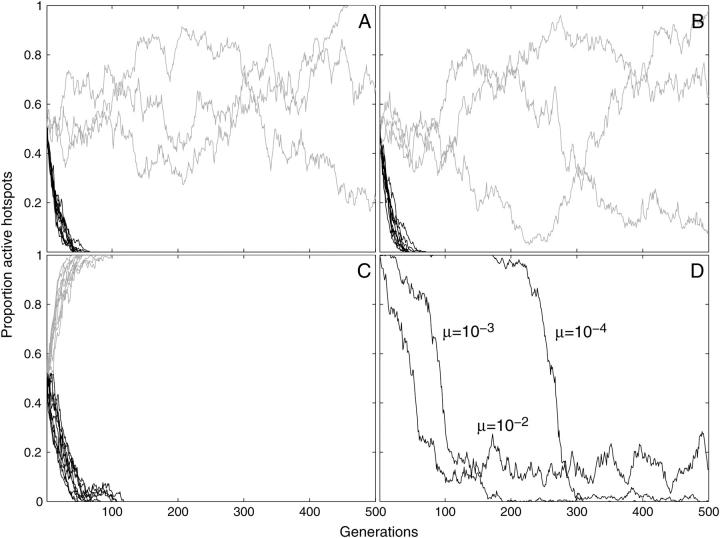
Figure 4.—

Results for chromosomes with 10 hotspot loci. All simulations had μ_F = μ_B = 0 and P_DSB = 0.1. Simulations in A–C were initiated with 50% active hotspot alleles with the following: (A) μ_v = 0, s = 0, P_A = 0 [solid bottom lines (n = 10), P_C = 1; shaded top lines (n = 10, three typical simulations shown), P_C = 0]; (B) μ_v = 0.01, s = 0.01, P_A = 0 [solid bottom lines (n = 10), P_C = 1; shaded top lines (n = 10, three typical simulations shown), P_C = 0]; and (C) μ_v = 0, s = 0, P_A = 0.5 [solid bottom lines (n = 10), P_C = 1; shaded top lines (n = 10), P_C = 0]. (D) Decline of mean population fitness. μ_v = 0.01, s = 0.01, P_C = 0, P_A = 0.5. Shaded top lines, all hotspot alleles active; solid bottom lines, all hotspot alleles inactive.

TABLE 2.

Effects of selection for nonmeiotic functions of hotspots

Selective cost of each inactive hotspot allele	PDSB = 0.01	PDSB = 0.02	PDSB = 0.05	PDSB = 0.1	PDSB = 0.2
A. Equilibrium frequency of active hotspot alleles
0.005	0.37	0.01	0.00	0.00	0.00
0.01	0.98	0.20	0.01	0.00	0.00
0.02	1.00	0.95	0.01	0.00	0.00
0.05	1.00	1.00	1.00	0.02	0.00
0.1	1.00	1.00	1.00	0.99	0.00
0.2	1.00	1.00	1.00	1.00	0.80
B. Equilibrium cost of fitness selection
0.005	0.06	0.099	0.10	0.10	0.10
0.01	0.00	0.16	0.19	0.19	0.19
0.02	0.00	0.01	0.34	0.34	0.34
0.05	0.00	0.00	0.00	0.64	0.64
0.1	0.00	0.00	0.00	0.01	0.88
0.2	0.00	0.00	0.00	0.00	0.53

Figure 5.—

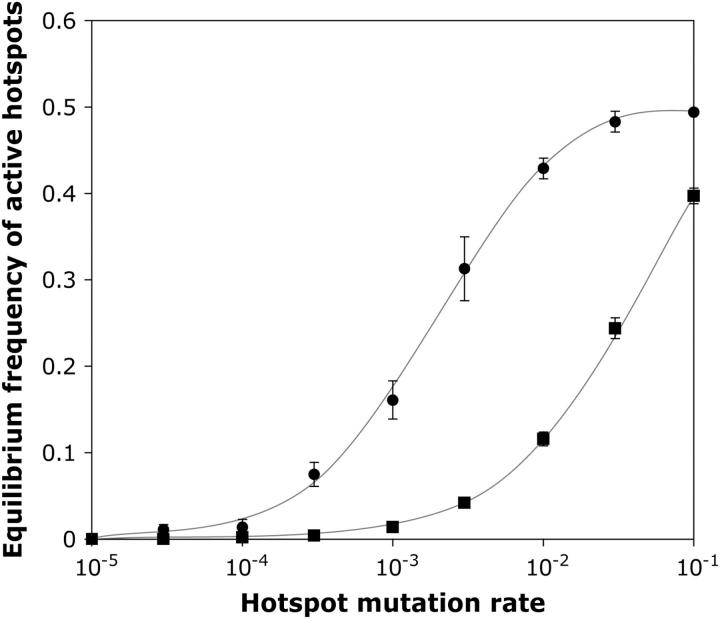
Equilibrium frequencies of active hotspot alleles in populations with different hotspot mutation rates. μ_F = μ_B, s = 0, μ_v = 0, P_C = 1, P_A = 0.5. Two replicates of each condition were run. Squares, P_DSB = 0.1, run for 500 generations; circles, P_DSB = 0.01, run for 2000 generations. Error bars indicate ±1 standard deviation (see materials and methods for details).

Figure 6.—

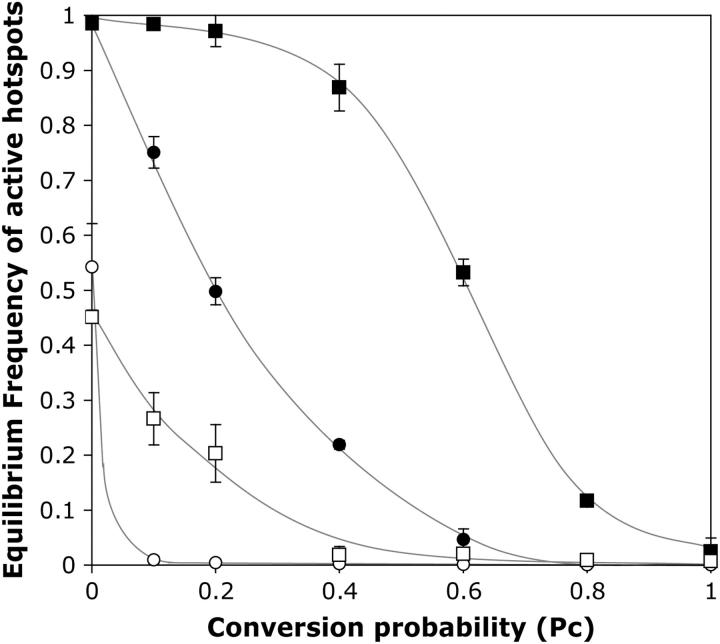
Equilibrium frequency of active hotspot alleles in populations with different hotspot conversion probabilities. μ_F = μ_B = 0.0001, s = 0, μ_v = 0. Solid squares, P_DSB = 0.1, P_A = 0.5; solid circles, P_A = 0.5, P_DSB = 0.01; open squares, P_A = 0, P_DSB = 0.1; open circles, P_A = 0, P_DSB = 0.01. Error bars indicate ±1 standard deviation (see materials and methods for details).

RESULTS

The primary goal of these simulations was to identify biologically plausible conditions that could allow active hotspot alleles to persist. To this end we devised a stochastic model that tracks all chromosomes in an obligately sexual diploid population with nonoverlapping generations and no separate sexes or mating types. The major events in each generation are (i) mutation of haploid gametes, (ii) random mating to form diploids, (iii) selection, (iv) meiosis (with DSBs causing conversion of hotspots and crossing over), and (v) segregation of chromosomes into gametes. These events are shown schematically in Figure 2 and described in detail in materials and methods. Key parameters of the model are listed in Table 1.

TABLE 1.

The main parameters of the model

Parameter	Significance	Usual value(s)
N	No. of chromosomes in the population	1000
μv	Mutation rate of viability loci	0.01
μF and μB	Rates of forward and back mutation at hotspots	10−4
s	Selection against viability mutations	0.01
PDSB	Probability of a DSB at an active hotspot	0.1 or 0.01
PC	Probability that a DSB destroys the hotspot	1.0
PX	Probability that a DSB becomes a crossover	0.5
PA	Probability of aneuploidy for a meiosis with no crossover	0.5 or 0

Single-hotspot chromosomes:

Our initial simulations were of chromosomes containing a single recombination hotspot. These provided the framework for interpreting the more complex simulations that followed and also allowed direct comparisons to the simulations of Boulton et al. (1997).

The first set of results (Figure 3A) shows how the gene conversion resulting from DSBs affects persistence of an active hotspot allele in the absence of any benefits of crossing over. In these tests fitness effects were absent because the viability loci that flank the hotspot suffered neither mutations nor selection (μ_v = 0 and s = 0; see materials and methods and Table 1), and chromatids segregated correctly with or without crossovers because aneuploidy was prevented (P_A = 0). The populations consisted of 500 diploid individuals (N = 1000). The simulations were initiated with half of the chromosomes carrying an inactive hotspot allele and half an active allele; each active allele had a 10% probability of initiating a hotspot-destroying double-strand break at meiosis (P_DSB = 0.1, P_C = 1). In all 10 runs shown in Figure 3A the frequency of active hotspot alleles (solid lines) fell rapidly, and all alleles were eliminated by generation 67 (mean generations to extinction 50 ± 8.7, n = 10). In contrast, control simulations where no conversion occurred (P_C = 0) showed no preferential loss of active alleles (shaded lines). Instead the allele frequencies changed only as a result of genetic drift and most populations remained polymorphic after 500 generations.

Additional control simulations (not shown) confirmed that, when conversion did occur (P_C = 1), the hotspot activity P_DSB determined the rate of loss and the time to extinction of active alleles, with more-active hotspot alleles being eliminated faster. These rates were comparable to those seen with the previous deterministic model (Boulton et al. 1997). Controls also showed that the loss of hotspots was independent of whether or not recombination events resulted in crossing over but did depend on whether or not DSBs destroyed hotspot sequences (considered in detail below). In summary, these simulations confirmed that, if unopposed, meiotic gene conversion leads to extremely rapid loss of active hotspot alleles.

Viability selection:

Could the genetic benefits of crossing over explain the persistence of active hotspots? The deterministic model found these benefits to be far weaker than the force of conversion, but was compromised by its assumption of an infinitely large population with no role for stochastic events such as genetic drift. To create a situation where crossing over was as beneficial as possible, the hotspots in our model were flanked with clusters of genes subject to recurrent deleterious mutation. In the absence of crossing over such viability mutations can lead to irreversible fitness decline when the best allele combinations are repeatedly lost due to genetic drift (a process called Muller's ratchet) (Muller 1964). This decline and the benefits of recombination in regenerating fitter combinations are largest when populations are small and when viability mutations are frequent and have low fitness costs, allowing drift to strongly influence the accumulation of mutations (Gessler and Xu 1999). To further enhance our ability to detect the fitness effect, the viability gene clusters were given the unrealistically high mutation rate of μ_v = 0.01.

To confirm that recombination between the two viability gene clusters did increase fitness under these conditions, simulations of populations with no active hotspots were compared to those with 100% active hotspots. Fitness declined in both types of population, but more slowly in the presence of recombination. After 10,000 generations, the mean fitness of 10 populations without crossing over (inactive hotspot allele fixed) had declined from 1.0 to 0.555 ± 0.05 (n = 10 replicate runs). Recombination at the hotspot located between the viability loci (active hotspot allele fixed, P_DSB = 0.1) slowed this decline, giving a final mean fitness of 0.724 ± 0.052 (n = 10).

Where populations contain both active and inactive hotspot alleles, the production of some high-fitness individuals by recombination is expected to generate indirect “hitchhiking” selection for active alleles, because these alleles remain tightly linked to the beneficial gene combinations they create. Hitchhiking is, however, weak because it is indirect and is often obscured by the very genetic drift that creates it (Gessler and Xu 1999). This is seen in Figure 3B. Although the mutation and selection parameters were identical to those giving the fitness differences described in the preceding paragraph, the outcomes were indistinguishable from those in the complete absence of fitness benefits, with all active alleles extinct by generation 72 when conversion was active (mean generations to extinction 49 ± 11, n = 10; compare to Figure 3A). This indicates that the stochastic benefits of recombination are too weak to detectably change the outcome of conversion, reinforcing Boulton et al.'s (1997) conclusion.

Fertility selection:

A potentially stronger benefit of crossovers is their ability to prevent aneuploidy by stabilizing the segregation of chromosomes into gametes. This fertility benefit was not present in the simulations shown in Figure 3, A and B, because the crossover requirement of the model had been turned off (P_A = 0). P_A was set to 0.5 in the simulations shown in Figure 3C, so chromosomes from meioses without crossovers had a 50% probability of producing aneuploid and inviable gametes. The shaded lines in Figure 3C show control simulations where crossovers affected segregation but where no conversion was allowed (P_C = 0). Here the benefits of correct segregation created strong selection favoring active hotspot alleles (mean generations to fixation 62 ± 19, n = 10). In contrast, when conversion was allowed (solid lines, P_C = 1), active alleles were still lost rapidly (mean generations to extinction 83 ± 25, n = 10), showing that even very strong fertility selection was unable to overcome the destruction of active hotspot alleles. The rates of loss of active alleles were again comparable to those seen under similar conditions with the deterministic model. Additional simulations combined both viability and fertility selection, to test whether interactions between these generated unexpected synergistic benefits. The outcomes, however (not shown), were indistinguishable from those in Figure 3C.

Mutation:

The results so far show that inactive hotspots can displace active ones in populations where they are already common. Figure 3D shows simulations examining the role of hotspot mutation in populations initially fixed for the active allele. The mutation rates used were unrealistically high (μ_F = μ_B = 10⁻⁴, 10⁻³, or 10⁻²) to give results within 500 generations in these small populations. The results of these runs were characterized by (1) an initial lag dependent on the rate of mutations creating inactive alleles (μ_F), (2) a rapid loss of active alleles due to conversion, and (3) a stable low-frequency equilibrium set by the balance between conversion and recurrent creation of active alleles by back mutation (μ_B). The initial lag was highly variable because mutations are infrequent, but the rate of loss was independent of mutation rate, with the frequency of active alleles falling from 80 to 20% in ∼50 generations. This analysis confirmed that conversion not only favors inactive alleles once they are common but also allows them to invade the population when they are rare.

Chromosomes with 10 hotspots:

It was necessary to extend the model to chromosomes with multiple hotspots for two reasons. First, such aspects of recombination as interference and competition depend on interactions between events at different hotspots. Second, although the single hotspots in Figure 3C experienced strong fertility selection due to their effect on segregation, crossovers in single-hotspot chromosomes were too infrequent to ensure proper segregation. Even when the activity of the hotspots was set to an unrealistic P_DSB = 0.5, 41% of the single-hotspot chromosomes had no crosssover. This is highly unrealistic, as in almost all organisms all chromosomes undergo at least one crossover in each meiosis. Although chromosomes with 25 hotspots best ensured accurate segregation, the computations were extremely slow. Chromosomes with 10 hotspots and 11 interspersed viability loci (illustrated in Figure 2B) best balanced the constraints of biological realism and computational practicality.

Initial simulations (Figure 4A) were run with no mutation of or selection on the viability loci (μ_v = 0, s = 0) and with crossovers not required for proper segregation (P_A = 0). In these simulations active hotspots were rapidly eliminated, with dynamics almost identical to those for the solitary hotspots in Figure 3A (n = 10; all active alleles extinct by 74 ± 8 generations). The graphs of control simulations without conversion show the effects of genetic drift (Figure 4A, shaded lines). After 500 generations all simulated populations remained polymorphic in at least 1 of their 10 hotspots. In the absence of conversion, active and inactive hotspots were equally likely to increase and decrease (mean frequency after 100 generations 0.494 ± 0.059) (n = 100 simulated populations), as expected from their initial 50:50 proportions.

Viability selection:

Viability selection was again introduced by setting μ_v = 10⁻² and s = 0.01. Because each chromosome now had 11 viability loci rather than 2, the fitness effects and recombination benefits were stronger than those in the single-hotspot simulations. Figure 4D shows how strongly recombination slowed the decline in fitness caused by accumulating deleterious mutations: after 2000 generations the populations with frequent crossovers had a mean fitness of 0.62 ± 0.04 (n = 12), whereas the fitness of populations with no crossovers had fallen to 0.20 ± 0.02 (n = 12).

However, the solid lines in Figure 4B show that this larger benefit of recombination still did not discernibly slow the loss of active hotspots by conversion (n = 10; all active alleles extinct by 77 ± 11 generations; compare to Figure 4A). The control simulations with no conversion (P_C = 0; Figure 4B, shaded lines) again show that the strong random effects of drift obscured any hitchhiking by active hotspot alleles due to the higher fitnesses they created (mean frequency after 100 generations 0.500 ± 0.075) (n = 100 simulated populations). As expected, simulations that reduced drift by increasing the population size from 1000 to 10,000 gave a proportionally weaker fitness benefit of recombination (not shown).

The 2000-generation fitness difference seen in Figure 4D (0.62–0.20 = 0.42) was used to estimate the per-generation viability benefit conferred by hotspot-dependent recombination as s_r = 0.00043 [the solution of (1 − s_r)²⁰⁰⁰ = 0.42]. Figure 4B shows that this recombination benefit is too small to affect the persistence of hotspots in the face of conversional loss. To determine how strong a benefit would be needed to maintain hotspots, active hotspot alleles were assigned a range of direct fitness benefits, s_h (see Nonmeiotic benefits of active hotspot alleles below). Hotspots persisted only when s_h was at least 0.1, suggesting that to maintain hotspots against conversion any recombination benefit would need to be at least 200-fold stronger than that generated by the mutation-accumulation model. Because the actual fitness benefits of recombination were so small, they were omitted from subsequent analyses by setting μ_v = 0 and s = 0.

Fertility selection:

The nature of fertility selection is also expected to change when chromosomes have multiple hotspots. Cells homozygous for 10 active hotspots with P_DSB = 0.1 have on average 1.9 crossovers per meiosis. Because a single crossover is sufficient to ensure accurate segregation in the model, an active hotspot receives no benefit from causing the second or third crossover in a meiosis, so the average benefit per crossover should be nearly halved. Furthermore, the segregation benefits of the crossovers caused by active alleles are shared by competing inactive alleles. Consistent with these expectations, the shaded (top) lines in Figure 4C show that in the absence of conversion active hotspots increased more slowly than the solitary hotspots in Figure 3C, and the mean fixation time per hotspot increased to 281 ± 79.

Although this fertility selection was much stronger than the viability selection shown in Figure 4B, it was still unable to overcome the loss of hotspots by conversion (Figure 4C, solid lines). The mean time to extinction of individual hotspots was 65 ± 9.2, reduced from 85 for the solitary hotspots in Figure 3C. This pattern held over a wide range of hotspot activities (P_DSB = 0.01–0.5; data not shown). The balance between fertility selection and hotspot conversion always favored inactive hotspot alleles. Reducing hotspot strength (P_DSB) simultaneously weakened both the fertility selection favoring active hotspots and the conversion eliminating them, allowing drift to play a larger role in determining which alleles were fixed.

Back mutation:

The role of back mutation in maintaining active hotspots was next investigated in more detail. Figure 5 shows how the interaction between hotspot strength and mutation rate affected the equilibrium persistence of active alleles. These simulations examined the biologically plausible P_DSB values of 0.1 and 0.01 (strong and weak hotspots, respectively) and elimination of hotspots by conversion and mutation (μ_F) was opposed by fertility selection and hotspot back mutation (μ_B). Strong hotspot alleles became rare (<2%) whenever mutation rates were <10⁻³, and weak hotspots were rare whenever the rates were <10⁻⁴. These mutation rates are much higher than those of biological systems, suggesting that creation of new hotspots by mutation is unlikely to be the process maintaining real hotspots. In the simulations that follow, the rates of forward and back mutations were set at 10⁻⁴. This was sufficiently high to ensure that loss or fixation of alleles by drift did not prevent identification of stable polymorphic equilibria, but low enough to not mask the effects of the factors under investigation.

Varying the probability of conversion:

An important improvement in this model is the ability to vary the probability that a DSB leads to conversion of the initiating hotspot allele. Although it is well established that DSBs and the associated sequence degradation at hotspots frequently cause conversion of the initiating allele, the specific conversion probabilities are not known. As these are likely to be critical factors affecting the persistence of hotspots, we have examined the effects of a range of values of the conversion probability P_C.

Figure 6 shows how strongly different values of P_C affected the long-term persistence of hotspots. Hotspots with high probabilities of conversion persisted at only low frequencies or became effectively extinct, but those with lower values of P_C were maintained. The key role of fertility selection in counteracting conversion is shown by the lack of hotspot persistence when aneuploidy was turned off. In both Figures 5 and 6, weak hotspots reached higher frequencies than strong hotspots. This was because mutations play a stronger role when conversion is weak and because fertility selection on the strong hotspots was diluted by the occurrence of more than one crossover per meiosis.

Interference:

Crossover interference regulates the number and positions of crossovers in most organisms, usually ensuring that crossovers are widely spaced and that each chromosome or chromosome arm receives at least one crossover, thus optimizing the segregation of homologous chromosomes (Hassold et al. 1991; Hawley et al. 1993; Kleckner 1996). Interference does not regulate the number or locations of DSBs (Stadler 1959; Mortimer and Fogel 1974), but instead controls the probability that repair of each DSB will lead to a crossover, as a function of its distance from other crossovers. Most of the properties of interference can be explained by a “counting” mechanism (Stahl et al. 2004), but the molecular processes are not understood.

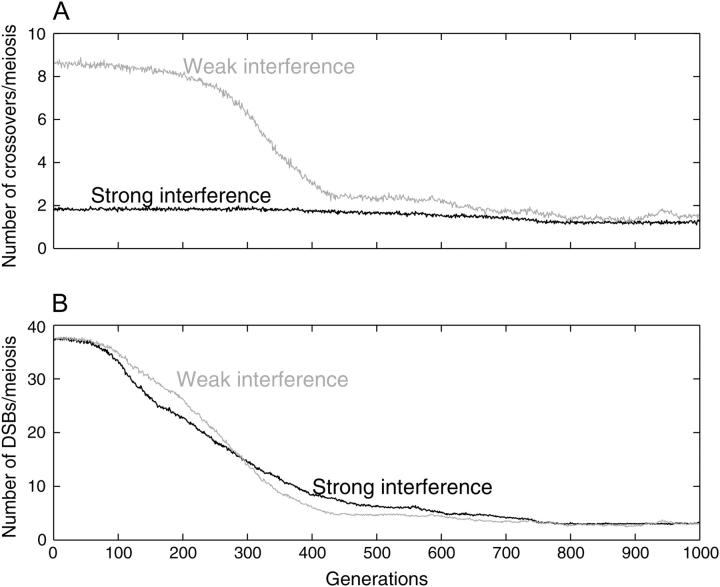
The model evaluated the effects of two different mechanisms of interference. In the first (mechanism A) interference acted by limiting the number of crossovers per chromatid, with strong interference allowing each chromatid to participate in only a single crossover and weak interference allowing five crossovers per chromatid. The second version of interference (mechanism B) used a counting model, which controlled the spacing of crossovers without reducing their frequency.

Mechanism A required meioses with many DSBs, so the number of hotspot loci per chromosome was increased to 25 and P_DSB was raised to 0.5. The strong hotspot activity necessitated reducing P_C to 0.1 to prevent immediate elimination of all the active hotspots by conversion. The crossover limits did not affect the number of DSBs created or their probability of undergoing hotspot conversion, and the data in Figure 7 confirm that they did not affect the loss of active hotspots. Figure 7A shows that strong interference worked as expected, keeping the number of crossovers per meiosis low even when the number of DSBs was high. With weak interference the average number of crossovers more closely paralleled the number of DSBs. Figure 7B shows the average number of DSBs per meiosis; these reflect the numbers of active hotspot alleles and decreased at the same rate under both strong and weak interference. Results of other simulations using mechanism A were consistent: strong interference reduced the number of DNA breaks that resulted in crossovers, but had no effect on the rate of hotspot loss or on the final results. The persistence of ∼10% active hotspots at equilibrium in these simulations is because P_C = 0.1, not because of interference.

Figure 7.—

Effect of crossover-limit interference. μ_F = μ_B = 0.0001, s = 0, μ_v = 0, P_DSB = 0.5, P_A = 0.5, P_C = 0.1. Each chromosome has 25 hotspot loci (interference mechanism A). (A) Crossovers per meiosis. (B). DSBs per meiosis. Solid lines, crossover limit = 1; shaded lines, crossover limit = 5.

Counting interference (mechanism B) also had 25 hotspots per chromosome and caused every fifth DSB to became a crossover and the other DSBs to become noncrossovers. It was compared to a random-crossover model with P_X = 0.2 (all other parameters identical). As expected, counting interference more efficiently allocated crossovers to meioses; when all hotspots were active only 1% of meioses lacked crossovers, whereas with random crossovers ∼13% lacked them. It was no more effective, however, at preserving active hotspot alleles (data not shown). Again, this is not unexpected, as the interference did not affect the occurrence or repair of DSBs.

Dependence of hotspot activity on competition with adjacent hotspots:

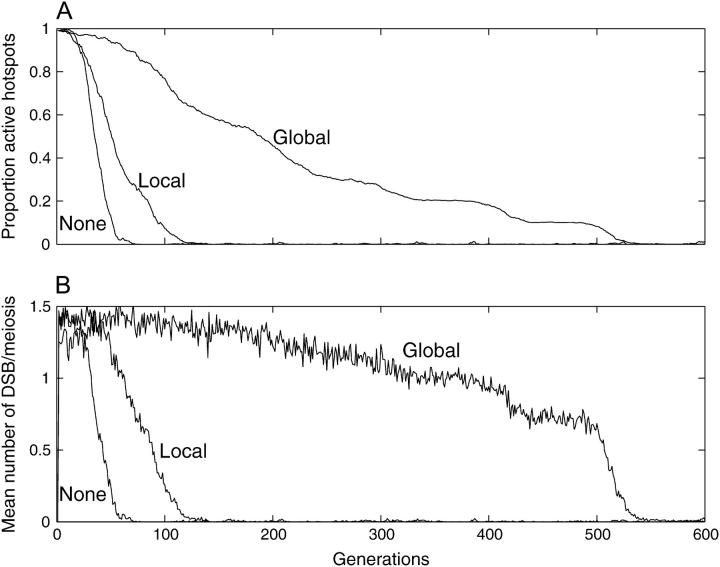
There is substantial evidence that the probability of one hotspot initiating recombination is affected by the activity of nearby hotspots. Specifically, deleting or otherwise inactivating one hotspot often increases the activity of nearby hotspots (Yoshino et al. 1994; Wu and Lichten 1995; Fan et al. 1997; Kaback et al. 1999; but see also Haring et al. 2003). Competition may arise because hotspots compete for nucleases or other factors that limit their activity and has been suggested to allow some hotspots to increase their activity only when nearby ones have been lost and thus to counteract the loss of hotspots by conversion (Carrington and Cullen 2004). Our model simulated competition in two ways, local and global. Under local competition the activity of each active allele decreased if one or both of the adjacent hotspot loci on its chromosome contained active alleles. Under global competition the activity of each active allele was decreased in proportion to the total number of active alleles on its chromosome.

Several different combinations of parameters were examined. In all, competition changed the dynamics of hotspot conversion but not the final outcome. Figure 8 shows the test that most closely fits the usual view of competition. It compared three populations whose hotspots all had equal intrinsic activity (i.e., were equally strong in isolation). The three populations also began with approximately the same total meiotic recombination activity, contributed by 2 noncompeting hotspots with very high constant activity, 4 locally competing hotspots with moderate initial activity due to competition, or 10 globally competing hotspots with weak initial activity due to competition. As the simulations progressed, the remaining locally competing and globally competing hotspots increased their activities as their competing neighbors were lost.

Figure 8.—

Effect of competition between active hotspot alleles. μ_F = μ_B = 0.0001, s = 0, μ_v = 0, P_C = 1, P_DSB = 0.1, P_A = 0.5, seeded with 1% inactive alleles. (A) Frequency of active hotspot alleles. (B) Mean DSBs per meiosis. Competition type is as indicated. See materials and methods for details.

Figure 8B shows that a population initiated with many hotspots whose low activity was due to competition could maintain its initial level of recombination for much longer than a population that began with a few noncompeting hotspots. Nevertheless, the competition delayed only the loss of the hotspots; Figure 8A shows that in all cases the hotspots were effectively extinct by generation 600. These tests were repeated with P_C set to 0.5, to simulate hotspots that frequently avoid self-conversion. The outcome was different in that each population retained active alleles at a single-hotspot locus (results not shown), but again the presence and type of competition did not affect the outcome.

Nonmeiotic benefits of active hotspot alleles:

Recombination hotspots commonly occur at sites of relatively open chromatin, where the SPO11 nuclease has access to chromosomal DNA (Ohta et al. 1999; Mizuno et al. 2001). In many cases this exposure reflects chromatin structures that function in nonmeiotic cells, for example, as promoters (Gerton et al. 2000). These functions led Nicolas et al. (1989) to suggest that active hotspots might persist because mutations that reduce or eliminate their DSB activity also reduce their contribution to viability and are thus eliminated by selection. The final set of simulations examined this possibility by assigning each inactive hotspot allele a fitness cost that reduced its chance of entering meiosis, independently of its participation in recombination. Each simulation followed chromosomes with 10 hotspots; aneuploidy selection was active but the viability loci flanking the hotspots made no contribution to fitness.

The data in Table 2A show that active hotspot alleles that contributed to fitness in this way could sometimes avoid extinction. Hotspots under weak selection were lost (Table 2A, boldface italics and italics) but those with strong contributions to fitness were effectively fixed if P_DSB was weak (regular type) or maintained as polymorphisms if selection was balanced by the DSB activity (underlined regular type).

This selection came at a cost—the ongoing cost of the deaths of all the unfit individuals with inactive hotspots. Table 2B shows the fitness costs associated with each entry in Table 2A (cost = 1 − mean fitness of the individuals in the population). Comparing the two parts of the table, we see that active alleles that were maintained close to fixation by strong selection (Table 2A, regular type) imposed only a very small fitness cost (Table 2B, regular type), because selection was strong enough to eliminate new inactive alleles before they could increase by conversion. Extinction of weakly selected hotspot alleles imposed a much larger cost (Table 2B, top two rows, underlined regular type). The most severe fitness costs were seen with strong hotspot alleles whose substantial fitness contributions were unable to entirely prevent conversion (Table 2B, italics and underlined boldface italics).

DISCUSSION

Our stochastic model of the population dynamics of recombination hotspots incorporated many of the key processes of meiotic recombination and facilitated exploration of the long-term requirements for hotspot persistence. The main results can be summarized as follows: unopposed hotspot conversion created a very strong force, able to drive strong hotspots from 50% representation to extinction within 70 generations. Although crossing over could substantially increase a population's fitness, the benefits did not significantly affect the hotspots responsible for the crossing over, which were lost as quickly as in the absence of selection. Hotspots could not be maintained by de novo mutation or by interference, which reduced their ability to cause crossovers without slowing the rate at which they were lost. Competition among hotspots also did not prevent their extinction, although it could slow their rate of loss. The fertility benefits of crossing over (prevention of aneuploidy) were large enough to substantially slow hotspot loss, and to prevent loss if at least some crossovers arose without hotspot conversion. Hotspots that contributed directly to fitness were maintained provided their fitness contribution was comparable to their probability of being lost by conversion. Loss of these hotspot alleles, however, often imposed severe fitness costs.

Processes that did not maintain hotspots:

In addition to identifying conditions under which active hotspot alleles were able to persist, the results also identified conditions that could not maintain active hotspot alleles. Here we briefly discuss these before considering the successful conditions in more detail.

Viability selection for crossing over:

The genetic benefits of recombination are commonly invoked to explain all aspects of meiosis. These benefits are, however, seen only under somewhat contrived conditions and are often overwhelmed by the costs of sex (Maynard Smith 1978; Barton and Charlesworth 1998; Otto and Nuismer 2004). Our results show that even when the potential benefits of crossing over are maximized by combining strong fitness selection with an unrealistically high mutation rate at viability loci, the genetic benefits of crossing over are >200-fold weaker than the biased conversion driving active hotspot alleles to extinction (Figures 3B and 4B). These results confirm the findings of Boulton et al. (1997). With a more realistic mutation rate the benefit of crossing over would be even smaller.

Mutation (forward and back):

Frequent creation of new hotspots or mutational activation of potential ones is often suggested as a solution to hotspot loss. Simulations incorporating recreation of hotspots by back mutation found that implausibly high mutation rates were needed to raise the equilibrium frequency of active hotspot alleles to biologically significant levels (Figure 5). More generally, unless the rate at which new hotspots arise is comparable to that at which they act, new alleles are expected to destroy themselves by conversion before they can rise to a significant frequency in the population. One might instead hypothesize that active hotspot alleles are constantly being created and destroyed by mutation at many thousands of sites throughout the genome and that, although these alleles rarely increase to high frequencies, each individual has enough hotspots for its own needs. However, the ability to map individual human hotspots across unrelated sperm donors (Jeffreys et al. 2004) contradicts this model's prediction that individuals independently drawn from a population will have very few or no hotspots in common.

Interference:

Because the mechanism of interference is not well established, we simulated it with two very different mechanisms. Both found that interference did not to contribute to hotspot persistence (Figure 7). This was not surprising, because interference is known not to limit gene conversion. In real chromosomes reducing the number of crossovers allowed per chromosome from five to one might be expected to increase (rather than decrease) the rate at which active hotspots are lost, as it would make crossing over a less probable consequence of DSBs and thus reduce their benefit to the organism. However, the negligible viability benefits of crossing over had been eliminated from this version of the model, and the fertility benefits required only a single crossover per chromosome.

Competition among hotspots:

There is substantial evidence for hotspot competition, although it does not appear to be universal (Yoshino et al. 1994; Wu and Lichten 1995; Fan et al. 1997; Kaback et al. 1999; Haring et al. 2003). To compensate for the lack of information about its mechanism, we chose to model two extreme modes of competition (global and local) under a range of initial conditions. None of these allowed hotspots to persist indefinitely, although populations initiated with many globally competing hotspots were able to maintain their baseline level of recombination for many generations while hotspots were being lost (Figure 8). It is important to recognize that the situations we modeled are unlikely to arise naturally, as mutations creating competition will be selected against because they reduce the organism's overall level of meiotic recombination.

Locus-specific hotspot strength:

The model considered only two categories of hotspot alleles, active and inactive, with all active alleles having the same strength in any one simulation. Alleles of intermediate strength are easy to create in the lab and have been found in natural populations (Jeffreys and Neumann 2002), and the fate of any new allele should depend only on the difference between its activity and that of other alleles at its locus. Thus the results for this model are expected to extend cleanly to a continuous model and to real hotspot alleles.

Processes that might maintain hotspots:

Fertility selection:

The role of crossovers in chromosome segregation, and thus in fertility, is well established in real meioses (Hassold et al. 1991; Hawley et al. 1993; Kleckner 1996), and in our model fertility selection is a strong force opposing hotspot conversion. The model's default assumption that 50% of DSBs lead to crossovers was, however, motivated less by experimental evidence than by our desire to give hotspots the benefit of the doubt. A 50% probability is predicted if recombination occurs by a single pathway in which isomerization of Holliday junctions completely randomizes the parental and recombinant orientations of the flanking duplex DNA (Holliday 1964). The available data indicate, however, that resolution is usually biased toward the parental configuration [e.g., 4- to 15-fold at the human hotspot DNA3 (Jeffreys and May 2004), 14-fold at the Neurospora am hotspot (Bowring and Catcheside 1996), and 5-fold at the Drosophila rosy locus (Hilliker et al. 1991)]. In most of our simulations the fertility benefits were the only force opposing loss by conversion, so incorporating more realistic crossover probabilities into the model would shift any equilibrium further toward inactive alleles. For example, if the model's crossover probability was reduced from 50 to 25%, the P_C = 0.4 values for P_DSB = 0.1 and P_DSB = 0.01 in Figure 6 would fall from 0.22 and 0.73 to 0.01 and 0.20, respectively. In simulations where fertility selection was reinforced by direct selection against inactive alleles (Table 2), decreasing the crossover probability would further reduce the population's ability to survive.

Another parameter affecting fertility selection is the probability that chromosomes without crossovers randomly assort into daughter cells at telophase of meiosis I. The model's assumption that chromosomes without crossovers suffered 50% aneuploidy maximized the strength of fertility selection. However, chromosomes in Drosophila males use a “distributive” segregation system to segregate normally despite the lack of crossing over (Carpenter 1991), and similar systems play back-up roles in chromosome segregation in at least some other organisms (Loidl et al. 1994; Sharif et al. 2002). Such systems will decrease the strength of fertility selection and thus make hotspot persistence even more difficult.

Probability that a DSB leads to conversion of the hotspot:

One feature of hotspot action revealed to be of critical importance was P_C, the probability that initiation of recombination destroys the initiating allele. The experimental data most useful for estimating real values of P_C are in Jeffreys and Neumann's (2002) analysis of non-Mendelian segregation proportions among gametes with crossovers at the human hotspot DNA2. Seventy-six percent of sperm from males heterozygous for the FG11G and FG11A hotspot alleles at this locus contained the less-active G allele. This degree of overtransmission is compatible with values of P_C ranging between 0.51 and 1.0, depending on the assumed activity difference of the two alleles. The lower value is obtained by assuming that all recombination at this hotspot is initiated by the A allele and the higher value by assuming that recombination is initiated 3.2-fold more often by the A allele than by the G allele. These values of P_C constrain the simulations in Figure 6 to the right-hand half of the graph, where active alleles are poorly maintained. Other data, mainly from fungal systems (Gutz 1971; Nag and Kurst 1997), are consistent with values of P_C in this range, although they are potentially confounded by recombination initiated at nearby hotspots and by mismatch repair of the heteroduplex DNA produced by processing of DSBs.

Direct contributions of active hotspot alleles to fitness:

The correspondence of many yeast hotspots with promoters led Nicolas et al. (1989) to suggest that selection for functional promoters may be sufficient to overcome hotspot loss by conversion. McKee (1996) explicitly assumed this when proposing that biased conversion might directly eliminate deleterious mutations caused by adjacent promoter-up mutations that also increased hotspot activity. Our analysis shows that the direct contributions that hotspots may make to fitness are indeed crucial, not only for their potential to maintain hotspots but also for the debilitating fitness costs this maintenance can impose. Most striking are the values in the bold italic underlined entries in Table 2B with fitnesses <0.5 (bottom right corner), where strong hotspots are unable to persist despite strong selection favoring them. Although our model assumes a constant population size, selective costs this high are likely to drive most natural populations extinct.

The fitness effects shown in Table 2 are likely to be underestimates for several reasons. First, these simulations assumed that nonfunctional promoter alleles are not recessive to functional alleles, making selection against them very efficient. Real loss-of-function mutations are usually recessive and are consequently eliminated very inefficiently because they are hidden from selection when heterozygous. Second, these simulations tracked only a single chromosome with a limited number of hotspots. Because mis-segregation of any one chromosome ruins the whole gamete, organisms with multiple chromosomes must have near-perfect segregation of all chromosomes if they are to keep aneuploidy at a tolerable frequency (e.g., 1% mis-segregation of each of 10 chromosomes would give 10% aneuploid gametes), entailing higher fitness costs. The underestimation is likely to be further compounded by other assumptions of the model, such as the assumed 50% crossover and aneuploidy probabilities.

Priorities and perspectives:

The results of this model situate the hotspot-maintenance paradox within the larger paradox of the evolutionary function of sexual recombination. A central problem is the ongoing inability of population geneticists to identify a benefit of recombination large enough to counter the conversion of active hotspots. In the absence of such a benefit, maintaining hotspots by selection for nonmeiotic functions is simply robbing Peter to pay Paul—the population would have higher fitness if it simply gave up sexual reproduction and retained its hotspot sequences for their nonmeiotic functions.

Even if the benefits of recombination responsible for the evolution of sex were identified, the DSBR mechanism of recombination initiation would remain problematic. The same number of selective deaths would still be needed to maintain hotspots in the face of their destruction by self-inflicted conversion, although more of the deaths would come from the indirect fitness reductions occurring in nonrecombining genomes and fewer from selection against the loss of nonmeiotic functions.

Thus hotspots remain at the heart of the paradox. More complex evolutionary models are not likely to provide a solution, as the present model is realistic where realism is practical and, where it is not, errs on the side of assumptions that favor hotspot persistence. We see three promising directions for experimental work: first, do mutations eliminating hotspot activity in organisms other than yeast usually reduce viability, and if so, is each hotspot's viability effect strong enough to maintain it close to fixation without compromising overall fitness? Second, are new hotspots created by a directed mutation process powerful enough to compensate for their eventual loss by conversion? Finally, is hotspot conversion much less pervasive than the experimental evidence to date suggests?

Each of these hypotheses could be dismissed as inconsistent with at least some experimental evidence, but the alternatives are even more problematic. An equal temptation is to simply assume that one or another is the correct explanation. But until the paradox has been resolved we cannot afford to have confidence in any aspect of the DSBR model, despite its strong experimental support.