Abstract
A decline in population size can lead to the loss of allelic variation, increased inbreeding, and the accumulation of genetic load through drift. We estimated the fitness consequences of these processes in offspring of controlled within-population crosses from 13 populations of the self-incompatible, clonal plant Ranunculus reptans. We used allozyme allelic richness as a proxy for long-term population size, which was positively correlated with current population size. Crosses between plants of smaller populations were less likely to be compatible. Inbreeding load, assessed as the slope of the relationship between offspring performance and parental kinship coefficients, was not related to population size, suggesting that deleterious mutations had not been purged from small populations. Offspring from smaller populations were on average more inbred, so inbreeding depression in clonal fitness was higher in small populations. We estimated variation in drift load from the mean fitness of outbred offspring and found enhanced drift load affecting female fertility within small populations. We conclude that self-incompatibility systems do not necessarily prevent small populations from suffering from inbreeding depression and drift load and may exacerbate the challenge of finding suitable mates.
THE recent history of population size is assumed to be a major determinant of population genetic variation (Frankham 1996). Both population size and genetic diversity in turn affect several processes relevant to fitness, such as inbreeding, the accumulation of deleterious mutations through genetic drift, and genetic incompatibility due to mating systems that disregard similar gametes (Frankham et al. 2002).
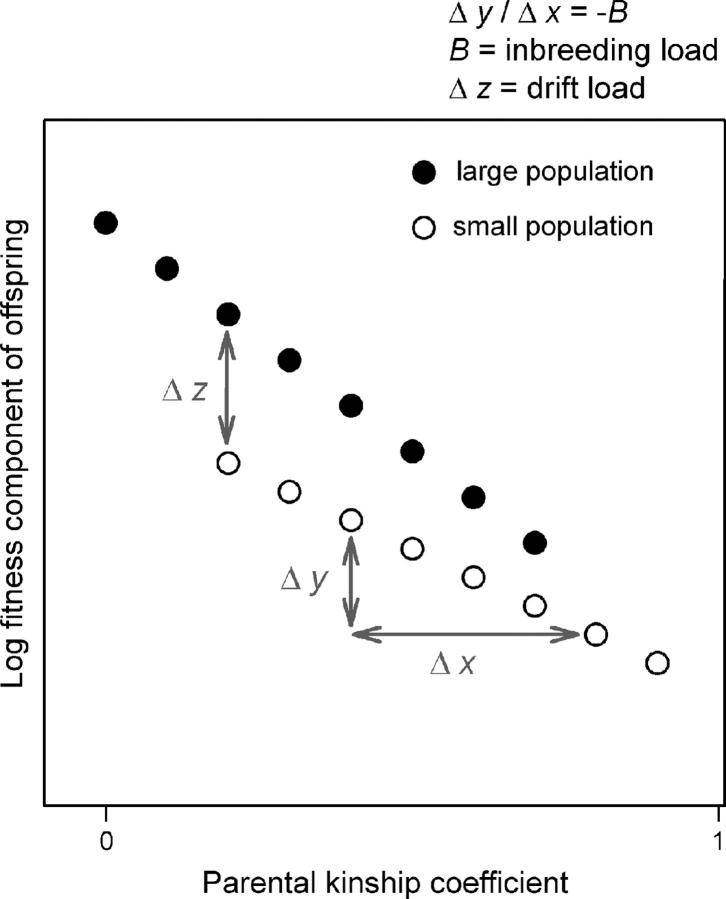
The two processes of inbreeding and genetic drift work differently and their magnitude of fitness relevance is thought to change over time in opposite directions in small populations. According to Wright (1977), the main causes of inbreeding depression, the fitness decline due to inbreeding, are general homozygosity and the demasking of deleterious alleles. The process of genetic drift is a change in gene frequency arising from random events (Wright 1977). When population size is small, these random events may outweigh the force of selection, leading to the loss of adaptive genetic variation and the fixation of deleterious alleles (Kimura et al. 1963; Lynch and Gabriel 1990; Charlesworth et al. 1993; Whitlock 2000). While genetic load through drift increases over time, inbreeding depression is expected to decrease after several generations. Purging eliminates deleterious mutations of large effect after exposure to selection in the homozygous stage (Lande and Schemske 1985; Waller 1993), and it is supposed to occur much more rapidly in small and inbred populations (Wang et al. 1999, but see Glémin 2003). Inbreeding depression should also decrease because mutations of small effect are likely to become fixed due to genetic drift and therefore can no longer cause inbreeding depression (Bataillon and Kirkpatrick 2000). Thus, in populations that have been small for some time, inbreeding load and hence inbreeding depression should decrease, while drift load should increase (Bataillon and Kirkpatrick 2000; Hedrick 2001) (Figure 1). Recent theoretical studies on population subdivision also predict a decrease in inbreeding depression with decreasing size of local populations and decreasing migration rate (Whitlock 2002; Glémin et al. 2003; Roze and Rousset 2004).
Figure 1.—
Expected relationship between parental kinship coefficient and offspring fitness for populations of different size. Large populations have a high inbreeding load, because inbreeding and thus purging of deleterious mutations have rarely happened. Small populations with some history of inbreeding have already lost deleterious mutations of large effect due to inbreeding. Consequently, their inbreeding load is low. On the other hand, drift load is expected to be higher in small populations, and so their outbred offspring are relatively less fit in comparison to those of large populations.
Many empirical studies have found that small populations exhibit reduced fitness due to inbreeding (reviewed in Keller and Waller 2002). However, selection against inbred individuals turns out to eliminate mainly recessive lethal or semilethal mutations; for other detrimentals, purging underlies a stochastic component and is probably not effective enough to reduce inbreeding load and hence inbreeding depression in small and inbred populations (Frankham 1995; Byers and Waller 1999; Miller and Hedrick 2001; Reed et al. 2003; Lienert and Fischer 2004). A number of studies have reported drift load in small populations, most prominently the Florida panther with its kinked tail and poor semen quality (Roelke et al. 1993). Still, studies focusing on population size affecting inbreeding depression and drift load have been unable to estimate them separately (e.g., Ouborg and Van Treuren 1994; van Oosterhout et al. 2000; Rowe and Beebee 2003). It is important to distinguish between the two, because they represent different mechanisms affecting fitness and are expected to depend on population history.
A further mechanism that can decrease mean fitness in small populations arises from genetic incompatibility systems. Many organisms of all five kingdoms have evolved mating systems that assure outbreeding. Self-incompatibility (SI) systems that prevent selfing and to some extent also biparental inbreeding are common in plants (Kao and McCubbin 1996; De Nettancourt 2001). Incompatibility processes involve a recognition step, with complex interactions between pollen and pistil that induce acceptance or rejection of the pollen (De Nettancourt 2001). An encounter of two incompatible types, leading to no offspring, is more likely in small populations. Depending on pollen loads, incompatibility may therefore reduce offspring production. On the other hand, incompatibility systems should prevent inbreeding effects in later life stages.
How can we distinguish between fitness reductions due to inbreeding, genetic drift, and incompatibility in natural populations? The effect of cross-incompatibility on individual fitness is relatively easy to distinguish in plants, if the genetically based incompatibility system causes no seed set after pollination among self-incompatible partners. Reciprocal pairings that fail completely can be interpreted as incompatible. Within-population inbreeding depression can be measured by estimating inbreeding load, the steepness of the slope of log-transformed offspring fitness against the inbreeding coefficient (Keller and Waller 2002). As pedigrees are usually unknown for natural populations, a marker-based estimate of parental relatedness can substitute for the inbreeding coefficient (Ritland 1996). This approach is more sophisticated than the usually applied comparison of self vs. outbred crosses for the estimation of inbreeding load, as it offers the advantage of accounting for differences in levels of biparental inbreeding in different populations. To estimate differences in drift load among natural populations due to population size, and to avoid confusion with inbreeding depression, we suggest a comparison of fitness between equally outbred offspring of populations of varying size.
This study relates inbreeding depression and drift load to population size in the gametophytically self-incompatible, tetraploid plant Ranunculus reptans. A common garden experiment with field-collected rosettes of this species had previously shown that rosettes sampled in small populations produced fewer daughter rosettes and flowers than did rosettes sampled in larger populations (Fischer et al. 2000). We studied 13 populations around Lake Constance, assuming that they had experienced similar population histories and differed mainly in size. We used two estimates of population size, one measured in the field and reflecting current size, and the other based on allelic diversity and reflecting long-term size. R. reptans is known to experience dramatic changes in population size (Peintinger et al. 1997), which led us to predict that drift load will mostly affect populations that have been chronically small rather than currently small. We focused on the following questions: (1) What is the effect of the SI system in populations of different size?, (2) What is the magnitude of inbreeding depression, and which life stages does it affect?, and (3) Do populations of different size differ in drift load?
MATERIALS AND METHODS
Study species:
R. reptans (Ranunculaceae) has a circumpolar distribution, mainly in the temperate to boreal-subarctic zones of Europe, Asia, and North America (Prati and Peintinger 2000). In central Europe, where this study was conducted, R. reptans usually occurs on the shores of prealpine lakes in relatively distinct populations, varying in size from a few square meters to a few thousand square meters. The persistence of these populations is associated with the regular occurrence of floods, because R. reptans is flood tolerant but a poor competitor.
This plant has a SI system, and self-incompatibility is maintained even in populations of very small size (Y. Willi, unpublished results). Studies of the genetic basis of incompatibility in the genus Ranunculus suggest that the species possesses a gametophytic SI system (Lundqvist 1990, 1994; De Nettancourt 2001). Furthermore, the plant grows clonally and nodes may develop roots. Consequently, the fitness of a clonal plant can be estimated by seed production and by clonal growth (Sackville Hamilton et al. 1987); these are the two fitness estimates used in this study. Clonal performance is especially important in R. reptans, because only rooted rosettes survive the annual floods caused by snow melt in May and June, and because in most years there is insufficient time for seed production and seedling establishment.
Plant material:
We used 163 plants that had been collected in spring 2002, derived from 13 R. reptans populations around Lake Constance. At each site, 14 individuals were collected at 5-m intervals along two transects separated by 5 m. The distance between the two transects was decreased to 4 m in four narrow populations. In five populations, the band of R. reptans along the shoreline was so short that we could sample only 8–12 individuals. The number of sampled individuals was not correlated with population size (P > 0.2).
After collection, plants were held indoors in a growth room until the beginning of the crossing experiment. Five original plants died during this propagation phase. In August 2002, we planted two groups of three R. reptans rosettes derived from the original rosette collected in the field into two tubs (17.2 × 12.2 × 5.5 cm). The tubs contained a 1:2 mixture of horticulture soil and sand, with a shallow gravel surface layer to prevent insects from laying eggs. About every 10 days, we treated plants with commercial insecticides, and once, just before crossings began, we added 300 mg of N-P-K fertilizer per tub.
Size of populations:
Population sizes were determined in spring 2003 by measuring the surface area and density of R. reptans aggregations. Surface area was estimated by careful mapping, while densities within aggregations were determined by haphazardly placing 0.25 m2 frames on the ground and counting the number of 5 × 5-cm squares that had at least one rosette with roots. The number of frame counts per aggregation ranged from 3–12, depending on the size of the plot. We defined the end of the population if there was no more than 5 m2 containing R. reptans over a shoreline distance of 100 m.
Allozyme analysis:
Field-collected plants were scored for eight loci of seven enzyme systems: AAT-1 (EC 2.6.1.1), ACON-1 (EC 4.2.1.3), GPI-2 (EC 5.3.1.9), MDH-2 (EC 1.1.1.37), MDH-3, MPI (EC 5.3.1.8), SKD (EC 1.1.1.25), and 6-PGDH (EC 1.1.1.44) according to standard methods (Hebert and Beaton 1993). R. reptans is known to have (2n =) 32 chromosomes. Allozyme studies in the genus Ranunculus suggest that this chromosome number is inherent to tetraploid taxa (Hörandl and Greilhuber 2002). Our zymograms supported this hypothesis and gave evidence for tetrasomic inheritance.
As a measure of genetic diversity, the allelic diversity (Hs) was calculated according to Nei (1973). Hs represented long-term population size under the assumption of mutation-drift balance (Frankham 1996). As a measure of relatedness between two individuals, kinship coefficients were estimated according to Ritland (1996) using the software program SPAGeDi (Hardy and Vekemans 2002). Kinship coefficients were computed only for pairs of individuals within populations, and the outbred reference was a sample within the same population.
Hand pollination:
We produced offspring resulting from random crosses to estimate inbreeding depression and drift load. Each genotype previously collected in the field was crossed with two randomly selected other genotypes from the same population. Thus, we measured the fitness of within-population crosses spanning ranges of relatedness that correspond to random mating. We performed 319 total crosses. Hand pollinations took place over a period of 2 months, from September 29 to November 27, 2002, except for six later crosses among late-blooming genotypes. Anthers from one flower were removed and stroked over the stigmas of the other flower. Crossings between different genotypes were performed reciprocally, so flowers were used as both pollen donors and pollen recipients. We harvested seeds ∼1 month after crossing and counted the number of developed seeds and ovules.
Measurements of offspring performance:
We measured sexual and clonal performance in adult plants of the F1 generation. In May 2003, seed families incubated in gibberellic acid (2 g in 1 liter of water) for 5 days before germinating indoors (16 hr daylight) on a 3:1 mixture of horticulture soil and sand. We rerandomized the locations of trays at weekly intervals.
Six weeks after germination began (June 16–18, 2003), we counted seedlings and haphazardly chose one individual per seed family for planting into a tub (10 × 10 × 11 cm) with a 1:2 mixture of horticulture soil and sand. We distributed tubs in random positions within outdoor beds covered with 50% shade cloth. Plants were watered daily, unless it rained. Checks for survival were performed after 3 days, 2 weeks, and 4 weeks. Of 519 plants, 19 died. As mortality was so low and its estimate was based on only one representative of a seed family, we did not calculate survival. Instead, we subtracted a dead plant from the number of seedlings emerged after germination and replaced it with another representative of the same seed family. Tub positions were rerandomized after 1 month, and after 2 months (August 11–20, 2003) both clonal and sexual reproduction of the one representative of each cross was assessed. We recorded the following parameters: number of rooted rosettes, number of flowers, number of flower buds, number of infructescenses, and fresh biomass (after drying plant surfaces with paper towels). We also scored the proportion of developed seeds of all infructescenses, categorized within two classes (0–50% and >50%) because there was insufficient time to count all undeveloped ovules and seeds.
Multiplicative offspring fitness measures:
Two offspring fitness measures were assessed for each cross, one based on the sexual, the other on the clonal performance of its progeny. Sexual performance was the proportion of ovules that produced seedlings multiplied by the total number of flowers and flower buds produced by the family representative and by a factor representing seed production (× 1 or × 2, for 0–50% seed production, or >50%). The estimate of clonal performance was the proportion of ovules that produced seedlings multiplied by the number of rooted rosettes of the family representative.
Statistical analysis:
In a first stage of analysis, population mean-fitness estimates were regressed against allelic diversity, our measure of long-term population size. Possible causes for the observed relationship between population size and measures of offspring fitness were then explored, in particular, differences in cross-compatibility, inbreeding depression, and drift load.
We analyzed variation in cross-compatibility by regressing the proportion of incompatible crosses (reciprocal crosses that produced no developed seed) within a population against allelic diversity. In total, we counted 15 incompatible crosses. These incompatible crosses were excluded from analyses investigating effects of inbreeding and drift load.
Inbreeding depression in each population was estimated as δ = 1 − e−B×F (Keller and Waller 2002). The inbreeding coefficient, F, reflects the degree of inbreeding in a population. As an estimate of F, we used the mean parental kinship coefficient of all randomly performed crosses (excluding incompatible crosses) within each population. Inbreeding load, B, is the slope of log-transformed offspring fitness against parental kinship coefficient. To calculate B, we first tested for differences among populations in a linear relationship between parental kinship coefficient and offspring performance with a model that included kinship coefficient, populations, and their interaction (GLM procedure in SAS; SAS Institute 1999). As the two dependent variables of sexual and clonal offspring performance were strongly correlated (r = 0.866, N = 304, P < 0.0001), we tested effects of independent variables with a multivariate analysis of covariance (MANCOVA). Second, we performed linear regressions between parental kinship coefficient and offspring performance for each population to obtain population-specific slopes B.
To estimate differences in drift load among populations due to differences in long-term population size and to exclude confusion with inbreeding depression, we compared mean performance between equally outbred offspring. The range of parental relatedness used to calculate performance of outbred offspring was determined by the smallest range of kinship coefficients for which all populations had at least five crosses (kinship coefficient: 0.04–0.18).
At each step of the analysis, we also tested four life-stage variables to determine at which stage differences arose: seed set in the parental generation; germination rate; F1 adult growth performance (the first component from a principal component analysis, PCA, on the number of rooted rosettes, the sum of flowers, buds, and infructescences, and wet biomass); and F1 seed production. The first eigenvector of the PCA explained 87% of the variance in the three adult fitness components (loadings: flowers = 0.579, rooted rosettes = 0.577, wet biomass = 0.576).
We did not adjust α for multiple comparisons because we adopted a hierarchical approach, first testing whether population mean performance varies with allelic diversity and then exploring mechanisms contributing to that relationship. We log transformed measures of population size and fitness except for proportions, which underwent an angular transformation (Sokal and Rohlf 1995), and offspring seed production, which remained untransformed. Fitness measures of reciprocal crosses were averaged and entered the analysis as cross means.
RESULTS
Population size and mean fitness:
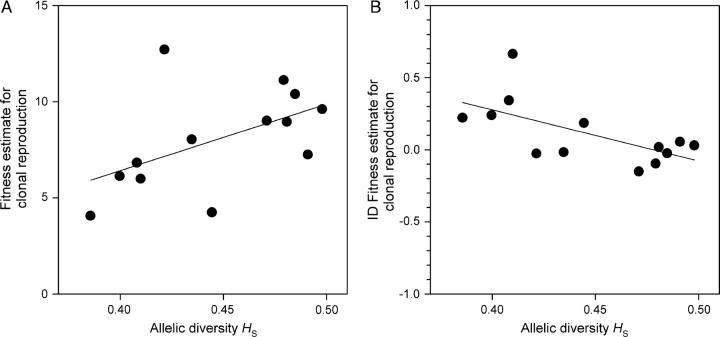
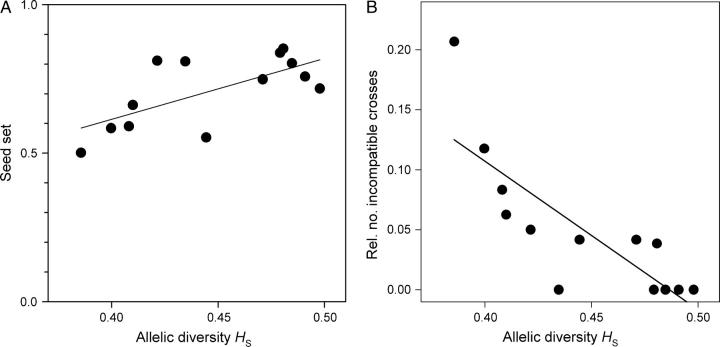
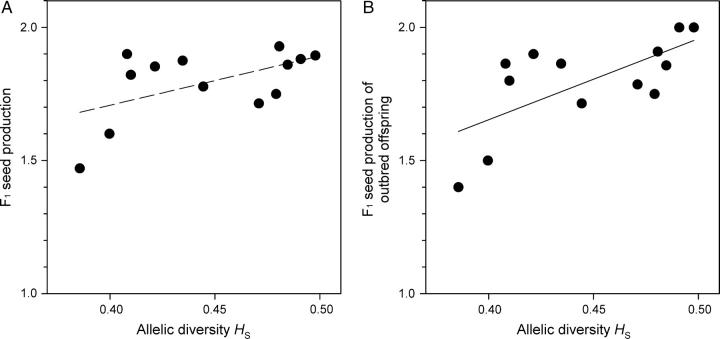
Mean clonal performance of populations was positively correlated with allelic diversity reflecting long-term population size (Table 1, Figure 2A), mostly because seed set was significantly lower in long-term small populations (Figure 3A). Furthermore, there was a tendency for reduced seed production in the offspring (Table 1, Figure 4A). Mean sexual performance was not related to allelic diversity (Table 1), indicating that one of its components, flower production, is not negatively affected by long-term small size. Although current population size was correlated with allelic diversity (r = 0.707, N = 13, P = 0.0069), current size did not explain performance variation among populations (P > 0.3 for sexual and clonal performance and four life-stage fitness components). Population surfaces varied between 38 m2 and 2182 m2, whereas population sizes, the product of surface area and plant density, varied between 5.2 m2 and 475.4 m2.
TABLE 1.
Linear relationship between allelic diversity, a measure of long-term population size, and population mean-fitness estimates
| Response variable
|
||||
|---|---|---|---|---|
| b | t | R2 | P | |
| Sexual performance: 4.18 | 1.53 | 0.18 | 0.1532 | |
| Clonal performance: 5.70 | 2.31 | 0.33 | 0.0413 | |
| Seed set | 3.01 | 3.17 | 0.48 | 0.0089 |
| Germination rate | 1.48 | 1.72 | 0.21 | 0.1137 |
| PC1-adult performance | 3.13 | 1.04 | 0.09 | 0.3187 |
| Seed production of offspring | 1.85 | 2.15 | 0.30 | 0.0547 |
Allelic diversity is considered a measure of long-term population size under mutation-drift balance. Underlining indicates P-values < 0.1 (N = 13).
Figure 2.—
Relationship between allelic diversity and (A) population means of clonal offspring fitness (untransformed data) and (B) inbreeding depression ID in clonal fitness after the exclusion of self-incompatible crosses (N = 13, values based on transformed data).
Figure 3.—
Relationship between allelic diversity and (A) population mean seed set (untransformed data) and (B) relative number of incompatible crosses (N = 13). The SI system leads to a reduced number of available mating partners in long-term small populations.
Figure 4.—
Relationship between allelic diversity and (A) population means in offspring seed production (untransformed data) and (B) drift load in offspring seed production after the exclusion of self-incompatible crosses (N = 13, means of untransformed data). Long-term small populations have a higher drift load.
Cross-compatibility:
Long-term small populations had significantly more reciprocal crosses that produced no seeds (R2 = 0.65, N = 13, P = 0.0008, Figure 3B). This result indicates low S-allele diversity in long-term small populations.
Inbreeding, inbreeding load, and inbreeding depression:
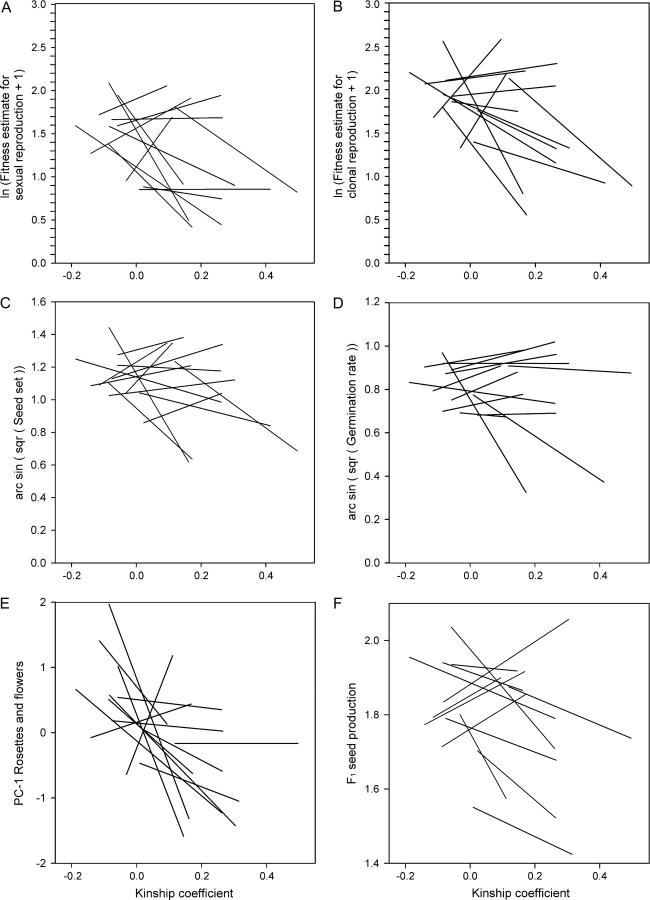
The linear model showed that populations of R. reptans differed significantly in multiplicative fitness estimates of sexual and clonal reproduction (Table 2, Figure 5) (incompatible crosses excluded). Furthermore, the significant interaction between population and kinship coefficient revealed that some populations exhibited negative relationships between parental kinship coefficient and the two fitness estimates, while others did not.
TABLE 2.
MANCOVA examining effects of population, kinship coefficient between plants crossed, and their interaction on two estimates of fitness, sexual and clonal offspring performance
|
F-ratio from univariate tests
|
||||||
|---|---|---|---|---|---|---|
| Source of variation | Error term | d.f. | Wilks' F | P | Sexual performance |
Clonal performance |
| Population | Pooled error | 24, 554 | 2.75 | <0.0001 | 3.12*** | 2.41** |
| Kinship coefficient | Population × kinship coefficient | 2, 11 | 0.64 | 0.5477 | 1.39 | 0.98 |
| Population × kinship coefficient | Pooled error | 24, 554 | 2.02 | 0.0029 | 2.00* | 2.09* |
Significance of univariate tests is indicated (*P < 0.05, **P < 0.01, ***P < 0.001; N = 304; R2 = 0.273 for sexual performance, and R2 = 0.271 for clonal performance).
Figure 5.—
Fitness estimates for sexual and clonal reproduction of R. reptans offspring (A and B) and four life-stage fitness components (C–F) regressed on kinship coefficient between the parents. Results from the 13 populations are represented by separate lines.
The slope of offspring performance against kinship coefficient, reflecting inbreeding load, was not related to population allelic diversity (Table 3). This runs counter to the expectation that inbreeding load is purged from smaller populations. On the basis of inbreeding load, we calculated expressed inbreeding depression considering the average relatedness between compatible individuals of the populations. Populations with a low allelic diversity, reflecting long-term small population size, had higher inbreeding levels; mean kinship coefficient of all randomly performed, compatible crosses showed a negative linear relationship with allelic diversity (R2 = 0.49, N = 13, P = 0.0081). This is an inevitable outcome of random mating and reduced allelic diversity in small populations. These long-term small populations suffered from more inbreeding depression in clonal performance and in seed production of F1 offspring (Table 3, Figure 2B).
TABLE 3.
Linear relationship between allelic diversity and population inbreeding load, inbreeding depression, and drift load
| Inbreeding load B
|
Inbreeding depression δ
|
Drift load
|
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Response variable: t | R2 | P | t | R2 | P | t | R2 | P | ||
| Sexual performance: −0.35 | 0.01 | 0.7302 | −1.30 | 0.13 | 0.2196 | 0.87 | 0.06 | 0.4045 | ||
| Clonal performance: −0.91 | 0.07 | 0.3824 | −2.76 | 0.41 | 0.0187 | 0.96 | 0.08 | 0.3587 | ||
| Seed set | −1.30 | 0.13 | 0.2213 | −1.58 | 0.18 | 0.1429 | 1.08 | 0.10 | 0.3032 | |
| Germination rate | −0.55 | 0.03 | 0.5926 | −1.57 | 0.18 | 0.1458 | 1.23 | 0.12 | 0.2456 | |
| PC1-adult performance | −0.44 | 0.02 | 0.6715 | −1.71 | 0.21 | 0.1159 | 1.05 | 0.09 | 0.3178 | |
| Seed production of offspring |
−0.69 | 0.04 | 0.5023 | −2.97 | 0.45 | 0.0127 | 3.04 | 0.46 | 0.0113 | |
Inbreeding load, B, is the slope of log-transformed offspring fitness of compatible within-population crosses against parental kinship coefficient, calculated for each population. Inbreeding depression in each population is δ = 1 − e−B×F (Keller and Waller 2002), where F represents mean relatedness of all randomly performed crosses (incompatible crosses excluded). Differences in drift load are based on the comparison of mean fitness between equally outbred offspring. Fitness estimates are clonal and sexual offspring performance of crosses within populations, with results for the separate life-stage fitness components presented in italics. Underlining indicates P-values < 0.1 (N = 13).
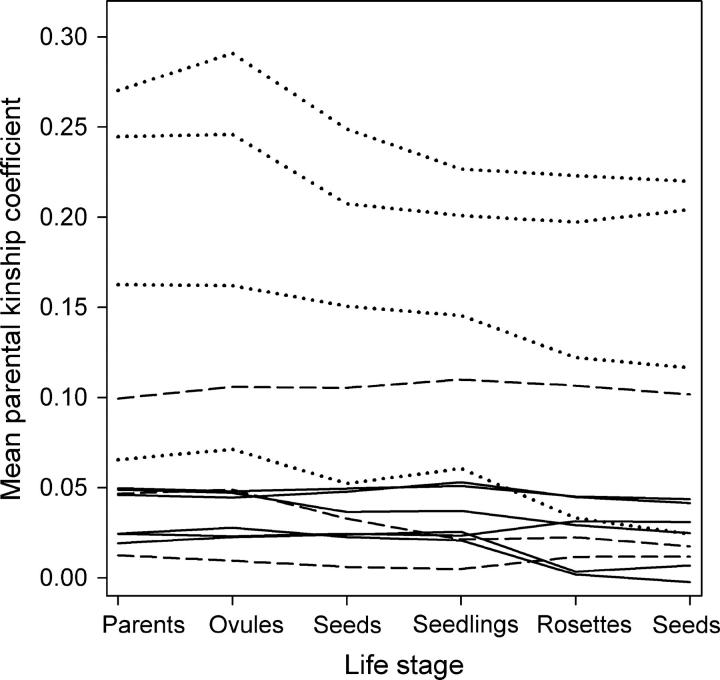
The effect of inbreeding depression was to create selection favoring less inbred offspring. This is visible in Figure 6 that shows the average parental relatedness of surviving offspring through a series of life stages from the parental generation to seed production by their F1 offspring. A significant effect of life stage in repeated measures analysis of mean parental kinship coefficient reflects the overall advantage of less inbred offspring (F5,55 = 6.02, Greenhouse-Geisser adjusted P = 0.0113). The effect of allelic diversity indicates that populations that were larger over the long term had higher kinship coefficients among crosses at all life stages (F1,11 = 10.64, P = 0.0076). The interaction term shows that the bias favoring less inbred offspring was greater in small than in large populations (F5,55 = 4.79, Greenhouse-Geisser adjusted P = 0.0236).
Figure 6.—
Mean parental kinship coefficient of all surviving individuals at six life stages of R. reptans. The six life stages are parents, ovules within crossed flowers, developed seeds, germinated seedlings, rooted rosettes, and seeds produced by the F1 offspring. The 13 populations are represented by separate lines: dotted lines for long-term small populations (Hs: 0.386–0.410), dashed lines for medium-sized populations (Hs: 0.421–0.444), and solid lines for large populations (Hs: 0.471–0.498). (The first two classes of 7 populations include the 6 populations with the smallest size measured in the field.) Small populations had on average the highest kinship coefficients between randomly chosen parents, and, after crossing, the SI system and selection acted most strongly against inbred crosses, leading to a decrease of mean parental kinship coefficient in adult offspring.
Drift load:
Drift load, defined as a decline in mean population performance of outbred offspring in small populations, was not detected for the two measures of sexual and clonal fitness (Table 3). However, mean seed production of F1 offspring was significantly lower in long-term small populations, suggesting drift load for female fertility (Figure 4B).
DISCUSSION
We found a threefold genetic Allee effect that can explain the reduced fitness observed in long-term small populations of R. reptans. Our simultaneous estimation of fitness consequences of inbreeding, genetic drift, and cross-compatibility in natural populations of different sizes revealed that the three processes simultaneously erode individual fitness of plants of small populations.
Cross-compatibility:
First, cross-compatibility was lower for long-term small populations, possibly because plants in small populations lack compatible partners carrying different S alleles. However, as negative frequency-dependent selection acts in favor of S-allele diversity, effective population size must be very small to enable drift to eliminate S alleles (Byers and Meagher 1992). For these small populations, Byers and Meagher (1992) predict lower seed set of individuals whose genotypes are more common. In fact, field studies of plants with self-incompatible mating systems find that seed set declines with population size only when the number of individuals drops below 10 (Luijten et al. 2000), 50 (Fischer et al. 2003), and 250 reproductive individuals (Widén 1993). Under these conditions a complete breakdown of the self-incompatibility system may even occur (Vekemans et al. 1998). So far, empirical studies do not show a trend toward the breakdown of self-incompatibility in small populations, perhaps due to accumulated deleterious mutations at loci linked to the S locus (Glémin et al. 2001).
Inbreeding, inbreeding load, and inbreeding depression:
Second long-term small populations experienced reduced clonal fitness due to inbreeding even after incompatible crosses were excluded from the analysis. Higher inbreeding depression in clonal fitness and in seed production (through open pollination in the common garden) in long-term small populations resulted from the higher degree of relatedness between parental plants. In large populations there was hardly any inbreeding, and therefore inbreeding depression was negligible.
The result of increased inbreeding and an associated fitness decline in long-term small populations stands in contrast to theoretical predictions about inbreeding in connection with incompatibility and tetraploidy. Incompatibility systems are thought to influence inbreeding depression in two opposing ways: the level of inbreeding is reduced if close relatives are prevented from reproducing with each other, while the lack of mating among relatives prevents purging over the long term (Lande and Schemske 1985). Our results suggest that self-incompatibility does not effectively prevent inbreeding among individuals in small populations, and therefore inbreeding depression occurs. On the other hand, we found no evidence that purging has been quantitatively important in small populations, perhaps because inbreeding is too infrequent for purging to happen.
Polyploidy is expected to decrease the chance of suffering from inbreeding as well (Husband and Schemske 1997). Since each locus has four alleles, all four must be identical for a complete recessive to be exposed (Frankham et al. 2002). Moreover, biparental inbreeding in autotetraploids leads to a slower decline of heterozygotes than in diploids (Bever and Felber 1992). The rate at which heterozygosity is lost depends on the extent to which chromosomes and chromatids segregate randomly during anaphase. As inbreeding leads to a slower loss of heterozygosity in polyploids, and the expression of (partially) recessive deleterious alleles is therefore rarer, equilibrium inbreeding depression is lower in polyploids than in diploids (but see Ronfort 1999). In line with our results, another study of a tetraploid plant has shown increased inbreeding in small populations and decreased values for some fitness components (Buza et al. 2000).
Our result of independence of inbreeding load from population size suggests that the predicted decline in inbreeding depression through purging may never happen in long-term small populations or may require an extremely long period of time. As noted above, this is especially likely in a tetraploid and self-incompatible species. Empirical studies indicate that purging is an inconsistent force and is ineffective in reducing inbreeding depression (Byers and Waller 1999, but see Crnokrak and Barrett 2002). Glémin (2003) argues that purging can result from two different processes: purging by nonrandom mating and purging through small population size. His models indicate that the first process is effective at eliminating deleterious mutations regardless of their dominance level, whereas only highly recessive mutations can be purged through small population size. Keller et al. (2002) hypothesize—in the context of substantial inbreeding depression found in Darwin's finches—that gene flow could lead to the reintroduction of deleterious recessive alleles that may have been purged in one population but not in a neighboring one. Even if purging occurs, overdominance could still cause inbreeding depression (Wright 1977).
A consequence of both self-incompatibility and inbreeding depression is that inbred offspring are eliminated, especially at the seed set stage. We found that long-term small populations had fewer inbred individuals in later life stages than expected on the basis of random mating. Selection against the most inbred individuals may thus maintain allelic diversity.
Drift load:
Third, the comparison between outcrossed offspring of the different populations revealed drift load at the late life stage of offspring seed production, yet multiplicative fitness estimates of clonal and sexual reproduction were not affected. Pollination in the common garden experiment was accomplished by accident as plants were randomly visited by insects, so reduced seed production in the offspring of long-term small populations must stem from reduced female fecundity.
It is surprising that long-term small populations suffered from drift load at the same life stage of offspring seed production. One expects the accumulation of deleterious mutations to occur randomly, affecting different populations at different life stages and in different traits. A possible explanation for the pattern of reduced fecundity is the self-incompatibility system: Bernacchi and Tanksley (1997) showed that several floral traits involved in pollination biology were linked to the S locus in Lycopersicon hirsutum. On the other hand, loci linked to the S locus are expected to have an increased mutation load, which is higher in small than in large populations (Glémin et al. 2001). Hence, the observed reduction in fecundity may be caused by the sheltering of deleterious alleles at loci coding for female traits, which are linked to the S locus.
It is noteworthy that the pattern of reduced genetic variation in small populations was revealed by sampling at a standard spatial scale in populations of all sizes. Differences among populations are therefore likely to reflect real differences in processes occurring within these populations, and not simply because smaller areas were sampled in smaller populations. Our approach is therefore conservative in comparison with random sampling of populations. Furthermore, our method of estimating inbreeding depression and drift load based on markers—instead of by comparing selfed and outcrossed offspring—has several advantages. First, it is the only reasonable approach for self-incompatible organisms. Second, it minimizes assumptions about the relationship between relatedness and offspring fitness, because the range of parental relatedness that is studied is the one important in the natural population. Third, our data show that convincing results are possible even though a marker-based approach introduces its own sampling variance.
Evolutionary implications:
Our results are especially interesting in the context of the evolution of mating systems. In contrast with small populations of a selfing species, those of a self-incompatible species suffer from a threefold genetic Allee effect. Self-incompatibility causes reduced mate availability, and yet biparental inbreeding is still not prevented by the SI system. As inbreeding load is not purged, inbreeding depression reduces offspring fitness. Finally, drift load causes a decline in female fertility. A prerequisite for the evolution of self-incompatibility seems to be large population size. Once this mating type dominates a population, it is very unlikely to break down even when the population becomes small because of the high genetic load it implies (Glémin et al. 2001). A recent study that estimated inbreeding load and drift load in the selfing species Gentianella germanica found that small populations suffered from drift load whereas larger populations had a tendency to suffer from both drift and inbreeding load (Paland and Schmid 2003). Purging must have eliminated unfixed load in this selfing species.
Conservation implications:
Simulation studies show that both inbreeding and drift load can lead to the decline and extinction of populations (Lynch et al. 1995). Furthermore, there is increasing evidence from studies in the wild that low genetic diversity, inbreeding depression, and drift load can substantially erode the prospects of small populations (Newman and Pilson 1997; Saccheri et al. 1998; Ahlroth et al. 2003). Our study indicates that several genetic Allee effects can simultaneously impact small populations of self-incompatible species, possibly causing negative population growth rates (Fischer and Matthies 1998). At that stage, the conservation of these populations is likely to depend on genetic restoration efforts and the introduction of plants from other populations.
Acknowledgments
We thank Susan Hoebee, Rolf Holderegger, Burgi Liebst, Uli Reyer, Sandy Röthlisberger, and Jakob Schneller for an introduction to allozyme electrophoresis, and Daniela Lang, Regula Langenauer, and Evelyn Underwood for help in the field. Esther Glaus gave support in harvesting and counting seeds. Josh Bizozzero, Marcel Zefferer, Claudia Kübler, Vanessa Summa, Rico Tuor, Gillianne Vergnerie, and Andrea Weidt transplanted seedlings. Simone Käppeli, Daniela Lang, Susanne Müller, Sabine Rahm, Romain Scalone, Gillianne Vergnerie, Anton Willi, Claudia Willi, and Edith Willi helped measuring offspring. Many thanks go to B. Rosemary Grant for fruitful discussions, and to Lukas Keller and Christoph Vorburger for constructive comments on earlier drafts. This work was supported by the Swiss National Science Foundation (NF-grants 31-56 809.99 and 31-67876.02) and the Institute of Environmental Sciences, University of Zürich.
References
- Ahlroth, P., R. V. Alatalo, A. Holopainen, T. Kumpulainen and J. Suhonen, 2003. Founder population size and number of source populations enhance colonization success in waterstriders. Oecologia 137: 617–620. [DOI] [PubMed] [Google Scholar]
- Bataillon, T., and M. Kirkpatrick, 2000. Inbreeding depression due to mildly deleterious mutations in finite populations: size does matter. Genet. Res. 75: 75–81. [DOI] [PubMed] [Google Scholar]
- Bernacchi, D., and S. D. Tanksley, 1997. An interspecific backcross of Lycopersicon esculentum × L. hirsutum: linkage analysis and a QTL study of sexual compatibility factors and floral traits. Genetics 147: 861–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bever, J. D., and F. Felber, 1992. The theoretical population genetics of autopolyploidy. Oxf. Surv. Evol. Biol. 8: 185–217. [Google Scholar]
- Buza, L., A. Young and P. Thrall, 2000. Genetic erosion, inbreeding and reduced fitness in fragmented populations of the endangered tetraploid pea Swainsona recta. Biol. Conserv. 93: 177–186. [Google Scholar]
- Byers, D. L., and T. R. Meagher, 1992. Mate availability in small populations of plant species with homomorphic sporophytic self-incompatibiliy. Heredity 68: 353–359. [Google Scholar]
- Byers, D. L., and D. M. Waller, 1999. Do plant populations purge their drift load? Effects of population size and mating history on inbreeding depression. Annu. Rev. Ecol. Syst. 30: 479–513. [Google Scholar]
- Charlesworth, D., M. T. Morgan and B. Charlesworth, 1993. Mutation accumulation in finite outbreeding and inbreeding populations. Genet. Res. 61: 39–56. [Google Scholar]
- Crnokrak, P., and S. C. H. Barrett, 2002. Perspective: purging the genetic load: a review of the experimental evidence. Evolution 56: 2347–2358. [DOI] [PubMed] [Google Scholar]
- De Nettancourt, D., 2001 Incompatibility and Incongruity in Wild and Cultivated Plants, Ed. 2. Springer-Verlag, Berlin.
- Fischer, M., and D. Matthies, 1998. Effects of population size on performance in the rare plant Gentianella germanica. J. Ecol. 86: 195–204. [Google Scholar]
- Fischer, M., M. van Kleunen and B. Schmid, 2000. Genetic Allee effects on performance, plasticity, and developmental stability in a clonal plant. Ecol. Lett. 3: 530–539. [Google Scholar]
- Fischer, M., M. Hock and M. Paschke, 2003. Low genetic variation reduces cross-compatibility and offspring fitness in populations of a narrow endemic plant with a self-incompatibility system. Conserv. Genet. 4: 325–336. [Google Scholar]
- Frankham, R., 1995. Conservation genetics. Annu. Rev. Genet. 29: 305–327. [DOI] [PubMed] [Google Scholar]
- Frankham, R., 1996. Relationship of genetic variation to population size in wildlife. Conserv. Biol. 10: 1500–1508. [Google Scholar]
- Frankham, R., J. D. Ballou and D. A. Briscoe, 2002 Introduction to Conservation Genetics. Cambridge University Press, Cambridge, UK.
- Glémin, S., 2003. How are deleterious mutations purged? Drift versus nonrandom mating. Evolution 57: 2678–2687. [DOI] [PubMed] [Google Scholar]
- Glémin, S., T. Bataillon, J. Ronfort, A. Mignot and I. Olivieri, 2001. Inbreeding depression in small populations of self-incompatible plants. Genetics 159: 1217–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glémin, S., J. Ronfort and T. Bataillon, 2003. Patterns of inbreeding depression and architecture of the load in subdivided populations. Genetics 165: 2193–2212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardy, O. J., and X. Vekemans, 2002. SPAGeDi: a versatile computer program to analyse spatial genetic structure at the individual or population levels. Mol. Ecol. Notes 2: 618–620. [Google Scholar]
- Hebert, P. D. N., and M. J. Beaton, 1993 Methodologies for Allozyme Analysis Using Cellulose Acetate Electrophoresis: A Practical Handbook. Helena Laboratories, Beaumont, TX.
- Hedrick, P. W., 2001. Conservation genetics: Where are we now? Trends Ecol. Evol. 16: 629–636. [Google Scholar]
- Hörandl, E., and J. Greilhuber, 2002. Diploid and autotetraploid sexuals and their relationships to apomicts in the Ranunculus cassubicus group: insights from DNA content and isozyme variation. Plant Syst. Evol. 234: 85–100. [Google Scholar]
- Husband, B. C., and D. W. Schemske, 1997. The effect of inbreeding in diploid and tetraploid populations of Epilobium angustifolium (Onagraceae): implications for the genetic basis of inbreeding depression. Evolution 51: 737–746. [DOI] [PubMed] [Google Scholar]
- Kao, T.-H., and A. G. McCubbin, 1996. How flowering plants discriminate between self and non-self pollen to prevent inbreeding. Proc. Natl. Acad. Sci. USA 93: 12059–12065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller, L. F., and D. M. Waller, 2002. Inbreeding effects in wild populations. Trends Ecol. Evol. 17: 230–241. [Google Scholar]
- Keller, L. F., P. R. Grant, B. R. Grant and K. Petren, 2002. Environmental conditions affect the magnitude of inbreeding depression in survival of Darwin's finches. Evolution 56: 1229–1239. [DOI] [PubMed] [Google Scholar]
- Kimura, M., T. Maruyama and J. F. Crow, 1963. The mutation load in small populations. Genetics 48: 1303–1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lande, R., and D. W. Schemske, 1985. The evolution of self-fertilization and inbreeding depression in plants. I. Genetic models. Evolution 39: 24–40. [DOI] [PubMed] [Google Scholar]
- Lienert, J., and M. Fischer, 2004. Experimental inbreeding reduces seed production and germination independent of fragmentation of populations of Swertia perennis. Basic Appl. Ecol. 5: 43–52. [Google Scholar]
- Luijten, S. H., A. Dierick, J. Gerard, B. Oostermeijer, L. E. L. Raijmann et al., 2000. Population size, genetic variation, and reproductive success in a rapidly declining, self-incompatible perennial (Arnica montana) in The Netherlands. Conserv. Biol. 14: 1776–1787. [DOI] [PubMed] [Google Scholar]
- Lundqvist, A., 1990. The complex S-gene system for control of self-incompatibility in the buttercup genus Ranunculus. Hereditas 113: 29–46. [Google Scholar]
- Lundqvist, A., 1994. The self-incompatibility system in Ranunculus repens (Ranunculaceae). Hereditas 120: 151–157. [Google Scholar]
- Lynch, M., and W. Gabriel, 1990. Mutation load and the survival of small populations. Evolution 44: 1725–1737. [DOI] [PubMed] [Google Scholar]
- Lynch, M., J. Conery and R. Bürger, 1995. Mutation accumulation and the extinction of small populations. Am. Nat. 146: 489–518. [Google Scholar]
- Miller, P. S., and P. W. Hedrick, 2001. Purging of inbreeding depression and fitness decline in bottlenecked populations of Drosophila melanogaster. J. Evol. Biol. 14: 595–601. [Google Scholar]
- Nei, M., 1973. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 70: 3321–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman, D., and D. Pilson, 1997. Increased probability of extinction due to decreased genetic effective population size: experimental populations of Clarkia pulchella. Evolution 51: 354–362. [DOI] [PubMed] [Google Scholar]
- Ouborg, N. J., and R. Van Treuren, 1994. The significance of genetic erosion in the process of extinction. IV. Inbreeding load and heterosis in relation to population size in the mint Salvia pratensis. Evolution 48: 996–1008. [DOI] [PubMed] [Google Scholar]
- Paland, S., and B. Schmid, 2003. Population size and the nature of drift load in Gentianella germanica. Evolution 57: 2242–2251. [DOI] [PubMed] [Google Scholar]
- Peintinger, M., I. Strang, M. Dienst and C. Meyer, 1997. Veränderung der gefährdeten Strandschmielengesellschaft am Bodensee zwischen 1989 und 1994. Zeitschrift für Ökologie und Naturschutz 6: 75–81. [Google Scholar]
- Prati, D., and M. Peintinger, 2000. Biological flora of Central Europe: Ranunculus reptans L. Flora 195: 135–145. [Google Scholar]
- Reed, D. H., E. H. Lowe, D. A. Briscoe and R. Frankham, 2003. Inbreeding and extinction: effects of rate of inbreeding. Conserv. Genet. 4: 405–410. [Google Scholar]
- Ritland, K., 1996. Estimators for pairwise relatedness and individual inbreeding coefficients. Genet. Res. 67: 175–185. [Google Scholar]
- Roelke, M. E., J. S. Martenson and S. J. O'Brien, 1993. The consequences of demographic reduction and genetic depletion in the endangered Florida panther. Curr. Biol. 3: 340–350. [DOI] [PubMed] [Google Scholar]
- Ronfort, J., 1999. The mutation load under tetrasomic inheritance and its consequences for the evolution of the selfing rate in autotetraploid species. Genet. Res. 74: 31–42. [Google Scholar]
- Rowe, G., and T. J. C. Beebee, 2003. Population on the verge of a mutational meltdown? Fitness costs of drift load for an amphibian in the wild. Evolution 57: 177–181. [DOI] [PubMed] [Google Scholar]
- Roze, D., and F. Rousset, 2004. Joint effects of self-fertilization and population structure on mutation load, inbreeding depression and heterosis. Genetics 167: 1001–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saccheri, I., M. Kuussaari, M. Kankare, P. Vikman, W. Fortelius et al., 1998. Inbreeding and extinction in a butterfly metapopulation. Nature 392: 491–494. [Google Scholar]
- Sackville Hamilton, N. R., B. Schmid and J. L. Harper, 1987. Life-history concepts and the population biology of clonal organisms. Proc. R. Soc. Lond. Ser. B 232: 35–57. [Google Scholar]
- SAS Institute, 1999 SAS OnlineDoc, Version 8. SAS Institute, Cary, NC.
- Sokal, R. R., and F. J. Rohlf, 1995 Biometry, Ed 3. W.H. Freeman, New York.
- van Oosterhout, C., W. G. Zijlstra, M. K. van Heuven and P. M. Brakefield, 2000. Inbreeding depression and drift load in laboratory metapopulations of the butterfly Bicyclus anynana. Evolution 54: 218–225. [DOI] [PubMed] [Google Scholar]
- Vekemans, X., M. H. Schierup and F. B. Christiansen, 1998. Mate availability and fecundity selection in multi-allelic self-incompatiblility systems in plants. Evolution 52: 19–29. [DOI] [PubMed] [Google Scholar]
- Waller, D. M., 1993 The statics and dynamics of mating system evolution, pp. 97–117 in The Natural History of Inbreeding and Outbreeding, edited by N. W. Thornhill. University of Chicago Press, Chicago.
- Wang, J., W. G. Hill, D. Charlesworth and B. Charlesworth, 1999. Dynamics of inbreeding depression due to deleterious mutations in small populations: mutation parameters and inbreeding rate. Genet. Res. 74: 165–178. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., 2000. Fixation of new alleles and the extinction of small populations: drift load, benficial alleles, and sexual selection. Evolution 54: 1855–1861. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., 2002. Selection, load and inbreeding depression in a large metapopulation. Genetics 160: 1191–1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widén, B., 1993. Demographic and genetic effects on reproduction as related to population size in a rare, perennial herb, Senecio integrifolius (Asteraceae). Biol. J. Linn. Soc. 50: 179–195. [Google Scholar]
- Wright, S., 1977 Evolution and the Genetics of Populations, Vol. 3: Experimental Results and Evolutionary Deductions. University of Chicago Press, Chicago.