Abstract
Linkage disequilibrium mapping has been used extensively in medical and evolutionary genetics to map causal polymorphisms within genes associated with disease status or phenotypic variation for a trait. However, the initial findings of most nonhuman studies have not been replicated in subsequent studies, due in part to false positives, as well as additional factors that can render true positives unreplicable. These factors may be more severe when the initial study is performed using an experimental population of organisms reared under controlled lab conditions. We demonstrate that despite considerable phenotypic differences for wing shape between a lab-reared experimental population and a wild-caught cohort of Drosophila melanogaster, an association between a putative regulatory polymorphism in Egfr and wing shape can be replicated. These results are discussed both within the framework of future association-mapping studies and within the context of the evolutionary dynamics of alleles in populations.
ONE of the primary goals of evolutionary genetics is to explore the characteristics of segregating polymorphisms that contribute to standing genetic variation for phenotypes. The dissection of the genetic architecture of trait variation is an important step in understanding the evolutionary response for these phenotypes. To understand the genetic architecture we must examine several aspects of the genetic contribution to traits, such as the number of loci responsible, the distribution of their effects, their frequency in wild populations, and how they interact with one another and the environment (Barton and Turelli 1989; Mackay 2001; Barton and Keightley 2002). Recent advances in molecular biology and statistical methodology have facilitated the mapping of these quantitative trait loci (QTL) by linkage to polymorphic markers, in both evolutionary and agriculturally relevant systems (Flint and Mott 2001; Mackay 2001). While the mapping of QTL has provided estimates of the number and distribution of genetic effects involved with trait variation, it does not have the resolution to map the actual polymorphisms responsible, which is required for estimation of allele frequencies, as well as functional verification and characterization (Flint and Mott 2001). Furthermore, a number of studies have demonstrated that some QTL effects do not resolve to single polymorphisms and may be due to the summation of several genetic effects in linkage disequilibrium (Podolin et al. 1998; Legare et al. 2000; Sawamura et al. 2004).
Another promising approach that has gained prominence is association mapping. Unlike QTL mapping, which experimentally derives linkage disequilibrium and then utilizes recombination to break it down, association mapping takes advantage of the long-term effects of demography and recombination to examine patterns of linkage disequilibrium (LD) between polymorphic sites and trait variation. This allows fine-scale resolution of genetic effects, limited by the extent of regional LD in the population of study. This approach has been used extensively to study human diseases and has also been used to examine quantitative traits of interest such as bristle number (Lai et al. 1994; Long et al. 1998; Robin et al. 2002), immune response (Lazzaro et al. 2004), cryptic variation for photoreceptor determination (Dworkin et al. 2003), heart rate (Nikoh et al. 2004), and wing shape (Palsson and Gibson 2004) in Drosophila melanogaster, as well as agriculturally relevant traits such as flowering time in maize (Thornsberry et al. 2001). In species such as D. melanogaster, where LD usually breaks down rapidly, on the order of 300–500 bp, it may be possible to map the causative polymorphisms (see Dworkin et al. 2003 and Palsson and Gibson 2004 for putative examples).
While the successes of LD mapping are notable, there is evidence that some of the initial significant associations observed in human genetic studies have in fact been false positives, possibly due to artifactual effects of population structure, sampling effects, and Beavis effects (Beavis 1994; Ioannidis et al. 2001). Well-studied associations, such as that observed between prostate cancer and the androgen receptor, have failed to be replicated in subsequent systematic studies (Freedman et al. 2005). In addition, it is still unclear what, if any, impact interpopulation variation for allele frequencies and for modifier alleles will have on genotype-phenotype associations. In a meta-analysis of gene-disease associations across human ethnic groups, there was little evidence for population effects (Ioannidis et al. 2004). However, both intra- and interlocus effects modulate the association between flowering-time genes and life-history traits in populations of Arabidopsis (Caicedo et al. 2004; Stinchcombe et al. 2004). Thus, it is still not clear what factors are most important for distinguishing true associations between genotype and phenotype and for subsequent confirmation.
In model experimental systems the problem of replication may be more severe, given that the conditions used to assess the initial association may in fact reduce the likelihood of successful replication. For instance, in many genetically tractable organisms, individuals from the wild are brought into the lab, and the genetic region of interest is made isogenic through either severe inbreeding (Dworkin et al. 2003) or chromosomal extraction (De Luca et al. 2003). Given that inbreeding changes the genetic and phenotypic variation of traits (Coyne and Beecham 1987; see Whitlock and Fowler 1999 for review) the use of inbred lines may result in associations between polymorphisms and phenotypes in the context of a genetic makeup that is improbable in nature. Furthermore it is not known if inbreeding changes the additive genetic variance via the fixation of rare alleles or by altering the allele frequencies of common polymorphisms (Falconer and Mackay 1996). Thus the effects of inbreeding could potentially render a true-positive association undetectable in a wild population.
Organisms raised in the lab are often reared under uniform environmental conditions, reducing random variation and restricting analysis to a small space of the norm of reaction. As well, with genetically tractable organisms it is possible to produce multiple individuals with identical genotypes that can further increase the precision of genotypic estimates. While these above two factors will augment the power to detect associations between genotype and phenotype, by increasing the ratio of genetic to environmental variance, an association detected in the lab may not be replicable in natural populations, unless it accounts for a very large percentage of the phenotypic variation.
Previously we demonstrated an association between a number of common, synonymous substitutions in the Epidermal growth factor receptor (Egfr) and cryptic variation for photoreceptor determination in D. melanogaster (Dworkin et al. 2003). Utilizing a modified case-control and transmission disequilibrium test (TDT) we replicated our initial findings in a wild-caught population of flies mated to females bearing a gain-of-function allele of Egfr. While we were able to replicate the initial association in this population, the phenotype scored could be observed only after mating to a mutant stock requiring one generation of rearing under lab conditions, potentially reducing environmental variation relative to wild populations.
In a related study, 289 common polymorphisms in Egfr, including all of the coding region and flanking noncoding sequences, were examined for associations with aspects of wing shape in a set of highly inbred lines (Palsson and Gibson 2004). For the current study we endeavored to replicate the significant association observed between a noncoding site, T30200C, ∼300 bp upstream of the alternative first exon of Egfr, and one aspect of geometrically described wing shape in D. melanogaster (Palsson and Gibson 2004). Specifically, this site was found to be associated with the first principal component (PC1) of shape variation for the central region of the wing, after procrustes superimposition. This axis of variation predominantly describes proximal-distal compression between the anterior crossvein (r-m) and the intersection of the posterior crossvein with the M1 vein (dm-cu), with respect to the R4 + 5 and M1 veins intersecting the wing margin (Palsson and Gibson 2004, Figure 1; also see Figure 4B). While the initial associations were performed on inbred lines reared under lab conditions, for the current study we utilized a cohort of ∼900 wild-caught male flies of D. melanogaster. We first examined the phenotypic differences between the inbred lab-reared population and the wild cohort and observed significant differences in many aspects of mean shape as well as overall shape variation, but allele frequencies did not differ. We then demonstrated that the initial association found for an aspect of wing shape could be replicated. These findings are discussed within the context of detecting genetic effects in wild populations.
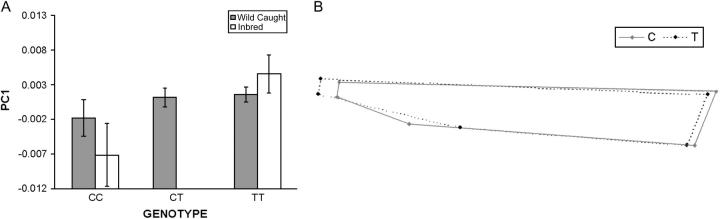
Figure 4.—
The effects of genotype on shape variation in the central region of the wing. (A) Bar graph demonstrating the mean differences (95% C.I.) for the genotypic classes for the wild-caught flies in comparison to the inbred lines. The genotypic effects are much greater in the inbred lines. (B) geometric representation of the allelic effects. Relative to the T genotype, the shape represented by the C allele appears to be compressed along the proximal-distal axis. This shape difference is extremely similar to that observed for the original association. Given that mean shape differences are subtle, individual values for the landmarks were taken from the top and bottom 10% of the distribution to magnify the effects.
METHODS
Collection of flies and digitization of wings:
All flies were collected within 3 consecutive days at a peach orchard located in West End, North Carolina (NC) in the summer of 2002. This is the same location we sampled in 2000 that was used to establish the NC inbred lines used in our previous association studies (Dworkin et al. 2003; Palsson and Gibson 2004). The left and right wings of male flies were removed and mounted between slides and coverslips and digitized using a SPOT camera mounted on a Nikon Eclipse microscope. Images were cropped in Adobe Photoshop (V5) and stored in TIFF format prior to morphometric analysis. (see Birdsall et al. 2000 for extensive protocol). Each carcass was stored individually in an Eppendorf tube with 70% ethanol until being genotyped.
Genotyping:
The site of interest, a C-T polymorphism in the noncoding region upstream of alternative exon 1 (Palsson and Gibson 2004; Palsson et al. 2004), was genotyped for ∼900 male flies. The allelic variant contained a restriction fragment length polymorphism (RFLP) for the DraIII restriction endonuclease. DNA extraction for single males followed previously published methods (Gloor et al. 1993). For PCR, the following primers were utilized: GTGGCTCGTAATGTGAAACT and GCGTTACTGGTGGGATGAATCAAG, according to standard procedures in 10-μl reactions (MgCl2, 2mm final concentration). PCR conditions were as follows: 94° for 5 min; 95° for 15 sec, 55° for 30 sec, 72° for 45 sec 38 times; and 72° for 10 min. Two microliters of PCR product from each sample was digested in a 20-μl reaction with 2 units of DraIII and 0.1 μl of BSA per reaction overnight at 37°. Products were scored manually on 2% agarose gels (uncut, 374 bp; cut, 273 bp). The final sample with both genotypic information and undamaged wings contained 871 individuals.
RT-PCR and quantitative PCR:
To confirm that alternative exon 1 of Egfr was expressed in the imaginal wing discs, 10 pairs of wing discs from wandering third instar larvae were dissected from the white; Oregon-R strain. Standard manufacturer-recommended protocols were used for RNA extraction using Trizol (GIBCO BRL, Gaithersburg, MD) and reverse transcription (Promega, Madison, WI). cDNA was then amplified with Egfr alternative exon 1-specific primers (TCGATTCCTATACCGCAGCAGTTC and CCCTTGACGAACTCGTTCTTGTTCT) and examined on an agarose gel. To quantify the relative abundance of the Egfr alternative first exon between T30200C genotype classes, we used the Quantitect SYBR green RT-PCR kit (QIAGEN, Valencia, CA) on a GeneAmp 5700 sequence detection system (Applied Biosystems, Foster City, CA). GAPDH2 (AATTAAGGCCAAGGTTCAGGAGGC and TCGTTTAGCGAAATGCCAGCCTTG) as well as a common exon (3) from Egfr were used as control genes for comparison (TTGCCAGAAGTTCAGCAAGCTCAC and GTTCTTGCAGGCGATGCAATCCTT). However, initial results suggested that this assay is not sensitive enough to detect expression differences less than twofold.
Morphometric analysis:
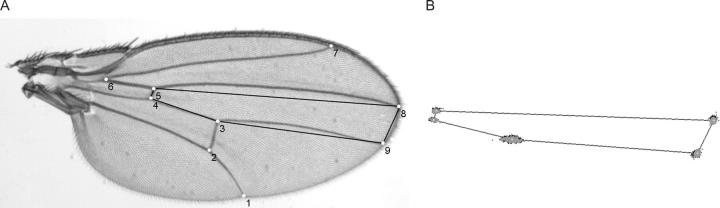
Landmark variation was captured manually for the digital images of wings using the TPS DIG program (v. 1.39; Rohlf 2003). Nine landmarks that encompass most of the variation in the wing blade were used for this study (Figure 1). As expected for a population of wild-caught flies, a number of samples were damaged prior to collection, and in general these specimens were excluded (∼5%) if landmarks could not be scored. For appropriate comparisons of shape variation to be made, the specimens for both the inbred lines of Palsson and Gibson (2004) and the new sample were combined for the generalized least-squares (GLS) procrustes superimposition. This procedure removes variation due to translation, rotation, and isometric scaling. However, allometric variation, a dependence of shape variation on centroid size, can still occur. For examination of variance-covariance matrices and MANOVAs we utilized the thin plate spline to derive the weight matrix, composed of the partial warps and uniform components of shape variation (Bookstein 1991). While the matrix is decidedly less biologically intuitive than one derived from the aligned specimens, it does have the appropriate degrees of freedom for statistical testing; thus no landmarks need to be dropped arbitrarily from the analysis. Furthermore, Rohlf (1999) demonstrated that the results of principal-components analyses are the same for both the weight matrix and the aligned specimens, as the two matrices are just rotations of one another. The superimposition and the extraction of centroid size, partial warp scores, and principal components were all performed using the TPS RELW program (v. 1.35; Rohlf 2003). All software is available freely at http://life.bio.sunysb.edu/morph/index.html.
Figure 1.—
Wing landmarks used in this study. (A) Nine landmarks on the dorsal surface of the wing blade were digitized per wing (1–9). The central region of the wing also utilized in the study is outlined with a solid line (landmarks 3, 4, 5, 8, and 9). (B) Residual variation in landmark position for the C region following procrustes superimposition. Solid circles represent individuals from the inbred lines, shaded areas represent the wild-caught flies, and open areas show the consensus configuration.
STATISTICAL ANALYSIS
Unless otherwise stated, all analyses were performed in SAS 8.2 (SAS Institute, Cary, NC).
Differences between groups:
To investigate the differences between the means for measures of wing shape between the inbred and wild cohort of flies we compared the principal components in a standard ANOVA using PROC GLM,
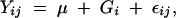 |
where i represents the group (inbred or wild cohort), and j is residual error. To determine if the levels of within-group variation were the same (homoscedasticity) between the two populations, we utilized Levene's statistic on the principal components.
While there are challenges with many methods for the comparison of variance-covariance matrices (Steppan et al. 2002), to examine underlying patterns of structure for the covariance weight matrix (partial warps and uniform components) we utilized common principal-components analysis (Flury 1988), which allows for a hierarchical decomposition of the similarities between the covariances from the two groups. The common principal components (CPC) program (Phillips and Arnold 1999, available at http://www.uoregon.edu/~pphil/programs/cpc/cpc.htm) was used to calculate the common principal components. Furthermore, the eigenvalues for the covariance matrices for each group separately were examined to compare whether they qualitatively shared patterns in terms of the distribution of phenotypic variation.
Associations:
To determine if the association in the central (C) region with site T30200C of Egfr could be replicated, we began with a multivariate analysis of variance (MANOVA). MANOVAs were not used extensively in the previous study (Palsson and Gibson 2004), since it was unclear whether the same axes of variation would be appropriate, even with a common consensus configuration. However, the relevant biological variation should be found in the central region of the wing. Therefore, all of the partial warp and uniform components of shape variation for the C region were used with the model
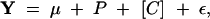 |
where Y represents the four partial warps and the two uniform components of shape variation derived from the least-squares mean (LSmean) estimates per individual, P is the polymorphism, and C is centroid size as a covariate. After examination of the initial model, the model including centroid size as a covariate was included to determine what, if any, effect centroid had on the strength of association.
For the most direct comparison with the results of Palsson and Gibson (2004), we also performed a univariate analysis of variance for the first principal component of shape variation for the central region. Two related univariate models with Y = PC1 were used to test between a purely additive vs. an arbitrary dominance model of genetic effects (Genissel et al. 2004). The additive model reduces to a linear regression on genotype, under the assumption that the mean heterozygous (CT) value is midway between the means of the two homozygous classes CC and TT. The arbitrary dominance model (ANOVA) makes no assumptions with regard to dominance and should give similar results to the additive model unless the mean value of the heterozygous class shows significant levels of dominance. For both models a priori we began with a conceptual hypothesis for the direction of genetic effects on shape variation captured in the first principal component, on the basis of the results of Palsson and Gibson (2004). Thus the critical value of F employed was equal to 2α (Sokal and Rohlf 1995, p. 223). After demonstrating that there was an overall genetic effect at this site, the least-squares means were contrasted to test whether the CT and TT genotypic classes had significantly greater metrics of shape on the basis of PC1, compared with the CC genotypes.
Genetic contributions to overall variance were examined according to Falconer and Mackay (1996). The additive genetic variance is VA = 2pq[a + d(q − p)]2, the dominance variance is VD = (2pqd)2, and the total genetic variance is VG = VA + VD, where p is the allele frequency of T, q is the allele frequency of C, a is the genotypic value for TT homozygotes (−a is the value for CC), and d represents the dominance estimate for the model (Falconer and Mackay 1996). These values were derived from estimates of the LSmean values for each genotype (best linear unbiased estimates were equal to the LSmeans for these data).
For the inbred lines, where we could not estimate d since there were no heterozygotes, a purely additive model with VA = 2pqa2 was used. The variance explained by site T30200C for these two groups is the additive or total genetic variance divided by the phenotypic variance of the group in question.
RESULTS
Phenotypic differences between the inbred lab lines and the wild-caught cohort:
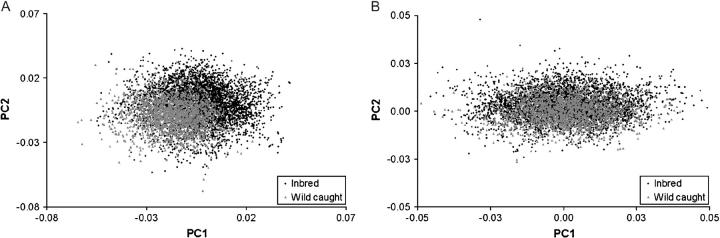
While previous work has demonstrated the environmental insensitivity of aspects of wing shape (Birdsall et al. 2000) relative to wing size, considerable evidence suggests that the process of inbreeding can affect both mean shape as well as its patterns of (co)variance (Coyne and Beecham 1987; Phillips et al. 2001; Whitlock et al. 2002). With this in mind, we tested for differences in patterns of phenotypic variation for wing shape between the two groups of study, namely the inbred lab lines and the wild-caught cohort of flies. This question was addressed with respect to shape variation for all landmarks, as well as for a subset of landmarks for the central region of the wing in which the original association was detected. Multivariate patterns of shape variation between these two groups exhibited highly significant differences, both for the full set of landmarks (λ = 0.545; F = 352.8; d.f. = 14, 5937; P < 0.0001) and for the central region (λ = 0.89; F = 115.4; d.f. = 6, 5945; P < 0.0001). However, the use of a MANOVA does not allow for easy interpretation of geometric shape variation. Therefore we utilized a principal-components analysis to extract new variates describing some of the axes of shape variation. When the shape variation based upon the principal components for all nine landmarks is used, there is a significant group effect for all of the PCs (Table 1, Figure 2), with the group effect explaining 29.3% of the total variation for PC1 as compared with centroid size (93.0% of the variation). Interestingly, while PC2–PC6 all show highly significant differences between the inbred and outbred groups for the central region of the wing (Table 1), there was no evidence for a significant effect with respect to the first principal component. This is particularly relevant given that this axis of variation, affecting the relative location of the anterior crossvein, was previously observed to be associated with site T30200C of Egfr (Palsson and Gibson 2004).
TABLE 1.
Summary of ANOVAs between the inbred and wild-caught flies
| Dependent | d.f. | SS | MS | F-value | P | Levene |
|---|---|---|---|---|---|---|
| A. ANOVA summary for the principal components for shape variation across the whole wing | ||||||
| PC1 | 1,5950 | 0.222 | 0.222 | 1063.232 | 1E-214 | 2.11E-16 |
| PC2 | 1,5950 | 0.082 | 0.082 | 431.859 | 1.17E-92 | 4.41E-22 |
| PC3 | 1,5950 | 0.101 | 0.101 | 796.289 | 1.6E-164 | 0.01 |
| PC4 | 1,5950 | 0.086 | 0.086 | 1105.086 | 2E-222 | 5.15E-13 |
| PC5 | 1,5950 | 0.012 | 0.012 | 215.687 | 5.42E-48 | 4.01E-09 |
| PC6 | 1,5950 | 0.017 | 0.017 | 334.545 | 9.41E-73 | 4.03E-05 |
| PC7 | 1,5950 | 0.002 | 0.002 | 57.129 | 4.7E-14 | 6.23E-31 |
| PC8 | 1,5950 | 0.001 | 0.001 | 36.162 | 1.92E-09 | 0.07 |
| B. ANOVA summary for the principal components for shape variation in the central region of the wing | ||||||
| PC1 | 1,5950 | 1.11E-04 | 1.11E-04 | 0.59 | 0.444 | 2.93E-11 |
| PC2 | 1,5950 | 0.012 | 0.012 | 218.63 | 1.3E-48 | 1.7E-07 |
| PC3 | 1,5950 | 0.006 | 0.006 | 205.56 | 7.37E-46 | 5.5E-05 |
| PC4 | 1,5950 | 1.34E-04 | 1.34E-04 | 9.27 | 0.002 | 2.62E-13 |
| PC5 | 1,5950 | 0.002 | 0.002 | 152.77 | 1.14E-34 | 1.79E-08 |
| PC6 | 1,5950 | 0.001 | 0.001 | 120.44 | 9.34E-28 | 4.9E-24 |
Note that the first principal component for the central region is not significantly different between groups. Levene, the P-value for Levene's test between groups for within-group variation. SS, sum of squares; MS, mean square.
Figure 2.—
Summary of phenotypic variation in PC1 and PC2 between groups. (A) Scatterplot of PC1 vs. PC2 for the whole wing, with highly significant differentiation between groups. (B) Scatterplot of PC1 vs. PC2 derived from the central region of the wing. Note that there is little differentiation between the two groups for the first principal component for the central region, unlike that for the complete set of landmarks.
Levene's test was used to contrast the levels of within-group variation. For all PCs, the phenotypic variance among the inbred lines was greater than that in the wild cohorts. While inbred lines are generally expected to show an increase in overall phenotypic variation due to amplification of between-line effects, this was expected to be attenuated by the increased environmental variation for the wild cohort.
One method to address whether there are underlying similarities in the overall structure of the covariance matrix for wing shape for the two groups is to utilize a hierarchical decomposition of the common principal components (Flury 1988). As discussed, utilizing the Flury hierarchy allows for decomposition of the patterns of similarities between the covariance matrices of the two groups, the inbred NC lines and the wild cohort of flies (Phillips and Arnold 1999). Using the CPC program of Phillips and Arnold (1999) there was no evidence for any common principal components for the data sets including all landmarks, while for the data set including only the central portion of the wing, there was evidence for only a single CPC (step up, χ2 = 43.739, d.f. = 4, P < 0.0001). This suggests that there is relatively little evidence for common patterns of covariation between these two groups. Previous work also demonstrated a low number of shared PCs between inbred and outbred populations for phenotypic covariance matrices (Phillips et al. 2001). However, this data should be interpreted with care as simulation work suggests that CPC does not perform well under many circumstances (Houle et al. 2002). The number of common principal components observed between species in the genus Drosophila is low (Galpern 2000) and may underestimate the patterns of shared structure.
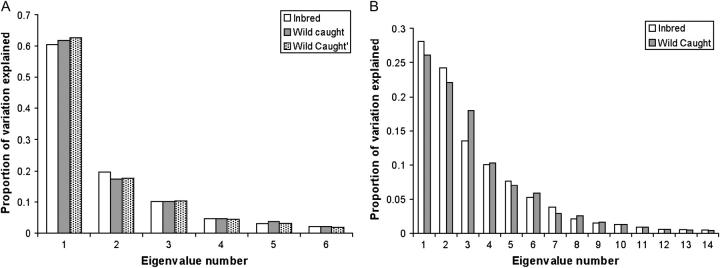
The observation of differences in the covariance matrices between the two groups raises the concern that even though all flies in this study underwent superimposition together, the principal components extracted from the two groups separately may differ somewhat. To address this, we simply examined the distribution of eigenvalues, representing the amount of variation explained by each new variate. The number of and percentage of variation explained by the eigenvalues are extremely similar for the two groups, both for the whole wing (Figure 3A) and the central region (Figure 3B). This lends some support to the presumption that there actually are commonalities in the covariance matrix. Interestingly, very similar results are obtained when the GLS procrustes superimposition is performed only on the wild cohort of flies (Figure 3A). This suggests common axes of variation are not dependent upon the consensus configuration for the landmarks for these data. This pattern may suggest some form of morphological stability due to selection, canalization, or a constraint operating on wing shape.
Figure 3.—
Distribution of eigenvalues by group (inbred vs. wild caught). (A) eigenvalues of the PCs for the C region of the wing appear to be very similar for both groups. Furthermore, the eigenvalues are also very similar for the wild-caught flies when they undergo procrustes superimposition alone (wild caught vs. wild caught′). (B) Eigenvalues for the PCs from all nine landmarks of the wing. Qualitatively there appear to be some differences for the first three eigenvalues.
Allele frequencies:
Any alteration of the allele frequencies of the polymorphisms of interest due to inbreeding would also alter the genetic variance, decreasing the likelihood of replicating the initial association. To test for such an effect, the genotype and allele frequencies from the wild cohort of flies were compared to the frequencies observed in the original association study (Table 2). From the cohort of wild-collected male flies, 892 were successfully genotyped. The allele frequency of the wild cohort and that of the inbred lines are not significantly different on the basis of a G-test, which suggests that the process of inbreeding did not alter the allele frequency at site T30200C. While the genotype frequencies are quite close to the expected value under Hardy-Weinberg equilibrium (HWE), a small but significant deficiency of heterozygotes was observed in the wild cohort (Table 2). It is unclear what if anything should be made by this small deviation; however, it is worth noting that two other sites in this gene were examined from a subsample of ∼300 of the wild-caught individuals, and in neither case did they deviate significantly from HWE (not shown).
TABLE 2.
Comparison of allele frequencies between the inbred and wild cohort of flies
| Allele | Frequency | Allele frequencies |
||
|---|---|---|---|---|
| NC inbred | ||||
| T | 85 | 0.72 | ||
| H | ||||
| C | 33 | 0.28 | ||
| Allele | Frequency | Allele frequencies |
Genotype frequencies |
HWE |
| NC wild cohort | ||||
| T | 489 | 0.73 | 0.55 | 474 |
| H | 323 | 0.36 | 352 | |
| C | 80 | 0.27 | 0.09 | 65 |
| χ2 | 0.046 | |||
There was no evidence for significant differences between the groups for allele frequencies on the basis of a G-test. However, the observed genotype frequencies showed a slight deficiency of heterozygotes relative to the expectations for the wild cohort.
Association:
Palsson and Gibson (2004) demonstrated that a noncoding site T30200C, ∼300 bp upstream of the alternative first exon of Egfr, was significantly associated with PC1 of shape variation for the central region of the wing in a panel of inbred lines. To assess whether this association is replicated in the wild cohort, an ANOVA with PC1 of the central region as the dependent variable was employed, facilitating direct comparison with the original study. Two related models described in methods examined the association between genotype and phenotypic variation, assuming an arbitrary dominance model or an additive model. As shown in Table 3, the results for these models are similar and suggest a significant association at P < 0.05, between shape variation in PC1 and the T30200C polymorphism. We then utilized one-way t-tests, corrected for multiple comparisons on the LSmeans, to determine if the CT and TT genotype classes had significantly higher values for the first principal component of shape variation for the central region of the wing, compared with CC. As demonstrated in Figure 4, both of these genotypes appear to have significantly greater means than the CC genotype (CC vs. CT, P = 0.05; CC vs. TT, P = 0.02) and are consistent with respect to direction of the effects observed with the inbred lines. Furthermore, the shape variation observed along this axis of variation (Figure 4B) is nearly identical to that seen by Palsson and Gibson (2004) and predominantly involves the placement of the posterior crossvein.
TABLE 3.
Summary of linear models for genotypic effects of site T30200C
| Source | d.f. | SS | MS | F-value | ProbF | |
|---|---|---|---|---|---|---|
| Additive | T30200C | 1 | 5.4E-04 | 5.4E-04 | 3.74 | 0.027 |
| Additive with covariate | T30200C | 1 | 5.2E-04 | 5.2E-04 | 3.65 | 0.028 |
| Centroid | 1 | 1.9E-03 | 1.9E-03 | 13.53 | 2.5E-04 | |
| AD model | T30200C | 2 | 7.7E-04 | 3.9E-04 | 2.68 | 0.035 |
| AD model with covariate | T30200C | 2 | 6.7E-04 | 3.3E-04 | 2.36 | 0.045 |
| Centroid | 1 | 1.8E-03 | 1.8E-03 | 12.95 | 3.0E-04 |
Additive models correspond to a linear regression under the assumption that the TC heterozygotes class shows no dominance. Arbitrary dominance (AD) equals a standard ANOVA, with no assumption about the degree of dominance. Covariate represents the inclusion of centroid size, which had minimal impact upon the strength of the association between genotype and shape variation. SS, sum of squares; MS, mean square; ProbF, probability of F.
Given the demonstrated differences of the variance-covariance matrices (Figures 2 and 3, Table 1) between the two groups, it could be argued that the first principal component for the central region from both data sets is not directly comparable. Therefore we also explored the variation in the central region using a MANOVA for the partial warps and uniform components of shape variation for the central region of the wing. As shown in Table 4, there is evidence for a significant effect of the T30200C polymorphism on multivariate shape variation for the central region of the wing. Thus it appears that even with the differences in patterns of phenotypic (co)variation, the association could be replicated.
TABLE 4.
Summary of MANOVA for the effects of site T30200C on multivariate shape variation
| Hypothesis | Error matrix | Wilk's λ | F-value | No. d.f. | Den d.f. | ProbF | |
|---|---|---|---|---|---|---|---|
| AD model | T30200C | Error SSCP | 0.97 | 2.17 | 12 | 1726 | 0.01 |
| AD model with covariate | T30200C | Error SSCP | 0.97 | 2.27 | 12 | 1724 | 0.01 |
| Centroid | Error SSCP | 0.91 | 14.44 | 6 | 862 | 9.6E-16 |
MANOVA for the partial warps and uniform components of variation for the central region of the wing. While there is a highly significant effect of centroid size on shape (allometry), there was no significant impact on the strength of the association with genotype. AD, arbitrary dominance; Den d.f., denominator degrees of freedom; ProbF, probability of F.
Size (as measured using centroid size) may have an allometric relationship with shape variation (since only isometric scaling effects have been removed). Therefore we utilized centroid size as a covariate in an ANCOVA to determine if any of the variation explained by site T30200C is dependent upon allometric scaling. While centroid size does significantly covary with both PC1 and the multivariate summary for the partial warps and uniform components of shape, there is no evidence that this alters the strength of association between the polymorphism and shape (Tables 3 and 4). This suggests that the association for this site is not in itself strongly dependent upon size.
The results discussed above are consistent with the association being replicated within the wild-caught cohort, but the mean genotypic effects are not as divergent as seen with the inbred lines (Figure 4A). Site T30200C explains 6.8% of the overall phenotypic variation for the inbred lines, while it explains only 0.4% of the variation in the wild-caught cohort. Surprisingly, this difference appears to be almost entirely due to genotypic estimates as opposed to an overall increase in phenotypic variance for this trait.
DISCUSSION
With the advent of new technical and statistical methods for LD mapping, it is clear that there are reasons to be optimistic with respect to the future mapping of many segregating variants involved with complex quantitative traits. However, with optimism must come the appropriate caution with respect to the resolution of genetic effects, in terms of both location and the limit on genetic effects detectable with a reasonable sample size. Additional power is also lost through the general problem of multiple contrasts between markers and phenotypes. It has been demonstrated that some significant associations that have been observed cannot be replicated, and it is often not clear if this is due to an initial false-positive result or if a number of confounding factors render the effect undetectable in different samples. Such effects include differences in allele frequencies or patterns of LD between markers and causal sites between populations (Zondervan and Cardon 2004).
Initial positive associations that are observed in the lab may be even more prone to failure for replication due to the addition of the effects of inbreeding on allele frequencies, phenotypic distributions, as well as changes in the relative levels of environmental variance. In a recent study of bristle number in a wild cohort of ∼2000 Drosophila individuals, there was no evidence of significant association with polymorphisms in the hairy gene (Macdonald and Long 2004), even though previous work did find such an association (Robin et al. 2002). It is unclear if the failure to detect any significant association was due to the fact that polymorphisms used in this study were not in LD with the markers found earlier or to some of the aforementioned effects. As well, previous work on bristle number has demonstrated that the genetic effects attributable to markers in another neurogenic locus, Delta, are environmentally sensitive (Geiger-Thornsberry and Mackay 2002). Efforts to successfully map causal variants to the nucleotide level in wild populations should be cognizant of what confounding conditions are likely.
In this study we have demonstrated that despite some phenotypic differences between wild and laboratory populations, the association between a polymorphic site in a conserved region with homology to a GAGA factor binding site could be successfully replicated in a wild cohort of 872 male D. melanogaster. The apparent success of mapping from wing-shape QTL (Zimmerman et al. 2000), to fine-scale mapping using deficiency complementation (Palsson and Gibson 2000), and finally to association mapping (Palsson and Gibson 2004), may be in part due to the relative environmental insensitivity of this trait with respect to genotype (Birdsall et al. 2000). There is still significant covariation of aspects of shape with size (Tables 3 and 4), and in other instances this may have an impact upon genotypic effects. However, despite the numerous statistical and biological issues associated with capturing the complexity of geometric structures such as wing shape, it appears to be a good model for the replication of naturally occurring polymorphisms in wild populations.
Nevertheless, it is worth considering some notes of caution regarding association studies on model organisms. Foremost, it is clear from this experiment that large sample sizes are required to detect even moderate genetic effects. While the T30200C site explained close to 6.8% of the overall phenotypic variation for this aspect of wing shape in the initial study, the estimates for variance explained for the wild cohort of flies are ∼0.4% of the variation. Surprisingly this change of phenotypic variance had less to do with an increase in overall phenotypic variation for the trait in the wild-caught population and was primarily due to a much larger estimate of effect size for this site in the inbred lab lines. It is unclear whether this is due to more precise estimates for the inbred lines or whether there was a sampling or Beavis effect resulting in an overestimate of effect size (Beavis 1994). This comparison of the variance explained assumes pure additivity for the inbred lines, while dominance effects are included for the estimates from the wild-caught cohort, but assuming a purely additive effect does not change the estimate for the wild cohort of flies. For future studies, special considerations must be made for detecting genetic effects of even moderate size, and it may be that without utilizing extremely large sample sizes, effects of just 1–2% of the phenotypic variation detected in the lab will not be replicable. As with the results of QTL effects, this ascertainment bias may skew the interpretation toward the inference that the average genetic effect size is much larger than what actually occurs in natural populations.
This raises the issue of the relationship between detection and the true distribution of allelic effects in natural populations. Using isogenic chromosomal regions, several studies have detected effect sizes within the range of 5–12% for bristles (Long et al. 1998) and 2.2% for longevity in Drosophila (De Luca et al. 2003). These can be contrasted with other traits such as insecticide resistance, immunity, or the evolution of domestication traits. For instance, polymorphisms in the Dwarf8 locus of maize explain between 12 and 32% of phenotypic variation for flowering time (Thornsberry et al. 2001), and a recent study examining immunity genes in Drosophila observed polymorphisms that explain between 0 and 13% of the phenotypic variation in response to bacterial challenge (Lazzaro et al. 2004). Another recently observed example at the extreme showed that resistance to DDT in D. melanogaster was almost entirely due to the presence of an Accord transposable element in the cyp6g1 gene (Daborn et al. 2002).
Are there any mechanisms that may help to explain these differences in phenotypic variance? It is perhaps worth considering the evolutionary history of the trait, i.e., what forms of selection pressures have shaped the underlying genetic variation. It is reasonable to assume that traits such as insecticide resistance and immune response and traits related to domestication in maize have undergone strong directional selection in the recent past. On the other hand, traits such as bristle number in Drosophila appear to have been under stabilizing selection (Santiago et al. 1992; Nuzhdin et al. 1995; Garcia-Dorado and Gonzalez 1996). Similarly, wing shape seems to demonstrate relative evolutionary stasis, possibly due to stabilizing selection as well (Weber 1990; Galpern 2000; Houle et al. 2003). Recent theoretical work on the trajectory of adaptation suggests that early on in the evolutionary history of a trait there is a possibility for the fixation of alleles of large effect (Kimura 1980; Orr 1998, 1999). But as the trait approaches its optimum the average effect size of an allele fixed in the population decreases. These effects may be further obscured if alleles that are fixed demonstrate epistatic interactions with the alleles of large effect; thus the relative contribution of the alleles may be further diminished (see Caicedo et al. 2004). From this argument, traits under recent directional selection may in fact possess alleles that are relatively easy to detect by association and will explain the largest amounts of phenotypic variation. However, they may also bias the expected distribution of allelic variation. Until much larger numbers of replicated and hopefully functionally verified polymorphisms are associated with trait variation, any conclusions regarding the impact of alleles of major effect on the genetic architecture of traits should be viewed with caution. Given the rate at which the genetic architecture of traits is being dissected, and the ability to functionally verify causal polymorphisms, it seems likely that precise estimates of genetic effects are coming soon.
Acknowledgments
We are grateful to Jenny Moser for help with the Q-PCR protocols. We thank Ellen Larsen for discussions on these topics. We thank Trudy Mackay, Corbin Jones, Phillip Awadalla, and two anonymous reviewers for comments on previous versions of the article. This work was supported by National Institutes of Health grant R01GM61600 to G.G.
References
- Barton, N. H., and P. D. Keightley, 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3: 11–21. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and M. Turelli, 1989. Evolutionary quantitative genetics: How little do we know? Annu. Rev. Genet. 23: 337–370. [DOI] [PubMed] [Google Scholar]
- Beavis, W. D., 1994 The power and deceit of QTL experiments: lessons from comparitive QTL studies, pp. 250–266 in Proceedings of the Forty-Ninth Annual Corn & Sorghum Industry Research Conference. American Seed Trade Association, Washington, DC.
- Birdsall, K., E. Zimmerman, K. Teeter and G. Gibson, 2000. Genetic variation for the positioning of wing veins in Drosophila melanogaster. Evol. Dev. 2: 16–24. [DOI] [PubMed] [Google Scholar]
- Bookstein, F. L., 1991 Morphometric Tools for Landmark Data: Geometry and Biology. Cambridge University Press, Cambridge, UK.
- Caicedo, A. L., J. R. Stinchcombe, K. M. Olsen, J. Schmitt and M. D. Purugganan, 2004. Epistatic interaction between Arabidopsis FRI and FLC flowering time genes generates a latitudinal cline in a life history trait. Proc. Natl. Acad. Sci. USA 101: 15670–15675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coyne, J. A., and E. Beecham, 1987. Heritability of two morphological characters within and among natural populations of Drosophila melanogaster. Genetics 117: 727–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daborn, P. J., J. L. Yen, M. R. Bogwitz, G. Le Goff, E. Feil et al., 2002. A single P450 allele associated with insecticide resistance in Drosophila. Science 297: 2253–2256. [DOI] [PubMed] [Google Scholar]
- De Luca, M., N. V. Roshina, G. L. Geiger-Thornsberry, R. F. Lyman, E. G. Pasyukova et al., 2003. Dopa decarboxylase (Ddc) affects variation in Drosophila longevity. Nat. Genet. 34: 429–433. [DOI] [PubMed] [Google Scholar]
- Dworkin, I., A. Palsson, K. Birdsall and G. Gibson, 2003. Evidence that Egfr contributes to cryptic genetic variation for photoreceptor determination in natural populations of Drosophila melanogaster. Curr. Biol. 13: 1888–1893. [DOI] [PubMed] [Google Scholar]
- Falconer, D., and T. Mackay, 1996 Introduction to Quantitative Genetics. Longman, Essex, UK. [DOI] [PMC free article] [PubMed]
- Flint, J., and R. Mott, 2001. Finding the molecular basis of quantitative traits: successes and pitfalls. Nat. Rev. Genet. 2: 437–445. [DOI] [PubMed] [Google Scholar]
- Flury, B., 1988 Common Principal Components and Related Multivariate Models. John Wiley & Sons, New York.
- Freedman, M. L., C. L. Pearce, K. L. Penney, J. N. Hirschhorn, L. N. Kolonel et al., 2005. Systematic evaluation of genetic variation at the androgen receptor locus and risk of prostate cancer in a multiethnic cohort study. Am. J. Hum. Genet. 76: 82–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galpern, P., 2000 The use of common principal component analysis in studies of phenotypic evolution: an example from the Drosophilidae. Master's Thesis, University of Toronto, Toronto, Ontario, Canada.
- Garcia-Dorado, A., and J. A. Gonzalez, 1996. Stabilizing selection detected for bristle number in Drosophila melanogaster. Evolution 50: 1573–1578. [DOI] [PubMed] [Google Scholar]
- Geiger-Thornsberry, G. L., and T. F. Mackay, 2002. Association of single-nucleotide polymorphisms at the Delta locus with genotype by environment interaction for sensory bristle number in Drosophila melanogaster. Genet. Res. 79: 211–218. [DOI] [PubMed] [Google Scholar]
- Genissel, A., T. Pastinen, A. Dowell, T. F. Mackay and A. D. Long, 2004. No evidence for an association between common nonsynonymous polymorphisms in Delta and bristle number variation in natural and laboratory populations of Drosophila melanogaster. Genetics 166: 291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gloor, G. B. P., D. M. Johnson-Schlitz, N. A. Nassif, R. W. Phillis, W. K. Benz et al., 1993. Type I repressors of P element mobility. Genetics 135: 81–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle, D., J. Mezey and P. Galpern, 2002. Interpretation of the results of common principal components analyses. Evolution 56: 433–440. [DOI] [PubMed] [Google Scholar]
- Houle, D., J. Mezey, P. Galpern and A. Carter, 2003. Automated measurement of Drosophila wings. BMC Evol. Biol. 3: 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis, J. P., E. E. Ntzani, T. A. Trikalinos and D. G. Contopoulos-Ioannidis, 2001. Replication validity of genetic association studies. Nat. Genet. 29: 306–309. [DOI] [PubMed] [Google Scholar]
- Ioannidis, J. P., E. E. Ntzani and T. A. Trikalinos, 2004. ‘Racial’ differences in genetic effects for complex diseases. Nat. Genet. 36: 1312–1318. [DOI] [PubMed] [Google Scholar]
- Kimura, M., 1980. Average time to fixation of a mutant allele in a finite population under continued mutation pressure: studies by analytical, numerical and pseudosampling methods. Proc. Natl. Acad. Sci. USA 77: 522–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai, C., R. F. Lyman, A. D. Long, C. H. Langley and T. F. Mackay, 1994. Naturally occurring variation in bristle number and DNA polymorphisms at the scabrous locus of Drosophila melanogaster. Science 266: 1697–1702. [DOI] [PubMed] [Google Scholar]
- Lazzaro, B. P., B. K. Sceurman and A. G. Clark, 2004. Genetic basis of natural variation in D. melanogaster antibacterial immunity. Science 303: 1873–1876. [DOI] [PubMed] [Google Scholar]
- Legare, M. E., F. S. Bartlett, II and W. N. Frankel, 2000. A major effect QTL determined by multiple genes in epileptic EL mice. Genome. Res. 10: 42–48. [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., R. F. Lyman, C. H. Langley and T. F. Mackay, 1998. Two sites in the Delta gene region contribute to naturally occurring variation in bristle number in Drosophila melanogaster. Genetics 149: 999–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald, S. J., and A. D. Long, 2004. A potential regulatory polymorphism upstream of hairy is not associated with bristle number variation in wild-caught Drosophila. Genetics 167: 2127–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay, T. F., 2001. Quantitative trait loci in Drosophila. Nat. Rev. Genet. 2: 11–20. [DOI] [PubMed] [Google Scholar]
- Nikoh, N., A. Duty and G. Gibson, 2004. Effects of population structure and sex on association between serotonin receptors and Drosophila heart rate. Genetics 168: 1963–1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzhdin, S. V., J. D. Fry and T. F. Mackay, 1995. Polygenic mutation in Drosophila melanogaster: the causal relationship of bristle number to fitness. Genetics 139: 861–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, H. A., 1998. The population genetics of adaptation: the distribution of factors fixed during adaptive evolution. Evolution 52: 935–949. [DOI] [PubMed] [Google Scholar]
- Orr, H. A., 1999. The evolutionary genetics of adaptation: a simulation study. Genet. Res. 74: 207–214. [DOI] [PubMed] [Google Scholar]
- Palsson, A., and G. Gibson, 2000. Quantitative developmental genetic analysis reveals that the ancestral dipteran wing vein prepattern is conserved in Drosophila melanogaster. Dev. Genes Evol. 210: 617–622. [DOI] [PubMed] [Google Scholar]
- Palsson, A., and G. Gibson, 2004. Association between nucleotide variation in Egfr and wing shape in Drosophila melanogaster. Genetics 167: 1187–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, A., A. Rouse, R. M. Riley-Berger, I. Dworkin and G. Gibson, 2004. Nucleotide variation in the Egfr locus of Drosophila melanogaster. Genetics 167: 1199–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips, P. C., and S. J. Arnold, 1999. Hierarchical comparison of genetic variance-covariance matrices I. Using the Flury hierarchy. Evolution 53: 1506–1515. [DOI] [PubMed] [Google Scholar]
- Phillips, P. C., M. C. Whitlock and K. Fowler, 2001. Inbreeding changes the shape of the genetic covariance matrix in Drosophila melanogaster. Genetics 158: 1137–1145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podolin, P. L., P. Denny, N. Armitage, C. J. Lord, N. J. Hill et al., 1998. Localization of two insulin-dependent diabetes (Idd) genes to the Idd10 region on mouse chromosome 3. Mamm. Genome 9: 283–286. [DOI] [PubMed] [Google Scholar]
- Robin, C., R. F. Lyman, A. D. Long, C. H. Langley and T. F. Mackay, 2002. hairy: a quantitative trait locus for Drosophila sensory bristle number. Genetics 162: 155–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohlf, F. J., 1999. Shape statistics: procrustes superimpositions and tangent spaces. J. Classif. 16: 197–223. [Google Scholar]
- Rohlf, F. J., 2003 tpsDig, digitize landmarks and outlines, Version 1.39. Department of Ecology and Evolution, State University of New York, Stony Brook, NY.
- Santiago, E., J. Albornoz, A. Dominguez, M. A. Toro and C. Lopez-Fanjul, 1992. The distribution of spontaneous mutations on quantitative traits and fitness in Drosophila melanogaster. Genetics 132: 771–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawamura, K., J. Roote, C. I. Wu and M. Yamamoto, 2004. Genetic complexity underlying hybrid male sterility in Drosophila. Genetics 166: 789–796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal, R. R., and F. J. Rohlf, 1995 Biometry. W. H. Freeman, New York.
- Steppan, S. J., P. C. Phillips and D. Houle, 2002. Comparative quantitative genetics: evolution of the G matrix. Trends Ecol. Evol. 17: 320–327. [Google Scholar]
- Stinchcombe, J. R., C. Weinig, M. Ungerer, K. M. Olsen, C. Mays et al., 2004. A latitudinal cline in flowering time in Arabidopsis thaliana modulated by the flowering time gene FRIGIDA. Proc. Natl. Acad. Sci. USA 101: 4712–4717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 28: 286–289. [DOI] [PubMed] [Google Scholar]
- Weber, K. E., 1990. Selection on wing allometry in Drosophila melanogaster. Genetics 126: 975–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock, M. C., and K. Fowler, 1999. The changes in genetic and environmental variance with inbreeding in Drosophila melanogaster. Genetics 152: 345–353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock, M. C., P. C. Phillips and K. Fowler, 2002. Persistence of changes in the genetic covariance matrix after a bottleneck. Evolution 56: 1968–1975. [DOI] [PubMed] [Google Scholar]
- Zimmerman, E., A. Palsson and G. Gibson, 2000. Quantitative trait loci affecting components of wing shape in Drosophila melanogaster. Genetics 155: 671–683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zondervan, K. T., and L. R. Cardon, 2004. The complex interplay among factors that influence allelic association. Nat. Rev. Genet. 5: 89–100. [DOI] [PubMed] [Google Scholar]