Strict rules determine arrangements of strands in sandwich proteins

Abstract

From a computer analysis of the spatial organization of the secondary structures of β-sandwich proteins, we find certain sets of consecutive strands that are connected by hydrogen bonds, which we call “strandons.” The analysis of the arrangements of strandons in 491 protein structures that come from 69 different superfamilies reveals strict regularities in the arrangements of strandons and the formation of what we call “canonical supermotifs.” Six such supermotifs account for ≈90% of all observed structures. Simple geometric rules are described that dictate the formation of these supermotifs.

The classification of the spatial organization of secondary structures, i.e., the classification of supersecondary structures, is central in our understanding the basic principles of protein structure formation (1–11). The key to classifying proteins is determining a set of sequence and structural properties shared by a given group of proteins. In this research, we focus on a large group of proteins, the so-called sandwich-like proteins (SPs). These proteins are distinctive [see the SCOP (10) and CATH (11) databases] because of the following structural features: they consist of only β-strands, which form two main β-sheets that pack face to face (Fig. 1a). This type of architecture unites a number of very different protein superfamilies, which have no detectable sequence homology.

Fig. 1.

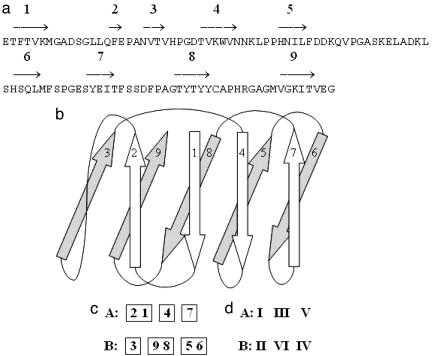
Schematic presentation of the structure of plastocyanin (PDB ID code 1baw). (a) The sequences of amino acids in chain A. The arrows show the strands, with strand numbers assigned sequentially from the N terminus of the sequence. (b) The domain consists of two sheets, containing the strands 2, 1, 4, and 7 in one sheet and the strands 3, 9, 8, 5, and 6 in the other one. (c) Secondary structure motif, representing the arrangement of the strands in sheets A and B. (d) Supersecondary structure supermotif, representing the arrangement of the strandons in sheets A and B.

Considerable progress has been made in protein structure analysis and structural classification with the discovery of certain supersecondary units, arrangements of consecutive secondary structure elements, such as parallel strands with an α-helix between them, the four-helix bundle, the Greek key arrangement of four strands, and others (12–16). Analysis of the arrangements of strands in SPs has revealed an invariant supersecondary substructure that consists of the two interlocked pairs of neighboring β-strands (17). Specific supersecondary structural rules satisfied by ≈90% of observed SPs were introduced in our recent work (18). Strand arrangements that satisfy these rules were called “canonical motifs” (19). Furthermore, a simple and systematic way for generating all possible canonical motifs was introduced in ref. 19, which is based on the so-called “geometric structures.” Each geometric structure generates a multitude of canonical motifs. Thus, geometric structures, whose number is dramatically less than that of canonical motifs, are fundamental structural units.

In this work, we introduce a previously undescribed supersecondary unit, a set of consecutive strands connected with hydrogen bonds (H-bonds) in a β-sheet. We call these sets “strandons.” The description of proteins in terms of strandons reveals that almost all SPs are described by very few variants of arrangements of strandons and that strict rules describe the regularity of these arrangements.

Results and Discussion

Object of Investigations.

We investigate the structures of the β-sandwich proteins, containing two main β-sheets [see SCOP database, 1.67 release (5)]. These proteins varied strongly in the number of strands and the arrangement of strands in the two sheets. According to the SCOP hierarchical classification, protein structures are divided into folds, superfamilies, families, and domains. The domains further are subdivided into groups, which usually describe different species in the domains. In our analysis we consider one protein structure from each group of species because the sequences of different proteins classified in the same species are very similar, and their secondary and tertiary structures are nearly always identical. In total, we have examined 491 protein structures, which are described by 38 folds, 69 superfamilies, and 105 families.

Construction of Supersecondary Structure.

For the purpose of our analysis, we introduce here the concept of a strandon. It is defined as the set of the maximum number of consecutive strands, which are connected by H-bonds between main-chain atoms. If a strand is not H-bonded to a consecutive strand, then this strand by itself makes up a strandon. Strandons will be denoted by Roman numerals, and strands belonging to the same strandons are shown in a box.

Let us consider, for example, the strandons in the structure of plastocyanin [Protein Data Bank (PDB) ID code 1baw]. The chain A in this protein forms a domain with nine strands (Fig. 1). The calculations of the interstrand H-bonds (symbolized here by −) reveal the following arrangement of these strands in the two β-sheets, termed here as A and B:

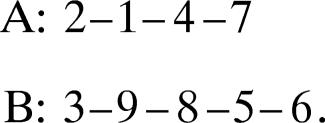Strands 1 and 2 are connected by H-bonds. There are no H-bonds between the consecutive strands 2 and 3. Thus, according to the definition, strandon I consists of strands 1 and 2. Strand 3 has no H-bonds with strand 2 or strand 4; thus, strandon II consists of only one strand. Similarly, we identify strandon III (strand 4), strandon IV (strands 5 and 6), strandon V (strand 7), and strandon VI (strands 8 and 9). Thus, the strands of the strandons of the structure of 1baw can be represented as in Fig. 1c. By analogy with the term motif, we call a “supermotif” the arrangement of strandons in the structure of Fig. 1d.

Analysis of Protein Structures.

Our analysis involves the following three steps.

Step 1. Identification of the secondary structure.

We have used the secondary structures indicated by the PDBSum database (20) for all but nine protein structures. In each of these nine structures there exists one strand located at the edge of a β-sheet consisting of one, two, or three residues.^‖ In our investigation, we do not take this short strand into account for the construction of strandons. We also consider two PDBsum-defined strands to be a single strand with a small bulge, if the two PDBsum strands are neighbors in a sequence, are parallel to each other, and both share H-bonds with the same strand in the structure.

Step 2. Finding the arrangement of strands.

To find the arrangement of the strands in each structure, we calculated the H-bonds between the main-chain atoms of residues in the different strands. In total, there are 99 different arrangements of strands that describe all 491 protein structures. Several of the most common supersecondary structural motifs are presented in Table 1. One motif can depict structures from several superfamilies. For example, the motif

Table 1.

The most popular supersecondary structural motifs and supermotifs in sandwich proteins

Supermotifs	Motifs		No. of motifs	No. of domains

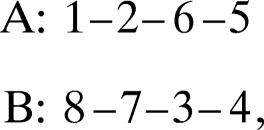describes the structures from 4 superfamilies, 6 families, and 27 domains.

Step 3. Determination of strandons and supermotifs.

From the analysis of the H-bonds between the main-chain atoms, we identified the groups of consecutive strands, which form the strandons. The set of strands containing strand 1 is numbered as strandon I. For the construction of strandons, the strands are numbered cyclically, i.e., the next strand after the last strands is 1. Thus, the last and first strands are considered to be consecutive.

The examination of the arrangement of the strandons in 491 structures reveals 14 different supermotifs. The six most common supermotifs, which describe 88% of all structures, are shown in Table 1. For example, the supermotif no. 2 describes 30 different motifs from 9 different protein folds, 27 superfamilies, and 35 families.

Rules of the Arrangement of Strandons in the Supermotifs.

The analysis of the arrangement of strandons in observed supermotifs (Table 1) has revealed the following two constraint rules.

Rule 1.

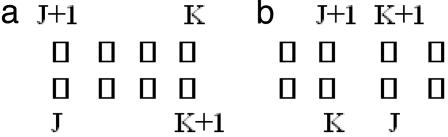
Two strandons located on the same edge (right or left) of the two sheets are always consecutive (Fig. 2a). For example, in supermotif 1 two pairs of consecutive strandons, namely pairs I and II, and IV and V, are located at the left and right edge of the β-sheets, respectively (Table 1).

Fig. 2.

The schematic representation of a consecutive pair of strandons at the edge of the sheets (a) and strandon interlock in a supermotif (b) consists of two consecutive pairs of strandons: J, J + 1 and K, K + 1. The open rectangles denote strandons.

Rule 2.

For any pair of consecutive strandons J and J + 1, where at least one strandon is not at the edge of a sheet, there always exist another pair of consecutive strandons, K and K + 1, such that the arrangement of these two pairs have the following characteristics (Fig. 2b):

1. Strandons J and K are neighbors in one sheet and strandons J + 1 and K + 1 are neighbors in the other sheet.

2. If strandon J is the right (left) of K, then J + 1 is the left (right) of K + 1. We call such a substructure a “strandon interlock.”

These rules imply that two consecutive strandons are always located on different sheets. A pair of strandons J and J + 1 is either located at the edge of the sheet (rule I) or forms the interlock (rule II). Thus, the number of strandons is always even, and the odd-numbered strandons are located in one sheet (the “odd sheet”), whereas the even strandons are located in the other sheet (the “even sheet”).

Supergeometric Structures and Permissible Arrangements.

We present here a simple algorithm for constructing all supermotifs with a given number of strandons. This construction is based on the concept of supergeometric structure, which is a natural extension of the concept of geometric structures introduced in ref. 19. A supergeometric structure consisting of 2N strandons is a collection of N strandon interlocks placed in sequence.

For example, the supergeometric structures consisting of four, six, and eight strandons are given in Fig. 3.

Fig. 3.

The supergeometric structures consisting of 4 (a), 6 (b), and 8 (c) strandons are shown. The open rectangles denote strandons.

Each supergeometric structure gives rise to several supermotifs as follows. Place numeral I at one of the strandons and then number the remaining strandons cyclically, taking in account a strandon interlock. After placing I at a strandon, there exist two choices for placing strandon II, and each of these choices yields a unique supermotif.

For example, after placing I at the top left strandon of Fig. 3a, there exist two choices for II: either at the bottom right strandon, which yields supermotif 2 of Table 1, or at the bottom left strandon, which yields supermotif 3 of Table 1. Similarly, after placing I at the top left strandon of Fig. 3b, there exist two choices for II: either at the bottom left strandon, which yields supermotif 1 of Table 1, or at the bottom middle strandon, which yields supermotif 5 of Table 1. Also, after placing I at the top middle strandon of Fig. 3b, there exist two choices for II: either at the bottom left strandon, which yields the supermotif 6 of Table 1, or at the bottom right strandon, which yields a supermotif equivalent to no. 6. It can be verified that by placing I at all other strandons of Fig. 3 a and b, one finds supermotifs that are equivalent to the above. Thus, supermotifs 2 and 3 and supermotifs 1, 5, and 6 are the only supermotifs consisting of four and six strandons, respectively. In the same way, one can find all supermotifs consisting of eight strandons.

Construction of Motifs.

Each supermotif gives rise to a multitude of motifs as follows. (i) Choose the number of strands in each strandon. (ii) Canonical motifs are constructed by placing the strands in each strandon cyclically. (iii) Noncanonical motifs are constructed by changing the order of the strands in one or more strandons.

Examples.

Example 1.

Consider supermotif 2 of Table 1 and suppose that the number of strands in strandons I, II, III, IV is as follows:

(a) 1, 1, 2, 2.

Then the unique canonical motif is

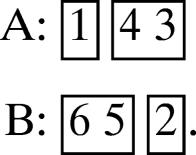The strands in the strandons are shown in boxes.

(b) 3, 1, 1, 1.

Then there exist the following three possible canonical motifs

(c) 3, 2, 1, 2.

Then one of the three possible canonical motifs is

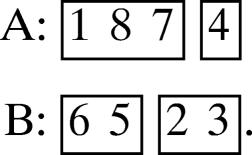(d) 4, 1, 1, 3.

Then one of the four possible canonical motifs is

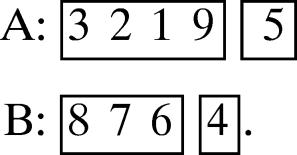Example 2.

Consider supermotif 3 of Table 1, and suppose that the number of strands in strandons I, II, III, IV, is as follows:

(a) 1, 1, 2, 2.

Then the unique canonical motif is

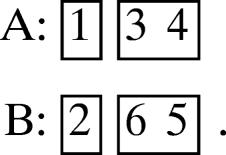(b) 2, 1, 1, 1.

Then the two possible canonical motifs are

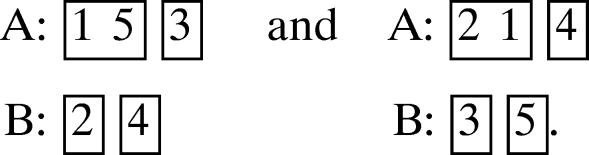Conclusions

It was observed in ref. 18 that ≈90% of observed motifs are canonical, i.e., they satisfy certain structural rules (see rules I–III of ref. 18). A systematic procedure for constructing all canonical motifs was introduced in ref. 19, based on the concept of geometric structures. A procedure for constructing the remaining few motifs, which are noncanonical, also was introduced in ref. 19. The geometric structures involving one, two, and three interlocks produce motifs that take the form of the supermotifs presented in Fig. 3 a–c, respectively, where each box consists of one or more strands. In this work, we have called the collection of these strands strandons. The introduction of strandons simplifies further the construction of both canonical and noncanonical motifs.

Our analysis suggests that the supersecondary structures of architecturally similar proteins are governed by well defined rules, which imply strict regularities. The knowledge of these supersecondary structure regularities can be used in several applications of structural analysis. For example, because they limit dramatically the number of allowed arrangements of supersecondary structure elements, they provide useful tools for structure prediction. Combination of these rules with other known regulations of chain topology, for example, right-handedness of strands in the β-sheet (21), may lead to further limitation of permissible supersecondary motifs.

Another important application is the possibility to align nonsimilar sequences that belong to the same motif or supermotif. In fact, the alignment of the four strands, which form an interlock, was used in ref. 17 to identify particular residues occupying eight common positions in all SPs. It was shown later (22) that these residues are crucial for the folding of a protein chain to a sandwich-like structure.

Abbreviations

PDB

Protein Data Bank

SP

sandwich-like protein.