Linkage Disequilibrium Grouping of Single Nucleotide Polymorphisms (SNPs) Reflecting Haplotype Phylogeny for Efficient Selection of Tag SNPs

Abstract

Single nucleotide polymorphisms (SNPs) have been proposed to be grouped into haplotype blocks harboring a limited number of haplotypes. Within each block, the portion of haplotypes is expected to be tagged by a selected subset of SNPs; however, none of the proposed selection algorithms have been definitive. To address this issue, we developed a tag SNP selection algorithm based on grouping of SNPs by the linkage disequilibrium (LD) coefficient r² and examined five genes in three ethnic populations—the Japanese, African Americans, and Caucasians. Additionally, we investigated ethnic diversity by characterizing 979 SNPs distributed throughout the genome. Our algorithm could spare 60% of SNPs required for genotyping and limit the imprecision in allele-frequency estimation of nontag SNPs to 2% on average. We discovered the presence of a mosaic pattern of LD plots within a conventionally inferred haplotype block. This emerged because multiple groups of SNPs with strong intragroup LD were mingled in their physical positions. The pattern of LD plots showed some similarity, but the details of tag SNPs were not entirely concordant among three populations. Consequently, our algorithm utilizing LD grouping allows selection of a more faithful set of tag SNPs than do previous algorithms utilizing haplotype blocks.

SINGLE nucleotide polymorphisms (SNPs) are stably inherited, highly abundant, and distributed throughout the genome. These variations are associated not only with diversity within and among populations, but also with individual responses to medication and susceptibility to diseases (Strachan and Read 2004). In particular, positional cloning of genes for disease susceptibility depends on linkage disequilibrium (LD) and correlations among alleles of neighboring variations, reflecting “haplotypes” descended from a common, ancestral chromosome. It has become clear that chromosomally mapped and ordered SNPs can be grouped into “haplotype blocks” harboring a limited number of distinct haplotypes (Gabriel et al. 2002). Several studies have shown that the human genome is structured with such segments within which there is strong LD among relatively common SNPs, but between which recombination has left little LD (Patil et al. 2001). When SNPs are in strong LD, the alleles of a few SNPs on a haplotype suggest the alleles of the other SNPs, which as a result provide redundant information. Consequently, a modest number of common SNPs selected from each segment would suffice to define the relevant haplotypes in presumably any population. This hypothesis has led to the HAPMAP project (http://www.hapmap.org), which aims at developing a map of common haplotype patterns throughout the genome in several ethnic populations. Once each gene (or chromosomal fragment) is subdivided into haplotype blocks, the haplotypes can be “tagged” by a subset of all available SNPs, the so-called tag SNPs. The construction of a haplotype map of the human genome and the definition of tag SNPs are expected to facilitate association studies of common genetic variation, in particular, to determine as-yet-unidentified disease-causing alleles.

However, in real data, LD among SNPs does not necessarily produce clear segmental structure, and selection of tag SNPs is not straightforward. When a well-defined haplotype block contains only a group of SNPs in almost complete LD, any SNP can be used as a tag SNP, and the selection is simple. For two groups of SNPs in no intergroup LD, genotype information of SNPs in one group is not useful to deduce genotype information of SNPs in the other group, and tag SNPs can be selected independently from each group. In most cases, however, because both SNPs in strong LD and those in weak LD mingle in certain chromosomal fragments, selection of tag SNPs has to be made by considering such a complex feature of LD relations. Moreover, as the number of SNPs under investigation increases, LD relations among them become complicated. Several tag SNP selection methods have been proposed (Zhang et al. 2002; Eskin et al. 2003), but none have been shown to be definitive so far.

We took this issue up by classifying SNPs in strong LD into separate groups and then selecting tag SNPs from each group independently. We first characterized a number of SNPs in five genes—ABCA1, ADPRT, F5, LPL, and SLC12A3—and tested our newly developed tag SNP selection algorithm on them. Among these five genes, we examined in detail the LPL (lipoprotein lipase) gene, which had been extensively studied for LD and haplotype structure (Clark et al. 1998; Nickerson et al. 1998; Templeton et al. 2000a,b; Morabia et al. 2003), because of the presence of highly abundant polymorphisms and because of its physio-pathological importance. Independently of observations from the previous reports, we investigated the LD relations with particular attention to ethnic diversity and studied the phylogenic tree of haplotypes to clarify the theoretical basis underlying our tag SNP selection algorithm. We also examined ethnic diversity in allele frequencies of SNPs more extensively with a set of 979 SNPs distributed throughout the genome.

MATERIALS AND METHODS

SNP discovery and genotyping in five genes:

To investigate LD and tag SNP selection, we used a number of SNPs from five genes—ABCA1, ADPRT, F5, LPL, and SLC12A3. These five genes were chosen because they had been shown to hold a large number of SNPs (25 or more) through our SNP discovery, which was part of our ongoing project on 150 atherosclerosis candidate genes. First, SNPs were screened by direct sequencing of genomic DNA derived from 48 Japanese subjects in all exons, 5′-untranslated regions (5′-UTRs), and 3′-UTRs of each gene. In addition to SNPs thus detected, those reported in previous publications and those listed in the assays-on-demand set (Applied Biosystems, Foster City, CA) were genotyped by either the TaqMan method (Applied Biosystems) or restriction fragment length polymorphism. The panel of DNA samples consisted of 113 Japanese volunteers, as well as 100 African Americans and 100 Caucasians, samples for both of which were purchased from the Coriell Cell Repositories (Camden, NJ). We selected SNPs that were consistent with Hardy-Weinberg equilibrium and had minor allele frequencies (MAFs) of at least 5% in an ethnic population. The threshold of 5% was chosen because it was considered to be the lowest MAF for a potentially causative SNP with a genotype relative risk of at least 2 being detectable with a sample size of 1000 in the case-control study design (Risch 2000). All subjects gave written consent for participation and the protocols were approved by the ethics committee of the International Medical Center of Japan.

Tag SNP selection:

First, in our strategy for tag SNP selection, SNPs in LD greater than a given threshold were grouped together, which was conceptually analogous to haplotype block partitioning. Then, independently in each group, the SNPs were divided into subgroups in complete LD with respect to haplotype classes in the individual groups. In any group, the selection of any one SNP from each of the subgroups could distinguish the haplotype classes. The collection of SNPs thus selected over all the groups was defined as a tag SNP set. Even when the SNPs as a whole spanned different haplotype blocks, those in an LD group were expected to reside within one haplotype block. The appropriate threshold for grouping was determined automatically in our algorithm as described below. (The computer program for the algorithm presented in this article is available from http://www.fumihiko.takeuchi.name/publications.html.) Our tag SNP selection algorithm consists of the following steps. Here, MAFs of SNPs were assumed to be at least 5%.

• Step 1. Compute LD coefficient r² between SNPs.

• Step 2. For s = 0.0, 0.1, 0.2, … , 1.0, where s is an arbitrarily definable threshold against r², do steps 3–6 to compute the LD groups (step 3), complete LD subgroups (step 5), and the “total frequency of neglected haplotype classes” (step 6) under respective thresholds.

• Step 3. Divide SNPs into LD groups: if two SNPs have r² ≥ s, they belong to the same LD group.

• Step 4. For each LD group, infer haplotype classes for the SNPs.

• Step 5. For each LD group, divide the SNPs into complete LD subgroups: the SNPs in complete LD (i.e., co-inherited) with respect to common haplotype classes (frequency ≥ 5%) belong to the same complete LD subgroup.

• Step 6. For each LD group consisting of more than one SNP, sum the frequencies of rare haplotype classes (frequency < 5%) and define the average value of the sum over a series of LD groups as the “total frequency of neglected haplotype classes.”

• Step 7. Find the minimum value, t, for a threshold, s, such that the total frequency of neglected haplotype classes (step 6) is at most 5% for s ≥ t, but not necessarily so for s < t. Output this r² threshold, t, and adopt the classifications of SNPs by LD groups (step 3) and complete LD subgroups (step 5) for this t. The selection of any one SNP from each of the complete LD subgroups constitutes a tag SNP set.

For tag SNPs thus selected, the imprecision in the allele-frequency estimation of nontag SNPs was guaranteed to be limited. In application, genotyping of the tag SNPs gives their allele frequencies, which in turn approximate allele frequencies of the nontag SNPs belonging to the same complete LD subgroup. Thus, the errors in this approximation involve those due to the noninclusion of rare haplotype classes (step 5), whose frequencies sum at most 5% on average (step 6 and 7), and those due to the imprecise inference of haplotypes, which seems to be negligible since the SNPs are in LD greater than the threshold to constitute one LD group (step 3). This error bound is valid as long as the genotyped populations have an LD structure similar to the population initially used for tag SNP selection.

The (minimum) threshold, t, providing such guarantee (step 7) always exists, because for s = 1, only the SNPs in complete LD (with respect to haplotypes inferable from all the SNPs) are grouped together in an LD group, and thus the haplotype classes of the LD group correspond to the alleles of the SNPs (which were assumed to have a frequency of at least 5%); hence the total frequency of neglected haplotype classes (step 6) becomes zero. Although a higher threshold value than the one computed in step 7 also guarantees limiting approximation errors, it will result in the selection of a larger tag SNP set.

The haplotypes were inferred by the SNPHAP software (Clayton 2004). LD coefficient r² and LD grouping were calculated with Mathematica (Wolfram Research 2003). [See, for example, the handbook (Balding et al. 2001) for the definition of the coefficient r², which is sometimes denoted as Δ².] A tag SNP set selected with our algorithm was evaluated for two factors: efficiency and imprecision. The efficiency of the selected tag SNP set was evaluated by the ratio between its size (which could equal the number of complete LD subgroups) and the number of polymorphic SNPs. The imprecision of allele-frequency estimation of nontag SNPs was evaluated by calculating the allele-frequency ranges (which were the differences between the maximum and minimum frequencies) of the SNPs in each complete LD subgroup consisting of more than one SNP and then by taking their mean. The maximum of the ranges was also calculated to demonstrate the maximum limit of imprecision.

Evaluation of ethnic diversity using an additional panel of SNPs:

To evaluate ethnic diversity in allele frequencies of SNPs more extensively, we genotyped 1380 SNPs in the HuSNP set (Affymetrix, Santa Clara, CA) in 12 Japanese volunteers according to the manufacturer's protocol. As for 979 SNPs that showed unambiguous genotype scores in >9 of the 12 subjects (genotyping success rate >75%), MAFs were calculated. The genotype results of the Japanese were compared to those of a reference panel that consisted of 113 Western Europeans, 10 African Americans, and 10 Asians provided by the manufacturer as supplementary data. In addition, by referring to the dbSNP (http://www.ncbi.nlm.nih.gov/SNP/), the genotyped SNPs were categorized into three positional classes—exon, intron, and UTR—when applicable.

Characterization of the phylogenic closeness of SNPs:

To investigate LD groups and complete LD subgroups of SNPs from a different viewpoint, we introduced the phylogenic closeness of SNPs to represent the proximity of SNPs in the phylogeny of haplotypes. First, haplotypes were inferred from genotype data by the SNPHAP software (see Table 1 for SNPs of the LPL gene and Table 2 for haplotypes of selected SNPs). Then, the most parsimonious phylogenic tree of haplotypes was computed by the PaupSearch (Genetics Computer Group 2001) and drawn by the TreeView software (Page 1996) (see Figure 1A). An edge connecting two haplotype nodes in the tree corresponds to the SNP(s) at which the haplotypes differ. The phylogenic closeness of SNPs was defined as a “relation” between the SNPs: two SNPs were thought to be related if their corresponding edges were connected to a common haplotype node in the tree. (For example, SNP13 and SNP24 are related, because their corresponding edges share HAP1 in Figure 1A, whereas SNP13 and SNP14 are not related.) This relation was reshaped into a diagram with nodes corresponding to the SNPs and edges between two related nodes, i.e., SNPs (see Figure 1B). When multiple SNPs were labeled on an edge in the phylogenic tree of haplotypes, the phylogenic closeness relation was defined as follows. A group of SNPs always appearing together in the tree (e.g., SNP9 and SNP10 in Figure 1A) were treated as identical. On the other hand, a pair of SNPs appearing together on some edges but separately on others (e.g., SNP17 and SNP20 appeared together between HAP8 and HAP9, but were separated by HAP13, in the lower-left and lower-right, respectively, of Figure 1A) were treated as different SNPs. In such a case, we enumerated all the possible trees [e.g., with respect to SNP17 and SNP20, either HAP8-SNP17-(undetected haplotype)-SNP20-HAP9 or HAP8-SNP20-(undetected haplotype)-SNP17-HAP9 are possible], and among the resulting relations we chose the one having the smallest number of related SNP pairs.

TABLE 1.

SNPs genotyped in theLPL gene

					Minor allele frequency (%)d					Previously studied SNPs in LPLe
Namea	In gene	SNPb	Amino Acidc	nt position (chromosome 8) RefSeq Build 34	Japanese	African Americans	Caucasians	dbSNP ID	JSNP ID	Templeton et al. (2000a)	Morabia et al. (2003)
SNP1f,g	Intron 1	G/A	—	19,809,412	0.0	11.2	23.2	—	—	—	—
SNP2f	Intron 1	C/T	—	19,812,675	88.5	18.5	52.0	rs10104051	—	—	—
SNP3	Intron 3	C/A	—	19,821,060	10.6	5.9	6.6	rs343	—	1	—
SNP4f	Exon 4	G/A	I/I	19,821,099	0.0	4.5	7.5	rs248	—	3	Exon 4_b.6
SNP5	Intron 4	T/C	—	19,821,279	6.3	10.2	9.6	rs249	—	4	—
SNP6	Intron 5	C/G	—	19,822,170	16.4	20.4	14.4	rs254	—	9	—
SNP7	Intron 6	T/G	—	19,823,940	18.5	41.6	17.4	rs269	IMS-JST003328	19	Exon 6_+73
SNP8	Intron 6	C/A	—	19,823,949	6.3	9.9	20.4	rs270	—	20	Exon 6_+82
SNP9	Intron 6	T/C	—	19,826,644	18.3	34.4	23.2	rs297	—	43
SNP10	Intron 7	T/C	—	19,827,207	15.0	33.0	23.5	rs301	IMS-JST185262	44	—
SNP11	Intron 7	G/C	—	19,828,270	7.7	27.3	11.2	rs312	—	51
SNP12	Exon 8	C/A	T/T	19,828,709	6.3	24.7	11.2	rs316	—	55	Exon 8_b.25
SNP13f	Intron 8	A/G	—	19,829,712	18.5	58.0	30.3	rs326	IMS-JST089898	65	—
SNP14	Intron 8	T/G	—	19,829,809	15.6	46.3	29.2	rs327	IMS-JST089899	66	Exon 9_-90
SNP15	Exon 9	C/G	S/X	19,829,997	9.6	7.2	9.2	rs328	IMS-JST089900	—	Exon 9_b.99
SNP16	Intron 9	C/T	—	19,833,083	9.5	7.7	10.5	rs11570891	—	—	Exon 10_-11
SNP17	Exon 10	G/A	—	19,833,103	6.3	13.8	16.0	rs4922115	—	—	Exon 10_b.10
SNP18	Exon 10	A/G	—	19,833,890	5.8	29.3	15.7	rs11570892	—	—	—
SNP19	Exon 10	A/T	—	19,833,921	14.7	55.6	28.6	rs3208305	—	—	—
SNP20	Exon 10	C/T	—	19,834,236	6.2	12.1	13.5	rs1059507	IMS-JST089901	—	—
SNP21	Exon 10	C/A	—	19,834,318	9.4	7.1	10.7	rs3735964	IMS-JST089902	—	—
SNP22	Exon 10	T/C	—	19,834,765	15.5	53.2	29.1	rs13702	—	—	—
SNP23	Exon 10	C/A	—	19,834,942	6.6	22.0	16.0	rs3866471	—	—	—
SNP24	3′-flanking	T/G	—	19,835,169	22.3	8.0	29.0	rs9644636	—	—	—
SNP25f	3′-flanking	C/T	—	19,841,194	10.9	44.4	12.0	rs10096633	—	—	—

^aThe number of an SNP corresponds with the location order in the LPL gene. Among them, SNP1 and SNP4 were not informative in the Japanese.

^bThe nucleotide to the left of the slash was the more frequent allele.

^cX denotes a stop codon.

^dIndividual SNPs were characterized in 113 Japanese, 100 African Americans, and 100 Caucasians as described in materials and methods.

^eWhen applicable, the identity of SNPs previously studied by two other groups of researchers is shown for the relevant SNPs characterized in this study.

^fSNPs derived from Assays-on-Demand (Applied Biosystems).

^gAssays-on-Demand ID was C_9642874_10.

TABLE 2.

Estimated haplotype frequencies in three ethnic populations for the central 16 SNPs in theLPL gene

		Japanese		African Americans		Caucasians
Haplotype class inferred from all 16 SNPsa	Haplotype (from SNP9 to SNP24)	Frequency (%)	(Order)b	Frequency (%)	(Order)b	Frequency (%)	(Order)b
HAP1	TTGCATCCGAACCTCT	63.9	(1)	31.5	(1)	42.5	(1)
HAP2	TTGCATCCGAACCTCG	20.2	(2)	6.4	(6)	26.5	(2)
HAP3	CCCAGGCCAGTTCCAT	5.3	(4)	10.5	(2)	11.0	(3)
HAP4	CCGCGGGTGATCACCT	6.9	(3)	6.5	(5)	9.9	(4)
HAP5	TTGCGTCCGATCCCCT	—	—	8.5	(4)	2.0	(6)
HAP6	CCCAGGCCGATCCCCT	—	—	9.3	(3)	—	—
HAP7	TTGCGGCCGGTCCCCT	—	—	5.9	(7)	—	—
HAP8	TTGCGGCCAGTTCCAT	—	—	—	—	5.0	(5)
HAP9	TTGCGGCCGGTCCCAT	—	—	3.4	(8)	—	—
HAP10	TTGCGTCCGAACCTCT	—	—	3.0	(9)	—	—
HAP11	CCCCGGCCGATCCCCT	—	—	2.1	(10)	—	—
HAP12	TTGCATCCGGACCTCT	—	—	2.0	(11)	—	—
HAP13	CCCAGGCCAGTCCCAT	—	—	2.0	(12)	—	—
HAP14	CCCAGGCCGGTCCCAT	—	—	2.0	(13)	—	—
Haplotype class inferred from 6 SNPs in SNP cluster A (SNP9, SNP10, SNP13, SNP14, SNP19 and SNP22)c
A-1 (HAP1 + 2 + 12)	TT--AT----A--T--	84.5	(1)	39.9	(1)	69.0	(1)
A-2 (HAP3 + 4 + 6 +   11 + 13 + 14)	CC--GG----T--C--	14.6	(2)	34.0	(2)	21.5	(2)
A-3 (HAP7 + 8 + 9)	TT--GG----T--C--	—	—	9.6	(3)	5.0	(3)
A-4 (HAP5)	TT--GT----T--C--	—	—	8.7	(4)	—	—
Haplotype class inferred from 4 SNPs in SNP cluster B (SNP17, SNP18, SNP20 and SNP23)c
B-1 (HAP1 + 2 + 4 +   5 + 6 + 10 + 11)	--------GA-C--C-	93.4	(1)	69.3	(1)	84.0	(1)
B-2 (HAP3 + 8)	--------AG-T--A-	5.8	(2)	12.0	(2)	16.0	(2)
B-3 (HAP7 + 12)	--------GG-C--C-	—	—	8.7	(3)	—	—
B-4 (HAP9 + 14)	--------GG-C--A-	—	—	6.4	(4)	—	—
Haplotype class inferred from 3 SNPs in SNP cluster C (SNP15, SNP16 and SNP21)c
C-1 (HAP1 + 2 + 3 +   5 + 6 + 7 + 8 +   9 + 10 + 11 + 12 +   13 + 14)	------CC----C---	90.7	(1)	92.0	(1)	89.5	(1)
C-2 (HAP4)	------GT----A---	9.3	(2)	6.9	(2)	9.9	(2)

^aAmong 25 SNPs genotyped in the LPL gene (Table 1, Figure 2C), the central 16 SNPs (SNP9–SNP24 spanning 8.5 kbp) were used for the estimation of haplotype classes because they formed a haplotype block. While a number of haplotype classes were inferred from these SNPs, 14 had a frequency of at least 2% in the Japanese, African American, or Caucasian population, and they were numbered by the frequency order calculated from the three ethnic populations combined.

^bThe frequency order shown in the parentheses was determined by calculating the percentage of the corresponding haplotype class in each ethnic group.

^cSNP clusters are defined in Figure 2B.

Figure 1.—

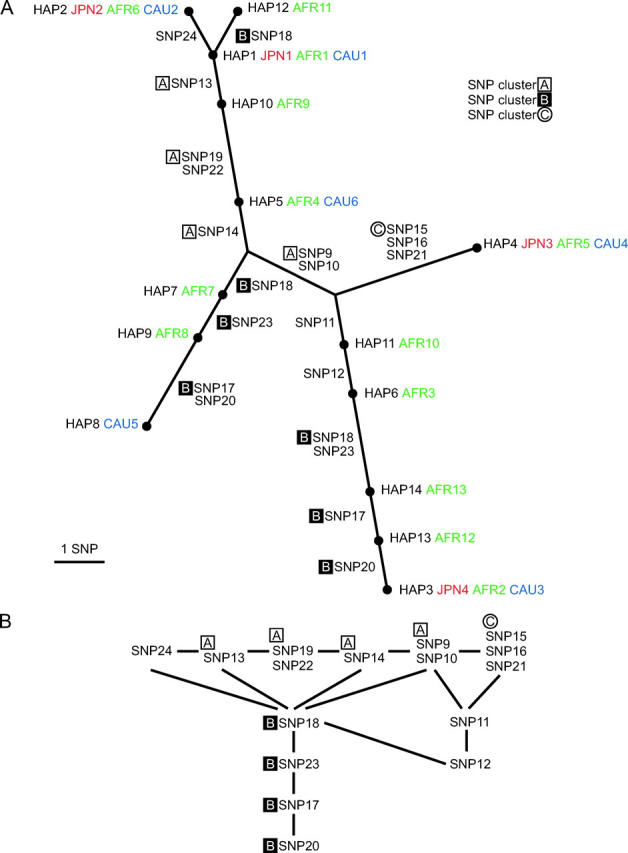
(A) The most parsimonious phylogenic tree of haplotypes for the central 16 SNPs in the LPL gene (see Table 2). For each haplotype, its number and its frequency order in the Japanese (JPN), African Americans (AFR), and Caucasians (CAU) are indicated. For each pair of haplotypes adjacent in the tree, the SNP(s) at which they differ is denoted on the edge between the pair. One of the pair of haplotypes might have been generated from the other one by mutation(s) at the SNP(s) or, alternatively, by recombination. (B) Schematic of the phylogenic closeness of SNPs. Two SNPs related in this closeness (i.e., SNPs with corresponding edges connected to the same haplotype node in A) are connected by an edge. In A and B, three clusters—A, B, and C—of SNPs (see Figure 2B) are marked.

RESULTS

Tag SNP selection and LD:

Our algorithm enabled us to select tag SNPs that reduced the number of SNPs necessary for genotyping down to 43%, on average, for five genes (Table 3). The imprecision of the allele-frequency estimation of the nontag SNPs from the tag SNPs was only 2% on average. The five genes studied in three ethnic populations showed a wide variety of LD relations (Figure 2, A and B), and the efficiency of tag SNP selection, i.e., the number of tag SNPs divided by the number of polymorphic SNPs, ranged widely from 24 to 76% (Table 3). When LD relations between SNPs were strong as a whole, which would be indicated as overall coloration of pixels toward redness in the LD plots, we observed that a small set of tag SNPs would be sufficient to capture genetic information of the gene. Indeed, among the five genes tested, ADPRT and F5 showed a high average value of pairwise LD (0.32 and 0.22 when averaged for three populations, respectively) despite a large number of SNPs and allowed considerable reduction in the number of tag SNPs (the efficiency of tag SNP selection was 28 and 30%, respectively). Moreover, among the three populations, pairwise LD in any gene appeared to be highest in the Japanese and lowest in African Americans, and accordingly the efficiency of tag SNP selection averaged for five genes ranged from 36% for the Japanese to 55% for African Americans. The r² thresholds for LD grouping (i.e., t in step 7) varied among the three populations as well, but were not necessarily associated with average values of pairwise LD or with the efficiency of tag SNP selection (Table 3). On the other hand, the imprecision of allele-frequency estimation was limited to a small range between 1 and 3% for five genes, independently of average values of pairwise LD in three ethnic populations, and the maximum limit of imprecision was estimated to be 9%. The overall differences in LD relations among three populations must be caused by a number of factors, such as diversity in population histories and some selection bias of SNPs, since the SNPs tested in the present study were mostly discovered in the Japanese.

TABLE 3.

Concordance between LD relations and tag SNP selection in five genes for three ethnic populations

		Japanese			African Americans			Caucasians
Gene name	No. of SNPs testeda	Average value of pairwise LDb	Threshold value of LD groupingc	No. of tag SNPs/no. of polymorphic SNPsd (%)	Average value of pairwise LD	Threshold value of LD groupingc	No. of tag SNPs/no. of polymorphic SNPsd (%)	Average value of pairwise LD	Threshold value of LD groupingc	No. of tag SNPs/no. of polymorphic SNPsd (%)
ABCA1	37	0.12	0.4	19/37 (51)	0.05	0.2	24/37 (64)	0.08	0.5	17/37 (45)
ADPRT	29	0.38	0.4	7/29 (24)	0.26	0.6	10/28 (35)	0.32	0.2	7/28 (25)
F5	41	0.25	0.7	12/41 (29)	0.18	0.6	15/41 (36)	0.22	0.2	10/40 (25)
LPL	25	0.31	0.5	9/23 (39)	0.14	0.5	17/25 (68)	0.23	0.4	12/25 (48)
SLC12A3	25	0.14	0.3	10/25 (40)	0.05	0.2	19/25 (76)	0.10	0.3	11/25 (44)

ABCA1, ATP-binding cassette, subfamily A (ABC1), member 1; ADPRT, poly (ADP-ribose) polymerase family, member 1; F5, coagulation factor V; SLC12A3, solute carrier family 12 (sodium/chloride transporters), member 3.

^aFrom exons, 5′-UTRs, and 3′-UTRs of each gene, SNPs with MAF of at least 5% in any of three populations were tested.

^bThe LD by coefficient r² was averaged over all possible pairs of polymorphic SNPs.

^cThe optimal r² threshold for defining LD groups of SNPs was chosen automatically within our algorithm (see the minimum value, t, in step 7).

^dThis ratio indicates the efficiency of tag SNP selection (see results).

Figure 2.—

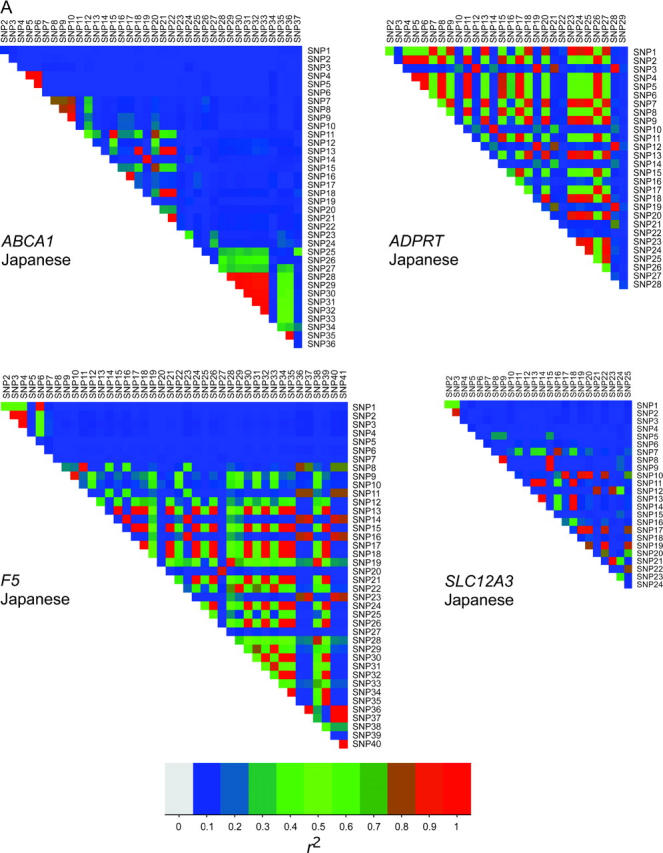
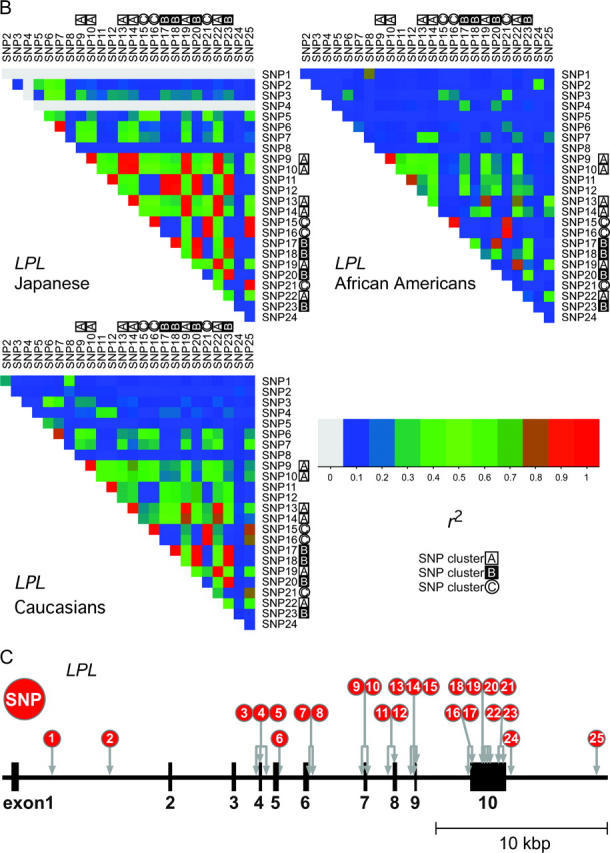
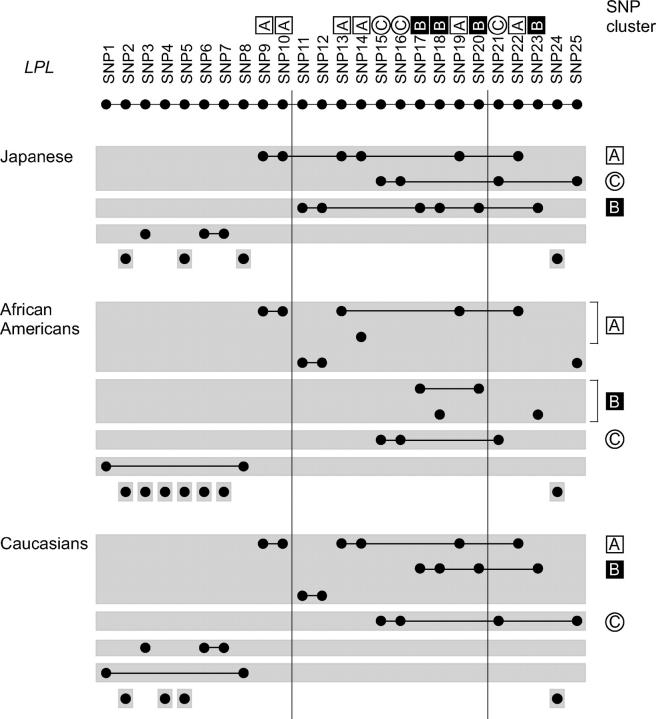
(A) Plots of LD by coefficient r² among SNPs in ABCA1, ADPRT, F5, and SLC12A3 for the Japanese. (B) Plots of LD among SNPs in LPL for the Japanese, African Americans, and Caucasians. In the Japanese, SNP1 and SNP4 are not polymorphic, and their pixels are in light gray. Three clusters of SNPs having strong intracluster LD are marked with A, B, and C. A mosaic pattern consisting of these LD clusters appeared to be common to the three ethnic populations. (C) The positions of 25 SNPs in the LPL gene (see Table 1).

LD structure of SNPs:

We further investigated the relationships among LD, LD groups, and complete LD subgroups (from which tag SNPs were selected) in the LPL gene. Of note is the fact that a mosaic pattern of high-LD pixels within an assumedly haplotype block was commonly observed in the LD plots for three ethnic populations (Figure 2B). This pattern was formed basically by three clusters (or groups) of SNPs in strong intracluster LD: the cluster A included SNP9, SNP10, SNP13, SNP14, SNP19, and SNP22; the cluster B included SNP17, SNP18, SNP20, and SNP23; and the cluster C included SNP15, SNP16, and SNP21. A mosaic pattern of LD plots could be explained by the finding that the physical positions of SNPs belonging to different clusters were mingled. Similarly, mosaic patterns were prominent in the ADPRT and F5 genes (Figure 2A), in which concordant patterns were observed not only for the Japanese but also for African Americans and Caucasians (data not shown).

In the LPL gene, while a concordant mosaic pattern of LD plots was observed across three populations, ethnic consistency was not entirely but partially supported by the concordant classification of LD groups and complete LD subgroups across the populations (Figure 3). Here, any of the three clusters of SNPs—A, B, and C—was found to constitute a class of SNPs in between the coarse classification by LD groups and the fine classification by complete LD subgroups, and this was pertinent to three ethnic populations. Meanwhile, not all the combinations of SNPs in LD groups and complete LD subgroups were identical among the populations. For example, SNP11 and SNP12 were included in an LD group together with cluster A in African Americans, but included in an LD group with cluster B in the Japanese.

Figure 3.—

LD groups and complete LD subgroups of SNPs in the LPL gene for three ethnic populations. SNPs in the same LD group are shaded together, and the SNPs in the same complete LD subgroup are joined by lines. Selection of one SNP from each of the complete LD subgroups constitutes a tag SNP set. For example, in the Japanese, there were seven LD groups. Among them, the topmost LD group consists of 10 SNPs, and it separates into two complete LD subgroups of size six (SNP9, SNP10, SNP13, SNP14, SNP19, and SNP22) and four (SNP15, SNP16, SNP21, and SNP25). As for the four LD groups at the bottom, each consists of one complete LD subgroup, including a single SNP. There are nine complete LD subgroups in total, and a selection of one SNP from each of them composes a tag SNP set of size nine. The SNP cluster name (defined in Figure 2B) to which a SNP belongs is indicated next to the SNP number. The SNP clusters were found as an “intermediate” level of SNP classifications between the two levels—LD groups and complete LD subgroups—in any of the populations. In fact, when compared to LD groups, any of the SNP clusters was included within one LD group; i.e., they were not split into multiple LD groups. On the other hand, when compared to complete LD subgroups, the SNP clusters were distinguishable in the sense that none of the complete LD subgroups were derived from more than one SNP cluster. For each SNP cluster, its name is denoted at the right, and the complete LD groups comprising the SNPs of the cluster are aligned at its left. The clusters highlight concordance in the classifications by LD groups and complete LD groups across ethnic populations. The vertical lines partition every 10 SNPs.

Ethnic diversity in frequencies of SNPs and haplotypes:

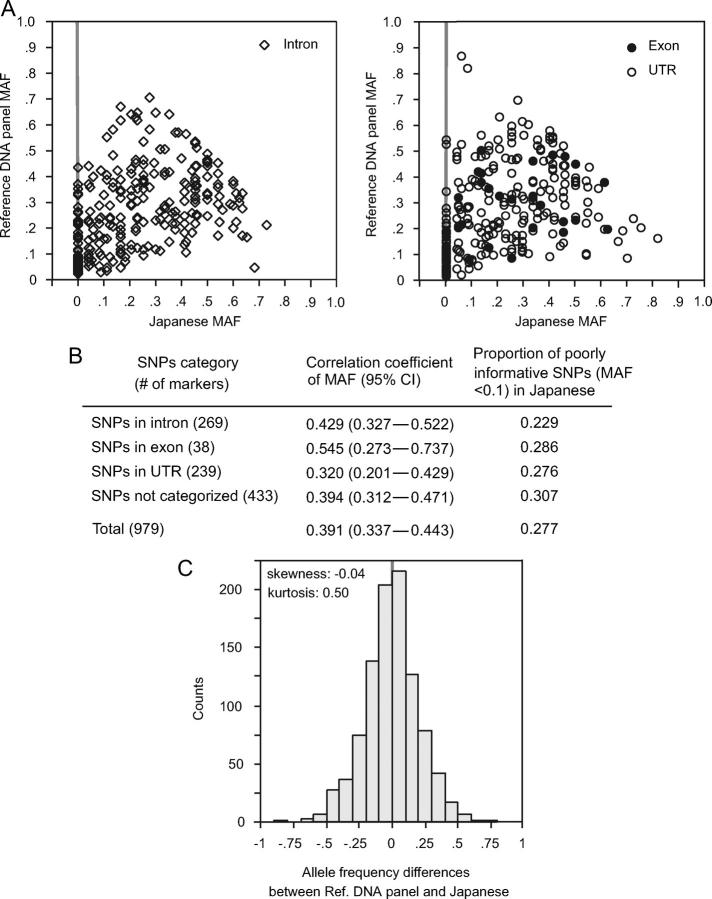
Although LD relations showed moderate ethnic consistency, the allele frequencies of SNPs varied widely among three ethnic populations. In the five genes tested, MAFs showed only weak correlation between the Japanese, African Americans, and Caucasians, and the correlation coefficients were mostly <0.6 (Table 4). To further study the correlation of MAFs on a larger scale, we tested SNPs from the HuSNP set. SNPs in the HuSNP set had been chosen on the basis of relatively high MAFs in a reference panel in which Caucasians constituted a predominant population, but a quarter of genotyped SNPs turned out to be poorly informative (MAF < 0.1) in the Japanese. MAFs of the SNPs did not show significant correlations between the Japanese and the reference panel: correlation coefficients were 0.55 for SNPs in exon, 0.43 in intron, and 0.32 in UTR (Figure 4, A and B). Here, although there were no significant differences in correlation coefficients among three positional classes of SNPs, they tended to be higher for SNPs in exons compared to those for SNPs in UTRs. Allele-frequency differences between the Japanese and the reference panel showed an almost normal distribution in terms of skewness but not in terms of kurtosis (Figure 4C).

TABLE 4.

Correlation coefficients of the MAFs of SNPs in five genes among three ethnic populations

		Correlation coefficients of MAFs between a pair of ethnic populations
Gene name	No. of SNPs	Japanese vs. African Americans	Japanese vs. Caucasians	African Americans vs. Caucasians
ABCA1	37	0.60a	0.28	0.55a
ADPRT	29	−0.09	−0.29	0.61a
F5	41	0.37a	−0.39a	0.46a
LPL	25	0.12	0.78a	0.42a
SLC12A3	25	0.24	0.34	0.58a

^aThe MAFs of SNPs were significantly correlated (i.e., the t-satistics testing no linear regression showed P-values <0.05).

Figure 4.—

(A) Allele-frequency comparison between the Japanese and a reference panel. The minor allele was set as the less-frequent allele in the combined population, and MAF was calculated in each population for the 979 SNPs analyzed. (B) Correlation coefficients of MAFs according to the positional classes of SNPs. MAFs of SNPs did not show significant correlations between the Japanese and a reference panel and there were no significant differences in correlations among three positional classes of SNPs. (C) Allele-frequency differences between the Japanese and a reference panel. Almost normal distribution was observed in terms of skewness (b₁ = −0.04) but not in terms of kurtosis (b₂ = 0.50, significantly different from normal distribution).

A tag SNP set commonly useful for different ethnic populations could be detected by our algorithm under two conditions: if the classification by LD groups was comparable among populations and if the haplotype classes in each LD group was comparable. For the first condition, as described above, LD groups were moderately concordant across ethnic populations. For the second condition, we estimated the extent to which haplotype classes were conserved in case arbitrarily defined classes of SNPs were comparable among populations. We took the SNP clusters A, B, and C in the LPL gene and separately computed haplotype classes with a frequency of at least 5% in three populations (Table 2). The frequency order of common haplotype classes was concordant across the populations, while the frequency of each haplotype class and the total number of common haplotype classes differed widely. For example, in the cluster A, the A-1 haplotype was the most frequent class in all of the three populations, but its frequency ranged from 39.9% in African Americans to 84.5% in the Japanese and the total number of common haplotypes ranged from four in African Americans to two in the Japanese. To statistically capture haplotype information covering all the populations, three tag SNPs were required to distinguish four common haplotype classes in African Americans, whereas any of the three tag SNPs was sufficient to distinguish two common haplotypes in the Japanese. This indicated that some redundancy of SNPs would be inevitable for a tag SNP set working universally for different ethnic populations.

Phylogenic closeness of SNPs:

We have defined LD groups and complete LD subgroups in statistical terms so far, and we next demonstrate that such grouping of SNPs may well be correlated with the “phylogenic closeness” of SNPs. To be precise, it is the inheritance of haplotypes that may determine their phylogeny, in which a SNP mutation or a recombination may generate a new haplotype from the existing ones. Thus, in general, SNPs themselves do not form a framework of phylogeny, but serve as “connections” between haplotypes that constitute phylogeny. Here we investigated the closeness of SNPs in the phylogeny. Among 25 SNPs genotyped in the LPL gene (Table 1, Figure 2C), we focused on the central 16 SNPs (SNP9–SNP24 spanning 8.5 kbp), which formed a haplotype block. While a number of haplotype classes were inferred for these SNPs, 14 had a frequency of at least 2% in the Japanese, African American, or Caucasian populations (Table 2). The resultant phylogenic tree of haplotypes was the most parsimonious tree (Figure 1A).

To depict the closeness of SNPs in this tree explicitly, we reshaped the diagram as shown in Figure 1B. In the preceding arguments, three clusters of SNPs in the LPL gene (Figure 2B) typically represent three aspects of LD relations of SNPs: patterns in LD plots, LD groups, and complete LD subgroups. Each cluster of SNPs was found to be congregated closely in the diagram. This supports the idea that these two independent approaches to partitioning SNPs—one by LD relations and the other by mutual proximity from the phylogenic viewpoint—were indeed consistent.

DISCUSSION

In this study, we developed a tag SNP selection algorithm that can spare, on average, ∼60% of SNPs required for genotyping and that can simultaneously limit the imprecision of allele-frequency estimation of the nontag SNPs (i.e., SNPs not directly characterized but assumed to be in strong LD with a tag SNP) to 2% in the five genes tested (Table 3). In our algorithm, SNPs are first classified into LD groups on the basis of LD relations calculated by coefficient r² and then each LD group is divided into complete LD subgroups such that a set of tag SNPs derived from the subgroups can distinguish common haplotype classes in the LD group. We have found that a mosaic pattern of LD plots exists and that three clusters of SNPs with strong intracluster LD form this pattern in the LPL gene (Figure 2B). Moreover, we have found that the grouping of SNPs by LD relations typically reflects their mutual proximity from the phylogenic viewpoint (Figure 1). While Carlson et al. (2004) previously reported a greedy algorithm for tag SNP selection based on the LD coefficient r² under a stringent threshold, we believe that our algorithm is unique in the sense that tag SNPs are selected on the basis of LD grouping of SNPs, which we have proven to be compatible with the structure of SNPs in the phylogeny of haplotypes.

Our algorithm has two major advantages over tag SNP selection algorithms previously proposed. First, most algorithms (Patil et al. 2001; Zhang et al. 2002; Eskin et al. 2003; Zhang and Jin 2003) assume the existence of haplotype blocks, which is appropriate only in the limited situations discussed below. Second, the input data required for many of them are haplotypes, whereas our algorithm requires genotypes of individual SNPs alone, which can be generated by current high-throughout typing technologies. In addition, tag SNP selection based on LD relations, which are equivalent to haplotypes for two SNPs, can be accurately performed by using fewer individuals than that based on haplotype inference of multiple SNPs, because haplotype inference for a larger number of SNPs generally requires higher computational load but results in lower precision.

Several features of SNPs and haplotypes have been brought up in the present study. First of all, ethnic diversity is an issue of interest. We found moderate conservation across three ethnic populations in the genetic makeup of SNPs but not in the allele frequencies of SNPs or haplotypes. In accordance with a previous report comparing African Americans and European Americans (Carlson et al. 2003), our SNP data in the HuSNP set (Figure 4) do not show significant correlations of MAFs between the Japanese and a reference population, and our SNP data in five genes have also led to similar observations in the Japanese, African Americans, and Caucasians (Table 4). In contrast, the patterns of LD plots have shown some similarity across the populations (Figure 2B) due to moderate conservation in the genetic makeup of SNPs, which is represented by the partially concordant classification of LD groups (Figure 3). However, the details of tag SNPs are not entirely concordant among three populations. As far as tag SNPs are concerned, similarity in the LD grouping, the frequency order of common haplotypes in an LD group, and discrepancy in the frequencies and the number of common haplotypes (Table 2) have indicated that, although tag SNP selection can be performed commonly across ethnic populations to some extent, part of the selected tag SNPs will become redundant in some populations.

Second, a mosaic pattern formed by LD groups is another issue of interest. This mosaic pattern emerges when multiple clusters of SNPs with strong intracluster LD are mingled in the physical order in a certain chromosomal segment. In the LPL gene, a number of LD groups and complete LD subgroups of SNPs exist, which are mingled as such within a conventionally inferred haplotype block, thereby resulting in a mosaic pattern (Figure 2B and 4). We have observed this kind of mosaic pattern in ADPRT and F5 as well (Figure 2A). Overall, three of five genes having 25 or more SNPs show an apparent mosaic pattern, suggesting that such a phenomenon may not be exceptional especially when SNPs are genotyped densely.

Third, the concept of haplotype blocks needs to be reconsidered with reference to the SNP classification by LD groups. The mosaic pattern formed by LD groups implies that the overall LD relations among SNPs are not faithfully represented by haplotype blocks, each of which is thought to comprise a consecutive set of SNPs on the chromosome. The representation of LD relations by haplotype blocks may be appropriate when we analyze SNPs sparsely placed on the chromosome. However, even for such SNPs, the potential presence of multiple LD groups could make it difficult to determine the exact boundaries of a given haplotype block. As for the LPL gene, the preceding publications have already shown the presence of a haplotype block from SNP9 to its downstream, a recombination hotspot in the upstream of SNP9 (Clark et al. 1998; Templeton et al. 2000a), and recombinational events within the haplotype block (Templeton et al. 2000b). By adopting the LD coefficient r², we have additionally discovered the presence of several LD groups involving three or more clusters of SNPs within the haplotype block.

Fourth, the coverage of genetic information by selected tag SNPs is critical. Our results for the LPL gene suggest that tag SNPs are selected on the basis of LD groups and complete LD subgroups rather than on the basis of haplotype blocks when the target gene is relatively large. For example, SNP24 constitutes a single LD group by itself and has been selected as a tag SNP. It is located between SNPs belonging to different LD groups (Figure 3). When tag SNP selection is performed primarily on the basis of haplotype blocks, SNP24 may be concealed by its flanking SNPs—SNP21, SNP22, SNP23, and SNP25—in the relevant haplotype block and may not be selected as a unique tag SNP any more. Because SNP24 shows a high MAF in the Japanese (22%) and in Caucasians (29%), the failure to select this SNP for genotyping decreases the statistical power of genetic association studies. In this context, tag SNP selection with equally spaced SNPs on the chromosome also puts studies at risk for losing genetic information.

In summary, we have developed a two-level grouping of SNPs by LD relations, and thereby we have demonstrated the efficiency of our tag SNP selection algorithm in the representative data. This enlightens our understanding of genetic polymorphisms and facilitates their use in genetic studies. We still need to examine a larger number of genes to validate the close relations between LD statistics and phylogenic structures and the moderate conservation of these relations among different ethnic populations. Also, in a larger sample set, we need to evaluate the efficiency of our tag SNP selection algorithm in more detail, particularly by comparing it with the preceding ones. Then, such studies will answer the question of how our observations of five genes are extendable to the entire genome.

APPENDIX:

EXTENSIVE EXAMINATION OF THE r² THRESHOLD AND LD GROUPS

In our tag SNP selection, the classification of SNPs by LD groups (step 3) changed according to the r² threshold (variable s in step 2). For example, in the two extremes, under s = 1, only the SNPs in complete LD were grouped together, whereas under s = 0, all the SNPs belonged together in a single LD group. For the sake of comprehensibility, we restricted the candidate values for the optimal threshold (the minimum value, t, in step 7) to s = 0.0, 0.1, 0.2, … , 1.0 (step 2) and did not examine all possibilities in the range 0 ≤ s ≤ 1. Also, correspondingly, not all possibilities were tested for the classifications by LD groups or complete LD subgroups.

Alternatively, we can examine LD groups extensively by a variation of our algorithm in which the statement in step 2 needs to be changed to “For 0 ≤ s ≤ 1, do step 3–6.” This caused more cases of LD groups to be examined in the LPL gene (Figure A1)

Figure A1.—

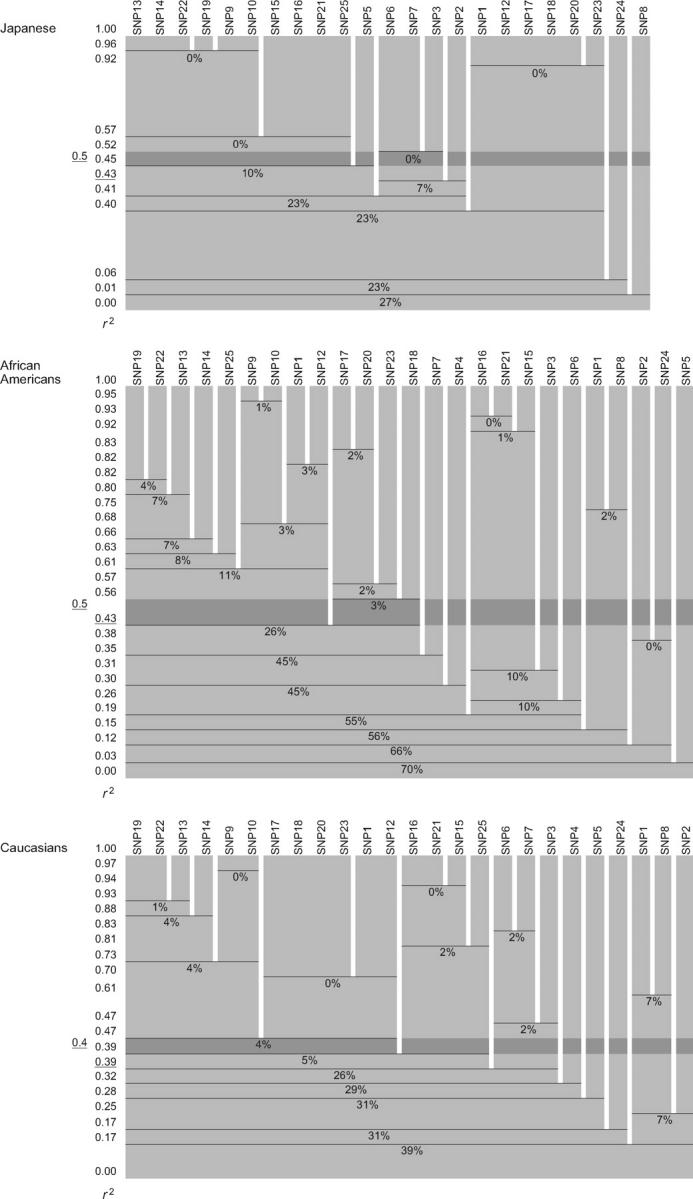
SNP classification by LD groups against various r² thresholds in the LPL gene in three ethnic populations. For any r² threshold between zero and one, locate its position in the vertical axis. The SNP classification by LD groups against a given threshold is at its right on the horizontal axis: the SNPs classified in the same LD group are placed together in a single shaded rectangle. Each rectangle outlined by two horizontal lines corresponds to an LD group, and the sum of the frequencies of rare haplotype classes (see step 6 of the tag SNP selection algorithm) is indicated as a percentage within the rectangle. Since the sum for LD groups against the r² threshold of one (e.g., a group of SNP13, SNP14, and SNP22 in the Japanese) is always 0%, the sum is not denoted for such cases. The average of the sums across a series of LD groups against the r² threshold value becomes the “total frequency of neglected haplotype classes” (see step 6). Note that even for this continuous range of the r² thresholds, there are only finite possibilities for classification by LD group. As the r² threshold decreases, separate clusters of SNPs are combined and form a larger LD group. Overall, the sum of the frequencies of rare haplotype classes for combined LD groups tends to become larger than that for separate clusters of SNPs. The optimal threshold value, t, in the original tag SNP selection algorithm is underlined at the far left, and the resultant classification by LD groups is indicated by dark shading (see also Figure 3). The optimal threshold for the continuous version (see appendix) is also underlined in the immediate left.

. However, as a conclusion, the optimal threshold value, t, and the resultant classification by LD groups were almost the same for the two versions. In the Japanese, with the original threshold of t = 0.5, we could detect three LD groups (indicated by dark shading in Figure A1) that included more than one SNP. This resulted in the total frequency of neglected haplotype classes being (0 + 0 + 0)/3 = 0% (see step 6). For the continuous version shown in Figure A1, the optimal threshold was t = 0.43, a little less than the original version, with which we could detect three LD groups as well (indicated just below the dark shaded row) that included more than one SNP. This resulted in the total frequency of neglected haplotype classes being (10 + 0 + 0)/3 = 3%, which was still <5% (see step 7). In the Caucasians, the threshold value for the continuous version was 0.39 instead of 0.4 for the original version, which caused two LD groups to be joined. On the other hand, in African Americans, the thresholds were 0.5 and 0.43, respectively, and this yielded identical LD groups. Nevertheless, for software implementation, we recommend the use of the more extensive continuous version.