Abstract
Our ability to predict long-term responses to artificial and natural selection, and understand the mechanisms by which naturally occurring variation for quantitative traits is maintained, depends on detailed knowledge of the properties of spontaneous polygenic mutations, including the quantitative trait loci (QTL) at which mutations occur, mutation rates, and mutational effects. These parameters can be estimated by mapping QTL that cause divergence between mutation-accumulation lines that have been established from an inbred base population and selected for high and low trait values. Here, we have utilized quantitative complementation to deficiencies to map QTL at which spontaneous mutations affecting Drosophila abdominal and sternopleural bristle number have occurred in 11 replicate lines during 206 generations of divergent selection. Estimates of the numbers of mutations were consistent with diploid per-character mutation rates for bristle traits of 0.03. The ratio of the per-character mutation rate to total mutation rate (0.023) implies that >2% of the genome could affect just one bristle trait and that there must be extensive pleiotropy for quantitative phenotypes. The estimated mutational effects were not, however, additive and exhibited dependency on genetic background consistent with diminishing epistasis. However, these inferences must be tempered by the potential for epistatic interactions between spontaneous mutations and QTL affecting bristle number on the deficiency-bearing chromosomes, which could lead to overestimates in numbers of QTL and inaccurate inference of gene action.
AT what loci do spontaneous mutations affecting quantitative traits occur? What are per-character and per-locus mutation rates and allelic effects of new polygenic mutations? What is the molecular nature of spontaneous mutations? Answers to these questions are critical if we are to predict long-term responses to artificial and natural selection and understand the extent to which naturally occurring variation for quantitative traits is caused by mutation-selection balance (Barton and Turelli 1989; Falconer and Mackay 1996).
As with many central questions in evolutionary quantitative genetics, answers remain elusive because the only quantity that can be measured with relative ease, the input of new mutational variance for the trait per generation (VM; Clayton and Robertson 1955; Hill 1982), is a composite parameter of the very quantities we wish to estimate separately: numbers of loci affecting the trait, mutation rates per locus, and variance of allelic effects. VM can be estimated from mutation-accumulation experiments, in which an initially homozygous strain is split into sublines, each of which is maintained for many generations either with random choice of parents or by artificial selection for extreme phenotypes. Under an additive, neutral model of mutational effects, VM can be estimated from the divergence among unselected sublines (Lynch and Hill 1986) or from response to selection (Hill 1982). These estimates center around 10−3 times the environmental variance (VE) for a variety of traits (Houle et al. 1996), but are biased downward by an amount that depends on the extent to which deleterious mutations affecting the trait are eliminated by natural selection (Keightley et al. 1993).
Nevertheless, substantial subline divergence and responses to selection from new mutations have been documented. Selection for increased and decreased Drosophila bristle number from a highly inbred base population led to an average divergence of 12.0 abdominal and 8.2 sternopleural bristles after 125 generations (Mackay et al. 1994) and 11.1 abdominal and 15.8 sternopleural bristles after 184 generations (Mackay and Lyman 1998). These differences are large enough to map the quantitative trait loci (QTL) at which new mutations occurred and thus directly address the questions of interest. However, mapping QTL in multiple mutation-accumulation lines poses special problems. Typically, Drosophila QTL are mapped by linkage to molecular markers in segregating mapping populations derived by crossing two inbred parental lines that differ for the markers and the trait (Mackay 2001). Informative markers are extremely rare in mutation-accumulation lines, since marker polymorphism must itself arise by mutation. There were very few transpositions of transposable elements (Nuzhdin and Mackay 1994, 1995) or microsatellite mutations (Schug et al. 1997, 1998) in these lines, evidence, in fact, for the absence of contamination by exogenous flies. Further, with two to three high- and three low-selection lines per trait, a comprehensive analysis of QTL would entail constructing all of the six to nine possible mapping populations for each trait. The solution to both problems is to map the QTL for each mutation-accumulation line separately, relative to an unrelated strain.
Here, we have used deficiency complementation mapping (Pasyukova et al. 2000) to map QTL harboring new spontaneous mutations affecting bristle number in these mutation-accumulation selection lines. We were able to estimate per-character mutation rates for bristle number from these data and infer extensive pleiotropy of mutations affecting numbers of sensory bristles as well as dependency of mutational effects on genetic background.
MATERIALS AND METHODS
Mutation-accumulation selection lines:
Twelve replicate lines were established from a highly inbred derivative of the Harwich P cytotype reference strain (Kidwell et al. 1977), and three replicates were selected for high (1HA, 2HA, 3HA) and low (1LA, 2LA, 3LA) abdominal and high (1HS, 2HS, 3HS) and low (1LS, 2LS, 3LS) sternopleural bristle number. Sternopleural bristle number was scored as the total number of bristles on the left and right sides, and abdominal bristle number was the number of microchaetae on the most posterior abdominal sternite, segment 6 in females and 5 in males. Up to generation 64, 10 pairs of parents were selected from 40 scored each generation; from generations 65–206, 10 pairs were selected from 20 scored. After 206 generations of artificial selection the lines were maintained by mass mating, with selection of extreme parents every second generation to maintain the bristle number phenotypes. Sternopleural line 1HS was discarded after generation 200 as molecular marker analysis showed it had become contaminated. All other lines were homozygous for transposable element and molecular markers, with occasional mutation events of the markers themselves (Nuzhdin and Mackay 1994, 1995; Schug et al. 1997, 1998).
Estimation of mutational variance from selection response:
The rate at which additive genetic variance is introduced by mutation can be estimated from response to selection under two alternative models, both of which assume that mutations have additive effects and are selectively neutral (Hill 1982). Under the infinitesimal model, mutations are assumed to have such small effects that selection has no effect on genetic variance. Under the large-effects model, mutations are assumed to have large enough effects that the asymptotic response rate is reached immediately. Under the infinitesimal model, response from new mutations to t generations of truncation selection (Rt) is given by
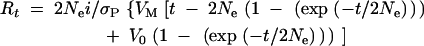 |
Under the large-effects model, response from new mutations to t generations of truncation selection (Rt) is given by
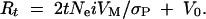 |
In both cases Ne is the effective population size, i is the selection intensity, σP is the phenotypic standard deviation, VM is the mutational variance, and V0 is the genetic variance in the base population (Hill 1982). For additive neutral genes, the expected equilibrium genetic variance in a full-sib inbred line is V0 = 4VM (Keightley et al. 1993). We estimated VM for each selection line by substituting Ne = 14 and i = [1.242(64) + 0.767(142)]/206 = 0.915 (Falconer and Mackay 1996, Appendix Table B) into the above expressions. Rt for each line was estimated as the difference between the mean of the last six generations of selection and the first six generations, and σP for each line was estimated as the square root of the average phenotypic variance (VP) taken over all 206 generations. The environmental variance, VE, was estimated as VP − VG, where the equilibrium genetic variance, VG, was estimated as 2NeVM (Hill 1982).
Deficiency mapping stocks:
The genotypes and cytogenetic breakpoints of 37 X chromosome, 60 chromosome 2, and 65 chromosome 3 deficiency stocks used in quantitative complementation tests are listed in supplementary Table S1 (http://www.genetics.org/supplemental/). All stocks were obtained from the Bloomington, Indiana, Drosophila Stock Center.
Quantitative complementation tests with deficiencies:
Each of the 11 mutation-accumulation selection lines was crossed to each of the deficiency stocks, yielding F1 progeny of genotype Df/Si and Bal/Si, where Df denotes the deficiency and Bal the dominantly marked balancer chromosome, and Si (i = 1, … , 11) indicates the selection line. Sternopleural and abdominal bristle numbers were scored on five males and five females from each of two replicate vials per genotype for the autosomal deficiencies; only females were scored for the X chromosome deficiencies. The sample size was thus 440 (220) for each autosomal (X chromosome) deficiency, for a total of ∼63,140 flies scored.
ANOVA was used to partition the variance in bristle number according to the three-way factorial, mixed model Y = μ + L + G + S + L × G + L × S + L × G × S + V(L × G) + S × V(L × G) + E, where L is selection line, G is F1 genotype (Df/Si or Bal/Si), S is sex, V is replicate vial, and E is the error variance. Terms including vial replicate were considered random effects; all others were treated as fixed effects. Reduced ANOVAs were also run for each sex separately. Quantitative failure to complement was inferred if the L × G and/or L × G × S terms were significant (Long et al. 1996; Mackay and Fry 1996; Lyman and Mackay 1998; Gurganus et al. 1999; Pasyukova et al. 2000).
As for all complementation tests using nonisogenic deficiency stocks, failure of QTL alleles to complement deficiencies could arise in four possible circumstances. First, the deficiency could uncover QTL mutant alleles affecting bristle number in one or more selection lines but not the others, leading to allelic failure to complement. Second, the deficiency could interact epistatically with a nonallelic mutation at a QTL affecting bristle number in one or more of the selection lines. In either case the QTL mapped in this manner affect variation in the trait between the strains tested; it just cannot be said whether their effect is direct or through interaction with another locus. Third, there could be epistatic interactions between mutations at bristle number QTL in the selection lines and genes affecting bristle number on the Bal chromosomes. For all genetic models except for complete dominance of mutant QTL alleles in the selection lines (in which case deficiency mapping is not useful), one expects the variance among hemizygous deficiency genotypes (Df/Si) to be greater than the variance among heterozygous balancer genotypes (Bal/Si) if the deficiency uncovers mutant QTL alleles in the selection lines. We attempted to account for this problem by computing the among-line variance components for Df/Si and Bal/Si genotypes. Although the critical value for formal significance (P = 0.05) of the F-statistic for the ratio of the variance of balancer to deficiency genotypes is F10,10 = 2.98, we applied the more stringent and conservative criterion that F10,10 = 1.6 (P = 0.25). We excluded all cases of observed failure to complement where the variance among Bal/Si genotypes was 1.6 or greater than that of the Df/Si genotypes as potentially arising from epistasis between mutant QTL alleles and the Bal chromosome. Note that such interactions are readily detected in genome-wide deficiency-mapping protocols, since the same Bal chromosomes are repeatedly crossed to the same selection lines (supplementary Table S1). Finally, failure to complement could occur in the case of epistatic interactions between spontaneous mutations and QTL affecting bristle number on the deficiency-bearing chromosomes. Such interactions represent true false positives.
To determine which line(s) contributed to significant complementation effects, we computed the mean and upper and lower confidence limits of the difference Df/Si − Bal/Si for each of the i selection lines. Lines for which the confidence limits for the difference did not overlap were considered to be significantly different. All analyses were performed using SAS statistical software.
RESULTS
Response to selection from new mutations:
The evolution of replicate lines derived from an inbred base population and selected for 206 generations for increased or decreased abdominal and sternopleural bristle number is shown in Figure 1. Spontaneous mutations affecting bristle number have caused an impressive divergence of 13.1 abdominal and 15.2 sternopleural bristles. However, inspection of Figure 1 reveals that the pattern of selection response is not that expected from independent additive, neutral mutations with symmetric effects (Hill 1982). This model predicts symmetrical responses to selection from new mutations, whereas observed selection responses for both traits were highly asymmetrical. Abdominal bristle number increased on average by 3.0 bristles but decreased by 10.1 bristles; sternopleural bristle number increased on average by 11.2 and decreased by 4.0 bristles. The infinitesimal and large-effects models of response to selection from new mutations both predict an asymptotic linear rate of response of 2NeiVM/σP per generation (Hill 1982). However, all abdominal bristle and the low sternopleural bristle lines have responded little from generation 120, and the high sternopleural bristle replicates have not evolved beyond generation 160. Further, in several instances responses actually ran counter to the direction of selection.
Figure 1.—
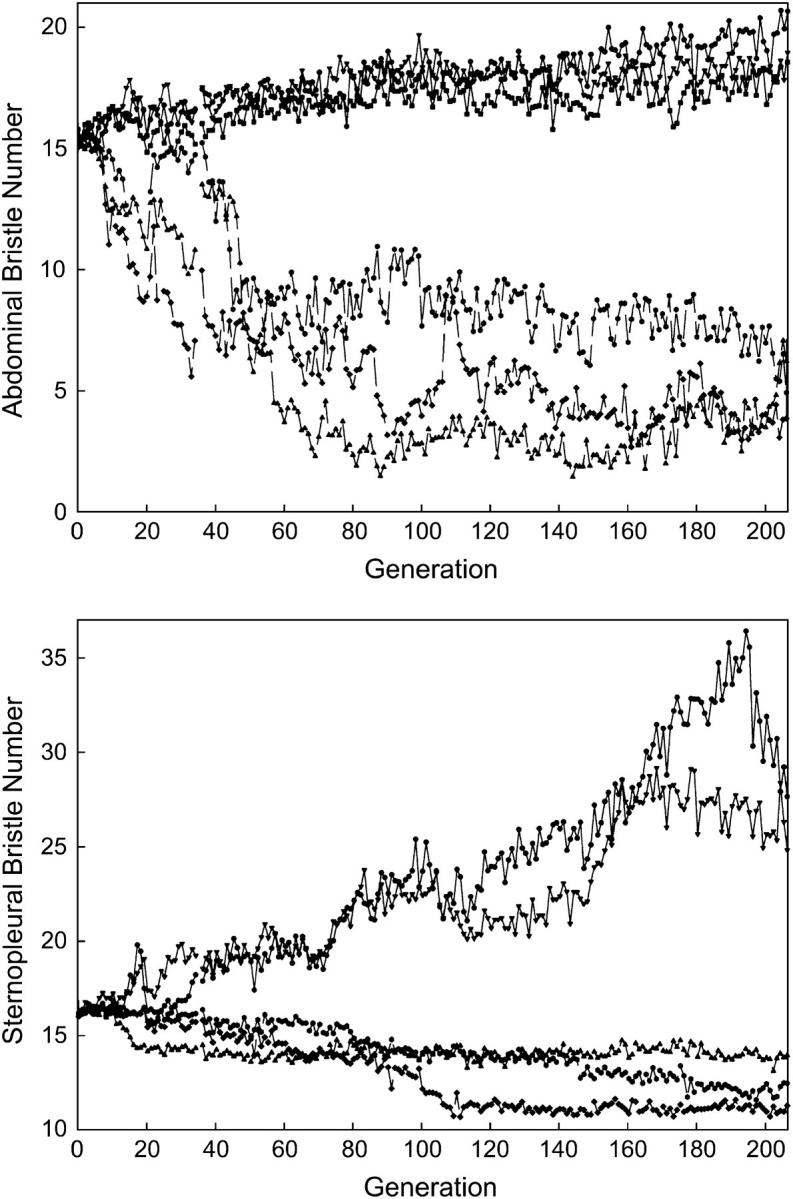
Response to selection from new spontaneous mutations affecting bristle number.
We estimated mutational variance in each selection line under both the infinitesimal and large-effects models of response to selection from new mutations (Hill 1982). These estimates are given in Table 1 for the total period of selection, as well as from generations 1–25 and 1–125 (Mackay et al. 1994) for comparison. Consistent with the static responses to selection in later generations, estimates of mutational heritabilities, VM/VE, were lower when based on the entire experiment than for earlier generations. For example, estimates of VM/VE from 206 generations of selection response under the infinitesimal model averaged 0.64 × 10−3 for abdominal bristle number and 0.92 × 10−3 for sternopleural bristle number, in contrast to average estimates of 4.32 × 10−3 for abdominal bristles and 3.71 × 10−3 for sternopleural bristles from the first 25 generations of selection. Note that estimates of VM under both models reflect the observed asymmetrical responses to selection, but that estimates of VM/VE are similar between the high and low selection lines. This is because the increased mutational variance in the low abdominal bristle number and high sternopleural bristle number selection lines is accompanied by increased variance—again in violation of the model assumptions.
TABLE 1.
Mutational parameters from selection response
| Infinitesimal model
|
Large-effects model
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| G1-206
|
G1-25a:
|
G1-125a:
|
G1-206
|
G1-25a:
|
G1-125a:
|
|||||
| Line | R206b | VPc |
VM × 10−3d |
VM/VE × 10−3d |
VM/VE × 10−3 |
VM/VE × 10−3 |
VM/VE × 10−3d |
VM/VE × 10−3d |
VM/VE × 10−3 |
VM/VE × 10−3 |
| 1HA | 4.24 | 3.60 | 1.72 | 0.49 | 1.44 | 0.60 | 1.50 | 0.42 | 0.62 | 0.39 |
| 2HA | 2.70 | 3.01 | 1.00 | 0.34 | 3.19 | 0.66 | 0.87 | 0.29 | 1.07 | 0.39 |
| 3HA | 2.14 | 2.94 | 0.79 | 0.27 | −0.05 | 0.47 | 0.68 | 0.23 | −0.34 | 0.31 |
| 1LA | −9.80 | 4.09 | 4.25 | 1.07 | 5.30 | 4.86 | 3.68 | 0.93 | 2.12 | 2.17 |
| 2LA | −11.41 | 5.34 | 5.66 | 1.09 | 9.73 | 3.95 | 4.90 | 0.95 | 4.37 | 0.93 |
| 3LA | −9.07 | 12.31 | 6.82 | 0.56 | 6.31 | 1.98 | 5.91 | 0.49 | 2.16 | 0.67 |
| 2HS | 12.88 | 7.43 | 7.53 | 1.04 | 3.81 | 2.47 | 6.52 | 0.90 | 0.68 | 1.26 |
| 3HS | 9.53 | 4.33 | 4.25 | 1.01 | 3.49 | 1.80 | 3.69 | 0.88 | 1.66 | 0.81 |
| 1LS | −2.53 | 0.96 | 0.53 | 0.56 | 7.93 | 2.43 | 0.46 | 0.49 | 3.70 | 0.50 |
| 2LS | −5.25 | 1.11 | 1.18 | 1.10 | 2.19 | 2.08 | 1.03 | 0.96 | 0.93 | 1.58 |
| 3LS | −4.14 | 1.11 | 0.93 | 0.87 | 1.13 | 1.01 | 0.80 | 0.76 | 0.51 | 0.78 |
From Mackay et al. (1994).
Difference between mean bristle number of last six and first six generations of selection.
Average phenotypic variance of all 206 selection generations.
See text for explanation.
There are several possible and nonmutually exclusive explanations for the decelerating responses to selection from new mutations: (1) Stabilizing selection increasingly opposes artificial selection as the means increasingly deviate from those of the base population; (2) mutations affecting bristle number have pleiotropic deleterious fitness effects, and there is epistasis for fitness such that additional mutations cause larger fitness reductions; (3) there is diminishing epistasis of new mutations affecting bristle number; and (4) there is a limited number of loci at which mutations affecting bristle number can occur and the lines have become saturated for these mutations.
Mapping of spontaneous mutations can help discriminate among these alternatives. For example, with direct stabilizing selection, mutations with opposite effects to the direction of selection are likely to be fixed. If mutations exhibit diminishing epistasis for bristle number, one would predict their effects would be greater in nonmutant backgrounds. Finally, mapping will yield direct estimates of the minimum number of loci at which mutations affecting each trait occurred and indicate whether the same mutations were found in replicate lines. The latter is expected if relatively few loci are harboring bristle number mutations, and consequently the mutation rate per locus is high.
Deficiency complementation tests:
Each of the 11 mutation-accumulation lines was crossed to 162 deficiencies, together uncovering ∼75% of the entire genome, and the F1 progeny were scored for abdominal and sternopleural bristle number. The presence of QTL harboring mutations in one or more selection lines was inferred if there was significant failure of the mutation-accumulation lines to complement a deficiency, as judged by a significant L × G interaction term from analysis of variance (and/or L × G × S interactions, for autosomal deficiencies) (Pasyukova et al. 2000). Cases of significant failure to complement were further scrutinized to ensure that the interaction was not attributable to the Balancer chromosome; interactions where the variance among Balancer [Var(Bal)] genotypes was 1.6 or greater than the variance among deficiency genotypes [Var(Df)] were excluded as possibly arising from epistasis. This constraint primarily affected the X chromosome analyses of sternopleural bristle number, where 18 of the 37 tested deficiencies exhibited significant failure to complement, and on average Var(Bal) was 3.4 times greater than Var(Df). Inspection of the line means revealed that all of the X chromosome balancer chromosomes increased sternopleural bristle number, regardless of genetic background, but that this increase was especially large in the 2HS and 3HS line backgrounds. Presumably these lines had accumulated at least one mutation that interacted with the mutations at the achaete-scute complex carried by all FM balancers. Therefore, X chromosome deficiency complementation analyses for sternopleural bristle number were assessed after excluding lines 2HS and 3HS.
A total of 66 deficiencies exhibited significant failure to complement bristle numbers of the mutation-accumulation lines (Tables 2–4). These data have not been corrected for multiple tests, because the deficiencies are overlapping and it is not obvious how many independent tests have been performed. However, it is clear that the fraction of significant deficiencies is far greater than that expected by chance. With 324 tests (162 deficiencies × two bristle traits), one expects 16 tests to be significant at P = 0.05 and 3 at P = 0.01, whereas we observed 41 significant tests (12.6%) with 0.01 < P < 0.05 and 22 (6.8%) with P < 0.01. Several of the deficiencies had sex-specific effects, as judged by significance of the L × G × S interaction term and/or significance of the L × G term in only one sex.
TABLE 2.
Deficiency mapping ofX chromosome QTL affecting sensory bristle number
| Trait | Deficiency | P(L × G) | Var(Df) | Var(Bal) | QTL |
|---|---|---|---|---|---|
| AB | Df(1)JC19 | 0.005 | 5.89 | 3.54 | 2F6;3C2–3 |
| Df(1)G4eLH24iR | 0.022 | 11.25 | 1.00 | 5E8;6B | |
| Df(1)C128 | 0.014 | 4.39 | 2.20 | 7D1;7D5–6 | |
| Df(1)9a4-5 | 0.002 | 6.57 | 2.63 | 8D8–9;8E1–2 | |
| Df(1)C52 | 0.031 | 4.14 | 4.26 | 8E;9B1–2 | |
| Df(1)N105 | 0.002 | 10.91 | 2.26 | 11D1 | |
| Df(1)HF396 | 0.000 | 12.72 | 5.60 | 18E1–2;20A | |
| STa | Df(1)260-1 | 0.021 | 2.27 | 1.63 | 1A1;1B4–6 |
| Df(1)9a4-5 | 0.044 | 1.19 | 0.81 | 8D8–9;8E1–2 | |
| Df(1)HF396 | 0.035 | 1.49 | 2.13 | 18E1–2;20A |
P-values are from the line × genotype term in the two-way deficiency complementation ANOVA. Var(Df) and Var(Bal) are among-line variance components for mutation-accumulation selection lines as hemizygotes against deficiencies and heterozygotes against balancer chromosomes, respectively.
Excluding Lines 2HS and 3HS. See text for explanation.
TABLE 4.
Deficiency mapping of autosomal QTL affecting sternopleural bristle number
| Both sexes
|
Females
|
Males
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deficiency | P(L × G) | P(L × G × S) | Var(Df) | Var(Bal) | P(L × G) | Var(Df) | Var(Bal) | P(L × G) | Var(Df) | Var(Bal) | QTL | Sex |
| Df(2L)al | 0.000 | 0.343 | 13.99 | 6.93 | 0.001 | 9.59 | 4.44 | 0.004 | 21.90 | 10.80 | 21B8–C1;21C8–D1 | B |
| Df(2L)ast2 | 0.003 | 0.119 | 2.73 | 4.33 | 0.008 | 2.14 | 2.95 | 0.388 | 5.24 | 6.49 | 21D1–2;22A2–3 | B |
| Df(2L)C144 | 0.045 | 0.179 | 5.10 | 5.42 | 0.523 | 2.93 | 4.13 | 0.008 | 8.39 | 7.61 | 23A1–2;23C3–5 | M |
| Df(2L)XE-2750 | 0.014 | 0.091 | 6.00 | 3.27 | 0.374 | 3.20 | 2.04 | 0.002 | 11.87 | 5.35 | 28C;28D3 | M |
| Df(2L)TE29Aa-11 | 0.591 | 0.000 | 3.22 | 2.73 | 0.466 | 1.54 | 1.63 | 0.015 | 8.24 | 4.71 | 28E4–7;29B2–C1 | M |
| Df(2L)r10 | 0.493 | 0.544 | 10.61 | 9.85 | 0.967 | 7.23 | 7.19 | 0.047 | 16.05 | 13.28 | 35F1–7;36A8–9 | M |
| Df(2L)TW161 | 0.063 | 0.439 | 6.81 | 5.59 | 0.041 | 4.32 | 3.55 | 0.440 | 10.94 | 8.92 | 38A6–B1;40A4–B1 | F |
| Df(2R)M41A4 | 0.000 | 0.002 | 13.65 | 6.70 | 0.000 | 12.36 | 3.67 | 0.335 | 17.60 | 12.73 | 41A | F |
| In(2LR)Gla | 0.028 | 0.149 | 7.49 | 9.47 | 0.239 | 5.65 | 5.88 | 0.034 | 10.36 | 15.07 | 41B;42A2–3 | B |
| Df(2R)cn9 | 0.001 | 0.473 | 13.94 | 7.76 | 0.124 | 8.85 | 5.08 | 0.008 | 22.24 | 12.43 | 43E15–18;43F | B |
| Df(2R)Np5 | 0.000 | 0.372 | 12.37 | 4.60 | 0.000 | 8.95 | 3.02 | 0.003 | 17.13 | 7.82 | 44F12;45A6–7 | B |
| Df(2R)w45-30n | 0.011 | 0.296 | 8.39 | 4.83 | 0.264 | 4.86 | 2.81 | 0.003 | 14.09 | 8.56 | 45D9–E1;45E2–3 | M |
| Df(2R)stan1 | 0.000 | 0.027 | 6.94 | 4.06 | 0.005 | 6.64 | 3.66 | 0.000 | 7.21 | 5.39 | 47A1;47D3 | B |
| Df(2R)P34 | 0.008 | 0.001 | 15.19 | 8.42 | 0.114 | 5.61 | 3.65 | 0.002 | 42.87 | 23.00 | 55F;56C1–11 | M |
| Df(2R)017 | 0.000 | 0.263 | 14.55 | 9.46 | 0.006 | 11.98 | 8.24 | 0.002 | 18.78 | 11.10 | 56F9–15 | B |
| Df(2R)Egfr5 | 0.003 | 0.363 | 6.29 | 5.11 | 0.028 | 3.88 | 3.74 | 0.085 | 10.27 | 7.32 | 57D11–12;58D1 | B |
| Df(2R)59AD | 0.010 | 0.641 | 11.10 | 4.95 | 0.026 | 8.44 | 4.09 | 0.082 | 14.78 | 6.49 | 59A1–3;59D1–4 | B |
| Df(3L)AC1 | 0.320 | 0.390 | 6.27 | 4.72 | 0.955 | 3.90 | 3.21 | 0.021 | 10.54 | 6.56 | 67B1;67D7–13 | M |
| Df(3L)lxd6 | 0.002 | 0.546 | 3.10 | 5.59 | 0.810 | 1.67 | 3.01 | 0.002 | 6.13 | 9.47 | 67E1–2;67F2–3 | B |
| Df(3L)brm11 | 0.000 | 0.336 | 8.75 | 3.47 | 0.005 | 4.83 | 1.91 | 0.002 | 16.03 | 6.26 | 72C1;72D10 | B |
| Df(3L)st-f13 | 0.000 | 0.067 | 9.43 | 2.78 | 0.010 | 5.77 | 2.12 | 0.000 | 15.20 | 3.70 | 72C1;72D10 | B |
| Df(3l)ri-79c | 0.017 | 0.942 | 8.37 | 4.06 | 0.048 | 5.47 | 2.64 | 0.223 | 11.43 | 7.08 | 77D1;77F–78A | B |
| Df(3R)Dfd13 | 0.028 | 0.594 | 6.87 | 4.97 | 0.019 | 4.97 | 3.34 | 0.220 | 9.54 | 7.68 | 83E3;84A1–2 | B |
| Df(3R)Scr | 0.036 | 0.578 | 10.10 | 7.11 | 0.085 | 8.64 | 5.38 | 0.306 | 11.99 | 9.14 | 84A4–5;84B1–2 | B |
| Df(3R)Antp17 | 0.063 | 0.098 | 10.81 | 6.56 | 0.300 | 9.30 | 4.42 | 0.011 | 13.06 | 10.73 | 84B1–2;84D3–5 | M |
| Df(3R)p-XT103 | 0.001 | 0.006 | 6.18 | 8.96 | 0.005 | 7.42 | 7.24 | 0.000 | 6.03 | 12.92 | 85A2;85C1–2 | B |
| Df(3R)M-Kx | 0.016 | 0.780 | 4.04 | 5.29 | 0.022 | 2.56 | 4.68 | 0.744 | 5.97 | 6.22 | 86C1;86E2–4 | B |
| Df(3R)P14 | 0.000 | 0.434 | 42.24 | 7.20 | 0.000 | 31.43 | 5.32 | 0.000 | 56.48 | 9.80 | 90C2–D1;91A1–2 | B |
| Df(3R)mbc-R1 | 0.174 | 0.037 | 4.90 | 3.13 | 0.034 | 3.59 | 2.08 | 0.126 | 6.84 | 5.19 | 95A5–7;95D6–11 | F |
| Df(3R)3450 | 0.042 | 0.485 | 12.02 | 4.59 | 0.018 | 8.52 | 1.81 | 0.496 | 16.09 | 10.49 | 98E3;99A1–2 | F |
| Df(3R)Dr-rv1 | 0.039 | 0.378 | 5.80 | 5.35 | 0.296 | 4.30 | 3.04 | 0.098 | 7.99 | 8.78 | 99A6–8;99B6–11 | B |
| Df(3R)tll-g | 0.025 | 0.632 | 9.72 | 6.66 | 0.024 | 6.49 | 4.62 | 0.236 | 14.61 | 9.89 | 99F1–2;100B4–5 | B |
| Df(3R)awd-KRB | 0.001 | 0.039 | 4.84 | 5.50 | 0.040 | 2.97 | 4.05 | 0.000 | 6.89 | 8.54 | 100C;100D | B |
P-values are from the line × genotype and line × genotype × sex terms in deficiency complementation ANOVAs. Var(Df) and Var(Bal) are among-line variance components for mutation-accumulation selection lines as hemizygotes against deficiencies and heterozygotes against balancer chromosomes, respectively.
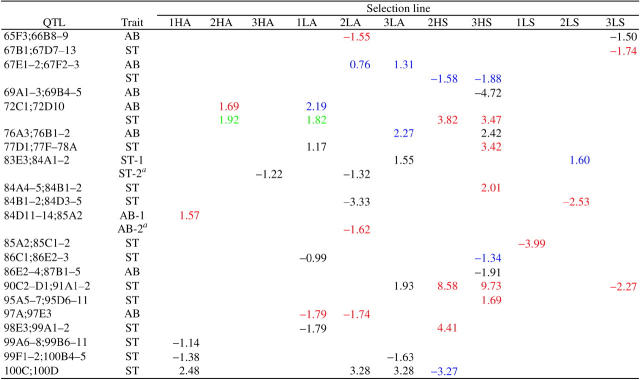
We infer from deficiency complementation mapping that there are at least 56 QTL at which mutations affecting bristle number arose (Table 5). In this test, a significant failure to complement indicates that there is variation among the selection lines in the sign and/or the magnitude of the complementation effect, defined for each of the i selection lines as the difference in mean bristle number between hemizygous and heterozygous genotypes (Df/Si − Bal/Si).
TABLE 5.
Complementation effects a
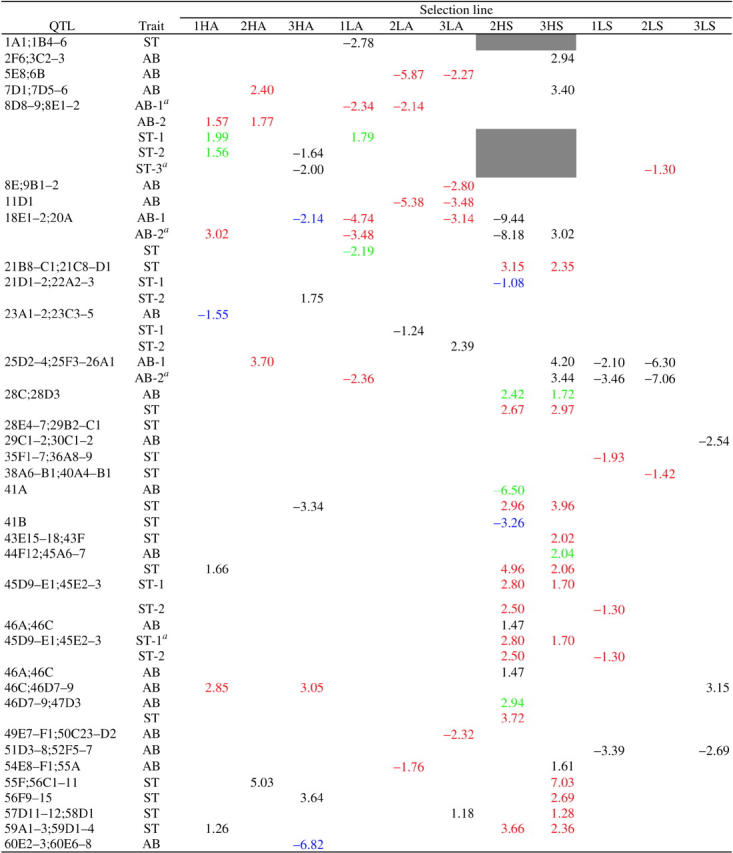
Complementation effects of spontaneous mutations on abdominal (AB) and sternopleural (ST) bristle number are shown. Red, blue, and green refer, respectively, to significant effects on bristle number in the direction of selection and opposite to the direction of selection and potential pleiotropic effects on the unselected trait. Black denotes neutral mutations. Shaded cells indicate exclusion of lines 2HS and 3HS from the X chromosome deficiency complementation tests. Alternative interpretations are given for cases of ambiguity.
The interpretation used in the computation of per-character mutation rates (see text for explanation).
Numbers of mutations:
To determine which line(s) contributed to failure to complement deficiencies, we computed the upper and lower confidence limits of the complementation effects for each selection line and grouped together lines with overlapping confidence limits. Given the origin of the selection lines, it is possible to use these groups to infer the minimum number of mutations that occurred. All lines derived from the same inbred base; therefore, if only one line accumulated a mutation uncovered by the deficiency, there would be a common group of 10 lines with mean complementation effects that did not differ significantly and one outlier. If two lines contained mutant alleles affecting bristle number, the mean complementation effects of 9 lines would define the common group. Therefore, the minimum number of mutations per deficiency was estimated as 11 − nc, where nc is the number of lines in the largest common group. The complementation effect of the deviant line(s) was then estimated as a deviation from the mean complementation effect of the common group. These estimates (and alternative interpretations for cases of ties for the largest common group) are given in Table 5.
The mutant complementation effects fall into four categories: those for which the trait affected and sign of the effect are consistent with a direct response to selection (S), those that could be construed as pleiotropic effects on the unselected trait (P), presumed neutral mutations affecting the unselected trait (N), and mutations with opposite effects on the selected trait (O). For cases with more than one possible interpretation, we have chosen the one with the largest number of direct responses, smallest number of responses in the opposite direction to selection, and largest number of possibly pleiotropic mutations as the most parsimonious (Table 5). The existence of mutations with opposite effects to the direction of selection could indicate a component of stabilizing natural selection for bristle number, fixation by drift, or hitchhiking with a favored allele. Under the pleiotropic model such mutations would also have deleterious fitness effects, and artificial and natural selection in the same direction would ensure they are not fixed.
Assuming effects on the unselected trait that occur in the same QTL as those that result from response to selection (S or O) result from pleiotropy, 62 independent mutations affect sternopleural bristle number and 44 affect abdominal bristle number, for a minimum of 106 mutations in total. This scales to 141 for the whole genome, assuming deficiency coverage of 75%. If the inferred pleiotropic mutations are at independent loci, the upper bound for the minimum number of mutations is 65 for sternopleural bristle number and 49 for abdominal bristle number, for a total of 114 (152 scaled to the whole genome).
Epistasis:
In the absence of epistasis, the complementation effect is an estimate of a − d (Falconer and Mackay 1996) for each deficiency, so the sum of the complementation effects for each line cannot be directly compared to the total selection responses without making assumptions about the average degree of dominance of mutations. Thus, the sum of the complementation effects for each line could be less than half of the total response if mutations are on average partly dominant, half of the total response for additive mutations, and equal to the total response for completely recessive mutations. If the sum of the complementation effects exceeds the total selection response, we can infer the mutations act epistatically, with effects that are contingent on the genetic background.
From Table 5, we compute the sums of the complementation effects as follows: 1HA, 4.32; 2HA, 4.09; 3HA, −3.77; 1LA, −7.78; 2LA, −19.3; 3LA, −7.29; 2HS, 32.62; 3HS, 45.52; 1LS, −5.92; 2LS, −3.65; and 3LS, −4.01. These are compared to total responses for each line (Table 1): 1HA, 4.24; 2HA, 2.70; 3HA, 2.14; 1LA, −9.80; 2LA, −11.41; 3LA, −9.07; 2HS, 12.88; 3HS, 9.53; 1LS, −2.53; 2LS, −5.25; and 3LS, −4.14. Thus, the deficiency mapping data concur well with the observed total responses to selection for lines 1HA, 2HA, 1LA, 3LA, 2LS, and 3LS, assuming mutations have recessive or partially recessive effects on bristle number. Line 3HA is peculiar in that the total complementation effect is negative, opposite to the direction of selection, due to an inferred mutation of large effect (−6.82) in the 60E2–3; 60E6–8 interval. This is explicable if one assumes other compensatory mutations in the direction of selection have been fixed in this line in regions not uncovered by the deficiencies or if this mutation is not expressed in the selection line background. Lines 2LA, 2HS, 3HS, and 1LS all have total complementation effects that exceed the total selection responses. These observations are consistent with diminishing epistasis for mutations affecting bristle number in the selection lines. An alternative interpretation that cannot be excluded is that complementation effects are apparently epistatic, but the true cause is false positive effects attributable to epistatic interactions between spontaneous mutations and QTL affecting bristle number on some deficiency-bearing chromosomes.
DISCUSSION
Per-character mutation rates:
We can estimate the minimum genomic mutation rate for bristle number (U = nμ, where n is the total number of loci at which mutations affecting bristle number can arise and μ is the mutation rate per locus) from the substitution rate, if we assume a single mutation per interval and that mutations are fixed in the selection lines. From classic population genetics theory, the substitution rate for neutral mutations is the genomic mutation rate (U), and the substitution rate of selectively favored mutations is 4NeUs, where Ne is the effective population size (Ne = 14 in these lines) and s is the selection coefficient of the favored mutation (Kimura 1983). If we knew the difference in bristle number phenotype between homozygous genotypes (2a) for each mutation, and this difference was small relative to the phenotypic standard deviation of the trait, we could estimate s as ai/σP (Kimura and Crow 1978). However, the homozygous effects that are relevant are those in the background of the mutation-accumulation lines, and we have inferred that at least some mutations affecting bristle number have effects that are conditional on the genetic background. Further, the magnitude of effects we have detected is of the same order or greater than the phenotypic standard deviation. Therefore, we conservatively take s = 1 for selectively favored mutations.
We have estimates of the number of neutral (N) and selected (S and O) mutations for both bristle traits. If all mutations have independent effects on abdominal and sternopleural bristles, the potentially pleiotropic mutations are counted both as neutral for the unselected trait and as S or O for the selected trait; otherwise, they are counted only as contributing to the selected trait. There are 1236 allele generations (six mutation-accumulation lines × 206 generations) for abdominal bristle number. Thus, assuming pleiotropy there are 26 selected and 18 neutral mutations and U = 1.5 × 10−2; assuming independent mutations there are 26 selected and 23 neutral mutations and U = 1.9 × 10−2. Scaled to the whole genome, these estimates are U = 2.0 × 10−2 (pleiotropy) and U = 2.5 × 10−2 (no pleiotropy). There are 1030 (five mutation-accumulation lines × 206 generations) for sternopleural bristle number. The estimates of U (scaled to the whole genome) for this trait are 3.3 × 10−2 (pleiotropy) and 3.7 × 10−2 (pleiotropy). Averaged over both bristle traits, 0.026 < U < 0.031.
The validity of these estimates of U depends on the power to detect QTL by deficiency complementation mapping. As with all QTL mapping experiments, we must regard the number of QTL to be minimum estimates, as more QTL, with smaller effects, could potentially be detected with increased sample sizes. On the other hand, increasing the stringency for declaring significance of complementation tests would reduce the estimated number of QTL. However, the estimates of U reported here are consistent with those obtained for abdominal (U = 0.018) and sternopleural (U = 0.086) bristle number in an independent mutation-accumulation experiment (García-Dorado et al. 1999), suggesting our estimates are not unduly biased.
Large mutational target size and extensive pleiotropy for sensory bristle number:
These estimates of genomic mutation rates for bristle number seem extraordinarily high and imply a large number of loci affecting bristle number (and hence extensive pleiotropy for genes affecting bristle number), high per-locus mutation rates, or both. The following considerations suggest that both may be true. We can estimate the total genomic mutation rate per generation (λ) in Drosophila from the sum of the base pair mutation rate and rate of transposition of transposable elements. Multiplying the estimate of 3.6 × 108 bp in the diploid Drosophila genome (Adams et al. 2000) by the estimate of the substitution rate at silent sites (2.2 × 10−9/generation, Keightley and Eyre-Walker 2000), which is the base pair mutation rate under neutrality, gives an estimate of 0.79 bp mutations per generation. There are four independent estimates of genomic transposition rates, ignoring the P element: 0.5 (Eggleston et al. 1988), 0.3 (Harada et al. 1990), 0.2 (Nuzhdin and Mackay 1995), and 0.12 (Maside et al. 2000), for an average of 0.28. However, the total rate of transposition is likely to be increased in strains with autonomous P elements, such as the Harwich strain used in this experiment. From the data of Eggleston et al. (1988) we estimate the P-element transposition rate in the P cytotype as 0.005 per element per generation. There are at least 50 P-element copies in Harwich (Mackay et al. 1994), for a total of 0.25 P-element transpositions per generation. Thus, λ in strong P strains could be 1.32, giving a per-locus mutation rate of nearly 10−4, assuming 13,600 genes (Adams et al. 2000).
The inference from the ratio of the estimated per-character mutation rate for bristle numbers to the total mutation rate (0.03/1.32) is that 2.3% of the genome—>300 loci—could affect abdominal or sternopleural bristle number. Is this reasonable? Lyman et al. (1996) and Norga et al. (2003) conducted screens for single P-element insertional mutations affecting abdominal and sternopleural bristle number, in co-isogenic genetic backgrounds. Remarkably, 9.9% (6.7%) of the inserts had effects on abdominal (sternopleural) bristle number exceeding the 99.9% confidence limits in the Lyman et al. (1996) screen, and 3.8% (4.0%) of the inserts had effects on abdominal (sternopleural) bristle number exceeding the 99.9% confidence limits in the Norga et al. (2003) screen. Although several insertions with significant effects on bristle number were in the same loci, these results are also consistent with a large mutational target size for each bristle trait—at least 2% of the genome—and consequently extensive pleiotropy.
Adult bristles are external sensory organs of the peripheral nervous system (PNS); therefore, one category of candidate genes for bristle number QTL is those affecting PNS development (Mackay 2001). Many of the first genes discovered to affect bristle development also affected sex determination (achaete-scute, daughterless) and eye and wing development (scabrous, Notch, Delta, Hairless) (FlyBase@flybase.bio.indiana.edu). Extensive pleiotropy of genes that are essential for PNS development is also indicated by the study of Prokopenko et al. (2000), who characterized 26 novel genes tagged by P-element insertions with aberrant development of the embryonic PNS. Few, if any, of these genes act only in the PNS, but affect other cellular and developmental processes in the embryo such as dorsal closure, cell cycle and cell division, cellular metabolism, and signal transduction and are probably also recruited at later developmental stages. Of the 56 QTL containing mutations affecting bristle number that were mapped using deficiency complementation, 32 contain candidate genes with effects on adult macrochaetae and microchaetae or PNS development; no such candidate genes were present in the remaining 24 (43%) QTL. This also suggests that genes affecting other processes can affect adult bristle number, that screens for genes affecting bristle number have not reached saturation, and that screens for quantitative effects of mutations are an efficient way to identify novel loci (Norga et al. 2003).
Maintenance of genetic variation:
Naturally segregating variation for bristle number must be at least partly maintained by a balance between the input of new mutations and their elimination by stabilizing selection. Stabilizing selection can act directly on the deviation of trait values from an intermediate optimum (Turelli 1984) and indirectly (“pleiotropic” stabilizing selection) through deleterious pleiotropic fitness effects of mutations affecting the trait (Barton 1990; Keightley and Hill 1990; Kondrashov and Turelli 1992; Caballero and Keightley 1994). Stabilizing selection acting on both bristle traits was shown by direct estimates of fitness of the selection lines and unselected mutation-accumulation lines derived from same base population (Nuzhdin et al. 1995) and from a statistical analysis of the covariance of line means of the unselected mutation-accumulation lines (Mackay et al. 1995). However, neither analysis was consistent with strictly “real” or strictly pleiotropic stabilizing selection, and both mechanisms probably occur (Zhang and Hill 2002). Our observations here of “compensatory” mutations in the opposite direction to selection indicate a component of real stabilizing selection on both bristle traits.
For characters under direct stabilizing selection, the equilibrium genetic variance under mutation-selection balance is VG = 4UVS, assuming a model of n equivalent loci, mutant effects are large relative to standing variation, per-locus mutation rates are small, and stabilizing selection is strong (Turelli 1984). Evaluation of this model with VG = VE seems to lead to the untenable conclusion that high heritabilities can be maintained only in the face of strong stabilizing selection (VS = 10–20VE) if per-locus mutation rates are extraordinarily high or if an apparently unreasonably large number of loci affect the trait (Falconer and Mackay 1996). Reevaluating this model with the minimum estimated per-character mutation rates for abdominal and sternopleural bristle number of 0.02 and 0.03, respectively, gives VS = 12.5VE for abdominal bristle number and VS = 8.33VE for sternopleural bristle number. Therefore, high heritabilities of bristle traits are compatible with strong direct stabilizing selection on bristle number. This treatment ignores pleiotropy; but, as noted above, it is valid only for large numbers of loci affecting each trait, which in turn implies extensive pleiotropy. Zhang and Hill's (2002) analysis of variation maintained by a balance between new mutations and the joint action of direct and pleiotropic stabilizing selection shows most VG is due to small-effect mutations with near neutral pleiotropic fitness effects, but most apparent stabilizing selection is due to genes with a large effect on the trait. Therefore, we must reconsider that a substantial fraction of segregating variation for bristle number might indeed be maintained by a balance between mutation and stabilizing selection, although the exact amount depends on the distribution of mutational effects on the trait and on fitness (Zhang and Hill 2002).
We have inferred that effects of mutations affecting sensory bristle number can be strongly conditional on genetic background—i.e., exhibit epistasis—from the failure in several instances of the sum of mutational effects in the mapping analyses to equal those of the selected lines. An alternative interpretation is that some instances of failure to complement occurred via interactions between mutations and QTL affecting bristle number on the deficiency-bearing chromosomes. The results of prior experiments using these lines are consistent with the former interpretation. Previously, we crossed lines selected in the same direction for the same trait in all possible pairwise combinations and continued selection from the F2 hybrids (Fry et al. 1995). The responses of the hybrids never approached the additive expectation of the sum of the responses of the two parental lines and in most cases did not even exceed that of the more extreme parent, despite high realized heritabilities. These results are also consistent with diminishing epistatic interactions between new mutations. With some forms of epistasis, conditions can be more favorable to maintaining high levels of genetic variation and strong pleiotropic stabilizing selection for a broad class of models incorporating mutation-selection balance, without excessive genetic load (Gavrilets and De Jong 1993). However, such models are sensitive to the exact nature of epistatic interactions, which are currently unknown.
Lessons from Drosophila bristles:
Drosophila sensory bristle numbers are commonly regarded as archetypical model quantitative traits, with simple genetic architecture (Falconer and Mackay 1996). This study illustrates that effects of accumulating spontaneous mutations are complex even for “simple” quantitative traits like bristle number. High per-character mutation rates, and the extensive pleiotropy this implies, complicate the task of identifying the genes at which mutations occurred by nominating positional candidate genes, since many genes could have unexpected bristle number phenotypes. Further, epistasis confounds our ability to map the mutations by linkage to molecular markers or complementation to deficiencies and mutations, since both of these designs require assessing mutational effects in unrelated backgrounds. The problem of identifying the loci at which mutations have occurred in long-term mutation-accumulation lines must await the time when we can count new mutations directly by whole genome resequencing. A more effective design for mutation-accumulation experiments may be to assess very large numbers of lines for shorter periods of time, such that each deviant line contains on average a single mutation. This could simplify mapping new mutations and determining their effects, singly and in combination.
It is important to determine to what extent segregating alleles, which are a selected subset of new mutations, have the same properties as new mutations. Several lines of evidence indicate that epistasis cannot be ignored as a general feature of the genetic architecture of complex traits, but that such interactions may not be as pervasive between segregating alleles within natural populations as between new mutations. While epistatic interactions with effects as large as main effects have been detected between bristle number QTL (Long et al. 1995; Gurganus et al. 1999; Dilda and Mackay 2002), the majority of QTL do appear to have additive gene action. [This statement must be tempered by the caveat that these studies underestimated the magnitude of epistasis because interactions were tested only between QTL that were themselves significant because of the low significance threshold that would need to be adopted to account for all possible n(n − 1)/2 pairwise interactions between n QTL.] Further, Drosophila QTL mapped by complementation to deficiencies and mutations have been confirmed by linkage disequilibrium mapping in independent samples (Long et al. 1998; Lyman et al. 1999; Robin et al. 2002; DeLuca et al. 2003), suggesting that epistasis is not a major confounding factor in identifying genes.
On the other hand, evidence is accumulating that an understanding of the nature of variation for complex traits, particularly between populations or strains that have undergone some evolutionary divergence, cannot be complete without taking nonadditive interactions between QTL into account. For example, two QTL (tb1 and T3L) for the number of staminate spikelets in the primary lateral inflorescence have been identified as segregating between maize and its presumed progenitor, teosinte. When teosinte alleles of these QTL are introgressed separately into a maize background, they have very small effects, but double homozygotes exhibit a high degree of synergistic epistasis, nearly recapitulating the teosinte phenotype (Lukens and Doebley 1999). Teosinte itself harbors cryptic variation for maize-like morphological traits that is apparent only in the presence of maize alleles (Lauter and Doebley 2002), suggesting the accumulation of teosinte QTL with diminishing epistasis that are decanalized by the maize alleles. This is not an uncommon phenomenon in interspecies crosses and has been observed for Drosophila bristle number in crosses between Drosophila melanogaster and D. simulans (Coyne 1985) and multiple morphological traits in crosses between Tribolium castaneum and T. freemani (Wade et al. 1997). It is tempting to speculate that our long-term mutation-accumulation experiment captures some of the essential features of long-term natural evolution, such that evolution under directional selection enriches for mutations that interact synergistically, whereas stabilizing selection favors diminishing interactions between new mutations.
TABLE 3.
Deficiency mapping of autosomal QTL affecting abdominal bristle number
| Both sexes
|
Females
|
Males
|
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Deficiency | P(L × G) | P(L × G × S) | Var(Df) | Var(Bal) | P(L × G) | Var(Df) | Var(Bal) | P(L × G) | Var(Df) | Var(Bal) | QTL | Sex |
| Df(2L)C144 | 0.016 | 0.326 | 3.44 | 4.13 | 0.115 | 4.19 | 4.63 | 0.028 | 3.32 | 4.01 | 23A1–2;23C3–5 | B |
| Df(2L)cl-h3 | 0.027 | 0.001 | 9.56 | 5.95 | 0.540 | 5.57 | 3.87 | 0.001 | 22.42 | 11.48 | 25D2–4;25F3–26A1 | M |
| Df(2L)XE-2750 | 0.073 | 0.037 | 1.84 | 0.52 | 0.107 | 2.79 | 0.29 | 0.017 | 1.73 | 1.06 | 28C;28D3 | M |
| Df(2L)N22-14 | 0.041 | 0.253 | 2.86 | 3.15 | 0.007 | 3.00 | 3.06 | 0.683 | 2.60 | 3.51 | 29C1–2; 30C1–2 | F |
| Df(2R)M41A4 | 0.023 | 0.028 | 0.31 | 0.77 | 0.016 | 2.86 | 0.46 | 0.085 | 0.59 | 0.64 | 41A | F |
| Df(2R)Np5 | 0.051 | 0.156 | 1.26 | 1.52 | 0.148 | 0.86 | 1.35 | 0.046 | 1.79 | 1.82 | 44F12;45A6–7 | M |
| Df(2R)B5 | 0.025 | 0.656 | 1.92 | 1.09 | 0.274 | 2.36 | 0.60 | 0.062 | 2.28 | 1.37 | 46A;46C | B |
| Df(2R)X1 | 0.115 | 0.023 | 1.24 | 1.05 | 0.007 | 2.90 | 1.53 | 0.266 | 1.58 | 1.75 | 46C;46D7–9 | F |
| Df(2R)stan1 | 0.021 | 0.737 | 1.06 | 1.05 | 0.214 | 0.56 | 0.83 | 0.043 | 2.27 | 2.24 | 46D7–9;47D3 | B |
| Df(2R)CX1 | 0.037 | 0.558 | 2.27 | 0.51 | 0.063 | 1.91 | 0.64 | 0.570 | 2.06 | 1.04 | 49E7–F1;50C23–D2 | B |
| Df(2R)Jp1 | 0.018 | 0.394 | 6.32 | 7.71 | 0.500 | 2.52 | 5.48 | 0.023 | 12.39 | 11.68 | 51D3–8;52F5–9 | B |
| Df(2R)Pcl7B | 0.030 | 0.272 | 1.63 | 1.70 | 0.129 | 0.91 | 1.38 | 0.095 | 3.62 | 1.86 | 54E8–F1;55A | B |
| Df(2R)M60E | 0.002 | 0.551 | 3.23 | 1.05 | 0.159 | 2.12 | 0.53 | 0.002 | 5.06 | 1.47 | 60E2–3; 60E6–8 | B |
| Df(3L)pbl-X1 | 0.015 | 0.776 | 3.10 | 1.32 | 0.219 | 3.27 | 1.02 | 0.162 | 2.72 | 1.51 | 65F3;66B8–9 | B |
| Df(3L)lxd6 | 0.022 | 0.997 | 4.21 | 6.54 | 0.472 | 4.28 | 6.09 | 0.442 | 3.91 | 5.45 | 67E1–2;67F2–3 | B |
| Df(3L)vin7 | 0.591 | 0.022 | 3.52 | 3.39 | 0.033 | 5.22 | 3.12 | 0.347 | 3.20 | 4.16 | 69A1–3;69B4–5 | F |
| Df(3L)brm11 | 0.011 | 0.945 | 6.22 | 2.99 | 0.182 | 6.07 | 2.05 | 0.426 | 5.68 | 3.30 | 72A1; 72D1–10 | B |
| Df(3L)st-f13 | 0.041 | 0.118 | 3.59 | 2.17 | 0.296 | 3.03 | 1.70 | 0.004 | 4.58 | 2.89 | 72D1–10;73A3 | M |
| Df(3L)VW3 | 0.009 | 0.015 | 2.66 | 3.21 | 0.024 | 3.68 | 4.49 | 0.005 | 2.97 | 3.29 | 76A3;76B1–2 | F, M |
| Df(3R)D8 | 0.033 | 0.904 | 6.31 | 3.14 | 0.196 | 7.16 | 3.88 | 0.323 | 5.71 | 2.64 | 84D11–14;85A2 | B |
| Df(3R)M-Kx | 0.288 | 0.011 | 3.39 | 4.53 | 0.010 | 4.61 | 5.84 | 0.243 | 2.81 | 4.18 | 86E2–4;87B1–5 | F |
| Df(3R)T-32 | 0.423 | 0.011 | 3.08 | 3.52 | 0.030 | 3.90 | 4.41 | 0.938 | 3.12 | 2.93 | 86E2–4;87B1–5 | F |
| Df(3R)Tl-P | 0.014 | 0.786 | 4.13 | 2.55 | 0.078 | 3.97 | 3.19 | 0.281 | 3.74 | 1.83 | 97A;97E3 | B |
P-values are from the line × genotype and line × genotype × sex terms in deficiency complementation ANOVAs. Var(Df) and Var(Bal) are among-line variance components for mutation-accumulation selection lines as hemizygotes against deficiencies and heterozygotes against balancer chromosomes, respectively.
References
- Adams, M. D., S. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne et al., 2000. The genome sequence of Drosophila melanogaster. Science 287: 2185–2195. [DOI] [PubMed] [Google Scholar]
- Barton, N., 1990. Pleiotropic models of quantitative variation. Genetics 124: 773–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton, N., and M. Turelli, 1989. Evolutionary quantitative genetics: How little do we know? Annu. Rev. Genet. 23: 337–370. [DOI] [PubMed] [Google Scholar]
- Caballero, A., and P. D. Keightley, 1994. A pleiotropic model of variation in quantitative traits. Genetics 138: 883–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton, G. A., and A. Robertson, 1955. Mutation and quantitative variation. Am. Nat. 89: 151–158. [Google Scholar]
- Coyne, J. A., 1985. Genetic studies of three sibling species of Drosophila with relationship to theories of speciation. Genet. Res. 46: 169–192. [DOI] [PubMed] [Google Scholar]
- DeLuca, M., N. V. Roshina, G. L. Geiger-Thornsberry, R. F. Lyman, E. G. Pasyukova et al., 2003. Dopa decarboxylase (Ddc) affects variation in Drosophila longevity. Nat. Genet. 34: 429–433. [DOI] [PubMed] [Google Scholar]
- Dilda, C. L., and T. F. C. Mackay, 2002. The genetic architecture of Drosophila sensory bristle number. Genetics 162: 1655–1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eggleston, W. B., D. M. Johnson-Schlitz and W. R. Engels, 1988. P-M hybrid dysgenesis does not mobilize other transposable element families in Drosophila melanogaster. Nature 331: 368–370. [DOI] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996 Introduction to Quantitative Genetics, Ed. 4. Addison Wesley Longman, Harlow, Essex, UK.
- Fry, J. D., K. A. DeRonde and T. F. C. Mackay, 1995. Polygenic mutation in Drosophila melanogaster: genetic analysis of selection lines. Genetics 139: 1293–1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Dorado, A., C. López-Fanjul and A. Caballero, 1999. Properties of spontaneous mutations affecting quantitative traits. Genet. Res. 74: 341–350. [DOI] [PubMed] [Google Scholar]
- Gavrilets, S., and G. De Jong, 1993. Pleiotropic models of polygenic variation, stabilizing selection and epistasis. Genetics 134: 609–625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurganus, M. C., S. V. Nuzhdin, J. W. Leips and T. F. C. Mackay, 1999. High resolution mapping of quantitative trait loci affecting sternopleural bristle number in Drosophila melanogaster. Genetics 152: 1585–1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harada, K., K. Yukuhiro and T. Mukai, 1990. Transposition rates of movable genetic elements in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 87: 3248–3252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill, W. G., 1982. Predictions of response to artificial selection from new mutations. Genet. Res. 40: 255–278. [DOI] [PubMed] [Google Scholar]
- Houle, D., B. Morikawa and M. Lynch, 1996. Comparing mutational variabilities. Genetics 143: 1467–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., and A. Eyre-Walker, 2000. Deleterious mutations and the evolution of sex. Science 290: 331–333. [DOI] [PubMed] [Google Scholar]
- Keightley, P. D., and W. G. Hill, 1990. Variation maintained in quantitative traits with mutation-selection balance: pleiotropic side-effects on fitness traits. Proc. R. Soc. Lond. Ser. B 242: 95–100. [Google Scholar]
- Keightley, P. D., T. F. C. Mackay and A. Caballero, 1993. Accounting for bias in estimates of the rate of polygenic mutation. Proc. R. Soc. Lond. Ser. B 253: 291–296. [DOI] [PubMed] [Google Scholar]
- Kidwell, M. G., J. F. Kidwell and J. A. Sved, 1977. Hybrid dysgenesis in Drosophila melanogaster: a syndrome of aberrant traits including mutation, sterility and male recombination. Genetics 86: 813–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M., 1983 The Neutral Theory of Molecular Evolution. Cambridge University Press, Cambridge, UK.
- Kimura, M., and J. F. Crow, 1978. Effect of overall phenotypic selection on genetic change at individual loci. Proc. Natl. Acad. Sci. USA 75: 6168–6171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov, A. S., and M. Turelli, 1992. Deleterious mutations, apparent stabilizing selection and the maintenance of quantitative variation. Genetics 132: 603–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauter, N., and J. Doebley, 2002. Genetic variation for phenotypically invariant traits detected in teosinte: implications for the evolution of novel forms. Genetics 160: 333–342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., S. L. Mullaney, L. A. Reid, J. D. Fry, C. H. Langley et al., 1995. High resolution mapping of genetic factors affecting abdominal bristle number in Drosophila melanogaster. Genetics 139: 1273–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., S. L. Mullaney, T. F. C. Mackay and C. H. Langley, 1996. Genetic interactions between naturally occurring alleles at quantitative trait loci and mutant alleles at candidate loci affecting bristle number in Drosophila melanogaster. Genetics 144: 1497–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., R. F. Lyman, C. H. Langley and T. F. C. Mackay, 1998. Two sites in the Delta gene region contribute to naturally occurring variation in bristle number in Drosophila melanogaster. Genetics 149: 999–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukens, L. N., and J. Doebley, 1999. Epistatic and environmental interactions for quantitative trait loci involved in maize evolution. Genet. Res. 74: 291–302. [Google Scholar]
- Lyman, R. F., and T. F. C. Mackay, 1998. Candidate quantitative trait loci and naturally occurring variation for bristle number in Drosophila melanogaster: the Delta-Hairless gene region. Genetics 149: 983–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyman, R. F., F. Lawrence, S. V. Nuzhdin and T. F. C. Mackay, 1996. Effects of single P element insertions on bristle number and viability in Drosophila melanogaster. Genetics 143: 277–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyman, R. F., C. Lai and T. F. C. Mackay, 1999. Linkage disequilibrium mapping of molecular polymorphisms at the scabrous locus associated with naturally occurring variation in bristle number in Drosophila melanogaster. Genet. Res. 74: 303–311. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and W. G. Hill, 1986. Phenotypic evolution by neutral mutation. Evolution 40: 915–935. [DOI] [PubMed] [Google Scholar]
- Mackay, T. F. C., 2001. Quantitative trait loci in Drosophila. Nat. Rev. Genet. 2: 11–20. [DOI] [PubMed] [Google Scholar]
- Mackay, T. F. C., and J. D. Fry, 1996. Polygenic mutation in Drosophila melanogaster: genetic interactions between selection lines and candidate quantitative trait loci. Genetics 144: 671–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay, T. F. C., and R. F. Lyman, 1998. Polygenic mutation in Drosophila melanogaster: genotype × environment interaction for spontaneous mutations affecting bristle number. Genetica 102/103: 199–215. [PubMed] [Google Scholar]
- Mackay, T. F. C., J. D. Fry, R. F. Lyman and S. V. Nuzhdin, 1994. Polygenic mutation in Drosophila melanogaster: estimates from response to selection of inbred strains. Genetics 136: 937–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay, T. F. C., R. F. Lyman and W. G. Hill, 1995. Polygenic mutation in Drosophila melanogaster: non-linear divergence among unselected strains. Genetics 139: 849–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maside, X., S. Assimacopoulos and B. Charlesworth, 2000. Rates of movement of transposable elements on the second chromosome of Drosophila melanogaster. Genet. Res. 75: 275–284. [DOI] [PubMed] [Google Scholar]
- Norga, K. K., M. C. Gurganus, C. L. Dilda, A. Yamamoto, R. F. Lyman et al., 2003. Quantitative analysis of bristle number in Drosophila mutants identifies genes involved in neural development. Curr. Biol. 13: 1388–1397. [DOI] [PubMed] [Google Scholar]
- Nuzhdin, S. V., and T. F. C. Mackay, 1994. Direct determination of retrotransposon transposition rates in Drosophila melanogaster. Genet. Res. 63: 139–144. [DOI] [PubMed] [Google Scholar]
- Nuzhdin, S. V., and T. F. C. Mackay, 1995. The genomic rate of transposable element movement in Drosophila melanogaster. Mol. Biol. Evol. 12: 180–181. [DOI] [PubMed] [Google Scholar]
- Nuzhdin, S. V., J. D. Fry and T. F. C. Mackay, 1995. Polygenic mutation in Drosophila melanogaster: the causal relationship of bristle number to fitness. Genetics 139: 861–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pasyukova, E. G., C. Vieira and T. F. C. Mackay, 2000. Deficiency mapping of quantitative trait loci affecting longevity in Drosophila melanogaster. Genetics 156: 1129–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prokopenko, S. N., Y. He, Y. Lu and H. J. Bellen, 2000. Mutations affecting the development of the peripheral nervous system in Drosophila: a molecular screen for novel proteins. Genetics 156: 1691–1715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robin, C., R. F. Lyman, A. D. Long, C. H. Langley and T. F. C. Mackay, 2002. hairy: a quantitative trait locus for Drosophila bristle number. Genetics 162: 155–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schug, M. D., T. F. C. Mackay and C. F. Aquadro, 1997. Low mutation rates of microsatellite loci in Drosophila melanogaster. Nat. Genet. 15: 99–102. [DOI] [PubMed] [Google Scholar]
- Schug, M. D., C. M. Hutter, K. A. Wetterstrand, M. S. Gaudette, T. F. C. Mackay et al., 1998. The mutation rate of di-, tri- and tetranucleotide repeats in Drosophila melanogaster. Mol. Biol. Evol. 15: 1751–1769. [DOI] [PubMed] [Google Scholar]
- Turelli, M., 1984. Heritable genetic variation via mutation-selection balance: Lerch's zeta meets the abdominal bristle. Theor. Popul. Biol. 25: 138–193. [DOI] [PubMed] [Google Scholar]
- Wade, M. J., N. A. Johnson, R. Jones, V. Siguel and M. McNaughton, 1997. Genetic variation segregating in natural populations of Tribolium castaneum affecting traits observed in hybrids with T. freemani. Genetics 147: 1235–1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, X.-S., and W. G. Hill, 2002. Joint effects of pleiotropic selection and stabilizing selection on the maintenance of quantitative genetic variation at mutation-selection balance. Genetics 162: 459–471. [DOI] [PMC free article] [PubMed] [Google Scholar]