Abstract
If colonization of empty habitat patches causes genetic bottlenecks, freshly founded, young populations should be genetically less diverse than older ones that may have experienced successive rounds of immigration. This can be studied in metapopulations with subpopulations of known age. We studied allozyme variation in metapopulations of two species of water fleas (Daphnia) in the skerry archipelago of southern Finland. These populations have been monitored since 1982. Screening 49 populations of D. longispina and 77 populations of D. magna, separated by distances of 1.5–2180 m, we found that local genetic diversity increased with population age whereas pairwise differentiation among pools decreased with population age. These patterns persisted even after controlling for several potentially confounding ecological variables, indicating that extinction and recolonization dynamics decrease local genetic diversity and increase genetic differentiation in these metapopulations by causing genetic bottlenecks during colonization. We suggest that the effect of these bottlenecks may be twofold, namely decreasing genetic diversity by random sampling and leading to population-wide inbreeding. Subsequent immigration then may not only introduce new genetic material, but also lead to the production of noninbred hybrids, selection for which may cause immigrant alleles to increase in frequency, thus leading to increased genetic diversity in older populations.
MANY populations exist as metapopulations, that is, as populations structured into interconnected demes with local “turnover” dynamics of extinction and recolonization (Andrewartha and Birch 1954; Hanski 1999). Evolutionary processes in metapopulations differ in many aspects from those in large, uniform populations because gene flow among demes is restricted, local demes may be small, and turnover dynamics lead to genetic bottlenecks during recolonization (Andrewartha and Birch 1954; Hanski and Gilpin 1997; Hanski 1999). Moreover, metapopulation structure may be important for evolutionary processes even in populations that do not exist as ecological metapopulations (i.e., with turnover dynamics too weak to influence demography). This is because many migrants are needed to homogenize the genetic structure of subdivided populations, whereas only a few individuals may be needed to recolonized an empty habitat patch (Ives and Whitlock 2002).
The impact of restricted gene flow and finite local population size on genetic diversity have been studied extensively (Wright 1969; Slatkin 1985; Hedrick 2000; Excoffier 2001). The question of how turnover dynamics affect genetic diversity has received less attention. Theory predicts that turnover dynamics mostly (but not invariably) lead to increased genetic differentiation and decreased local genetic diversity as compared to similarly structured populations without extinction and recolonization dynamics (Slatkin 1977; Wade and McCauley 1988; Whitlock and McCauley 1990; Austerlitz et al. 1997, 2000; Le Corre and Kremer 1998; Pannell and Charlesworth 1999).
This can be studied empirically in metapopulations in which the age of local demes is known. If turnover dynamics increase genetic differentiation, young demes should be more strongly differentiated than old demes, because age structure in metapopulations is a direct consequence of turnover. Indeed, a number of empirical studies have found decreasing differentiation with population age (Whitlock 1992a; McCauley et al. 1995; Nurnberger and Harrison 1995; Giles and Goudet 1997; Ingvarsson et al. 1997; Mopper et al. 2000; but see Dybdahl 1994).
The reason why turnover dynamics mostly increase genetic differentiation and decrease local genetic diversity is that recolonization events usually involve a smaller number of individuals than the demes can eventually support, and extinction limits the life time of demes, during which subsequent gene flow can ameliorate the effect of these founder events. Whereas this shows why recently colonized demes are predicted to be more differentiated and to have reduced levels of local genetic diversity compared to older demes, the magnitude of these differences may be small, especially if turnover rates are high, local populations are large, and migration rates are low. This is because under these circumstances, return rates to equilibrium are so low that most local populations may become extinct before subsequent immigration has significantly changed the effect of the founder events (Crow and Aoki 1984; Whitlock 1992b). In such metapopulations it may thus be difficult to detect genetic consequences of turnover by studying how local genetic diversity and genetic differentiation change with population age.
Yet in metapopulations with strong founder effects not only neutral but also selective processes may influence genetic differences between young and old populations. Genetic bottlenecks during colonization lead to local inbreeding (e.g., Kirkpatrick and Jarne 2000; Haag et al. 2002) and as a consequence, noninbred, hybrid crosses between immigrants and local residents may have a selective advantage (“hybrid vigor”; Whitlock et al. 2000; Ebert et al. 2002; Saccheri and Brakefield 2002). Hybrid vigor has the potential to increase effective migration rate and to decrease genetic differentiation because it gives an advantage to immigrant genes, which are initially rare but represent half of the hybrid genome (Pamilo et al. 1999; Ingvarsson and Whitlock 2000; Ebert et al. 2002). Hybrid vigor may thus lead to changes in local genetic diversity and genetic differentiation after colonization that are faster than changes driven only by the neutral processes of drift during colonization and subsequent migration.
The aim of this study was to assess how local genetic diversity and genetic differentiation change with population age in metapopulations of two co-occurring Daphnia species. Both metapopulations are characterized by high yearly turnover rates (∼17%/year), stressing the potential importance of turnover dynamics for the genetic population structure. The two metapopulations are further characterized by large populations (often >10,000 individuals) and low migration rates, indicating that neutral rates of change after colonization may be low (Crow and Aoki 1984; Whitlock 1992b). Therefore, the observation of hybrid vigor after immigration in one of the species (Ebert et al. 2002) may be crucial for understanding the patterns of change in genetic structure with age.
This study also profits from detailed knowledge of demographic and ecological parameters of the studied metapopulations. Age of local populations was recorded by one of us (V. I. Pajunen) by monitoring 507 local patches (pools) for 20 years. We also recorded several ecological variables, which may either confound a possible association between population age and genetic structure or lead to spurious correlations because they themselves may be correlated to both genetic structure and population age. Genetic structure was assessed with allozymes, which allowed us to screen a large number of local populations (77 and 49 for the two species, respectively). Finally, investigating the genetic structure of newly colonized populations only, we tentatively estimated the number of colonizers, which for several reasons is believed to be small, but has never been studied explicitly (Ebert et al. 2002; Haag et al. 2002).
Daphnia rock pool populations form metapopulation systems with discrete habitat patches and frequent extinction and recolonization (Ranta 1979; Hanski and Ranta 1983; Pajunen 1986; Bengtsson 1989; Ebert et al. 2001; Pajunen and Pajunen 2003). In our study area, the average proportion of pools containing D. magna or D. longispina populations in a given year is 17% for D. longispina and 18% for D. magna and the yearly extinction probabilities are 17 and 16%, respectively. Since 1982, the number of extinctions, on average, is balanced by the number of new colonizations (Pajunen 1986; Pajunen and Pajunen 2003). Even though the two species have slightly different habitat preferences (the pools vary in size, salinity, humic acid content, pH, calcium concentration, etc.; Ranta 1979), they often occur together (Pajunen and Pajunen 2003). The two species thus have a very similar metapopulation ecology.
MATERIALS AND METHODS
The study system:
We studied metapopulations of the small filter-feeding freshwater crustaceans Daphnia longispina and D. magna (Cladocera). In our study area in the skerry archipelago of southern Finland, the two species occur in rock pools, small water-filled depressions in the bare rock that are often found along the Baltic Sea coast. Rock pools represent a patchily distributed and discrete environment and mostly freeze solid in winter. Both species reproduce by cyclical parthenogenesis, in which phases of asexual reproduction are intermitted by sexual reproduction. In rock pools Daphnia survive the winter as resting eggs. In spring, only females hatch and start to reproduce asexually. Because resting eggs can be produced only sexually, each hatchling female is the founder of a genetically unique clone. The number of hatchlings is estimated to be at least in the hundreds to thousands (C. R. Haag, personal observation) and local populations often contain tens of thousands of individuals. The length of an asexual generation (hatching to first reproduction) is 10–20 days and there are typically ∼8–12 generations during the season (∼5 months in our study area). The production of males is triggered by the environment (Hobaek and Larsson 1990; Kleiven et al. 1992), and males are genetically identical to their clonal sisters (environmental sex determination; Hebert and Ward 1972). During sexual reproduction, resting eggs, which are resistant to drought and freezing, are produced. They are also the main dispersal stage, carried passively by wind, water, and birds. Because of the possibility of clonal reproduction, a single hatchling female from a blown-in resting egg may found a new population, and subsequent mating among her male and female clonal offspring is genetically equivalent to selfing.
The study area:
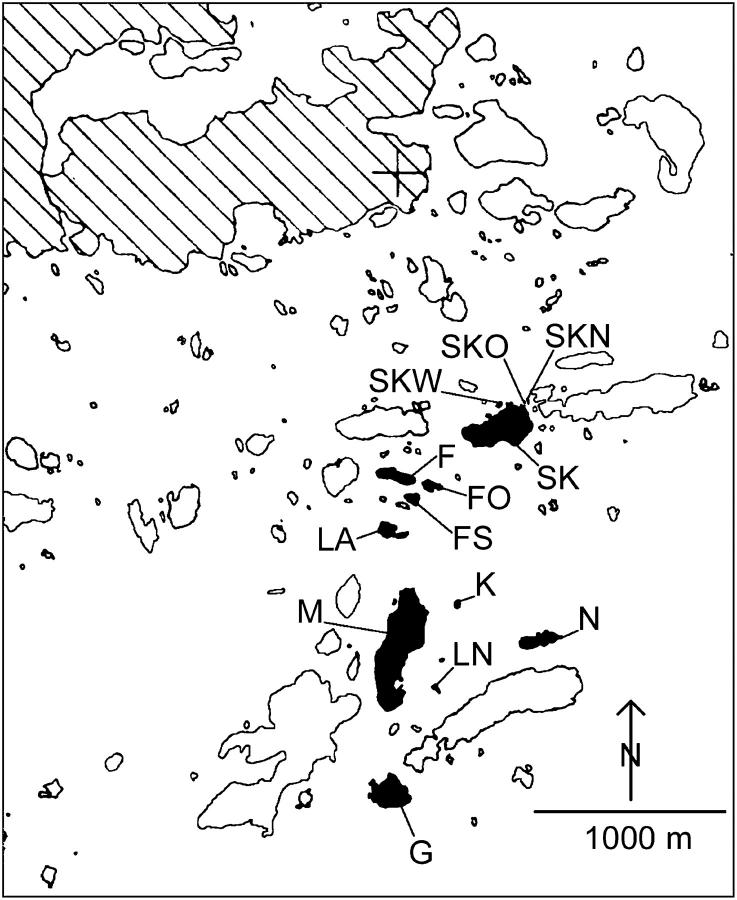
Our study area is in the archipelago of southern Finland at Tvärminne on the Hanko peninsula (59°50′N, 23°15′E; Figure 1), where we collected samples of D. longispina between July 17 and August 17, 1999, and samples of D. magna between June 12 and August 23, 1998. All samples were taken from an area consisting of 13 islands and a total of 507 pools. At the time of sampling, 13% of the pools were inhabited by D. longispina and 19% by D. magna. However, we included only isolated pools; that is, we excluded pools receiving water from other pools because these cannot be considered independent. This resulted in a total of 49 populations of D. longispina on 8 islands and 77 populations of D. magna on 13 islands, separated by distances of 6–2077 m and 1.5–2180 m, respectively (Table 1). The geographic location of each pool was recorded by the use of a differential global positioning system (with accuracy to the nearest meter).
Figure 1.—
Map of the study area on the Baltic coast of southern Finland. Islands included in this study are solid and labeled with abbreviations of island names as in Table 1. To our knowledge, there are no populations of either of the two species present on the mainland (hatched area) within 20 km, but populations are present on many other islands. The cross within the hatched area indicates the location of the Tvärminne Zoological Station at 59°50′N and 23°15′E.
TABLE 1.
Coordinates and number of sampled pools for each island included in this study
| No. of pools
|
|||
|---|---|---|---|
| Island | Coordinates | D. longispina | D. magna |
| Fyrholmen (F) | 57.861/35.466 | 5 | 1 |
| Prackan (FO) | 58.121/35.432 | 4 | 1 |
| Nameless skerry (FS) | 58.041/35.366 | 5 | 8 |
| Granbusken (G) | 57.849/33.861 | 14 | 21 |
| Flatgrund (K) | 58.245/34.856 | 0 | 1 |
| Lasarettet (LA) | 57.943/35.198 | 1 | 7 |
| Nameless skerry (LN) | 58.140/34.420 | 0 | 1 |
| Mellanskär (M) | 57.992/34.497 | 4 | 3 |
| Storgrundet (N) | 58.699/34.636 | 14 | 24 |
| Skallotholmen (SK) | 58.510/35.739 | 4 | 6 |
| Nameless skerry (SKN) | 58.606/35.857 | 0 | 1 |
| Nameless skerry (SKO) | 58.595/35.837 | 0 | 1 |
| Nameless skerry (SKW) | 58.468/35.834 | 0 | 2 |
Abbreviations of names correspond to labels in Figure 1. Coordinates are in kilometers, according to the Finnish coordinate system.
Data collection
Genetic data:
Samples were collected with a hand net with equal effort in all parts of a pool. Samples were brought to the laboratory, where they were kept alive at 12° and at low density to prevent selective mortality. Random samples of usually 22 individuals (range 20–22 in D. longispina; 8–22 in D. magna) were screened for allozyme polymorphism by cellulose acetate electrophoresis (Hebert and Beaton 1993) within 3 days of collection. The following polymorphic loci were studied: aspartate amino transferase (Aat, enzyme commission number EC 2.6.1.1), fumarate hydratase (Fum, 4.2.1.2), glucose-6-phosphate isomerase (Gpi, 5.3.1.9, only D. longispina), malic enzyme (Me, 1.1.1.40, only D. longispina), phosphoglucomutase (Pgm, 5.4.2.2.), and a peptidase locus with leucyleglycine as dipeptide substrate (Pep, 3.4.11., only D. longispina).
Temporal data:
One of us (V. I. Pajunen) has visited the 507 pools of the study area twice every year since 1982 (for detailed methodology see Pajunen 1986; Pajunen and Pajunen 2003). During each visit, the presence and absence of Daphnia was recorded, and the identity of present Daphnia species was determined. From this data, we calculated the age (in years) of the populations for each species separately (the age of newly established populations was 0). Note that maximum age was 17 in D. longispina (18 populations) and 16 in D. magna (16 populations). These populations may be of even older age, because they were colonized before or in 1982. For statistical analysis they were treated as if they had been colonized in 1982 (see discussion). A population was assumed to be absent only if it was not found during three consecutive sampling dates. After this period, reestablishment of a population from local resting eggs was considered to be unlikely on the basis of the observation that, using this criterion, the likelihood of recolonization depended on distance to the nearest occupied pool, and no resting eggs were found in sediment samples of empty pools (Pajunen and Pajunen 2003; V. I. Pajunen, unpublished data).
Ecological variables:
For each sampled pool, we recorded the following ecological variables, which may be correlated with genetic diversity and population age (Table 2): pool volume, isolation, relative distance to the sea, and presence of competitor species.
TABLE 2.
Description of population parameters used in this study
| Parameter | Mean (SD) | Range | N |
|---|---|---|---|
| D. longispina | |||
| Dependent variables | |||
| Allelic richness | 7.70 (0.97) | 6–10 | 49 |
| Genotypic richness | 4.05 (2.67) | 1–10.8 | 49 |
| Pairwise FST within islands | 0.28 (0.25) | −0.02–1 | 48 |
| Explanatory variables | |||
| Age of population (yr) | 8.57 (7.23) | 0–17+ | 49 |
| Volume (m3) | 2.40 (6.10) | 0.048–31.1 | 49 |
| Distance to neighbor (m) | 29.5 (54.4) | 6–337 | 49 |
| Relative distance to sea | 0.44 (0.25) | 0.084–0.93 | 49 |
| Pairwise distance within islands (m) | 66.8 (55.6) | 6–361 | 48 |
| D. magna | |||
| Dependent variables | |||
| Allelic richness | 3.43 (0.66) | 3–5.59 | 77 |
| Genotypic richness | 1.45 (0.90) | 1–4.82 | 77 |
| Pairwise FST within islands | 0.27 (0.26) | −0.02–1 | 63 |
| Explanatory variables | |||
| Age of population (yr) | 5.86 (6.22) | 0–16+ | 77 |
| Volume (m3) | 1.25 (3.67) | 0.007–24.2 | 77 |
| Distance to neighbor (m) | 19.72 (43.42) | 1.5–198 | 77 |
| Relative distance to sea | 0.72 (1.00) | 0.013–5.44 | 77 |
| Pairwise distance within islands (m) | 50.1 (45.6) | 1.5–478 | 63 |
Age of population indicates number of years since colonization. Age = 0 indicates a pool newly colonized in 1998 (D. magna) or 1999 (D. longispina). Populations colonized before or in 1982 (age 17+ in D. longispina and 16+ in D. magna) were assumed to have been colonized in 1982. Genetic data are based on genotypes of usually 22 individuals/population. Pairwise variables (FST and geographic distance) were calculated only within islands. N indicates the number of pools for which at least one pairwise value was calculated. Two additional explanatory variables were the island on which a pool was located and the presence of competitors (both categorical) with N = 49 and N = 77 in D. longispina and D. magna, respectively.
Pool volume:
For each pool, we recorded the greatest length at the surface, the greatest width perpendicular to it, and the maximum depth. Pool volume was estimated by assuming the shape of an inverted pyramid (length × width × depth/3). We considered pool volume as a potential correlate of genetic diversity because larger pools may contain larger populations and receive more immigrants than smaller pools. Because of its potential effect on turnover rates, pool volume may also be correlated with population age.
Isolation:
As a measure of the isolation of a pool, we calculated the distance to the nearest pool inhabited by the same Daphnia species (“distance to neighbor”) from the pool coordinates. We used distance to neighbor rather than connectivity (Hanski 1994) because the latter differed strongly among islands and was therefore confounded with the “island” variable. Isolation may be inversely correlated with genetic diversity, because more isolated pools may receive fewer immigrants (isolation by distance). Isolation may also be negatively correlated with population age because decreased migration rates make genetic and demographic rescue effects (Brown and Kodric-Brown 1977; Richards 2000) less probable.
Relative distance to the sea:
Rock pools in our study area occur in the treeless zone between the shore and the forest. The width of this zone varies between 4 m in sheltered places to ∼100 m in places that are most exposed to wind and waves. As a measure of the impact of the sea on the pools, we calculated the relative distance of the pool to the sea, that is, the distance of the pool to the sea divided by the width of the treeless zone at the location of the pool. For the five small treeless islands that were each harboring one or two populations (D. magna only), the width of the treeless zone was set to 100 m because this was the maximum distance recorded for pools on islands with trees and reflects strong exposure. Relative distance to the sea may be correlated with genetic diversity because exposed pools may represent a less stable environment than sheltered pools (e.g., due to sudden changes in salinity), and thus population sizes may be reduced. Due to their lower stability, exposed pools may also have higher extinction rates, and exposure may thus be negatively correlated with population age.
Presence of competitor species:
For D. longispina interspecific competition was considered to be high if D. magna and/or D. pulex (a third co-occurring species of Daphnia) were present in the same pool at the sampling date. For D. magna the presence of D. longispina and/or D. pulex was considered. Competitor species were present in 31 and 36% of D. longispina and D. magna populations, respectively. We considered interspecific competition as a potential confounding factor because it may influence population sizes and extinction rates (Bengtsson 1989).
Data analysis
Description of genetic diversity and differentiation:
As measures of genetic diversity, allelic richness and genotypic richness were calculated for each population. Allelic richness and genotypic richness represent measures for the number of alleles and the number of multi-locus genotypes in a population, independent of sample size (El Mousadik and Petit 1996; Goudet 2001). Allelic richness was also calculated for each locus separately, to give an impression of the contribution of the different loci to total genetic diversity. As alternative measures of genetic diversity, we also calculated gene diversity (Nei 1973) and Simpson's diversity index (Stoddart 1983) for genotypes. These two measures give less weight to rare polymorphisms than to common ones. However, the results obtained with these two measures did not differ from the results obtained with allelic richness and genotypic richness and therefore only their summary statistics are reported.
Genetic differentiation was assessed by means of F-statistics (Weir and Cockerham 1984). Using the program FSTAT (Goudet 2001), we estimated overall FST and pairwise FST values between all pairs of pools.
Associations between explanatory variables and genetic diversity:
We used allelic richness and genotypic richness as dependent variables to investigate which of the explanatory variables listed in Table 2 were associated with genetic diversity. The analysis was carried out in two steps. First, we tested for associations between genetic diversity and each of the explanatory variables separately. For continuous variables, this was done using linear regression and, for class variables, using one-way analysis of variance (factor island) or t-test (presence of competitors). Whenever an island was considered as a factor, we excluded islands with only one pool.
In a second step, we used multiple regression models to investigate the combined effect of explanatory variables on measures of genetic diversity. Because these models included island as a factor, they were carried out only for pools from islands with more than one pool. We used a forward selection procedure (P to include 0.05, P to exclude 0.1; Sokal and Rohlf 1981) to determine explanatory variables that had a significant effect after correcting for other significant factors. We also used Akaike's information criterion (AIC) to identify the model that best explained the data.
For all statistical analyses, volume, distance to neighbor, and the relative distance to the sea were log10 transformed. After transformation, the variables showed approximately normal distribution, although deviations were significant in some cases. Yet, nonparametric alternatives for association tests with single explanatory variables yielded almost identical results and therefore we report the parametric test only.
In D. magna, our loci showed only limited polymorphism, resulting in very skewed distributions of measures of genetic diversity. For statistical reasons, we restricted association analyses between measures of genetic diversity and explanatory variables to polymorphic D. magna populations only; that is, we excluded all pools that contained only a single, all-homozygous multi-locus genotype. We are confident that the exclusion of monomorphic pools did not have a strong influence on our results because rank tests on the whole data set showed very similar results.
Association between explanatory variables and pairwise FST:
Genetic differentiation is a measure defined among several pools or between pairs of pools, whereas all our explanatory variables were defined for each pool. To circumvent this problem, we used simple and partial Mantel tests (analogous to simple and multiple regression) with pairwise FST as the dependent variable and mean pairwise age, mean pairwise volume (log10 transformed), and geographic distance (log10 transformed) as explanatory variables. Relative distance to the sea and distance to neighbor were not considered because they were nonlinearly related to geographic distance. Mean pairwise age and mean pairwise volume are means for pairs of pools. This has the disadvantage that intermediate values can represent either two pools with intermediate values or two pools with opposite extreme values.
We calculated pairwise FST only for pairs of pools on the same islands to avoid inclusion of pools that very rarely exchange migrants (C. R. Haag, unpublished data). Because of many undefined values in D. magna, this analysis could be carried out only for D. longispina. In D. longispina, we carried out the Mantel test separately for each of the two islands with >10 pools and obtained a combined test by Fisher's method for combining P-values (Sokal and Rohlf 1981). Mantel tests were first carried out as simple Mantel regressions and in a second step as partial regressions using the program FSTAT (Goudet et al. 1996) and tested with 10,000 randomizations. The reliability of partial Mantel tests has recently been questioned (Raufaste and Rousset 2001), but the main point here was not to obtain an exact P-value, but rather to see whether the patterns would fundamentally change by controlling for potentially confounding variables.
To test simple associations between population age and pairwise genetic differentiation for both species and for all islands, we grouped pools in three age classes: young (0–2 years), intermediate (3–10 years), and old (>10 years). For each age class, we calculated average pairwise FST (arithmetic mean) for all pairs with both pools on the same island and in the same age class. Standard statistical tests for differences in pairwise FST among age classes are not available, because data points come from matrices and are therefore nonindependent, but these matrices are not complete. As a conservative approximation, we used a test based on the number of pools in each age class, for which at least one pairwise estimate was calculated. One less than the number of pools is the number of independent data points. Standard errors were therefore calculated using the observed variance in pairwise FST values in each group and the number of pools on which these estimates were based. Degrees of freedom were also based on the number of pools in each class. F-tests were based on these estimates of standard errors and degrees of freedom.
Number of colonizers:
The number of colonizers in rock pool populations of D. magna is known to be very low (Ebert et al. 2002; Haag et al. 2002). The year 1998 appeared to be an exceptionally good year for new colonizations, as the number of new colonizations in both species in our study area was more than twice the average for the period 1984–1997 (Pajunen and Pajunen 2003). Consequently, our genetic sample contained a large proportion of the D. magna population that were in their first year (28 of 77 populations) whereas 11 of 49 D. longispina populations, sampled in 1999, were in their second year. In 1999 there were 5 newly colonized populations of D. longispina.
To obtain a quantitative estimate of the number of colonizers, for all genotypes that were found in newly colonized populations we calculated the probability of twice obtaining an individual with this genotype by picking two random individuals from the total metapopulation (migrant pool model of colonization). From this, for each pool we calculated the probability that a pool was colonized by a given number of individuals.
RESULTS
Descriptive parameters of genetic diversity are given for each locus and species in Table 3. Within pools, between 6 and 10 alleles were found in D. longispina (summed over six polymorphic loci) and between 3 and 6 alleles were found in D. magna (summed over three polymorphic loci). In D. magna the overall level of polymorphism was low, possibly not due to a lack of genetic diversity, but rather due to a lack of suitable markers. Whereas 62% of all D. magna populations contained only a single, all homozygous multi-locus genotype, this was the case in only 8% of the D. longispina populations.
TABLE 3.
Descriptive parameters of genetic diversity for each locus and species
| Parameter | Aat | Fum | Pgm | Gpi | Me | Pep | All | Pool mean |
|---|---|---|---|---|---|---|---|---|
| D. longispina | ||||||||
| No. of alleles | 3 | 2 | 2 | 2 | 2 | 2 | 13 | 7.71 |
| Allelic richness | 3 | 2 | 1.87 | 1.93 | 1.29 | 1.41 | 11.50 | 7.70 |
| Gene diversity | 0.65 | 0.38 | 0.09 | 0.12 | 0.02 | 0.03 | 0.22 | 0.09 |
| No. of genotypes | — | — | — | — | — | — | 55 | 4.14 |
| Genotypic richness | — | — | — | — | — | — | 44.01 | 4.05 |
| G0 | — | — | — | — | — | — | 11.57 | 2.93 |
| Polymorphic pools | 0.86 | 0.22 | 0.10 | 0.08 | 0.06 | 0.06 | 0.92 | — |
| D. magna | ||||||||
| No. of alleles | 3 | 3 | 2 | — | — | — | 8 | 3.53 |
| Allelic richness | 2.35 | 1.50 | 1.15 | — | — | — | 5.00 | 3.43 |
| Gene diversity | 0.27 | 0.07 | 0.02 | — | — | — | 0.07 | 0.03 |
| No. of genotypes | — | — | — | — | — | — | 14 | 1.69 |
| Genotypic richness | — | — | — | — | — | — | 2.80 | 1.45 |
| G0 | — | — | — | — | — | — | 1.82 | 1.36 |
| Polymorphic pools | 0.30 | 0.17 | 0.01 | — | — | — | 0.38 | — |
Genotypic measures are given only for multi-locus genotypes. G0 refers to Simpson's diversity index of genotypes. Proportion of polymorphic pools are given with respect to alleles, not genotypes. Sample sizes were 49 pools for D. longispina and 77 pools for D. magna. “All” indicates the total across all loci and pools; “pool mean” indicates the average within a pool across all loci.
Genetic differentiation among pools was strong, averaging 0.59 for D. longispina and 0.56 for D. magna at the level of the whole metapopulation (P < 0.0001 in both species). Within islands, average FST between pairs of pools was 0.28 in D. longispina and 0.27 in D. magna (Table 2). This is not the most accurate method to estimate within-island differentiation (Goudet 2001), but is used here because association tests with population age were based on pairwise values. A hierarchical analysis of genetic differentiation for a larger data set, including the data of this study, will be reported elsewhere.
Correlations among explanatory variables:
Before testing for associations between the variables listed in Table 2 and genetic diversity, we tested to what degree these variables were independent from each other (Table 4). Relative distance to the sea was positively correlated with population age in both species, and there was also a trend for a positive correlation between population age and pool volume. Furthermore, several variables showed significant variation among islands and, in D. magna, populations in larger pools were more likely to have a competitor species. After correction for multiple testing (sequential Bonferroni), only variation in relative distance to the sea among islands in D. magna remained significant.
TABLE 4.
Matrix of association among explanatory variables
| Variable | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| D. longispina | |||||
| 1. Age of population | r = 0.31* | r = −0.24 | r = 0.39** | t = 1.41 | F = 0.83 |
| 2. Volume | r = −0.09 | r = 0.10 | χ2 = 1.41 | F = 0.80 | |
| 3. Distance to neighbor | r = −0.09 | χ2 = 0.20 | F = 2.35* | ||
| 4. Relative distance to sea | χ2 = 2.20 | F = 3.73** | |||
| 5. Presence of competitors | Fisher** | ||||
| 6. Island | |||||
| D. magna | |||||
| 1. Age of population | r = 0.31 | r = 0.17 | r = 0.49** | t = 0.72 | F = 5.96** |
| 2. Volume | r = 0.22 | r = 0.16 | χ2 = 6.07* | F = 0.46 | |
| 3. Distance to neighbor | r = 0.03 | χ2 = 1.09 | F = 1.70 | ||
| 4. Relative distance to sea | χ2 = 2.38 | F = 21.72**** | |||
| 5. Presence of competitors | Fisher | ||||
| 6. Island | |||||
Association among continuous variables was tested with the Pearson correlation coefficient (r). Associations between continuous and class variables were tested with t-test (t), logistic regression (Wald-χ2), or one-way analysis of variance (F). Associations among class variables were tested with Fisher's exact tests (Fisher). Sample sizes are 49 for D. longispina and 29 for D. magna. Significance levels are given without correcting for multiple testing. *P < 0.05, **P < 0.01, ****P < 0.0001.
Correlations among dependent variables:
The two measures of genetic diversity, allelic richness and genotypic richness, were highly positively correlated (r = 0.89, N = 49, P < 0.0001 in D. longispina and r = 0.81, N = 29, P < 0.0001 in D. magna). Nevertheless, we decided to use both as measures of genetic diversity, because several populations were fixed for a heterozygous genotype, in which case the two measures of genetic diversity differ considerably.
Single explanatory variables:
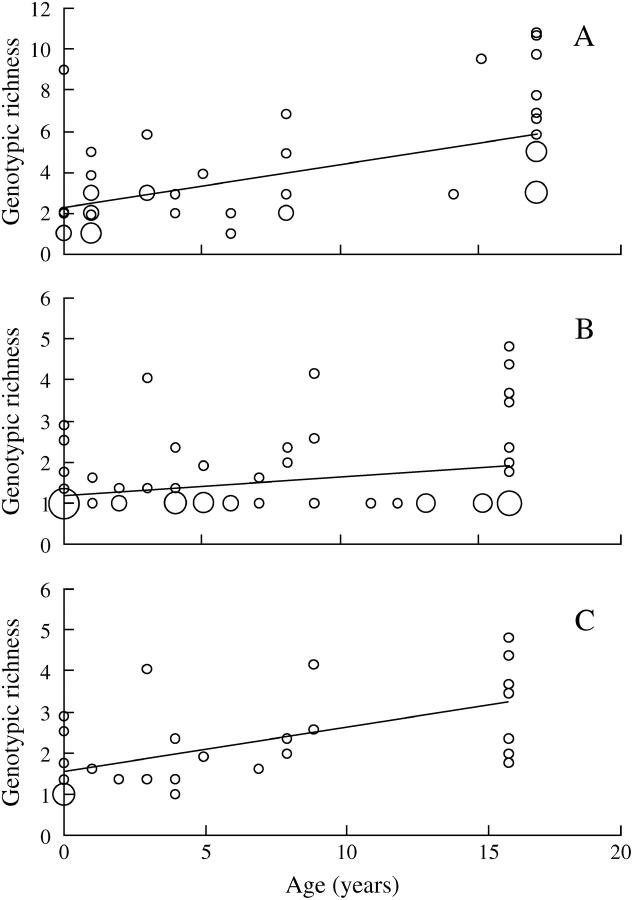
As a single explanatory variable (i.e., without correcting for potential confounding factors), population age was associated with both measures of genetic diversity in both species (Table 5, Figure 2). In D. magna, the regression for allelic richness was nonsignificant after correcting for multiple testing, but population age was overall clearly the variable that showed the closest association with genetic diversity, explaining 18–37% of the total variance, depending on measure and species.
TABLE 5.
Associations between measures of genetic diversity and single explanatory variables
| Allelic richness
|
Genotypic richness
|
||||||
|---|---|---|---|---|---|---|---|
| Explanatory variable | Type of data | Slope | Statistics | N | Slope | Statistics | N |
| D. longispina | |||||||
| Age of population | Continuous | 0.08 | t = 5.23**** | 49 | 0.21 | t = 4.70**** | 49 |
| Volume | Continuous | 0.81 | t = 4.61**** | 49 | 2.45 | t = 5.29**** | 49 |
| Distance to neighbor | Continuous | −0.84 | t = −2.46* | 49 | −1.84 | t = −1.93 | 49 |
| Relative distance to sea | Continuous | 1.33 | t = 2.86** | 49 | 2.94 | t = 2.23* | 49 |
| Presence of competitor | Class | — | t = 0.63 | 49 | — | t = 1.15 | 49 |
| Island | Class | — | F = 1.56 | 48 | — | F = 1.46 | 48 |
| D. magna | |||||||
| Age of population | Continuous | 0.04 | t = 2.39* | 29 | 0.11 | t = 3.92*** | 29 |
| Volume | Continuous | −0.05 | t = −0.34 | 29 | 0.22 | t = 0.72 | 29 |
| Distance to neighbor | Continuous | 0.28 | t = 1.28 | 29 | 0.50 | t = 1.12 | 29 |
| Relative distance to sea | Continuous | 0.20 | t = 1.03 | 29 | 0.64 | t = 1.73 | 29 |
| Presence of competitor | Nominal | — | t = 0.579 | 29 | — | t = 0.087 | 29 |
| Island | Nominal | — | F = 8.70*** | 25 | — | F = 3.39* | 25 |
Reported statistics are either F-values (island) or t-values (all other variables). The regression slope is given only for continuous variables. N, the number of pools for which a given statistic was calculated. Significant values after correction for multiple testing (sequential Bonferroni correction) are underlined. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.
Figure 2.—
Relationship between genotypic richness and population age in D. longispina (A) and D. magna (B and C). B shows all D. magna populations and C shows only those populations that were not fixed for the most common genotype. The size of the dots indicates the number of populations with the same value.
In D. longispina, pool volume, distance to neighbor, and relative distance to the sea also were significantly associated with at least one diversity estimate. All slopes went in the expected direction; that is, age, volume, and relative distance to the sea were positively correlated and distance to neighbor was negatively correlated with genetic diversity (Table 5). In D. magna, both measures of diversity differed significantly among islands, but none of the other variables, except population age, was significantly associated with genetic diversity (Table 5).
Multiple regression analysis:
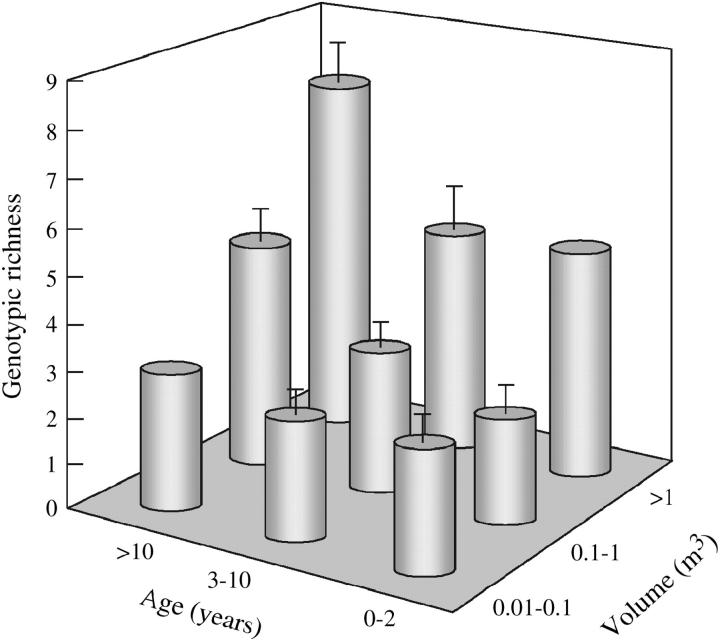
The results of the multiple regression with stepwise selection are given in Table 6. In both species and for both measures of genetic diversity, population age entered in the model and remained significant after controlling for all other significant factors in the final model. In D. longispina, volume and, in the case of allelic richness, distance to neighbor were the other significant factors in the final model. This shows that both population age and pool volume have an effect on genetic diversity in D. longispina, even when the other factor is controlled for (Figure 3). In D. magna, the model for allelic richness included island and relative distance to the sea in addition to population age. Population age, on the other hand, was the only significant factor in the model for genotypic richness in D. magna. Overall, the models explained 31–76% of the total variance in genetic diversity.
TABLE 6.
Multiple regressions between measures of genetic diversity and explanatory variables
| Dependent variable | Explanatory variable | Slope | d.f. | Statistics | r2 |
|---|---|---|---|---|---|
| D. longispina | |||||
| Allelic richness | Age of population | 0.06 | 44 | t = 16.55*** | 0.56 |
| Volume | 0.59 | 44 | t = 14.97*** | ||
| Distance to neighbor | −0.56 | 44 | t = 4.22* | ||
| Genotypic richness | Age of population | 0.15 | 45 | t = 14.42*** | 0.52 |
| Volume | 1.94 | 45 | t = 20.14**** | ||
| D. magna | |||||
| Allelic richness | Age of population | 0.04 | 19 | t = 3.22** | 0.76 |
| Relative distance to sea | 0.58 | 19 | t = 2.56* | ||
| Island | — | 3/19 | F = 15.04**** | ||
| Genotypic richness | Age of population | 0.10 | 23 | t = 3.23** | 0.31 |
Only variables with significant effects (P < 0.05) remained in the final model. Slopes and P-values are given after correcting for all other factors in the model. Reported statistics are F-values (island) or t-values (all other variables). One r2-value is given for each complete model. *P < 0.05, **P < 0.01, ***P < 0.001, ****P < 0.0001.
Figure 3.—
Genotypic richness in D. longispina depending on population age and volume. Error bars indicate 1 SE.
Models based on the lowest AIC values usually included more factors, with goodness-of-fit P-values ranging from 0.05 to 0.4. Additional factors included were island in D. longispina and island, volume, and relative distance to the sea in D. magna. Yet, inclusion of these factors did not qualitatively change the association between genetic diversity and explanatory variables present in the stepwise models. Therefore only the stepwise models are reported.
Association between explanatory variables and pairwise FST:
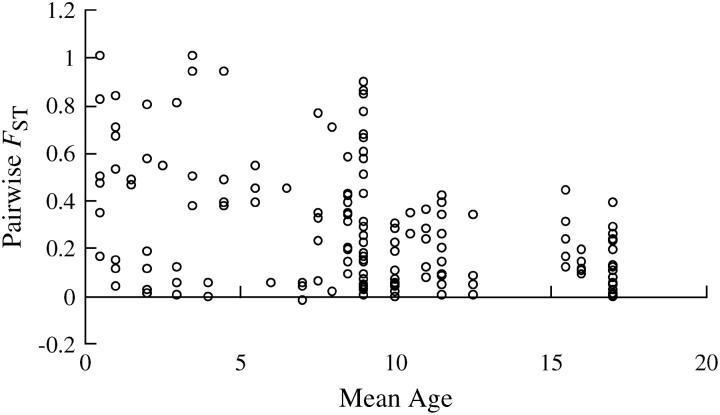
The Mantel regression on the two islands with the highest number of D. longispina pools showed that genetic differentiation was negatively correlated with population age, indicating that younger populations were more strongly differentiated than older populations (Table 7, Figure 4). This was evident in a simple regression as well as in a multiple regression after correcting for volume and distance. The Mantel regression further showed a significantly negative correlation between genetic differentiation and volume as well as a positive correlation between genetic differentiation and distance.
TABLE 7.
Mantel regressions for associations between pairwiseFST and explanatory variables on the two islands with the highest number ofD. longispina pools (Granbusken, 14 pools; Storgrundet, 12 pools)
| Explanatory variable | Island | Test statistic |
Value |
|---|---|---|---|
| Mean age | Granbusken | r | −0.46*** |
| Storgrundet | r | −0.30* | |
| Combined | χ2 | 26.96**** | |
| Mean volume | Granbusken | r | −0.18 |
| Storgrundet | r | −0.43*** | |
| Combined | χ2 | 22.07*** | |
| Distance | Granbusken | r | 0.22* |
| Storgrundet | r | 0.41*** | |
| Combined | χ2 | 21.25*** |
Combined tests were calculated according to Fisher's method of combining probabilities. The Mantel r-values from simple regression are given. The underlined values are also significant (P < 0.05) in a multiple regression after correcting for all other factors.
Figure 4.—
Decrease in pairwise FST with mean population age in D. longispina. The data represented are from all within-island pairs on the two islands on which the Mantel tests were based.
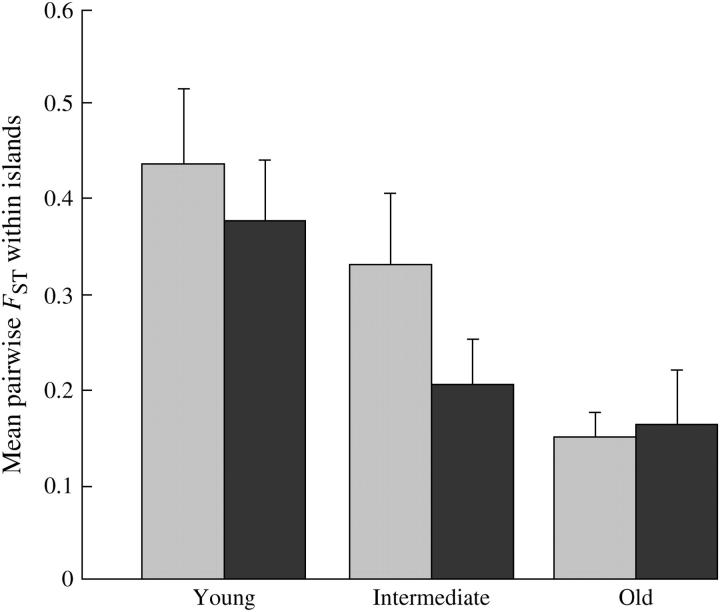
Comparing the means of all defined within-island pairwise FST estimates for each age class showed that pairwise FST decreased with age in both species (Figure 5). Our approximate test indicated that this decrease was significant in both species (D. longispina: F2,42 = 7.07, P = 0.002; D. magna: F2,48 = 3.81, P = 0.03).
Figure 5.—
Mean pairwise FST between populations of young (0–2 years), intermediate (3–10 years), and old (>10 years) in D. longispina (shading) and D. magna (solid). Only pairs with both pools on the same island are included. Error bars indicate 1 SE, calculated from observed variances of pairwise FST within each age class and the number of pools (not the number of pairs) in a given class.
Number of colonizers:
In D. magna, 19 of 28 newly colonized populations contained only a single homozygous genotype, and 5 populations were fixed for a single heterozygous genotype. In D. longispina, 1 of 5 newly colonized populations was fixed for a homozygous and 1 for a heterozygous genotype.
For D. magna populations, 16 populations (57%) were fixed for the most common homozygous genotype. The overall frequency of this genotype in the metapopulation was 73%. Assuming two randomly picked genotypes from the whole metapopulation (migrant pool migration), the probability of twice obtaining the most common genotype is 53%. We thus assumed that these 16 pools were colonized by an average of 1.8 individuals (because this number of colonizers would result in 57% of newly colonized populations fixed for the most common genotype). For the other monomorphic populations, the probability that they were founded by two individuals of the same genotype was <10%. Therefore, we assumed that these populations were founded by one individual. Assuming further that polymorphic populations were founded by the number of individuals equal to the number of genotypes that they contained (two or three), we obtained an overall estimate of 1.7 colonizers (range 1–3)/population. For D. longispina, these calculations lead to an estimate of 3.2 colonizers (range 1–9), which is higher, because 1 newly colonized population contained nine genotypes. Without this population, the estimate is 1.75 colonizers (range 1–2).
DISCUSSION
In the studied metapopulations of Daphnia, genetic differentiation was stronger among young populations than among old populations and young populations were also genetically less diverse. Because variation in population age is a direct consequence of extinction and recolonization, this pattern, which is highly consistent between the two species, suggests that turnover leads to decreased local genetic diversity and to increased genetic differentiation in these metapopulations.
It is likely that both the increase in genetic diversity with age and the decrease in genetic differentiation with age reflect the same processes. Colonization by a small number of colonizers creates strong genetic bottlenecks (founder events) and consequently, newly founded populations have a low local genetic diversity and are strongly differentiated from each other. Subsequent immigration may introduce new genetic material, increasing local genetic diversity and decreasing differentiation. This effect has been analyzed by Whitlock and McCauley (1990), who found that turnover dynamics always lead to increased differentiation if the number of colonizers is less than twice the number of migrants. In Daphnia, wind-blown resting eggs are thought to be the main source of both colonizers and migrants. Because this form of dispersal is entirely passive, it may be assumed that colonization and migration are qualitatively the same; that is, colonization is migration into a pool that happens to be empty. The number of colonizers may therefore be assumed to be equal to the number of migrants and turnover is thus expected to increase differentiation in this system.
Our analyses indicate that the number of colonizers (and thus the assumed number of migrants) is very low compared to the large local population sizes. Migrant frequencies in populations are thus expected to be small, and, in a neutral model, most immigrant genes would disappear by drift, and even the few that increase would increase slowly. Thus, the equalizing effect of migration on gene frequencies will be small and most populations may become extinct before genetic diversity has significantly increased (Crow and Aoki 1984; Whitlock 1992b). This means that with the parameters given by the Daphnia metapopulations it should be difficult to detect a change of genetic population structure with age. This can best be seen in a numerical example, which is intended to reflect the general properties of Daphnia metapopulations but makes the simplifying assumption of the island model of population structure, that is, that migrants and colonizers are drawn at random from the whole metapopulation. We calculated equilibrium FST in the absence of turnover, assuming local demes of 1000 individuals (N = 1000) exchanging on average one migrant per generation (Nm = 1, m = 0.001) in the presence of a turnover rate of 17% with the number of colonizers, k, being equal to the number of migrants (i.e., k = Nm = 1, which implies that colonization is migration into empty patches). With these parameters, expected equilibrium FST in the absence of turnover is 0.2. With turnover, expected FST among newly colonized populations is 0.5 (Wade and McCauley 1988), showing the strong effect of turnover. However, the expected overall FST of a metapopulation described by these parameters is 0.49 (Wade and McCauley 1988), which is only slightly less than that among newly colonized populations. The reason for this small difference, which would make it almost impossible to detect differences in genetic differentiation between young and old populations, is that the time required to return halfway back to FST = 0.2 is 277 generations due to the large population size and the low migration rates (Whitlock 1992b).
We therefore think that the observed increase in local genetic diversity and the reduction in genetic differentiation with population age across a period of only 17 years is unlikely to be explainable on the basis of a neutral model only, but may be better explained if immigrants have a selective advantage. One effect that may cause such an advantage is hybrid vigor (Whitlock et al. 2000), which we have earlier shown to be present in the D. magna metapopulation (Ebert et al. 2002). In this metapopulation, local populations appear to be strongly inbred due to founder events. Particularly if populations are founded by single individuals, resting eggs can be produced only by within-clone mating, and thus all hatchlings in the following season will be the result of selfing with an inbreeding coefficient of 0.5. If subsequent immigrants mate successfully with the resident population, they produce noninbred hybrids, which have a selective advantage. During selection for hybrids, all genes introduced by immigrants rapidly increase in frequency because they represent half of the hybrid's genes, whereas the initial frequency of immigrant genes in the pool is likely to be much lower. Immigration, even by a few individuals, can thus have a strong effect on genetic diversity if the immigrants succeed in mating with residents to produce hybrids. Hybrid vigor thus leads to an increased effective migration rate (Ingvarsson and Whitlock 2000) and reduces population differentiation (Pamilo et al. 1999) and hence may represent a mechanism by which genetic population structure in metapopulations may be closely related to the age structure of local demes. Other possible selective advantages of immigrants may further contribute to this pattern, as, for instance, locally adapted parasites, which may reduce the fitness of local residents more than they affect the fitness of immigrants.
A number of other studies have found a decrease of genetic differentiation or an increase in genetic diversity with population age (Whitlock 1992a; McCauley et al. 1995; Nurnberger and Harrison 1995; Giles and Goudet 1997; Ingvarsson et al. 1997; Mopper et al. 2000). It is not clear to which degree hybrid vigor has contributed to these studies. In plant metapopulations, an important factor contributing to higher numbers of migrants than of colonizers is that colonization has to take place by seeds, whereas subsequent gene flow can also be mediated by pollen (McCauley et al. 1995; Giles and Goudet 1997). However, in all studies genetic bottlenecks occurred during colonization. A possible contribution of hybrid vigor should therefore not be neglected.
We have estimated the number of colonizers using assumptions of the migrant pool model. In reality, colonizers may come mainly from a close-lying pool (Pajunen and Pajunen 2003), indicating that our estimate is likely to be an underestimate of the real number of colonizers because colonizers may be genetically more similar to one another and a larger propagule size would thus not be detected as easily. Yet the repeated occurrence of fixed heterozygous populations among newly colonized populations (6 of 33 newly colonized populations, summed across species) indicates that the number of colonizers is indeed low. This is because fixed heterozygous populations must have been colonized by heterozygous individuals only. Furthermore, the number of colonizers calculated under the assumption of migrant pool colonization may come close to the effective number of colonizers (Ingvarsson 1998), that is, to the number of colonizers that would have the same effect on genetic differentiation if colonization happened according to the migrant pool model.
In D. longispina, genotypic richness increased from 2.5 to 5.8 over the time span of the whole study and in D. magna from 1.2 to 2.2 (monomorphic populations not excluded). At the same time pairwise FST estimates decreased from 0.43 to 0.15 in D. longispina and from 0.37 to 0.16 in D. magna (see also Figures 2 and 5). Yet the oldest populations may in fact be older than 16 or 17 years because they were founded before the onset of the study. This indicates that a class of old and relatively stable populations may exist, which may act as a reservoir of genetic diversity (Pajunen and Pajunen 2003). We think that this does not change our general conclusion for two reasons. First, the associations among population age genetic differentiation as well as the association between population age and local genetic diversity do not rely only on these oldest populations. Populations of intermediate age (colonized after 1982) in both species had intermediate local genetic diversities and intermediate levels of genetic differentiation. Second, these old and stable populations occur mainly in deep pools and are therefore unlikely to dry out during summer droughts. We think, however, that it is during these droughts, when the sediment is dry and exposed to wind, that dispersal mainly occurs. Hence, the stable and old populations may not be the main source of migrants.
In addition to population age, a number of other ecological variables explain part of the population genetic structure in our Daphnia metapopulations. These patterns were less consistent between the two species than population age, and it is unclear whether these inconsistencies reflect real differences in the ecology of the two species or a lack of statistical power. At least in D. longispina, pool volume appeared to be an important factor, both for genetic diversity and for genetic differentiation, but our analysis does not allow us to identify the reason for these correlations. The effect of pool volume may be because of increased drift in smaller pools (due to smaller population size), but also because larger pools may receive more immigrants (because of their larger surface area) or because they have a lower extinction rate (because they are less likely to dry out during the summer). Yet, it was important to include these ecological variables in this study because they were also correlated with population age and correlations between genetic measures and population age without controlling for ecological variables may have been spurious. Our analysis indicates that this was not the case (see also Figure 3). Nevertheless, our study shows that a number of ecological factors can play an important role in determining genetic population structure.
In conclusion, we found that older populations had a higher genetic diversity and that genetic differentiation among pools decreased with population age. In the studied metapopulations, this pattern seems unlikely to be caused by neutral processes alone because large population sizes and low migration rates predict that long time spans would be required for the observed patterns to become evident. We therefore think that the results are more easily explained if immigrant genes are selectively favored, for instance, by hybrid vigor, which has been shown for one of the metapopulations. This mechanism suggests that genetic bottlenecks during colonization cause low genetic diversity of young populations and population-wide inbreeding. Subsequent immigration leads to hybrid vigor, which gives a selective advantage to immigrant genes. Thus, even with large local population sizes and low nominal (as opposed to effective) migration rates, increases in diversity may be observed within a reasonable time because hybrid vigor increases the effective migration rate.
Acknowledgments
We thank the staff of the Tvärminne Biological Station, B. Gimelli, and I. Pajunen for support and technical assistance. We greatly profited from comments and advice from J. Goudet, P. Jarne, T. J. Kawecki, C. Liautard, C. Pampoulie, and an anonymous reviewer. We thank the Swiss National Science Foundation, the Handschin-Stiftung, Max Husmann-Stiftung, Josef & Olga Tomcsik-Stiftung, the Werenfels-Fonds, and the Roche Research Foundation for support. This is part of project no. 97524006 at Tvärminne Zoological Station.
References
- Andrewartha, H. G., and L. C. Birch, 1954 The Distribution and Abundance of Animals. University of Chicago Press, Chicago.
- Austerlitz, F., B. Jung-Muller, B. Godelle and P.-H. Gouyon, 1997. Evolution of coalescence times, genetic diversity and structure during colonization. Theor. Popul. Biol. 51: 148–164. [Google Scholar]
- Austerlitz, F., S. Mariette, N. Machon, P.-H. Gouyon and B. Godelle, 2000. Effects of colonization processes on genetic diversity: differences between annual plants and tree species. Genetics 154: 1309–1321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson, J., 1989. Interspecific competition increases local extinction rate in a metapopulation system. Nature 340: 713–715. [Google Scholar]
- Brown, J. H., and A. Kodric-Brown, 1977. Turnover rates in insular biogeography: effect of immigration on extinction. Ecology 58: 445–449. [Google Scholar]
- Crow, J. F., and K. Aoki, 1984. Group selection for a polygenic behavioural trait: estimating the degree of population subdivision. Proc. Natl. Acad. Sci. USA 81: 6073–6077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dybdahl, M. F., 1994. Extinction, recolonization, and the genetic structure of tidepool copepod populations. Evol. Ecol. 8: 113–124. [Google Scholar]
- Ebert, D., J. W. Hottinger and V. I. Pajunen, 2001. Temporal and spatial dynamics of parasites in a Daphnia metapopulation: Which factors explain parasite richness? Ecology 82: 3417–3434. [Google Scholar]
- Ebert, D., C. Haag, M. Kirkpatrick, M. Riek, J. W. Hottinger et al., 2002. A selective advantage to immigrant genes in a Daphnia metapopulation. Science 295: 485–488. [DOI] [PubMed] [Google Scholar]
- El Mousadik, A., and R. J. Petit, 1996. High level of genetic differentiation for allelic richness among populations of the argan tree (Argania spinosa (L.) Skeels) endemic to Morocco. Theor. Appl. Genet. 92: 832–839. [DOI] [PubMed] [Google Scholar]
- Excoffier, L., 2001 Analysis of population subdivision, pp. 271–307 in Handbook of Statistical Genetics, edited by D. Balding, M. Bishop and C. Cannings. John Wiley & Sons, New York.
- Giles, B. E., and J. Goudet, 1997. Genetic differentiation in Silene dioica metapopulations: estimation of spatiotemporal effects in a successional plant species. Am. Nat. 149: 507–526. [Google Scholar]
- Goudet, J., 2001 FSTAT, A Program to Estimate and Test Gene Diversities and Fixation Indices, Version 2.9.3. http://www.unil.ch/izea/softwares/fstat.html.
- Goudet, J., M. Raymond, T. deMeeus and F. Rousset, 1996. Testing differentiation in diploid populations. Genetics 144: 1933–1940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haag, C., J. Hottinger, M. Riek and D. Ebert, 2002. Strong inbreeding depression in a Daphnia metapopulation. Evolution 56: 518–526. [PubMed] [Google Scholar]
- Hanski, I., 1994. A practical model of metapopulation dynamics. J. Anim. Ecol. 63: 151–162. [Google Scholar]
- Hanski, I., 1999 Metapopulation Ecology. Oxford University Press, Oxford.
- Hanski, I., and M. Gilpin, 1997 Metapopulation Biology: Ecology, Genetics and Evolution. Academic Press, San Diego.
- Hanski, I., and E. Ranta, 1983. Coexistence in a patchy environment: three species of Daphnia in rock pools. J. Anim. Ecol. 52: 263–279. [Google Scholar]
- Hebert, P. D. N., and M. J. Beaton, 1993 Methodologies for Allozyme Analysis Using Cellulose Acetate Electrophoresis, Ed. 2. Helena Laboratories, Beaumont, TX.
- Hebert, P. D. N., and R. D. Ward, 1972. Inheritance during parthenogenesis in Daphnia magna. Genetics 71: 639–642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick, P. W., 2000 Genetics of Populations. Jones & Bartlett, Boston.
- Hobaek, A., and P. Larsson, 1990. Sex determination in Daphnia magna. Ecology 71: 2255–2268. [Google Scholar]
- Ingvarsson, P. K., 1998. Kin-structured colonization in Phalacrus substriatus. Heredity 80: 456–463. [Google Scholar]
- Ingvarsson, P. K., and M. C. Whitlock, 2000. Heterosis increases the effective migration rate. Proc. R. Soc. Lond. Ser. B 267: 1321–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingvarsson, P. K., K. Olsson and L. Ericson, 1997. Extinction-recolonization dynamics in the mycophagous beetle Phalacrus substriatus. Evolution 51: 187–195. [DOI] [PubMed] [Google Scholar]
- Ives, A. R., and M. C. Whitlock, 2002. Inbreeding and metapopulations. Science 295: 454–455. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., and P. Jarne, 2000. The effects of a bottleneck on inbreeding depression and the genetic load. Am. Nat. 155: 154–167. [DOI] [PubMed] [Google Scholar]
- Kleiven, O. T., P. Larsson and A. Hobaek, 1992. Sexual reproduction in Daphnia magna requires three stimuli. Oikos 65: 197–206. [Google Scholar]
- Le Corre, V., and A. Kremer, 1998. Cumulative effects of founding events during colonisation on genetic diversity and differentiation in an island and stepping-stone model. J. Evol. Biol. 11: 495–512. [Google Scholar]
- McCauley, D. E., J. Raveill and J. Antonovics, 1995. Local founding events as determinants of genetic structure in a plant metapopulation. Heredity 75: 630–636. [Google Scholar]
- Mopper, S., P. Stiling, K. Landau, D. Simberloff and P. Van Zandt, 2000. Spatiotemporal variation in leafminer population structure and adaptation to individual oak trees. Ecology 81: 1577–1587. [Google Scholar]
- Nei, M., 1973. Analysis of gene diversity in subdivided populations. Proc. Natl. Acad. Sci. USA 70: 3321–3323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nurnberger, B., and R. G. Harrison, 1995. Spatial population structure in the whirligig beetle Dineutus assimilis: evolutionary inferences based on mitochondrial DNA and field data. Evolution 49: 266–275. [DOI] [PubMed] [Google Scholar]
- Pajunen, V. I., 1986. Distributional dynamics of Daphnia species in a rock-pool environment. Ann. Zool. Fenn. 23: 131–140. [Google Scholar]
- Pajunen, V. I., and I. Pajunen, 2003. Long-term dynamics in rock pool Daphnia metapopulations. Ecography 26: 731–738. [Google Scholar]
- Pamilo, P., S. Pálsson and O. Savolainen, 1999. Deleterious mutations can reduce differentiation in small, subdivided populations. Hereditas 130: 257–264. [Google Scholar]
- Pannell, J. R., and B. Charlesworth, 1999. Neutral genetic diversity in a metapopulation with recurrent local extinction and recolonization. Evolution 53: 664–676. [DOI] [PubMed] [Google Scholar]
- Ranta, E., 1979. Niche of Daphnia species in rock pools. Arch. Hydrobiol. 87: 205–223. [Google Scholar]
- Raufaste, N., and F. Rousset, 2001. Are partial Mantel tests adequate? Evolution 55: 1703–1705. [DOI] [PubMed] [Google Scholar]
- Richards, C. M., 2000. Inbreeding depression and genetic rescue in a plant metapopulation. Am. Nat. 155: 383–394. [DOI] [PubMed] [Google Scholar]
- Saccheri, I. J., and P. M. Brakefield, 2002. Rapid spread of immigrant genomes into inbred populations. Proc. R. Soc. Lond. Ser. B 269: 1073–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin, M., 1977. Gene flow and genetic drift in a species subject to frequent local extinctions. Theor. Popul. Biol. 12: 253–262. [DOI] [PubMed] [Google Scholar]
- Slatkin, M., 1985. Gene flow in natural populations. Annu. Rev. Ecol. Syst. 16: 393–430. [Google Scholar]
- Sokal, R. R., and F. J. Rohlf, 1981 Biometry, Ed. 2. Freeman, New York.
- Stoddart, J. A., 1983. A genotypic diversity measure. J. Hered. 74: 489–490. [Google Scholar]
- Wade, M. J., and D. E. McCauley, 1988. Extinction and recolonization: their effects on the genetic differentiation of local populations. Evolution 42: 995–1005. [DOI] [PubMed] [Google Scholar]
- Weir, B. S., and C. C. Cockerham, 1984. Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., 1992. a Nonequilibrium population-structure in forked fungus beetles: extinction, colonization, and the genetic variance among populations. Am. Nat. 139: 952–970. [Google Scholar]
- Whitlock, M. C., 1992. b Temporal fluctuations in demographic parameters and the genetic variance among populations. Evolution 46: 608–616. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., and D. E. McCauley, 1990. Some population genetic consequences of colony formation and extinction: genetic correlations within founding groups. Evolution 44: 1717–1724. [DOI] [PubMed] [Google Scholar]
- Whitlock, M. C., P. K. Ingvarsson and T. Hatfield, 2000. Local drift load and the heterosis of interconnected populations. Heredity 84: 452–457. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1969 Evolution and the Genetics of Populations, Vol. 2: The Theory of Gene Frequencies. University of Chicago Press, Chicago.