Diffusion of isolated DNA molecules: Dependence on length and topology

Abstract

The conformation and dynamics of circular polymers is a subject of considerable theoretical and experimental interest. DNA is an important example because it occurs naturally in different topological states, including linear, relaxed circular, and supercoiled circular forms. A fundamental question is how the diffusion coefficients of isolated polymers scale with molecular length and how they vary for different topologies. Here, diffusion coefficients D for relaxed circular, supercoiled, and linear DNA molecules of length L ranging from ≈6 to 290 kbp were measured by tracking the Brownian motion of single molecules. A topology-independent scaling law D ∼ L^−ν was observed with ν_L = 0.571 ± 0.014, ν_C = 0.589 ± 0.018, and ν_S = 0.571 ± 0.057 for linear, relaxed circular, and supercoiled DNA, respectively, in good agreement with the scaling exponent of ν ≅ 0.588 predicted by renormalization group theory for polymers with significant excluded volume interactions. Our findings thus provide evidence in support of several theories that predict an effective diameter of DNA much greater than the Debye screening length. In addition, the measured ratio D_Circular/D_Linear = 1.32 ± 0.014 was closer to the value of 1.45 predicted by using renormalization group theory than the value of 1.18 predicted by classical Kirkwood hydrodynamic theory and agreed well with a value of 1.31 predicted when incorporating a recently proposed expression for the radius of gyration of circular polymers into the Zimm model.

While many eukaryotic genomes are linear, prokaryotic genomes and most cloned DNA constructs are circular (1). Indeed, a commonly stated motivation for theoretical calculations on circular polymers is that they may be applicable to understanding the behavior of DNA. However, four of the five previously reported studies on the diffusion of circular polymers have used synthetic polymers, and only two of these, both using synthetic polymers, examined the dependence of the diffusion coefficient on molecular length. The dependence of D on length for relaxed circular DNA has never been measured. Here, we examine linear, relaxed circular, and supercoiled DNA molecules covering a wide range of lengths (≈6 to 290 kbp).

For long linear polymers in a good solvent, where excluded volume effects are appreciable, polymer physics theory (2) predicts D ∼ 1/R_G ∼ L^−ν with ν ≅ 0.588, where R_G is radius of gyration. The same scaling exponent has been calculated for both dynamic (D ∼ L^−ν) and static (R_G ∼ L^ν) quantities, with nearly identical results determined by using a wide range of methods. Static scaling has been examined by using Monte Carlo simulations (3), bead-rod simulations (4), and cylindrical self-avoiding polygon models (5). Renormalization group theory methods have been used in both static (3, 6) and dynamic (7) calculations, and bond-fluctuation simulations (8) were used to measure and compare both scaling relationships. The predicted scaling exponent is close to our previous experimental finding of ν = 0.61 ± 0.016 for linear DNA (9). Although the primary purpose of the present study is to examine the effect of topology on diffusion, more accurate results on linear DNA were also obtained because we used DNA constructs of defined lengths, whereas previously we only estimated the lengths of the longest molecules.

Theoretical studies and numerical calculations further predict that the scaling exponent ν should be unaffected by a topological change from linear to circular form (3, 6, 10, 11). Although the two previous synthetic polymers experiments examining the dynamical scaling behavior of both linear and circular molecules in good solvent found such topological invariance, they did not find an exponent in accord with the predicted scaling exponent of 0.588. Rather, reported exponents were in agreement with the 0.5 exponent predicted for a polymer in a theta solvent and thus not subject to excluded volume. Light-scattering methods were used, and scaling exponents of ν = 0.48 to 0.53 were reported (12, 13).

While the scaling exponent is predicted to be topologically invariant, the ratio of diffusion coefficients of circular and linear species C = D_C/D_L is predicted to be greater than unity and independent of length for long molecules. The exact value is still debated and is found to be sensitive to how solvent conditions, hydrodynamic interactions, and excluded volume interactions are treated. Faster diffusion of circles compared with linear molecules can be qualitatively understood as being due to a reduced mean square end-to-end distance caused by the conformational constraint of closure. However, it is important to note that increased hydrodynamic screening and an altered sensitivity to excluded volume effects are also expected to play a role (14).

Calculations based on classical Kirkwood hydrodynamic theory (15) predict C = 3π/8 ≅ 1.18, whereas more recent renormalization group calculations using the Edwards Hamiltonian (7) predict C = e^3/8 ≅ 1.45. Three of the aforementioned experiments on synthetic polymer solutions (12, 13, 16) report values of C = 1.11–1.2, in reasonable agreement with the calculations using Kirkwood theory, whereas one (17) reports C = 1.36, in closer agreement with the renormalization group theory calculation. To our knowledge, the ratio C has only been measured for one short plasmid DNA molecule, ColE₁ (≈6.6 kbp), by light scattering, and a value of C = 1.24 was reported (18). An alternative approach for estimating C has involved using R_G predictions for circles in an expression for hydrodynamic drag predicted by the Zimm model (19). Whether this approach leads to reasonable predictions will be considered below.

Besides being of inherent interest in biophysics, DNA is now well established as a useful model system for studying basic polymer physics phenomena and holds several advantages (20–22). DNA replication yields a homogeneous sample of molecules of exactly the same length, and DNA topology can be precisely controlled. Supercoiled molecules can be completely converted to relaxed circular or linear form by treatment with appropriate enzymes. Furthermore, single-molecule imaging of DNA allows for visualization of single-polymer dynamics (21, 22). Here, imaging of the Brownian motion of single DNA molecules provides the simplest and most direct way of determining the diffusion behavior of isolated polymers in the limit of infinite dilution. Bulk methods such as light or neutron scattering are usually made at higher concentrations where the diffusion is concentration-dependent, and thus extrapolation is required for determining the behavior of isolated molecules. In the present single-molecule experiments, the average distance between molecules is hundreds of times R_G. Thus, such measurements are complementary to traditional bulk methods.

Results and Discussion

Linear and Relaxed Circular DNA.

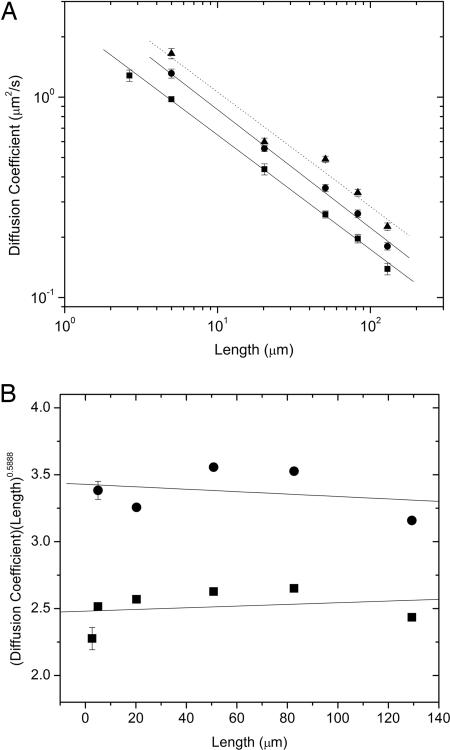
We have measured the scaling of D with L (Fig. 1A) for both linear and relaxed circular molecules and find ν_L = 0.571 ± 0.014 and ν_C = 0.589 ± 0.018, respectively. These scaling exponents were determined by a linear fitting of log D vs. log L and are in good agreement with the predicted value of ν ≅ 0.588. The present value is also more accurate than our previously measured value of ν_L = 0.61 ± 0.016 for linear DNA (9) because here we used DNA constructs of defined lengths, whereas previously we only estimated the lengths of the longest molecules. To confirm the validity of this power-law behavior, we have compared our results with the predicted scaling by plotting D·L^0.588 versus L for both linear and circular molecules (Fig. 1B). Linear fits to both data sets yield values of 6.27 × 10⁻⁴± 0.001 and −9.07 × 10⁻⁴± 0.001 for linear and circular forms, respectively. The predicted power-law behavior is therefore within the error bars of these measurements, and the relatively small errors in these fits show the accuracy of our reported scaling laws.

Fig. 1.

Scaling of diffusion coefficients. (A) Diffusion coefficient (D) vs. chain length (L) for isolated DNA molecules. The points are the data obtained by tracking fluorescently labeled linear (squares), relaxed circular (circles), and untreated (mostly supercoiled circular) (triangles) DNA. The solid lines are power-law fits having exponents ν_L = 0.571 ± 0.014 and ν_C = 0.589 ± 0.018. The dashed line is a fit to the supercoiled DNA data with ν_S = 0.571 ± 0.057. The error bars indicate σ_D from bootstrap analysis. (B) Comparison of measured scaling of diffusion coefficient (D) with chain length (L) to predicted scaling of −0.588. Plot of D·L^0.588 vs. L (data points and error bars are the same as those in A). The solid lines are linear fits to the data that yield values of 6.27 × 10⁻⁴± 0.001 and −9.07 × 10⁻⁴± 0.001 for linear and circular molecules, respectively.

Our ν_C value is higher than those previously reported for circular synthetic polymers (ν_C = 0.52) (12, 13). Although these previous studies were done in good solvent conditions, the findings were noted to be in closer agreement with the value ν = 0.5 expected for a theta solvent. It was proposed in ref. 12 that this difference could be due to a reduced excluded volume effect for low-molecular-weight polymers. Here, we covered a range of ≈70 to 1,900 persistence lengths, which extends to five times higher than that in ref. 12.

On the other hand, DNA differs from many synthetic polymers in that the persistence length is ≈25 times larger than the double-helix diameter, which suggests that the excluded volume effect might be less significant for DNA than for typical synthetic polymers. However, we measure a scaling exponent of ν ≅ 0.58 extending to much shorter molecules. This value is in agreement with ν ≅ 0.588 predicted when including the excluded volume effect rather than that of ν = 0.5 predicted with negligible excluded volume. The most likely explanation for our finding is the electrostatic self-repulsion of charged DNA molecules. It is often assumed that the effective diameter of DNA should correspond to the solvent-dependent Debye length rather than the natural helix diameter. Here, we use a solvent containing 10 mM NaCl that gives a Debye length λ_D of ≈3 nm (λ_D = 0.3 nm/[NaCl]^1/2) (23), which is not much larger than the bare diameter of 2 nm. Using this Debye length, Marko and Siggia (24) have estimated using Flory theory that the excluded volume effect would only be expected to be marginally important for DNA molecules of ≈100 kbp and longer. However, early theoretical calculations by Stigter (25) predict an effective diameter in 10 mM Na⁺ of ≈16 nm, which is much larger than the Debye length. Moreover, Toan and Micheletti (26) have recently predicted that the electrostatic contribution is even larger and estimated an effective diameter value of ≈24 nm in 10 mM Na⁺. This value would imply a persistence length only approximately two times the effective diameter, leading to a much stronger excluded volume effect than that expected for bare double-stranded DNA. Our present results, as well as recent studies of knotted DNA (27), provide experimental data in support of these theoretical predictions.

Our ratios of C = D_C/D_L, which were similar for all of the molecules studied, yield a mean value of C = 1.32 ± 0.014 (Table 1). This value is significantly higher than that predicted by first-order perturbation theory based on the Kirkwood hydrodynamic model (C ≅ 1.18) and those reported in scattering experiments on synthetic polymers (C = 1.11–1.2) (12, 13, 16). Our value is also higher than C = 1.24 reported for ColE₁ DNA (18) and is in closer accord with a pulsed-gradient-spin-echo NMR measurement on poly(ethylene oxide) (17) of C ≅ 1.36. Our result along with that in ref. 17 is closer to the prediction of the most recent renormalization group calculation (C ≅ 1.45) (10). Furthermore, although this predicted value is higher than our finding, the authors note that their theory allows for knotted circular conformations and could thus lead to a slightly overestimated value compared with that obtained experimentally with unknotted circular polymers.

Table 1.

Diffusion coefficients, inferred radii of gyration, and topology-dependent diffusion ratios and radius of gyration ratios for linear, relaxed circular, and supercoiled DNA molecules

DNA construct	Size, kbp	Length,* μm	DL, μm2/s	RG,L, μm	DC, μm2/s	RG,C, μm	Ds,† μm2/s	C = DC/DL	G = RG,L/RG,C
pYES2‡	5.9	2.65	1.28	0.213
pPIC9K〈TRL5〉	11.1	4.99	0.976	0.279	1.31	0.173	1.65	1.35	1.61
pCC1FOSTM45	45	20.25	0.437	0.624	0.554	0.410	0.598	1.27	1.52
CTD-2342K16	112.8	50.81	0.260	1.05	0.35	0.645	0.490	1.36	1.63
CTD-2609C22	183.5	82.66	0.197	1.38	0.26	0.867	0.334	1.33	1.60
CTD-2657L24	287.1	129.32	0.139	1.96	0.180	1.26	0.226	1.30	1.56

*Accounting for the increase in length caused by YOYO-I, as described in ref. 56.

^†Samples had ≈50–80% supercoiled molecules, as described in the text.

^‡Relaxed circular and supercoiled pYES2 moved too quickly to accurately track with our current setup.

Although relatively few previous studies have considered the diffusion of circular versus linear polymers, a number of previous investigations have considered the effect of topology on the radius of gyration. The ratio G = R_G,L/R_G,C has been calculated by using a variety of models. The Bloomfield–Zimm model (28) predicts G = 1.45, renormalization field theory applied to Fixman’s cluster expansion (6) gives G = 1.33, and, most recently, a modified Yu–Fujita model has been proposed (14) that predicts G = 1.54. The defining differences in these theories are the method of calculating the mean square distance for cyclic polymers as well as the means of introducing excluded volume effects. In addition, a number of Monte Carlo simulations (29–34) have been performed, and values ranging from G = 1.32 to G = 1.38 were reported. Finally, small-angle neutron scattering (35), light scattering (36, 37), and size-exclusion chromatography (37) measurements on synthetic ring polymers reported values in the range G ≅ 1.37–1.39, whereas a light-scattering measurement (18) on ColE₁ DNA found G = 1.39.

We are unable to accurately measure R_G with our experimental setup because of the limited resolution of optical microscopy. Other techniques such as static light scattering were considered, but such measurements are extremely difficult for long molecules and become virtually impossible for molecules longer than ≈60 μm (38). Therefore, although there is no apparent way to directly measure R_G for our entire range of molecular lengths, we can still examine whether our data are consistent with theories that relate R_G and D. The hydrodynamic radius R_H can be calculated from D by using the Stokes–Einstein relation D = k_BT/6pηR_H, where k_B is Boltzmann’s constant, T is temperature (≅297 K), and η is solvent viscosity (≅1.2 cPa). We may then combine predictions for G with the predicted relationship between R_H and R_G to test these predictions and compare our results with those previously reported. For linear polymers, the ratio of these radii is predicted by the Zimm model (15) to be R_G,L/R_H,L = 8/3π^1/2 ≅ 1.508, whereas for circular polymers this ratio is predicted (19) to be R_G,C/R_H,C = (π/2)^1/2 ≅ 1.253, leading to a net prediction G ≅ 1.2C. Within this estimate our results imply G = 1.58 ± 0.017, which is in good agreement with a recent prediction of G ≅ 1.54 based on a modified Yu–Fujita model (14). This model predicts less swelling of circles due to the excluded volume interaction than the Bloomfield–Zimm model.

Sedimentation measurements have also been reported for certain linear and circular DNAs in a limited length range. The ratio of sedimentation coefficients for circular and linear molecules, S⁰_C/S⁰_L, is theoretically predicted to equal D_C/D_L and thus can be compared with our measured ratio. S⁰_C/S⁰_L = 1.23 was measured for ColE₁ (18), whereas a ratio of 1.10 was reported for polyoma DNA (≈4,815 bp) (39). Lambda DNA (48,502 bp) has also been measured, and ratios of 1.18, 1.13, and 1.14 have been reported (40). These ratios are systematically lower than our finding of D_C/D_L = 1.32 and that of 1.45 predicted by renormalization group calculations.

Supercoiled DNA.

We have also measured D for our untreated DNA samples containing ≈50–80% supercoiled molecules. The varying fractions of supercoiled species produced increased scatter in our data compared with data for the linear and relaxed circular samples. In addition, we did not attempt to characterize the degree of supercoiling of the molecules, although a single band was observed in gel electrophoresis. With these caveats in mind, we can still compare our results with previously reported theories and experiments. Interestingly, we find a scaling exponent of ν_S = 0.571 ± 0.057, which is similar to the scaling exponents we found for the linear and relaxed circular forms. Flow field-flow fractionation has previously been used to estimate D for three short supercoiled molecules (≈2.7–7.4 kbp), and a value of ν_S = 0.66 was reported (41), whereas light scattering measurements for five short supercoiled DNAs (42) (2.1–10.2 kbp) found ν_S = 0.6. Theory of the conformation and hydrodynamics of supercoiled DNA is less developed than that of the relaxed circular form, and multiple opposing models have been proposed (42–44). One model proposes a rod-like conformation for supercoiled DNA with ν_S ≅ 0.8, whereas another model predicts that supercoiled molecules would have a constantly changing conformation, like linear and relaxed circular molecules, and have the same scaling exponent (ν_S ≅ 0.6) as the other forms (44). Our findings and the previous findings with shorter DNA molecules appear to be in agreement with this latter model.

We also measured the ratios between the diffusion coefficients of the three different forms of our molecules. We found that the ratio between supercoiled and relaxed circular forms (D_S/D_C) ranged from ≈1.1 to 1.4, whereas the ratios between supercoiled and linear forms (D_S/D_L) ranged from ≈1.4 to 1.9. No systematic trend in these ratios with length was observed, and thus these variations may simply be due to the aforementioned sample variations. Previous measurements of diffusion coefficient ratios have been limited to relatively short molecules (≈1–10 kbp) and were made at finite concentrations by using bulk methods. In light scattering studies, D_S/D_C = 1.251 was reported for a 3.7-kbp DNA molecule (44) and D_S/D_C = 1.18 and D_S/D_L = 1.46 were reported for ColE₁ DNA (18). Photon correlation spectroscopy has also been used to study a 2.7-kbp molecule, and a ratio of D_S/D_L = 1.48 was reported (45). Sedimentation ratios have been measured as well, finding S⁰_S/S⁰_C = 1.26 and S⁰_S/S⁰_L = 1.56 for ColE₁ DNA (18) and S⁰_S/S⁰_C = 1.25 and S⁰_S/S⁰_L = 1.38 for polyoma DNA (46). Surprisingly, although the presence of relaxed circular molecules in our sample would be expected to decrease both ratios, our average values were actually slightly higher than previously reported experimental values, suggesting that the supercoiled form is more compact than previously thought.

Fluorescent Labeling Effects.

A potential concern in our measurements is whether the YOYO-I dye may alter the DNA twist. It is well known that the binding of certain dyes, such as ethidium bromide, may cause unwinding of DNA. As the dye:base pair ratio is increased, negatively supercoiled DNA stained with ethidium unwinds to a relaxed circular form and then begins to accumulate positive supercoils (47). Circular DNA prerelaxed by topoisomerase I is thus expected to become positively supercoiled when stained with ethidium. However, we have found that no such supercoiling occurs upon labeling with YOYO-I dye in the conditions used in our experiment. Because many researchers now use this dye, this observation constitutes an additional finding worthy of description.

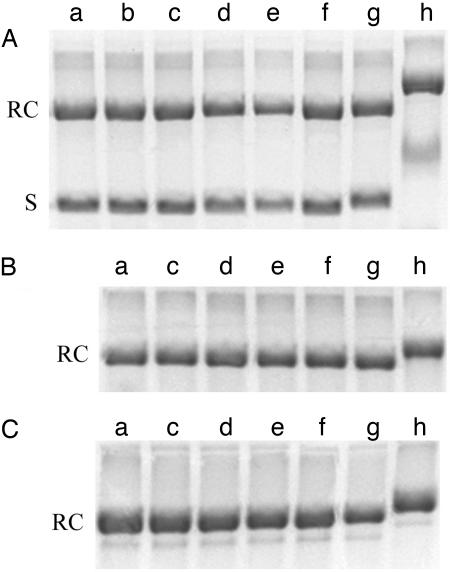
We performed several experiments using pPIC9K〈TRL5〉 DNA to examine the effect of YOYO-I. First, we carried out gel electrophoresis measurements on prelabeled molecules. The high binding constant of YOYO-I ensures stability of the DNA–dye complex during electrophoresis (48), and YOYO-I fluorescence was observed on gel bands corresponding to labeled samples, confirming this stability. Furthermore, it has been shown that DNA supercoiling may be quantified by electrophoresis because the mobility increases with increasing supercoiling (49–51). We compared the supercoiled form, the relaxed circular form produced by treatment with topoisomerase I, and the relaxed circular form produced by nicking the DNA with a nicking endonuclease (Nt.Bst.NBI) (52). The relaxed circle produced by topoisomerase I has the potential to accumulate twist, whereas the nicked form does not (53). As shown in Fig. 2, we observed no change in mobility of any of the three forms of circular DNA at the level of YOYO-I staining used in our experiments.

Fig. 2.

Agarose gel electrophoresis of YOYO-I-labeled pPIC9K〈TRL5〉 DNA samples containing an initial mixture of supercoiled (S) and relaxed circular (RC) species (A), a relaxed circular form produced by treatment with topoisomerase I (B), and a nicked circular form (C). The staining level was varied as follows (in base pairs per dye molecule): lane a, unlabeled DNA; lane b, 500:1; lane c, 50:1; lane d, 5:1; lane e, 1:2; lane f, 1:20; lane g, 1:200; lane h, 1:2,000. The samples were incubated in the dark for 2 h at 50°C to ensure homogeneous labeling. A 1% agarose gel was run using tris-acetate-EDTA buffer and poststained with ethidium bromide to make the bands uniformly visible.

To confirm this finding, we also compared the diffusion of these different species. The value of D for molecules relaxed by topoisomerase I differed by <3% from the value for nicked molecules, whereas D measured for the sample containing supercoiled molecules was 20% higher. Thus, the relaxed circular DNA does not become supercoiled under the conditions of our experiments.

Conclusion

In conclusion, power-law scaling was observed for the relaxed circular, linear, and supercoiled DNA forms, in good agreement with certain theoretical predictions (6, 7, 44). We report the first measurement of the dependence of the diffusion coefficient on molecular length for relaxed circular DNA. Our observation of a scaling exponent of ν_C ≅ 0.59 is the first experimental finding for any circular polymer of an exponent that agrees with theoretical predictions for long molecules in a good solvent. Furthermore, the findings provide evidence in support of several theories that predict an effective diameter of DNA much greater than the Debye screening length. We also report the measurement of a length-independent ratio of diffusion coefficients for linear and circular relaxed DNA molecules (D_C/D_L ≅ 1.32). This measured ratio is significantly greater than that predicted by the classical Kirkwood theory and is in closer agreement with predictions of more recent renormalization group calculations.

Materials and Methods

Six samples of double-stranded DNA molecules were prepared by replication of plasmid, fosmid, and bacterial artificial chromosome constructs in Escherichia coli (Table 1). It is well known that such DNA molecules replicated in E. coli adopt unknotted, negatively supercoiled configurations (54). We extracted and purified the DNA constructs by alkaline lysis, isopropanol precipitation, phenol-chloroform extraction, and dialysis, and characterized them by gel electrophoresis. After purification, ≈50–80% of molecules were found to be in supercoiled form while the remainder were in the relaxed circular form. To prepare linear molecules, samples were digested with restriction endonucleases that cut at only one site. BamHI, ApaI, and MluI were used to cut the plasmids, fosmid, and BACs, respectively. To prepare relaxed circles, samples were digested with topoisomerase I under conditions where this enzyme is known to relax all supercoils in double-stranded DNA without inducing knots (53). To verify that the molecules were fully relaxed after treatment with topoisomerase I, we compared them with molecules treated with the nicking endonuclease Nt.Bst.NBI, which makes the DNA torsionally unconstrained and relaxes all supercoiling without inducing knots (52, 53). No difference was observed between these two samples in either gel electrophoresis measurements [which can resolve knots and supercoils (53)] or diffusion measurements, thus showing that the molecules treated by topoisomerase I were fully relaxed and unknotted.

DNA was labeled with a fluorescent dye, YOYO-I (Molecular Probes), as described in ref. 9, and imaged in an aqueous buffer solution containing 10 mM Tris·HCl (pH 8), 1 mM EDTA, 10 mM NaCl, 4% (vol/vol) β-mercaptoethanol, 30% (wt/vol) glucose, 10 μg/ml glucose oxidase, and 120 μg/ml catalase. Gel electrophoresis and diffusion measurements were used to confirm that the dye did not cause supercoiling of the relaxed circular species, as discussed in further detail above. Molecules were imaged with a custom-built epifluorescence microscope consisting of a 100-W mercury lamp (Nikon), a ×60, 1.2 numerical aperture plan-apochromat, water-immersion microscope objective (Olympus), a YOYO-I fluorescence filter set (Chroma Technology), a 300-mm imaging lens, and an intensified CCD camera (IC-300B; Photon Technology International).

The center of mass (x, y) coordinates of >1,000 paths of >20 different molecules for each construct were tracked every 8/30 sec, and the Einstein relationship 〈x²〉 = 〈y²〉 = 2Dt was used to determine the diffusion coefficient. Errors were estimated by using the bootstrap method to calculate D for 1,000 subensembles of molecules (55). To check the calibration of our apparatus, we measured D for a 0.87-μm-diameter polystyrene microsphere in water and obtained a value within 1% of that predicted by the Stokes–Einstein law. We also measured D for our 45-kbp DNA molecule in five solutions of increasing viscosity and found that D decreased as the −0.99 ± 0.18 power of viscosity, in accord with theoretical expectations.