Abstract
Using multiple diallelic markers, variance component models are proposed for high-resolution combined linkage and association mapping of quantitative trait loci (QTL) based on nuclear families. The objective is to build a model that may fully use marker information for fine association mapping of QTL in the presence of prior linkage. The measures of linkage disequilibrium and the genetic effects are incorporated in the mean coefficients and are decomposed into orthogonal additive and dominance effects. The linkage information is modeled in variance-covariance matrices. Hence, the proposed methods model both association and linkage in a unified model. On the basis of marker information, a multipoint interval mapping method is provided to estimate the proportion of allele sharing identical by descent (IBD) and the probability of sharing two alleles IBD at a putative QTL for a sib-pair. To test the association between the trait locus and the markers, both likelihood-ratio tests and F-tests can be constructed on the basis of the proposed models. In addition, analytical formulas of noncentrality parameter approximations of the F-test statistics are provided. Type I error rates of the proposed test statistics are calculated to show their robustness. After comparing with the association between-family and association within-family (AbAw) approach by Abecasis and Fulker et al., it is found that the method proposed in this article is more powerful and advantageous based on simulation study and power calculation. By power and sample size comparison, it is shown that models that use more markers may have higher power than models that use fewer markers. The multiple-marker analysis can be more advantageous and has higher power in fine mapping QTL. As an application, the Genetic Analysis Workshop 12 German asthma data are analyzed using the proposed methods.
IN linkage disequilibrium (LD) mapping or association study, one may use one marker a time. However, the resolution of the single-marker analysis strategy can be low. In addition, utilizing different markers may lead to different results, since the power to detect allelic association depends on specific properties of the markers. This complicates the interpretation of an analysis. It is interesting and important to build models that use multiple markers simultaneously for high-resolution mapping of genetic traits. A unified analysis using multiple markers gives a unique result and may lead to greater resolution. Moreover, large numbers of single-nucleotide polymorphisms (SNPs) are available, and high-throughout genotyping approaches are emerging (International SNP Map Working Group 2001). This encouraging development facilitates high-resolution fine mapping of genetic traits. It is natural and necessary to develop high-resolution multiple-marker-based methods to dissect genetic traits.
In our previous work, variance component models using two markers are proposed for high-resolution linkage and association mapping of quantitative trait loci (QTL) based on population and pedigree data (Zhao et al. 2001; Fan and Xiong 2002, 2003; Fan and Jung 2003; Fan et al. 2005). The genetic effects are orthogonally decomposed into summation of additive and dominance effects. In Abecasis et al. (2000a)(b, 2001), Cardon (2000), Fulker et al. (1999), and Sham et al. (2000), an association between-family and association within-family (AbAw) approach is proposed to decompose the genetic association into effects of between pairs and within pairs. The models of our previous work differ from the AbAw approach in the following senses: (1) The AbAw approach uses only one marker in analysis, but we use two diallelic markers, and (2) the way of modeling mean coefficients is different. Fan and Jung (2003) compare our method with the AbAw approach and find that our method is advantageous for sib-pair data. In addition, Fan et al. (2005) confirm that our approach is more powerful than the AbAw approach for large pedigrees. One may note that it is not clear how to extend the AbAw approach to use more than one marker in analysis (R. Fan and G. R. Abecasis, personal communication).
This article extends our previous work and investigates variance component models in high-resolution linkage and association mapping of QTL using multiple diallelic markers. The models jointly take linkage and linkage disequilibrium information into account. The linkage information is modeled in the variance-covariance matrix, and the linkage disequilibrium information is modeled in mean coefficients of trait values such as the AbAw approach. By modeling the linkage information in the variance-covariance matrix, we may take advantage of much research on variance component models (Haseman and Elston 1972; Amos et al. 1989; Goldgar and Oniki 1992; Amos 1994; Fulker et al. 1995; Almasy and Blangero 1998; George et al. 1999; Pratt et al. 2000). In the mean time, the linkage disequilibrium information is incorporated into the mean coefficients via indicator variables of marker genotypes, whose validity can be justified intuitively (Fan and Xiong 2002, pp. 608–609).
Using the models developed in this article, test statistics can be developed for high-resolution association mapping of QTL. The procedure is to perform appropriate linkage analysis on the basis of a sparse genetic map for prior linkage evidence. Then association study can be carried out on the basis of a dense genetic map for high-resolution mapping of QTL in the presence of prior linkage information. Likelihood-ratio tests (LRT) can be carried out in high-resolution association studies. For large-sample data, likelihood-ratio criteria are accurate. On the basis of general theory of linear models, F-test statistics can be built to test the association between trait locus and markers in the presence of prior linkage evidence (Graybill 1976). The analytical formulas for the noncentrality parameter approximations are derived for the F-test statistics. The merits of the proposed method are investigated by power and sample size comparison. Using the simulation program LDSIMUL kindly provided by G. R. Abecasis, simulation study is performed to explore the power and type I error rates of the proposed test statistics. The proposed methods are compared with the AbAw approach (Abecasis et al. 2000a). Moreover, the method is applied to analyze the Genetic Analysis Workshop (GAW) 12 German asthma data (Wjst et al. 1999; Meyers et al. 2001).
MODEL
Assume that k diallelic markers Mj, j = 1, · · · , k, are typed in a region of one chromosome. Suppose a quantitative trait locus Q is located in the region, which has two alleles Q1 and Q2 with frequencies q1 and q2, respectively. For marker Mj, there are two alleles Mj with frequency PMj and mj with frequency Pmj, respectively. For a nuclear family of l children and two parents, let y = (yf, ym, y1, · · · , yl)τ be their quantitative trait column vector and Gj = (Gfj, Gmj, G1j, · · · , Glj)τ be their genotype column vector at the jth marker locus Mj. Here yf is the trait value of the father, and Gfj is the genotype of the father at the jth marker. Likewise, the other notations of the mother and the ith child are defined accordingly with subscripts m and i, respectively. The superscript τ denotes the transpose of a vector or a matrix. Under the assumption of multivariate normality, we consider the mixed-effect model
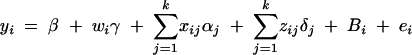 |
1 |
(Searle et al. 1992; Pinheiro and Bates 2000), where β is the overall mean of fixed effect, wi is a row vector of covariates such as sex and age, γ is a column vector of fixed-effect regression coefficients of wi, Bi is the familial effect of random effects, and ei is the error term. Assume that ei is normal N(0, σ2e), and Bi is normal N0,σ2s + σ2Ga, where σ2e is error variance, σ2s is the variance of shared environment effect, and σ2Ga is the variance of additive polygenic effect. Moreover, Bi and ei are independent. For j = 1, · · · , k, αj and δj are fixed-effect regression coefficients of the dummy variables xij and zij, respectively. Here xij and zij are indicator variables and are defined as follows:
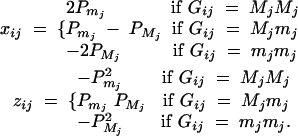 |
2 |
Following the traditional quantitative genetics, the variance-covariance matrix of model (1) is a (l + 2) × (l + 2) square matrix and is given by
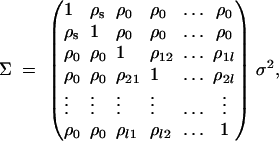 |
where 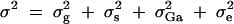 . Here σ2g is variance explained by the putative QTL Q. The genetic variance
. Here σ2g is variance explained by the putative QTL Q. The genetic variance 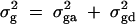 is decomposed into additive and dominance components.
is decomposed into additive and dominance components. 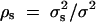 is the correlation between the parents. Let
is the correlation between the parents. Let 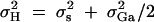 be the variance of familial effects that include shared environment variance σ2s and half of the additive polygenic variance.
be the variance of familial effects that include shared environment variance σ2s and half of the additive polygenic variance. 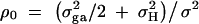 is correlation between parents and children;
is correlation between parents and children; 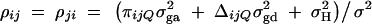 is the correlation between the ith child and the jth child, where πijQ is the proportion of alleles shared identical by descent (IBD) at putative QTL Q by the ith child and the jth child, and ΔijQ is the probability that both alleles at the putative QTL Q shared by the ith child and the jth child are IBD (Cotterman 1940; Pratt et al. 2000; Zhu and Elston 2000; Lange 2002). On the basis of the above discussion, the log-likelihood function of the mixed-effect model (1) is given by
is the correlation between the ith child and the jth child, where πijQ is the proportion of alleles shared identical by descent (IBD) at putative QTL Q by the ith child and the jth child, and ΔijQ is the probability that both alleles at the putative QTL Q shared by the ith child and the jth child are IBD (Cotterman 1940; Pratt et al. 2000; Zhu and Elston 2000; Lange 2002). On the basis of the above discussion, the log-likelihood function of the mixed-effect model (1) is given by
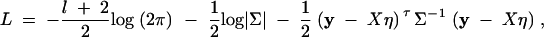 |
3 |
where η = (β, γτ, α1, · · · , αk, δ1, · · · , δk)τ is a vector of regression coefficients, and X is the model matrix, accordingly.
One may wonder why we use model (1) to describe the phenotypes. Here we provide an intuitive rationale. Suppose that QTL Q coincides with one marker, e.g., marker M1, and trait allele Q1 coincides with marker allele M1 and allele Q2 coincides with allele m1. Let μij be the effect of genotype QiQj, i, j = 1, 2. Denote genotypic value a = μ11 − (μ11 + μ22)/2 and d = μ12 − (μ11 + μ22)/2. The average effect of gene substitution is αQ = a + (q2 − q1)d, i.e., the difference between the average effects of the trait locus alleles, and dominance deviation is δQ = 2d in view of traditional quantitative genetics (Falconer and Mackay 1996). Fan and Xiong (2002) show that yi can be expressed as yi = μ0 + xi1αQ + zi1δQ + Bi + ei, where μ0 is overall population mean of the quantitative trait. Hence, marker M1 may fully describe the trait values if it coincides with the QTL Q. In practice, the information of QTL Q is unknown. Instead, model (1) is proposed to describe trait value yi using marker information. Two marker models were used in previous work (Fan and Xiong 2002, 2003; Fan and Jung 2003; Fan et al. 2005). Model (1) uses multiple markers and is a natural generalization of model of our previous work. The objective is to use marker information fully for fine high-resolution mapping of QTL. In the following, we show that model (1) and log-likelihood (3) can be used in joint linkage and association mapping of QTL.
PROPERTY OF REGRESSION COEFFICIENTS AND ASSOCIATION TESTS
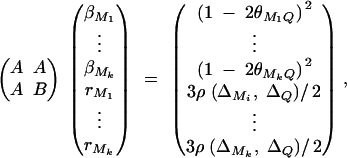
Denote the measure of LD between trait locus Q and marker Mi by 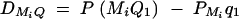 , i = 1, · · · , k and the measure of LD between marker Mi and marker Mj by
, i = 1, · · · , k and the measure of LD between marker Mi and marker Mj by 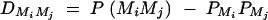 , i < j, i, j = 1, · · · , k. Let the additive and dominance variance-covariance matrices of the indicator variables defined in (2) be (appendix A)
, i < j, i, j = 1, · · · , k. Let the additive and dominance variance-covariance matrices of the indicator variables defined in (2) be (appendix A)
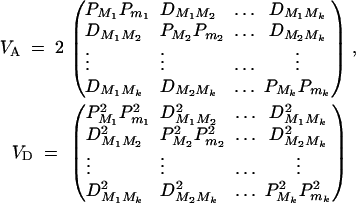 |
4 |
In appendix A, the coefficients of model (1) are derived as
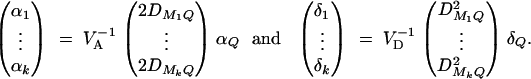 |
5 |
Equations (5) show that the parameters of LD (i.e., DMiQ and DMiMj) and gene effect (i.e., αQ and δQ) are contained in the mean coefficients. Model (1) simultaneously takes care of the LD and the effects of the putative trait locus Q. The gene substitution effect αQ is contained only in αi; and the dominance effect δQ is contained only in δi, i = 1, · · · , k. Therefore, model (1) orthogonally decomposes genetic effect into summation of additive and dominance effects.
Assume that all markers Mi and Mj are in linkage equilibrium (i.e., 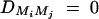 , i, j = 1, · · · , k, i ≠ j). The coefficients of additive and dominance effects are given by
, i, j = 1, · · · , k, i ≠ j). The coefficients of additive and dominance effects are given by 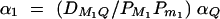 , · · ·,
, · · ·, 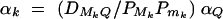 , and
, and 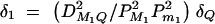 , · · · ,
, · · · , 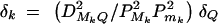 . That means markers M1, · · · , Mk independently contribute to the analysis of the trait values. Usually, the markers Mi can be in LD, especially when they are located in a narrow chromosome region. Equations (5) correctly use the LD information of markers Mi in the analysis.
. That means markers M1, · · · , Mk independently contribute to the analysis of the trait values. Usually, the markers Mi can be in LD, especially when they are located in a narrow chromosome region. Equations (5) correctly use the LD information of markers Mi in the analysis.
Linkage analysis can be performed by considering a reduced variance component model,
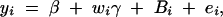 |
6 |
by using the traditional method of variance component models (Amos et al. 1989; Amos 1994; Almasy and Blangero 1998). This initial study can identify prior linkage evidence of the trait values to a specific chromosome region on the basis of a sparse genetic map. Suppose that prior linkage evidence is provided by an initial linkage study. On the basis of a dense genetic map, high-resolution association mapping of the QTL can be carried out by fitting the full model (1). First, assume that linkage is confirmed in a chromosome region by the significant presence of both the gene substitution and dominance effects, i.e., αQ ≠ 0 and δQ ≠ 0. On the basis of Equations 5, the existence of LD between markers Mi (i = 1, · · · , k) and trait locus Q can be tested by Had: α1 = · · · = αk = δ1 = · · · = δk = 0. Second, assume that linkage is supported by the significant presence of the gene substitution effect, but not the dominance effect, i.e., αQ ≠ 0 and δQ = 0. The existence of LD can be tested by Ha: α1 = · · · = αk = 0. Third, assume that linkage is supported by the significant presence of the dominance effect, but not the gene substitution effect, i.e., αQ = 0 and δQ ≠ 0. The existence of LD can be tested by Hd: δ1 = · · · = δk = 0.
Evidence of association can be evaluated by the LRT procedure. For instance, let Lad be the log-likelihood under the alternative hypothesis of Had and L0 be the log-likelihood under the null hypothesis Had. Then, the likelihood-ratio test statistic 2[Lad − L0] is asymptotically distributed as χ2. The degrees of freedom for this test are determined as follows. Under the null hypothesis Had, there are only k measures of LD, DM1Q, · · · , DMkQ, of which only k − 1 are independent since 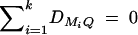 . Thus, the number of coefficients αi, δi, i = 1, · · · , k, which is significantly different from 0, should be ≤k − 1 in a data analysis. This number is the degrees of freedom of the likelihood-ratio test statistic 2[Lad − L0]. The likelihood-ratio test is accurate and robust for large sample data based on the statistical theory.
. Thus, the number of coefficients αi, δi, i = 1, · · · , k, which is significantly different from 0, should be ≤k − 1 in a data analysis. This number is the degrees of freedom of the likelihood-ratio test statistic 2[Lad − L0]. The likelihood-ratio test is accurate and robust for large sample data based on the statistical theory.
Theoretically, it is not easy to evaluate the power of the likelihood-ratio test statistics. The reason is that it is very hard to calculate the approximations of noncentrality parameters of the likelihood-ratio test statistics. Sham et al. (2000) performed power analysis of the AbAw approach by deriving the approximations of the noncentrality parameters of the likelihood-ratio test statistics, which is rather complicated in our opinion. In addition to the likelihood-ratio test statistics, we develop an F-test procedure based on linear model theory in this article (Graybill 1976). Utilizing the formulas of noncentrality parameters in chapter 6 of Graybill (1976), the approximations of the noncentrality parameters of the F-tests are calculated readily. Moreover, we show that the type I error rates and power of the F-test are very close to those of the likelihood-ratio test statistics (Tables 2 and 3), which are actually guaranteed by the construction of the F-test for large samples (Graybill 1976, pp. 187–188). Therefore, both the likelihood-ratio test procedure and the F-test procedure are useful. Before introducing the F-test procedure, we discuss the parameter estimations first.
TABLE 2.
Type I error rates (%) of test cases of Table 1 at a 0.05 significance level
| Error rates when total no. of offspring is
|
|||||||
|---|---|---|---|---|---|---|---|
| 120
|
240
|
480
|
|||||
| No. of offspring in each family | Test case | LRT | F̂1,a | LRT | F̂1,a | LRT | F̂1,a |
| 1 | Null | 5.0 | 4.9 | 5.1 | 5.1 | 5.8 | 5.8 |
| Familiality | 5.4 | 5.3 | 5.2 | 5.2 | 5.3 | 5.3 | |
| Admixture | 3.9 | 3.8 | 5.2 | 5.2 | 5.3 | 5.3 | |
| 2 | Null | 4.6 | 4.5 | 4.8 | 4.7 | 4.5 | 4.5 |
| Familiality | 4.2 | 4.1 | 3.6 | 3.6 | 4.7 | 4.8 | |
| Admixture | 5.0 | 4.8 | 5.5 | 5.5 | 4.9 | 5.1 | |
| Linkage | 5.5 | 5.4 | 5.0 | 4.3 | 5.0 | 5.1 | |
| Composite | 5.6 | 5.8 | 5.8 | 5.9 | 5.6 | 5.7 | |
| 4 | Null | 4.9 | 5.0 | 4.3 | 4.3 | 3.6 | 3.6 |
| Familiality | 5.2 | 5.3 | 4.2 | 4.3 | 4.8 | 4.8 | |
| Admixture | 5.5 | 5.6 | 5.4 | 5.8 | 4.2 | 4.2 | |
| Linkage | 5.3 | 5.5 | 5.4 | 5.4 | 4.9 | 5.0 | |
| Composite | 5.3 | 5.5 | 5.3 | 5.3 | 4.1 | 4.2 | |
| 8 | Null | 4.2 | 4.4 | 5.0 | 5.1 | 4.7 | 4.7 |
| Familiality | 4.7 | 5.3 | 5.1 | 5.5 | 4.4 | 4.4 | |
| Admixture | 3.5 | 4.4 | 5.5 | 6.0 | 4.4 | 4.6 | |
| Linkage | 6.1 | 6.8 | 4.3 | 4.6 | 4.6 | 4.8 | |
| Composite | 5.8 | 6.7 | 5.5 | 5.9 | 3.7 | 3.9 | |
The parameters are the same as those of Abecasis et al. (2000a)(Table 2).
TABLE 3.
Power comparison with results of Abecasiset al. (2000a, Table 4)
| No. of families/sample size N
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| One sib per family: 480/1440 |
Two sibs per family: 240/960 |
Three sibs per family: 160/800 |
Four sibs per family: 120/720 |
Five sibs per family: 96/672 |
Six sibs per family: 80/640 |
Eight sibs per family: 60/600 |
|||||||||
| D′ % | No. of simulated data sets |
AbAw |
F1,a, F̂1,a, LRT |
AbAw |
F1,a, F̂1,a, LRT |
AbAw |
F1,a, F̂1,a, LRT |
AbAw |
F1,a, F̂1,a, LRT |
AbAW |
F1,a, F̂1,a, LRT |
AbAw |
F1,a, F̂1,a, LRT |
AbAw |
F1,a, F̂1,a, LRT |
| 0 | 0.2 | 0.1 | 0.0 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.0 | 0.1 | |
| 1,000 | 0.1 | 0.1 | 0.1 | 0.0 | 0.1 | 0.1 | 0.0 | ||||||||
| 1,000 | 0.1 | 0.1 | 0.1 | 0.0 | 0.1 | 0.1 | 0.0 | ||||||||
| 20,000a | 0.105 | 0.10 | 0.105 | 0.09 | 0.105 | 0.095 | 0.09 | ||||||||
| 20,000b | 0.105 | 0.10 | 0.105 | 0.09 | 0.085 | 0.085 | 0.09 | ||||||||
| 25 | 2.1 | 33.1 | 1.8 | 15.4 | 2.0 | 10.6 | 2.6 | 8.5 | 3.0 | 7.4 | 2.1 | 6.7 | 2.1 | 5.8 | |
| 1,000 | 33.0 | 14.8 | 11.2 | 7.3 | 8.2 | 5.3 | 4.3 | ||||||||
| 1,000 | 32.9 | 14.7 | 10.9 | 7.2 | 7.4 | 4.9 | 3.8 | ||||||||
| 50 | 19.5 | 99.2 | 22.9 | 89.4 | 24.8 | 78.6 | 26.7 | 70.7 | 26.7 | 65.2 | 27.2 | 61.2 | 23.9 | 56.0 | |
| 1,000 | 99.4 | 90.5 | 76.7 | 69.9 | 63.7 | 55.5 | 47.5 | ||||||||
| 1,000 | 99.4 | 90.4 | 76.4 | 69.0 | 62.8 | 54.1 | 45.0 | ||||||||
| 75 | 69.3 | 100 | 72.6 | 100 | 74.2 | 99.8 | 76.9 | 99.3 | 76.0 | 98.7 | 76.5 | 98.1 | 75.4 | 96.9 | |
| 1,000 | 100 | 100 | 99.9 | 99.2 | 98.9 | 97.3 | 94.6 | ||||||||
| 1,000 | 100 | 100 | 99.9 | 99.2 | 98.8 | 97.2 | 93.8 | ||||||||
| 100 | 97.4 | 100 | 97.7 | 100 | 98.3 | 100 | 98.4 | 100 | 98.2 | 100 | 98.4 | 100 | 98.5 | 100 | |
| 1,000 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||||||||
| 1,000 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | ||||||||
In the AbAw columns, the power (%) is taken from Abecasis et al. (2000a)(Table 4). In columns 4, 6, 8, 10, 12, 14, and 16 the power (%) of F1,a is calculated on the basis of the theoretical approximation of noncentrality parameter λ1,a of test statistic F1,a at a 0.001 significance level; the empirical power (%) of F̂1,a and LRT are calculated as the proportions of 1000 or 20,000 simulated data sets that give significant results at the 0.001 significance level on the basis of F1,a and the likelihood-ratio test statistic, respectively. The parameters are the same as those of Abecasis et al. (2000a)(Table 4): 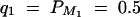 , h2 = 0.1, σ2 = 100,
, h2 = 0.1, σ2 = 100, 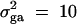 ,
, 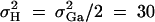 ,
, 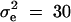 . In addition,
. In addition, 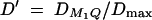 and
and 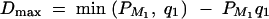 .
.
Results of the row are calculated on the basis of F̂1,a.
Results of the row are calculated on the basis of LRT.
PARAMETER ESTIMATIONS
IBD estimations:
Denote the recombination fraction between the trait locus Q and marker Mi by θMiQ, i = 1, · · · , k. Likewise, the recombination fraction between markers Mi and Mj is defined by θMiMj. Following Fulker et al. (1995) and Almasy and Blangero (1998), we propose a multipoint interval mapping method to estimate the proportion πijQ of allele sharing IBD at a putative QTL Q for a sib-pair i and j by
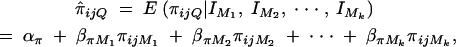 |
7 |
where πijMl is the proportion of alleles shared IBD at the marker Ml for l = 1, · · · , k. The coefficients απ, βπM1, · · · , βπMk are derived in appendix B as follows:
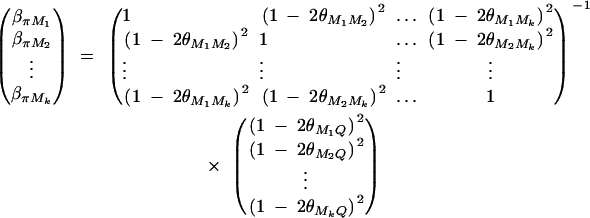 |
And απ is estimated as 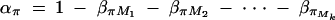 . If marker Ml coincides with QTL Q, it can be shown that
. If marker Ml coincides with QTL Q, it can be shown that 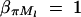 and απ = 0,
and απ = 0, 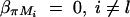 . Hence
. Hence 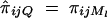 . To estimate ΔijQ of the probability of sharing two alleles IBD for a sib-pair, consider
. To estimate ΔijQ of the probability of sharing two alleles IBD for a sib-pair, consider
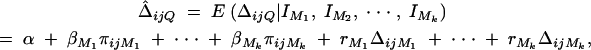 |
8 |
where ΔijMl is the probability of sharing two alleles IBD at marker Ml for l = 1, · · · , k. The coefficients rM1, · · · , rMkτ are derived in appendix C as follows:
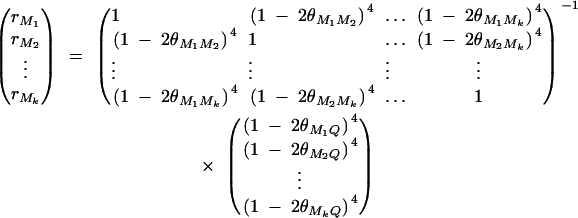 |
The remaining coefficients are given in appendix C by
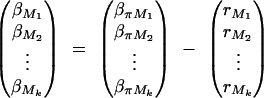 |
The α in Equation 8 is 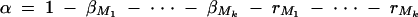 . Again, if marker Ml coincides with QTL Q, it can be shown that
. Again, if marker Ml coincides with QTL Q, it can be shown that  .
.
Estimations of model coefficients and variance-covariance matrix:
As an example, assume that the data are composed of three subsamples: n individuals of a population; m trio families, each having both parents and a single child; and s nuclear families, each having both parents and two offspring. Furthermore, we assume that n, m, and s are sufficiently large, so that large sample theory applies. We may include data of nuclear families with both parents and more than two offspring. The principle of the following paragraphs can be extended to such families if the number of families is large enough to apply the large sample theory. To estimate the parameters, one may take the method of interval mapping proposed by Fulker et al. (1995) and Almasy and Blangero (1998). That is to say, for each location of the QTL on the chromosome with fixed recombination fractions, the IBD estimations are performed first. Then one may estimate parameters of Σ and η as follows.
Consider the overall log-likelihood 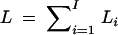 , I = n + m + s, where Li is the log-likelihood of trait vector or value yi of the ith family or individual. Let Σi be the variance-covariance matrix of trait vector or value yi and Xi be its model matrix. Denote the total trait values by y = (yτ1, · · · , yτI)τ, the total variance-covariance matrix by Σ = diag(Σ1, · · · , ΣI), and the model matrix by X = (Xτ1, · · · , XτI)τ. Let N = n + 3m + 4s be the total number of individuals. On the basis of the log-likelihood
, I = n + m + s, where Li is the log-likelihood of trait vector or value yi of the ith family or individual. Let Σi be the variance-covariance matrix of trait vector or value yi and Xi be its model matrix. Denote the total trait values by y = (yτ1, · · · , yτI)τ, the total variance-covariance matrix by Σ = diag(Σ1, · · · , ΣI), and the model matrix by X = (Xτ1, · · · , XτI)τ. Let N = n + 3m + 4s be the total number of individuals. On the basis of the log-likelihood 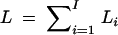 , parameters of Σ and η can be estimated by Newton-Raphson or Fisher scoring algorithms (Jennrich and Schluchter 1986). Let Σ̂ = diag(Σ̂1, · · · , Σ̂I) be the maximum-likelihood estimates of Σ. Then the estimate of η is
, parameters of Σ and η can be estimated by Newton-Raphson or Fisher scoring algorithms (Jennrich and Schluchter 1986). Let Σ̂ = diag(Σ̂1, · · · , Σ̂I) be the maximum-likelihood estimates of Σ. Then the estimate of η is
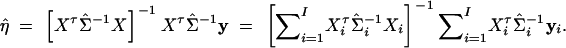 |
For each location of the QTL on the chromosome, the likelihood-ratio test or F-test statistics can then be calculated using the estimates Σ̂ and η̂. The location that gives the best result can be treated as the location of the QTL. In practice, some of the parameters (e.g., the variance parameter σ2gd) may not be estimable and identifiable due to the redundancy. For specific types of data, one needs to specify the model carefully.
F-TESTS AND NONCENTRALITY PARAMETER APPROXIMATIONS
On the basis of linear regression model theory, one may construct F-test statistics of genetic effects and LD coefficients (Graybill 1976). Moreover, the noncentrality parameters of the F-test statistics can be calculated readily. To evaluate the power of the F-test statistics, it is necessary to calculate the approximations of the noncentrality parameters. The procedure is as follows. First, one may construct an F-test statistic for each of three hypotheses:
Had: α1 = · · · = αk = δ1 = · · · = δk = 0;
Ha: α1 = · · · = αk = 0;
Hd: δ1 = · · · = δk = 0.
The noncentrality parameter of each F-test statistic can be calculated using the theory in Graybill (1976)(Chap. 6). Assume that there are no covariates. Then the coefficients of model (1) can be written as η = (β, α1, · · · , αk, δ1, · · · , δk)τ. For each hypothesis, there is a q × (2k + 1) matrix H, such that the hypothesis can be written as Hη = 0, where q is the rank of H. On the basis of Graybill (1976), the F-test statistic for hypothesis Hη = 0 is
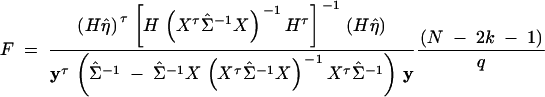 |
with a noncentral F(q, N − (2k + 1), λ) distribution under the alternative hypothesis, where λ is the noncentrality parameter given by λ = (Hη)τ[H(XτΣ−1X)−1 Hτ]−1(Hη).
Combined analysis of population and family data:
Again, assume that the data are composed of three subsamples: n individuals of a population; m trio families, each having both parents and a single child; and s nuclear families, each having both parents and two offspring. To calculate the approximations of the noncentrality parameters, assume that the sample sizes n, m, and s are large enough that the large-sample theory applies. We show in appendix d the approximation
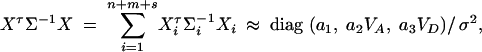 |
9 |
where a1, a2, and a3 are constants given by Equations (D7) in appendix D.
The additive variance 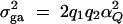 and the dominance variance
and the dominance variance 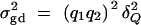 are expressed in terms of the average effect of gene substitution αQ and the dominance deviation δQ. Let Ik and I2k be k and 2k dimension identity matrices. Moreover, let Ok×l be a k × l zero matrix. To test hypothesis Ha: α1 = · · · = αk = 0, the test matrix H = (Ok×1, Ik, Ok×k). Let us denote the test statistic as Fk,a. The noncentrality parameter is approximated by
are expressed in terms of the average effect of gene substitution αQ and the dominance deviation δQ. Let Ik and I2k be k and 2k dimension identity matrices. Moreover, let Ok×l be a k × l zero matrix. To test hypothesis Ha: α1 = · · · = αk = 0, the test matrix H = (Ok×1, Ik, Ok×k). Let us denote the test statistic as Fk,a. The noncentrality parameter is approximated by
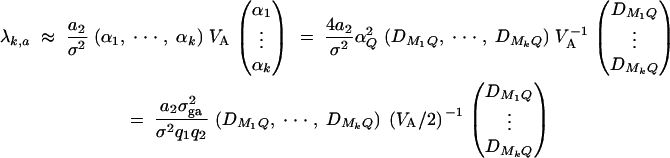 |
To test hypothesis Hd: δ1 = · · · = δk = 0, the test matrix H = (Ok×1, Ok×k, Ik). Let us denote the test statistic as Fk,d. The noncentrality parameter is approximated by
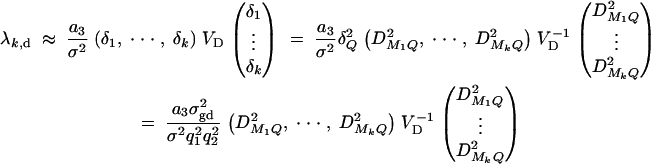 |
To test hypothesis Had: α1 = · · · = αk = δ1 = · · · = δk = 0, the test matrix H = (O2k×1, I2k). Let us denote the test statistic as Fk,ad. The noncentrality parameter is λk,ad ≈ λa + λd; i.e., λk,ad is decomposed into the summation of additive and dominant noncentrality parameters.
Nuclear family data:
To make a comparison with the results of Abecasis et al. (2000a)(Table 4), we consider I families, each having both parents and l offspring. Let N = I(l + 2) be the total number of individuals. The other notations are defined in a similar way as above. Suppose that variance-covariance matrices of the I families are the same, i.e., Σ1 = · · · = ΣI. Denote 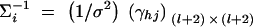 . If the sample size N is large enough, we show in appendix E that
. If the sample size N is large enough, we show in appendix E that
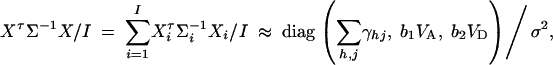 |
10 |
where b1 and b2 are constants given by Equations (E1) in appendix E. The approximation of the noncentrality parameter of statistic Fk,a is
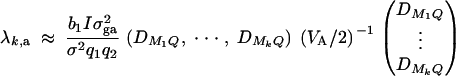 |
TYPE I ERROR RATES
To evaluate the type I error rates of the proposed method, simulation program LDSIMUL kindly provided by G. R. Abecasis is used to generate data sets. Nuclear families are generated in simulation. Five test cases are considered in type I error rate calculation, which are taken from Abecasis et al. (2000a)(Table 2). Table 1 presents parameters of four test cases. Trait values are constructed by a normal distribution with mean 0 and total variance σ2 = 100 except for test case of Admixture. Here 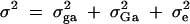 is the summation of the additive major gene effect σ2ga, the variance of polygenic effect σ2Ga, and the error variance σ2e. In each model except the Admixture, a diallelic marker M1 is simulated with allele frequency
is the summation of the additive major gene effect σ2ga, the variance of polygenic effect σ2Ga, and the error variance σ2e. In each model except the Admixture, a diallelic marker M1 is simulated with allele frequency 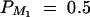 . In the test cases of Null, Familiality, and Admixture, no major gene effect is assumed, i.e.,
. In the test cases of Null, Familiality, and Admixture, no major gene effect is assumed, i.e., 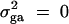 . In the test cases of Linkage and Composite, major gene effect is assumed, and marker M1 coincides with the QTL Q, i.e., recombination fraction
. In the test cases of Linkage and Composite, major gene effect is assumed, and marker M1 coincides with the QTL Q, i.e., recombination fraction 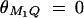 ; in the meantime, linkage equilibrium is assumed between QTL Q and the marker M1, i.e.,
; in the meantime, linkage equilibrium is assumed between QTL Q and the marker M1, i.e., 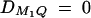 . In the test case of Admixture, population admixture is generated by mixing families equally drawn from one of two subpopulations A and B. In both subpopulations A and B, no major gene effect or familial effect is assumed, i.e.,
. In the test case of Admixture, population admixture is generated by mixing families equally drawn from one of two subpopulations A and B. In both subpopulations A and B, no major gene effect or familial effect is assumed, i.e., 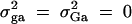 . However, the trait mean of subpopulation A is fixed at 10 and the variance is fixed at 100, and the marker allele frequency PM1 is taken as 0.7 in subpopulation A. The trait mean of subpopulation B is fixed at 0 and the variance is fixed at 100, and the marker allele frequency PM1 is taken as 0.3 in subpopulation B. Therefore, the total variance in the mixing population is σ2 = 125. The admixture contributed to (10 − 0)2/[4 × 125] = 0.20 of the total variance.
. However, the trait mean of subpopulation A is fixed at 10 and the variance is fixed at 100, and the marker allele frequency PM1 is taken as 0.7 in subpopulation A. The trait mean of subpopulation B is fixed at 0 and the variance is fixed at 100, and the marker allele frequency PM1 is taken as 0.3 in subpopulation B. Therefore, the total variance in the mixing population is σ2 = 125. The admixture contributed to (10 − 0)2/[4 × 125] = 0.20 of the total variance.
TABLE 1.
The parameters of the simulated genetic cases
| Test case | σ2ga | σ2Ga | σ2e | σ2 | θM1Q | β | PM1 | q1 | DM1Q |
|---|---|---|---|---|---|---|---|---|---|
| Null | 0 | 0 | 100 | 100 | Not applied | 0 | 0.5 | Not applied | Not applied |
| Familiality | 0 | 50 | 50 | 100 | Not applied | 0 | 0.5 | Not applied | Not applied |
| Linkage | 30 | 0 | 70 | 100 | 0 | 0 | 0.5 | 0.5 | 0 |
| Composite | 20 | 30 | 50 | 100 | 0 | 0 | 0.5 | 0.5 | 0 |
The total variance is fixed at 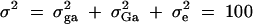 and
and 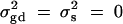 . Admixture: no major gene effect or familial effect
. Admixture: no major gene effect or familial effect 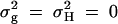 , but with population admixture (see text for explanation).
, but with population admixture (see text for explanation).
To calculate the type I error rates, 1000 data sets are simulated for each test case. Each data set contains a certain number of related pedigrees. For instance, 120 trio families are generated for test case Null if the total number of offspring is 120 and the number of offspring in each family is 1; but only 15 families are generated if the number of offspring in each family is 8 and the total number of offspring is 120. Using the data sets, we fit the model
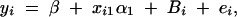 |
where Bi is normal N(0, σ2Ga), yi is normal N(β + xi1α1, σ2), and 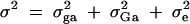 . The null hypothesis is H1,a: α1 = 0. Since the QTL Q is in linkage equilibrium with marker M1, an empirical test statistic that is larger than the cutting point at a 0.05 significance level is treated as a false positive. On the basis of either the likelihood-ratio test or the F-test, type I error rates are calculated as the proportions of the 1000 simulation data sets that give a significant result at the 0.05 significance level based on F1,a and the likelihood-ratio test statistic, respectively. Table 2 presents type I error rates of likelihood-ratio tests and F-test statistics. The results show that the type I error rates are around the 0.05 nominal significance level in almost all cases. Hence, the proposed model is robust. In addition, the type I error rates of F-tests are similar to those of the likelihood-ratio tests. In an association study, false positives due to population stratifications are usually a big issue. From the results of Table 2, the type I error rates in the Admixture case are reasonable.
. The null hypothesis is H1,a: α1 = 0. Since the QTL Q is in linkage equilibrium with marker M1, an empirical test statistic that is larger than the cutting point at a 0.05 significance level is treated as a false positive. On the basis of either the likelihood-ratio test or the F-test, type I error rates are calculated as the proportions of the 1000 simulation data sets that give a significant result at the 0.05 significance level based on F1,a and the likelihood-ratio test statistic, respectively. Table 2 presents type I error rates of likelihood-ratio tests and F-test statistics. The results show that the type I error rates are around the 0.05 nominal significance level in almost all cases. Hence, the proposed model is robust. In addition, the type I error rates of F-tests are similar to those of the likelihood-ratio tests. In an association study, false positives due to population stratifications are usually a big issue. From the results of Table 2, the type I error rates in the Admixture case are reasonable.
Table 2, bottom, shows a notable variability in the range of type I errors when the number of offspring is 8 and the sample sizes are small. For example, the type I error rates of the F-test F̂1,a are 6.7% for test case of Composite when the total number of offspring is 120. This is most likely due to the small sample size and multivariate normality. When the total number of offspring is 120, there are only 15 pedigrees, each consisting of two parents and 8 offspring; and the variance-covariance matrix Σ is a big 10 × 10 square matrix. Hence, the parameter estimations are hardly accurate, which makes the deviation from the nominal level greater. When the sample size increases (i.e., the total number of offspring is 240 or 480), the type I error rates are close to the nominal level of 0.05. The results of Table 2 are based on 1000 simulated data sets, which may not be always reliable. To further investigate the issue, we perform a calculation in the next section based on 20,000 simulated data sets for another Composite test case in Table 3. The results of Table 3 confirm that the type I error rates are close to the nominal level for large-sample data.
POWER CALCULATION AND COMPARISON
Comparison with the AbAw approach:
Denote the heritability by h2, which is defined as 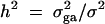 (Falconer and Mackay 1996). To compare the method proposed in this article with the AbAw approach of Abecasis et al. (2000a), we present a power comparison in Table 3. The parameters are the same as those of Abecasis et al. (2000a)(Table 4):
(Falconer and Mackay 1996). To compare the method proposed in this article with the AbAw approach of Abecasis et al. (2000a), we present a power comparison in Table 3. The parameters are the same as those of Abecasis et al. (2000a)(Table 4): 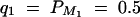 , h2 = 0.1, σ2 = 100,
, h2 = 0.1, σ2 = 100, 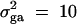 ,
, 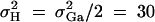 ,
, 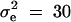 . In addition,
. In addition, 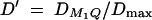 and
and 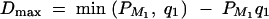 . In the AbAw columns in Table 3, the results are taken from Abecasis et al. (2000a)(Table 4). In the (F1,a, F̂1,a, LRT)τ columns, the power (%) of F1,a is calculated on the basis of approximation of noncentrality parameter λ1,a of test statistic F1,a at a 0.001 significance level; the power (%) of F̂1,a and the LRT are calculated as the proportions of 1000 or 20,000 simulation data sets that give a significant result at the 0.001 significance level based on F1,a and the likelihood-ratio test statistic, respectively. For each simulated data set, a certain number nuclear families are simulated via LDSIMUL. For instance, for one sib per family, 480 trio families are simulated in each simulated data set.
. In the AbAw columns in Table 3, the results are taken from Abecasis et al. (2000a)(Table 4). In the (F1,a, F̂1,a, LRT)τ columns, the power (%) of F1,a is calculated on the basis of approximation of noncentrality parameter λ1,a of test statistic F1,a at a 0.001 significance level; the power (%) of F̂1,a and the LRT are calculated as the proportions of 1000 or 20,000 simulation data sets that give a significant result at the 0.001 significance level based on F1,a and the likelihood-ratio test statistic, respectively. For each simulated data set, a certain number nuclear families are simulated via LDSIMUL. For instance, for one sib per family, 480 trio families are simulated in each simulated data set.
The results of Table 3 clearly show that the proposed F-tests F1,a and likelihood-ratio tests are much more powerful than the AbAw approach. When 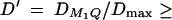 25%, it is possible to achieve considerable power. When
25%, it is possible to achieve considerable power. When 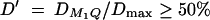 , the statistic F1,a is powerful for a sample with a total number of 480 sibs. In addition, the results of Table 3 show that the empirical power of F̂1,a is similar to that of the likelihood-ratio test. This implies that in a large sample the two tests provide similar power (Graybill 1976). The AbAw approach presented in Abecasis et al. (2000a) utilized only the trait values of sibships in the model and discarded the trait values of parents. This is, obviously, not an efficient way. The proposed methods, on the other hand, incorporate both parental and sibship phenotypes into the models. This considerably increases the power as shown in Table 3.
, the statistic F1,a is powerful for a sample with a total number of 480 sibs. In addition, the results of Table 3 show that the empirical power of F̂1,a is similar to that of the likelihood-ratio test. This implies that in a large sample the two tests provide similar power (Graybill 1976). The AbAw approach presented in Abecasis et al. (2000a) utilized only the trait values of sibships in the model and discarded the trait values of parents. This is, obviously, not an efficient way. The proposed methods, on the other hand, incorporate both parental and sibship phenotypes into the models. This considerably increases the power as shown in Table 3.
In Table 3, the first row of results corresponds to the case when D′ is zero, i.e., a situation when the null hypothesis of no association is true. Hence, the power results for all these tests are simply the type I error rates. It can be seen that the type I error rates are close to the nominal level 0.001 = 0.1% when the number of simulated data sets is 20,000. This is consistent with the conclusion of Table 2; i.e., the proposed model is robust. To make a comparison with the results of Abecasis et al. (2000a)(Table 4), the results of F̂1,a and the LRT of 1000 simulated data sets are also presented. In most cases, the entries are equal to the nominal level 0.001 = 0.1%; i.e., one of the 1000 data sets leads to a significant result, but some entries are 0 since none of the 1000 data sets leads to a significant result.
In Table 3, there is a trend that the power of (F1,a, F̂1,a, LRT)τ to detect association decreases with the increasing sibship sizes. This is partly because the sample size N decreases although the total number of offspring is the same, 480: For 480 trio families of one sib per family, the total number of individuals is N = 1440; for 60 families of eight sibs per family, the total number of individuals is N = 600. For the AbAw approach presented in Abecasis et al. (2000a), the total number of offspring that are used in the model is the same, 480. Since our models use phenotypes of both parents and offspring, the sample sizes N are different. On the other hand, for the same total number of typed individuals N, families of large sibship sizes contain less LD information than families of small sibship sizes. The readers may note that this result is consistent with findings in Fan and Xiong (2003). In Fan and Xiong (2003)(p. 131, Figure 3), the population-based method is shown to be more powerful than the family-based method for the same number of individuals.
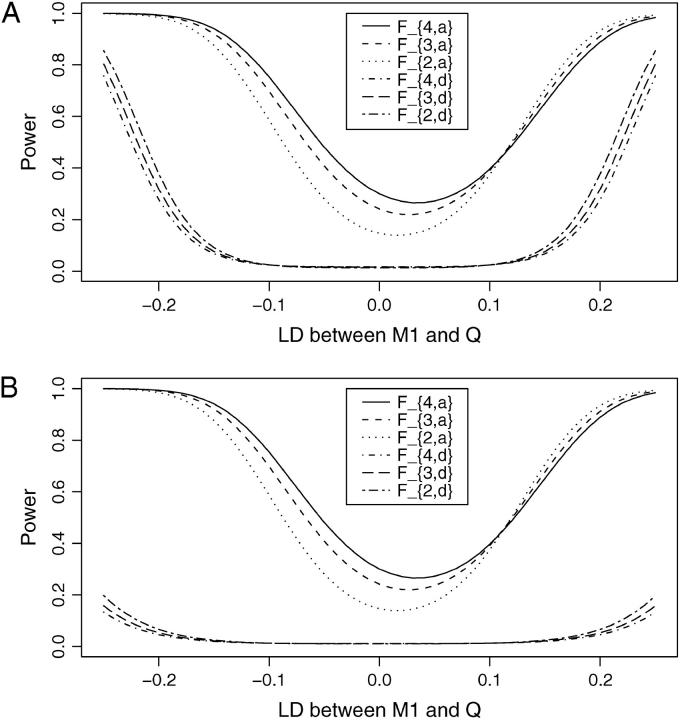
Comparisons of sample size and power of LD mapping:
Power and sample size calculations are performed to investigate the merits of the proposed method. Figure 1 shows the power curves of the test statistics F4,a, F3,a, F2,a, F4,d, F3,d, and F2,d against the linkage disequilibrium coefficient DM1Q at a 0.01 significance level for a dominant mode of inheritance (a = d = 1.0) and a recessive mode of inheritance (a = 1.0, d = −0.5). The related parameters are given in the Figure 1 legend. Generally, the power of F4,a using four markers in the model is higher than that of F3,a using three markers, which in turn is higher than that of F2,a using two markers. Hence, multiple-marker analysis is advantageous. The power of Fk,d is usually minimal unless the LD between locus Q and marker M1 is very strong for the dominant mode of inheritance. Note the power curves of Figure 1 are not symmetric with respect to DM1Q. This is due to 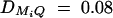 , i = 2, 3, 4,
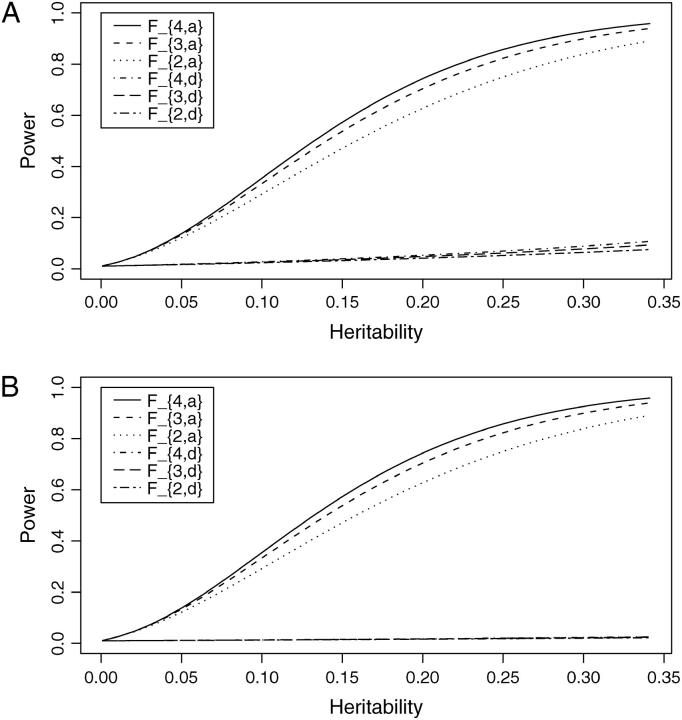
, i = 2, 3, 4, 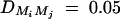 , i ≠ j, and so the power curves do not have to reach a minimum value when DM1Q is zero. Instead, they are shifted to the right, so that the minimum is at a point when DM1Q > 0. Figure 2 provides the power of the test statistics F4,a, F3,a, F2,a, F4,d, F3,d, and F2,d against heritability h2 at a 0.01 significance level for a dominant mode of inheritance (a = d = 1.0) and a recessive mode of inheritance (a = 1.0, d = −0.5), respectively. In addition to the merits shown in Figure 1, the power of the test statistics F4,a, F3,a, F2,a is high when heritability h2 is >0.10 for both modes of inheritance.
, i ≠ j, and so the power curves do not have to reach a minimum value when DM1Q is zero. Instead, they are shifted to the right, so that the minimum is at a point when DM1Q > 0. Figure 2 provides the power of the test statistics F4,a, F3,a, F2,a, F4,d, F3,d, and F2,d against heritability h2 at a 0.01 significance level for a dominant mode of inheritance (a = d = 1.0) and a recessive mode of inheritance (a = 1.0, d = −0.5), respectively. In addition to the merits shown in Figure 1, the power of the test statistics F4,a, F3,a, F2,a is high when heritability h2 is >0.10 for both modes of inheritance.
Figure 1.—
Power curves of test statistics F4,a, F3,a, F2,a, F4,d, F3,d, and F2,d against the measure of LD between M1 and Q at a 0.01 significance level, when q1 = 0.5, 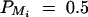 , i = 1, 2, 3, 4,
, i = 1, 2, 3, 4, 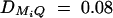 , i = 2, 3, 4,
, i = 2, 3, 4, 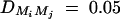 , i ≠ j, π12Q = 0.5, δ12Q = 0.25, heritability h2 = 0.15, polygenic effect variance
, i ≠ j, π12Q = 0.5, δ12Q = 0.25, heritability h2 = 0.15, polygenic effect variance 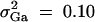 and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
Figure 2.—
Power of test statistics F4,a, F3,a, F2,a, F4,d, F3,d, and F2,d against the heritability h2 at a 0.01 significance level, when q1 = 0.5, 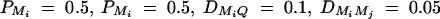 , i, j = 1, 2, 3, 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25,
, i, j = 1, 2, 3, 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25, 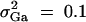 and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
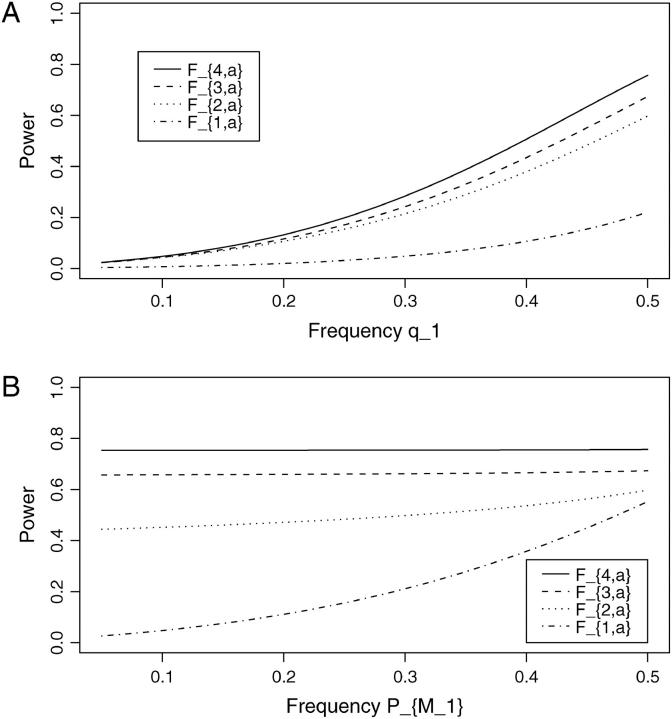
Figure 3 shows the power of test statistics F4,a, F3,a, F2,a, and F1,a against the trait allele frequency q1 (Figure 3A) or marker allele frequency PM1 (Figure 3B) at a 0.01 significance level for an additive mode of inheritance a = 1.0, d = 0.0, respectively. The other parameters are given in the Figure 3 legend. From Figure 3A, it can be seen that the power of Fk,a increases as the trait allele frequency q1 increases. Figure 3B shows that the power of F4,a and F3,a is almost constant; in addition, the power of F2,a increases slowly, and the power of F1,a increases as the marker allele frequency PM1 increases. In general, the power of F4,a and F3,a depends heavily on the trait allele frequency q1, but not on the marker allele frequency PM1. At first glance, it is strange that the power of F4,a and F3,a does not depend very much on the marker allele frequency PM1. The mystery is that the LD measures 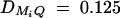 , i = 2, 3, 4 are already high. That is why the contribution of marker M1 matters not very much to the power of F2,a, F3,a, and F4,a. This adds one more piece of information to the advantage of multiple-marker analysis. That is, as long as some markers are in strong linkage disequilibrium with the trait locus, the power to detect the association is high.
, i = 2, 3, 4 are already high. That is why the contribution of marker M1 matters not very much to the power of F2,a, F3,a, and F4,a. This adds one more piece of information to the advantage of multiple-marker analysis. That is, as long as some markers are in strong linkage disequilibrium with the trait locus, the power to detect the association is high.
Figure 3.—
Power of test statistics F4,a, F3,a, F2,a, and F1,a against the trait allele frequency q1 (A) or marker allele frequency PM1 (B) at a 0.01 significance level for an additive mode of inheritance a = 1.0, d = 0.0, when 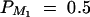 or q1 = 0.5, respectively. The other parameters are given by h2 = 0.15,
or q1 = 0.5, respectively. The other parameters are given by h2 = 0.15, 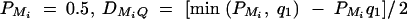 ,
, 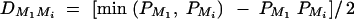 ,
, 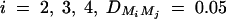 , i, j = 2, 3, 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25,
, i, j = 2, 3, 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25, 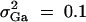 and sample size n = 40, m = 30, s = 20.
and sample size n = 40, m = 30, s = 20.
Assume that the LD is due to historical mutations T generations ago at QTL Q. At the initial generation when the mutation occurred, the LD coefficient is 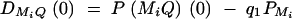 , where P(MiQ)(0) is the frequency of haplotype MiQ. The LD coefficient is reduced by a factor 1 − θMiQ in each subsequent generation. The LD between marker Mi and Q is
, where P(MiQ)(0) is the frequency of haplotype MiQ. The LD coefficient is reduced by a factor 1 − θMiQ in each subsequent generation. The LD between marker Mi and Q is 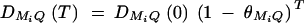 at the current generation. Assume that the marker M1 locates at position 0 cM, marker M2 locates at position 1 cM, marker M3 locates at position 2 cM, and marker M4 locates at position 3 cM. Under the assumption of no interference, we may calculate the recombination fraction
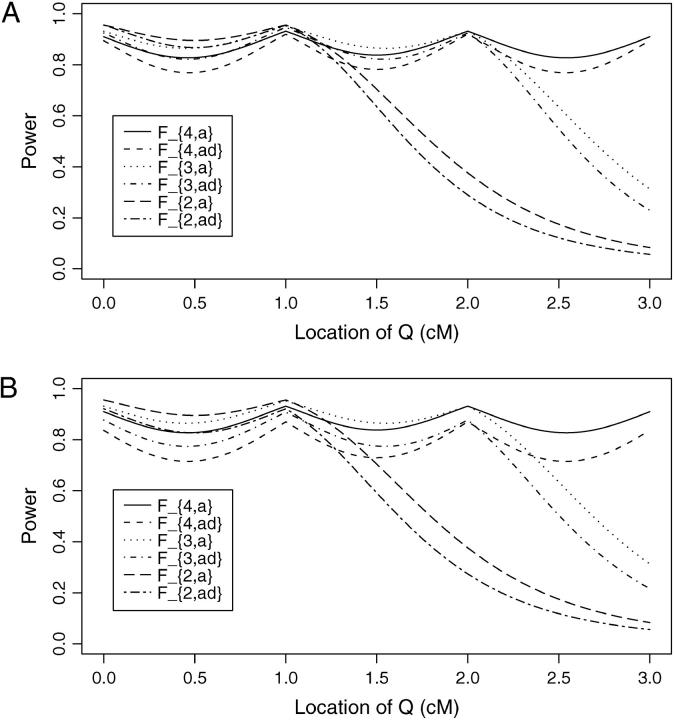
at the current generation. Assume that the marker M1 locates at position 0 cM, marker M2 locates at position 1 cM, marker M3 locates at position 2 cM, and marker M4 locates at position 3 cM. Under the assumption of no interference, we may calculate the recombination fraction 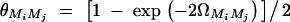 by Haldane's map function, where ΩMiMj is the map distance between marker Mi and marker Mj. Similarly, the recombination fraction θMiQ can be calculated by the distance ΩMiQ between QTL Q and marker Mi, i = 1, · · · , 4. Suppose that the QTL Q is located along the horizontal axis; i.e., it moves from 0 to 3 cM. Figure 4 shows the power curves of the test statistics F4,a, F4,ad, F3,a, F3,ad, F2,a, and F2,ad against the location of QTL Q for a dominant mode of inheritance (a = d = 1) and a recessive mode of inheritance (a = 1.0, d = −0.5), respectively. The powers of F4,a and F4,ad with four markers in the model are generally high across the location of QTL Q, since at least one marker is close to the QTL Q. The power of F3,a and F3,ad using three markers in the model is similar to that of four markers, except that QTL Q locates far above marker M3, i.e., λM1Q ≥ 2.3cM. The power of F2,a and F2,ad using two markers in the model is high when the QTL is close to markers M1 and M2. However, once the QTL is far above marker M2 (i.e., λM1Q ≥ 1.3cM ), the power of F2,a and F2,ad using two markers in the model decreases very quickly. Figure 4 implies that multiple-marker LD analysis has high power in fine mapping of QTL. Moreover, the power of test statistic Fk,a, which tests only the additive effect, is higher than that of Fk,ad, which tests both the additive and dominance effects through the proposed model. The reason is that the degrees of freedom of test statistics increases if the dominance effect is added to the test statistics. Figure 5 shows the power curves of test statistic F4,ad against the position of markers M1, · · · , M4 for different mutation age at a 0.01 significance level. The trait locus Q locates at position 10 cM. The four markers flank the trait locus Q; two markers are on each side of the QTL with equal distance to each other as follows: M2 = 5 + M1/2, M3 = 15 − M1/2, M4 = 20 − M1. Here Mi also denotes the location in centimorgans of marker Mi. As the mutation ages, the power decreases and the power can be high only when the markers are close to the trait locus.
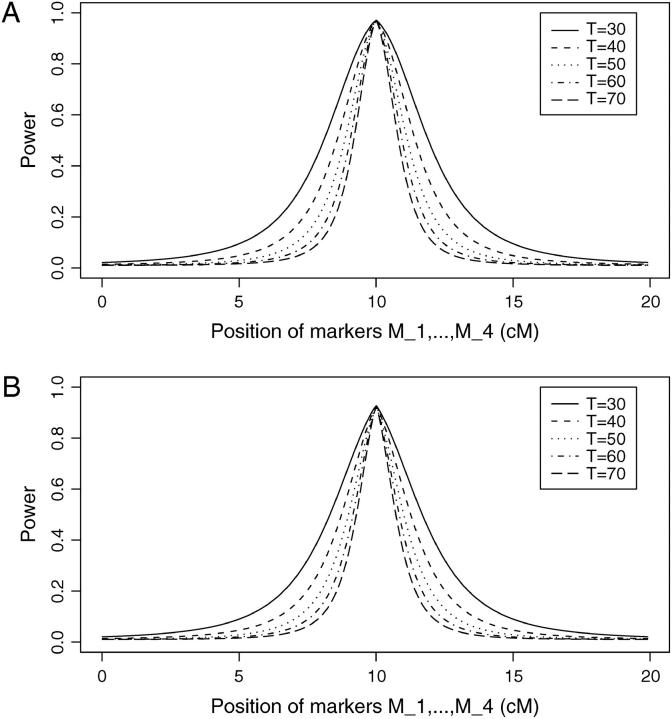
by Haldane's map function, where ΩMiMj is the map distance between marker Mi and marker Mj. Similarly, the recombination fraction θMiQ can be calculated by the distance ΩMiQ between QTL Q and marker Mi, i = 1, · · · , 4. Suppose that the QTL Q is located along the horizontal axis; i.e., it moves from 0 to 3 cM. Figure 4 shows the power curves of the test statistics F4,a, F4,ad, F3,a, F3,ad, F2,a, and F2,ad against the location of QTL Q for a dominant mode of inheritance (a = d = 1) and a recessive mode of inheritance (a = 1.0, d = −0.5), respectively. The powers of F4,a and F4,ad with four markers in the model are generally high across the location of QTL Q, since at least one marker is close to the QTL Q. The power of F3,a and F3,ad using three markers in the model is similar to that of four markers, except that QTL Q locates far above marker M3, i.e., λM1Q ≥ 2.3cM. The power of F2,a and F2,ad using two markers in the model is high when the QTL is close to markers M1 and M2. However, once the QTL is far above marker M2 (i.e., λM1Q ≥ 1.3cM ), the power of F2,a and F2,ad using two markers in the model decreases very quickly. Figure 4 implies that multiple-marker LD analysis has high power in fine mapping of QTL. Moreover, the power of test statistic Fk,a, which tests only the additive effect, is higher than that of Fk,ad, which tests both the additive and dominance effects through the proposed model. The reason is that the degrees of freedom of test statistics increases if the dominance effect is added to the test statistics. Figure 5 shows the power curves of test statistic F4,ad against the position of markers M1, · · · , M4 for different mutation age at a 0.01 significance level. The trait locus Q locates at position 10 cM. The four markers flank the trait locus Q; two markers are on each side of the QTL with equal distance to each other as follows: M2 = 5 + M1/2, M3 = 15 − M1/2, M4 = 20 − M1. Here Mi also denotes the location in centimorgans of marker Mi. As the mutation ages, the power decreases and the power can be high only when the markers are close to the trait locus.
Figure 4.—
Power of test statistics F4,a, F4,ad, F3,a, F3,ad, F2,a, and F2,ad against location of QTL Q at a 0.01 significance level. The parameters are given by, q1 = 0.5, 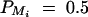 ,
, 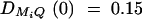 ,
, 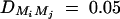 , i, j = 1, · · · , 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25, familial effect variance
, i, j = 1, · · · , 4, i ≠ j, π12Q = 0.5, δ12Q = 0.25, familial effect variance 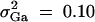 , heritability h2 = 0.15 and sample size n = 100, m = 50, s = 30, mutation age T = 60 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively. Marker M1 locates at position 0 cM, marker M2 locates at position 1 cM, marker M3 locates at position 2 cM, and marker M4 locates at position 3 cM. The location of QTL Q is along the horizontal axis; i.e., it moves from 0 to 3 cM.
, heritability h2 = 0.15 and sample size n = 100, m = 50, s = 30, mutation age T = 60 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively. Marker M1 locates at position 0 cM, marker M2 locates at position 1 cM, marker M3 locates at position 2 cM, and marker M4 locates at position 3 cM. The location of QTL Q is along the horizontal axis; i.e., it moves from 0 to 3 cM.
Figure 5.—
Power of test statistic F4,ad for mutation age T = 30, T = 40, T = 50, T = 60, T = 70 against position of markers Mi, i = 1, · · · , 4 at a 0.01 significance level. The QTL Q locates at position 10 cM. The four markers flank the trait locus Q; two markers are on each side of the QTL with equal distance to each other as follows: M2 = 5 + M1/2, M3 = 15 − M1/2, M4 = 20 − M1. q1 = 0.5, 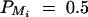 ,
, 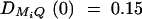 ,
, 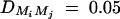 , i, j = 1, · · · , 4, i ≠ j, heritability h2 = 0.15, polygenic effect variance
, i, j = 1, · · · , 4, i ≠ j, heritability h2 = 0.15, polygenic effect variance 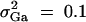 and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
and sample size n = 40, m = 30, s = 20 for (A) a dominant mode of inheritance a = d = 1.0 and (B) a recessive mode of inheritance a = 1.0, d = −0.5, respectively.
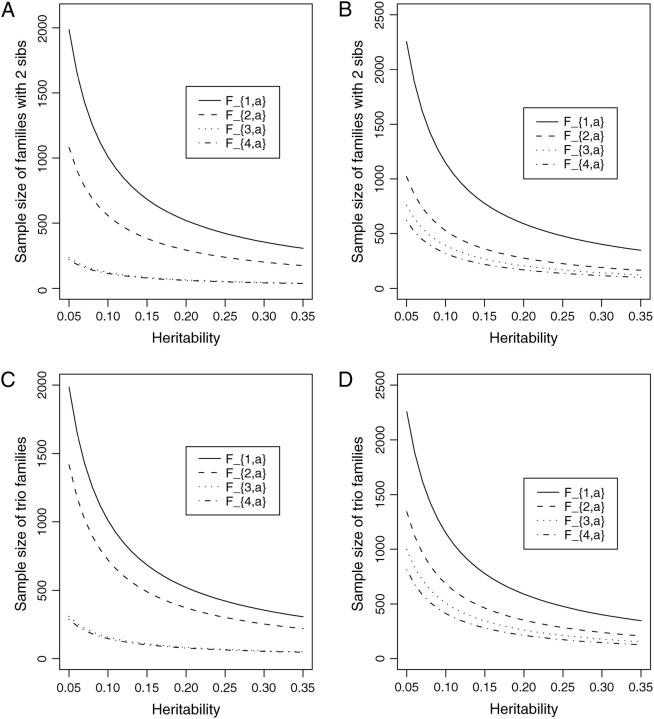
Figure 6 shows the required number of trio families or families with both parents and two offspring for the test statistics F4,a, F3,a, F2,a, and F1,a against heritability h2 at a significance level 0.01 and power 0.8. For a favorable case (Figure 6, A and C), the parameters are given by  , and
, and 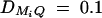 for i, j = 1, · · · , 4, i ≠ j. For a less favorable case (Figure 6, B and D), the parameters are given by q1 = 0.2,
for i, j = 1, · · · , 4, i ≠ j. For a less favorable case (Figure 6, B and D), the parameters are given by q1 = 0.2, 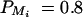 ,
, 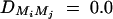 , and
, and 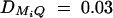 for i, j = 1, · · · , 4, i ≠ j. For the favorable case, the required number of families of test statistics F4,a and F3,a is <200 and that of F2,a is <600 if heritability h2 is >0.1. For the less favorable case, the required number of families of test statistics F4,a and F3,a is <500 and that of F2,a is <700 if heritability h2 is >0.1. The required number of families of test statistics F1,a is very large for both favorable and less favorable cases.
for i, j = 1, · · · , 4, i ≠ j. For the favorable case, the required number of families of test statistics F4,a and F3,a is <200 and that of F2,a is <600 if heritability h2 is >0.1. For the less favorable case, the required number of families of test statistics F4,a and F3,a is <500 and that of F2,a is <700 if heritability h2 is >0.1. The required number of families of test statistics F1,a is very large for both favorable and less favorable cases.
Figure 6.—
Sample size of test statistics F1,a, F2,a, F3,a, and F4,a against heritability h2 at a 0.01 significance level and 0.80 power for a dominant mode of inheritance a = d = 1.0. For a favorable case (A and C), q1 = 0.5, 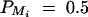 ,
, 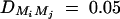 ,
, 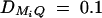 , i, j = 1, 2, 3, 4, i ≠ j; for a less favorable case (B and D), q1 = 0.2,
, i, j = 1, 2, 3, 4, i ≠ j; for a less favorable case (B and D), q1 = 0.2, 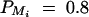 ,
, 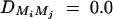 ,
, 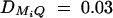 , i, j = 1, 2, 3, 4, i ≠ j. In addition, the polygenic effect variance
, i, j = 1, 2, 3, 4, i ≠ j. In addition, the polygenic effect variance 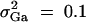 .
.
AN EXAMPLE
The proposed method is applied to the Genetic Analysis Workshop 12 German asthma data (Meyers et al. 2001). The data consist of 97 nuclear families, including 415 persons. Seventy-four families have two children, 19 have three children, and 4 have four children. Wjst et al. (1999) perform linkage analysis for total serum IgE by a nonparametric statistic of MAPMAKER/SIBS 2.1. Three markers on chromosome 1 are shown to be linked with immunoglobulin E (IGE) level, i.e., marker D1S207 at position 118.1 cM, marker D1S221 at position 146.7 cM, and marker D1S502 at position 151.2 cM. In Fan and Jung (2003), we analyze the data using sibships and confirm the result of Wjst et al. (1999). By the method proposed in this article, we analyze the data again. The dominance variance of log(IGE) is significantly >0 at position 149.85 cM (P-value, 0.00075; compared with the P-value of 0.01 in Fan and Jung 2003). On this basis, we collapse alleles 6, 8, and 10 as allele M1 at marker D1S207 and others as allele m1. At marker D1S221, alleles 5, 6, and 7 are collapsed as allele M2 and other alleles as allele m2. At marker D1S502, we collapse alleles 7, 8, and 12 as allele M3 and others as allele m3. Then, we find that coefficient δ2 is significantly different from 0 at position 149.85 cM, with a P-value of 0.034 by likelihood-ratio test (compared with the P-value of 0.0475 in Fan and Jung 2003) and a P-value 0.034 by F-test (compared with the P-value 0.0484 in Fan and Jung 2003). The estimation is δ̂2 = 0.76. Hence, we are able to confirm the result of Wjst et al. (1999) and find that marker D1S221 is associated with log(IGE).
Compared with the results of Fan and Jung (2003), the evidence in the above paragraph is stronger since the P-values are smaller. There are two reasons for this. In this article, all family members are used in the analysis (compared with only sibships used in Fan and Jung 2003). This article used three markers in the analysis (compared with only two markers used in Fan and Jung 2003). Hence, the proposed model improves the performance of the previous method.
DISCUSSION
On the basis of multiple diallelic markers, this article proposes variance component models for high-resolution joint linkage and association mapping of QTL. The models extend our previous work using two diallelic markers in analysis and incorporate genetic-marker information into the models (Fan and Xiong 2002, 2003; Fan and Jung 2003; Fan et al. 2005). By analytical analysis, it is shown that linkage disequilibrium measures and genetic effects are incorporated in the mean coefficients. On the basis of marker information, a multipoint interval mapping method is provided to estimate the proportion of allele-sharing IBD and probability of sharing two alleles IBD at a putative QTL for a sib-pair. It is shown that recombination fractions, i.e., linkage information, are contained in variance-covariance matrices. Therefore, the proposed methods model both association and linkage in a unified model.
In the literature, there is plenty of research for linkage mapping of QTL (Amos 1994; Fulker et al. 1995; Almasy and Blangero 1998). The linkage evidence can be detected by fitting model (6) as the first step on the basis of a sparse genetic map. In this article, we put more effort into high-resolution linkage disequilibrium mapping of QTL in the presence of prior linkage evidence. To test the association between the trait locus and the markers, both likelihood-ratio tests and F-tests can be constructed on the basis of the proposed models. In addition, analytical formulas of noncentrality parameter approximations of the F-test statistics are provided. After comparing it with the AbAw approach, it is found that the method proposed in this article is more powerful and advantageous on the basis of simulation study and power calculation. By power and sample size comparison, it is shown that models that use more markers may have higher power than models that use less markers. Multiple-marker analysis can be more advantageous and has higher power in fine mapping QTL.
In an association study, population stratification can have a huge impact on a study, which leads to high false positives (Ewens and Spielman 1995). Zhao and Xiong (2002) proposed unbiased quantitative population association tests to investigate the issue. In this article, we perform type I error calculations. We allow for the very extreme form of population admixture, in which each family is drawn from a different stratum (Abecasis et al. 2000a). Type I error rates of the proposed test statistics are calculated to investigate the behaviors of the test statistics under the null distribution. Five test cases including population admixture are considered to investigate the type I error rates. The results show the proposed models and methods have correct type I error rates for most cases and are robust.
In a QTL mapping study, a strategy may be taken as follows. First, linkage analysis can be carried out using a sparse genetic map. Then, an association study can be performed using a dense genetic map for high-resolution mapping of the trait. The basic idea is to take advantage of linkage analysis for prior linkage information. In the meantime, one can take advantage of the high-resolution association study for fine mapping a genetic trait. It is well known that linkage analysis is robust; i.e., the false-positive rates are not high. However, the resolution of linkage analysis can be low. On the other hand, the resolution of the association study is high. But the association study is prone to false positives caused by population stratifications. Using the method proposed in this article, it is more likely to avoid high false-positive rates by performing an association study in the presence of prior linkage. The low resolution of a prior linkage analysis can be remedied by the follow-up high-resolution association study.
In recent years, there has been great interest in linkage disequilibrium mapping of QTL (Allison 1997; Rabinowitz 1997; Zhang and Zhao 2001). Various methods of joint analysis of linkage and association are proposed by researchers (Almasy et al. 1999; George et al. 1999; Martin et al. 2000). On the basis of variance component models, a combined linkage and association AbAw approach has been developed to decompose association effects into within- and between-family components (Fulker et al. 1999; Abecasis et al. 2000a,b, 2001; Cardon 2000; Sham et al. 2000). However, most research is limited to using one diallelic marker a time to model the association of QTL. This article proposes use of multiple markers to model the association and linkage. The genetic effects are orthogonally decomposed into additive and dominance effects. The method has the advantage of high-resolution dissection of genetic traits in an era in which dense marker maps are available (International SNP Map Working Group 2001; Kong et al. 2002). It is hoped that the current research may stimulate more interest in building models for joint linkage disequilibrium and linkage mapping of QTL.
In a genetics study, the first-hand data are usually genotyping information. The methods developed in this article can be directly used in analyzing quantitative and genotyping data of nuclear families by combining linkage and association information together. In the meantime, one may argue the use of haplotype data in an analysis that can be constructed on the basis of genotyping data. The question is an important issue as the haplotype map project will soon be completed and haplotype data will be readily available (International HapMap Consortium 2003; HapMap project, http://www.hapmap.org). The proposed method deals with diallelic markers. When the markers are not diallelic as is the case in the analyzed data, we collapse alleles into two groups to form two allele types. The hidden question is whether this collapsing has any consequence in type I error because the collapsing is not unique, which leads to the selection issue. It is important to develop appropriate models and handy algorithms in linkage and association mapping of complex diseases using haplotype/multiallelic marker data. It would be interesting to see a comparison of the two approaches. In Jung et al. (2004), a population-based regression approach is explored for association mapping of QTL using haplotype data. It is important to extend the research to utilize both population and pedigree data based on multiallelic markers/haplotypes.
One potential problem of using multiple markers in analysis is that the degrees of freedom of test statistics can be large, which may lead to low power. Moreover, the number of LD measures can be large. Thus, selection of appropriate markers for analysis is one issue that needs careful consideration. The optimal number of markers needed depends on a specific trait in a study. Also, it depends on the LD measures among the QTL and the markers. In data analysis, the markers that show significance in the model can be included in the final analysis. On the one hand, it would not be a good strategy to use many diallelic markers in the model. More markers will lead to higher degrees of freedom in test statistics. The number of markers that show significance is unlikely to be too large. Usually, using three or four relevant markers in an analysis would be worthwhile, since it may have higher power than a two- or one-marker analysis. In the meantime, the degrees of freedom of test statistics and number of LD measures would not be too big using three or four markers in an analysis. The second problem is the existence of a dominance trait effect. If the dominance effect is present, one may lose power by excluding it from analysis (Fan and Xiong 2002). However, one may get low power by testing hypothesis α1 = · · · = αk = δ1 = · · · = δk = 0, if the dominance effect is not significantly present to influence the trait values, due to the increase of degrees of freedom of test statistics.
So far, only one trait locus Q is assumed to be located in the chromosome region. Suppose that there are multiple QTL in the region. The mixed-effect model (1) can still be used in QTL mapping. In addition, suppose that the trait value is influenced by unlinked trait loci in different regions. Then model (3) needs to be generalized to use markers from different regions in analysis (Hoh and Ott 2003). If multiple-trait loci are present, other issues such as epistasis need more in-depth investigation. For IBD estimation, we follow the method proposed by Fulker et al. (1995) and Almasy and Blangero (1998). If there is LD between the trait and markers, LD among markers would also be expected and needs to be incorporated in estimating IBD. However, it is not clear how to achieve this. This is a very interesting and important research area for future study. Better IBD estimates would lead to a fitted variance-covariance structure that is a better approximation of the true variance-covariance structure. This would improve the performance of the proposed models.
Acknowledgments
We thank G. Gibson for kindness and patience in handling this article; and we thank two anonymous reviewers for very detailed and thoughtful critiques, which improved the article greatly. We are grateful to G. R. Abecasis for kindly providing the simulation program LDSIMUL to generate simulated data sets. R. Fan was supported partially by a research fellowship from the Alexander von Humboldt Foundation, Germany, by an international research travel assistance grant, Texas A&M University, and by the National Science Foundation Grant DMS-0505025.
APPENDIX A
Taking variance-covariance among xij, zij, yi of the mixed-effect model (1) leads to the following variance-covariance equations:
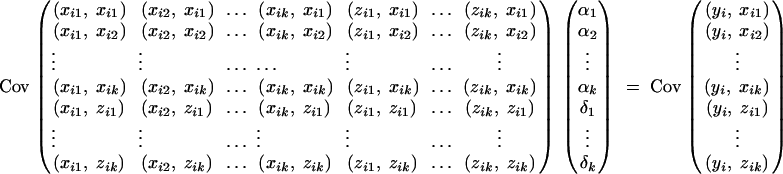 |
A1 |
In a similar way to that in Fan and Xiong (2002)(Appendix A), the following expectations, variance, and covariances can be derived accordingly: Exij = 0, Ezij = 0, 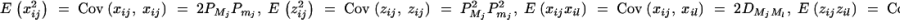 for j, l = 1, · · · , k, j ≠ l. Plugging the above quantities into (A1) gives
for j, l = 1, · · · , k, j ≠ l. Plugging the above quantities into (A1) gives
 |
Therefore, the coefficients of (5) are derived.
APPENDIX B
To simplify notations, we omit subscripts ij from πijQ, πijM1, · · · , πijMk, ΔijM1, · · · , ΔijMk in appendixes b and c. Taking variance-covariance among πQ, πMj, yi of Equation 7 leads to
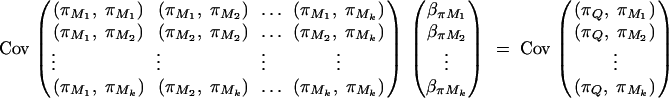 |
B1 |
From Elston and Keats (1985) and Almasy and Blangero (1998), we have
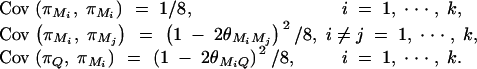 |
Plugging the above quantities into Equation B1 gives
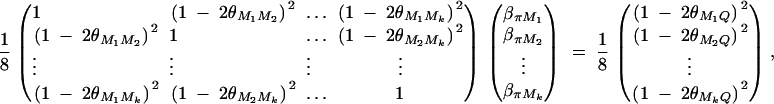 |
which leads to
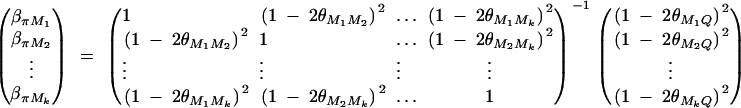 |
APPENDIX C
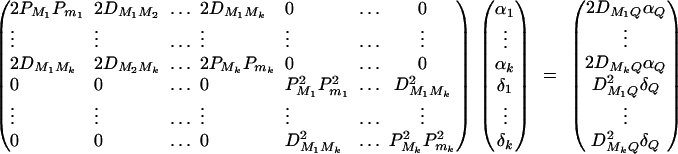
Taking variance-covariance among ΔQ, πMj, ΔMl of Equation 8 leads to
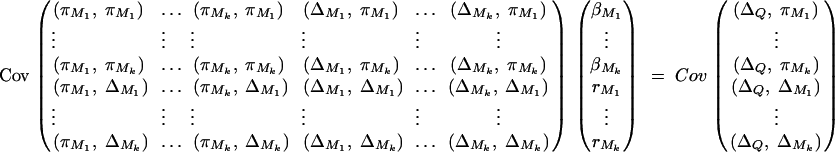 |
C1 |
As in appendix B, the following covariances are from Elston and Keats (1985), Almasy and Blangero (1998), and Fan and Jung (2003),
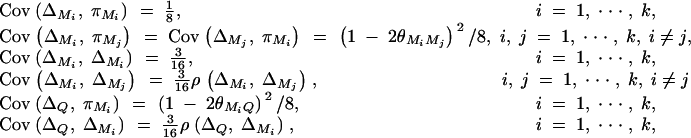 |
where 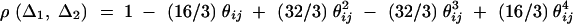 . Plugging the above results into the equation (C1), we have a submatrix block equation,
. Plugging the above results into the equation (C1), we have a submatrix block equation,
 |
where
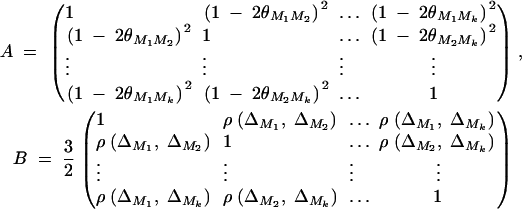 |
Therefore, we have from Harville (1997) that
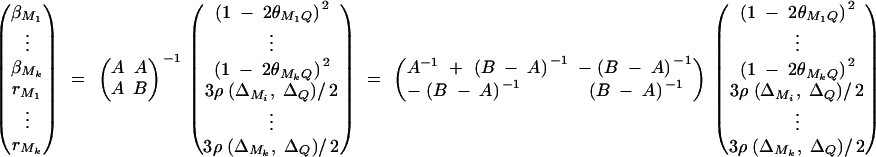 |
The equation 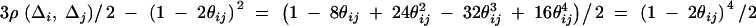 leads to
leads to
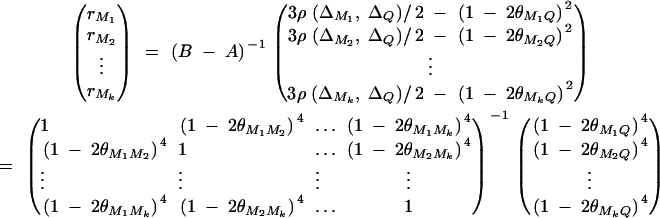 |
Moreover, we have
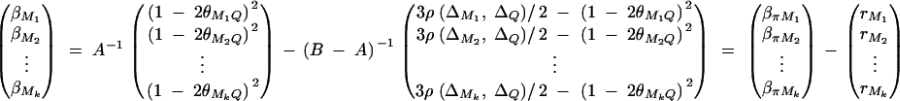 |
APPENDIX D
To derive a1, a2, a3 in approximation (9), we assume three subsamples of a population: n individuals; m trio families, each having both parents and a single child; and s nuclear families, each having both parents and two offspring.
- For each yi of the n individuals, Σi = σ2 and Xi = (1, xi1, · · · , xik, zi1, · · · , zik), i = 1, · · · , n. When the sample size n of individuals is large, the large number law leads to
Therefore, we have the approximation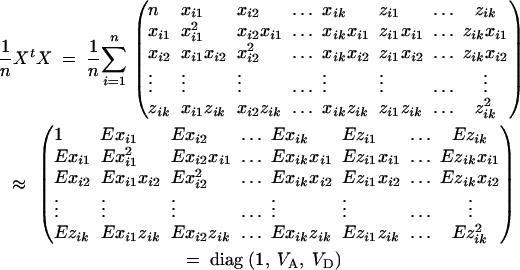
where VA and VD are additive and dominance variance-covariance matrices defined by (4).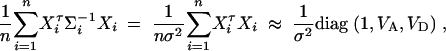
D1 - For the ith trio family, let (yfi, ymi, yi1)τ be the trait values and Xi = (Xfi, Xmi, Xi1)τ be the related model matrix, i = n + 1, · · · , n + m. In the same way as that of Fan and Xiong (2003)(Appendix A), the covariance matrix between parents and their offspring can be shown to be
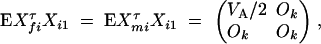
D2
where Ok is a zero k × k matrix. For each of the m trio families, the variance-covariance matrix
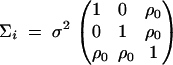 |
The inverse matrix of Σi is
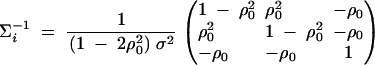 |
By the above formulas, we can show the following:
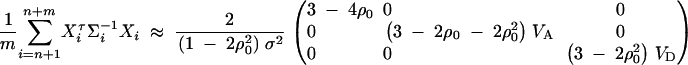 |
D3 |
- For the ith family that is composed of both parents and two offspring, let (yfi, ymi, yi1, yi2)τ be the trait values and Xi = (Xfi, Xmi, Xi1, Xi2)τ be the related model matrix, i = n + m + 1, · · · , n + m + s. In the same way as that of Fan and Xiong (2003)(Appendix C), it can be shown that
For each of the s families, the inverse variance-covariance matrix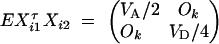
D4
where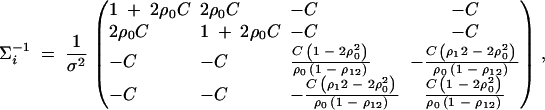
D5 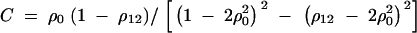 . Using (D2), (D4), and (D5), we can show
. Using (D2), (D4), and (D5), we can show
where the constants are given by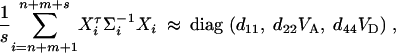
D6 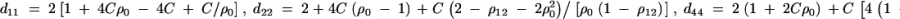 . Combining the n individuals, m trio families, and s families with two offspring, the equations (D1), (D3), and (D6) lead to
. Combining the n individuals, m trio families, and s families with two offspring, the equations (D1), (D3), and (D6) lead to 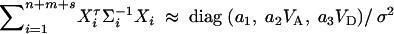 , where
, where 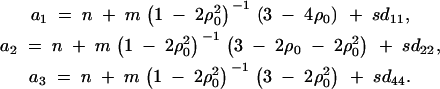
D7
APPENDIX E
Using (D2) and (D4), we can show approximation (10). The constants b1 and b2 are given by
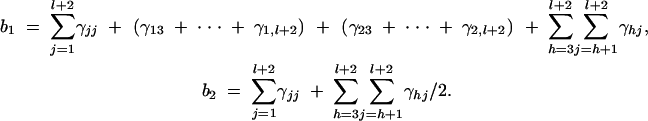 |
E1 |
References
- Abecasis, G. R., L. R. Cardon and W. O. C. Cookson, 2000. a A general test of association for quantitative traits in nuclear families. Am. J. Hum. Genet. 66: 279–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abecasis, G. R., W. O. C. Cookson and L. R. Cardon, 2000. b Pedigree tests of linkage disequilibrium. Eur. J. Hum. Genet. 8: 545–551. [DOI] [PubMed] [Google Scholar]
- Abecasis, G. R., W. O. C. Cookson and L. R. Cardon, 2001. The power to detect linkage disequilibrium with quantitative traits in selected samples. Am. J. Hum. Genet. 68: 1463–1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison, D. B., 1997. Transmission-disequilibrium tests for quantitative traits. Am. J. Hum. Genet. 60: 676–690. [PMC free article] [PubMed] [Google Scholar]
- Almasy, L., and J. Blangero, 1998. Multipoint quantitative trait linkage analysis in general pedigrees. Am. J. Hum. Genet. 62: 1198–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almasy, L., J. T. Williams, T. D. Dyer and J. Blangero, 1999. Quantitative trait locus detection using combined linkage/disequilibrium analysis. Genet. Epidemiol. 17(Suppl. 1): S31–S36. [DOI] [PubMed] [Google Scholar]
- Amos, C. I., 1994. Robust variance-components approach for assessing linkage in pedigrees. Am. J. Hum. Genet. 54: 534–543. [PMC free article] [PubMed] [Google Scholar]
- Amos, C. I., R. C. Elston, A. F. Wilson and J. E. Bailey-Wilson, 1989. A more powerful robust sib-pair test of linkage for quantitative traits. Genet. Epidemiol. 6: 435–449. [DOI] [PubMed] [Google Scholar]
- Cardon, L. R., 2000. A sib-pair regression model of linkage disequilibrium for quantitative traits. Hum. Hered. 50: 350–358. [DOI] [PubMed] [Google Scholar]
- Cotterman, C. W., 1940 A calculus for statistico-genetics. Ph.D. Thesis, Ohio State University, Columbus, OH.
- Elston, R. C., and B. J. B. Keats, 1985. Genetic analysis workshop III: sib pair analyses to determine linkage groups and to order loci. Genet. Epidemiol. 2: 211–213. [Google Scholar]
- Ewens, W. J., and R. S. Spielman, 1995. The transmission/disequilibrium test: history, subdivision, and admixture. Am. J. Hum. Genet. 57: 455–464. [PMC free article] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996 Introduction to Quantitative Genetics, Ed. 4. Longman, London. [DOI] [PMC free article] [PubMed]
- Fan, R., and J. Jung, 2003. High resolution joint linkage disequilibrium and linkage mapping of quantitative trait loci based on sibship data. Hum. Hered. 56: 166–187. [DOI] [PubMed] [Google Scholar]
- Fan, R., and M. Xiong, 2002. High resolution mapping of quantitative trait loci by linkage disequilibrium analysis. Eur. J. Hum. Genet. 10: 607–615. [DOI] [PubMed] [Google Scholar]
- Fan, R., and M. Xiong, 2003. Combined high resolution linkage and association mapping of quantitative trait loci. Eur. J. Hum. Genet. 11: 125–137. [DOI] [PubMed] [Google Scholar]
- Fan, R., C. Spinka, L. Jin and J. Jung, 2005. Pedigree linkage disequilibrium mapping of quantitative trait loci. Eur. J. Hum. Genet. 13: 216–231. [DOI] [PubMed] [Google Scholar]
- Fulker, D. W., S. S. Cherny and L. R. Cardon, 1995. Multiple interval mapping of quantitative trait loci, using sib-pairs. Am. J. Hum. Genet. 56: 1224–1233. [PMC free article] [PubMed] [Google Scholar]
- Fulker, D. W., S. S. Cherny, P. C. Sham and J. K. Hewitt, 1999. Combined linkage and association sib-pair analysis for quantitative traits. Am. J. Hum. Genet. 64: 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George, V., H. K. Tiwari, X. F. Zhu and R. C. Elston, 1999. A test of transmission/disequilibrium for quantitative traits in pedigree data, by multiple regression. Am. J. Hum. Genet. 65: 236–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldgar, D. E., and R. S. Oniki, 1992. Comparison of a multipoint identity-by-descent method with parametric multipoint linkage analysis for mapping quantitative traits. Am. J. Hum. Genet. 50: 598–606. [PMC free article] [PubMed] [Google Scholar]
- Graybill, F. A., 1976 Theory and Application of the Linear Model. Wadsworth & Brooks/Cole Advanced Books & Software, Pacific Grove, CA.
- Harville, D. A., 1997 Matrix Algebra From a Statistician's Perspective. Springer, Berlin/Heidelberg, Germany/New York.
- Haseman, J. K., and R. C. Elston, 1972. The investigation of linkage between a quantitative trait and a marker locus. Behav. Genet. 2: 3–19. [DOI] [PubMed] [Google Scholar]
- Hoh, J., and J. Ott, 2003. Mathematical multi-locus approaches to localizing complex human trait genes. Nat. Rev. Genet. 4: 701–709. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium, 2003. The international HapMap project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]
- International SNP Map Working Group, 2001. A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature 409: 928–933. [DOI] [PubMed] [Google Scholar]
- Jennrich, R. I., and M. D. Schluchter, 1986. Unbalanced repeated-measures models with structured covariance matrices. Biometrics 42: 805–820. [PubMed] [Google Scholar]
- Jung, J., R. Fan and L. Jin, 2004 Haplotype association mapping of quantitative trait loci, a population based approach. Abstracts of the 54th Annual Meeting of the American Society of Human Genetics, Toronto, Abstract 1970.
- Kong, A., D. F. Gudbjartsson, J. Sainz, G. M. Jonsdottir, S. A. Gudjonsson et al., 2002. A high resolution recombination map of the human genome. Nat. Genet. 31: 241–247. [DOI] [PubMed] [Google Scholar]
- Lange, K., 2002 Mathematical and Statistical Methods for Genetic Analysis, Ed. 2. Springer, Berlin/Heidelberg, Germany/New York.
- Martin, E. R., S. A. Monks, L. L. Warren and N. L. Kaplan, 2000. A test for linkage and association in general pedigrees: the pedigree disequilibrium test. Am. J. Hum. Genet. 67: 146–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyers, D. A., M. Wjst and C. Ober, 2001. Description of three data sets: collaborative study on the genetics of asthma (CSGA), the German affected sib pair study, and the Hutterites of South Dakota. Genet. Epidemiol. 21(Suppl. 1): S4–S8. [DOI] [PubMed] [Google Scholar]
- Pinheiro, J. C., and D. M. Bates, 2000 Mixed-Effects in S and S-plus. Springer, New York.
- Pratt, S. C., M. Daly and L. Kruglyak, 2000. Exact multipoint quantitative-trait linkage analysis in pedigrees by variance components. Am. J. Hum. Genet. 66: 1153–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabinowitz, D., 1997. A transmission disequilibrium test for quantitative trait loci. Hum. Hered. 47: 342–350. [DOI] [PubMed] [Google Scholar]
- Searle, S. R., G. Casella and C. E. McCulloch, 1992 Variance Components. John Wiley & Sons, New York.
- Sham, P. C., S. S. Cherny, S. Purcell and J. K. Hewitt, 2000. Power of linkage versus association analysis of quantitative traits, by use of variance-components models, for sibship data. Am. J. Hum. Genet. 66: 1616–1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wjst, M., G. Fischer, T. Immervoll, M. Jung, K. Saar et al., 1999. A genome-wide search for linkage to asthma. Genomics 58: 1–8. [DOI] [PubMed] [Google Scholar]
- Zhang, S. L., and H. Y. Zhao, 2001. Quantitative similarity-based association tests using population samples. Am. J. Hum. Genet. 69: 601–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao, J., and M. Xiong, 2002. Unbiased quantitative population association test. Am. J. Hum. Genet. 71(Suppl.): 568. [Google Scholar]
- Zhao, J., W. Li and M. Xiong, 2001. Population based linkage disequilibrium mapping of QTL: an application to simulated data in an isolated population. Genet. Epidemiol. 21(S1): S655–S659. [DOI] [PubMed] [Google Scholar]
- Zhu, X. F., and R. C. Elston, 2000. Power comparison of regression methods to test quantitative traits for association and linkage. Genet. Epidemiol. 18: 322–330. [DOI] [PubMed] [Google Scholar]