Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2005 Jul;170(3):1001–1008. doi: 10.1534/genetics.105.040741

Epistasis and the Adaptability of an RNA Virus

Rafael Sanjuán *, José M Cuevas *,†, Andrés Moya *, Santiago F Elena ‡,1
PMCID: PMC1451175  PMID: 15879507

Abstract

We have explored the patterns of fitness recovery in the vesicular stomatitis RNA virus. We show that, in our experimental setting, reversions to the wild-type genotype were rare and fitness recovery was at least partially driven by compensatory mutations. We compared compensatory adaptation for genotypes carrying (1) mutations with varying deleterious fitness effects, (2) one or two deleterious mutations, and (3) pairs of mutations showing differences in the strength and sign of epistasis. In all cases, we found that the rate of fitness recovery and the proportion of reversions were positively affected by population size. Additionally, we observed that mutations with large fitness effect were always compensated faster than mutations with small fitness effect. Similarly, compensatory evolution was faster for genotypes carrying a single deleterious mutation than for those carrying pairs of mutations. Finally, for genotypes carrying two deleterious mutations, we found evidence of a negative correlation between the epistastic effect and the rate of compensatory evolution.

THE process of adaptation is sometimes visualized as populations walking throughout an adaptive landscape. If this landscape is rugged, then natural selection will trap populations in particular, historically determined, adaptive peaks. Under the shifting-balance hypothesis (Wright 1931, 1932, 1982), episodes of genetic drift would play an essential role in adaptation, because they would allow populations to cross through valleys of low adaptive value and then to reach new adaptive peaks once the selective regime gets restored. The basic idea of this classic model has deep implications for the understanding of diversity (Stephan 1996), the maintenance of historical contingencies, and the genesis of complexity (Lynch and Conery 2003). Its validity depends on the existence of rugged landscapes that in turn critically depend on the abundance and strength of epistasis (Whitlock et al. 1995). Despite having deserved considerable experimental effort, detecting epistasis has been somehow elusive (de Visser et al. 1997; Elena and Lenski 1997; Elena 1999; Burch et al. 2003). However, during the last year, experiments with RNA viruses have contributed to shedding some light on this topic. Bonhoeffer et al. (2004), Burch and Chao (2004), and Sanjuán et al. (2004b), found evidence for positive epistasis in the human immunodeficiency virus type-1 (HIV-1), the bacteriophage φ6, and the vesicular stomatitis virus (VSV), respectively. Still, finding evidence of frequent genetic interactions does not necessarily provide information about the contribution of epistasis to adaptation.

A population that has accumulated deleterious mutations can respond to selection by simply reverting them to the ancestral state or, alternatively, by fixing compensatory changes at different loci. Compensatory mutations can be defined as those masking the effect of deleterious mutations. Reversion guarantees a complete fitness recovery in a single step, whereas this is not necessarily the case for compensation (Burch and Chao 1999). The relative amount of evolutionary reversals and compensations depends on the effective population size (Ne): the larger the Ne, the more mutations will arise and, consequently, the higher the chance for a reversion to appear and get fixed (Burch and Chao 1999).

Compensatory changes necessarily invoke epistastic interactions (Wright 1932), that is, the existence of rugged adaptive landscapes. Therefore, the magnitude and frequency of genetic interactions determine the extent to which fitness can be recovered via compensatory adaptation. In general, an increased genetic complexity, defined as the number of different gene functions and the connectivity of the network of interactions among them, should give more opportunities for compensation; whereas those genomes under intense functional constraints should be prone to higher rates of genetic reversion. RNA viruses are the prototypic system in which evolution proceeds under extremely large population sizes, enormous mutational supply, and considerable functional constraints (Holland et al. 1982; Holmes 2003; Moya et al. 2004). Therefore, RNA viruses provide an interesting tool for exploring whether evolutionary reversal is more common than compensatory evolution. Previous studies with VSV have shown that the same beneficial mutations appear many times in independently evolving populations (Cuevas et al. 2002; Novella and Ebendick-Corpus 2004), suggesting that adaptive solutions might be quite limited. A similar pattern of convergent adaptive evolution has been also described for the DNA bacteriophage φX174 (Bull et al. 1997).

Fitness-recovery experiments in which both the mutated and the wild-type genotypes are genetically characterized offer an exceptional opportunity for testing several evolutionary predictions. For example, it has been predicted that increasing Ne would result in speeding up the rate of adaptive evolution (Orr 2000b; Wilke 2004), but also positively biasing the fitness effect associated with each mutation fixed (Gerrish and Lenski 1998; Rozen et al. 2002). These predictions remain valid for the case of compensatory evolution, as shown in the bacteriophage φ6 (Burch and Chao 1999). Similarly, at the first stages of the evolutionary process, it is expected that the rate of adaptation positively correlates with the fitness distance to the optimal genotype (Elena et al. 1998; Moore et al. 2000). Later, the rate of adaptation should slow down as the genetic distance to the optimum reduces, partly because the expected beneficial selection coefficient per mutation is smaller (Orr 2000a,b). The use of genotypes that have accumulated more than one deleterious mutation is also useful for addressing the relationship between the type and strength of epistasis and the rate of adaptation. It has been suggested that those genotypes in which the accumulated deleterious mutations show negative epistasis should regain wild type's fitness faster than those showing multiplicative effects, because the reversion or the compensation would confer a larger marginal gain (Moore et al. 2000). Similarly, fitness improvements should be faster under multiplicative effects than in the presence of positive epistasis, because the reversion or the compensation of the first mutation would uncover the entire effect of the second mutation. Therefore, a negative correlation between the epistatic effect and the rate of compensatory adaptation should be observed.

VSV is a negative-stranded RNA virus belonging to the Rhabdoviridae family that has been used extensively for experimental viral evolution studies (reviewed in Novella 2003 and Moya et al. 2004). The VSV genome is constituted by a single 11,161-nucleotides-long molecule encoding five genes. In this study, we used a collection of single- and double-nucleotide substitution mutants created by site-directed mutagenesis (Sanjuán et al. 2004a,b) to perform a set of fitness-recovery experiments. We are especially interested in exploring the role of compensatory mutations rather than in reversions to the wild-type genotype. Therefore, to minimize the chances of reversion, our evolution experiments elapsed for only ∼20 replication cycles, a particularly short time for this type of evolution experiment. After the evolution phase, we measured the fitness of the evolved populations and we calculated the relative rate of fitness improvement. First, reversions were discarded by confirming the presence of the original mutations in the evolved populations. Second, we used the fact that the potential for adaptation of genotypes carrying strongly deleterious mutations should be greater than that for those carrying milder changes (Elena et al. 1998) to demonstrate compensatory evolution. Finally, we tested the predictions mentioned above about the influence of Ne, the selection coefficient of deleterious mutations, the number of ancestral mutations, and their epistatic effect in determining the rate of adaptation.

MATERIALS AND METHODS

Mutant genotypes:

Single-nucleotide (Sanjuán et al. 2004a) and double-nucleotide (Sanjuán et al. 2004b) substitution mutants were obtained from a full-length infectious cDNA clone (Whelan et al. 1995) by site-directed mutagenesis as previously described (Sanjuán et al. 2004a,b). Sequencing of the mutant cDNAs was done to confirm that each desired mutation was successfully incorporated. All mutations were introduced in the same reference genotype, called MARM RSV (Sanjuán et al. 2004a), which differs from the wild type by a neutral (see below) single-nucleotide substitution that confers the ability to grow in the presence of the I1 monoclonal antibody (mAb) at concentrations that completely inhibit the wild type (Vandepol et al. 1986). Viruses were recovered from transfected BHK21 cells as detailed in Whelan et al. (1995) and Sanjuán et al. (2004a). The presence of plaque-forming units (PFU) 96 hr postinoculation indicated the successful recovery of infectious VSV particles. Post-transfection titers, which ranged from 104 to 106 PFU/ml, were equalized to ∼5 × 106 PFU/ml prior to the competition assays to avoid any possible density effect on fitness. Transfection experiments were done for the mutants, the nonmutated wild type, and the MARM RSV clone. A large volume of wild type was produced and kept at −80°. This stock constituted our common competitor for fitness assays.

Table 1 shows the genetic properties and fitness values, W, of each one of the 12 mutant genotypes used in this study. For the double mutants, the estimated epistasis parameter (ε), estimated as the difference between the observed fitness of a double mutant and the value expected under a multiplicative model (Sanjuán et al. 2004b), is also shown. Two genotypes had significant negative epistasis; two had significant positive epistasis; and in the last two cases ε was not significant and therefore is considered as multiplicative effects.

TABLE 1 .

Nature of the mutations used in this study

Mutation 1 Mutation 2 Original fitness [W(0)] Strength of epistasis (ε)
T1323A (F421L) N gene 0.584 ± 0.022
G4459T (W461L) G gene 0.701 ± 0.011
T3192C (Y39H) G gene 0.717 ± 0.004
G6376C (L549F) L gene 0.859 ± 0.029
T3709C (L211P) G gene 0.842 ± 0.179
T10809C (I2026T) L gene 0.861 ± 0.024
A8787T (N1352I) L gene T1323A (F421L) N gene 0.592 ± 0.035 0.078 ± 0.038*
G7128T (C799F) L gene T5496A (L255Q) L gene 0.625 ± 0.010 −0.065 ± 0.025*
G7128T (C799F) L gene A8787T (N1352I) L gene 0.657 ± 0.005 −0.027 ± 0.021
T1585A (S64T) N gene T4398C (F411L) G gene 0.837 ± 0.016 −0.042 ± 0.048
A2018T (Q208L) P gene T5124A (I131N) L gene 0.841 ± 0.016 0.112 ± 0.022*
T6010C (synonymous) L gene T1585A (S64T) N gene 0.867 ± 0.014 −0.078 ± 0.034*
Open in a new tab

The first two columns show the nucleotide (and amino acid) changed and the corresponding gene. The fitness of each original mutant genotype, relative to the reference MARM RSV strain, and the estimated strength of epistasis (± SEM) are shown.

*

Significantly different from ε = 0 (one sample t-test).

Evolution experiments:

Six single- and six double-nucleotide substitution mutants (Table 1) were used to initiate the evolution experiment. All of them had a significant reduction in fitness compared to the MARM RSV reference genotype (Sanjuán et al. 2004a,b). Each of these mutants was used to initiate three independent replica populations at two effective population sizes each (Ne = 2 × 102 PFU and Ne = 2 × 104 PFU) in six 12-well plates (one well in one plate for each replicate) containing fresh BHK21 cell monolayers. Infected cell cultures were incubated for 48 hr, so that the cytopathic effect could be completed even by clones carrying mutations with large deleterious fitness effect, and the number of PFU produced after this time (Nf) was estimated by titration as described elsewhere (Holland et al. 1991).

The effective population size in a fluctuating passage regime can be estimated as

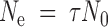graphic file with name M1.gif 1

(Lenski et al. 1991), where N0 stands for the size of the inoculum at the beginning of each passage and τ for the number of generations (here, replication cycles) per passage. In the particular case of a negative-strand lytic virus that exhausts the entire cell culture, τ can be estimated as

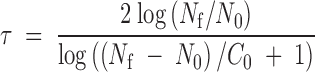graphic file with name M2.gif 2

(Miralles et al. 2000), where C0 stands for the number of cells initially present in the well, and it was determined by direct counting using a hemocytometer (∼8 × 105 cells/well). Therefore, Ne can be adjusted by numerically solving Equations 1 and 2 for different values of τ and N0.

Forty-eight hours postinoculation, the number of infectious particles per well was in the order of 109 PFU and hence, for Ne = 2 × 102 PFU, the inoculum was set to N0 ≈ 41.986, the number of replication cycles per passage being thus τ ≈ 4.764. Four passages were done under this regime and thus ∼19.056 replication cycles elapsed during this evolution experiment. For Ne = 2 × 104 PFU, the inoculum was set to N0 ≈ 5.925 × 103 PFU, and the number of replication cycles per passage was thus τ ≈ 3.375. Six passages were done under this regime and hence ∼20.250 replication cycles elapsed in this evolution experiment. Therefore, all our evolution experiments expanded for approximately the same number of replication cycles (20) regardless of the Ne imposed. Specific details concerning cell culture conditions can be found elsewhere (Elena et al. 1998).

Relative fitness assays:

The fitness of each mutant relative to the wild type was assessed by seeding ∼2.5 × 103 PFU of each competing genotype into ∼105 cells. Ten hours postinoculation, the titers of both genotypes were determined by plating an appropriate dilution in the presence and absence of I1 mAb. Exponential growth occurred during this time interval (Sanjuán et al. 2004a) and, therefore, intrinsic growth rates, r, were calculated as the slope of the log-titer against time (hours postinoculation). The fitness of population i relative to the wild type can then be calculated as ωi = exp(ri − rwild type).

Fitness assays were done in five independent blocks for the ancestors (Sanjuán et al. 2004a,b) and in three independent blocks for each one of the 72 evolved populations. Fitness estimates of each ith mutant genotype (Wi) were adjusted by dividing ωi by the grand-mean fitness of MARM RSV. MARM RSV was effectively neutral relative to the wild type (ωMARM RSV = 0.997 ± 0.009; t59 = 0.405, P = 0.687).

The magnitude of fitness improvement experienced by the kth evolved populations compared with its corresponding ancestrals after the ∼20 replication cycles of experimental evolution was assessed using the relative change in fitness: Rk = Wk(20)/Wk(0) − 1.

Consensus sequences:

Viral RNA was extracted from the supernatant of the infected cultures using the High Pure viral nucleic acid kit and following the instructions provided by the manufacturer (Roche, Indianapolis). The anti-genomic VSV cDNA was synthesized using the reverse transcriptase of the Moloney murine leukemia virus (Promega, Madison, WI) plus a battery of random hexamers (Promega). The genomic region containing the original mutations was amplified by PCR using Taq polymerase (Amersham, Arlington Heights, IL) and automatically sequenced in an ABI310 machine (Applied Biosystems, Foster City, CA) to determine whether a reversion had occurred. The sets of primers used for sequencing were the same as those used in Cuevas et al. (2002).

RESULTS

Evidence for reversions and beneficial mutations:

Each of the six single- and six double-nucleotide substitution deleterious mutants was evolved in triplicate for ∼20 replication cycles at two effective population sizes (Ne = 2 × 102 PFU and Ne = 2 × 104 PFU). We checked in each of the 72 lineages whether the original mutation had reverted to its ancestral wild-type state by performing consensus population sequencing. Among the 18 single-nucleotide mutant-derived lineages evolved at the smaller Ne = 2 × 102 PFU, none showed a complete reversion to the wild-type allele, and only 1 showed a partial reversion (i.e., a polymorphism between the mutant and wild-type alleles), whereas 4 out of 18 reversions were observed for the larger Ne = 2 × 104 PFU. Analogous results were obtained for the double mutants. Only 1 case of partial reversion in one of the two mutated sites was observed among the 18 double-nucleotide mutant-derived lineages evolved at Ne = 2 × 102 PFU, whereas 6 reversions (3 were polymorphisms and 3 were fixed reversions) were observed in at least one site among the 18 lineages evolved at Ne = 2 × 104 PFU. Therefore, within this evolutionary time frame, reversions were rare for the smaller Ne (∼5%, regardless of whether they were fixed or polymorphic), but their frequency (∼28%) significantly increased (χ2 = 6.400, P = 0.011) as Ne increased two orders of magnitude.

When the fitness reached by each putative revertant genotype, Wk(20), was compared (one-sample t-test) with the fitness of the MARM RSV, three cases showed values that were significantly lower than expected (P ≤ 0.044), in apparent contradiction with the observed molecular reversion to the ancestral allele. However, if we apply the Bonferroni method, accounting for the multiplicity of tests for the same hypothesis (Rice 1989), only one case, A8787T/T1323A, remained significant (P = 0.004). Nonetheless, this is not surprising at all since (i) the first mutated site was polymorphic whereas the second still retained the mutant allele and (ii) positive epistasis existed between these two mutations (Table 1) and, hence, the entire deleterious effect associated with the T1323A mutation can be expressed. In conclusion, complete reversion to the wild-type allele fully recovers fitness, as expected.

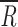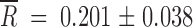The mean relative fitness gains, Inline graphic, for the revertants were Inline graphic and Inline graphic for the small and large Ne, respectively. The average fitness gain was larger for Ne = 2 × 104 PFU than for 2 × 102 PFU (Mann-Whitney's test: U = 1, 1-tailed P = 0.027). These gains can be attributed to reversions, but also to additional beneficial mutations taking place elsewhere in the genome. In fact, for Ne = 2 × 104 PFU, in those populations in which no reversion to the wild-type allele had occurred, fitness improved as well (Inline graphic). However, as expected, the magnitude of fitness recovery was smaller than that for the reverting group (U = 36, 1-tailed P < 0.001). Regarding the case of Ne = 2 × 102 PFU, those populations in which no reversion had occurred also recovered fitness (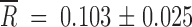Inline graphic), although to an extent similar to that of the reverting group (U = 15, 1-tailed P = 0.095). The above results indicate that, in addition to reversions to the wild-type alleles, other beneficial mutations appeared in at least some populations. However, these results do not give insights into the putative fixation of compensatory changes.

Evidence for compensatory adaptation:

After excluding partial and complete reversions, the variability in fitness gains observed during the evolution experiments can be attributed to several factors. First, we can distinguish between single- and double-nucleotide mutants. Second, the evolution of each mutant genotype can be conditioned by the peculiarities of the associated ancestral mutations. Third, the rate of adaptation of each genotype is expected to be different for the two Ne's employed. Finally, for each genotype and each Ne, the outcome of the three parallel evolution lines can differ simply by intrinsic stochastic factors. We assessed the contributions of each of these factors by means of a nested ANOVA in which each factor was nested within the preceding one. This analysis (Table 2) indicates that the fitness gain experienced by a single genotype that has been evolved at a fixed Ne depends on the evolution lineage (P < 0.001), something that is not surprising given that beneficial mutations are random and rare events. Moreover, for the same reason, the higher the Ne, the higher the fitness gain should be, as confirmed by the nested ANOVA (P = 0.004). More interestingly, the magnitude of fitness gains can vary depending on the starting genotype: significant differences exist between single- and double-nucleotide mutants (P < 0.001), but also among those genotypes in which the same number of mutations has been introduced (P < 0.001). Given that the 12 evolved lineages showing signs of reversion have been excluded from this analysis, the results show that beneficial changes arising during the evolution experiment interacted with the ancestral deleterious mutations.

TABLE 2 .

Nested ANOVA for fitness recovery data

Source of variation SS d.f. F P
No. of mutations 5.270   2 74.530 <0.001
Mutant genotype 2.786  10  7.880 <0.001
Ne 1.249  11  3.211 0.004
Evolution lineage 1.308  37  4.988 <0.001
Error 0.851 120
Open in a new tab

Each factor is nested within the one immediately above. All factors were treated as fixed except the evolution lineage.

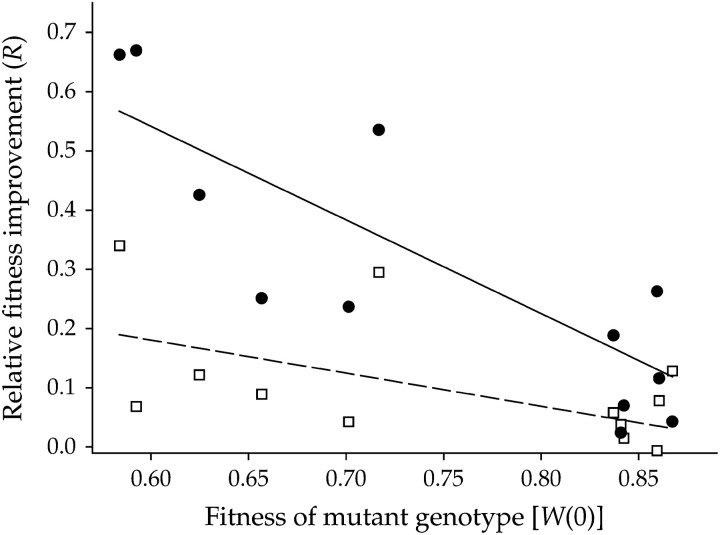
Several properties of the ancestral mutant genotypes can be involved in determining the relative rate of adaptation, one of these being their fitness value. To explore this possibility, the genotype factor can be substituted by its corresponding fitness value, Wk(0), and included in the nested ANOVA as a covariable. After doing so, the effect of Wk(0) is highly significant (F1,167 = 52.764, P < 0.001), showing that the starting fitness strongly influenced further adaptability. Indeed, as illustrated in Figure 1, the lower the Wk(0), the higher the fitness gain (partial correlation controlling for Ne: r = −0.487, 57 d.f., P < 0.001).

Figure 1.—

Figure 1.—

Open in a new tab

Negative correlation between ancestral fitness and the magnitude of fitness improvement. Each point represents the mean of the three evolution lineages. Open squares and the dashed least-squares regression line show Ne = 2 × 102 PFU; solid circles and the solid least-squares regression line show Ne = 2 × 104 PFU.

After excluding reversions from the analyses, the following three findings support the existence of compensatory mutations: (i) the presence of beneficial mutations, (ii) the evidence for genetic interactions between fixed mutations and ancestral genotype (genetic background), and (iii) the negative correlation between ancestral fitness and the magnitude of fitness improvement.

Epistasis and the rate of adaptation:

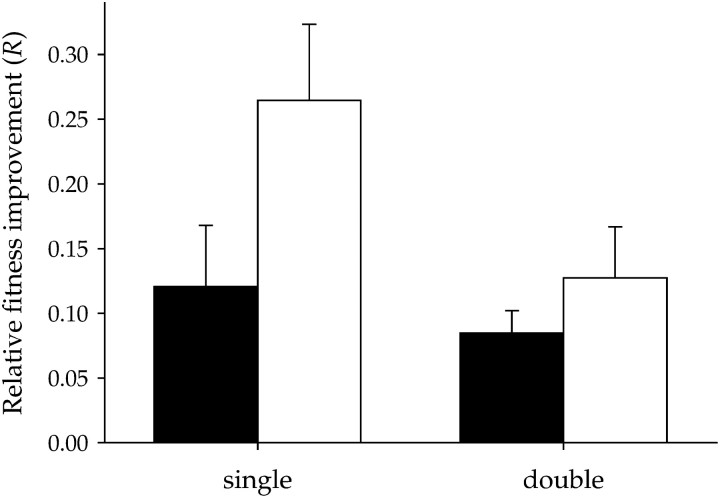
According to the results shown in Figure 1, and given that single and double mutants were chosen in such a way that they had similar Wk(0) (Table 1), both groups should display a similar fitness recovery rate if compensation was complete, that is, if all mutational effects had been masked. On the contrary, this is not the case (Table 2: P < 0.001) and single mutants recovered fitness to a larger extent than did double mutants (Figure 2), therefore indicating that the evolutionary time elapsed during the experiment has not been enough for full compensation of two mutations.

Figure 2.—

Figure 2.—

Open in a new tab

Average fitness improvement for single- and double-nucleotide substitution mutants, for the two effective population sizes. Solid bars show Ne = 2 × 102 PFU and open bars show Ne = 2 × 104 PFU. Error bars show standard errors of the means.

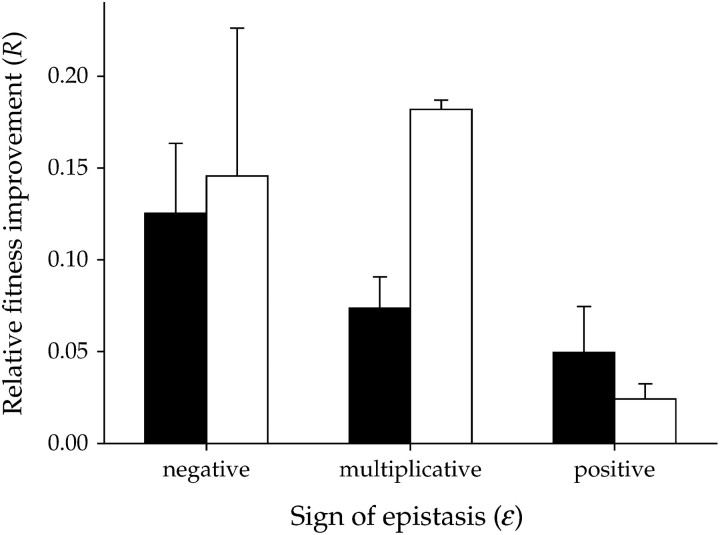
Given that deleterious fitness effects of most double mutants have not been fully compensated, we expect epistasis between ancestral mutations to have an effect on the observed magnitude of fitness gain. Our prediction is that the latter should negatively correlate with the sign of epistasis: as we have argued above, negative epistasis should speed up the rate of adaptation compared with multiplicative effects whereas positive epistasis should slow it down. To test this prediction, the “genotype” factor in the nested ANOVA can be substituted by two covariables: (i) its corresponding Wk(0), as before, and (ii) the epistatic term, ε. This analysis, restricted to double mutants, revealed that in addition to Wk(0) (F1,79 = 132.358, P < 0.001), ε also played a role in determining the extent of fitness improvement (Figure 3: F1,79 = 7.556, P = 0.007). Indeed, as hypothesized, a significant partial correlation (controlling for both Ne and the initial fitness value) between the sign of epistasis and the observed fitness gain was found (r = −0.355, 26 d.f., 1-tailed P = 0.032). A Friedman's test for randomized blocks also provides statistical support (χ2 = 5.828, 1 d.f., P = 0.016) to the following rank of epistasis affecting the extent of fitness recovery: negative > multiplicative > positive.

Figure 3.—

Figure 3.—

Open in a new tab

Average fitness improvement as a function of the type of epistasis characteristic of the two mutations carried by the double mutants, for the two effective population sizes. Solid bars show Ne = 2 × 102 PFU and open bars show Ne = 2 × 104 PFU. Error bars show standard errors of the means.

DISCUSSION

The relative amount of reversions and compensatory changes in fitness recovery experiments provides valuable information about the influence of epistasis in adaptation, which in turn sheds light on the topology of adaptive landscapes, a key issue for our understanding of the evolutionary process. The reversion probability should increase with population size and evolutionary time (Levin et al. 2000). Compensatory-evolution experiments with RNA viruses confirm this prediction. For example, Novella and Ebendick-Corpus (2004) identified five compensatory mutations and nine back mutations in 17 VSV populations that recovered fitness during 10 laboratory passages after having accumulated deleterious mutations. In this experiment, the evolutionary time was longer than in ours and the effective population size was presumably >2 × 105 PFU. These two differences clearly account for the larger fraction of reversions observed by Novella and Ebendick-Corpus (2004). Our results indicate that in VSV, the amount of back mutations relative to compensatory mutations increases with Ne, suggesting that the former are less likely than the latter, but that their beneficial selection coefficient is larger. This means that compensatory mutations can only partially restore fitness. As a second example, bacteriophage φ6 populations that had fixed single deleterious mutations recovered fitness by small steps, suggesting that several compensatory events are needed to restore the wild-type fitness. Additionally, the beneficial effect of these changes positively correlated with population size (Burch and Chao 1999). As a final example, the analysis of genetic substitutions associated with fitness recoveries in the foot-and-mouth disease virus (Escarmís et al. 1999) revealed the existence of multiple compensatory molecular pathways, although back mutations were also reported.

Evolutionary reversals and compensatory changes have been explored beyond those in RNA viruses. For example, bacteriophage φX174 populations that had fixed two to three deleterious mutations in the major capsid gene were able to back mutate most of these changes under massive population passages (Crill et al. 2000). In contrast, Bull et al. (2003) found that compensations and not reversions were responsible for the partial fitness recoveries observed in two lineages of bacteriophage T7 whose genomes were previously crippled with deleterious mutations. Similarly, Moore et al. (2000) reported that in Escherichia coli, compensatory adaptation is the main responsible for fitness recovery, although in this case the deleterious mutations studied were gene knockouts produced by transposon insertions. Compensation in E. coli and other bacteria has been demonstrated several times. For instance, the cost of antibiotic resistance can be reduced by fixing secondary mutations that are epistatic to the primary resistance change (Björkman et al. 1998). Further, the double mutants can be even fitter than each single mutant, thus avoiding posterior evolutionary reversals (Schrag et al. 1997). Therefore, current evidence indicates that, at least in the short term, fitness recovery preferentially takes place by means of compensatory adaptation, suggesting that epistasis and rugged adaptive landscapes might be the norm. Hence, the shifting-balance hypothesis (Wright 1931, 1932, 1982) seems a powerful tool for understanding both evolutionary diversification and historical contingencies.

Current evidence also indicates that the reversion rate increases with population size, suggesting that peak shift can occur by pure natural selection. Similarly, the pattern of adaptation also depends on the nature of the ancestral deleterious mutations. For example, compensation is the only plausible mechanism for restoring knocked-out functions, at least for complex genomes in which partially redundant genetic pathways can be used for the restoration (Moore et al. 2000; Rokyta et al. 2002). Taken together, these observations suggest that chances for compensatory adaptation should be related to genome complexity, a possibility that needs further experimental confirmation. Finally, the nature of epistasis between primary and secondary mutations should also be involved in determining evolutionary reversibility and, more precisely, the stability of compensation (Schrag et al. 1997; Whitlock et al. 2003).

Whenever evolutionary time is not long enough to allow all deleterious mutations present in a genome to be compensated, the rate of compensatory adaptation is expected to negatively correlate with the strength of epistasis between these ancestral mutations, as shown by Moore et al. (2000) for E. coli. This is also the case in our experiments. First, for a given initial fitness, single-nucleotide substitution mutants show a higher fitness gain than double-nucleotide substitution mutants, thus indicating that compensation is not complete. Second, as expected, there is a partial negative correlation between the sign of the epistatic interaction and the compensation rate. Although the sample size is too small to provide a conclusive statistical proof, a negative correlation should be expected for reversions as well. Furthermore, epistasis between back mutations can be directly obtained from epistasis between forward mutations. If we call W00, W10, W01, and W11 the wild type, both single-mutant, and the double-mutant fitnesses, respectively, forward epistasis is usually defined (Wolf et al. 2000) as Inline graphic, whereas backward epistasis can be defined analogously as Inline graphic. Combining these two equations it comes out that forward and backward epistasis are proportional, εb = (W00/W11)2εf. Indeed, if we defined epistasis in a slightly different way, ε = log(W11W00/W01W10), then we would simply have εb = εf. This relationship means that negative epistasis between beneficial back mutations should speed up the rate of fitness recovery. Qualitatively, the very same argument should be valid for compensatory changes.

In a broader sense, a fitness recovery experiment is representative of a general adaptation experiment, because fitness starts at an arbitrarily low value and rises up to an upper bound (the ancestral wild type in fitness recovery experiments and any adaptive peak otherwise). Therefore, in general, negative epistasis between beneficial mutations is expected to speed up the rate of adaptation. This kind of epistasis has been documented in bacteriophage φX174 (Bull et al. 2000) and VSV (Sanjuán et al. 2004b) [although decompensatory epistasis (i.e., the fitness of the double mutant was lower than that for each single mutant) was the norm].

Although a significant negative relationship between the sign of epistasis and the magnitude of fitness recovery was observed, Figure 3 reveals that actually, for Ne = 2 × 104 PFU, the maximum adaptation rate may occur at intermediate epistasis value. By contrast, a clear negative trend was apparent for Ne = 2 × 102 PFU. Regardless of this difference being biologically real or simply a consequence of noisy measurements, the pattern in Figure 3 has to be understood as a consequence not only of epistasis, but also of underlying individual mutational effects. Recall that there is a negative correlation between the selection coefficient of the deleterious mutation carried by each genotype and its rate of adaptation. Moreover, as just mentioned, the rate of adaptation negatively correlates with the sign of epistasis. Finally, both theoretical work (Wilke and Adami 2001) and simulations with digital organisms (Wilke and Adami 2001; Edlund and Adami 2004) and of RNA folding (Wilke and Adami 2001), as well as in silico models of the bacteriophage T7 infectious cycle (You and Yin 2002), suggest a trade-off between the strength of epistasis and the selective value of deleterious mutations. Therefore, a strongly positive epistasis will per se slow down the rate of adaptation, but if epistasis shifts to highly negative values, the rate of fitness gain will also be diminished, since mutations will be less deleterious. Consequently, a maximum rate of adaptation could be reached for intermediate epistasis. This tantalizing prediction needs to be further explored from an experimental approach.

Acknowledgments

We are indebted to Y. Michalakis, C. O. Wilke, and a quasi-anonymous reviewer for constructive comments and suggestions. This research was supported by grants BMC2001-3096 (Ministerio de Educación y Ciencia-FEDER), GRUPOS02/204 (Generalitat Valenciana), and 071979 (Wellcome Trust) to A.M. and by grants BMC2003-00066 (MEC-FEDER), GRUPOS03/064, and GV04B280 (Generalitat Valenciana) and the European Molecular Biology Organization Young Investigator Program to S.F.E. R.S. acknowledges a predoctoral fellowship from the Spanish MEC. J.M.C. is funded by the Wellcome Trust.

References

  1. Björkman, J., D. Hughes and D. I. Andersson, 1998. Virulence of antibiotic-resistant Salmonella typhimurium. Proc. Natl. Acad. Sci. USA 95 3949–3953. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bonhoeffer, S., C. Chappey, N. T. Parkin, J. M. Whitcomb and C. J. Petropoulos, 2004. Evidence for positive epistasis in HIV-1. Science 306 1547–1550. [DOI] [PubMed] [Google Scholar]
  3. Bull, J. J., M. R. Badgett, H. A. Wichman, J. P. Huelsenbeck, D. M. Hillis et al., 1997. Exceptional convergent evolution in a virus. Genetics 147 1497–1507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bull, J. J., M. R. Badgett and H. A. Wichman, 2000. Big-benefit mutations in a bacteriophage inhibited with heat. Mol. Biol. Evol. 17 942–950. [DOI] [PubMed] [Google Scholar]
  5. Bull, J. J., M. R. Badgett, D. Rokyta and I. J. Molineux, 2003. Experimental evolution yields hundreds of mutations in a functional viral genome. J. Mol. Evol. 57 241–248. [DOI] [PubMed] [Google Scholar]
  6. Burch, C. L., and L. Chao, 1999. Evolution by small steps and rugged landscapes in the RNA virus φ6. Genetics 151 921–927. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Burch, C. L., and L. Chao, 2004. Epistasis and its relationship to canalization in the RNA virus φ6. Genetics 167 559–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Burch, C. L., P. E. Turner and K. A. Hanley, 2003. Patterns of epistasis in RNA viruses: a review of the evidence from vaccine design. J. Evol. Biol. 16 1223–1235. [DOI] [PubMed] [Google Scholar]
  9. Crill, W. D., H. A. Wichman and J. J. Bull, 2000. Evolutionary reversals during viral adaptation to alternating hosts. Genetics 154 27–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cuevas, J. M., S. F. Elena and A. Moya, 2002. Molecular basis of adaptive convergence in experimental populations of RNA viruses. Genetics 162 533–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. de Visser, J. A. G. M., R. F. Hoekstra and H. van den Ende, 1997. Test of interaction between genetic markers that affect fitness in Aspergillus nidulans. Evolution 51 1499–1505. [DOI] [PubMed] [Google Scholar]
  12. Edlund, J. A., and C. Adami, 2004. Evolution of robustness in digital organisms. Artif. Life 10 167–179. [DOI] [PubMed] [Google Scholar]
  13. Elena, S. F., 1999. Little evidence for synergism among deleterious mutations in a nonsegmented RNA virus. J. Mol. Evol. 49 703–707. [DOI] [PubMed] [Google Scholar]
  14. Elena, S. F., and R. E. Lenski, 1997. Test of synergistic interactions among deleterious mutations in bacteria. Nature 390 395–398. [DOI] [PubMed] [Google Scholar]
  15. Elena, S. F., M. Dávila, I. S. Novella, J. J. Holland, E. Domingo et al., 1998. Evolutionary dynamics of fitness recovery from the debilitating effects of Muller's ratchet. Evolution 52 309–314. [DOI] [PubMed] [Google Scholar]
  16. Escarmís, C., M. Dávila and E. Domingo, 1999. Multiple molecular pathways for fitness recovery of an RNA virus debilitated by operation of Muller's ratchet. J. Mol. Biol. 285 495–505. [DOI] [PubMed] [Google Scholar]
  17. Gerrish, P. J., and R. E. Lenski, 1998. The fate of competing beneficial mutations in an asexual population. Genetica 102–103 127–144. [PubMed] [Google Scholar]
  18. Holland, J. J., K. Spindler, F. Horodyski, E. Grabau, S. Nichol et al., 1982. Rapid evolution of RNA genomes. Science 215 1577–1585. [DOI] [PubMed] [Google Scholar]
  19. Holland, J. J., J. C. de la Torre, D. K. Clarke and E. A. Duarte, 1991. Quantitation of relative fitness and great adaptability of clonal populations of RNA viruses. J. Virol. 65 2960–2967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Holmes, E. C., 2003. Error thresholds and the constraints to RNA virus evolution. Trends Microbiol. 11 543–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lenski, R. E., M. R. Rose, S. C. Simpson and S. C. Tadler, 1991. Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2000 generations. Am. Nat. 138 1315–1341. [Google Scholar]
  22. Levin, B. R., V. Perrot and N. Walker, 2000. Compensatory mutations, antibiotic resistance and the population genetics of adaptive evolution in bacteria. Genetics 154 985–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Lynch, M., and J. S. Conery, 2003. The origins of genome complexity. Science 302 1401–1404. [DOI] [PubMed] [Google Scholar]
  24. Miralles, R., A. Moya and S. F. Elena, 2000. Diminishing returns of population size in the rate of RNA virus adaptation. J. Virol. 74 3566–3571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Moore, F. B., D. E. Rozen and R. E. Lenski, 2000. Pervasive compensatory adaptation in Escherichia coli. Proc. R. Soc. Lond Ser. B 267 515–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Moya, A., E. C. Holmes and F. González-Candelas, 2004. The population genetics and evolutionary epidemiology of RNA viruses. Nat. Rev. Microbiol. 2 279–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Novella, I. S., 2003. Contributions of vesicular stomatitis virus to the understanding of RNA virus evolution. Curr. Opin. Microbiol. 6 399–405. [DOI] [PubMed] [Google Scholar]
  28. Novella, I. S., and B. E. Ebendick-Corpus, 2004. Molecular basis of fitness loss and fitness recovery in vesicular stomatitis virus. J. Mol. Biol. 342 1423–1430. [DOI] [PubMed] [Google Scholar]
  29. Orr, H. A., 2000. a Adaptation and the cost of complexity. Evolution 54 13–20. [DOI] [PubMed] [Google Scholar]
  30. Orr, H. A., 2000. b The rate of adaptation in asexuals. Genetics 155 961–968. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Rice, W. R., 1989. Analyzing tables of statistical tests. Evolution 43 223–225. [DOI] [PubMed] [Google Scholar]
  32. Rokyta, D., M. R. Badgett, I. J. Molineux and J. J. Bull, 2002. Experimental genomic evolution: extensive compensation for loss of DNA ligase activity in a virus. Mol. Biol. Evol. 19 230–238. [DOI] [PubMed] [Google Scholar]
  33. Rozen, D. E., J. A. G. M. de Visser and P. J. Gerrish, 2002. Fitness effects of fixed beneficial mutations in microbial populations. Curr. Biol. 12 1040–1045. [DOI] [PubMed] [Google Scholar]
  34. Sanjuán, R., A. Moya and S. F. Elena, 2004. a The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA 101 8396–8401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Sanjuán, R., A. Moya and S. F. Elena, 2004. b The contribution of epistasis to the architecture of fitness in an RNA virus. Proc. Natl. Acad. Sci. USA 101 15376–15379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Schrag, S. J., V. Perrot and B. R. Levin, 1997. Adaptation to the fitness costs of antibiotic resistance in Escherichia coli. Proc. R. Soc. Lond. Ser. B 264 1287–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Stephan, W., 1996. The rate of compensatory evolution. Genetics 144 419–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Vandepol, S. B., L. Lefrancois and J. J. Holland, 1986. Sequences of the major antibody binding epitopes of the Indiana serotype of vesicular stomatitis virus. Virology 148 312–325. [DOI] [PubMed] [Google Scholar]
  39. Whelan, S. P., L. A. Ball, J. N. Barr and G. T. W. Wertz, 1995. Efficient recovery of infectious vesicular stomatitis virus entirely from cDNA clones. Proc. Natl. Acad. Sci. USA 92 8388–8392. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Whitlock, M. C., P. C. Phillips, F. B. G. Moore and S. J. Tonsor, 1995. Multiple fitness peaks and epistasis. Ann. Rev. Ecol. Syst. 26 601–629. [Google Scholar]
  41. Whitlock, M. C., C. K. Griswold and A. D. Peters, 2003. Compensating for the meltdown: the critical effective population size of a population with deleterious and compensatory mutations. Ann. Zool. Fenn. 40 169–183. [Google Scholar]
  42. Wilke, C. O., 2004. The speed of adaptation in large asexual populations. Genetics 167 2045–2053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Wilke, C. O., and C. Adami, 2001. Interaction between directional epistasis and average mutational effects. Proc. R. Soc. Lond. Ser. B 268 1469–1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Wolf, J. B., E. D. Brodie, III and M. J. Wade, 2000 Epistasis and the Evolutionary Process. Oxford University Press, Oxford.
  45. Wright, S., 1931. Evolution in Mendelian populations. Genetics 16 97–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Wright, S., 1932. The roles of mutation, inbreeding, crossbreeding and selection in evolution. Proc. Sixth Int. Congr. Genet. 1 356–366. [Google Scholar]
  47. Wright, S., 1982. The shifting balance theory and macroevolution. Annu. Rev. Genet. 16 1–19. [DOI] [PubMed] [Google Scholar]
  48. You, L., and J. Yin, 2002. Dependence of epistasis on environment and mutation severity as revealed by in silico mutagenesis of phage T7. Genetics 160 1273–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES