An autocorrelation model with place dependence to account for the effect of harmonic number on fundamental frequency discrimination

Abstract

Fundamental frequency (f₀) difference limens (DLs) were measured as a function of f₀ for sine-and random-phase harmonic complexes, bandpass filtered with 3-dB cutoff frequencies of 2.5 and 3.5 kHz (low region) or 5 and 7 kHz (high region), and presented at an average 15 dB sensation level (approximately 48 dB SPL) per component in a wideband background noise. Fundamental frequencies ranged from 50 to 300 Hz and 100 to 600 Hz in the low and high spectral regions, respectively. In each spectral region, f₀ DLs improved dramatically with increasing f₀ as approximately the tenth harmonic appeared in the passband. Generally, f₀ DLs for complexes with similar harmonic numbers were similar in the two spectral regions. The dependence of f₀ discrimination on harmonic number presents a significant challenge to autocorrelation (AC) models of pitch, in which predictions generally depend more on spectral region than harmonic number. A modification involving a “lag window” is proposed and tested, restricting the AC representation to a limited range of lags relative to each channel's characteristic frequency. This modified unitary pitch model was able to account for the dependence of f₀ DLs on harmonic number, although this correct behavior was not based on peripheral harmonic resolvability.

I. INTRODUCTION

Psychophysical studies of the pitch of harmonic tone complexes have demonstrated a relationship between the ability to discriminate small differences in fundamental frequency (f₀), and the harmonic numbers presented, i.e., the ratios between the frequencies of the individual harmonic components and f₀ of the stimulus (Houtsma and Goldstein, 1972; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003). Harmonic complexes containing components with frequencies less than ten times the f₀, i.e., harmonic numbers below the tenth, generally yield good f₀ discrimination performance, while those containing only harmonics above the tenth yield poorer f₀ discrimination performance, at least for f₀'s in the 100 to 200 Hz range. The different f₀ discrimination results yielded by low- and high-order harmonics have traditionally been explained in terms of harmonic resolvability (Carlyon and Shackleton, 1994; Shackleton and Carlyon, 1994). The individual frequency components of a harmonic complex are spaced linearly in frequency, while auditory filter bandwidths are approximately proportional to the filters' characteristic frequencies (CFs). The frequency spacing between low-order harmonics will be wider than the bandwidths of the auditory filters they excite. As a result, one low-order harmonic will dominate the output of a single auditory filter, and will therefore be resolved by the auditory system. Conversely, multiple high-order harmonics fall within a single auditory filter and will therefore be unresolved by the auditory system. To estimate the f₀, the individual frequencies of resolved low-order resolved components, derived from either rate-place or temporal phase-locking cues, could be compared to an internally stored harmonic template (Goldstein, 1973; Wightman, 1973; Terhardt, 1974, 1979; Srulovicz and Goldstein, 1983). A separate temporal mechanism could estimate the f₀ for unresolved harmonics, by acting on the temporal envelope resulting from the interaction of several components within a single auditory filter, which has a periodicity corresponding to the f₀ (Moore, 1977; Shackleton and Carlyon, 1994; Cariani and Delgutte, 1996a).

Certain results in the literature have provided evidence that f₀ discrimination performance is related to harmonic resolvability. One such result concerns the effect of phase on f₀ discrimination. Houtsma and Smurzynski (1990) showed that both the magnitude and the phase-dependency of f₀ difference limens (DLs) varied with harmonic number in the same way. Complexes containing low-order harmonics yielded small f₀ DLs that were not affected by the relative phase of the individual harmonics, whereas complexes containing only high-order components yielded large f₀ DLs that were phase-dependent. The phase relationship between harmonics should only affect f₀ discrimination if the harmonics are unresolved and interact within a single auditory filter (Moore, 1977; Shackleton and Carlyon, 1994). Therefore, the co-occurrence of large and phase-dependent f₀ DLs suggests that f₀ discrimination performance also depends on harmonic resolvability. Another important result concerns the ability to hear out the frequency of an individual harmonic of a complex, which is a more direct estimate of harmonic resolvability. Bernstein and Oxenham (2003) found that f₀ DLs showed the same dependence on harmonic number as listeners' abilities to hear out harmonic frequencies. Below about the tenth harmonic, f₀ DLs were small and the frequency of an individual harmonic could be heard out. Above the tenth harmonic, f₀ DLs became large, and individual component frequencies were no longer discriminable from nearby pure-tone frequencies.

These studies have shown that f₀ discrimination performance has the same dependence on harmonic number as two different measures that clearly depend on harmonic resolvability. Nevertheless, this is not conclusive evidence that f₀ discrimination is directly dependent on harmonic resolvability. In fact, several results in the literature suggest that f₀ discrimination performance does not depend on harmonic resolvability per se. Bernstein and Oxenham (2003) showed that the dichotic presentation of harmonic complexes, where even and odd components were presented to opposite ears, did not increase the harmonic number of the transition between good and poor f₀ discrimination, even though twice as many peripherally resolved components were available. Similar results were shown with the dichotic presentation of two-tone complexes in normal-hearing (Houtsma and Goldstein, 1972) and hearing-impaired listeners (Arehart and Burns, 1999). These results raise the possibility that the correlation between the dependencies of f₀ DLs and harmonic resolvability on harmonic number is epiphenomenal and not causal.

As an alternative to harmonic template theories, pitch could be derived from a single temporal mechanism that acts on timing information from all frequency channels, regardless of resolvability (Licklider, 1951; Meddis and Hewitt, 1991a,b; Cariani and Delgutte, 1996a; Meddis and O'Mard, 1997; de Cheveigné, 1998). A recent implementation of these timing-based models is the Meddis and O'Mard (1997) unitary autocorrelation (AC) model of pitch perception. The Meddis and O'Mard model performs an AC of the probability of firing as a function of time in each simulated auditory nerve fiber (ANF). These individual autocorrelation functions are then summed across all frequency channels to produce a summary autocorrelation function (SACF). The AC in each channel contains peaks at a period equal to the inverse of the f₀ whether it responds to the envelope of the waveform of several interacting components or to an individual resolved frequency component at a multiple of the f₀. Therefore, the SACF will contain a large peak at the inverse of the f₀, allowing the extraction of the f₀. This mathematical formulation is analogous to calculating the all-order interval histogram based on spike times in the auditory nerve (Cariani and Delgutte, 1996a). Meddis and O'Mard (1997) have argued that this AC model can account for the effect of harmonic number on f₀ discrimination indicated by the psychophysical results of Shackleton and Carlyon (1994). They claimed that the AC responds inherently differently to resolved and unresolved harmonics, yielding the requisite f₀ discrimination behavior.

However, Carlyon (1998) disputed this claim, suggesting that any deterioration in f₀ discrimination seen in the AC model is a function of the roll-off of phase locking with absolute frequency, as was seen in the physiological recordings of Cariani and Delgutte (1996a), and not a function of harmonic number as seen in psychophysical studies (Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003). According to Carlyon (1998), the most important shortcoming of the Meddis and O'Mard (1997) AC model is that it fails to predict the effect of harmonic number on f₀ discrimination seen in the psychophysics: two harmonic complexes with different f₀'s, bandpass filtered in the same spectral region, yield very different f₀ discrimination performance when one complex contains low-order harmonics and the other does not (Shackleton and Carlyon, 1994).

The present study addressed this controversy. The Meddis and O'Mard (1997) unitary AC model of pitch perception was tested for its ability to account for the effects of harmonic number on f₀ discrimination. A psychophysical experiment measuring f₀ DLs as a function of f₀ for fixed spectral regions was performed in order to provide more data points than the six (two f₀'s times three spectral regions) tested by Shackleton and Carlyon (1994). The same stimuli were then passed through the Meddis and O'Mard (1997) AC model to determine its ability to predict the experimental results. Overall, the AC model failed to predict the experimental results. Whereas the experimental results (described in Sec. II) showed decreasing f₀ DLs with increasing f₀, the model predictions (described in Sect. III) showed the opposite trend. A number of possible modifications to the model were then tested. Of these, the most successful was one similar to that suggested by Moore (1982), in which place dependency is introduced into the model, such that each frequency channel responded only to a limited range of periodicities related to the channel's CF.

II. EXPERIMENT: F₀ DLs WITH A FIXED SPECTRAL ENVELOPE

A. Rationale

This experiment was intended to provide a larger data set than that provided by Shackleton and Carlyon (1994) with which to test the ability of the AC model to account for the effects of harmonic number on f₀ discrimination. This experiment also addressed two issues surrounding the mechanisms underlying pitch processing: the roles of phase and temporal fine-structure in f₀ discrimination.

1. Phase

Previous results have shown that the phase relationship between harmonics affects f₀ DLs (Houtsma and Smurzynski, 1990): harmonic stimuli with “peakier” wave forms, such as sine- or cosine-phase complexes, yield smaller f₀ DLs than those with “flatter” waveforms, such as random-or negative Schroeder-phase (Schroeder, 1970) complexes. However, this phase effect was not apparent in the results of Bernstein and Oxenham (2003). There are two possible reasons for this discrepancy. First, different groups of listeners were tested for the two phase relationships (random and sine phase) in the Bernstein and Oxenham (2003) study, yielding an analysis of variance (ANOVA) with less statistical power than would be expected if the same subjects had been tested for both phase relationships. Second, as discussed by Bernstein and Oxenham (2003), listeners in their study may have performed the f₀ discrimination task without extracting the f₀, by listening for a change in the frequency of the lowest harmonic present. Although the lowest harmonic number presented was randomized from interval to interval, a large enough change in f₀ would overcome this small amount of randomization. Data analysis showed that for complexes containing only high-order harmonics, f₀ DLs were large enough that subjects may have been using the lowest harmonic cue, rather than f₀ cues, to perform the task, especially for the random-phase stimuli. If subjects were not using f₀ to perform the task, then the effects of phase on f₀ extraction would not be apparent in the results.

To address the possibility that the lack of a significant phase effect resulted from different groups of listeners participating in two phase conditions, all subjects in the present study participated in both the sine-phase and random-phase conditions. To address the possibility that listeners had used the frequency of the lowest harmonic rather than f₀ cues to perform the f₀ discrimination task, the experiment described in the following attempted to eliminate lowest harmonic cues by using harmonic stimuli with a fixed spectral envelope, and measuring f₀ DLs as a function of f₀. Although the frequency of the lowest harmonic increases with increasing f₀, a lower-numbered harmonic will also begin to appear at the low end of the spectrum. Thus, the cochlear excitation pattern will remain roughly constant, at least for those complexes containing only unresolved harmonics where the lowest harmonic cue may have played a role. As f₀ increases, the lowest harmonic number present in the passband decreases, allowing a direct comparison with the f₀ DL measurements of Bernstein and Oxenham (2003). Results indicating larger f₀ DLs in this experiment would indicate that subjects may have been using the lowest harmonic cue in the previous study.

2. Temporal fine structure

The effects of phase on f₀ discrimination have provided evidence that the pitch of complexes containing unresolved harmonics is derived from the repetition rate of peaks in the temporal envelope. Negative Schroeder-phase complexes, which have flatter envelopes than sine-phase complexes, yield larger f₀ DLs (Houtsma and Smurzynski, 1990). When unresolved harmonics are presented in alternating sine and cosine phase, yielding temporal envelopes with two peaks per period, the resulting pitch percept is judged to be twice the f₀ (Shackleton and Carlyon, 1994). Still, this does not rule out that periodicity information could be extracted from the fine structure of unresolved harmonic complexes in some conditions. Hall et al. (2003) demonstrated that phase manipulations affected amplitude-modulation (AM) rate discrimination performance for unresolved components in a high spectral region, but had little effect in a relatively low spectral region. Their interpretation was that fine-structure cues, which are unaffected by phase manipulations, are used in the low-frequency region, while envelope cues, which are affected by phase manipulations, are used in the high-frequency region where there is little phase-locking to the fine structure. Similarly, Bernstein and Oxenham (2003) found that for unresolved complexes containing the same harmonic numbers, f₀ DLs were larger for a 200- than a 100-Hz f₀, which may reflect reduced fine-structure information in the higher spectral region occupied by the 200-Hz complexes. Furthermore, deterioration in phase locking to the frequencies of individual partials could affect f₀ DLs for complexes containing resolved harmonics.

This experiment tested whether the presence of phase-locking to the fine-structure in the low region aided performance, in a task more closely related to pitch processing than the AM rate discrimination task of Hall et al. (2003). Fundamental frequency DLs were measured in two conditions: a “low spectrum” condition (2.5–3.5 kHz), in which phase-locking to fine structure is thought to be more available, and a “high spectrum” condition (5–7 kHz), in which phase-locking to the fine-structure information is greatly reduced, at least in mammalian species that have been tested so far (Rose et al., 1968; Johnson, 1980; Palmer and Russell, 1986; Weiss and Rose, 1988). Testing f₀ DLs in two different frequency regions also provided a control to verify that f₀ discrimination performance depends primarily on harmonic number, and not f₀ per se.

B. Methods

Five subjects participated in the experiment (ages 18–21, three female). All subjects had normal hearing (15 dB HL or less re ANSI-1969 at octave frequencies between 250 Hz and 8 kHz) and were self-described amateur musicians with at least 5 years of experience singing or playing a musical instrument.

All stimuli were presented in modified uniform masking noise (UMN_m ; Bernstein and Oxenham, 2003). This noise is similar to uniform masking noise (UMN; Schmidt and Zwicker, 1991), in that it is intended to yield pure-tone masked thresholds at a constant sound pressure level (SPL) across frequency, but the spectrum is somewhat different; UMN_m has a long-term spectrum level that is flat (15 dB/Hz SPL in our study) for frequencies below 600 Hz, and rolls off at 2 dB/octave above 600 Hz. The noise was low-pass filtered with a cutoff at 16 kHz. Thresholds for pure tones at 200, 500, 1500, and 4000 Hz in UMN_m in the left ear were estimated via a three-alternative forced-choice, 2-down, 1-up adaptive algorithm (Levitt, 1971). For each subject, pure tone thresholds in UMN_m fell within a 5 dB range at all four frequencies tested, such that harmonic components presented at equal SPL had nearly equal sensation level (SL). As an approximation, we defined 0 dB SL for each subject as the highest of the thresholds across the four frequencies tested, which ranged from 31 to 33.3 dB SPL across all subjects.

The stimuli were generated digitally and played out via a soundcard (LynxStudio LynxOne) with 24-bit resolution and a sampling frequency of 32 kHz. The stimuli were then passed through a programmable attenuator (TDT PA4) and headphone buffer (TDT HB6) before being presented to the subject via Sennheiser HD 580 headphones. Subjects were seated in a double-walled sound-attenuating chamber.

Fundamental frequency DLs as a function of a complex's f₀ were estimated via a three-alternative forced-choice, 2-down, 1-up adaptive algorithm tracking the 70.7% correct point (Levitt, 1971). The f₀ difference (Δf₀) was initially set to 10% of the f₀. The starting step size was 2% of the f₀, decreasing to 0.5% after the first two reversals, and then to 0.2% after the next two reversals. The f₀ DL was estimated as the average of the f₀'s at the remaining six reversal points. If the standard deviation of the last six reversal points was greater than 0.8%, the data were rejected and the run repeated. In each trial, two of the three intervals contained harmonic complexes with a base f₀(f_0,base), while the other interval contained a complex with a higher f₀(f_0,base+Δf₀). Subjects were informed that two of the intervals had the same pitch, while the third interval had a higher pitch, and were asked to identify the interval with the higher pitch. DLs were estimated for six different f₀'s in each spectral condition (low: 50, 75, 100, 150, 200, and 300 Hz; high: 100, 150, 200, 300, 400, and 600 Hz). The f₀'s tested in the high condition were double those tested in the low condition such that the harmonic numbers presented were the same in each spectral region. Measurements were repeated four times per subject for each combination of frequency region, phase, and f₀, except for one subject who completed only two runs for the random-phase conditions.

Stimuli were resynthesized for each trial of the experiment. First, diotic harmonic complexes containing equal-amplitude harmonics of the f₀ up to 10 kHz were synthesized. These harmonic complexes were then filtered with both fourth-order low-pass and fourth-order high-pass digital Butterworth filters. The 3-dB filter cutoff frequencies for the high- and low-pass filters, respectively, were 2.5 and 3.5 kHz in the low condition, and 5 and 7 kHz in the high condition. The filter weights for the high-pass filters were scaled such that the double filtering operation gave a 0-dB maximum amplitude response. The duration of the stimulus in each trial of the experiment was 500 ms, including 30-ms Hanning window onset and offset ramps.

Following the filtering operations, the stimulus in the interval with the higher f₀ was scaled in amplitude to have equal rms power to that of the two other intervals. The complexes were presented at an average level per component (before filtering) of 15 dB SL per component (adjusted individually based on tone-in-noise detection thresholds). In order to prevent the use of loudness cues, amplitude randomization was applied by roving the amplitude of the complex in each interval by ±5 dB, uniformly distributed. On the average, the following −15 dB (re max) frequency bands contained harmonics above threshold: 1.56–5.35 kHz and 3.28–9.37 kHz in the low and high spectral conditions, respectively.

The resulting signals were then added to the UMN_mnoise. Because of the rms normalization step, the average presentation level per harmonic was somewhat higher for the interval with (f_0,base+f₀) then for the intervals with f_0,base. However, this difference was quite small relative to the 10 dB random amplitude variation, reaching only about 0.6 dB for the largest measured f₀ DL of 15%. Complexes were presented in either sine or random phase. For the random-phase stimuli, the phase of each harmonic was newly chosen from a uniform random distribution ranging from −π to +π in each interval of the experiment.

C. Results and discussion

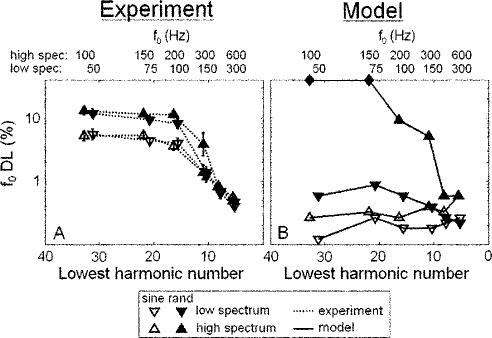
For each frequency region condition and f₀, the lowest detectable harmonic number (N) was estimated by dividing the average lowest detectable frequency in the passband (1.56 and 3.28 kHz in the low and high conditions, respectively) by the f₀. Figure 1(a) shows the estimated f₀ DLs as a function of N. The corresponding f₀'s in the low- and high-spectrum conditions are shown along the top axis. Figure 1(b) shows the f₀ DLs predicted by the autocorrelation model, which will be discussed in Sec. III. The main findings of this experiment are (i) f₀ DLs increase with increasing N (decreasing f₀), independent of spectral region, (ii) the relative phase relationship between partials affected f₀ DLs for high, but not low N, and (iii) there was a small but significant effect of spectral region on f₀ DLs. Each of these effects will be discussed in turn.

FIG. 1.

Fundamental frequency DLs(a) measured psychophysically and (b) predicted by the optimal detector autocorrelation model, as a function of the lowest harmonic number present within the passband. Stimulus f₀'s corresponding to the lowest harmonic numbers are listed at the top. Optimal model predictions in (b) are calculated as the minimum value of δ such that d′ exceeds the value of d₀′=190 depicted in Fig. 3. Closed diamonds plotted along the top horizontal axis indicate that d₀′ was not reached at the maximum tested value of δ=0.3.

A repeated-measures analysis of variance (RMANOVA) with three within-subject factors (spectral region, phase, and N) was conducted in order to determine the influence of each factor on f₀ discrimination. Values of p<0.05 were taken to be statistically significant. The RMANOVA was performed with logarithmically transformed data in an attempt to satisfy the equal-variance assumption, and the Greenhouse–Geisser (Geisser and Greeenhouse, 1958) correction for sphericity was included wherever necessary, with corrected values for degrees of freedom reported. However, neither manipulation affected the statistical significance of any main effect or interaction. Data from the subject who completed only two runs in the random-phase conditions were excluded from the RMANOVA. While the six f₀'s tested in the high-spectrum conditions were exactly double those tested in the low-spectrum condition, the low edge frequency in the high-spectrum conditions was not exactly double that of the low-spectrum conditions. As a result, N's differed by approximately 5% in the two spectral conditions. Nevertheless, for the purpose of performing the RMANOVA, we assumed that the N's were identical. For example a 100 Hz low-spectrum stimulus was assumed to have the same N as a 200 Hz high-spectrum stimulus. This small 5% shift in the value of N was unlikely to affect the RMANOVA results. The results of this analysis are shown in Table I.

TABLE I.

Results of the RMANOVA for the f₀ DL experiment. Asterisks indicate statistical significance (p<0.05). Degrees of freedom are adjusted based on the Geisser-Greenhouse correction.

	Effect	F	df	p
Main	N	161	(2.12, 6.37)	<0.0005*
effects	Phase	4180	(1, 3)	<0.0005*
	Spectral region	12.9	(1, 3)	0.037*
Two-way	N* spectral region	0.827	(1.45, 4.35)	0.827
interactions	N*phase	25.1	(2.37, 7.11)	<0.0005*
	Phase* spectral region	0.144	(1, 3)	0.318
Three-way	N* phase* spectral region	0.226	(1.87, 5.59)	0.15
interaction

There is clear transition from large to small f₀ DLs as f₀ increases (N decreases) in both the low- and high-spectrum conditions. The dependence of f₀ DLs on N is supported by a significant main effect of N. The transition to small f₀ DLs occurs as the approximately tenth harmonic [the highest resolved harmonic as estimated by Bernstein and Oxenham (2003)] begins to appear at the low end of the passband, consistent with previous results (Houtsma and Smurzynski, 1990). When plotted as a function of N, the low- and high-spectrum data overlap, indicating that f₀ DLs in these conditions depend mainly on harmonic number and not on f₀ or spectral region. This conclusion is supported by the fact that there was no significant interaction between spectral region and N.

Phase effects are apparent in these results, but only for those complexes with N>10, where random-phase f₀ DLs are larger than sine-phase f₀ DLs, consistent with previous findings (Houtsma and Smurzynski, 1990; Bernstein and Oxenham, 2003). The significant main effect of phase and a significant interaction between phase and N is consistent with the observation that phase effects are only observed for stimuli with high N. For low f₀'s (N>10), the random-phase relationship of the harmonics gives f₀ DLs of 11%–13%, which are much poorer than had been previously measured for random-phase complexes containing only high-order harmonics (Bernstein and Oxenham, 2003). This result indicates that the previous estimates of f₀ DLs in the 6%–8% range for high-order, random-phase complexes likely reflected the influence of the “lowest harmonic present” cue (see Bernstein and Oxenham, 2003). The relatively small f₀ DLs (∼4%–6%) measured for the sine-phase, high-order complexes were approximately the same as those measured in the Bernstein and Oxenham (2003) study, suggesting that the lowest harmonic cue did not play a role in the sine-phase conditions. With the elimination of the confounding “lowest harmonic” cue that affected random-phase but not sine-phase f₀ DLs, the effects of phase on f₀ discrimination are found to be significant, in line with Houtsma and Smurzynski (1990). The large f₀ DLs would make music perception based on unresolved complexes difficult, since musical semitones are only 6% apart in frequency.

While there was a significant main effect of spectral region, f₀ DLs for the same N did not generally appear to be different between the low- and high-spectrum conditions, with one exception: performance was notably worse for the high-spectrum stimulus in the random-phase, N≈10 case. This difference was only observed for two of the five subjects, one of whom showed very large variability across runs, and does not constitute a general trend in the data. Although there was neither a significant two-way interaction between spectral region and either N or phase, nor a significant three-way interaction, the main effect of spectral region disappeared when the N≈10 data were excluded from the RMANOVA analysis [F(1,3)=4.8, p=0.12]. This implies that phase locking to the stimulus fine structure did not play a significant role overall in f₀ discrimination for the stimuli used in this experiment.

The lack of a main effect of spectral region or a significant interaction between N and spectral region conflicts with the results of Hoekstra (1979), who also measured f₀ DLs as a function of f₀ for bandpass-filtered harmonic complexes in various spectral regions. Comparing similar spectral regions to those used in the current experiment, Hoekstra found that f₀ DLs were larger at higher spectral regions for complexes with small N, but not large N, suggesting that phase-locking to the stimulus fine-structure is more important for low-order, resolved harmonics. The discrepancy between the results of Hoekstra (1979) and the current study may be related to the bandwidths of the spectral regions used in the two studies. Hoekstra's 1/3-octave filters yielded only one audible partial for those stimuli with a low enough N to yield small f₀ DLs, while the approximately one-octave filters used in the current study produced multiple audible partials for all stimuli. The different results obtained in the two studies suggest that phase-locking to the stimulus fine structure may be more important for pure-tone frequency discrimination than for complex-tone f₀ discrimination. Alternatively, it may be that temporal fine-structure information is important for complex-tone f₀ discrimination, but that a large effect of spectral region was not observed in the present study because of the frequency ranges chosen for the two spectral conditions. The 3-dB bandpass-filter cutoff frequencies were chosen such that phase-locking should have been greatly reduced in the high-spectrum condition relative to the low-spectrum condition. However, the filter slopes yielded an audible frequency range in the high-spectrum condition that extended down to 3.28 kHz, where phase-locking to the stimulus fine structure might still have been available.

III. SIMULATIONS WITH THE AUTOCORRELATION MODEL

A. Introduction

Meddis and O'Mard (1997) showed that the autocorrelation model successfully accounted for the results of Houtsma and Smurzynski (1990): for stimuli with a fixed f₀, f₀ DLs increased as the order of the harmonics increased. Carlyon (1998) suggested that the model's successful prediction was due not to its dependence on harmonic number and harmonic resolvability, but to the reduction of phase-locking with increasing absolute frequency. Because Houtsma and Smurzynski (1990) tested only one stimulus f₀ of 200 Hz, it was not clear from their results whether the increase in f₀ DLs was due to effects of harmonic number and resolvability, or to effects of spectral region. Consistent with earlier studies (Shackleton and Carlyon, 1994; Kaernbach and Bering, 2001; Bernstein and Oxenham, 2003), the present experiment, which measured f₀ DLs in two different spectral regions, demonstrated that f₀ discrimination performance depended mainly on harmonic number, and not spectral region or f₀. These data provide a basis for testing the Meddis and O'Mard (1997) autocorrelation model to determine its ability to predict the dependence of f₀ discrimination on harmonic number.

B. Model description

The stimuli from our psychophysical experiment were passed through the Meddis and O'Mard (1997) autocorrelation model to determine its ability to account for the psychophysical f₀ discrimination results. This model consists of an outer/middle ear bandpass filter, a basilar membrane gamma-tone filterbank (Patterson et al., 1992), inner hair cell half-wave rectification and low-pass filtering, and the translation of the inner hair cell membrane potential into a probability of firing versus time in the auditory nerve fiber. The model used to generate ANF firing information in these simulations was identical to that used by Meddis and O'Mard (1997), except for the following two changes. First, 40 channels, consisting of only those CFs falling within the stimulus passband (1.5–5 kHz and 3–10 kHz for the low- and high-spectrum conditions, respectively) were used, with CFs spaced according to the Greenwood (1961) human scale. CFs falling outside these ranges, where the harmonic complex stimuli would not be detectable in the psychophysical experiment, were not included. Second, the inner hair-cell and auditory nerve models were replaced by a newer model (Sumner et al., 2002) that allowed for stochastic spike generation. All ANFs were modeled as high spontaneous-rate fibers. The bandwidths of the model's gammatone filters were derived from the equivalent rectangular bandwidth (ERB_N) formula described by Glasberg and Moore (1990), just as in the Meddis and O'Mard study. Because the only physiologically derived cochlear mechanical filtering data available for humans (Shera et al., 2002) are only appropriate for very low-level stimuli, the psychophysical bandwidths derived by Glasberg and Moore (1990) form a reasonable substitute.

Two different methods for converting from ANF firing to a psychophysical f₀ DL estimate were tested. The first method was that used by Meddis and O'Mard (1997), whereby discriminability was estimated by the Euclidean distance (D) between autocorrelation functions (ACFs) calculated from the ANF probabilities of firing as a function of time, p(t). The second method was an optimal detector model based on stochastic firing of the ANFs. These methods are described in the following two sections.

1. Euclidean distance measure

Meddis and O'Mard's (1997) procedure for estimating discrimination thresholds was also used here. The main difference was that whereas Meddis and O'Mard based all of their computations on p(t,k), the probability of firing (p) as a function of time (t) for each ANF channel index (k), the current simulations were based on stochastic ANF responses. This allowed for the possible influence of ANF refractoriness on the results. The inner hair cell/auditory nerve complex was set to “spike” mode (Sumner et al., 2002), yielding stochastic boolean responses s(t,k), whereby a one or a zero represented the presence or absence of a spike at each point in time. Each stimulus was resynthesized and presented to the model n=15 times (although n was increased to 60 and 100 for the simulations to be described in Secs. IV B and IV E, respectively) and p(t,k) was estimated by averaging across the n outputs s(t,k) obtained for each k.

The autocorrelation function (ACF) of p(t,k) was then calculated in each fiber according to the formulation of Meddis and O'Mard:

$$\begin{array}{cc}& h(t_0,l,k)=\frac{1}{\tau }\sum _{i=1}^{\infty }p(t_0-T,k)p(t_0-T-l,k)e^{-T∕\tau }dt\end{array}$$ (1)

where h(t,l,k) is the channel's ACF, t₀ is the point in time at which the autocorrelation was measured, l is the autocorrelation lag, τ is the autocorrelation time constant, dt is the sampling interval, 25 μs, and T=idt. Because of the exponential window used in the ACF formulation, the autocorrelation will tend to fluctuate with time. In these simulations, t₀was chosen to be an integer number of periods of each stimulus, just before the beginning of the offset ramp. This is in contrast to the Meddis and O'Mard study, where a “snapshot” of the SACF was taken at the end of the stimulus. The only other difference in the autocorrelation calculation in this study as compared to Meddis and O'Mard (1997) was that here τ was selected to be 25 ms, whereas Meddis and O'Mard used a shorter τ of 10 ms. The τ used in the current study, being longer than the period corresponding to the minimum f₀ tested, 50 Hz, tended to smooth out the SACF variation across time. A summary autocorrelation function, SACF(f₀,l), was computed by summing the individual channel ACFs. The range of lags was fixed throughout the modeling from zero to a maximum lag (l_max) of 25 ms. This value of l_max corresponds to a minimum frequency of 40 Hz, which is below the minimum f₀ of 50 Hz used in our psychophysical experiment.

For each combination of f₀, spectral region, and phase, ACFs and SACFs were calculated for stimuli with f₀ increased by small perturbations, Δf₀, with 30 values of δ=Δf₀/f₀ logarithmically spaced across the range 0.001≤δ ≤0.3. Following Meddis and O'Mard (1997), the squared Euclidean distance between the SACFs of the unperturbed stimulus (δ=0) and each of the perturbed stimuli was then calculated:

$$\begin{array}{cc}& D^2(f_0,\delta )=\sum _{i=0}^{l_{\max }∕dt}{[\mathrm{SACF}((1+\delta )f_0,idt)-\mathrm{SACF}(f_0,idt)]}^2.\end{array}$$ (2)

The procedure to convert from the D² statistic to an estimate of the f₀ DL was to choose a criterion based on a threshold $D^2\left(D_0^2\right)$,which served as a free parameter in fitting the model predictions to the psychophysical data. The lowest value of δ producing a D² that exceeded $D_0^2$ was taken to be the estimated f₀ DL. (In practice, to reduce erroneous results due to noise in the data, D² was judged to exceed $D_0^2$ only if it did so for two consecutive values of δ.) Because $D_0^2$ was allowed to vary as a free parameter, the D² measure was unable to predict an absolute f₀ DL that could be directly compared with experimental data. Rather, this statistic yielded a measure of the relative discriminability between stimulus pairs, providing a way to compare trends in the SACF and trends in measured f₀ DLs across different conditions.

2. Optimal detector model

The D² measure is a potentially flawed decision variable. Because D² is simply the distance between two SACF functions, it is likely to be sensitive to changes in stimulus dimensions that are unrelated to the stimulus pitch. For example, whereas psychophysical f₀ discrimination performance is fairly robust to changes in stimulus bandwidth, Pressnitzer et al. showed that such changes affect the SACF amplitude, and therefore model predictions based on the D² statistic. Similarly, Carlyon (1998) demonstrated that the D² statistic is susceptible to changes in stimulus amplitude, such as those introduced by level roving in the current study. Although calculating the D² between SACF functions averaged across many stimulus trials would reduce the influence of level roving on the model predictions, such a strategy would be likely to fail on a trial-by-trial basis due to its sensitivity to SACF amplitude fluctuations. An optimal detector model, with the ability to incorporate the variance associated with level roving into the decision statistic, was tested as a possible alternative.

The operation of the optimal detector was based on signal detection theory (Green and Swets, 1966). Up to four different sources of noise were present in the model: (1) the stochastic firing of the ANF; (2) stimulus level roving; (3) the background noise; and (4) phase randomization. Only the first two noise sources were always present in the simulations. For the initial simulations, background noise was not used, while phase randomization was only present in the random-phase conditions. These noise sources produced SACF variation at each lag, allowing the performance of an optimal detector to be computed based on the statistical properties of the SACF variation.

The decision variable was assumed to be a vector $\Delta \overline{\mathrm{SACF}}(f_{0A},f_{0B})$ containing the SACF differences (ΔSACF) yielded at each lag by two stimuli with different f₀'s (f_0A and f_0B):

$$\begin{array}{cc}& \Delta \mathrm{SACF}(f_{0A},f_{0B},l)=\mathrm{SACF}(f_{0A},l)-\mathrm{SACF}(f_{0B},l).\end{array}$$ (3)

In this model, the optimal detection strategy—the weighting of the information obtained at different lags—will vary depending on the f₀ and Δf₀. As in the D² model, each stimulus was presented n=15 times for the each combination of f₀, frequency region, phase, and δ. Each s(t,k) was substituted for p(t,k) in Eq. (1) to yield stochastic individual channel ACFs, which were then summed across channels to yield n stochastic SACFs.

The performance (d′) achieved by an optimal detector for discriminating stimuli on the basis of f₀ was estimated to be

$${\left(d^{\prime }\right)}^2=\Delta {\overline{m}}^T{G}^{-1}\Delta \overline{m},$$ (4)

where $\Delta \overline{m}$ was the mean of the $\Delta \overline{\mathrm{SACF}}\mathrm{s}$ across the n stimulus trials, and G is the covariance matrix, calculated from the n $\Delta \overline{\mathrm{SACF}}\mathrm{s}$ (Van Tress, 2001). In practice, both the mean and variance of ΔSACF were nearly zero for a subset of lags, such that G was often nearly singular and not easily invertible. To resolve this problem, a very small amount of independent noise (variance=10⁻⁸) was added to each lag by augmenting the variances along the diagonal of G.

Because the d′ estimates obtained from Eq. (4) will vary depending on the number of nerve fibers and the number of lag points used in the simulation, no attempt was made to predict the experimental d′ value of 1.26 (2-up, 1-down, 3AFC, Hacker and Ratcliff, 1979) using the model simulations. The extremely large d′ estimates reported in the following are a result of the large number of individual observations of f₀-related activity available across the lag range, and are not reliable estimates of absolute performance. Instead, a similar procedure to the D² method was used, whereby a d′ criterion ($\left(d_0^{\prime }\right)$) was chosen in order to predict an f₀ discrimination threshold, allowing relative performance comparisons across conditions.

C. Stimuli

The stimuli were produced in the same manner as those in our experiment, including level roving and phase randomization applied independently to each of the n stimulus presentations. There were three main differences between the stimuli used in the experiment and those used in the modeling simulations. First, the stimuli used in the modeling were reduced in duration to 200 ms in order to reduce computational load. The shorter duration should have no effect on the model predictions, since the autocorrelations were calculated only near the end of each stimulus, with a relatively short τ=25 ms and an l_max of 25 ms. Furthermore, decreasing the stimulus duration has little effect on f₀ DLs until durations fall below about 100 ms (Plack and Carlyon, 1995). Thus, it can be assumed that these 200-ms stimuli would yield similar results to the 500 ms stimuli used in our psychophysical experiment.

Second, no background noise was used in the initial model simulations. The main reasons for using a background noise in the psychophysical experiment (to mask distortion products and to promote the fusion of individual components into a single object) are not issues for the autocorrelation model with linear gammatone filters. However, because the presence of a background noise may still affect the ANF response to the complex tone stimuli, the possible influence of a background noise on the simulation results is examined in Sec. II E.

Third, the method of setting the signal levels differed from the psychophysical experiment. Because the model contained only high spontaneous-rate ANFs, the dynamic range available to human listeners was not available to the model. Stimulus levels similar to those actually used in the experiment tended to saturate the ANF outputs. To determine a reasonable operating level for the modeling simulations, it was assumed that for a given stimulus level, an optimal detector would choose to use those ANFs that yield the best possible performance, and discard those ANFs that yield little information, as in the “selective listening hypothesis” (Delgutte, 1982, 1987; Lai et al., 1994). In these simulations, rather than adjusting the model ANF spontaneous rates and thresholds to find those that yielded the optimal performance for a given stimulus level, the ANF parameters were kept fixed and the stimulus level was adjusted. Pilot tests indicated that the best overall performance (in terms of both D² and d′) occurred when the firing rate (r) of an ANF with CF at the center of the stimulus passband was at approximately the 90% point of the operating range, that is, when r=r_sp+0.90(r_max−r_sp), where r_sp and r_max are the spontaneous and maximum ANF firing rates, respectively. Therefore, in the simulations all stimulus levels were set such that a pure tone at the level and frequency of a harmonic component at the center of the stimulus passband yielded an r at 90% of the operating range of an ANF with CF at the tone frequency. Although the absolute model performance was best at this stimulus level, the relative performance of the model across the various conditions was generally unaffected by the stimulus level, provided the stimuli were above rate threshold.

D. Model results

The two main findings of the simulations are that (1) the D² and d′ formulations of the model yield virtually identical predictions, and (2) neither formulation was successful in accounting for the psychophysical results, especially for the sine-phase conditions.

1. Comparison of the D² and d′ measures

The Euclidean distance and optimal detector procedures produced virtually identical results. Because both procedures yield the same results, only the optimal detector model will be shown and discussed for the remainder of the paper. That these two procedures yielded similar results is perhaps not surprising, since both measures involve taking the sum of the squares of the differences between SACF functions. The main difference between the two methods is that the d′ method weights these differences based on the variances at different lags across stimulus trials, whereas the D² statistic weights each lag equally. The similar results seen for the two methods suggests that the weighting was of little consequence—lags falling between SACF peaks added little to the sum of squared differences between SACFs, regardless of the weighting strategy. The finding implies that the D² measure was in fact sensitive to f₀-related activity in the SACFs, and that weighting the lags equally yields results similar to those yielded by an optimal strategy.

It is important to note that in these simulations, the Euclidean distance procedure was not challenged with level roving, which was essentially eliminated by averaging SACFs across stimulus trials. On a trial-by-trial basis, the simple Euclidean distance measure might be more sensitive to the level roving than to the changes in f₀, prohibiting it from detecting changes in f₀. In contrast, the optimal detector formulation took into account the variance due to level roving. The similarity of the two sets of results suggests that the optimal detector model was able to ignore level roving effects in discriminating f₀.

2. Optimal detector predictions

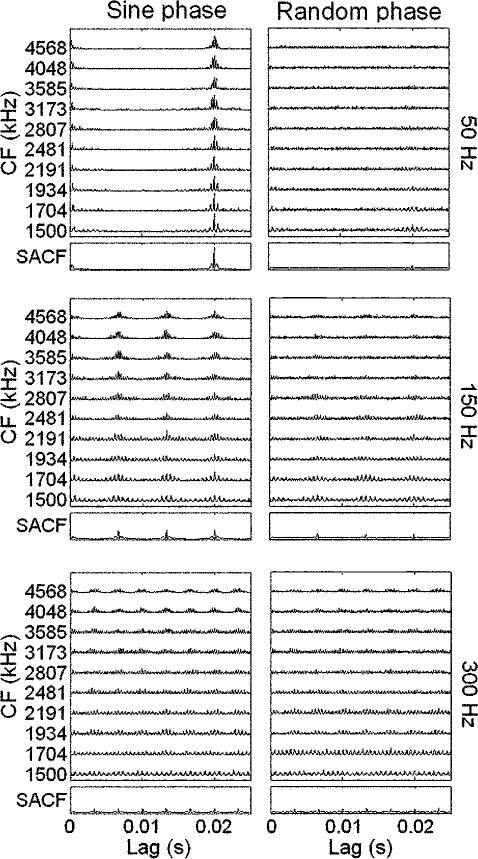
Figure 2 shows SACFs and individual channel ACFs for low-spectrum complexes with three different f₀'s. Sine-phase stimulus responses are shown in the left column. For the lowest f₀ of 50 Hz, harmonics are all unresolved and interact within each model filter, such that the ACFs in each channel are phase-locked to the stimulus envelope. For the middle f₀, 150 Hz, harmonics begin to be resolved for the lowest CFs, and ACFs in these channels become phased-locked to individual sinusoids rather than stimulus envelopes. At 300 Hz, harmonic resolvability extends further, up to about 2.4 kHz. Amplitudes of SACF peaks are largest for the 50 Hz case where the f₀ appears to be coded mainly by the envelope, and diminish with increasing f₀, as resolved harmonics appear. A similar effect was observed in the high-spectrum conditions, where the SACF peaks were even smaller (not shown).

FIG. 2.

Sample ACFs (top ten plots in each panel) for a subset of model ANFs with CFs as indicated along the vertical axis, for low-spectrum stimuli with three selected f₀'s under both phase conditions. The corresponding SACFs are shown in the bottom plot of each panel.

The observed decrease in SACF peak amplitude with increasing f₀ for sine-phase stimuli is reflected in the model's f₀ DL predictions. Figure 3 shows the model's predicted d′ as a function of δ, the fractional change in f₀. Figure 1(b) shows the minimum values of δ such that $d^{\prime }>d_0^{\prime }$, where $d_0^{\prime }=190$ was arbitrarily selected (horizontal dashed line in Fig. 3) to yield predicted f₀ DLs in the general range of the psychophysical results. For the sine-phase stimuli (open symbols), predicted f₀ DLs generally increase with increasing f₀, opposite to the trend seen in the psychophysical data. This is the case in both spectral regions. Note that this trend would occur independently of the chosen $d_0^{\prime }$, since the d′(δ) functions (Fig. 3) rarely cross. These results indicate that phase-locking to the envelope of unresolved harmonics was stronger than phase-locking to individual resolved harmonics, yielding smaller predicted f₀ DLs for lower stimulus f₀'s. This result may depend on the relatively high stimulus spectral regions tested. Phase-locking to resolved components would most likely be stronger for stimuli with energy below 1.5 kHz, the frequency at which phase locking begins to roll off in the guinea pig-based model used here.

FIG. 3.

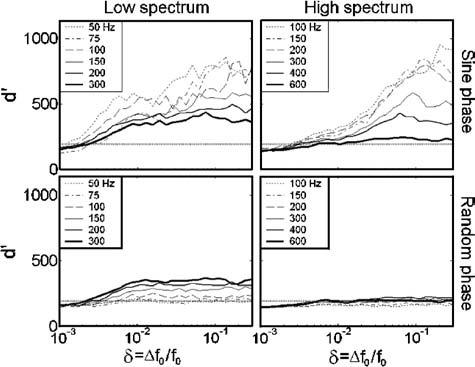
Plots of the estimated d′ as a function of δ, the fractional change in f₀, as predicted by an optimal detector model. For sine-phase stimuli, slopes decrease with increasing f₀, while for random-phase stimuli, slopes increase with increasing f₀. Horizontal dotted lines indicate the arbitrary $d_0^{\prime }$ used to predict f₀ discrimination thresholds plotted in Fig. 1(b). The plots rarely cross, indicating that the predicted f₀ DL vs f₀ trend is independent of the chosen value of $d_0^{\prime }$.

For random-phase stimuli [closed symbols in Fig. 1(b)], f₀ DLs predicted by the model tended to decrease with increasing f₀, consistent with the general trend seen in the psychophysical results. Diamonds indicate that d′ failed to exceed $d_0^{\prime }$ for the largest tested value of δ=0.3. The heights of the SACF peaks did not appear to change substantially with f₀ (Fig. 2, right column), suggesting that the decrease in f₀ DLs is most likely a result of the additional SACF peaks present for stimuli with larger f₀'s. This correct behavior for the random-phase conditions is a result of a very large phase effect that is present mainly for low f₀'s, where the predicted f₀ DLs for the same f₀ are drastically different between the two phase conditions. The presence of such a phase effect in the model (albeit much larger than that seen in the data) is consistent with previous studies that have found phase effects in the AC for harmonic complexes containing high-order harmonics, but not for those containing low-order harmonics (Patterson et al., 1995; Meddis and O'Mard, 1997; Carlyon and Shamma, 2003). Since the autocorrelation operation discards relative timing information across channels, but remains sensitive to timing information within each channel, we expect the relative phase of harmonics to affect the resulting SACFs only in cases where the harmonics are unresolved by the cochlear filters, i.e., for the lowest f₀'s presented.

For similar harmonic numbers present in the passband, the AC model predicts larger f₀ DLs in the high-spectrum conditions [triangles in Fig. 11(b)] than in the low-spectrum conditions (inverted triangles), suggesting an effect of spectral region in the model that was not seen in the psychophysical data. This is consistent with Carlyon's (1998) conclusion that, in contrast to the psychophysical results, the AC model is sensitive to spectral region effects, as a result of the decline in phase-locking with increasing absolute frequency.

E. Effects of added noise

The simulations described above were performed without the presence of background noise. To test the possibility that background noise could affect the model simulation results, a subset of the simulations were repeated with background noise present. In our psychophysical experiment, the background noise level was held fixed and the stimulus level set relative to the detection threshold for a pure tone in the noise. Repeating a similar strategy to determine an appropriate noise level for the modeling simulations would require a model for signal-in-noise detection based on ANF responses, which is outside the scope of this paper. Instead, we chose to examine the influence of background noise over a range of levels. The nominal signal level was the same as that used in our original simulations. The background noise levels were chosen such that the signal-to-noise ratio (SNR) ranged from −10 dB to + ∞ (no noise) relative to the average SNR used in the experiment (SNR_expt). The background noise was turned on 100 ms before, and off 100 ms after, the harmonic stimulus.

Figure 4 shows the predicted f₀ DLs at various SNRs (re SNR_expt) for the sine-phase conditions. Low-spectrum and high-spectrum results are plotted in the left and right panels, respectively. The predictions are largely unaffected by the background noise until the SNR reaches the SNR_expt. Interestingly, for a narrow window of SNRs near SNR_expt, the trend in f₀ DLs as a function of f₀ actually switches, and f₀ DLs decrease with increasing f₀ as in the experimental data. One aspect of this behavior with respect to SNR is consistent with previous psychophysical data. Hoekstra (1979) showed that f₀ DLs generally increase with decreasing SNR, and that this effect is most pronounced in a given fixed frequency region for low f₀'s at low SNRs. In the model simulations, the predicted f₀ DLs increase more rapidly with decreasing SNR for low f₀'s than for high f₀'s. However, Hoekstra (1979) also showed that the general trend for f₀ DLs to improve with increasing f₀ for a fixed spectral region was unaffected by SNR. In contrast, the model only shows a trend for f₀ DLs to increase with f₀ for a narrow range of SNRs, and is therefore unsatisfactory as a predictor of f₀ DL data.

FIG. 4.

Effects of the introduction of background noise on model predictions. Signal level was held constant while the noise level was adjusted; SNR (dB) are described relative to the SNR used in the psychophysical experiment. For SNRs 5 dB or greater than that used in the experiment, the background noise has little effect on model predictions. As in Fig. 1, closed diamonds plotted along the top axis indicate that d₀′ was not reached for the highest δ tested of 0.3.

Overall, this analysis shows that the model predictions are relatively unaffected by the presence of background noise, provided the SNR is above a certain threshold. For the remainder of the simulations described in the following, no noise background was used.

IV. MODEL MODIFICATIONS

To account for a variety of psychophysical effects, various modifications to autocorrelation models of pitch have been suggested. These include SACF normalization (Patterson et al., 1996; Yost et al., 1996; Patterson et al., 2000), SACF weighting functions (Pressnitzer et al., 2001; Krumbholz et al., 2003; Cedolin and Delgutte, 2005), a lag-dependent AC time constant (Wiegrebe, 2001) a nonlinear filterbank (Lopez-Poveda and Meddis, 2001), and a CF-dependent ACF weighting function (Moore, 1982). In the model simulations described in the following five sections, the CF-dependent weighting function was the most successful in accounting for the effect of harmonic number observed in these psychophysical results of Sec. II. Each of these possible modifications is discussed in turn.

A. SACF normalization

The height of the SACF peak normalized to the value at zero lag has been successful in predicting the pitch strength of iterated rippled noises (Patterson et al., 1996; Yost et al., 1996; Patterson et al., 2000). Cariani and Delgutte (1996a,b); performed an analysis similar to SACF normalization by using the peak-to-background ratio in the all-order interval histogram as a neural estimate of the pitch salience. They were able to successfully account for a wide range of psychophysical pitch phenomena using this type of analysis. However, when the optimal detector model was adjusted to include SACF normalization (results not shown), there was virtually no change from the results seen in Fig. 5. The reason for this is that the optimal detector inherently normalizes the SACF function to the standard deviation at each lag. In essence, the extra normalization step scales the mean and standard deviation of the SACF equally, leaving d′ unaffected. SACF normalization did serve to reduce the noise associated with level roving, increasing the overall d′. However, this effect was similar across all conditions, such that when d₀′ was adjusted accordingly, normalized and unnormalized SACFs yielded virtually identical f₀ DL predictions.

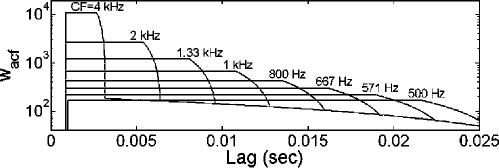
FIG. 5.

Sample w_ACF's [Eq. (6)] for a range of CFs, with parameters that yielded the best fit to the experimental data as shown in Fig. 7.

B. SACF weighting function

An SACF weighting function that generally gives more weight to short lags should yield a larger estimated d′ for high-f₀ stimuli that contain SACF peaks at short lags. Thus, such a weighting function may have the potential to account for the better discrimination performance observed for high f₀'s. For example, Pressnitzer et al. (2001) found that the Meddis and O'Mard (1997) model, modified to include a linear SACF weighting function, successfully predicted an increase in the lowest f₀ that could convey melody for higher spectral regions. In the optimal detector formulation, weighting the SACF would have no effect, since the weights would alter both the mean and standard deviations by the same factor, thus not affecting d′. Instead, independent noise with variance ${\sigma }_w^2\left(l\right)$ was added along the diagonal of the covariance matrix G in Eq. (4), according to

$${\sigma }_w^2\left(l\right)=w{\left(l\right)}^{-2},$$ (5)

where w(l) is the analogous SACF weighting function. Three different versions of w(l) were tested: a linear function, w=1−l/l_max (Pressnitzer et al., 2001), a power function, w=1−(l/l_max)^α with α ranging from 1/64 to 1 (Krumbholz et al., 2003), and an exponential function, w=exp(−l/λ) with λ ranging from 0.3 to 30 (Cedolin and Delgutte, 2005). For each w, the model was tested both with and without SACF normalization. The most promising results were produced by the combination of an exponential w(l) with 3<λ<4 ms, and SACF normalization. For low-spectrum stimuli, this modified model yielded f₀ DLs that decreased with increasing f₀ for low-spectrum stimuli, consistent with the experimental data (results not shown). However, this combination of modifications was unable to account for the high-spectrum data, and was therefore unsatisfactory. None of the other functions produced desirable results.

C. A lag-dependent time constant

Another lag-dependent AC modification was suggested by Wiegrebe (2001), whereby the AC time constant [τ in Eq. (1)] increases with increasing lag. Like the SACF weighting function of Pressnitzer et al. (2001), a lag-dependent τ would affect the SACF differently for different stimulus f₀'s, and could therefore influence the model's f₀ DL predictions. However, this modification would most likely not account for the results of the experiment described in Sec. II, because the longer time constant associated with low f₀'s would tend to increase the amplitudes of peaks in the SACF, yielding smaller f₀ DLs than for high f₀'s. Thus, Wiegrebe's (2001) modification would be likely to skew the model predictions even more heavily in favor of low f₀'s.

D. A nonlinear filterbank

The described above model simulations used a bank of linear gammatone filters (Patterson et al., 1992) to represent the basilar membrane. A more accurate nonlinear filter model that includes the compressive input—output function observed at the level of the basilar membrane (Rhode, 1971; Ruggero et al., 1997) has been shown to be important for a number of psychophysical phenomena (e.g. Oxenham and Bacon, 2003), and might better account for the f 0 DL data. The inclusion of a basilar membrane nonlinearity (e.g., Lopez-Poveda and Meddis, 2001) might compress the “peaky” sine-phase waveform more than the “flat” random-phase waveform yielded by interacting unresolved harmonics (Carlyon and Datta, 1997), possibly reducing the size of the phase effect predicted by the AC model. However, simulations using the dual-resonance nonlinear (DRNL) filterbank (Lopez-Poveda and Meddis, 2001) yielded unsatisfactory results (not shown), similar to those seen with the gammatone model. Thus, although the compression offered by this model is similar to that observed physiologically, it was not substantial enough to account for these data.

E. A CF-dependent “lag window”

Section III showed that for sine-phase stimuli, the Meddis and O'Mard (1997) AC model responded preferentially to low f₀'s for stimuli bandpass filtered in fixed spectral regions. Therefore, to successfully predict the improved f₀ discrimination for higher f₀'s seen in the human performance, the AC model must be modified in such a way as to impair performance for low f₀'s within a given spectral region. One way to accomplish this is to limit the range of lags for which the autocorrelation is calculated in each frequency channel in a CF-dependent manner (Moore, 1982). With this lag-window limitation, the AC will respond best to f₀'s that have certain harmonic numbers falling within each channel's bandwidth. Schouten (1970) first proposed the idea that “each pitch extractor has a limited range of measurable time intervals” in order to account for Ritsma's (1967) demonstration of the dominance of low-order harmonics in complex pitch perception. Moore (1982) further quantified the lag window, suggesting that a mechanism based on first-order interspike intervals operates over a range of lags between about 0.5/CF and 15/CF. Thus the AC in a particular channel will respond to f₀'s that are 1/15 to 2 times the channel's CF. In other words, the AC will respond to a given f₀ only if at least one of the f₀'s first to fifteenth harmonics fall near the CF. Ghitza (1986) implemented a similar idea, whereby the interspike interval analysis window length was roughly inversely proportional to each channel's CF.

After experimenting with various possibilities, we found that a piecewise-linear weighting function was able to account for the psychophysical data with some success. The CF-dependent weighting function consisted of four segments:

$$\begin{array}{cc}& w_{\mathrm{ACF}}(l,CF)=\{\begin{array}{cc}0,\hfill & l<\frac{0.5}{CF}\hfill \\ \frac{C{F}^2}{C{F}_0},\hfill & \frac{0.5}{CF}\le l<\frac{N_C}{CF}\hfill \\ \frac{C{F}^2}{C{F}_0}-m\left(l-\frac{N_C}{CF}\right),\hfill & \frac{N_C}{\mathrm{CF}}\le l<\frac{(N_C+N_{\Delta })}{CF}\hfill \\ A-\frac{A}{l_0}l,\hfill & l\ge \frac{(N_C+N_{\Delta })}{CF},\hfill \end{array}\phantom{\}}\end{array}$$ (6)

where l is the lag, CF₀=1500 Hz, the lowest CF used in the simulations, N_C is the cutoff between the second and third segments relative to CF, N_Δ is the width of the third segment relative to CF, A is the amplitude of the fourth segment at l=0, l₀ is the lag for which the fourth segment reaches zero, and m, the slope of the third segment, is defined as

$$m=\frac{{\mathrm{CF}}^2-A+\frac{A}{l_0}\left(\frac{N_C+N_{\Delta }}{\mathrm{CF}}\right)}{N_{\Delta }∕\mathrm{CF}}.$$ (7)

The fourth segment, independent of CF, is identical to the linear SACF weighting function of Pressnitzer et al. (2001). The zero-crossing of this segment (l₀) was set to 33 ms as suggested by Pressnitzer et al., consistent with a 30 Hz lower limit of melodic pitch. Finally, in some conditions, the estimated d′ reflected activity at low lags completely unrelated to the stimulus f₀. To prevent this phenomenon, w_ACF for each CF was set to zero for all values of l<0.875 ms. Sample w_ACF functions for various CF are shown in Fig. 5. (The linear segments of the functions appear curved because they are plotted on a logarithmic scale.) The lag window was applied to the ACF for each simulated ANF, and these windowed ACFs were summed to create the SACF just as before.

The CF-dependent windowing procedure described here was notably different from the SACF weighting described in Sec. IV B. There, the addition of independent noise was used as a substitute for a SACF-weighting function, which would have scaled the mean and standard deviation equally, yielding no net effect on d′. Here, the weighting functions (w_ACF) were applied to the individual ACFs before summing them to produce the SACF. Thus, the statistical properties of the SACF at each lag tended to reflect the statistical properties of the ACFs for channels that were most heavily weighted at that lag.

Estimates of d′ were generally noisier than in the unmodified model because the lag window tended to reduce the total number of ANF spikes that were used in the calculation. Therefore, two minor modifications were made. First, thenumber of stimulus repetitions n was increased to 100. Second, d′ was determined to exceed threshold only if it did not fall below d₀′ again for a higher value of δ. This ensured that the threshold was not exceeded due to random fluctuations in the d′ estimates.

The modified AC model was fit to the sine-phase experimental data of Sec. II with four free parameters (N_C, N_Δ, A, and d₀′). The two most important aspects of the experimental data were the dependence of f₀ DLs on N, and the lack of an effect of spectral region on f 0 DLs. Therefore, the fitting procedure minimized the sum of two error measures: the root-mean-squared difference between the logarithms of predicted and actual f₀ DLs, and the root-mean-squared difference between the logarithms of the predicted f₀ DLs for stimuli with equivalent N's in the low- and high-spectrum conditions. The strong model nonlinearities and limited range of δ values tested prohibited the successful use of an automated fitting procedure, such as the Nelder—Mead simplex method used by MATLAB's fminsearch function. Instead, a parameter-space search method was used, where coarse step-sizes allowed for a reduction in computation time. Thus, we caution that a somewhat different set of parameters may yield a better fit than those reported here.

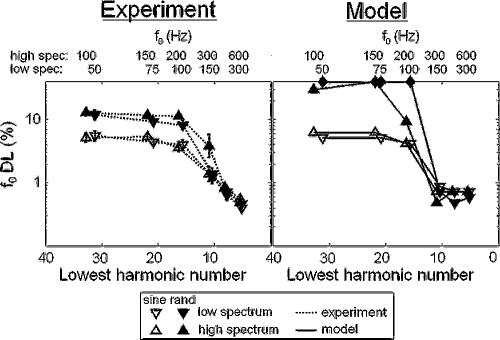
Figure 6 shows d′ as a function of δ for the modified model with parameters that yielded the best fit to the sine-phase experimental data: N_C=10.8, N_Δ=2 and A=200. The sample w_ACF functions depicted in Fig. 5 reflect these parameter values. The best-fitting d₀′ of 7.91×10⁴ is depicted as a horizontal dashed line in each panel of Fig. 6. Figure 7(b) shows the modified model's f₀ DL predictions as a function of N, based on these best-fitting parameters. The f₀'s corresponding to the N's are shown along the top axis. The psychophysical results from Fig. 1(a) are replotted in Fig. 7(a) for direct comparison with the model predictions. The modified model yielded a reasonable fit to both sets of data, and captured three main features of the data. First, f₀ DLs generally decrease with increasing f₀. Second, the model predictions for the two spectral regions overlap when plotted as a function of N, such that f₀ DL are mainly dependent on harmonic number. The separation of stimuli into two groups based on N is clearly seen in Fig. 6: those stimuli with low f₀'s, such that N>12, have shallow d′ vs δ slopes, yielding large f₀ DLs, while those with high f₀'s, such that N<12, have steeper slopes, yielding small f₀ DLs. Third, phase effects are only present for complexes with large N. For small N, sine- and random-phase stimuli yield similar f₀ DL predictions.

FIG. 6.

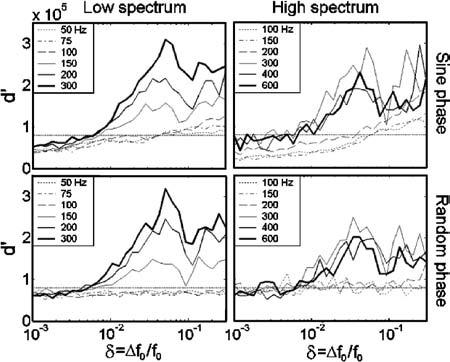
Model estimates of d′ vs δ using the lag windows described in Eq. (6) and pictured in Fig. 5, with parameters N_C=10.8, N_Δ=2, and A=200 that best fit the sine-phase data. Stimulus f₀'s are clearly divided into two groups, with lower f₀'s yielding gradual d′ slopes, and higher f₀'s yielding steeper d′ slopes.

FIG. 7.

(a) Psychophysical f₀ DLs from Fig. 1(a) are replotted for direct comparison with the model predictions. (b) Model f₀ DL predictions based on d′ estimates shown in Fig. 6 using the lag window [Eq. (6)], plotted as a function of N. As in Fig. 1, f₀'s corresponding to values of N for the lowand high-spectrum conditions are plotted above each panel, and closed diamonds plotted along the top horizontal axis indicate that d′₀ was not reached at the maximum tested value of δ =0.3. Both experimental and model f₀ DLs generally overlap for stimuli with the same N, indicating the modified model successfully accounts for effects of N on f₀ discrimination performance.

The one major failure of the modified model is that it overpredicted the phase effect for low f₀'s. The variability in the envelopes associated with low-f₀, unresolved, random-phase complexes was so large relative to the mean envelope that d′ was not affected by increasing δ. Thus, the model failed to reach threshold at the highest tested value of δ=0.3, and was unable to predict discrimination thresholds for these complexes. This problem was also observed for the original, unmodified model. The inclusion of a compressive nonlinearity in the model might help to reduce the magnitude of this phase effect by compressing “peaky” sine-phase envelope more than “flat” random-phase envelopes. However, because substituting DRNL filters (Lopez-Poveda and Meddis, 2001) for gammatone filters did not greatly affect the predictions of the unmodified model (Sec. IV D), it is also unlikely to greatly influence the predictions of the modified model.

Nonmonotonicities were observed in d′ estimates at the three highest f ₀'s tested in each condition. For values of δ near 0.1, d′ estimates suddenly decreased then increased. This nonmonotonic behavior can be understood by examining the sample SACF functions in Fig. 8. For the relatively high f₀ of 200 Hz, the SACF contains multiple sharp peaks at lags near 1/f₀, reflecting the stimulus fine structure. As δ increases, these closely spaced peaks move in and out of alignment with one another, yielding the observed nonmonotonic behavior. In contrast, the SACF representations for low f₀'s (e.g., 50 and 100 Hz) are dominated by a single large peak at each multiple of 1/f₀, with relatively small side bands. As a result, nonmonotonic behavior is not observed for these stimuli. This analysis suggests that the model uses fine-structure information to discriminate f₀ for low-order, but not for high-order harmonics. Regardless, these nonmonotonicities occur for f₀ separations well above the discrimination threshold, and therefore do not impact the model's f₀ DL predictions.

FIG. 8.

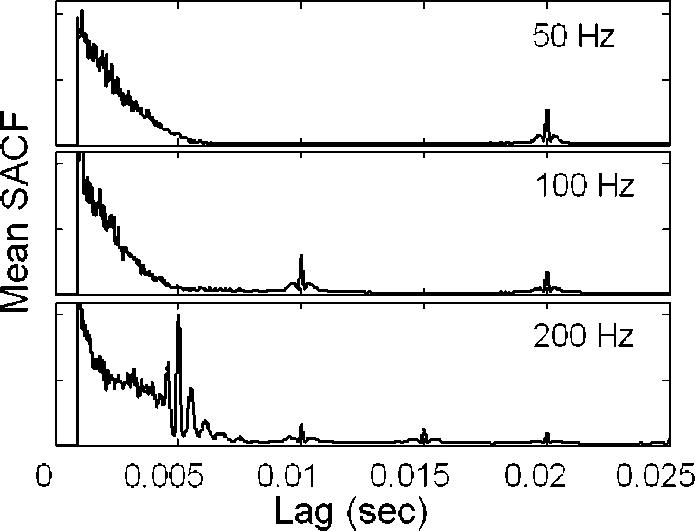
Mean SACFs produced with the lag-window modification [Eq. (6); Fig. 5] for sine-phase stimuli with various f₀'s. For higher f₀'s (e.g., 200 Hz), the large SACF peak at l=5 ms contains large fine-structure side peaks, causing the nonmonotonic behavior of d′ observed in Fig. 6. For lower f₀'s (50 and 100 Hz), the SACF side peaks are small relative to the central SACF peak; nonmonotonic d′ behavior is not observed for these stimuli.

V. DISCUSSION

The analysis of Sec. III showed that the Meddis and O'Mard unitary AC model of pitch perception is unable to account for the dependence of f₀ DLs on harmonic number. Whereas experimental data presented both here and elsewhere (Hoekstra, 1979; Houtsma and Smurzynski, 1990; Carlyon and Shackleton, 1994; Shackleton and Carlyon, 1994; Kaernbach and Bering, 2001) show that discrimination performance deteriorates with increasing lowest harmonic number within a given passband, the Meddis and O'Mard model predicts just the opposite for the stimuli used here. This result is consistent with the results of Cedolin and Delgutte (2005), who estimated pitch salience based on all-order interval analysis of cat ANF spikes. They found that pitch salience estimated in this way was maximal for the lowest f₀'s tested, where individual harmonics are not well resolved by the cat's auditory periphery.

We have shown (Sec. IV) that this failure of the AC model is not fatal to the idea that a single mechanism based on temporal information can account for the perceived pitch based on both resolved and unresolved harmonics. With the introduction of a CF-dependent lag window similar to that described by Moore (1982), the model was able to predict the dependence of f₀ discrimination on harmonic number. This was achieved because the modification reverses the original model's “preference” for high-order harmonics by applying a weighting function that amplifies the AC response to low-order harmonics, and attenuates the response to high-order harmonics.

The success of the modified AC model where the original model has failed supports the idea that temporal information alone is not enough to yield a salient pitch percept, and that the temporal information must be presented at the correct place on the cochlear partition in order to yield good f₀ discrimination performance (Oxenham et al., 2004). The lag window modification effectively codes “place” information into the AC model by weighting each channel's contribution based on its relationship to the stimulus f₀. For a given CF, a range of lags between 0.5/CF and N_C/CF are weighted most heavily. The ACF will respond most readily to a certain range of stimulus f₀'s that contain peaks falling within this lag range.

It is important to note that the correct behavior of the modified model with regard to the effects of harmonic number is not based on harmonic resolvability. The modified model responds preferentially to complexes containing low harmonics because of the introduction of the CF-dependent w_ACF. This could be considered a major failing of the model, if good f₀ discrimination performance were directly dependent on the presence of resolved harmonics. On the other hand, the direct dependence of the modified model's f₀DL predictions on harmonic number is consistent the results of several studies (described in Sec. I) suggesting that f₀ discrimination performance may depend only on harmonic number, and not on harmonic resolvability per se (Houtsma and Goldstein, 1972;Arehart and Burns, 1999; Bernstein and Oxenham, 2003).

The AC model was modified to fit the f₀ discrimination data described in Sec. II, and has not yet been tested on other data sets. Nevertheless, the dependence of predictedf₀ performance on harmonic number is a direct result of the w_ACF modification, suggesting that the modified model should be able to account at least qualitatively for the results of other studies that have shown an increase in f₀ DLs with increasing N. These include f₀ discrimination studies with bandpass-filtered harmonic complexes (Houtsma and Goldstein, 1972; Hoekstra, 1979; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003), as well as those that manipulate N for complexes with a fixed f₀ (Houtsma and Goldstein, 1972; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994; Bernstein and Oxenham, 2003). Furthermore, because this modification relies on harmonic number rather than peripheral resolvability, it is likely to account for results indicating that the diotic presentation of alternating harmonics does not improve f₀ discrimination performance (Houtsma and Goldstein, 1972;Arehart and Burns, 1999; Bernstein and Oxenham, 2003) despite the improvement in peripheral resolvability (Bernstein and Oxenham, 2003).

In contrast to the behavior of the modified model with respect to N, its correct behavior with respect to phase effects is most likely based on harmonic resolvability. The original model predicted a large effect of phase on f₀ DLs for low f₀'s containing unresolved harmonics, where the SACF mainly reflects phase-locking to the envelope (Fig. 2). In these conditions, the envelope resulting from the interaction of multiple harmonics within one filter was much “peakier” with sine-phase complexes than with random-phase complexes, yielding smaller predicted f₀ DLs. While the modified model predicts that stimuli yielding large f₀ DLs should also yield phase-dependent f₀ DLs, the two effects rely on different processes. The dependency of f₀ DLs on harmonic number derives from the w_ACF modification. The dependency on phase derives from inherent differences in the way the model processes resolved and unresolved harmonics, and is correctly predicted by both the original and modified AC models.

How is the mathematical formulation of a lag window to be interpreted in terms of physiological mechanisms? Licklider (1951) formulated an AC model of pitch perception in terms of a system of neurons, where every cochlear frequency channel is associated with its own bank of AC neurons, and each neuron in the bank is tuned to one of a wide range of periodicities. The ACF [Eq. (1)] represents the responses of each of the neurons in the bank, and the lag window is a weighting function applied to these responses. In the physiological interpretation, a larger number of neurons associated with a given lag will reduce the noise in the periodicity representation, yielding smaller predicted f₀ DLs for the f₀ associated with that lag.

In a manner similar to that described in the harmonic template model of Shamma and Klein (2000), the autocorrelation mechanism might develop over time to detect only those temporal correlations that tend to occur in the outputs of individual ANFs in response to generic wideband stimuli. The CF-dependent lag windows described here [Eq. (6) and Fig. 5] could emerge naturally based on the statistical properties of ANF outputs in response to such stimuli. Since the temporal extent of the impulse response of a bandpass filter is inversely proportional to the filter's bandwidth, the narrower filters associated with lower CFs will yield a wider range of lags over which a filtered wideband input stimulus will correlate with itself. Mirroring the properties of these naturally occurring autocorrelations, the system would be tuned to detect ANF response correlations at longer lags for low CFs than for high CFs. De Cheveigné and Pressnitzer (2005) have proposed a similar idea that relates filter impulse response times to pitch processing.

With the addition of a CF-dependent lag window, a single pitch mechanism based on temporal information can account for the poorer f₀ discrimination performance associated with high N. However, it does not address other evidence relating to frequency modulation (FM) detection and temporal integration that points to the possible existence of two separate pitch mechanisms. Plack and Carlyon (1995) showed that f₀ discrimination was affected by decreasing stimulus durations below 100 ms more for unresolved than for resolved complexes. They suggested that the exceptionally poor FM detection performance (relative to the f₀ DL) measured for unresolved complexes resulted from an absence of the longer integration time needed to extract the f₀. Because the modified autocorrelation model needs the same integration time for a given f₀ (i.e., somewhat longer than a single pitch period, in order to yield an SACF peak at l=1/f₀) regardless of resolvability, it is not likely to account for this result. It may be possible to interpret the CF-dependent weighting function as a manifestation of two pitch mechanisms. In this interpretation, the second segment of the lag-window [Eq. (6)] corresponds to the mechanism for low-order resolved harmonics, the CF-independent fourth segment represents the more poorly performing mechanism for high-order, unresolved harmonics and the third segment represents the transition between the two.

The autocorrelation model outlined here and elsewhere (e.g., Meddis and Hewitt, 1991a, b; Cariani and Delgutte, 1996a, b; Meddis and O'Mard, 1997) takes into account all-order intervals between ANF spikes. Kaernbach and Demany (1998) challenged the view that the f₀ detection mechanism takes into account anything but first-order interspike intervals. They showed that a click-train with f₀ information in its first-order interspike interval statistics was easier to discriminate from a random click train than a click train containing f₀ information in its second- and higher-order interval statistics, even though the waveform autocorrelation showed a similar peak at a lag corresponding to the f₀ in both cases. However, Pressnitzer et al. (2002) showed that an all-order autocorrelation based on simulated ANF responses, rather than the raw waveform, may be able to account for this phenomenon, as a result of the auditory filtering and neural transduction present in the model.

VI. SUMMARY AND CONCLUSIONS

Measurements of f₀ DLs for bandpass-filtered harmonic stimuli demonstrated that f₀ discrimination performance depends largely on harmonic number: as the ratio of a complex's f₀ to the frequency of its lowest component increases, f₀ discrimination improves. The Meddis and O'Mard (1997) unitary AC model of pitch perception fails to predict this effect of harmonic number on f₀ discrimination. While psychophysical measurements show an improvement in f₀ discrimination with increasing f₀ for bandpass filtered harmonic stimuli, the AC model predicts the opposite behavior, at least for sine-phase complexes. In order for the model to correctly predict the psychophysical results, an ad hoc modification was made, whereby the lags for which the AC was measured in each frequency channel were weighted in a CF-dependent manner. This yielded f₀ DL predictions that decreased with increasing f₀, and depended mainly on harmonic number, consistent with the data. This modification works by forcing the model to respond preferentially to low numbered harmonics. The correct behavior of the model in no way reflects a preference for resolved harmonics, per se. Instead, the model introduces a dependence on harmonic number, without regard to harmonic resolvability.

In conclusion, this study has shown that a single autocorrelation mechanism, modified to include CF dependency, is sufficient to account for the dependence of f₀ DLs on harmonic number. Consequently, two pitch mechanisms may not be needed to explain this effect. Nevertheless, the modified autocorrelation model may not account for other evidence for two pitch mechanisms, such as the differences observed between resolved and unresolved harmonics in the temporal integration of f₀ information (Plack and Carlyon, 1995).