Oscillator representations and systems of ordinary differential equations

Abstract

Using representation-theoretic methods, we determine the spectrum of the 2 × 2 system

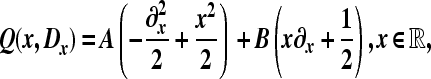with A, B ∈ Mat₂(ℝ) constant matrices such that A = ^tA > 0 (or <0), B = −^tB ≠ 0, and the Hermitian matrix A + iB positive (or negative) definite. We also give results that generalize (in a possible direction) the main construction.

1. Introduction

It is a natural and important problem to find an efficient and invariant way of studying the spectrum of systems of differential equations. We deal first with the spectral problem of particular systems that are the Weyl quantization of noncommutative quadratic form (that we shall call noncommutative harmonic oscillators) of the kind

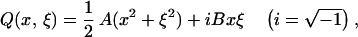where (x, ξ) ∈ ℝ² ≃ T*ℝ, A, B ∈ Mat₂(ℝ) are constant 2 × 2-matrices with A = ^tA definite, either positive or negative, B = −^tB ≠ 0, and A + iB > 0 (or < 0). The Weyl quantization of the above noncommutative quadratic form is

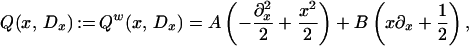Q(x, D_x): 𝒮(ℝ; ℂ²) → 𝒮(ℝ; ℂ²), Q(x, D_x): 𝒮′(ℝ; ℂ²) → 𝒮′(ℝ; ℂ²) continuously, and it is important to remark that in the above hypotheses the system Q(x, D_x), as an unbounded operator in L²(ℝ; ℂ²) (with maximal domain B²(ℝ; ℂ²) := {u ∈ L²(ℝ; ℂ²); x^α∂_x^β u ∈ L²(ℝ; ℂ²), ∀α, β, 0 ≤ α + β ≤ 2}) is self-adjoint with discrete spectrum made of eigenvalues μ_k ∈ ℝ (with finite multiplicities) such that |μ_k| → +∞ as k → +∞. The main problem in analyzing the spectrum of such systems comes from two sources: the noncommutativity of matrices and the noncommutativity of the quantized variables x and ξ.

Our aim is in the first place to find a systematic way of solving algebraically in L²(ℝ; ℂ²) (that is, taking into account L²-convergence or, at most, 𝒮′-convergence) the above kind of systems. The operator Q(x, D_x) naturally possesses an sl₂(ℝ)-action (and more generally a metaplectic group action), due to the Weyl quantization. Hence, the algebraic viewpoint consists of using this sl₂(ℝ)-symmetry and the symmetries carried by A and B to develop a method that determines, as a first step, a candidate for an eigenvalue along with the formal sequence of coefficients of a potential eigenfunction belonging to that eigenvalue (in the sense that the eigenfunction has that sequence as coefficients with respect to some Schwartz L²-basis obtained by means of the oscillator representation of sl₂(ℝ); this may be thought of as a necessary condition). Then the second step consists of determining which candidate eigenvalues can be actual ones, by studying the convergence properties (in L² or 𝒮′) of the related formal sequences of coefficients (see ref. 1). In Section 2, we shall give a survey of the results of refs. 2 and 3 described above. As it will be seen below, the key step is to obtain a three-term recurrence system that can be “diagonalized.” In Section 3, we shall next consider a different system of ordinary differential operators and treat the relative spectral problem by employing the tensor-product of the oscillator representation and the vector (standard) representation of sl₂(ℝ). That system (which is also interesting, for the most general noncommutative harmonic oscillator is given by A(−∂_x²/2) + B(x∂_x + 1/2) + C(x²/2) + D, with A = ^tA, B = −^tB, C = ^tC and D = ^tD) might look more difficult at first glance than the ones considered in Section 2, because of the presence of a zeroth-order nonconstant matrix-valued term. However, the difficulty is only “virtual,” for the use of the aforementioned tensor product representation of sl₂(ℝ) allows one to treat the eigenvalue problem in a completely straightforward way: the above system is just a pair of “harmonic oscillators” in disguise. We shall also exhibit a family of systems parametrized by ɛ ∈ ℝ, which “interpolates” the pair of “harmonic oscillators” and a system of the above type. This family possesses the remarkable property that all the eigenvalues have multiplicity 1, provided ɛ ∉ (1/2)ℤ. This approach will be generalized in ref. 4 to treat more general 2 × 2-systems and higher-rank cases in a unified way.

Applications of the study of the spectrum of N × N noncommutative harmonic oscillators are in the field of lower bounds and hypoellipticity of systems of pseudodifferential operators (see refs. 5–10).

We finally remark that the spectral problem for Q(x, D_x) can be translated into a family of Fuchsian type third-order equations with four regular singularities, in the complex unit disk (see ref. 11). We believe that the results on the multiplicity of the spectrum of Q(x, D_x) may provide a crucial information to determine the monodromy of the ordinary differential equation discussed in ref. 11.

2. Study of the Spectrum of Q

The condition that the Hermitian matrix A + iB be definite, either positive or negative, is equivalent to requiring that det A > (pf(B))², and also equivalent to requiring that the operator Q(x, D_x) be elliptic, i.e., det Q(x, ξ) ≠ 0 for (x, ξ) ≠ (0, 0), det Q(x, ξ) being positively homogeneous of degree 4 in (x, ξ). Hence, Q(x, D_x), as an unbounded operator with domain (maximal domain)

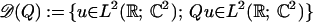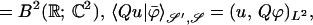for any given ϕ ∈ 𝒮(ℝ; ℂ²), has a discrete spectrum made of real eigenvalues with finite multiplicities, diverging (in absolute value) to +∞.

Define

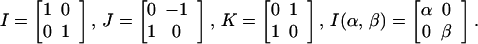Since B = ±pf(B)J, and by the commutativity of J with SO(2), one can easily reduce the study of Q to that of

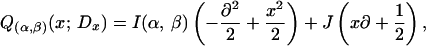where, after possibly conjugating by K, we may assume α, β > 0. We may thus suppose A = I(α, β), B = J. Set ℓ = 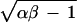> 0, and define

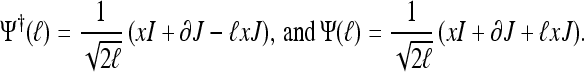1

Since [Ψ(ℓ), Ψ^†(ℓ)] = I, putting

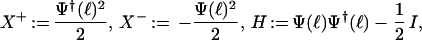yields that H, X⁺, X⁻ satisfy the commutation-relations of sl₂(ℝ)

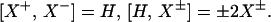2

This gives in fact the tensor product of the oscillator representation and the two-dimensional trivial representation of sl₂(ℝ). For v ∈ ℂ²∖{0}, set

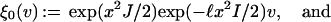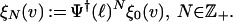Since X⁻ annihilates ξ₀(v) [ξ₀(v) is a lowest-weight vector], ξ_N(v) is a weight vector of H with weight N + 1/2, and it also follows that whenever v and w are nonzero vectors such that 〈v, w〉_ℂ² = 0, {ξ_N(v), ξ_N(w)}_N∈ℤ+ is an orthogonal basis of L²(ℝ; ℂ²). The operator Q_(α,β) is unitarily equivalent to (ℓ/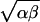)Q̃, where Q̃ := A^1/2HA^1/2. The problem is therefore to understand the structure of the spectrum of Q̃. There are now (at least) two ways of studying the spectral problem for Q̃: (1) studying the equivalent problem of finding λ and η such that (H − λA⁻¹)η = 0 (the twisted eigenvalue problem); and (2) studying directly the eigenvalue problem (Q̃ − λI)η = 0. In both cases, the key point is to get an appropriate recurrence formula that allows one to control the coefficients of the eigenfunctions. (One can easily see that an expansion in terms of the usual Hermite functions is not “convenient” for this purpose.) As we shall explain below, we get a system of recurrence equations that, by suitable rotations, can be diagonalized into a scalar three-term recurrence equation (this is highly nontrivial, for we do not know a priori that that is possible). We remark that the crucial point is the choice of the basis to be used in the discussion. Since A⁻¹ = σ₊I + σ₋KJ, A^1/2 = μ₊I + μ₋KJ, in both problems 1 and 2 the action of the operator K appears. Since K does not commute with H (whereas J does), what is missing here is the explicit formula for the action of K on the ξ_N(v) in terms of the ξ. Set ξ_N^j = ξ_N(e_j), j = 1, 2, where {e₁, e₂} is the canonical basis of ℂ², and, for v₊ := [_−i¹], define ξ_N⁺ := ξ_N(v₊).

Lemma 2.1. The set B_mix := {ξ_N⁺, Kξ_N⁺}_N∈ℤ+ is an orthogonal basis of L²(ℝ; ℂ²).

As the system preserves parity, we shall consider hereafter only the even case.

Dealing with Problem 1.

Since the action of H on the Kξ_N involves both the ξ and Kξ, we use both bases B_can⁺ := {ξ_2N¹, ξ_2N²}_N∈ℤ+ and B_can^+,K := {Kξ_2N¹, Kξ_2N²}_N∈ℤ+ at the same time, and the fact that they are related by K. The latter means that if ({a_N}_N∈ℤ+, {b_N}_N∈ℤ+) are the coordinates of a solution η to the twisted eigenvalue problem with respect to the basis B_can⁺, and ({c_N}_N∈ℤ+, {d_N}_N∈ℤ+) those of η with respect to the basis B_can^+,K, then there exists an involutive linear function

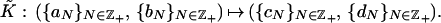Using K̃, we get a nonconstant matrix-coefficient system of recurrence equations in ℂ⁴ for the (a_N, b_N, c_N, d_N) that can be reduced to two recurrence systems for (a_N, b_N) and (c_N, d_N) plus a linear relation between (a_N, b_N) and (c_N, d_N). At this point there exists an explicitly known constant matrix M₀(ℓ) such that (1/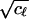) M₀(ℓ) ∈ SO(2), where

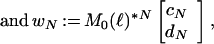we arrive at the recurrence equations

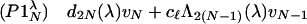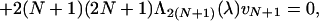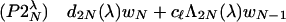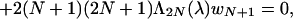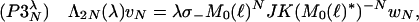where N ∈ ℤ₊, v₋₁ = w₋₁ = 0 and

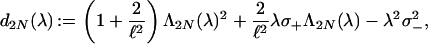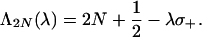The key point now is the compatibility condition: Suppose λ gives rise to a solution ({a_N}_N∈ℤ+, {b_N}_N∈ℤ+) to (P1_N^λ) that defines a function u₁ := ∑_N=0^+∞ (a_Nξ_2N¹ + b_Nξ_2N²) ∈ L²(ℝ; ℂ²), then with ({a_N}_N∈ℤ+, {b_N}_N∈ℤ+) we associate, in an algebraic fashion through (P3_N^λ), a solution ({c_N}_N∈ℤ+, {d_N}_N∈ℤ+) to (P2_N^λ) that corresponds to a function u₂ := ∑_N=0^+∞ (c_NKξ_2N¹ + d_NKξ_2N²) ∈ L²(ℝ; ℂ²), for which u₁ = u₂iff K̃(({a_N}_N∈ℤ+, {b_N}_N∈ℤ+)) = ({c_N}_N∈ℤ+, {d_N}_N∈ℤ+). In this and only in this case, η = u₁ = u₂is a solution to the twisted eigenvalue problem.

To study the recurrence (P1_N^λ), we first observe that by virtue of the initial condition v₋₁ = 0, it is actually a scalar recurrence, depending only on the initial condition v₀ ∈ ℂ². At this point, all the solutions to (P1_N^λ) [and hence to (P2_N^λ)] are of the form h(λ) ⊗ v₀, for some sequence h(λ) = {h_N(λ)}_N∈ℤ+ ∈ ℂ^ℤ₊ depending only on λ. One next sees that it is possible to construct, for λ ∈ ℝ, only two kinds of solutions: the ones for which there exists N₀ such that h_N(λ) = 0 for all N ≥ N₀ + 1 [such solutions are called finite-type (λ, N₀)-solutions] that are hence obviously associated with Schwartz candidates as solutions to the twisted eigenvalue equation; the ones that are not of finite type, for which there exists N₀ ≥ 0 such that h_N(λ) = 0 for every N ≤ N₀ − 1 and h_N(λ) ≠ 0 for infinitely many N ≥ N₀ [one sets h₋₁(λ) ≡ 0]. The latter solutions are not in general associated with any reasonable distribution in 𝒮′(ℝ; ℂ²) unless λ satisfies an equation of the kind q_N0(λ) = f_N0(λ), where q_N0 is a suitably defined rational function and f_N0 is a suitably defined continued fraction [both depending on Λ_2N(λ) and d_2N(λ)], case in which the associated function is actually a Schwartz function [such solutions are called infinite-type (λ, N₀)-solutions]. Notice that the algebraic-companion solutions k(λ) ⊗ w₀ to (P2_N^λ), algebraically obtained from a solution h(λ) ⊗ v₀ of (P1_N^λ) (of finite or infinite type) through (P3_N^λ), are automatically associated with Schwartz functions. Hence, for a fixed λ that gives rise to finite-type or infinite-type solutions, we get at least two solutions, for we have the freedom of the choice of v₀ ∈ ℂ². On the other hand, the aforementioned compatibility condition rules out that freedom: if one defines for h(λ)(≠ 0) of finite or infinite type

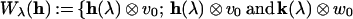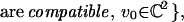then dim_ℂ W_λ(h) ≤ 1. The reason why W_λ(h) might be zero-dimensional (corresponding to v₀ = w₀ = 0) comes from the fact that the operator K̃ acts in a highly unknown fashion, and we cannot a priori conclude that a solution h(λ) ⊗ v₀ to (P1_N^λ) and the algebraic companion k(λ) ⊗ w₀ relative to (P2_N^λ) are related (for the same λ) through the compatibility condition.

Let us define

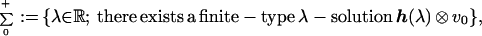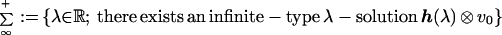(and analogously the sets ∑₀⁻ and ∑_∞⁻ relative to the odd case). One has also the following description of ∑₀⁺: upon defining polynomials j_2N ∈ ℝ[λ] inductively by the recurrence formula

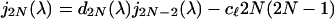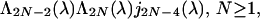j₋₂(λ) = 1, j₀(λ) = d₀(λ) [they appear as determinants of particular Jacobi matrices (see ref. 2)], then

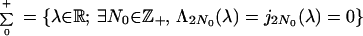(and analogously in the odd case). Put ∑₀ := ∑₀⁺ ∪ ∑₀⁻, ∑_∞ := ∑_∞⁺ ∪ ∑_∞⁻, and for λ ∈ ∑₀ ∪ ∑_∞ define V_λ⁺ := {u ∈ L²(ℝ; ℂ²); Q̃(x, D_x)u = λu and u is even} and V_λ⁻ := {u ∈ L²(ℝ; ℂ²); Q̃(x, D_x)u = λu and u is odd}. It is important to notice that at this point we do not know as yet that the V_λ^± are eigenspaces belonging to λ (because we do not know as yet that any given λ in ∑₀ ∪ ∑_∞ is an eigenvalue). Thus, as proved in ref. 2, we have the following theorem (that might be thought of as the first half of Theorem 2.4 below).

Theorem 2.2. One has

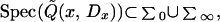and

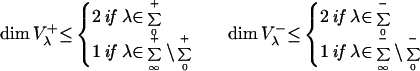Dealing with Problem 2.

In this case, the key ingredients for dealing directly with problem 2 are the formula

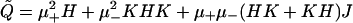and the use of the basis B_mix (see Lemma 2.1). Again, we restrict to the even-eigenfunction case. Hence, consider the equation (Q̃ − λI)η = 0, with η of the form η = ∑_N=0^+∞ (a_Nξ_2N⁺ + b_NKξ_2N⁺). Upon setting a₋₁ = b₋₁ = 0, z_N := ℓ^−2N (1 − iℓ)^N (μ₋a_N − iμ₊b_N), we get the recurrence equations

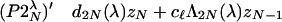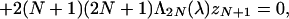i.e., exactly the recurrence equations (P2_N^λ). It is a key observation now, and the reason why the basis B_mix is of fundamental importance, that the compatibility condition is automatically satisfied. Hence, since λ ∈ ∑₀ ∪ ∑_∞ gives rise to Schwartz solutions to the eigenvalue equation, it follows from (P2_N^λ) = (P2_N^λ)′ that λ ∈ Spec(Q̃). Thus Spec(Q̃(x, D_x)) = ∑₀ ∪ ∑_∞. Now, since any finite-type (λ, N₀ + 1)-solution of (P1_N^λ) corresponds to a finite-type (λ, N₀)-solution of (P2_N^λ), and hence of (P2_N^λ)′, we have the following crucial fact.

Lemma 2.3. One has ∑₀⁺ ⊂ ∑_∞⁺ and ∑₀⁻ ⊂ ∑_∞⁻.

As a consequence of this approach and of Theorem 2.2 above, we get, as proved in ref. 3, the following rather complete description.

Theorem 2.4. One has

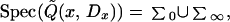and

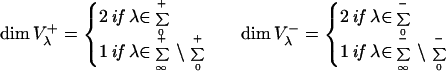Remark 2.5: In general ∑₀^± ≠ ∅ (see ref. 2).

3. A New System

As an example of some possible directions of generalization of the system defined by the operator

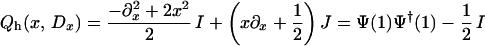(see Eq. 1), we propose here the spectral problem relative to the operator

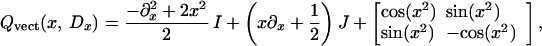i.e., the study of the equation

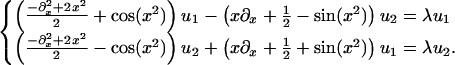Notice that, as an unbounded operator in L²(ℝ; ℂ²) with domain B²(ℝ; ℂ²), Q_vect(x, D_x) is self-adjoint with compact resolvent (this again by virtue of the global ellipticity of its principal part). It seems quite nontrivial to obtain the eigenvalues of Q_vect(x, D_x). We want to show that exploiting the oscillator representation allows one to solve the spectral problem. Notice that Q_h(x, D_x) is unitarily equivalent (through a symplectic scaling) to Q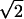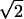_(,)(x, D_x) (in the notations of Section 2). The main problem here is to treat the zeroth-order part of Q_vect(x, D_x). That seems difficult, but that is not the case, by virtue of the tensor product representation of sl₂(ℝ) to be constructed below. Hence, let {H, X⁺, X⁻} be the basis of sl₂(ℝ), which satisfies Eq. 2. Put

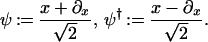Then it is clear that [ψ, ψ^†] = 1, and hence the map ω: sl₂(ℝ) → End_ℂ (𝒮(ℝ))

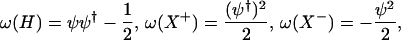gives the oscillator representation of sl₂(ℝ) on 𝒮(ℝ). Because the action of sl₂(ℝ) leaves the parity invariant, we have

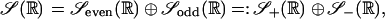the irreducible decomposition of ω. Put ω^± := ω|_𝒮±(ℝ). Then v₀ = e^−x2/2 (resp. ψ^†v₀) gives the lowest weight vector of the irreducible representation of (ω⁺, 𝒮₊(ℝ)) (resp. of (ω⁻, 𝒮₋(ℝ))) (see ref. 12). Let (π, V) (V ≃ ℂ²) be the vector representation of sl₂(ℝ):

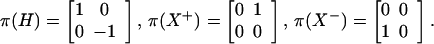We have the following proposition.

Proposition 3.1. Put ρ(H) := Q_vect(x, D_x),

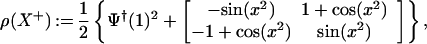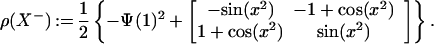Then (ρ, 𝒮(ℝ; ℂ²)) defines a representation of sl₂(ℝ). Furthermore, ρ is equivalent to the tensor product representation (ω ⊗ π, 𝒮(ℝ) ⊗ ℂ²). In fact, the operator exp(x² J/2) defines the intertwining operator between these representations:

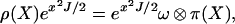where, recall, ω ⊗ π(Y) = ω(Y) ⊗ 1 + 1 ⊗ π(Y) [we have here identified 𝒮(ℝ) ⊗ ℂ² with 𝒮(ℝ; ℂ²)]. In particular, the system defined by the operator Q_vect(x, D_x) is unitarily equivalent to the system defined by the operator ω ⊗ π(H).

Proof: All the statements follow from the fact

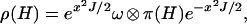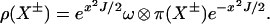Details are left to the reader.

Using the irreducible decomposition of the tensor product representation ω ⊗ π we have the following theorem.

Theorem 3.2. Put ξ₀^± := e^x2J/2 ϕ₀^± and ξ₁^± := e^x2J/2 ϕ₁^±, where

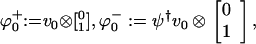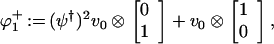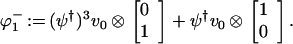Define, for N ≥ 0, ξ_0,N^± := ρ(X⁺)^N ξ₀^±, ξ_1,N^± := ρ(X⁺)^N ξ₁^±. Then

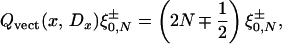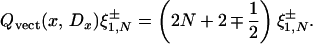Remark 3.3: As an sl₂(ℝ)-module, the above theorem implies the irreducible decomposition of (ρ, 𝒮(ℝ; ℂ²)):

where the closure refers to the 𝒮-topology (the same decomposition holds for L²(ℝ; ℂ²) with closure in the L²-topology). In particular, ξ₀⁺, ξ₁⁺ and ξ₀⁻, ξ₁⁻ give the lowest-weight vectors of the irreducible summands, respectively. The L²-structure of Spec(Q_vect(x, D_x)) is given by

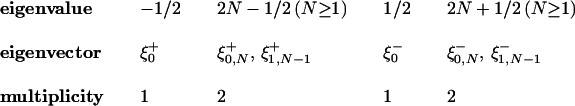Furthermore, the proof of the above theorem gives the following result (see ref. 4).

Theorem 3.4. Let

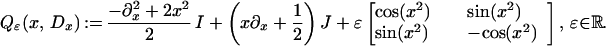The system Q_ɛ(x, D_x) interpolates systems Q_h(x, D_x) and Q_vect(x, D_x), it has spectrum given by the numbers 2N + 1/2 ± ɛ (with even relative eigenfunctions) and 2N + 3/2 ± ɛ (with odd relative eigenfunctions), where N ∈ ℤ₊, with multiplicity one for any N ≥ 0 when ɛ ∉ (1/2)ℤ.

Remark 3.5: We remark that the eigenfunctions of Q_ɛ(x, D_x) do not depend on ɛ (see ref. 4). This is the main reason why we think the eigenfunction basis of Q_ɛ may serve as a useful tool for studying more general systems.

We shall give further generalizations in ref. 4. One of our main motivations is to provide a class of examples whose spectral problems can be explicitly solved in a unified way. Indeed, if we take any unitary transformation U(x) in place of e^x2J/2 in Proposition 3.1, we may write down a number of examples that look more difficult, but that actually are obviously all unitarily equivalent to system Q_vect(x, D_x). Moreover, it is also quite interesting to consider the eigenvalue problem for

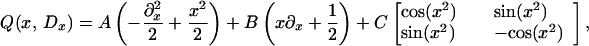even for the special case C = A, for one may write

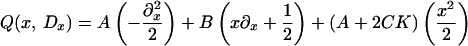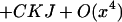(A and C are real self-adjoint matrices, B real skew-adjoint).