2-Aminopurine fluorescence quenching and lifetimes: Role of base stacking

Abstract

2-Aminopurine (2AP) is a fluorescent analog of guanosine and adenosine and has been used to probe nucleic acid structure and dynamics. Its spectral features in nucleic acids have been interpreted phenomenologically, in the absence of a rigorous electronic description of the context-dependence of 2AP fluorescence. Now, by using time-dependent density functional theory, we describe the excited-state properties of 2AP in a B-form dinucleotide stacked with guanosine, adenosine, cytosine, or thymine. Calculations predict that 2AP fluorescence is quenched statically when stacked with purines, because of mixing of the molecular orbitals in the ground state. In contrast, quenching is predicted to be dynamic when 2AP is stacked with pyrimidines, because of formation of a low-lying dark excited state. The different quenching mechanisms will result in different experimentally measured fluorescence lifetimes and quantum yields.

The nucleotide 2-aminopurine (2AP) has been used as a site-specific probe of nucleic acid structure and dynamics (1–11) because it base pairs with cytosine in a wobble configuration (4, 5, 12) or with thymine in a Watson–Crick geometry (7, 11). Thermodynamic measurements of DNAs containing 2AP:C or 2AP:T show that the former pairing is more destabilizing (11, 12). Incorporating 2AP into DNA quenches its fluorescence (2, 8, 11), reducing its quantum yield from that of the free nucleoside (0.65 in aqueous solution). This reduction is attributed to stacking interactions with nearest neighbor nucleobases, and, therefore, fluorescence properties of 2AP have been used to probe the equilibrium stacking properties of DNA duplexes containing these mismatched pairs (2, 8, 10). Although the fluorescence decay of 2AP in solution is single exponential, with a lifetime of ≈10 ns, in the context of a DNA molecule, four decay components, from 50 ps to 8 ns, are typically needed to describe its lifetime (2). The short decay time observed for 2AP in a duplex is attributed to the fully stacked state, whereas the longest lifetime comes from unstacked 2AP (2, 7). The distribution of stacked states can be altered by temperature, solvent, flanking bases, and bound protein, and so all of these conditions can be probed by using 2AP fluorescence. Dynamics of stacked bases adjacent to a mutagenic mismatch in DNA (such as 2AP:C and 2AP:T) may be part of the recognition mechanism by replication/repair enzymes (3, 13), so interpretation of 2AP fluorescence data is critical for describing these environments.

To understand the effect of base stacking on fluorescent properties of 2AP, we have used time-dependent density functional theory (TDDFT) (14, 15) to calculate the excited-state properties of 2AP alone and in stacked B- and A-form dinucleotides (dimers). Analysis of monomer calculations indicates the accuracy with which TDDFT describes spectral properties: excited-state transition energies, transition dipole directions, and oscillator strengths for 2AP, thymine, cytosine, adenine, and guanine (see figures) are in excellent agreement with experimental measurements (16–18) and with complete active subspace self-consistent field calculations (19, 20). Therefore, ^5′2AP-N dimers of these bases were built, and TDDFT calculations done on these “supermolecules,” so-called because their electronic properties are neither a sum nor perturbation of monomer properties.

Materials and Methods

GAUSSIAN 98 (21) was used for TDDFT calculations. All reported results were obtained by using the triple-ζ 6-311 + G(d) basis set with the B3LYP exchange–correlation functional. Larger basis sets gave virtually identical results for all properties. Dimer calculations were done on a dedicated 550-MHz Pentium III PC (Linux) and took approximately 150 h of computer time.

2AP-N dimers were constructed in INSIGHT II (22) from canonical B- and A-form x-ray structures, mutating adenine to 2AP and removing the sugar and phosphate atoms. Each base was optimized separately at the MP2/6-31G(d,p) level, maintaining the dimer starting structure. 2AP was minimized under C_s symmetry constraints to account for the flattening of the amino group as it would be in a duplex structure.

Calculations of monomers and dimers used different numbers of basis functions (e.g., 451 functions for the 2AP-T dimer vs. 235 and 216 functions for 2AP and thymine, respectively). Spurious differences on account of that difference (i.e., basis set superposition errors) were assessed by using the Counterpoise method (23): ground- and excited-state energies, dipole moments, and transition dipole moments were computed for each monomer and compared with dimer calculations where one base was replaced with ghost atoms (no nuclear charge or electrons) to effectively calculate monomer properties as they would appear in the dimer. Computed properties for monomers and ghost dimers were identical within 1%.

Results

^5′2AP-Thymine Dimers.

B-form.

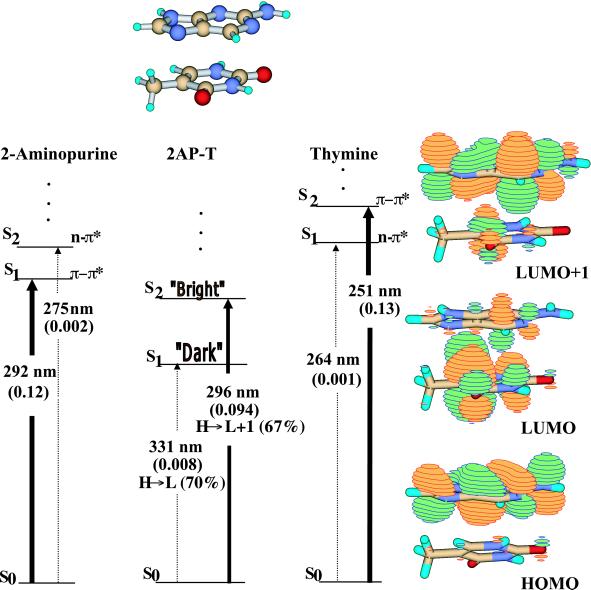
Results for the B-form 2AP-T dimer are summarized in Fig. 1. Several features are immediately notable: first, the ground state (S₀) to second excited-state (S₂) vertical transition has a strong oscillator strength (intensity); the transition dipole is only 4° out of plane. This absorption, dominated by the highest occupied molecular orbital (HOMO)→ lowest unoccupied molecular orbital (LUMO) + 1 transition, is similar to that of 2AP, and should produce similar fluorescent emission. However, and most significantly, there is a lower-lying S₁ state in the molecule. The S₀→S₁ absorption is very weak and arises predominantly from the HOMO (with electron density almost exclusively on 2AP) →LUMO transition (with electron density mostly on thymine). Invoking Kasha's rule, which predicts that rapid internal conversion will occur from S₂ to S₁, the (nearly) dark S₁ state would serve as a nonradiative sink for energy originally deposited in the bright (2AP-like) S₂ state. As a result, the lifetime of 2AP-like fluorescence from the S₂→S₀ transition would be significantly shortened. This prediction agrees with experimental observation that there is a short component of the fluorescent lifetime for 2AP in a duplex.

Figure 1.

Singlet excited-state transitions of B-form ^5′2AP-T as determined by TDDFT [B3LYP/6-311 + G(d)]. Jablonski diagrams for both monomer and dimer are shown. Oscillator strengths are shown in parentheses as are the dominant one-electron orbital contributions for the dimer transitions. Orbital amplitudes for the HOMO-1, HOMO and LUMO, LUMO + 1 are shown. The widths of the lines denoting the excited-state transitions reflect the relative oscillator strengths of the monomer and dimer transitions.

A-form.

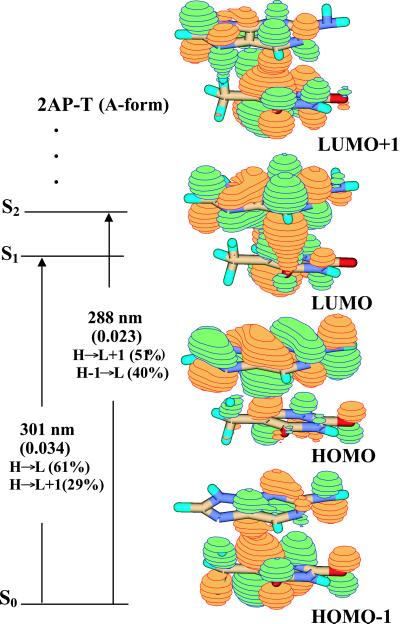
Because the nucleobases are conjugated π-systems, different stacking geometries that alter the extent of base overlap are predicted to alter their electronic properties. B-form and A-form geometries differ in the relative orientations of the stacked nucleobases, with A-form having more extensive overlap of the six-membered rings. A-form ^5′2AP-T (Fig. 2) shows a different composition of electronic states than does the B-form dimer. Most notably, the S₀→S₁ and S₀→S₂ transitions have comparable oscillator strengths (about one-fourth that of 2AP) and energies (Δλ_abs = 13 nm), and both receive contributions primarily from HOMO→LUMO and HOMO→LUMO + 1 configurations. Electron density in the HOMO is localized on 2AP, but there is significant thymine character in both LUMO and LUMO + 1. The S₀→S₁ transition is polarized about 25° out of plane, indicating that it has significant charge–transfer character (24, 25). The radiative lifetime of the (vertical) S₁→S₀ transition is predicted to be ≈40 ns (2AP radiative lifetime is 16 ns in solution), and thus nonradiative processes would effectively compete to reduce the fluorescence quantum yield.

Figure 2.

Jablonski diagram and orbital amplitudes for the A-form of the ^5′2AP-T dimer obtained at the B3LYP/6-311 + G(d) level.

^5′T-2AP B-Form Dimer.

The dimers analyzed above contain 2AP stacked 5′ to the flanking nucleobase, which of course is only one geometry within a nucleic acid strand. Stacking geometry can alter the fluorescent properties of 2AP, as illustrated by the A-form and B-form 2AP-T dimers, and therefore, a ^5′T-2AP dimer was also studied.

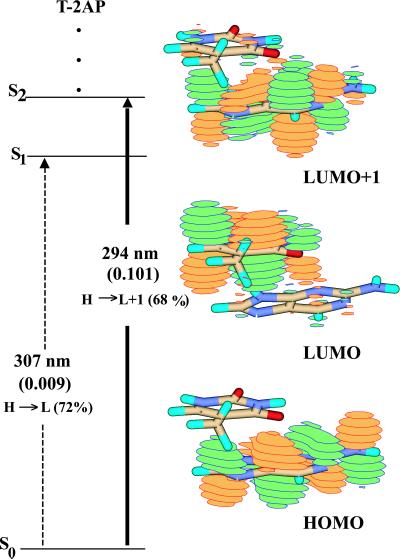
As illustrated in Fig. 3, the electronic properties of this dimer are similar to that of the ^5′2AP-T B-form dimer. Again, there is a dark state (S₁) below the state with 2AP character (S₂, the bright state), which indicates that there will be rapid internal conversion from S₂→S₁, resulting in a short experimentally observed lifetime. There is little evidence of charge transfer in the S₂ excited state (its transition dipole moment is only 4° out of plane), which is mostly 2AP-like. The lower-lying S₁ state has more electronic overlap, and its transition dipole moment is ≈31° out of plane. The prediction is that 2AP stacked 5′ or 3′ to T will show similar fluorescent characteristics.

Figure 3.

Jablonski diagram and orbital amplitudes for B-form ^5′T-2AP obtained at the B3LYP/6-311 + G(d) level.

Quenching Mechanisms in 2AP-T Dimers.

A comparison of the electronic transitions and electron densities of the A-form and B-form 2AP-T molecules indicates that all should result in quenched 2AP fluorescence. However, the mechanisms of quenching are quite different. In the case of the B-form molecules, quenching is predicted to result from loss of energy in the S₂ excited state through its decay to the S₁ state. A nonradiative transition (internal conversion) from S₂ to S₁ will be rapid, and its rate (k_nrad) will decrease the observed fluorescence lifetime [t = 1/(k_rad + Σ k_nrad)] of any S₂→S₀ emission. In contrast, fluorescence in the A-form dimer will be quenched because of stacking geometry that results in weak oscillator strengths (and slower radiative rates/longer radiative lifetimes) of nearly degenerate S₁→S₀ and S₂→S₀ transitions.

^5′2AP-Cytosine B-Form Dimer.

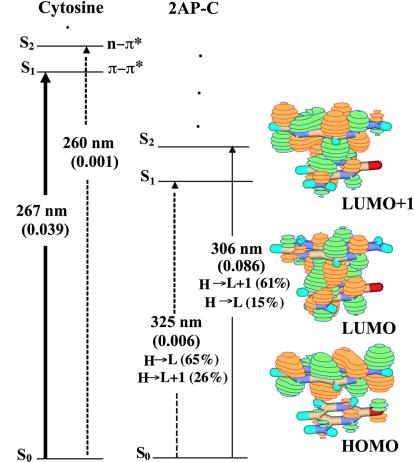
The predicted electronic character of this dimer is similar to that of the 2AP-T B-form dimer, suggesting that it is a property of 2AP flanked by pyrimidine bases (Fig. 4). Again, there is a very weakly allowed S₀→S₁ transition (oscillator strength 0.006), and a stronger S₀→S₂ transition. In the S₂ state, the dominant electronic configuration comes from LUMO + 1, which here has mostly 2AP character (the transition dipole is 1° out of plane). Decay of this state will most probably be to the S₁ state, where much of the electron density is localized on the cytosine ring (there is significant charge-transfer character, with the transition dipole 25° out of plane). The internal conversion from S₂→S₁ will be rapid, and the transition from S₁→S₀ will be dark, so, again, little fluorescence is anticipated from this dimer.

Figure 4.

Jablonski diagrams for cytosine and B-form ^5′2AP-C and orbital amplitudes for ^5′2AP-C obtained at the B2LYP/6-311 + G(d) level.

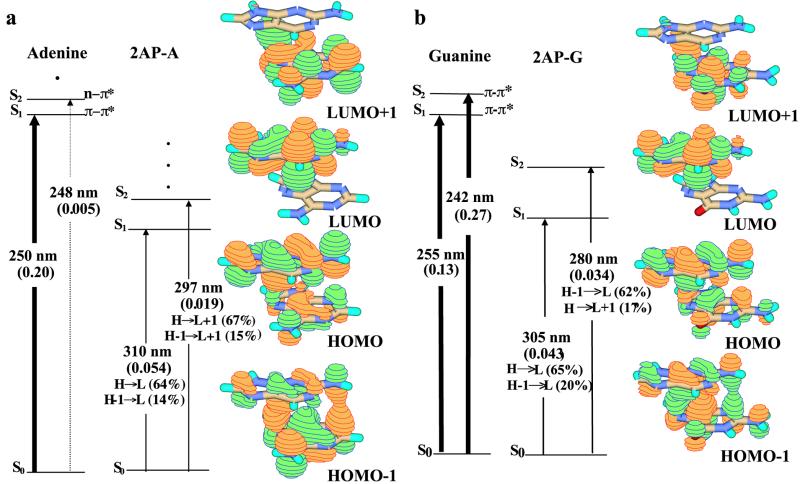
^5′2AP-Purine B-Form Dimers.

To explore the context dependence of 2AP fluorescence, TDDFT calculations were done with B-form 2AP-A and 2AP-G, as shown in Fig. 5. The electronic configurations of both supermolecules appear very similar, showing substantial electron delocalization in HOMO-1 and HOMO, excitations from which dominate the ground-state contributions to the S₀→S₁/S₂ transitions. For 2AP-A, the S₁ state has predominantly 2AP character (LUMO), but S₂ resembles adenine (67% LUMO + 1): an S₁→S₀ transition would be expected to have a radiative lifetime twice that of 2AP (t_rad ≈32 ns), but very little fluorescence is anticipated from the S₂→S₀ transition. The S₁ and S₂ states of 2AP-G both have 2AP-like features because of major contributions from the LUMO configuration: their transition dipoles are in the plane of the base. Oscillator strengths of S₀→S₁ and S₀→S₂ transitions are roughly one-third that of the 2AP S₀→S₁ transition, because of electron delocalization in the ground state [and radiative lifetimes are proportionately longer (t_rad ≈35 ns)]. Fluorescence could arise from both S₂→S₀ and S₁→S₀ transitions, but fluorescence yield will be low, because of the mixed ground-state configuration.

Figure 5.

Jablonski diagrams for (a) adenine and B-form ^5′2AP-A and (b) guanine and B-form ^5′2AP-G obtained at the B3LYP/6-311 + G(d) level. Orbital amplitudes for the dimers are also shown.

Discussion

2-AP has been used for nearly 30 years as a probe of nucleic acid properties. The observed quenching of its fluorescence on introduction into a nucleic acid strand (usually a duplex) is commonly assumed to result from stacking of adjacent nucleobases. The several fluorescent lifetimes observed are interpreted as an indication of contributions from an ensemble of stacking geometries. With the theoretical results described here, it may now be possible to ascribe experimentally observed fluorescent properties of 2AP to a physical origin with more confidence.

Most dimers constructed here mimic 2AP on the 5′ end of a DNA strand. The TDDFT calculations clearly show the influence of the neighboring base on electronic structure and fluorescence of 2AP. With the caveat that these calculations are done in vacuo, which leaves out static and dynamic solvent effects on the emitting states, several predictions of 2AP fluorescence properties result. (i) In B-form ^5′2AP-T, ^5′2AP-C and ^5′T-2AP, the presence of a lower-lying S₁ “dark” state is predicted to cause a loss of fluorescence intensity and a short decay time for S₂ emission, by means of a dynamic process (internal conversion). (ii) Stacking geometry of A-form 2AP-T will quench fluorescence because of the reduction of transition intensity (static quenching) with consequently longer radiative lifetimes. (iii) Both B-form 2AP-A and 2AP-G will exhibit a reduced fluorescence yield as a result of electron delocalization in the ground state (static quenching) and are expected to have longer radiative lifetimes.

2-AP fluorescence is quenched as a result of base stacking, but these calculations show that the mechanism of intensity loss can be static (electron delocalization with weak oscillator strengths) or dynamic (internal conversion). The absolute quantum yield cannot be derived from TDDFT calculations, because rates for nonradiative relaxation out of the excited states are unknown. Quenching of 2AP when in a duplex is characterized by two behaviors during a thermal denaturation experiment: the first is an increase in fluorescence as the duplex is melted (base pairing disrupted and strands separate); the second is a subsequent loss of fluorescence from 2AP in the single-strand state as the temperature continues to increase. Based on these calculations, the first increase in fluorescence because of duplex melting can be ascribed to disruption of stable stacking with its mixed electronic states that quench fluorescence. Loss of 2AP fluorescence from the single-strand state is presumably because of collisional quenching with solvent or other species in solution (any residual stacking in the single strand will be transient because of higher temperature).

Several 2AP fluorescent lifetimes are commonly observed when the nucleobase is part of a DNA or RNA duplex, and these lifetimes are ascribed to degrees of 2AP stacking with nearest neighbors. The ensemble of stacked states could be static or dynamic; as the calculations show, a given stacking geometry would give rise to a lifetime specific to its electronic properties. It seems most likely that there is a continuum of stacked states, as 2AP and its neighboring base pairs “breathe” (exchange of the hydrogen-bonded nucleobase labile hydrogens with bulk water is a rapid process in nucleic acids, and indicates that base pairs are continually opening and closing). The identification of four lifetimes to describe the decay of 2AP fluorescence would thus be optimistic for describing the number of stacked states. If the time scale of base excursion away from the canonical stacked structure is rapid on the scale of fluorescence decay, then there will be many more geometries extant than reported on. If, however, the excursions are slow on the timescale of fluorescence decay rates, then the observed lifetimes may report on the most populated (statically) stacked states.

As a final scenario, it is possible that quenching of 2AP fluorescence occurs most efficiently within a single stacked conformation. The extent of quenching observed (with a characteristic lifetime) would thus report on the probability of that conformation occurring, and would vary with solution conditions, temperature, and nearest neighbors. In this case, the event that leads to loss of fluorescence could be described as diffusion in a single well in the potential energy landscape of conformational space; such a representation has been used to describe the coupling of low frequency torsional motion and nonradiative electronic relaxation in a variety of systems (26), and may apply here.

2AP in a Nucleic Acid.

Addition of a second stacked nucleobase, M-2AP-N, is certain to unpredictably alter 2AP fluorescent properties, and these calculations will be necessary to fully understand behavior of 2AP in this common biological context. Given that TDDFT calculations show significant charge–transfer (or orbital overlap) of stacked nucleobases, it is also worth considering the contributions of next-nearest neighbors to the electronic properties of 2AP (and its resulting fluorescence).

In a nucleic acid duplex, 2AP can hydrogen bond with thymine, uracil, or cytosine. TDDFT calculations of 2AP base-paired to cytosine or thymine, with and without solvent, will show the effects of hydrogen-bonding on the π–π* and n–π* transitions and state ordering. TDDFT results clearly indicate that any structural interpretation of 2AP fluorescence decay laws and steady state yields in a DNA or RNA strand will be complicated by contributions not only from the ensemble of stacked states but also from unique electronic properties because of nearest neighbor bases. Subsequent calculations should greatly improve our ability to interpret the spectra of 2AP-containing nucleic acids, and thus extend our description of their structure and dynamics.

Abbreviations

2AP

2-aminopurine

TDDFT

time-dependent density functional theory

HOMO

highest occupied molecular orbital

LUMO

lowest unoccupied molecular orbital