Role of the N-terminal negative charges of actin in force generation and cross-bridge kinetics in reconstituted bovine cardiac muscle fibres

Abstract

Mutant yeast actins were used to determine the role of actin's N-terminal negative charges in force generation. The thin filament was selectively removed from bovine cardiac skinned muscle fibres by gelsolin, and the actin filament was reconstituted from purified G-actin. In this reconstitution, yeast wild-type actin (2Ac: two N-terminal negative charges), yeast mutant actins (3Ac and 4Ac), and rabbit skeletal muscle actin (MAc) were used. The effects of phosphate, ATP and ADP on force development were studied at 25°C. With MAc, isometric tension was 77% of the initial tension owing to the lack of a regulatory system. With 2Ac, isometric tension was 10% of the initial tension; with 3Ac, isometric tension was 23%; and with 4Ac, isometric tension was 44%. Stiffness followed a similar pattern (2Ac < 3Ac < 4Ac < MAc). A similar trend was observed during rigor induction and relaxation. Sinusoidal analysis was performed to obtain the kinetic constants of the cross-bridge cycle. The results showed that the variability of the kinetic constants was ≤ 2.5-fold among the 2Ac, 4Ac and MAc muscle models. When the cross-bridge distribution was examined, there was no significant reapportionment among these three models examined. These results indicate that force supported by each cross-bridge is modified by the N-terminal negative charges of actin, presumably via the actomyosin interface. We conclude that two N-terminal negative charges are not adequate, three negative charges are intermediate, and four negative charges are necessary to generate force.

The interaction of actin with myosin to form the actomyosin complex can be characterized by two binding states: the initial formation of a weak interaction followed by an isomerization to a strong interaction during which the power stroke occurs that produces the force necessary for muscle contraction. The difference in these two states can be seen by the resistance of the actomyosin complex to increasing ionic strength suggesting that a major component of the strong interaction involves a series of hydrophobic interactions in the actin–myosin interface. This hypothesis is consistent with the interpretation of experiments in which an elevation of temperature resulted in larger force generation (Zhao & Kawai, 1994a; Coupland et al. 2001) and a larger association constant of actin and myosin (Tonomura et al. 1962; Highsmith, 1977). A computerized docking study demonstrated the significance of the hydrophobic and stereospecific interactions between actin's α-helix (residues 338–354) and myosin's helix–loop–helix motif (residues 516–558) (Rayment et al. 1993a; Holmes et al. 2004).

In contrast, the weak interaction is believed to be dictated in large part by an electrostatic interaction between the acidic N-terminal finger of actin and the cationic loop 2 (residues 633–642 of myosin) that joins the 50K and 20K domains of the myosin head. In muscle myosin, this loop contains five positively charged Lys residues. The N-terminus of actin contains between two negative charges (yeast actin) and four negative charges (mammalian and avian muscle actins). Neither the myosin loop 2 (Rayment et al. 1993b) nor the actin acidic N-terminal finger (Kabsch et al. 1990) is ordered in crystal structures of the two proteins. The first evidence that actin's N-terminal acidic residues were involved in actin-activated ATP hydrolysis rate of myosin S1 came from blocking experiments with antibodies directed toward residues 1–7 of muscle actin (DasGupta & Reisler, 1989, 1992). The results showed that this antibody had a major inhibitory effect both on the actomyosin binding and the ATP hydrolysis rate. In another study, substitution of the N-terminal acidic residues in Dictyostelium discoideum actin with His abolished actomyosin ATPase activity and the movement of actin filaments in an in vitro motility assay (Sutoh et al. 1991), but the movement could be restored by the inclusion of methylcellulose, which prevented the filaments from diffusing away from the anchored myosin molecules (Johara et al. 1993).

The involvement of these N-terminal residues in the actomyosin interaction was addressed further by a series of studies using mutant yeast actins in which the number of N-terminal negative charges was varied from 0 to 4 (Cook et al. 1993; Crosbie et al. 1994; Miller et al. 1996). In solution, wild-type (WT) yeast actin (two negative charges) only produced about 10% of the activation of the muscle myosin S1 ATPase activity as is observed with muscle actin (Cook et al. 1993). However, they showed that simply increasing the N-terminal acidic residues from two to the four contained in muscle actins increased the effectiveness of the yeast actin activation to about 35–40% of that achieved with muscle actin, although only two acidic residues were necessary for maximal binding of actin to myosin under weak or strong binding conditions. These results led to the interpretation that, in addition to facilitating formation of the weak interaction, the actin N-terminal acidic residues play a significant role in the isomerization of the complexes from the weak to the strong interaction.

Although the above results have suggested that actin's N-terminal acidic residues may be important in force generation, the significance of these charges has not been established in muscle fibres in which force can be directly measured. A recent establishment of the system in which we can selectively remove the thin filament from cardiac muscle fibres and replace the filament with exogenous proteins to reconstitute a force-generating fibre (Fujita et al. 1996, 2002; Lu et al. 2003) has now enabled us to address the question of the significance of actin's N-terminal negative charges on force generation. We show that yeast actin can be used to reconstitute the actin filament in cardiac muscle fibres in which the thin filament is extracted, and that these fibres allow the measurement of force generation and the use of sinusoidal analysis. With this system, we report that force is minimal for fibres reconstituted with wild-type yeast actin with two negative charges (2Ac) and that force increases as the negative charge is increased from two to three (3Ac), and three to four (4Ac). The greatest force was generated by muscle actin (MAc), demonstrating that factors other than N-terminal negative charge also play an important role. With sinusoidal analysis, we found that there is no large scale reapportionment in cross-bridge states, indicating that the actin's N-terminal negative charge affects force supported by each cross-bridge.

Methods

Solutions

The details of solution compositions used in the current report were published in Lu et al. (2003). In brief, the relaxing solution contained (mm): 6 K₂H₂EGTA (EGTA), 2.2 Na₂MgATP (MgATP), 5 Na₂K₂ATP (ATP), 8 K_1.5H_1.5PO₄ (P_i), 41 sodium propionate (NaProp), 75 potassium propionate (KProp), 40 2,3-butanedione 2-monoxime (BDM), and 10 3-(N-morpholino) propane sulphonic acid (Mops). The standard activating solution (5S8P) contained 6 K₂CaEGTA (CaEGTA), 5.8 MgATP, 1.36 ATP, 8 P_i, 15 Na₂CP (CP), 1 NaProp, 73 KProp, 10 NaN₃, 10 Mops, and 320 units ml⁻¹ creatine kinase (CK). It is important to note here that, in reconstituted muscle fibres in the absence of Tm and Tn, 40 mm BDM is used to inhibit the actomyosin interaction and force generation (Herrmann et al. 1992; Zhao & Kawai, 1994b), and its absence permits fibre activation. Ca²⁺ was included for consistency. Any other activating solutions are variations of this solution. The pCa (=−log[Ca²⁺]) of all activating solutions was 4.36–4.66, the Mg²⁺ concentration was 0.5 mm, the total Na was 55 mm, ionic strength was 200 mm, and pH was adjusted to 7.0. Other than those used for the ADP study (0D–3D series), all activating solutions contained 15 mm CP and 320 units ml⁻¹ (0.64 mg ml⁻¹) CK. The rigor solution contained 55 NaProp, 122 KProp, 8 P_i, and 10 Mops.

Measurements to assess active force generation and cross-bridge kinetics were performed at 25°C; extraction, reconstitution, and relaxation of cardiac muscle fibres were performed at 0–2°C.

Na₂CP, Na₂H₂ATP, Na₂H₂ADP, Mops, H₄EGTA, and P¹,P⁵-di(adenosine-5′) pentaphosphate (lithium salt) were purchased from Sigma Chemical Co. (St Louis, MO, USA); CaCO₃, Mg(OH)₂, NaOH, KOH, KH₂PO₄, K₂HPO₄, NaN₃, and propionic acid from Fisher Scientific Co. (Itasca, IL, USA); and CK from Boehringer Mannheim (Indianapolis, IN, USA).

Muscle fibres and proteins

Fresh bovine hearts were obtained from a slaughterhouse and immediately cooled with ice. The muscle bundles (∼2 mm in diameter, ∼10 mm in length) were excised from a straight portion of the right ventricular trabecular muscles and soaked in a Na-skinning solution which consisted of (mm): 2 DTT (dithiothreitol), 30 BDM, 10 EGTA, 5 ATP, 2 MgATP, 122 NaProp and 10 Mops (pH 7.0) for 2.5 h at 0°C to minimize contraction. Then the solution was replaced with a K-skinning solution containing 2 DTT, 30 BDM, 10 EGTA, 5 ATP, 2 MgATP, 122 KProp and 10 Mops (pH 7.0), and stored overnight at 0°C. The Na⁺-based solution, low temperature, BDM, EGTA and MgATP were used to relax the preparation and to minimize force generation. The solution was further replaced twice with the storage solution containing 50% (v/v) glycerol, 2 DTT, 30 BDM, 10 EGTA, 5 ATP, 2 MgATP, 122 KProp and 10 Mops (pH 7.0) and stored at −20°C.

The yeast actins were purified by DNAase I affinity chromatography as described by Cook et al. (1992). Muscle actin was extracted and purified from acetone powder (Kondo & Ishiwata, 1976) of rabbit white skeletal muscles as described by Spudich & Watt (1971). The acetone powder was a gift from Professor Shin'ich Ishiwata of Waseda University, Tokyo. For wild-type yeast actin, the source was yeast cakes obtained from a local bakery. 4Ac actin was prepared from a 4Ac yeast strain as previously described (Cook et al. 1993).

Generation of yeast 3Ac actin

Using the QuickChange site-directed mutagenesis kit from Stratagene, the WT yeast actin coding sequence contained on a centromeric plasmid pRS314 was changed at Ser³ (TCT) and Glu⁴ (GAG) to Glu³ (GAG) and Asp⁴ (GAT), respectively, using the following complementary set of DNA primers obtained from Integrated DNA Technologies (Coralville, IA, USA). (5′-CTGAATTAACCATGGATGAGGATGTTGCTGCTTTGGTTTG-3′). A haploid yeast strain expressing the mutant actin, referred to as 3Ac, as the sole actin in the cell was generated using a plasmid shuffling procedure as previously described by Chen et al. (1995). The mutant plasmid was then rescued from the cell and sequenced to verify that the desired mutation remained intact.

Muscle preparations for mechanical analysis

A thin strip of bovine cardiac muscle fibres (∼3 mm in length, 85–145 μm in width) was dissected from the stock bundle and glued to the experimental apparatus by nail polish: one end was connected to the tension transducer, and the other end to the length driver via stainless steel wires (210 μm in diameter). Care was taken to minimize the amount of nail polish used. The preparation was further skinned in a relaxing solution that contained 1% (v/v) Triton X-100 for 20–25 min at 25°C. Muscle length was adjusted to give minimal tension in the relaxing solution. The average sarcomere length was 2.0 μm, and it ranged between 1.9 and 2.1 μm as detected by confocal microscopy (Fujita et al. 2002) and electron microscopy (Lu et al. 2003). At this time, the length (L₀) and the diameter were measured. From the diameter, the cross-sectional area was estimated assuming a circular shape.

Extraction and reconstitution of the thin filament

The preparation was briefly activated with the standard activating solution at 25°C to assess the initial tension (T_init). The preparation was then treated by an extracting solution that contained 0.3 mg ml⁻¹ gelsolin, 2 mm CaEGTA, 2.2 mm ATP, 4.25 mm MgCl₂, 121 mm KCl, 2 mm leupeptin, 2 mm DFP, 40 mm BDM, and 20 mm Mops (pH 7.0) for 50–90 min to remove the thin filaments (Fujita et al. 1996, 2002); gelsolin was prepared from bovine plasma as described by Kurokawa et al. (1990). The extent of the removal was examined by monitoring the active tension at 25°C. When the active tension was almost gone (∼6%), the extraction was stopped by replacing the solution with the relaxing solution that included BDM.

Fibres from which the thin filament had been extracted were reconstituted in a solution that contained 1 mg ml⁻¹ G-actin, 4 mm EGTA, 4 mm MgATP, 40 mm BDM, 80 mm KI, 8 mm KCl, 20 mm P_i, and pH adjusted to 7.0 (Fujita et al. 1996, 2002). We used the following four kinds of G-actin for reconstitution: (a) yeast wild-type actin which has two N-terminal negative charges (acetyl-Met-Asp-Ser-Glu-Val-…) (2Ac), (b) yeast mutant actin with three N-terminal negative charges (acetyl-Met-Asp-Glu-Asp-Val-…) (3Ac), (c) yeast mutant actin with four N-terminal negative charges (acetyl-Met-Asp-Glu-Asp-Glu-Val-…) (4Ac), and (d) rabbit skeletal muscle actin with four N-terminal negative charges (acetyl-Asp-Glu-Asp-Glu-Thr-…) (MAc). The four kinds of reconstituted fibres are referred to as the 2Ac (muscle) model, the 3Ac (muscle) model, the 4Ac (muscle) model, and the MAc (muscle) model, respectively. The reconstitution solution was replaced every 7 min 8 times (56 min total) to avoid spontaneous nucleation of actin in the muscle chamber. The volume of the muscle chamber was 80 μl. The reconstituted fibres were spontaneously active, because they lacked the troponin–tropomyosin regulatory system normally present on the thin filament. For this reason, 40 mm BDM was used to relax the preparation. Relaxation was performed at 0°C, because low temperature diminishes force production (Zhao & Kawai, 1994a; Coupland et al. 2001).

Sinusoidal analysis and the kinetic scheme

The length driver was controlled by a PC with 386 CPU (Industrial Computer Source, San Diego, CA, USA) equipped with a 14-bit digital-to-analog converter, and the time course data of length and force signals were collected by two 16-bit analog-to-digital converters. The data were processed to yield complex stiffness, which is the ratio of the force change to the length change expressed in the frequency (f) domain. The complex stiffness was then normalized according to the physical size of the fibre (length and cross-sectional area) to yield the complex modulus Y(f), which is a vector consisting of the real and the imaginary numbers. The dynamic modulus is defined as the length of the vector (= |Y(f)|), which is an indicator of the muscle stiffness at each frequency. Phase shift is defined as the angle measured from the real axis of the Y(f) vector (= arg[Y(f)]). The real part of the complex modulus is called the ‘elastic modulus’, which is an indicator of work storage; the imaginary part is called the ‘viscous modulus’, which is an indicator of work absorption. The ‘Nyquist plot’ is drawn to plot the elastic modulus in the abscissa, and the viscous modulus in the ordinate, with the frequency as an intervening parameter. The details of the sinusoidal analysis were published previously (Kawai & Brandt, 1980).

The complex modulus data were fitted to eqn (1) to determine the apparent rate constants (2πb, 2πc) and their respective magnitudes (B, C) (Kawai & Brandt, 1980; Wannenburg et al. 2000):

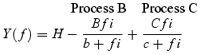(1)

where

and H is a constant. Stiffness is defined as Y_∞=H–B+C. Process B is a middle frequency exponential lag represented by the negative B term in eqn (1). Process C is a fast frequency exponential lead represented by the positive C term in eqn (1). Processes B and C, and Y_∞ correspond to phases 3, 2 and 1, respectively, of step length change analysis as defined by Heinl et al. (1974) and Huxley (1974). Process A or phase 4 is absent in cardiac preparations.

The apparent rate constants were studied as functions of ligand (P_i, MgATP, MgADP) concentrations, and they were analysed in terms of the cross-bridge scheme shown below (Scheme 1) (Kawai & Halvorson, 1991). A is actin, M is myosin, D is MgADP, S is MgATP, P is P_i, phosphate. The upper-case letter K indicates the association or equilibrium constant, and the lower-case letter k indicates the rate constant. These are as a whole called kinetic constants of elementary steps of the cross-bridge cycle.

The equations which relate the apparent rate constants to the kinetic constants of the elementary steps are (Kawai & Halvorson, 1991):

(2)

(3)

where

(4)

and

(5)

In these equations S, D, and P indicate the concentration of respective ligands: S is [MgATP], D is [MgADP], and P is P_i. For the P_i and ATP studies, K₀D is set to 0 in eqn (4). It can be seen from eqns (2)–(5) that both sum and product are hyperbolic functions of ligand concentrations. In particular, eqns (2)–(5) are increasing and saturating functions of S and P, whereas eqns (2)–(4) are decreasing and saturating functions of D.

Sodium dodecyl sulphate (SDS)–polyacrylamide gel electrophoresis (PAGE)

Cardiac muscle fibres at each step of extraction and reconstitution were pooled and dissolved in a sample-diluting buffer (2% SDS, 25% glycerol, 5%β-mercaptoethanol, 62.5 mm Tris-HCl, pH 6.8) and heated for 5 min at 90°C. Ten fibres were dissolved in 60 μl diluting buffer, and 6–15 μl were loaded in each lane of the gel. SDS-PAGE was carried out according to the method of Laemmli (1970) with an 8–16% linear gradient running gel and a 4% stacking gel (Bio-Rad, Hercules, CA, USA). Protein was stained using Coomassie Brilliant Blue R-250. The gel images were photographed by a digital camera and the intensity of bands was quantified by UN-SCAN-ITTM gel (version 5.1) software.

Statistical analysis

Data are expressed as means ±s.e.m. Data were analysed with Student's t test. Statistical comparisons were performed using R program (version 1.7.1, Bell Laboratories, Murray Hill, NJ).

Results

Initial active tension and four muscle models with four actins

The initial tension under the standard activating condition averaged T_init= 32 ± 2 kPa (±s.e.m., n= 49) at 25°C. This value was used to normalize the subsequent tension and complex modulus data. In this way, errors associated with the estimate of the cross-sectional area could be avoided. The thin filament was selectively removed subsequently as described in the Methods. At this stage, the remaining tension averaged 6.6 ± 0.9% (n= 32) of the initial tension. This much of remaining tension is necessary for successful reconstitution of the actin filament (Fujita et al. 1996, 2002). The actin filament was reconstituted from (a) yeast wild type actin which has two N-terminal negative charges (2Ac), (b) yeast mutant actin with three N-terminal negative charges (3Ac), (c) yeast mutant actin with four N-terminal negative charges (4Ac), and (d) rabbit skeletal muscle actin (MAc) (see Methods).

Tension and stiffness of the actin filament reconstituted fibres under the standard activating condition

Under the standard activating condition, tension of the MAc model was 77% of initial tension (T_init) (Table 1). This value is less than 100% because of the absence of the regulatory system. Addition of the regulatory system increases isometric tension to approximately 100% (Fujita et al. 2002; Fujita & Kawai, 2002). Tension of the 2Ac model was 10%, the 3Ac model was 23%, and the 4Ac model was 44% of the initial tension on average (Table 1). The tension values include residual tension (about 6.6%) after gelsolin treatment. Similarly, stiffness (in the T_init unit) of the 2Ac model was 10 ×, the 3Ac model was 25 ×, the 4Ac model was 39 ×, and the MAc model was 71 ×T_init (Table 1). Both tension and stiffness among the four muscle models were significantly different (P < 0.05) from each other as seen from the small s.e.m. in Table 1. Thus, the 3Ac model developed 30% (= 23/77) of tension and 35% (= 25/71) of stiffness generated by the MAc model. Similarly, the 4Ac model developed 57% (= 44/77) of tension and 55% (= 39/71) of stiffness generated by the MAc model. In contrast, the 2Ac model developed only 13% (= 10/77) of tension and 14% (= 10/71) of stiffness of the MAc model. The tension:stiffness ratio was in the vicinity of 1.0–1.1%L₀ in all four muscle models (Table 1).

Table 1.

Isometric tension and stiffness of actin filament reconstituted bovine myocardium in the standard activating solution

Parameter	Unit	2Ac	3Ac	4Ac	MAc
Tension	%Tinit	10 ± 2	23 ± 4	44 ± 4	77 ± 10
Stiffness	Tinit	10 ± 2	25 ± 4	39 ± 2	71 ± 6
Ratio	%L0	1.07 ± 0.17	0.97 ± 0.11	1.13 ± 0.09	1.08 ± 0.09
N		13	11	11	14

Measurements were performed at 25°C, and tension and stiffness were normalized to the initial tension (T_init= 32 ± 2 kPa, n= 49). Data are means ±s.e.m, and the number of experiments (N) is shown in the last row. Statistical analysis demonstrated that both tension and stiffness among four muscle models were significantly different (P < 0.05) from each other. Isometric tension values include the residual active tension (6.6 ± 0.9%, N= 32) after thin filament extraction with gelsolin.

Stiffness during rigor induction and relaxation

The above results concerning active tension and stiffness suggest that actomyosin linkage may be stronger when more negative charges are present in actin's N-terminus. To test this possibility directly, each muscle model was brought into the ‘high rigor’ condition (rigor following high active tension: Kawai & Brandt, 1976), and rigor stiffness and tension were compared (Table 2A). This Table demonstrates that rigor stiffness (in T_init unit) is least for 2Ac (15 ×), intermediate for 3Ac (72 ×), moderate for 4Ac (89 ×), and largest for MAc (127 ×). Statistical analysis demonstrated that the stiffness among the four muscle models was significantly different from each other (P < 0.05), except for the 3Ac and 4Ac muscle models. Rigor tension followed the same pattern (Table 2A). Tension among four muscle models was significantly different (P < 0.05) from each other, except between 4Ac and MAc. These observations indicate that the actomyosin linkage becomes progressively stronger in the order 2Ac < 3Ac < 4Ac < MAc. The ratio of tension/stiffness was in the range of 0.6–0.9%L₀ in all four muscle models, and less than that during activation (Tables 1 and 2A). Quite interestingly, stiffness measured during BDM relaxation at 0°C showed the similar pattern, and their values were in the order 2Ac < 3Ac < 4Ac < MAc (Table 2B). They are statistically different (P < 0.05) from each other except between 3Ac and 4Ac.

Table 2.

Isometric tension and stiffness of actin filament reconstituted myocardium in the rigor solution (A), and Stiffness of actin filament reconstituted myocardium in the relaxing solution (B)

Parameter	Unit	2Ac	3Ac	4Ac	MAc
A
Tension	%Tinit	11 ± 3	42 ± 9	78 ± 6	98 ± 20
Stiffness	Tinit	15 ± 2	72 ± 10	89 ± 7	127 ± 13
Ratio	%L0	0.59 ± 0.10	0.56 ± 0.06	0.90 ± 0.07	0.77 ± 0.12
N	15	8	11	12	12
B
Stiffness	Tinit	4.0 ± 0.8	15.2 ± 2.0	20.7 ± 2.0	32.9 ± 4.3
N		14	10	11	11

T_init= 32 kPa. Statistical analysis demonstrated that rigor tension among four muscle models was significantly different (P < 0.05) from each other, except for the 4Ac and MAc muscle models (P= 0.37); rigor stiffness among the four muscle models was significantly different from each other (P < 0.05), except for the 3Ac and 4Ac muscle models (P= 0.17). Stiffness was measured at 100 Hz.

Analysis of muscle proteins by SDS-PAGE

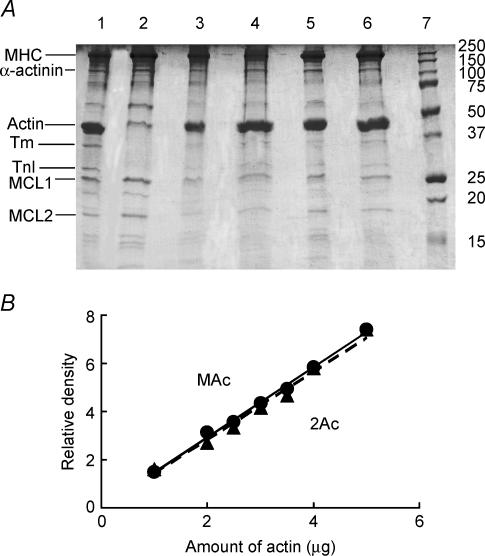
SDS-PAGE was performed to examine the degree of actin reconstitution in four muscle models, and the results are shown in Fig. 1A. Lane 1 is control fibres. Lane 2 is gelsolin-treated fibres: actin, Tm, TnT (underneath the actin band) and TnI are significantly decreased. However, myosin heavy chain (MHC), myosin light chains (MLC1, MLC2), and α-actinin appear to be the same. These results indicate that thin filament proteins were extracted, while thick filament and Z-line proteins were not extracted. Lane 3 is muscle actin reconstituted fibres; lane 4 is 2Ac actin reconstituted fibres; lane 5 is 3Ac actin reconstituted fibres; and lane 6 is 4Ac actin reconstituted fibres. As seen in these lanes, similar amounts of actin are restored in all four muscle models.

Figure 1. SDS-PAGE and the standard curves for MAc and 2Ac actins.

A, SDS-PAGE of cardiac muscle fibres. Lane 1: control myocardium without extraction or reconstitution. Lane 2: gelsolin-treated myocardium. Lane 3: MAc-reconstituted myocardium. Lane 4: 2Ac-reconstituted myocardium. Lane 5: 3Ac-reconstituted myocardium. Lane 6: 4Ac-reconstituted myocardium. Lane 7: molecular mass markers; their molecular masses in kDa are indicated. MHC, myosin heavy chain; MLC, myosin light chain. B, proportionality of the amount of G-actin and relative density on gel. The abscissa values indicate the amount of actin (μg) loaded to one lane of SDS-PAGE. The concentration of G-actin was determined from the absorbance at 290 nm using the extinction coefficient of 0.63 mg⁻¹ ml cm⁻¹. The straight lines are linear regression lines that go through the origin, and the slope is 1.462 for MAc actin, and 1.418 for 2Ac actin.

To quantitatively determine the amount of actin in each lane, the density values of α-actinin and LC1 bands were also obtained in addition to the density of the actin band, and their ratios were averaged and summarized in Table 3A (against LC1) and Table 3B (against α-actinin). In Table 3A, because this ratio was 5.9 in control fibres and it represents 100% of actin, all the ratios in Table 3A were divided by this number to obtain the relative amount of actin in each lane. Similarly in Table 3B, all the ratios were divided by 3.8 to obtain the relative amount of actin in each lane. These results indicate that the amount of actin reconstituted was in the neighbourhood of 100% and approximately the same whether it was normalized against LC1 or α-actinin, indicating that the amount of the actin filament reconstituted may not be too different among the four muscle models. Therefore, the difference in isometric force observed in four muscle models is inherent in the difference in the actin molecule and does not reflect a difference in the extent of reconstitution. The value 20% (Table 3A) or 29% (Table 3B) for gelsolin-treated fibres may appear large, but this is reasonable because the thin filament at the I-band was not extracted and such fibres developed on the average 6.6% of the initial tension, indicating a presence of 6.6% overlap between thick and thin filaments. This amount of residual actin is essential for the successful reconstitution of the actin filament (Fujita et al. 1996, 2002). The proportionality between the actin concentration (in the range used) and the actin intensity on the gel was tested in a separate experiment, and the result is shown in Fig. 1B. As seen here, the proportionality is satisfactory. The Figure also demonstrates that the actin stainability is just about the same for both MAc and 2Ac.

Table 3.

Relative amount of actin based on LC1 (A) and α-actinin (B)

Parameters	Control	Gelsolin	2Ac	3Ac	4Ac	MAc
A
Actin/LC1	6.16 ± 0.56	1.26 ± 0.21	6.64 ± 2.20	6.10 ± 1.43	6.18 ± 1.17	6.92 ± 1.03
*Relative amount of actin (%)	100	20 ± 4	108 ± 37	99 ± 25	100 ± 21	112 ± 20
N	13	5	3	3	3	6
B
Actin/α-actinin	3.80 ± 0.35	1.10 ± 0.21	4.00 ± 0.47	3.06 ± 0.55	5.13 ± 0.36	3.96 ± 0.42
*Relative amount of actin (%)	100	29 ± 6	105 ± 16	81 ± 16	135 ± 16	104 ± 15
N	14	3	5	3	4	4

The intensity of α-actinin, actin, and LC1 bands was measured from SDS-PAGE, the actin intensity was normalized against LC1 intensity in A, and the actin intensity was normalized against α-actinin in B, and averaged. Means ±s.e.m. are shown.

^*The relative amount of actin was obtained by dividing the ratio by that of the control (6.16 ± 0.56 in A, 3.80 ± 0.35 in B) and the errors were propagated.

Effect of phosphate, MgATP and MgADP on fibre tension and stiffness

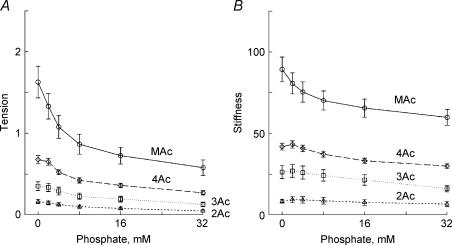
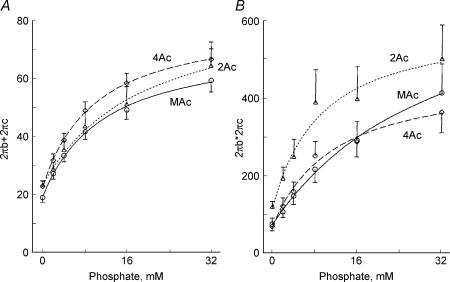
To characterize the force generation and phosphate release steps, we determined the effect of 0–32 mm added P_i on isometric tension and stiffness (Fig. 2). The experiments were carried out in the presence of 5 mm MgATP, 15 mm CP, 320 U ml⁻¹ CK and pCa 4.66. Tension and stiffness decreased with an increase in the P_i concentration in all muscle models. This effect of P_i is consistent with earlier studies on skeletal muscle fibres (Rüegg et al. 1971; Brandt et al. 1982; Cooke & Pate, 1985; Kawai, 1986; Nosek et al. 1987; Hoar et al. 1987; Bowater & Sleep, 1988; Pate & Cooke, 1989; Stienen et al. 1990; Wang & Kawai, 1997; Pate et al. 1998), on skeletal myofibrils (Tesi et al. 2002), as well as on cardiac muscle fibres (Herzig & Rüegg, 1977; Herzig et al. 1982; Kawai et al. 1993; Zhao & Kawai, 1996; Fujita et al. 2002; Lu et al. 2003). In our study, both tension and stiffness were minimal for the 2Ac model, intermediate for the 3Ac model, large for the 4Ac model, and largest for the MAc model. These results are consistent with those in Tables 1 and 2.

Figure 2. The effects of phosphate on tension (A) and stiffness (B).

Experiments were carried out in the presence of 5 mm MgATP. Tension and stiffness were normalized to the initial tension (T_init) that was measured in the standard activating solution, and the averaging was performed for 11–16 experiments. The mean and s.e.m. are shown. ▵, 2Ac reconstituted myocardium (n= 16); □, 3Ac reconstituted myocardium (n= 11); ♦, 4Ac reconstituted myocardium (n= 11); ○, muscle actin (MAc) reconstituted myocardium (n= 14). 0 mm P_i indicates the solution to which no P_i was added.

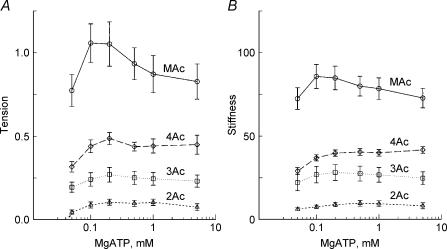
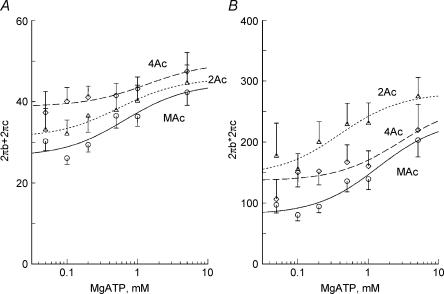
Next, we determined the MgATP dependence of tension and stiffness to characterize steps associated with MgATP binding. The experiments were carried out in the presence of 8 mm P_i, 15 mm CP and 320 U ml⁻¹ CK at pCa 4.36–4.66. A higher P_i concentration than that of in situ (1–3 mm, Maughan & Godt, 1989) was used, because high P_i pushes back the equilibrium of step 5 to steps 2 and 4, hence the resolution of processes B and C are better. As seen in Fig. 3, both tension and stiffness peaked at 0.1–0.2 mm MgATP and almost saturated at 1–5 mm MgATP after a small subsequent decline. This result is consistent with earlier results in skeletal muscle fibres (Kawai & Brandt, 1977; Orentlicher et al. 1977; Ferenczi et al. 1982; Kawai & Halvorson, 1989; Wang & Kawai, 1996) and cardiac muscle fibres (Kawai et al. 1993; Fujita et al. 2002). As in the P_i study, both tension and stiffness increased progressively in the order of 2Ac < 3Ac < 4Ac < MAc.

Figure 3. The effects of MgATP on tension (A) and stiffness (B).

Experiments were carried out in the presence of 8 mm P_i. Average of 11–16 experiments. ▵, 2Ac reconstituted myocardium (n= 16); □, 3Ac reconstituted myocardium (n= 11); ♦, 4Ac reconstituted myocardium (n= 11); ○, muscle actin (MAc) reconstituted myocardium (n= 14). The data were normalized to the initial tension and averaged.

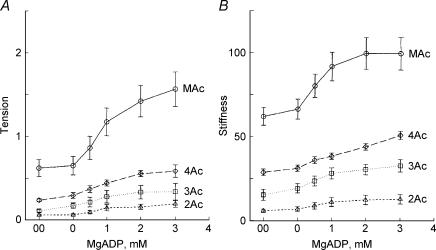
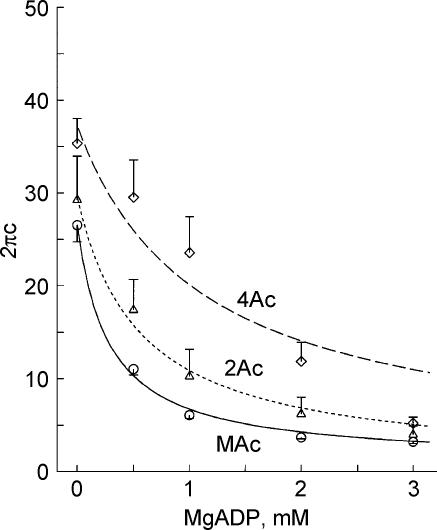
We then determined the MgADP dependence of tension and stiffness to characterize the ADP release step in the four muscle models, and the results are plotted in Fig. 4. The experiments were performed in the presence of 2 mm MgATP and 8 mm P_i at pCa 4.46–4.56 in the absence of CP/CK, but in the presence of 0.2 mm P¹,P⁵-di(adenosine-5′) pentaphosphate, an adenylate kinase inhibitor. With an increase in the MgADP concentration, tension and stiffness increased and approached saturation at high concentration. This result is consistent with earlier results on skeletal muscle fibres (Kawai & Halvorson, 1989; Wang & Kawai, 1996) and cardiac muscle fibres (Fukuda et al. 1998). For a comparative purpose, a special solution named 00D was created that contained CP/CK, but otherwise the same as the 0 mm MgADP (0D) solution. As seen from Fig. 4, the tension and stiffness in the 00D solution were almost the same as in the 0D solution. This result indicates that ADP has very little effect on mechanics at the concentrations in the 0D and 00D solutions, in agreement with previous study (Chase & Kushmerick, 1995). As in the P_i and ATP studies, both tension and stiffness increased progressively in the order of 2Ac < 3Ac < 4Ac < MAc.

Figure 4. The effects of MgADP on tension (A) and stiffness (B).

Experiments were carried out in the presence of 2 mm MgATP and 8 mm P_i. Average of 11–16 experiments. The means and s.e.m. are shown. ▵, 2Ac reconstituted myocardium (n= 16); □, (3Ac reconstituted myocardium (n= 7); ♦, 4Ac reconstituted myocardium (n= 8); ○, muscle actin (MAc) reconstituted myocardium (n= 14). The data were normalized to the initial tension and averaged.

Kinetic analysis of the actin reconstituted muscle models

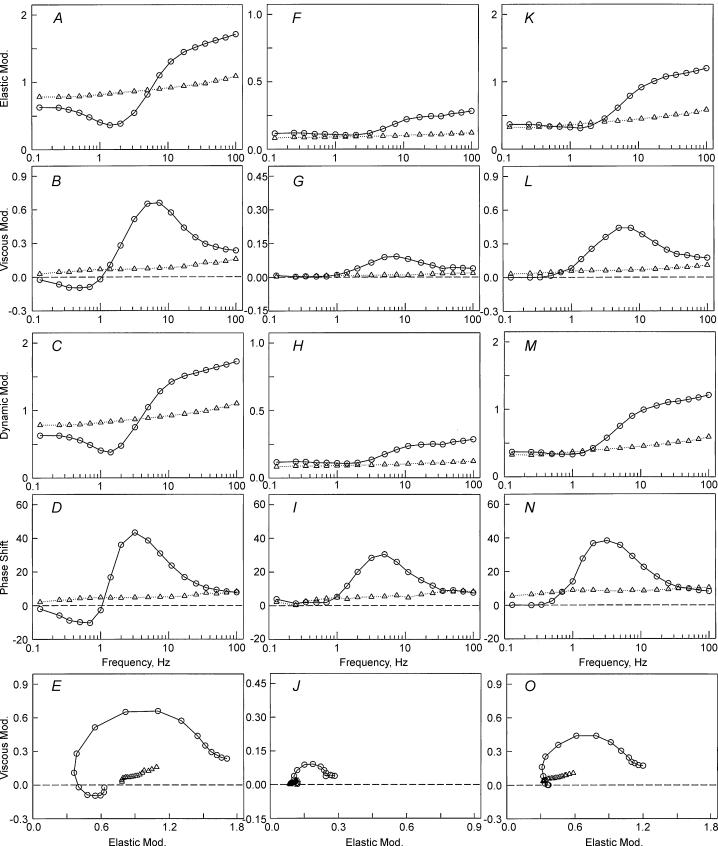
To determine if the variation in tension among four muscle models is based on the change in cross-bridge distribution, sinusoidal analysis was performed at each activation to obtain the kinetic constants of the elementary steps of the cross-bridge cycle (scheme 1). When steady tension developed, the length of the fibres was oscillated in 18 frequencies ranging from 0.13 Hz to 100 Hz with an amplitude of 0.125%L₀, and the complex modulus data Y(f) were obtained taking about 40 s. Because tension of the 2Ac model was only ∼10%, the complex modulus data were noisy and often not suitable for fitting to eqn (1). Therefore, the data from many (11–16) experiments were pooled, and Y(f) was averaged at each frequency. The complex moduli of the other muscle models were treated in the same way, and the results are shown in Fig. 5 at the standard activating condition for MAc, 2Ac and 4Ac muscle models (open circles). The frequency response of actin reconstituted fibres is in general similar to that of the control cardiac muscle fibres (Rossmanith et al. 1986; Shibata et al. 1987; Kawai et al. 1993; Zhao & Kawai, 1996; Wannenburg et al. 2000; Fujita et al. 2002). The dynamic modulus data of the 2Ac model were smallest of the three muscle models, those of the 4Ac model were in the middle, and those of the MAc model were largest. The complex modulus data of relaxed fibres at 0°C are also included in Fig. 5 (open triangles). Figure 5A and K demonstrates that, at frequencies less than ∼5 Hz, the dynamic modulus of activated fibres is smaller than that of relaxed fibres. In other words, activated fibres were less stiff than relaxed fibres at these frequencies. Figure 5A and K also demonstrates that, at frequencies greater than ∼5 Hz, the dynamic modulus is larger than that of relaxed fibres. demonstrates that oscillatory work is present in the MAc model, as evidenced by the negative phase shift or negative viscous modulus, but the oscillatory work is barely visible or not detectable in 4Ac and 2Ac models. further demonstrates that the resting stiffness is progressively larger in the order of 2Ac < 4Ac < MAc, which is consistent with the results in Table 2B. These results imply that the resting stiffness in these fibres is also carried by actin, hence by actomyosin cross-bridges, although the frequency response is typical of biopolymers (monotonic and weakly increasing function of frequency), and does not exhibit cycling cross-bridge characteristics.

Figure 5. The complex modulus Y(f) of reconstituted myocardium.

The complex modulus Y(f) of reconstituted myocardium based on muscle actin (A–E), 2Ac (F–J) and 4Ac (K–O). ○, obtained during standard activation; ▵, obtained during BDM relaxation. A, F and K, plots of elastic modulus versus frequency. B, G and L, plots of viscous modulus versus frequency. C, H and M, plots of dynamic modulus versus frequency. D, I and N, plots of phase shift versus frequency. E, J and O, Nyquist plots. The units of elastic, viscous and dynamic moduli are MPa; the units of phase are degrees. Note the reduced scale in F, G, H and J. The complex modulus data are based on the average of 11–16 experiments. Frequencies used are (Hz): 0.13, 0.25, 0.35, 0.5, 0.7, 1.0, 1.4, 2.0, 3.1, 5.0, 7.1, 11, 17, 25, 35, 50, 70 and 100.

The complex modulus data were fitted to eqn (1), and the apparent rate constants 2πb and 2πc were deduced. Because in cardiac muscle fibres, 2πc is not very much larger than 2πb, it may be more proper to use the sum and product of these rate constants (eqns (2) and (3)) than their approximate formulae to deduce the kinetic constants of elementary steps of the cross-bridge cycle (scheme 1). This method was used earlier in ferret cardiac muscle fibres (Kawai et al. 1993). The sum and product were plotted in Fig. 6 for the P_i study, and in Fig. 7 for the MgATP study for the same experiments shown in Figs 2 and 3, respectively. With an increase in the P_i concentration, both sum and product increased and approached saturation at high P_i concentrations (Fig. 6). Similarly, with an increase in the MgATP concentration, both sum and product increased and approached saturation at high MgATP concentrations (Fig. 7). In general, plots from all muscle models were similar and may not be significantly different from each other. The effect of P_i on the apparent rate constants is consistent with earlier data on fast twitch skeletal muscle fibres (Hibberd et al. 1985; Kawai, 1986; Fortune et al. 1991; Kawai & Halvorson, 1991; Dantzig et al. 1992; Walker et al. 1992), slow twitch skeletal muscle fibres (Wang & Kawai, 1997), and cardiac muscle fibres (Kawai et al. 1993; Zhao & Kawai, 1996; Fujita et al. 2002; Lu et al. 2003). Similarly, the effect of MgATP on the apparent rate constants is consistent with earlier data on fast twitch skeletal muscle fibres (Kawai, 1978; Kawai & Halvorson, 1989), slow twitch skeletal muscle fibres (Wang & Kawai, 1996) and cardiac muscle fibres (Kawai et al. 1993; Zhao & Kawai, 1996; Lu et al. 2003).

Figure 6. The effects of phosphate on the sum (A) and the product (B) of 2πb and 2πc.

The data were obtained from the same experiments shown in Fig. 2. ▵, 2Ac reconstituted myocardium (n= 13–15); ○, 4Ac reconstituted myocardium (n= 9); ♦, muscle actin (MAc) reconstituted myocardium (n= 13–14). Continuous curves are based on eqns (2) and (3) with best fit parameters. Units of the ordinates are s⁻¹ (A) and s⁻² (B).

Figure 7. The effect of MgATP on sum (A) and product (B) of the rate constants 2πb and 2πc.

The data were obtained from the same experiments shown in Fig. 3. The sum and product of the rate constants 2πb and 2πc are plotted as a function of the MgATP concentration. ▵, 2Ac reconstituted myocardium (n= 6–14); ♦, 4Ac reconstituted myocardium (n= 5–10); ○, muscle actin (MAc) reconstituted myocardium (n= 13–14). Continuous curves are based on eqns (2) and (3) with best fit parameters.

Figure 8 plots the apparent rate constant 2πc against the MgADP concentration. As seen in Fig. 8, 2πc decreased hyperbolically and approached saturation with an increase in the MgADP concentration. The rate constant 2πc was smallest for the MAc model, intermediate for the 2Ac model, and largest for the 4Ac model, but this difference may not be significant.

Figure 8. The effect of MgADP on the rate constant 2πc.

The rate constant 2πc is plotted as a function of ADP concentration. The data were obtained from the same experiment shown in Fig. 4. ▵, 2Ac reconstituted myocardium (n= 8–16); ♦, 4Ac reconstituted myocardium (n= 9–11); ○, muscle actin (MAc) reconstituted myocardium (n= 8). Continuous curves are based on eqn (2) with best fit parameters.

The data in Figs 6–8 were fitted to eqns (2)–(5), and the kinetic constants that characterize cross-bridge scheme 1 were deduced for the three muscle models (Table 4). The MgADP association constant (K₀) decreased by 80% going from 2Ac to 4Ac actin, and the MgATP association constant (K₁) decreased by 60% over the same change. The equilibrium constant for the cross-bridge detachment step (K₂) decreased by 40%. The equilibrium constant of the force generation step (K₄) was about the same, and the P_i association constant (K₅) increased by 100%. The rate constants of steps 2 and 4 changed slightly. If we exclude K₀, then the biggest change among the kinetic constants is × 2.5 in K₁.

Table 4.

The kinetic constants of actin filament reconstituted myocardium

Constant	Unit	2Ac	4Ac	MAc
K0	mm−1	9.4	2.1	16.8
K1	mm−1	1.81	0.74	1.50
K2	—	0.67	0.40	1.00
K4	—	0.24	0.26	0.12
K5	mm−1	0.052	0.099	0.086
k2	s−1	14.6	10.8	17.9
k−2	s−1	21.9	27.3	17.9
k4	s−1	15.6	14.7	6.2
k−4	s−1	65	57	54

The apparent rate constants 2πb and 2πc were fitted to eqns (2)–(5) to find the kinetic constants. The best fit parameters are listed. All measurements were performed at 25°C.

Probability of cross-bridges at various states

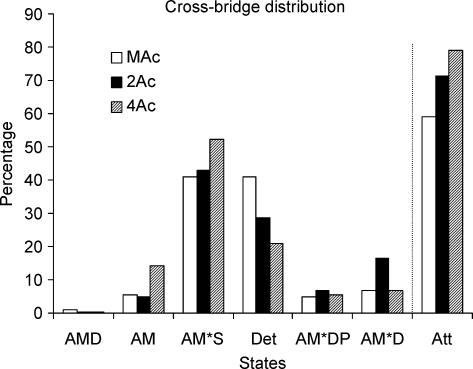
To examine how much the observed change in the kinetic constants affects the distribution of cross-bridges at the various states in three muscle models, the probability in each state was calculated based on eqns (8)–(13) of Zhao & Kawai (1996), the equilibrium constants listed in Table 4, and the standard activating condition (5 mm MgATP, 8 mm P_i). Because CP/CK are present in these solutions, the ADP concentration is estimated to be ∼0.01 mm (Meyer et al. 1985), therefore K₀ does not affect the distribution much. The result is plotted in Fig. 9. The last column in Fig. 9 labelled ‘Att’ is the sum of strongly attached states. It can be seen in this Figure that the total number of strongly attached cross-bridges increased by 8% (= 79–71%) from the 2Ac model to the 4Ac model. From the 4Ac to MAc model, the number of strongly attached cross-bridges decreased by 20% (= 59–79%). From these, it can be concluded that the variation in the cross-bridge distribution in the strongly attached states (∼10% if any) is much less than the variation in tension (4- to 8-fold) among three muscle models.

Figure 9. Cross-bridge distribution.

Calculated cross-bridge distribution in muscle actin reconstituted myocardium (open bars), 2Ac reconstituted myocardium (filled bars) and 4Ac reconstituted myocardium (hatched bars). The bars labelled Det are the sum of all detached states (MS, MDP) and weakly attached states (AMS, AMDP) and the same as X₃₄ in scheme 1. The bars labelled Att are the sum of all strongly attached states (AM, AM*S, AM*DP, AM*D, and AMD). The estimate of the error for this plot is about 20% of the value.

Force generated (or supported) by each cross-bridge

Because the total force can be modelled as the sum of force generated by each cross-bridge that is arranged in parallel in a half sarcomere, and because each cross-bridge state supports a specific amount of tension, the total isometric tension can be calculated by eqn (6) (Kawai & Zhao, 1993; Wang & Kawai, 1997):

(6)

where X_j is the probability of cross-bridges at state j and as defined in scheme 1, and T_j is the tension if all the cross-bridges are at state j. T_j was experimentally deduced on rabbit soleus slow twitch fibres (Wang & Kawai, 1997): T₀= 1.31T_c, T₁= 1.12T_c, T₂= 0.81T_c, T₃₄= 0, T₅= 1.29T_c, and T₆= 1.29T_c, where T_c is the control tension and depends on the muscle model. From eqn (6) and Fig. 9, the following theoretical isometric tension can be deduced.

Tension = 0.71T_c for the 2Ac model, 0.75T_c for the 4Ac model, and 0.56T_c for the MAc model. By equating the observed tension (Table 1) to the theoretical tension, 0.10 T_init= 0.71T_c (2Ac model), 0.44T_init= 0.74T_c (4Ac model), and 0.77T_init= 0.56T_c (MAc model) can be obtained. From this, T_c can be deduced as: T_c= 0.10/0.71T_init= 0.14T_init for the 2Ac model. Similarly, T_c= 0.44/0.74T_init= 0.59T_init for the 4Ac model, and T_c= 0.77/0.56T_init= 1.38T_init for the MAc model can be deduced (Table 5). As seen in these T_c values, each cross-bridge of the 2Ac model develops 10% tension (= 0.14/1.38) of the MAc model, and each cross-bridge of the 4Ac model develops 43% tension (= 0.59/1.37) of the MAc model.

Table 5.

Relative tension and stiffness on each cross-bridge

Parameter	Unit	2Ac	4Ac	MAc
Tension (Tc)	%Tinit	14	59	138
Stiffness (Ya)	Tinit	14	49	120
Tc/Ya	%L0	1.01	1.20	1.15

These values were deduced as described in Results

Stiffness of each cross-bridge

To a first approximation, the stiffness is the same for all strongly attached cross-bridges (Kawai & Halvorson, 1991; Kawai & Zhao, 1993). Therefore, the total stiffness (Y_∞) is given by:

(7)

where X_a is the probability of strongly attached cross-bridges (X_a=X₀+X₁+X₂+X₅+X₆), and Y_a is the stiffness of the fibres if all the cross-bridges are strongly attached. X_a is calculated and shown in Fig. 9 (Att), and Y_a depends on the muscle model. X_aY_a can be equated to the observed stiffness in Table 1, such as 0.71Y_a= 10T_init, from which Y_a= 10/0.71T_init= 14T_init can be deduced for the 2Ac model. Similarly, 0.79Y_a= 39T_init, from which Y_a= 39/0.79T_init= 49T_init can be deduced for the 4Ac model; and 0.59Y_a= 71T_init, from which Y_a= 71/0.59T_init= 120T_init can be deduced for the MAc model (Table 5). As seen in these Y_a values, each cross-bridge of the 2Ac model supports 12% of the stiffness (= 14/120) of the MAc model, and each cross-bridge of the 4Ac model supports 41% of the stiffness (= 49/120) of the MAc model. These values are similar to the force supported by each cross-bridge as mentioned above; hence, the ratio T_c/Y_a is about the same for all three muscle models, and ranges from 1.0 to 1.2%L₀ (Table 5).

Discussion

The focus of this study was to assess the importance of the role played by the N-terminal negative charge of actin in force generation using reconstituted cardiac muscle fibres at 200 mm ionic strength. This physiologically relevant system is a more direct approach than previously employed methods: the actin-activated S1 ATPase measurement and in vitro motility assay, both of which are carried out in low ionic strength (∼50 mm) solutions. Our studies demonstrate that we can reconstitute a muscle fibre with yeast actins, and that the extent of reconstitution is independent of the actin's N-terminal negative charge density (Fig. 1, Table 3). This reconstituted yeast/muscle system develops force and was amenable to sinusoidal analysis to assess elementary steps of the cross-bridge cycle. Most importantly, we were able to demonstrate that force development correlated with increasing negative charge density at the actin's N-terminus (Table 1).

It has been recognized for some time that the negatively charged actin N-terminus (Vandekerckhove & Weber, 1978; Ng & Abelson, 1980) is essential for the initial interaction of actin and myosin (Sutoh, 1982a; Sutoh & Hatano, 1986; Cook et al. 1993; Crosbie et al. 1994; Miller et al. 1996; Hansen et al. 2000). The reason postulated for this involvement is an electrostatic attractive force between the negatively charged N-terminus of actin and the positively charged loop 2 of myosin containing five Lys residues, which leads to an initial weak binding between the two proteins (Sutoh, 1982b; Rayment et al. 1993a; Miller et al. 1996). This weak binding would lead to a stronger, more stereospecific binding between the actin and myosin involving hydrophobic residues from both proteins leading to force generation (Tonomura et al. 1962; Highsmith, 1977; Rayment et al. 1993a; Zhao & Kawai, 1994a; Murphy et al. 1996; Kawai, 2003).

Our results with the reconstituted cardiac muscle fibre system demonstrate that both isometric tension and stiffness doubled when 3Ac yeast actin (3 negative charges) was used instead of 2Ac actin, that these values doubled again when 4Ac yeast actin was used instead of 3Ac, and that they doubled further when MAc (4 negative charges) was used instead of 4Ac actin (Table 1). A similar trend was found during rigor induction (Table 2A) and relaxation (Table 2B). These results correlate well with those obtained from S1 ATPase measurement in solution and in vitro motility assays. Replacement of the negatively charged N-terminal acidic residues with positively charged His in Dictyostelium discoideum actin led to a decreased movement in in vitro motility assay and an inactivation of S1 ATP hydrolysis rate in solution (Sutoh et al. 1991). Miller et al. (1996) used NEM-HMM to add a load to the reconstituted filament in an in vitro motility system in which they compared two yeast actins 2Ac and 4Ac. They found that at low ionic strength and in the presence of methylcellulose, which promotes the actomyosin interaction, the velocity of the 4Ac actin filament was much faster than that observed with the 2Ac actin filament and suggested that this reflected an increase in force that was dependent on the increased N-terminal negative charge density. Similarly, the fourfold increase in force we observed from 2Ac to 4Ac muscle models (Table 1) can be attributed to the increase in N-teminal negative charge density. Furch et al. (1998) carried out a complementary study on the effect of an added positive charge to myosin loop 2 on actomyosin ATPase activity. They observed that an increased positive charge led to an increased rate of association of actin and myosin: the increased electrostatic force between two proteins enhanced actomyosin interaction, in agreement with our results.

The enhanced interaction and force generation as a result of increased actin N-terminal negative charge density could result from a number of factors singly or in combination. (1) It could facilitate formation of the weak interaction providing a greater opportunity for the development of force-producing heads; (2) it could be actively involved in the change from the weak to strong interaction at the actin–myosin interface; and (3) it could allosterically affect the ability of myosin to bind actin and hydrolyse ATP. Our results with sinusoidal analysis help discriminate among these possibilities. Both tension and stiffness increase significantly (∼4-fold) in the order from 2Ac to 4Ac muscle models during the standard activation (Table 1), which cannot be explained by the small increase (∼10%) of the strongly attached cross-bridges as projected in Fig. 9. The mechanism which could explain both the tension and the stiffness data in 2Ac–4Ac muscle models is that an increase in the N-terminal negative charges of actin somehow results in an increase in the stereospecific and hydrophobic interaction between actin and myosin molecules. When the interaction is stronger, both tension and stiffness become larger. This mechanism is consistent with our results on rigor tension and stiffness, which become progressively stronger in the order 2Ac < 3Ac < 4Ac (Table 2). Thus, we conclude that the ionic interaction between actin's N-terminal and myosin's loop 2 initiates a conformational change of actin and/or myosin at their interface for better stereospecific and hydrophobic interaction, resulting in an increased stiffness and force. That is, the N-terminal negative charge of actin controls not only the weak interaction, but also the strong interaction between actin and myosin, and concomitant force generation and ATP hydrolysis rate.

An alternative mechanism may be that, from 2Ac to 4Ac models, tension and stiffness increase as a result of an increased number of tension and stiffness generating cross-bridges at the expense of non-tension and non-stiffness generating cross-bridges, i.e. a shift of equilibrium from weak to strong cross-bridges. If this is the case, then the rigor tension and stiffness must be the same among various muscle models, because the rigor is an extreme case of such equilibrium shift. This apparently is not the case, because rigor tension and stiffness are significantly different among the muscle models as shown in Table 2A. Our results on the distribution of cross-bridges (Fig. 9) also does not favour the equilibrium shift argument.

Our interpretation is consistent with the results of Cook et al. (1993) using the same actins (2Ac and 4Ac) in solution studies. Based on their observations, they proposed that the main difference between the behaviour of the 2Ac and 4Ac actins was exhibited at the isomerization step between the A.M**ADP.Pi and the A.M′.ADP.P_i state following ATP cleavage that represents the switch from the weak to strongly bound state. In our kinetic scheme, this isomerization occurs between step 3 and step 4, or during step 4 (scheme 1). Our interpretation is also consistent with that of Karatzaferi et al. (2004) who stated that the force exerted by a cross-bridge depends on the strength of the ‘actomyosin bond’. Our interpretation is further consistent with the results of DasGupta & Reisler (1989, 1992) who found that binding of S1 to actin and actin-activated ATPase were inhibited when antibody was attached to the first seven amino acid residues of actin's N-terminus.

Our results also demonstrate that the actin N-terminal negative charge density affects the binding of nucleotides and P_i to their sites on the myosin head (K₀, K₁ and K₅; Table 4). The distance of this site from the actin binding site is 5 nm (Schröder et al. 1993; Rayment et al. 1993b; Geeves & Holmes, 1999), which suggests that the effect is allosteric. This mechanism is consistent with a proposal made by Cook et al. (1993) and with the data from our own laboratory showing that increased tension leads to a decrease in K₁ (Zhao et al. 1996). Although we observe changes in the kinetic constants with the mutant actins (Table 4), the magnitude of these changes is not sufficient to account for the large difference in force and stiffness. Taken as a whole, the line of evidence indicates that the increased negative charge at the actin N-terminus primarily increases the tightness of the actomyosin interface resulting in the increased force and stiffness (Table 5). The effect of the N-terminal negative charge is similar to the case of the Tm→Δ23Tm substitution (or Tm deletion) where we found lines of evidence that Tm modifies the conformation of actin so as to increase stereospecific and hydrophobic interactions between actin and myosin molecules (Fujita & Kawai, 2002; Fujita et al. 2002; Lu et al. 2003).

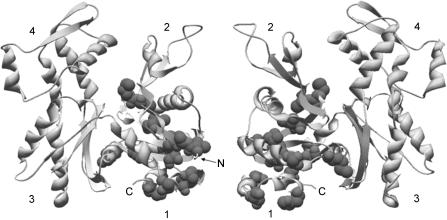
The difference between the ability of 4Ac yeast actin and MAc muscle actin to generate force in the reconstituted filament system (Table 1) implies that some other difference in the primary structure between yeast and muscle actins is also important for force generation. These two proteins differ in 50 out of 375 positions, and in most of those variant pairs, the two amino acids are similar in nature (Ng & Abelson, 1980). In addition to the difference in the N-terminal residues, 14 positional differences exist in subdomain 1, a major binding site for the myosin head. These differences might directly affect the interface between the two proteins or, alternatively, cause allosteric changes in thin filament conformation that results in an alteration of the actin–myosin interface. There is an increasing body of evidence that indicates that the actin filament exists in a number of different conformations. For example, actin has been crystallized in both open and closed conformations (Kabsch et al. 1990; Chik et al. 1996), and Egelman and coworkers have shown through EM studies that the filament itself can assume at least three different identifiable conformations (Galkin et al. 2002). It has been suggested based on the EM data that the yeast actin filament is in a more open state than the muscle actin filament, and this in turn may affect actin's ability to interact with myosin (Orlova et al. 1997). This difference may result in part from the absence of methylation of His⁷³ in yeast and other fungal actins compared to the presence of methylation of His⁷³ in muscle actin (Kalhor et al. 1999; Yao et al. 2002).

A clue to this difference in filament conformation might also be obtained from the positions of the variant residues in the actin structure. Figure 10 shows that, on a yeast actin background, the variant residues in subdomain 1 form a core that connects the N- and C-terminal regions with the nucleotide-binding site at the bottom of the interdomain cleft and within a shell of unaltered secondary structural elements. In actin, the nucleotide bridge connects the two major domains and determines their interrelationship. One can easily imagine that this core of variant residues affects both surface topology of subdomain 1 and the interdomain spatial relationship leading to an altered filament behaviour resulting in the change in force generation we observe. Our ability to generate site-directed mutants in yeast actin, coupled with the ability to use the yeast actin in the reconstituted muscle fibre system, provides means for identifying the role of a particular variant residue that may be important in affecting the actomyosin interaction that results in force generation under the physiologically relevant condition.

Figure 10. Muscle specific substitutions in subdomain 1 of yeast actin.

Muscle specific substitutions in subdomain 1 of yeast actin are depicted as space-filled residues in the ribbon structure of yeast actin (protein data base identification: 1YAG, Vorobiev et al. 2003). Both faces of the actin molecule are shown and the N- and C-termini are marked where visible. The numbers denote the four actin subdomains. ATP housed in the cleft has been omitted from the structure.