Slow volume transients in amphibian skeletal muscle fibres studied in hypotonic solutions

Abstract

The influence of extracellular hypotonicity on the relationship between cell volume (V_c) and resting membrane potential (E_m) was investigated in Rana temporaria skeletal muscle. V_c was measured by confocal microscope imaging of fibres through their transverse (xz) planes, and E_m was determined using standard microelectrode techniques. Hypotonic solutions first elicited a rapid increase in fibre volume, ΔV_R+ that fulfilled expectations of simple osmotic behaviour described in earlier reports. However, this was consistently followed by a slow increase in V_c (ΔV_S+) to 10–15% above osmotic predictions. Longer (>1 h) exposures to hypotonic solutions permitted a subsequent slow decrease in V_c (ΔV_S−), the eventual magnitude of which exceeded that of the preceding ΔV_S+. Restoration of isotonic conditions elicited a prompt recovery in V_c that matched simple osmotic predictions and thus left a net change in V_c. Such alterations in V_c attributable to ΔV_S+ then gradually reversed, while those due to ΔV_S− persisted. Both ΔV_S+ and ΔV_S− persisted under conditions of Cl⁻ deprivation. The depolarization of E_m that accompanied ΔV_R+ was consistent with dilution of intracellular [K⁺]. E_m did not significantly alter during the subsequent ΔV_S transients. These empirical features of ΔV_S+ and ΔV_S− were analysed using the quantitative charge-difference model of Fraser and Huang, published in 2004. This attributed the ΔV_S+ to an electroneutral increase in the effective osmotic activity of normally membrane-impermeant intracellular anions. In contrast, the ΔV_S− could only be explained by an efflux of such anions and was accordingly comparable to organic anion-dependent regulatory volume decreases reported in other cell types.

Skeletal muscle shows significant changes in both intracellular and extracellular osmolarity during both exercise and a variety of disease states. For example, exhaustive exercise can markedly increase intracellular lactate concentration and increase muscle fibre volume (V _c) by up to 20% (Sjogaard et al. 1985). Yet while most cell types perform regulatory volume decreases (RVD) in response to swelling (reviewed by Lang et al. 1998a), RVD has not been demonstrated in mature skeletal muscle (Sejersted & Sjogaard, 2000). Conversely, the steady-state V_c of muscle fibres decreases linearly with increases in extracellular tonicity (Adrian, 1956; Blinks, 1965; Ferenczi et al. 2004). In Cl⁻-depleted frog skeletal muscle these decreases in V_c were accompanied by shifts in resting membrane potentials (E_m) that followed expectations from the corresponding increases in intracellular potassium concentration ([K⁺]_i) and the K⁺ Nernst equation (Adrian, 1956).

However, recent investigations of the response of skeletal muscle to extracellular hypertonicity in more physiological Cl⁻-containing Ringer solutions (Geukes Foppen et al. 2002; Ferenczi et al. 2004) demonstrated more complex relationships between E_m and V_c. In contrast to the hyperpolarization of muscle fibres following fibre shrinkage, where K⁺ was the only significantly membrane-permeant ion (Adrian, 1956), similar osmotic reductions in V_c in such Cl⁻-containing solutions produced little change in E_m. This stabilization of E_m despite an increased [K⁺]_i appeared to result from elevation (‘splinting’) of [Cl⁻]_i above its electrochemical equilibrium concentration by the activity of cation−Cl⁻ cotransport systems, including the Na⁺–K⁺–2Cl⁻ cotransporter (NKCC; Geukes Foppen et al. 2002; Ferenczi et al. 2004). Thus, whereas the activity of such ion transporters is responsible for regulatory volume increase (RVI) in many other cell types (Lang et al. 1998a; Russell, 2000), it appears to regulate E_m without significant influence upon V_c in skeletal muscle exposed to hypertonic solutions. Subsequent modelling showed that the high Cl⁻ permeability (P_Cl) of skeletal muscle precluded a significant effect of cation−Cl⁻ cotransport systems upon V_c without a far greater influence upon E_m. In addition, any such changes to V_c or E_m would reverse on cessation of the cation−Cl⁻ cotransport activity, in contrast to the sustained changes to V_c and/or E_m that could result from changes to intracellular impermeant anion content (X_i) and/or its effective mean valency (z_X; Fraser & Huang, 2004).

The present experiments complement those recent studies of the effects of extracellular hypertonicity upon the relationship between V_c and E_m (Ferenczi et al. 2004) by an examination of the effects of extracellular hypotonicity on this relationship, using measurements of V_c obtained using confocal xz-plane imaging and of E_m using standard microelectrode techniques. The findings were then analysed in terms of a recent model (Fraser & Huang, 2004) that clarified the relationship between V_c and E_m and described the possible mechanisms for their control in skeletal muscle.

Methods

All solutions were titrated to pH 7.0 (as measured with a combination pH electrode) and their osmolarities (θ) measured using a standard, calibrated vapour pressure osmometer. All experiments were conducted at 20–22°C. The control, isotonic, solutions used were: (A) standard Cl⁻-containing Ringer solution (mm): 115 NaCl, 2.5 KCl, 1.8 CaCl₂, 3 Hepes, θ 227 mosmol l⁻¹; (B) standard SO₄²⁻ Ringer solution: 75 Na₂SO₄, 1.25 K₂SO₄, 8 CaSO₄, 3 Hepes, θ 225 mosmol l⁻¹. The compositions of the hypotonic test solutions were identical to those of either solution A or B apart from a reduction in the concentration of the principal solute (NaCl or Na₂SO₄). The isotonic test solutions, which were used to control for the reduced extracellular ion concentrations in the hypotonic test solutions, contained extracellular ion concentrations that matched those in the corresponding hypotonic solutions, but additionally contained sufficient sucrose to render their tonicities equal to the isotonic control solutions.

Sartorius and cutaneous pectoris muscles from cold-adapted Rana temporaria frogs (Blades Biological, Edenbridge, Kent, UK) previously killed by concussion followed by pithing (Schedule 1: Animals (Scientific Procedures) Act, Home Office, UK), were dissected in solution A. Several studies have reported comparable electrophysiological and osmotic properties in these two muscle types (Adrian, 1956; Ferenczi et al. 2004; Chin et al. 2004). For those experiments conducted under conditions of Cl⁻ deprivation, the muscles were then gradually equilibrated with Cl⁻-free solutions by exposing them to a succession of Ringer solutions in which the Cl⁻ content was progressively halved approximately every 5 min before a final transfer from 1 mm Cl⁻ Ringer solution to Cl⁻-free Ringer solution. This protocol of gradual Cl⁻ reduction avoided muscle twitching or contraction, in contrast to procedures that used more rapid removals of extracellular Cl⁻.

Cell volumes (V_c) were measured in groups of three to seven adjacent fibres in one- to three-fibre-thick cutaneous pectoris muscles mounted ventral side uppermost onto a coverslip that formed the base of a 0.5 ml microscope chamber. The chamber was sealed between solution changes to prevent evaporation. All solutions used to perfuse the muscle contained Sulphorhodamine B (Lissamine rhodamine B200: 75%; Aldrich-Sigma, UK) at a concentration of 62.5 μg ml⁻¹ (Ferenczi et al. 2004). This membrane-impermeable dye stained the extracellular space and thereby highlighted muscle fibre edges, without influencing membrane electrophysiological properties (Gallagher & Huang, 1997). A Zeiss LSM-510 laser-scanning confocal microscope, incorporating an Axiovert 100M inverted microscope, was used to obtain images of fibres in the xz-plane using a 40× oil immersion objective. The Sulphorhodamine B was activated with a 543 nm wavelength laser and fluorescence emission captured at >560 nm. This generated images with a fluorescent extracellular space and dark fibre cross-sections.

Initial pilot scans in the xy-plane were obtained in order to ensure that the x-axes of the xz scans ran perpendicular to the fibre long axes. The definitive images were then obtained every 5–60 s in the xz-plane and in-house image analysis software was used to calculate the fibre cross-sectional areas. This software first corrected the fluorescence attenuation associated with scanning of the deeper fibre areas, according to calibration data obtained earlier and fully described by Ferenczi et al. (2004), then applied a noise filter and a threshold function. The cross-sectional area of each fibre in the field of view was then calculated. Since the muscle was secured at a constant length throughout each experiment, changes in the measured cross-sectional areas provided a direct indication of changes in cell volume. These cell volumes, V_c, were standardized relative to steady-state values obtained during an initial 10 min period in one of the control solutions, A or B. Volume recordings were not performed in muscles showing any evidence of reduced viability such as movement, contraction, T-system vacuolation or divergent volume changes between fibres within the field of view. Preliminary experiments showed that fibre lysis, indicated by the entry of dye into the cytoplasm, generally occurred within an hour of such changes.

These measurements of V_c were then compared with the corresponding predictions of cell volumes assuming that muscle fibres showed perfect osmometric behaviour. Thus, if V_p denotes such a predicted volume, V_c(a) the cell volume before the solution change, and θ_e(a) and θ_e(b) the extracellular osmolarity, measured using a vapour pressure osmometer, before (a) and after the solution change (b), respectively:

(1a)

This formulation would be expected to overestimate volume changes in the event that the osmotically exchangeable solvent fraction of fibres was <100%, as has been suggested in earlier work. For example, Blinks (1965) showed that skeletal muscle fibre volume changes were predicted most closely from an assumption that the solvent fraction was 0.67 of the cell volume in isotonic solutions, which would lead eqn (1a) to overestimate volume changes by almost 50%. However, estimates of the solvent fraction of skeletal muscle fibres vary in the literature (Dydynska & Wilkie, 1963; Ferenczi et al. 2004). More generally, then, if the solvent fraction of the muscle is given the symbol x, then:

(1b)

As will be seen, the present study identifies volume changes in response to hypotonicity that exceed osmotic expectations. Experimental volume changes were therefore compared to V_p (eqn (1a)) because this provided an upper limit prediction that was independent of the value of the solvent fraction, x, in the present preparation.

Membrane potentials (E_m) were measured in sartorius muscles, known to have properties that closely resemble those of frog cutaneous pectoris muscles (Adrian, 1956), but providing considerably more fibres for electrophysiological study. They were mounted in a Perspex bath and pinned out stretched to ∼1.5 times their in situ length in accordance with previous electrophysiological studies (Koutsis et al. 1995; Ferenczi et al. 2004), to give centre sarcomere lengths (2.4–2.5 μm), measured using the microscope eyepiece graticule, that were similar to the cutaneous pectoris fibres studied under confocal microscopy. The experiments were all carried out at room temperature (20–22°C) to enable results of the electrophysiological and volume studies to be compared. Test solutions were added to or withdrawn from the bath when necessary, with two washes between the additions of new solutions.

Significance of results was assessed using Student's paired two-tailed t test to a significance level of P < 0.05. Significance of volume changes was assessed by comparing mean V_c over 100 s periods (mean of at least 5 images, where n was defined as the number of fibres in each image) at predefined time points. Pilot experiments using both hypertonic and hypotonic solutions showed that passive volume changes took approximately 300 s and the slow volume increase that resulted from exposure to hypotonic solutions reached a maximum volume after approximately 60 min. Therefore, the time points at which volume changes were assessed for significance were the 100 s periods immediately prior to, 300 s after and 60 min after each solution change, or at the end of the experimental period. Mean V_c at each of these time periods was compared to mean V_c at the previous time period using Student's paired t test, or to the predicted volume (V_p) using Student's single-sample t test, as stated. In addition, in those experiments involving the return of fibres to isotonic Ringer solution following a period in hypotonic Ringer solution, V_c at the end of the experimental period was compared with that at the beginning.

Results

Slow increases in fibre volume, ΔV_S+, follow the initial passive volume response, ΔV_R+, to exposures to hypotonic solutions

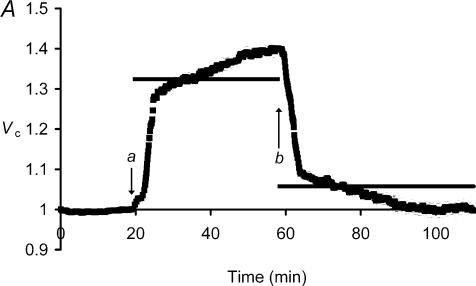
Figure 1 exemplifies the volume changes shown by groups of muscle fibres initially placed in a standard isotonic Ringer solution, then treated with a hypotonic Ringer solution. Application of the hypotonic extracellular solution initiated a pattern of volume changes (ΔV) that differed significantly from the straightforward linear relationships between V_c and extracellular osmolarity reported previously (Blinks, 1965; Ferenczi et al. 2004).

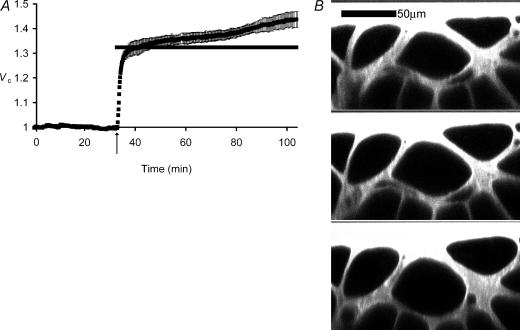
Figure 1. The response of skeletal muscle fibres to reduced extracellular tonicity.

A, mean (±s.e.m.) normalized volumes (V_c) of fibres (n= 3) in a muscle initially bathed in normal isotonic (227 mosmol l⁻¹) Ringer solution and transferred after 32 min (arrow) to hypotonic (171 mosmol l⁻¹) Ringer solution. The horizontal bar marks the predicted relative fibre volume (V_p, see Methods) assuming simple osmotic behaviour. Note that where the s.e.m. is not shown, it is smaller than the data point. Muscle fibres swelled rapidly (ΔV_R+) to volumes close to V_p, but then continued to swell slowly (ΔV_S+) over the next ∼1 h. B, confocal xz scans of muscle fibres before (top panel) and after transfer to hypotonic Ringer solution, showing fibres 300 s (middle panel) and 1 h (bottom panel) after solution change. Note that the ΔV_S+ volume transient is associated with a change in fibre shape to more circular profiles, but not with predictable diameter changes. Thus, fibre diameters were 1.11 ± 0.04 at 300 s and 1.09 ± 0.05 at 1 h following the solution change (non-significant difference, P > 0.05), despite the significant increase in cross-sectional area.

Figure 1A thus shows an initial relatively rapid volume increase, ΔV_R+, to a normalized of V_c to 1.32 ± 0.03 (n= 4 fibres) at 5 min after the solution change, close to the predicted volume assuming simple osmotic behaviour and corresponding to a rate of volume increase of ∼5% of the initial volume per minute. The rate of this initial swelling was similar to the rate of passive osmotic volume changes following applications of hypertonic solutions (Ferenczi et al. 2004). However, V_c then showed a much slower increase (ΔV_S+) at a rate of ∼0.5% min⁻¹ to reach a significantly (P < 0.01 on Student's paired t test versus the value of V_c at 5 min) larger V_c of 1.44 ± 0.03 at 60 min. Eleven muscles, in which V_c was recorded in 3–6 fibres of each, demonstrated similar rapid swelling to a mean value of V_c= 1.30 ± 0.02 after 5 min exposures to hypotonic Ringer solution but an eventual V_c= 1.42 ± 0.03 after 60 min, significantly exceeding the osmotic predictions (P≪ 0.01 on Student's single-sample t test). Figure 1B demonstrates that muscle fibre cross-sections in isotonic solutions were angular rather than circular in shape and that these volume changes largely involved changes in fibre shape to more circular profiles without predictable changes in fibre diameter.

Figure 2 shows typical confocal images in the xy-plane of single muscle fibres in standard Ringer solution (Fig. 2A) and after a 60 min exposure to hypotonic Ringer solution (Fig. 2B) through regions of interest that transected the xz-plane used for volume measurements. These show no significant differences in sarcomere length, as reflected in unchanged longitudinal distances between successive T-tubules. The ΔV_S+ was therefore not explicable in terms of an unexpected localized fibre shortening that could increase the local cross-sectional area whilst conserving total V_c. Figure 2 also shows that ΔV_S+ could not have resulted from an increase in T-tubular luminal as opposed to true cytosolic volume; to account for this ∼10% increase in V_c, the fractional tubular volume would have had to have increased >300-fold from its normal value of ∼0.003 (Peachey, 1965) to >0.10, contrasting with the similarity of the tubular appearances in Fig. 2A and B. Furthermore, although the T-tubules of amphibian muscle are too narrow (<20 nm) for accurate light microscopic measurements of their diameters (Martin et al. 2003), upper limits on the contribution of the T-system to these volume changes could be estimated using Delesse's principle, that the volume fraction, V_v, of an object embedded within a larger reference volume such as a muscle fibre is directly proportional to its area fraction in random sections. V_v was accordingly estimated by point counting (Weibel, 1979), using a transparent grid placed randomly over each of the digital images and containing a quadratic set of 0.5 μm spaced points generated by intersections on the grid. If P_i denotes the number of points falling on T-tubular lumina and P_tot the total number of points made upon the reference area, then the volume fraction is the dimensionless ratio V_v=P_i/ P_tot. This gave statistically indistinguishable (P > 0.05) upper limits of tubular luminal volume fractions of 0.081 ± 0.011 (n= 6) in standard Ringer solution and 0.065 ± 0.009 (n= 6) in hypotonic Ringer solution.

Figure 2. The influence of hypotonicity on T-tubular system.

Fibres were imaged in the xy-plane using confocal microscopy in standard isotonic (227 mosmol l⁻¹) Ringer solution (A) and in hypotonic (171 mosmol l⁻¹) Ringer solution (B). T-system appearance remained unchanged and neither the mean distances between successive T-tubules nor T-system volume fractions, measured using Delesse's principle, were significantly altered by the exposure to hypotonic Ringer solution.

ΔV_S+ varies with the degree of extracellular hypotonicity

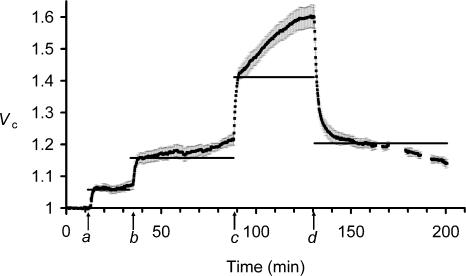
Figure 3 follows changes in V_c through a sequence of graded reductions in extracellular tonicity, followed by a final return of the fibres to standard isotonic Ringer solution. It illustrates a number of consistent features of the ΔV_R+ and ΔV_S+ phenomena. Fibres swelled rapidly on the introduction of 216 mosmol l⁻¹ Ringer solution (a) to reach V_c values of 1.06 ± 0.01 (n= 4 fibres) 5 min after the solution change, consistent with the simple osmotic prediction, V_p (horizontal bar). The subsequent ΔV_S+ changes increased V_c non-significantly (P > 0.05) to 1.07 ± 0.02 (n= 4) over the next 20 min. However, the subsequent larger tonicity changes elicited progressively greater ΔV_S+ components. Thus, the transition from 216 to 200 mosmol l⁻¹ Ringer solution (b) resulted in an initial ΔV_R+ that similarly matched osmotic expectations 5 min after the solution change. However, this was followed by a larger ΔV_S+ transient from 1.15 ± 0.02 at 5 min to 1.21 ± 0.02 (P < 0.05) prior to the next solution change 50 min later, a rate of volume increase of 0.11 ± 0.05% min⁻¹. In contrast, during the ΔV_S+ following transfer to 171 mosmol l⁻¹ Ringer solution (c) V_c increased from 1.43 ± 0.02 to 1.60 ± 0.04 (P < 0.01) in 40 min, a mean volume increase of 0.4 ± 0.1% min⁻¹ that was significantly (P < 0.05) greater and more rapid than the increase that resulted from the transfer from 216 to 200 mosmol l⁻¹ Ringer solution.

Figure 3. The influence of successive step changes in extracellular tonicity upon muscle fibre volume.

Filled squares denote mean normalized volumes, V_c (±s.e.m., n= 4 fibres except between 75 and 135 min, when n= 3 as cell swelling reduced the number of fibres that could be visualized in each frame). The horizontal bars denote predicted volumes, V_p, after each step change in osmolarity, taking into account the actual normalized volumes, V_c, recorded immediately before each such change (see Methods). Initial extracellular osmolarity was 227 mosmol l⁻¹, and this was reduced in steps to 216 mosmol l⁻¹ (a), 200 mosmol l⁻¹ (b) and 171 mosmol l⁻¹ (c). Finally, the bathing solution was replaced with standard 227 mosmol l⁻¹ Ringer solution once more (d). Note that fibres remained residually swollen on return to standard Ringer solution (from d), but then showed gradual volume recovery, in contrast to the ΔV_S+ seen in similarly swollen fibres (from b) in hypotonic solutions.

The successive sequence of ΔV_R+ followed by ΔV_S+ transients through each solution change finally resulted in an overall increase in V_c that significantly exceeded the simple osmotic expectations. Thus, the fibres in 171 mosmol l⁻¹ Ringer solution eventually reached mean normalized volumes of 1.601 ± 0.037, against a V_p of 1.327 relative to the cell volume initially observed in 227 mosmol l⁻¹ Ringer solution. The excess volume initially persisted on return to standard isotonic Ringer solution (d). Thus the return to isotonic 227 mosmol l⁻¹ Ringer solution produced a rapid decrease in V_c to a value close to that predicted by assuming simple osmotic behaviour (V_p=V_c(a)× (θ_e(a)/θ_e(b)) = 1.601 × (171/227) = 1.206). However, this passive osmotic shrinkage thus left a ∼20% residual elevation of V_c compared to its original value in standard Ringer solution that reflected the preceding, cumulative ΔV_S+ changes. This contrasted with the previously reported complete volume recovery in fibres returned to isotonic solutions following a sequential increase in extracellular tonicity (Ferenczi et al. 2004).

The adjustments in V_c that then followed were consistent with the ΔV_S+ being the consequence of an increased V_c under hypotonic, but not isotonic conditions. Thus, Fig. 3 indicates that fibres with similar V_c values showed contrasting slow volume transients, the directions of which depended on whether they were bathed in hypotonic Ringer solution (b) or demonstrated the residual swelling (d) that followed the exposures to extracellular hypotonicity. In the former case (b) fibres demonstrated the slow increase in volume, ΔV_S+, whereas in the latter case (d) there was a gradual recovery in volume to a significantly reduced V_c of 1.139 ± 0.013 (P < 0.01, n= 4) at the end of the experimental period. The ΔV_S+ volume transients are thus not intrinsic consequences of increases in V_c above their resting values. Nor could the ΔV_S+ phenomenon be attributed to the reduction in the extracellular NaCl concentration ([NaCl]_e); fibre volumes were not significantly altered by a 3 h exposure to isotonic, low [NaCl]_e solutions (normalized V_c=−0.002 ± 0.003, n= 8 fibres, 2 muscles after 3 h exposure) whose ionic composition equalled that of the 171 mosmol l⁻¹ hypotonic Ringer solution used in Figs 1 and 3 (85 mm NaCl) but additionally contained sufficient sucrose to preserve normal tonicity (227 mosmol l⁻¹).

ΔV_S+ persists under conditions of Cl⁻ deprivation

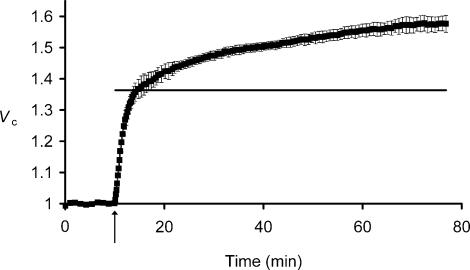
Many cell types exhibit regulatory volume increase (RVI) or decrease (RVD) phenomena (Lang et al. 1998a,b; O'Neill, 1999) that result from cation−Cl⁻ cotransporter activity mediated by the Na⁺–K⁺–2Cl⁻ cotransporter (NKCC; Russell, 2000) or K⁺–Cl⁻ cotransport (KCC; Lauf & Adragna, 2000), both of which have been identified in skeletal muscle (Hiki et al. 1999; Wong et al. 1999). Furthermore, many cell types increase their membrane Cl⁻ permeabilities in response to swelling (Nilius et al. 1996; Okada et al. 2001). Experiments that exposed muscle fibres to hypotonic solutions in Cl⁻-free environments further excluded such a potential role of Cl⁻-dependent processes in these ΔV_S+ changes. Thus, Fig. 4 follows the mean relative volumes of a group of fibres that were exposed to hypotonic Cl⁻-free Ringer solution. The volume changes were similar to those in Cl⁻-containing Ringer solutions (Fig. 1) in that fibres showed an initial ΔV_R+ until V_c approximated V_p (horizontal bar) ∼5 min after the solution change. This was followed by a ΔV_S+ that gradually increased V_c (at a rate of ∼0.2% min⁻¹) to 1.577 ± 0.025 after a 60 min exposure, significantly exceeding the simple osmotic expectations (V_p= 1.36). ΔV_S+ thus persisted under conditions in which membrane-permeant anions were absent from the extracellular medium.

Figure 4. The influence of extracellular hypotonicity upon muscle fibre volume under conditions of Cl⁻ deprivation.

Filled squares denote mean relative volumes, V_c (±s.e.m., n= 4 fibres), of a group of muscle fibres, initially equilibrated with isotonic Cl⁻-free SO₄ ²⁻ Ringer solution (225 mosmol l⁻¹), then transferred (arrow) to hypotonic Cl⁻-free Ringer solution (168 mOsm l⁻¹). Where the s.e.m. is not shown, it is smaller than the data point. The horizontal bar shows the relative volume, V_p, predicted by assuming simple osmotic behaviour. After rapidly swelling to this predicted volume (ΔV_R+), the fibres continued to swell gradually over the course of the next 1 h (ΔV_S+).

ΔV_S+ is followed by a delayed slow volume decrease, ΔV_S−

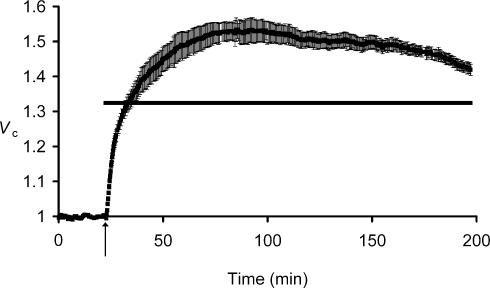
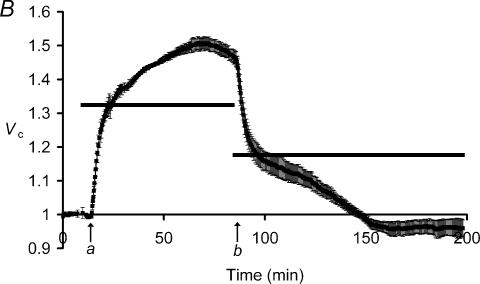
The ΔV_S+ phenomenon was further investigated in fibres exposed to hypotonic solutions for longer periods. This revealed that the ΔV_S+ transients were followed after ∼60–70 min by a slow volume decrease, ΔV_S−. Figure 5 shows typical fibre volumes following ∼3 h exposures to hypotonic Cl⁻-containing Ringer solutions, demonstrating a slow and sustained volume decrease, ΔV_S−, beginning after the ΔV_S+ transient.

Figure 5. Cell volume eventually reaches a maximum during long exposures to extracellular hypotonicity and then declines.

Muscle fibres were exposed to hypotonic Cl⁻-containing Ringer solution (arrow) for almost 3 h. Mean fibre volumes (±s.e.m., n= 5 fibres) are shown over this period, compared to the volume predicted by assuming simple osmotic behaviour (V_p, horizontal bar). Cell volume rapidly increased to close to this predicted value (ΔV_R+), and this was followed by a slower volume increase, ΔV_S+, to a maximum V_c of 1.53 ± 0.03, against the prediction of 1.32. However, fibres then showed a much slower volume reduction, ΔV_S−, lasting for the remainder of the experimental period. Thus, V_c eventually reduced to 1.42 ± 0.02 at 200 min, significantly lower than the previous maximum (P < 0.05).

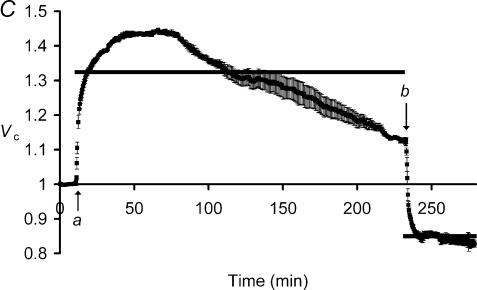
Figure 6 shows the mean normalized V_c of fibres in three muscles that were initially equilibrated with Cl⁻-free isotonic SO₄ ²⁻ Ringer solution and then exposed to hypotonic Cl⁻-free SO₄ ²⁻ Ringer solutions (a) for different periods before being returned to isotonic Cl⁻-free SO₄ ²⁻ Ringer solution (b). The slow V_c decrease, ΔV_S−, persisted with accelerated kinetics under conditions of Cl⁻ deprivation. These increased rates of ΔV_S+ and ΔV_S− in Cl⁻-free compared to Cl⁻-containing solutions made it possible to demonstrate several additional features of these slow volume transients within the ∼3–4 h period over which measurements of V_c in viable muscle fibres were possible, as follows.

Figure 6. The influence of long exposures to hypotonic solutions under Cl⁻-free conditions.

Three muscles (A, B and C) were equilibrated with isotonic (225 mosmol l⁻¹) Cl⁻-free SO₄ ²⁻ Ringer solution, exposed to hypotonic (170 mosmol l⁻¹) Cl⁻-free Ringer solution (a) for different durations and finally returned to isotonic Cl⁻-free Ringer solution (b). Data points show mean relative volume, V_c (±s.e.m., n≥ 4 fibres in each case). Horizontal bars denote predicted cell volume, V_p, after each solution change.

(1) In each case in Fig. 6 the exposure to hypotonicity (a) elicited an initial rapid volume increase, ΔV_R+, increasing V_c to values close to V_p (horizontal bar), as expected from a simple osmotic hypothesis. (2) A slow volume increase, ΔV_S+, that was nevertheless more rapid than its counterpart in Cl⁻-containing solutions then followed, increasing V_c to significantly above V_p (P < 0.01). (3) Exposures to extracellular hypotonicity of >1 h (Fig. 6B and C) then permitted an abrupt onset of a slow volume decrease, ΔV_S−, after ∼60–70 min, in common with the situation in the corresponding Cl⁻-containing solutions (Fig. 5). (4) This persisted at a constant rate that was faster than the ΔV_S− observed in Cl⁻-containing solutions (0.2% min⁻¹ in Cl⁻-free versus 0.1% min⁻¹ in Cl⁻-containing solutions) for at least 150 min (Fig. 6C). (5) The ΔV_S− process could eventually reduce V_c to significantly less than V_p (P < 0.01) for the prevailing extracellular tonicity (Fig. 6C), as opposed to simply reversing the preceding ΔV_S+ process.

Figure 6 also demonstrates the effects of (b) returning fibres to isotonic Cl⁻-free Ringer solution after long exposures to hypotonic Cl⁻-free Ringer solution, as follows. (1) In each case, the restoration to isotonic Ringer solution resulted in a rapid initial decrease in V_c, the magnitude of which matched the preceding ΔV_R+ and accordingly followed osmotic predictions (V_p, horizontal bar) that took into account the actual V_c immediately before the solution change. However, (2) V_c was then left with a residual difference from its baseline value, reflecting the volume changes attributable to the slow volume transients (ΔV_S++ΔV_S−), corrected for the relative extracellular tonicities (θ_e(hypo)/θ_e(iso)). Thus, the shift in V_c from baseline values was close to (ΔV_S++ΔV_S−) × (θ_e(hypo)/θ_e(iso)) in each case. (3) The initial passive, rapid decrease in V_c was then followed (Fig. 6A and B) by a much slower volume decrease that eventually equalled the magnitude of the ΔV_S+, corrected for the change in extracellular tonicity (thus, ΔV_S+× (θ_e(hypo)/θ_e(iso))). It was not possible to demonstrate this correction for very long exposures to hypotonicity; although a downward trend was observed (Fig. 6C), it was non-significant (P > 0.05) at the limits of viability of the preparation. (4) In contrast to this apparent eventual correction of the volume gain during ΔV_S+, any volume loss attributable to a previous ΔV_S− persisted (Fig. 6B and C). Thus, fibres that showed a significant ΔV_S− remained residually shrunken on return to isotonic Cl⁻-free Ringer solution such that final V_c was significantly reduced from its initial baseline value (P < 0.01).

Resting membrane potentials, E_m, during the volume changes

Adrian (1956) pointed out that osmotically induced changes in V_c would correspondingly concentrate or dilute any conserved intracellular ions and thereby potentially alter the resting membrane potential, E_m. For example, increases in [K⁺]_i/[K⁺]_e resulting from osmotically induced reductions in V_c hyperpolarize the K⁺ Nernst potential, E_K, and produce a corresponding shift in E_m in fibres studied in Cl⁻-free hypertonic solutions (Adrian, 1956; Hodgkin & Horowicz, 1959). Such a relationship permits the influence of V_c upon E_m to be predicted following a change in extracellular osmolarity. Thus, if the subscripts (iso) and (hypo) denote isotonic and hypotonic extracellular solutions, respectively, while the symbol θ denotes osmolarity:

if

(2)

then

(3)

and so

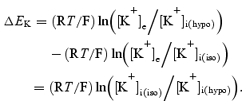(4)

Then, if

(5)

(6)

Equation (6) contains four implicit assumptions: (1) intracellular K⁺ content is conserved during changes in V_c; (2) V_c follows simple osmotic predictions (see Methods) over the range of extracellular osmolarities considered here; (3) Cl⁻ is passively distributed; and (4) membrane Na⁺ permeability is low relative to that of K⁺. Any deviation of measured E_m from these predictions might then reveal evidence of E_m or V_c regulation.

The following control experiments therefore first confirmed that these assumptions were reasonable under steady-state conditions in isotonic solutions. First, E_m was measured in fibres exposed to Ringer solutions in which sucrose partly but isosmotically replaced NaCl. This separated the effects upon E_m of the reduced tonicity of hypotonic solutions from the effects of their reduced [NaCl]_e and thus paralleled the investigation of V_c in solutions with similar isosmotic replacements of extracellular NaCl described above. Reductions in [NaCl]_e from 120 to 85 mm then yielded no significant differences (P≫ 0.05 on Student's unpaired t test) between E_m values as recorded over a 30 min period in standard isotonic Ringer solution (−90.4 ± 1.2 mV, n= 13) and those obtained over 10 min periods immediately following (−90.1 ± 1.2 mV, n= 9) and ∼60 min after the solution change (−89.3 ± 0.8 mV, n= 34), respectively. Similar results were obtained after solution changes to 45 mm NaCl Ringer solution (−92.2 ± 1.3 mV, n= 16 immediately following and −90.8 ± 1.0 mV, n= 12 at ∼60 min; P > 0.05).

The second set of control experiments assessed the validity of assumption (3) above. Although early reports had suggested that Cl⁻ is in electrochemical equilibrium across the membrane of resting skeletal muscle in isotonic solutions (Adrian, 1956; Hodgkin & Horowicz, 1959), more recent reports had suggested that E_m in both mouse skeletal muscle in isotonic solutions and amphibian fibres in hypertonic solutions is slightly depolarized relative to E_K owing to a combination of an elevated [Cl⁻]_i/[Cl⁻]_e due to cation−Cl⁻ transporter activity and a high ratio of Cl⁻ to K⁺ permeability, P_Cl/P_K (Geukes Foppen et al. 2002; Ferenczi et al. 2004). The experiments accordingly examined E_m in fibres in isotonic solutions under conditions of Cl⁻ depletion, which would abolish any such cation−Cl⁻ cotransport. Similar values of mean E_m were obtained from fibres during an initial 30 min period in standard Ringer solution (−89.5 ± 1.3 mV, n= 16 fibres, 2 muscles) between 20 and 40 min (−92.3 ± 0.9 mV, n= 16 fibres, 2 muscles) and between 41 and 60 min after gradual equilibration with Cl⁻-free Ringer solution (−91.3 ± 0.5 mV, n= 24 fibres, 2 muscles). Therefore Cl⁻ deprivation did not significantly affect values of E_m under isotonic conditions (P > 0.05 in each case on Student's unpaired two-tailed t test versus values in standard Ringer solution).

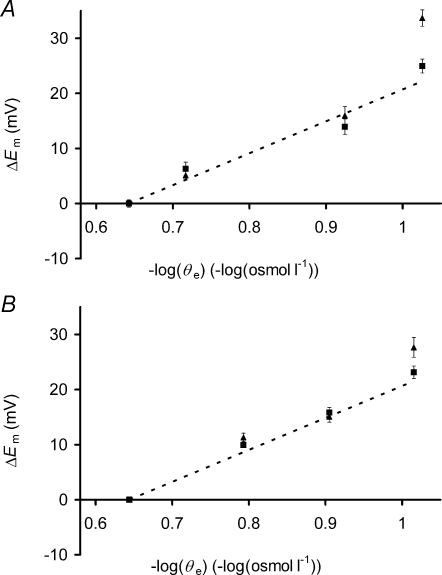
Figure 7A then compares the influence of exposures to extracellular hypotonicity upon E_m with the corresponding predicted values of E_m (eqn (6)) over a wide range of tonicities, including those under which the V_c changes were examined. The muscle fibres were transferred from standard Cl⁻-containing Ringer solution to a hypotonic Cl⁻-containing Ringer solution and E_m was measured soon after the solution change, to record E_m changes due to ΔV_R+, and after 60 min, to record any additional changes due to ΔV_S+. Progressive reductions in tonicity produced increasing depolarizations of the E_m measured between 5 and 15 min compared to values in isotonic Ringer solution (P≪ 0.01 in each case) that were close to predicted values of ΔE_m (dashed line) calculated from eqn (6) above. At tonicities of 192 and 119 mosmol l⁻¹, E_m remained stable after this initial depolarization. Only at the lowest tonicity (94 mosmol l⁻¹) was there any significant depolarization (P < 0.01) between the early and late measurement periods, possibly reflecting the reduced fibre survival, loss of normal striations and inability to return to basal conditions that may follow such extreme reductions in extracellular tonicity (Paris et al. 1965). Even longer exposures to 171 mosmol l⁻¹ solutions gave an E_m of −87.1 ± 1.06 mV between 170 and 190 min (P > 0.05 against earlier time bins), demonstrating continued E_m stability despite the ΔV_S− phenomenon. Figure 7B confirms similar relationships between extracellular tonicity and E_m under Cl⁻-free conditions; decreases in extracellular tonicity depolarized E_m as predicted by eqn (6) above (dashed line), giving stable ΔE_m values. Very long exposures to 164 mosmol l⁻¹ solutions gave E_m of −82.1 ± 1.06 mV between 170 and 190 min (P > 0.05 against earlier time bins), similarly demonstrating continued E_m stability despite the marked ΔV_S− transient observed under similar conditions of Cl⁻ deprivation.

Figure 7. The influence of reduced extracellular tonicity upon E_m .

The change in E_m (ΔE_m) compared to resting E_m in isotonic Ringer solutions is plotted against −log(extracellular osmolarity) (−log(osmol l⁻¹)) for muscle fibres exposed to hypotonic Ringer solutions in Cl⁻-containing (A) or Cl⁻-free solutions (B). In each case, mean ΔE_m (±s.e.m., n≥ 50 fibres from ≥2 muscles in each case) is shown soon (5–15 min) after the solution change (▪) and after a much longer (50–70 min) exposure period (▴). Where the s.e.m. is not shown, it is smaller than the data point. ΔE_m closely followed predictions assuming conservation of [K⁺]_i and simple osmotic behaviour (dashed line), and except at the very lowest tonicity (96 mosmol l⁻¹) remained stable following the initial depolarization despite the ΔV_S+ process that occurs over this period. Cl⁻ deprivation did not influence the relationship between extracellular osmolarity and ΔE_m.

Thus, with the exception of long exposures to the lowest tonicity used here, the results showed that ΔE_m following the application of hypotonic solutions conformed to predictions that assumed perfect osmotic behaviour, conservation of intracellular K⁺ and dependence of E_m upon E_K. Furthermore, the subsequent slow volume transients produced no additional detectable ΔE_m in either Cl⁻-free or Cl⁻-containing Ringer solutions.

Mathematical modelling of the relationship between E_m and V_c during ΔV_S+ and ΔV_S−

Skeletal muscle fibres exposed to hypotonic solutions thus showed: (1) slow volume transients, which followed an initial passive osmotic change (ΔV_R+), that first increased (ΔV_S+) and then decreased cell volume (ΔV_S−); and (2) accompanying alterations in E_m that simply reflected a K⁺ Nernst equation in which osmotically induced increases in V_c directly altered [K⁺]_i/[K⁺]_e, in contrast to the stable values of E_m observed in hypertonic solutions (Ferenczi et al. 2004). Both (1) and (2) persisted in Cl⁻-free solutions, which contain an insignificant concentration of membrane-permeable anions. This associated them with alterations in the intracellular membrane-impermeant solute (X_i) content, its osmotic activity, or its mean charge valency (z_X), rather than Cl⁻-dependent transport processes (Fraser & Huang, 2004). However, the relationships between intracellular impermeant anion content (X_i), its mean charge valency per osmole (z_X), V_c and E_m are potentially complex. On the one hand, an efflux of charged X could alter its intracellular content, X_i, whilst preserving z_X. On the other hand, the total intracellular charge carried by X_i would be unchanged following a flux of uncharged X or changes in the osmotic activity of X, and so such alterations in X_i would necessarily alter z_X and in turn influence E_m (Fraser & Huang, 2004). Nevertheless, it proved possible to model the effects of exposure of skeletal muscle to extracellular hypotonicity using the charge difference method of Fraser & Huang (2004) modified (see Appendix), to permit explicit modelling of changes in extracellular osmolarity.

Such modelling first assumed that the total charge carried by X_i was conserved within the cell unless there was a transmembrane flux of X. Secondly, [X]_e was set to zero, as in the experimental solutions, and so no net inward fluxes of X were possible. Instead, X_i could be increased by simulating either an increase in its osmotic activity or cleavage of larger molecules. In this case, the total charge carried by X_i was conserved by keeping the product V_c×[X]_i×z_X constant by altering z_X in inverse proportion to any change in [X]_i×V_c. In contrast, decreases in total X_i content were modelled either by a similar charge-conserving mechanism or by the introduction of a small permeability term to X, permitting efflux of X and thus reducing the product V_c×[X]_i×z_X whilst preserving z_X.

The model first demonstrated that an increase in X_i could result in a volume increase of comparable magnitude to ΔV_S+ without significant alteration of E_m, despite the resultant decrease in z_X. The simulation was started with extracellular solute concentrations similar to that of the isotonic low-[NaCl] Ringer solution, semiarbitrary intracellular concentrations, and with all other parameters, such as Na⁺–K⁺–ATPase density and ion permeabilities, as described by Fraser & Huang (2004) until all variables settled to stable values, at which point V_c was assigned a value of 1. Figure 8 illustrates results from the subsequent period of modelling, beginning with isotonic extracellular conditions. At point a extracellular tonicity was reduced and the system permitted to re-equilibrate. This reproduced the experimental findings of a rapid volume increase (ΔV_R+) and accompanying depolarization of E_m. However, also note a rapid and small initial hyperpolarization on exposure to hypotonicity attributable to a transient Cl⁻ influx secondary to the initial dilution of [Cl⁻]_i.

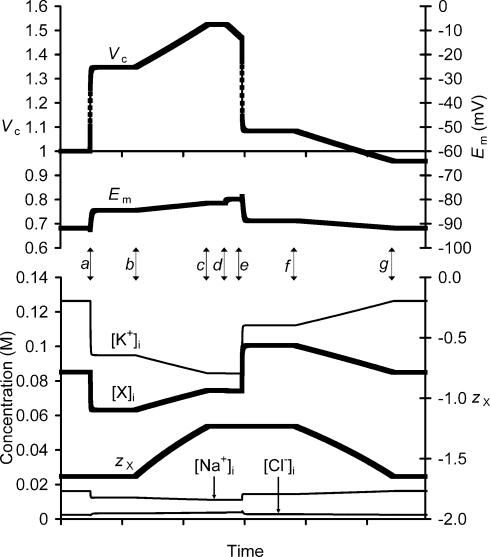
Figure 8. Charge difference modelling of an exposure to hypotonicity.

The charge difference method of Fraser & Huang (2004) was used to model intracellular events in amphibian skeletal muscle during exposure to hypotonicity. Thus, following equilibration with isotonic (230 mosmol l⁻¹) Ringer solution, extracellular tonicity was reduced to 172 mosmol l⁻¹ (a) and the model permitted to stabilize. ΔV_S+ was then modelled by gradually increasing X_i content (b) whilst proportionally reducing the magnitude of z_X to maintain a constant product V_c×[X]_i×z_X, as described in the text, until point c, where the model was once again permitted to stabilize. At point dΔV_S− was modelled by the introduction of a small permeability term to X⁻, permitting X⁻ efflux and thus a reduction in total intracellular charge, with conservation of z_X. At point e this efflux was stopped and extracellular isotonicity restored. At point f the process introduced at point b was reversed. These changes were stopped at point g, when [X]_i and z_X had reached their initial baseline values, allowing full recovery of E_m, [K⁺]_i, [Na⁺]_i, [Cl⁻]_i and [X]_i, but a net reduction in V_c.

At point b a gradual increase in cellular X_i content was modelled at a constant rate, following the assumptions above. The increase in X_i caused a gradual increase in V_c, while the accompanying decrease in z_X resulted in a small depolarization of E_m. Note that an increase in cellular X_i content alone, without any change in z_X, would be expected to change V_c such that [X]_i remained constant (Fraser & Huang, 2004). However, in this case the simultaneous reduction in the magnitude of z_X effectively dampens the V_c increase caused by increasing X_i content, permitting [X]_i to increase. However, during a ΔV_S+ of similar magnitude to that demonstrated in Fig. 6B (V_c from 1.34 to 1.52), E_m depolarized by only 2.9 mV, which is too close to the standard errors of the E_m measurements to have been detected in the present study, and is thus compatible with the experimental data. The increase in X_i content was then stopped at point c.

At point d an efflux of X was modelled by assigning a small permeability term to X_i such that the permeability ratio P_X:P_K was 0.0001. This resulted in a volume decrease analogous to ΔV_S−, accompanied by a small depolarization, as would be expected for any process that increased overall anion efflux, but which was too small to be detected in the present study. However, E_m stabilized at this slightly depolarized value, permitting the efflux of X_i to reduce V_c indefinitely, without further perturbation of E_m or any intracellular ion concentrations (Fraser & Huang, 2004).

However, the efflux was stopped at point e after a ΔV_S− of similar magnitude to that demonstrated in Fig. 6B, and the extracellular conditions returned to those at the start of the modelling period. This increase in extracellular osmolarity resulted in a rapid V_c decrease. V_c then stabilized above its baseline value, due to the net increase in the total osmotic activity of X_i that took place during the ΔV_S+ and ΔV_S− processes. However, E_m remained slightly depolarized (∼3 mV) compared to baseline values due to the reduction in z_X and concomitant decrease in [K⁺]_i.

Finally, at point f X_i content was gradually reduced in a reversal of the process started at point c, thus returning z_X to its baseline value over the same period. This process was continued until both z_X and [X]_i reached their respective baseline values (g), at which point V_c was decreased from its original value, due to the loss of X_i content during the ΔV_S− process between points d and e. In contrast, E_m, [K⁺]_i, [Na⁺]_i, [Cl⁻]_i and [X]_i were restored precisely to their original values.

A possible alternative mechanism for ΔV_S− was also modelled, in which the total intracellular charge carried by X (V_c×[X]_i×z_X) was conserved, as opposed to the net loss of charge during the ΔV_S− phase shown in Fig. 8. However, this did not permit reconstruction of the experimental results shown in Fig. 6C, where ΔV_S− reduced V_c from its maximum value to 1.15. A volume decrease of this magnitude with conservation of intracellular charge was shown to require approximately a doubling of z_X, as the increase in cellular cation content resulting from the increase in z_X magnitude would oppose the volume decrease caused by decreasing X_i content and additionally permit a significant increase in [K⁺]_i, causing a hyperpolarization of ∼6 mV. Such a hyperpolarization was not detected (Fig. 7A and B). Further decreases in V_c from this value were shown to imply increasingly unrealistic values of z_X, with a further doubling required to decrease V_c to 1, contrasting strongly with the indefinite V_c decreases possible with a simple efflux of X, which do not further perturb E_m (Fraser & Huang, 2004).

Discussion

This study explored the relationship between increases in cell volume (V_c) and the resulting alterations in resting membrane potential (E_m) in amphibian skeletal muscle fibres during extended (3–4 h) exposures to extracellular solutions of reduced tonicity. V_c was measured in cutaneous pectoris muscles using confocal microscope scanning in the xz plane (Ferenczi et al. 2004), and E_m was measured in sartorius muscles using conventional microelectrodes (Adrian, 1956).

The experiments first confirmed that exposure of skeletal muscle fibres to hypotonic solutions elicited a rapid (>5% min⁻¹) volume increase, ΔV_R+, that closely followed simple osmotic predictions as previously reported (Dydynska & Wilkie, 1963; Blinks, 1965). However, this swelling was followed by slower volume transients, not observed on earlier occasions, which may represent cellular volume regulatory phenomena. Their detection in the present study is likely to reflect the long exposure times used here (cf. Blinks, 1965) and the increased accuracy afforded by assessment of V_c using confocal xz-plane scanning rather than measurements of fibre diameter (cf. Reuber et al. 1963).

The slow volume transients showed two distinct phases. First, an initial slow (<0.5% min⁻¹) volume increase, ΔV_S+, immediately followed ΔV_R+ and lasted approximately 50–60 min. ΔV_S+ produced increases in V_c to final values ∼10–15% greater than osmotic predictions, and was therefore suggestive of increases in total intracellular osmotic activity. It occurred in solutions of even slightly reduced relative tonicity (relative tonicity = 0.88). ΔV_S+ took place at a rate that gradually decreased until a maximum V_c was reached after approximately 50–60 min, contrasting sharply with the 2–5 min time courses of the passive ΔV_R+ volume changes and the passive volume changes previously reported in response to increases in extracellular tonicity (Ferenczi et al. 2004).

Second, a slow (<0.5% min⁻¹) volume decrease, ΔV_S−, then began quite abruptly ∼60–70 min after the ΔV_R+. It was not possible to assess the maximum duration of the ΔV_S− phase because it continued beyond the limits of tissue viability in the isolated tissue preparation used here. However, it was observed to continue for at least 3 h, over which time the volume decrease could exceed the magnitude of the preceding ΔV_S+; fibre volumes then eventually decreased below the predicted values for the prevailing extracellular tonicity. This suggested that the ΔV_S− process did not simply represent a reversal of the preceding ΔV_S+ process.

Both the ΔV_S+ and ΔV_S− phenomena persisted, and indeed assumed more rapid kinetics, under conditions of Cl⁻ deprivation. These features exclude possible mechanisms involving cation−Cl⁻ cotransport systems or other Cl⁻-dependent processes, instead suggesting that Cl⁻ redistribution (Hodgkin & Horowicz, 1959) otherwise limited the rates of both ΔV_S transients. Finally, fibres exposed to isotonic solutions with concentrations of NaCl that were reduced to levels identical to those of the hypotonic solutions used here showed stable volumes, suggesting that the slow volume transients were not a consequence of reduced extracellular ion concentrations.

Fibres that had been exposed to hypotonicity for various durations were then returned to the original isotonic solutions. This resulted in an initial cell shrinkage that was similar in magnitude and rate to the initial ΔV_R+ and therefore compatible with passive osmotic behaviour. However, the overall V_c changes during ΔV_S+ and ΔV_S− were then reflected in a residual V_c deviation from its baseline value. This permitted the identification of a second difference between the ΔV_S+ and ΔV_S− processes. After the initial rapid osmotic volume decrease on transfer from hypotonic to isotonic Ringer solution, fibres then showed a gradual volume decrease that was eventually equal in magnitude to the preceding ΔV_S+, allowing for the change in extracellular tonicity, at which point cell volumes stabilized. Cell volumes therefore returned precisely to their original resting values if the duration of exposure to hypotonic Ringer solution was insufficient to permit ΔV_S− to occur, demonstrating the full reversibility of ΔV_S+. However, if the exposures to hypotonicity were of sufficient duration to permit ΔV_S− the subsequent return to isotonic conditions continued to elicit a complete reversal of the ΔV_S+ process. This left final stable volumes that were less than the initial baseline volumes, suggesting that ΔV_S− produced a sustained loss of intracellular solute. Fibres that had undergone a period of ΔV_S+ and were then returned to isotonic Ringer solution additionally demonstrated that ΔV_S+ did not result from the fibre swelling per se. Thus, while swollen fibres in hypertonic Ringer solution demonstrated the ΔV_S+ phenomenon, fibres residually swollen to similar extents on return to isotonic Ringer solution due to a preceding ΔV_S+ phase instead showed volume recovery.

However, despite these slow volume transients, the changes in membrane potential (ΔE_m) during these exposures to hypotonic solutions remained close to predictions that assumed simple osmotic behaviour, conservation of intracellular K⁺, and a dependence of E_m upon E_K. Thus, exposures to hypotonic solutions with a range of relative tonicities from 0.75 to 0.42 caused rapid depolarizations compatible with a directly proportional reduction in the ratio [K⁺]_i/[K⁺]_e. Similar depolarizations were observed in Cl⁻-containing and Cl⁻-free solutions, thereby excluding any cation−Cl⁻ cotransport-dependent stabilization of E_m, in contrast to the E_m stabilization reported in osmotically shrunken fibres (Ferenczi et al. 2004). Return to isotonic Ringer solution then permitted full recovery of E_m to its resting value.

The present findings thus sharply contrast with the splinting of E_m but a relatively simple dependence of V_c upon extracellular osmolarity in fibres studied in hypertonic solutions (Ferenczi et al. 2004). Nevertheless, they proved similarly amenable to a recent, charge-difference approach to quantitative modelling (Fraser & Huang, 2004) that invoked osmotic activity in charged intracellular impermeant anions and their possible transmembrane fluxes rather than the Cl⁻-dependent transport processes that had successfully accounted for the earlier observations in hypertonic solutions. Thus, such modelling suggested that the ΔV_S+ that immediately followed the hypotonic volume expansion, ΔV_R+, without detectable further depolarization of E_m could reflect a reversible increase in osmotic activity in normally membrane-impermeant intracellular anions (X_i), whilst conserving the total intracellular charge carried by X_i (=V_c×[X]_i×z_X) through a proportional decrease in z_X. While such reductions in the magnitude of z_X would reduce the maximum polarization of E_m, the predicted depolarization was too small (<2–3 mV) for detection in the present study. ΔV_S+ may thus simply represent an unavoidable, even if inappropriate, consequence of the dilution of cellular contents, which might result in an increase in the osmotic pressure of X_i, for example due to the depolymerization of proteins (Lew & Bookchin, 1991), an alteration of cellular polymer water compartments (Bookchin et al. 1994), or a significant increase in the osmotic coefficient (φ) of X_i with dilution. However, it is also conceivable that ΔV_S+ might represent a functional response to reduced X_i content that is inappropriately activated when X_i is diluted secondary to fibre swelling under hypotonic conditions. Under conditions of stable extracellular osmolarity, a reduction in [X_i] would tend to cause volume decrease (Fraser & Huang, 2004), rather than simply reflecting such a dilution of cellular contents, and therefore a mechanism analogous to ΔV_S+ that could increase X_i content or osmotic activity towards normal might then be an appropriate corrective response.

However, modelling showed that a converse decrease in X_i and conservation of the product V_c×[X]_i×z_X was not compatible with the magnitude of ΔV_S− observed experimentally, since such a mechanism would require an increase in the magnitude of z_X to unreasonable values, thereby producing a significant hyperpolarization of E_m, contrary to experimental observation. Rather, the delayed ΔV_S− could be readily explained in terms of a simple efflux of X_i, thereby reducing the total intracellular charge carried by X_i but conserving z_X and hence E_m while reducing the product V_c×[X]_i×z_X. This, together with the observed delay prior to its initiation, would be compatible with ΔV_S− representing an RVD phenomenon dependent on organic anion efflux that is activated by cell swelling, as has been described in other cell types (Lang et al. 1998a,b). Such a scheme is then compatible with the observed reversibility of ΔV_S+ and apparent irreversibility of ΔV_S−. If so, ΔV_S− would represent, to the best of our knowledge, the first demonstration of RVD in mature skeletal muscle.

Appendix

The model of Fraser & Huang (2004) was modified in order to model the effects of step changes in extracellular osmolarity, θ_e. Previously, the model simply made the assumption that membrane water permeability greatly exceeded ion permeabilities, and therefore ion movements were assumed to be accompanied by sufficient water to maintain equal intracellular and extracellular osmolarities. However, in order to model step changes in extracellular osmolarity, it was necessary to model transmembrane water fluxes explicitly. Thus a permeability term was introduced for H₂O (P_H2O= 1.56 × 10⁻⁴ cm s⁻¹: Frigeri et al. 2004) and transmembrane water movements were then modelled as for any other uncharged molecule. The equations described below replaced eqn (5) in Fraser & Huang (2004), and were calculated in the order that they are presented here.

The concentration of H₂O in pure water was taken as 55.55 m, and the osmotic coefficient (φ) of each ion was assumed to be unity, such that solution osmolarities were numerically equal to the sum of their constituent ion concentrations. Therefore, the extracellular and intracellular H₂O concentrations ([H₂O]_e and [H₂O]_i, respectively) were given by:

and

θ_e denotes total extracellular osmolarity, and was thus simply the sum of the concentrations of the extracellular ions. Thus, at the end of each iteration cycle, inward water flux, J_H2O, was calculated:

Intracellular water was then assumed to occupy precisely the same volume per mole as in pure water, and so the change in cell volume, ΔV_c, after each iteration was simply:

Preliminary simulations showed that the results described by Fraser & Huang (2004) could be precisely reconstituted. However, this change did influence the time course of V_c and E_m changes following alterations in extracellular tonicity.