Adaptation and generalization in acceleration dependent force fields

Abstract

Any passive rigid inertial object that we hold in our hand, e.g., a tennis racquet, imposes a field of forces on the arm that depends on limb position, velocity, and acceleration. A fundamental characteristic of this field is that the forces due to acceleration and velocity are linearly separable in the intrinsic coordinates of the limb. In order to learn such dynamics with a collection of basis elements, a control system would generalize correctly and therefore perform optimally if the basis elements that were sensitive to limb velocity were not sensitive to acceleration, and vice versa. However, in the mammalian nervous system proprioceptive sensors like muscle spindles encode a nonlinear combination of all components of limb state, with sensitivity to velocity dominating sensitivity to acceleration. Therefore, limb state in the space of proprioception is not linearly separable despite the fact that this separation is a desirable property of control systems that form models of inertial objects. In building internal models of limb dynamics, does the brain use a representation that is optimal for control of inertial objects, or a representation that is closely tied to how peripheral sensors measure limb state? Here we show that in humans, patterns of generalization of reaching movements in acceleration dependent fields are strongly inconsistent with basis elements that are optimized for control of inertial objects. Unlike a robot controller that models the dynamics of the natural world and represents velocity and acceleration independently, internal models of dynamics that people learn appear to be rooted in the properties of proprioception, nonlinearly responding to the pattern of muscle activation and representing velocity more strongly than acceleration.

Introduction

When we hold rigid objects firmly in our hand, the resulting dynamics of our arm+object is a field of forces that depends on the motion of our limb, i.e., limb position, velocity, and acceleration. If this field is represented in the intrinsic coordinates of the limb, e.g., joint coordinates where θ , is the vector of angular positions, then irrespective of the mass distribution of the rigid object or the arm, the field is linearly separable into two components (Slotine and Li, 1991): the forces due to limb acceleration (inertial field) and the forces due to limb velocity (coriolis and centripetal field) . That is,

$$\tau =I\left(\theta \right)\ddot{\theta }+C(\theta ,\dot{\theta })\dot{\theta }$$

where τ is a vector representing torques and θ is a vector representing limb position. The matrices I and C represent inertia and coriolis/centripetal terms and include constant terms like link lengths and position of centers of mass. Holding an arbitrary rigid object firmly in hand will change these constants, but will not affect the structure of the equation. If we wish to build a robot that can learn to reach while firmly holding passive rigid objects, we might rely on a model of inverse dynamics $(\theta ,\dot{\theta },\ddot{\theta })\to \widehat{\tau }$ that estimates the forces $\widehat{\tau }$ that are necessary to achieve a particular desired state $\theta ,\dot{\theta },\ddot{\theta }$ via a set of basis elements:

$$\widehat{\tau }=\sum p_i{g}_i(\theta ,\dot{\theta },\ddot{\theta }).$$

To learn most efficiently, we would structure this internal model by carefully choosing basis elements that reflect the natural relationships between states and forces (Schaal and Atkeson, 1998). For example, because the effect of velocity and acceleration remains linearly separable when holding an object, a reasonable coding might be:

$$\widehat{\tau }=\sum _i{p}_{1,i}{g}_{1,i}(\theta ,\dot{\theta })+\sum _j{p}_{2,j}{g}_{2,j}(\theta ,\ddot{\theta }).$$

That is, prior knowledge of physics instructs us to form the internal model with linearly separable sets of basis elements, one sensitive to limb velocity and position the other sensitive to acceleration and position. Indeed, sensors that one finds on robots independently measure joint position, velocity, and acceleration.

Unlike the robotic sensors, the proprioceptive sensors in our body, i.e., muscle spindles, do not code limb velocity and acceleration in a linearly separable way (Houk et al., 1973;Matthews, 1981). A linear superposition of muscle stretch velocity and acceleration cannot fit the complex discharge rate of spindles (Houk et al., 1981;Prochazka and Gorassini, 1998). Instead, muscle spindles encode all these variables non-linearly but with maximum sensitivity to stretch velocity (Lennerstrand, 1968;Lennerstrand and Thoden, 1968;Hasan, 1983;Lin and Crago, 2002). If the internal model that people learn for controlling the dynamics of their limb is compatible with the way proprioception encodes state of the limb, then the basis elements will not encode velocity and acceleration in a linearly separable way. If on the other hand the internal model that people learn was optimized for controlling dynamics of passive inertial objects, then the internal representation should linearly separate limb velocity from acceleration.

In a recent report, we showed that a large body of data on reach adaptation can be explained with the theory that the brain represents state of the limb in terms of a coding similar to that found in muscle spindles (Hwang and Shadmehr, 2005). However, because most previous experiments considered velocity dependent force fields, the results were also consistent with a linearly separable coding of velocity and acceleration. As we show in the theoretical development that follows, the learning strategies structured to match the physical dynamics of the world will be quite different from learning strategies structured to reflect how our sensors encode those properties. These two different ways of coding will produce different patterns of generalization. Here we distinguish between these two strategies by studying the generalization patterns of the human motor learning system during voluntary reaching movements.

Theory

Suppose we ask a subject to hold an arbitrary rigid object in hand. The mass of that object will produce a field of forces on the hand that depends on hand acceleration as well as the configuration of the mass with respect to the arm. If the mass is held rigidly, the forces on the hand will take the form:

$$f=M\left(\theta \right)\ddot{x}$$ (1)

where f is a force vector due to the motion of the object, M(θ) is a position dependent mass matrix, and $\ddot{x}$ is hand acceleration. Rather than handing the subject an object to hold, we can use a robot to actively produce the forces in Eq. (1). In this case, we have f_a ≈ f , where f_a represents the active forces produced by the robot. [We use the term active force so to distinguish these forces from passive forces that are inherent in holding on to the handle of a robot and moving it about. We can eliminate most of these passive forces using algorithms that compensate for robot’s passive dynamics.] We can represent this field in terms of the joint coordinates of the limb,

$${\tau }_a=J^{T}MJ\ddot{\theta }+J^{T}M\left[\begin{array}{ccc}\hfill {\left(\frac{d{J}_{1,1}}{d\theta }\right)}^T\dot{\theta }\hfill & \hfill \cdots \hfill & \hfill {\left(\frac{d{J}_{1,n}}{d\theta }\right)}^T\dot{\theta }\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\left(\frac{d{J}_{m,1}}{d\theta }\right)}^T\dot{\theta }\hfill & \hfill \hfill & \hfill {\left(\frac{d{J}_{m,n}}{d\theta }\right)}^T\dot{\theta }\hfill \end{array}\right]\dot{\theta }$$ (2)

where τ_a represents the active torques the robot imposes on the subject’s arm, J is the arm’s position-dependent Jacobian matrix, and J_i,j indicates an element of this matrix. From Eq. (2) we can now conclude that regardless of the mass structure of the rigid object, the acceleration dependent and velocity dependent torques remain linearly separable in the intrinsic coordinates of the limb.

Hypothesis

Suppose that during the process of adaptation, the CNS learns a map that associates limb states to forces $(\theta ,\dot{\theta },\ddot{\theta })\to \widehat{\tau }$ , and that this map is computed with a set of basis elements. Our concern here is to infer the sensitivity of the basis elements to limb acceleration from the patterns of generalization. Consider two scenarios: 1) The basis elements that are sensitive to limb acceleration are not sensitive to limb velocity and the basis elements that are sensitive to limb velocity are not sensitive to limb acceleration:

$$\widehat{\tau }=\sum _i{p}_{1,i}{g}_{1,i}(\theta ,\dot{\theta })+\sum _j{p}_{2,j}{g}_{2,j}(\theta ,\ddot{\theta })$$ (3)

Such a coding would be optimal for learning control of rigid inertial objects. 2) The basis elements that are sensitive to limb acceleration are also sensitive to limb velocity but sensitivity to velocity is stronger than sensitivity to acceleration. This second scenario is motivated by the observation that spindle afferent discharge is a strong function of limb velocity, but is also affected by limb position and acceleration (Hasan, 1983).

If we choose M to be an anti-symmetric constant matrix, e.g. $M=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill \end{array}\right]N\cdot s^2∕m$, the result is a curl field in acceleration space. If one reaches toward a target, the field will push the hand perpendicular to the acceleration vector. In a stereotypical reach, movements are straight with a symmetric hand velocity profile. For these movements hand velocities that are visited in the first half of the reach are again visited in the second half of the reach. However, because the acceleration vector changes sign from the first half to the second half of the reach, a given hand velocity during the reach will experience opposite forces in the first and second halves of the movement. These forces cancel and produce zero net force in hand velocity space. Therefore, in this field a typical reach is expected to experience zero net force in terms of hand velocity. This simply implies that learning to reach in an acceleration dependent field would be impossible with bases that are only sensitive to limb velocity. It also implies that if learning is with bases described in scenario 1, the velocity sensitive basis elements cannot make a significant contribution to $\widehat{\tau }$. Rather, learning to reach in a curl acceleration field will be dominated by the acceleration dependent basis elements.

Note that two reaching movements that are in opposite direction visit exactly the same part of the acceleration space (but opposite parts of the velocity space). Therefore, acceleration dependent bases that were used to learn the task in scenario 1 will produce a strong generalization to movements in the opposite direction. The coding of scenario 1 predicts that learning of an acceleration field in one direction should strongly generalize to the opposite direction. In simple terms this means that if one can represent acceleration independent of velocity, then learning to move a mass in one direction will generalize to movements in the opposite direction although these two movements involve very different patterns of muscle activation.

In contrast, in scenario 2 we assumed that the bases are simultaneously sensitive to limb position, velocity, and acceleration but are most sensitive to limb velocity. Learning to represent the field of Eq. (1) will be more difficult than a velocity dependent field because of the weaker sensitivity to acceleration. Importantly, generalization will be incomplete or absent from movements from one direction to the opposite direction. Here we performed an experiment to test whether adaptation to an acceleration dependent field generalizes from one direction of movement to the opposite direction.

Methods

Six healthy individuals (3 women and 3 men) participated in this study. Average age was 25 years (range: 23 to 26 years). The study protocol was approved by the Johns Hopkins University School of Medicine Institutional Review Board and all subjects signed a consent form.

Experimental setup

Subjects sat on a height adjustable chair in front of a 2D robotic manipulandum (InMotion2, Cambridge MA) and held its handle. A vertical monitor was placed about 75 cm in front of subjects and displayed a cursor (diameter 3 mm) representing hand position and circles (diameter 10 mm) representing start and target positions of reaching.

The task was to reach to a displayed target (displacement of 15 cm) within 550±50 ms. Onset of movement was determined using an absolute velocity threshold of 0.03 m/s. Feedback on performance was provided immediately after target acquisition. If the target was acquired within a 100 ms window around the required movement time (500-600 ms), the target “exploded” and the computer made a sound. If the target location was acquired too slowly or too quickly, the target turned blue or red, respectively. Target configuration is shown in the Fig. 1a. The reaching movements were in an out-and-back pattern. In Fig. 1a, the targets for the odd number trials are displayed as black arrows. In the even trials, the target always appeared at the center position. The direction of movement in the even numbered trials is displayed with gray arrows in Fig. 1a.

Figure 1.

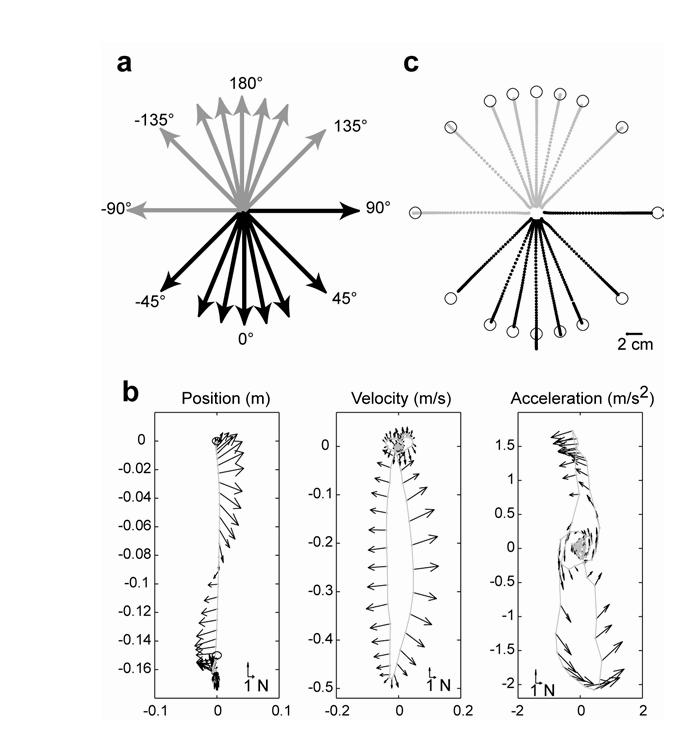
Experiment setup. (a) The experiment consisted of one baseline (null field) and five force field sets. During the baseline set, the first field set, and the fifth field set, subjects made movements in all 16 directions in a random order. However, center-out movements were always followed by out-center movements. The black lines indicate center-out movements and the grey lines indicate out-center movements. The out-center movements were drawn at the shifted positions for the purpose of clarity. Movements in all directions other than 0° were always in a force channel. During the second, third and fourth field sets, subjects made movements only in the 0° and 180° directions. (b) In field trials, an acceleration dependent curl field was imposed on the hand for movements toward 0°. Representative hand trajectory and the robot imposed forces are plotted here in position, velocity, and acceleration space of the hand. The example is from a representative trial in the last field set. Dots are sampled hand position every 20ms. (c) Movements in the force channel. Dots are sampled hand position (200 Hz) from single trials in the force channel from the fifth field set.

We used the robot to produce dynamics of an inertial object. In some trials, the robot produced active forces f_a on the hand that depended on hand acceleration (Eq. 1). where $M=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill \end{array}\right]N\cdot s^2∕m$. Hand acceleration was measured using an accelerometer mounted on the handle (Crossbow Technology Inc). Eq. (1) describes only the active forces that were applied to the hand. We estimated that in our robot, passive dynamics resulted in forces that were as large as 87% of the active forces. Therefore, the passive forces were not negligible. How could we be sure that the subjects learned an internal model of the active forces? We used three different approaches to deal with this issue. First, in addition to the forces that are described in Eq. (1), we used a control law on the robot to actively compensate for the passive dynamics. To do this, we used a system identification procedure to model the robot’s passive dynamics and then used the robot’s motors to cancel 50% of the forces due to its own inertia (we could not safely cancel more of the passive dynamics due to stability concerns). The passive dynamics cancellation control law remained in place during all phases of the experiment. Second, we used an extensive training period (see Experimental Procedure) to ensure that the subjects adapted to the (reduced) passive dynamics before we added the active inertial forces. Third, to independently measure the level of adaptation to the active forces, we used a force channel (see below) to compare the forces that the subjects produced during training in the inertial field with the forces that they produced at the end of training with the passive robot.

Force channel

We hypothesized that with adaptation, subjects learned an internal model of f_a , i.e., ${\widehat{f}}_a$ . To test our hypothesis, we used an important technique that was recently introduced by Scheidt et al. (2000). In this technique, in both the null and field sets a force channel is imposed on some trials so that it prevents movements from straying from the straight line that connects the start and end points of the movement. Depending on the strength of the channel walls, one can severely limit the kinematic errors in the trial (in our case, typically around 1mm). The channel pushes back with a force that is nearly equal to the force that the subject imposes on the walls. In this way, the channel allows the experimenter to readout the forces that the subject is producing perpendicular to the direction of motion without allowing those forces to produce kinematic errors. We were interested in measuring how training in an inertial field changed the forces that the subjects produced perpendicular to the direction of motion. We compared the forces that subject produced in the channel trials of the null set (termed f_n ), with the forces that the subject produced in the channel trials of the field set (termed f_f ). The difference in hand forces was assumed to be the result of adaptation of the internal model:

$${\widehat{f}}_a=f_f-f_n$$ (4)

In the channel trials, the walls had a stiffness of 1000 N/m and a viscosity of 200 N.s/m. Fig. 1c shows the hand paths of a typical subject in the channel trial. We measured the forces that the subjects produced during the channel trials using a six degree of freedom load cell mounted at the handle of the robot (Assurance Technology). The forces that we present in this report were post processed with a zero delay ten-point moving average digital filter. Sampling rate was 200Hz.

Experimental procedure

To familiarize the volunteers with the task, i.e., dynamics of the passive robot and other characteristics of the task, subjects began with four to seven sets of 96 movements in the null field. Once this pre-training was completed, the main experiment began with one set of 96 movements in the null field (baseline set) followed by five sets of 96 movements in a force field. During the baseline, first field, and last field sets, subjects made movements in all sixteen directions. However, movements in all direction except 0° were always in the channel. During the second, third and fourth field sets, subjects made movements only in 0° and 180°. Movement toward 180° was always in the channel. For movements at 0°, the channel was present occasionally (probability of 1/12∼1/5). For the remaining trials, movements were in the force field.

Performance measures

An acceleration dependent field makes movements somewhat unstable by forcing the hand to make a spiral path as it approaches the target. Therefore, a possible measure of performance in an acceleration dependent field is the total path length.

With training, hand path lengths can improve either because the nervous system learns to predict the environmental forces or because the arm stiffens and better reacts to perturbations in general. To test between these scenarios, we quantified forces that the hand produced in the channel trials. Because the robot imposed (active) forces were known, we calculated the forces subjects needed to produce to fully compensate for the external forces as: $-I\ddot{x}$ . We also measured forces that the subjects actually produced in the channel ${\widehat{f}}_a$ . To compare ${\widehat{f}}_a$ with $-I\ddot{x}$ , we computed three related measures: a correlation coefficient, a regression coefficient, and a mean squared error. The correlation coefficient is simply the covariance of the two signals divided by the square root of the individual variances. However, note that a correlation coefficient will indicate perfect correlation even when ${\widehat{f}}_a=-kI\ddot{x}$ and $k\ne 1$. Therefore, in addition to the correlation coefficient we computed the regression coefficient k:

$$k=\frac{\mathrm{cov}({\widehat{f}}_a,-I\ddot{x})}{\mathrm{var}(-I\ddot{x})}=\frac{\mathrm{cov}({\widehat{f}}_a,-I\ddot{x})}{\sqrt{\mathrm{var}(-I\ddot{x})}\cdot \sqrt{\mathrm{var}\left({\widehat{f}}_a\right)}}\cdot \frac{\sqrt{\mathrm{var}\left({\widehat{f}}_a\right)}}{\sqrt{\mathrm{var}(-I\ddot{x})}}$$ (5)

We also computed the mean squared difference between ${\widehat{f}}_a$ and $-I\ddot{x}$ along a sampled trajectory of the two variables during a movement.

Results

We considered the process of adapting reaching movements in inertial force fields. Subjects experienced the field for only the movements toward target at 0° (Fig. 1a). In this field (Eq. 1), forces on the hand were always perpendicular to the hand acceleration vector. Fig. 1b provides an example hand trajectory in a well adapted state. The forces initially push the hand to the right. When the hand reaches peak velocity, forces return to zero. As hand velocity decreases, forces reverse direction and push the hand to the left. The subplots in Fig. 1b also show the forces that the hand experiences when the reach trajectory is viewed in hand velocity and acceleration space. When the forces are viewed in hand velocity space (Fig. 1b, middle subplot), we note that very similar hand velocities are paired with opposite forces. The straighter the reaching movement, the more difficult it is to fit a smooth function to these forces in velocity space. At the limit (a perfectly straight reach with symmetric speed profile), the mean force at any hand velocity is close to zero. Similar properties hold for torques viewed in joint velocity space. The implication is that in order to adapt to this field, an internal model that utilizes linearly separable bases to encode limb position and acceleration (as in Eq. 3) would have to rely nearly exclusively on position/acceleration dependent bases.

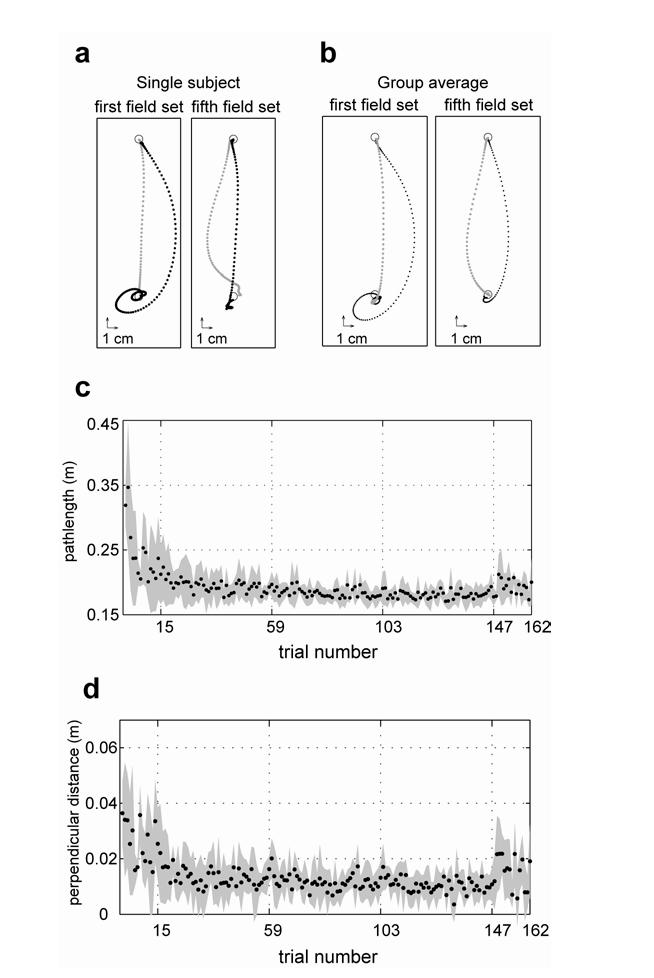
Fig. 2a displays a representative hand path from a null field trial (grey dots) as well as a trial in the first training set (black dots). When no external forces were applied to the hand, the movement was nearly straight. As the acceleration dependent curl field was applied, the movement curved to the right because the hand initially had negative acceleration. As the movement progressed and the hand decelerated, hand acceleration became positive and the direction of forces reversed, making the movement come back toward the straight line and go beyond it. As the hand missed the target, corrective movements via feedback control were made repetitively but these corrective movements were also perturbed in the direction perpendicular to the acceleration. As a result, movements exhibited a spiral about the target. Spirals were a consistent characteristic of this field, as illustrated by the cross-subject averaged hand paths in Fig. 2b.

Figure 2.

Hand trajectories during adaptation. (a) Hand paths in a typical subject for four representative trials, sampled at 200 Hz. Grey dots are from a trial in the null field. Black dots are from a trial in the force field. (b) Averaged hand paths across six subjects in the same format as (a). Movements were aligned to hand position at peak hand speed. (c) Path length as a function of trial number for movements toward 0°. The shaded area represents the standard deviation across subjects. Vertical dotted lines indicate each of the 5 field sets. In the first and last field sets, movements were performed in all 16 directions whereas in the middle 3 field sets, movements were only toward 0° and 180°. (f) Perpendicular distance at peak speed as a function of trial number (mean+/-SD).

Fig. 2a also displays a representative hand path from the last training set (black dots). The movement became straighter and the spiral at the end clearly decreased. The last movement in the fifth training set was a catch trial during which the external force was removed (this was the only catch trial in all the sets). During this trial, the movement was curved in the opposite direction to the movement in the field trial, indicating that subjects predicted some of the forces in the field. However, note that the large loops at the end of the movement in the field trials were not present in this catch trial, suggesting that the subjects might have increased their arm stiffness to stabilize the hand during the end of movements.

Fig. 2c displays the averaged path length across six subjects as a function of trial number. The path length gradually decreased with the training. At the end of training (the last force trial), path length was significantly smaller than that at the beginning of the training (the first force field trial) (t-test, t=5.06, d.f.=10, p=2.4×10^-4). We also measured the lateral deviation at the peak speed for each movement, which is the perpendicular distance from the straight line between the start and end positions. Fig. 2c displays the averaged perpendicular error across subjects as a function trial number. Similarly to the path length, the perpendicular error decreased with the training, suggesting adaptation to the force field.

Improvement in performance is likely due to both feed-forward mechanisms that associate desired limb states to forces $(\theta ,\dot{\theta },\ddot{\theta })\to \widehat{\tau }$ and feedback mechanisms that learn to better respond to errors that are sensed online (Wang et al., 2001;Burdet et al., 2001). We interspersed channel trials during the field sets to quantify the feed-forward forces. In the channel, the maximum deviation from a straight line was 1.4 ± 0.3 mm (mean+/-SD of maximum deviation across the 6 subjects). Because the channel minimized kinematic errors perpendicular to the movement direction, the forces at the hand could not be due to online compensation of kinematic errors or increased arm stiffness.

Fig. 3a shows the forces ${\widehat{f}}_a$ (Eq. 3) that a subject produced in the first and last channel trials in the field sets. Note that two field trials preceded the first channel trial. In the first channel trial, ${\widehat{f}}_a$ in this subject begins by pushing to the left, but at halfway into the movement (near peak velocity), the forces are near zero. By the end of training, ${\widehat{f}}_a$ is now very similar to the forces in the acceleration dependent field. That is, this subject produced forces that pushed initially to the left and then at middle of the movement switched and pushed to the right. Fig. 3b shows the average ${\widehat{f}}_a$ across six subjects in the first and last channel trials. Little compensation is present in the first channel trial. However, in the last channel trial a clear acceleration-like force pattern is present.

Figure 3.

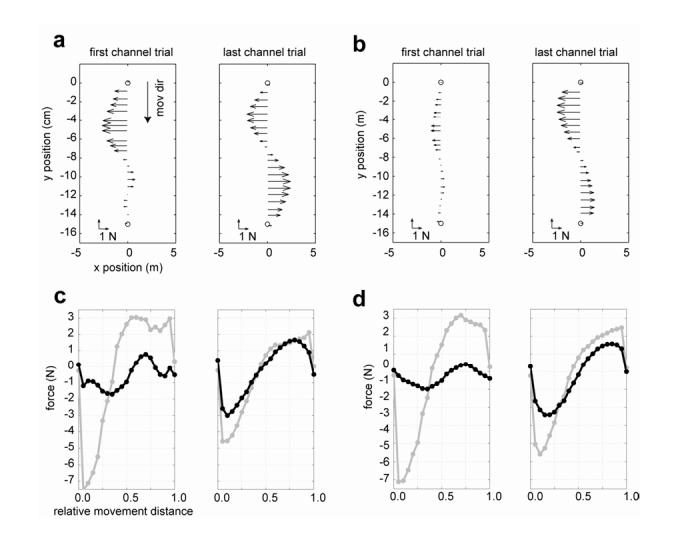
Forces that subjects produced in the channel trials for movements to target at 0°. (a) Forces ${\widehat{f}}_a$ (Eq. 3) produced by a typical subject in the first and last channel trials plotted as a function of hand position between start and end of the movement. (b) Across subject averaged forces for the first and last channel trials. (c) Comparison of forces ${\widehat{f}}_a$ produced in the channel trials and forces required for compensation of the field, f_a (Eq. 1). The black trace is ${\widehat{f}}_a$ produced by a typical subject as a function of movement displacement in the first and last channel trials. The grey trace is f_a . (d) Averaged ${\widehat{f}}_a$ and f_a across six subjects.

We examined how well ${\widehat{f}}_a$ matched the theoretical force $-I\ddot{x}$ required to counter the robot imposed field of forces. For each channel trial, we considered 21 evenly spaced points along the movement direction. The black line in Fig. 3c is ${\widehat{f}}_a$ for a single subject in a single trial. The grey line is the quantity $-I\ddot{x}$ .(The data for the black line in Figs. 3c and 3d are same as the data in Figs. 2a and 2b.) In the first channel trial, ${\widehat{f}}_a$ did not match the estimated external forces very well. However, in the last channel trial, ${\widehat{f}}_a$ was quite similar to the external force. Fig. 3d shows the cross-subject averaged ${\widehat{f}}_a$ and $-I\ddot{x}$ for the first and last trials. With training, the forces that subjects produced in channel trials approximated what was need to counter the field.

Fig. 4a shows the correlation between ${\widehat{f}}_a$ and $-I\ddot{x}$ for each channel trial, averaged across subjects. By the end of training the two variables were highly correlated (r=0.89±0.04) and the measure appeared to plateau by the second training set. Because correlation is insensitive to linear dependence between the variables, a large correlation is indicative of a high similarity between the shapes of the waveforms but not necessarily a match between the absolute values of the waveforms. We therefore computed a regression coefficient k (Eq. 5), where ${\widehat{f}}_a=-kI\ddot{x}$ . In the beginning of training, k was close to zero but it gradually increases to about 0.6 by the end of training. The data in Fig. 4b indicates that the rise time for k was somewhat slower than the correlation coefficient. Fig. 4c plots the mean squared difference between ${\widehat{f}}_a$ and $-I\ddot{x}$ (solid line). The dotted line indicates the expected difference when there is no compensation for the field, i.e., ${\widehat{f}}_a=0$ . The ratio between the solid and dotted line is a decreasing function (not shown) that starts at 1 and plateaus near the middle of the third set to around 0.4. This implies that by the end of training, ${\widehat{f}}_a$ compensated for around 60% of the external forces. Thus, using various measures we found ${\widehat{f}}_a$ was highly correlated with the time-dependent waveform of the external forces f_a but ultimately compensated for only about 60% of these forces. Because the various measures converged in the second or third sets, it is unlikely that further training would have significantly changed this incomplete compensation.

Figure 4.

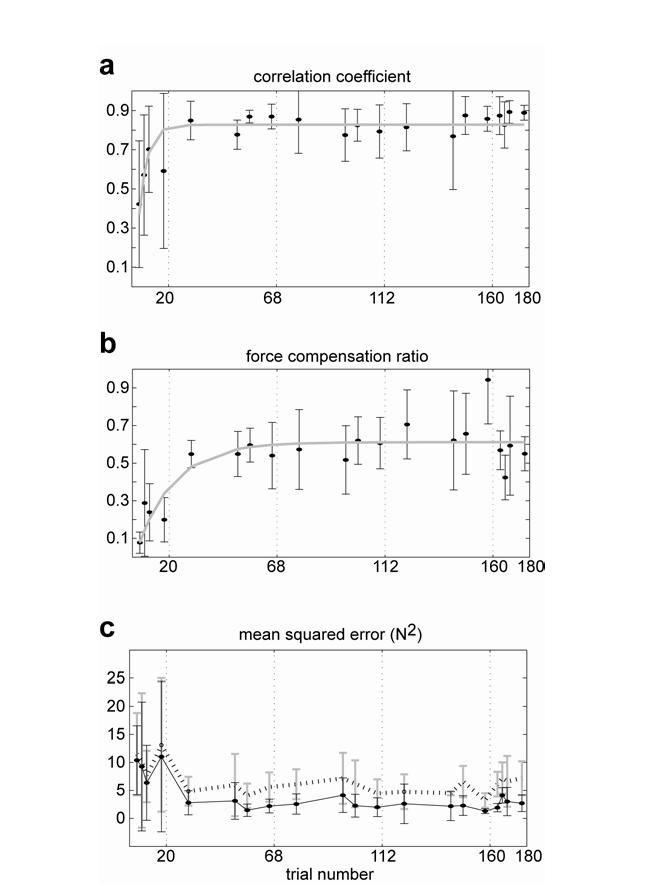
Evolution of forces during adaptation. (a) Correlation coefficient between forces ${\widehat{f}}_a$ produced in the channel trials and forces f_a required for compensation of the field. Each dot indicates a channel trial (mean+/SD). The solid line is an exponential fit to the data. (b) Slope of the linear regression between ${\widehat{f}}_a$ and f_a (Eq. 4). (c) Mean squared error between ${\widehat{f}}_a$ and f_a . The dotted line indicates the expected difference when there is no compensation for the field, i.e., ${\widehat{f}}_a=0$ .

We next examined how learning an acceleration dependent field in one direction was generalized to other directions. Fig. 5a shows $\widehat{f}$ for all sixteen directions during the last set of training. Note that all movements were performed in the channel except for some trials in 0° where the acceleration dependent field was present. Fig. 5a shows that in directions near the training direction, there are acceleration dependent force patterns but this generalization decayed quickly with angular distance. To quantify generalization, we computed the regression coefficient (Eq. 1) between ${\widehat{f}}_a$ and $-I\ddot{x}$ for each movement direction. Fig. 5b shows this measure for all sixteen directions. Generalization decayed quickly with the angular distance. Only in directions -22.5°, -11.25°, and 11.25°, significant amount of generalization was observed (t-test, p<0.01). Beyond ±45°, there is no significant generalization.

Figure 5.

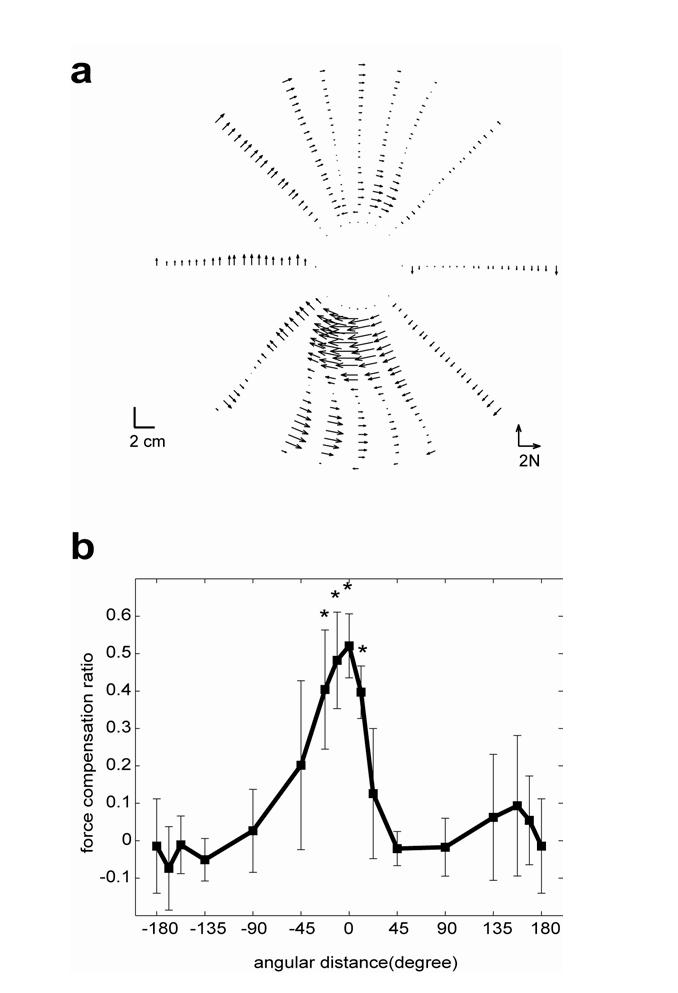
Generalization of the acceleration dependent field. (a) Across subject averaged ${\widehat{f}}_a$ recorded in force channels plotted as a function of displacement. The trained direction is for the downward movement at 0° and all other movements are measures of generalization. The data comes from the last set of training. (b) Generalization as a function of angular distance of the movements in the last training set. The measure is regression coefficient (Eq. 4) between ${\widehat{f}}_a$ and f_a in the last training set. Error bars are standard deviation. ^* indicates that the measure is significantly different from zero (p<0.01).

Note that movements in 180° experience nearly the same acceleration and deceleration as the 0° direction (our analysis finds that only 25±12 % of acceleration values in 180° lie outside the acceleration space that is covered in 0° direction). Despite this large overlap of acceleration, there is no generalization in the 180° direction. If learning were with two separate groups of basis elements, one that was sensitive to limb acceleration and one that was sensitive to limb velocity (scenario 1), then subjects should have learned a pure acceleration and force relationship and there should be near perfect force compensation for 180° direction. Instead, subjects seemed to have learned a more specific mapping, i.e., force as a function of all available arm states including arm acceleration, velocity and position, consistent with the scenario 2.

Discussion

We examined adaptation of reaching in a force field that depended exclusively on hand acceleration. Our first result was that in force channels that prevented the hand from moving outside of a straight line, the adapted system produced forces at the hand that closely approximated the acceleration dependent external forces along the entire hand trajectory. This is a crucial prediction of the hypothesis that the CNS learned a model of inverse dynamics of the task. Our second result was that this internal model generalized locally to directions ±45° with respect to direction of training. Importantly, adaptation did not generalize to 180°. Because movements to 180° visited nearly the same acceleration space as the trained movements but at very different velocities, the lack of generalization suggests that the basis elements that form the internal model cannot be linearly separated into groups that are exclusively sensitive to limb acceleration but not velocity. Instead, it agrees with our second hypothesis that the basis elements are sensitive to both acceleration and velocity. Indeed, the lack of generalization suggests that the sensitivity to limb velocity is the dominant factor.

Traditionally, adapting to altered dynamics of reaching has been assessed by examining change in kinematic features of reaching. Uncompensated dynamics tend to displace the hand from a straight line trajectory to the target, and with adaptation this displacement declines in field trials while the displacement increases in catch trials (Shadmehr and Mussa-Ivaldi, 1994;Lackner and Dizio, 1994;Singh et al., 2003). Here we found that in an acceleration dependent field, movements became straighter and clear after effects existed. It is possible that this improvement was due to formation of an internal model that mapped desired states of the limb to forces. Alternatively, performance improvements might have occurred because of adaptive changes in arm compliance (Burdet et al., 2001) or because of adaptive changes in how the CNS responded to kinematic errors that occurred during a movement (Wang et al., 2001). For example, in an acceleration-dependent field where forces change direction at maximum hand speed, it is possible that subjects learned to predict only the forces that were present during the initial part of the movement and then relied on feedback-error measures to correct for the forces that were present in the later part of the trial. This strategy is particularly relevant in acceleration dependent fields because the main effect is a spiraling of the hand near the target. Increased stiffness of the arm as it nears the target is a potential strategy for improving control. This strategy does not involve learning to predict an acceleration dependent force pattern and yet could account for both the improved straightness and the after effects of training. Indeed, the trajectories in catch trials did not show the consistent spiraling pattern near the target that we had observed in field trials. Therefore, kinematic analysis of field and catch trials could not provide strong evidence that the CNS learned to predict the acceleration dependent forces.

The internal model theory assumes that the CNS learns to associate desired states of the limb with forces. Therefore, if the limb follows the desired state trajectory, the force ${\widehat{f}}_a$ produced by the subject should predict the external dynamics. Scheidt et al. (2000) pioneered the use of a force channel to directly measure ${\widehat{f}}_a$ . In a force channel, changes in limb stiffness or improved error feedback control can not produce field-specific changes in hand forces because hand position does not deviate significantly from a straight line (presumably the intended trajectory). Scheidt et al. (2000) demonstrated that in a velocity dependent field ${\widehat{f}}_a\approx f_a\left(\dot{x}\right)$ . Here we used their approach and measured ${\widehat{f}}_a$ when the field depended on hand acceleration $\ddot{x}$. We found that with practice, ${\widehat{f}}_a$ became highly correlated with f_a . Therefore, the data appeared in agreement with a crucial prediction of the hypothesis that during adaptation, the CNS learned a map from limb states to forces. However, the regression coefficient between ${\widehat{f}}_a$ and f_a saturated around 0.6. This implies that the “feed-forward” motor commands learned only about 60% of the external force. The regression coefficient appears to saturate, implying that further practice was unlikely to significantly alter this result.

Subjects experienced the acceleration field only for movements to a single target. Movements to all other target directions were in a channel. This allowed us to directly measure the generalization pattern from the trained region of the limb state space to neighboring regions. Despite the fact that subjects moved in all directions but never experienced error in any direction but one, they generalized this error to neighboring directions. The pattern of generalization was similar to the generalization patterns in a task where a rigid object was attached to the arm (Sainburg et al., 1999). Therefore, the limited generalization pattern is likely not due to the unusual nature of the acceleration dependent field. Importantly, we did not observe significant generalization to movements at 180° away from the direction of training. This lack of generalization may be due to two reasons. First, movements at 180° include the same accelerations as the trained movements but in reversed temporal order. Second, movements at 180° involve very different limb velocities than movements in 0°. (In our experiment design, movements were out-and-back. Therefore, movements at 180° visited precisely the same limb position and very similar limb acceleration space of movements at 0°). Therefore, lack of generalization may have been due to either the fact that there was a difference in the temporal order in which the states were visited in the trained and test movements or the fact that the two movements had very different limb velocities.

The temporal order difference is unlikely because movements made in straight lines generalize to circular movements (Conditt et al., 1997;Conditt and Mussa-Ivaldi, 1999). This suggests that as long as the states of the two movements are similar, the temporal order in which those states are visited generally does not affect generalization. Furthermore, note that the accelerations experienced at the same velocity in straight and circular movements are very different. Despite that, the velocity dependent force field learned in straight line movements generalize to the circular movements as if subjects learned a velocity dependent force field in the circular movements (Conditt et al., 1997;Conditt and Mussa-Ivaldi, 1999). Thus, the receptive field of the basis elements must be relatively wide in acceleration space compared to velocity space. This suggests that the lack of generalization to 180° was due to the difference between those two movements in velocity space.

Our results reject the hypothesis that internal models for arm movement have basis elements that separately specialize in each limb state (position, velocity, and acceleration). Instead, the basis elements probably encode all state variables in a combined way. For example, a previous study used patterns of generalization to suggest that the basis elements encoded limb position and velocity via multiplicative coding: at a given velocity, the bases were globally and possibly linearly sensitive to limb position but at a given position, the bases were locally sensitive to limb velocity with possibly a Gaussian-like function (Hwang et al., 2003). This produces an ability to learn dynamics that is a non-linear function of both limb position and velocity, and produces global generalization in terms of limb position (Shadmehr and Moussavi, 2000) but local generalization in terms of limb velocity (Thoroughman and Shadmehr, 2000).

One possibility is that the basis functions that encode the internal model represent limb state in a way that is similar to how limb state is sensed by proprioception (Hwang and Shadmehr, 2005). For example, a common representation of position, velocity, and acceleration of the limb in muscle spindles is with firing rates that encode these variables multiplicatively (Hasan, 1983). In this coding, limb position is coded very broadly, limb velocity has strong directional bias, and limb acceleration is coded weakly. The linearly separable effects of acceleration and velocity of inertial objects is not reflected in this coding. Indeed, several neurophysiological studies have reported that no cell or only a small population of cells in both the peripheral and central nervous system have activities correlated with limb acceleration (Ashe and Georgopoulos, 1994;Hasan, 1983;Hasan and Houk, 1975;Matthews, 1981). All of these observations appear inconsistent with a control system that is optimized for learning dynamics of inertial objects.

Our data suggests that in a novel inertial field, the feed-forward mechanisms of the internal model at best compensated for 60% of the forces. In contrast, in a viscous field the compensation is nearly 100% (Scheidt et al., 2000). This is consistent with a strong representation of limb velocity in the CNS. However, we cannot reject the possibility that the learning control of a simple inertial object like a point mass (e.g., an apple held in hand) might be different from the adaptation we recorded for curl fields. For example, significant amount of force imposed by the mass in the hand can be compensated by simply scaling up the force output without a fine tuning of force as a function of velocity or acceleration.

In sum, our results suggest that the brain builds internal models of acceleration dependent forces with basis elements that encode limb acceleration, velocity and position in a combined way and not through specialized basis elements that are responsive to limb acceleration independent of limb velocity. In this combined representation, encoding of limb velocity appears to dominate acceleration. This type of coding of limb state is inconsistent with a system that is optimized to learn control of inertial objects. Rather, it raises the possibility that in the computation of the internal model, limb state is represented in a way that closely matches how limb state it is coded by sensors in the peripheral nervous system.