The Effect of Polymorphisms in the Enhancer of split Gene Complex on Bristle Number Variation in a Large Wild-Caught Cohort of Drosophila melanogaster

Abstract

The Enhancer of split complex [E(spl)-C] in Drosophila encompasses a variety of functional elements controlling bristle patterning and on the basis of prior work is a strong candidate for harboring alleles having subtle effects on bristle number variation. Here we extend earlier studies identifying associations between complex phenotypes and polymorphisms segregating among inbred laboratory lines of Drosophila and test the influence of E(spl)-C on bristle number variation in a natural cohort. We describe results from an association mapping study using 203 polymorphisms spread throughout the E(spl)-C genotyped in 2000 wild-caught Drosophila melanogaster. Despite power to detect associations accounting for as little as 2% of segregating variation for bristle number, and saturating the region with single-nucleotide polymorphisms (SNPs), we identified no single SNP marker showing a significant (additive over loci) effect after correcting for multiple tests. Using a newly developed test we conservatively identify six regions of the E(spl)-C in which the insertion of transposable elements as a class contributes to variation in bristle number, apparently in a sex- or trait-limited fashion. Finally, we carry out all possible 20,503 two-way tests for epistasis and identify a slight excess of marginally significant interactions, although none survive multiple-testing correction. It may not be straightforward to extend the results of laboratory-based association studies to natural populations.

ASSOCIATION mapping is potentially a powerful approach with which to dissect the genetic basis of complex traits (Risch and Merikangas 1996; Long and Langley 1999). Association mapping is especially attractive in comparison with quantitative trait locus (QTL) mapping as the resolution of genetic effects is much finer and potentially the actual causal site(s) can be uncovered. Also, as SNP genotyping becomes more cost effective the prospects for mapping complex phenotypes in whole-genome association studies are increasingly favorable (reviewed by Carlson et al. 2004; Hirschhorn and Daly 2005; Wang et al. 2005). Drosophila has proved a valuable model for understanding the genetic basis of complex traits (reviewed by Mackay 2001), and a number of recent association studies using laboratory inbred lines have aimed at identifying genetic variation for bristle number (Robin et al. 2002), photoreceptor determination (Dworkin et al. 2003), aging (De Luca et al. 2003), immune response (Lazzaro et al. 2004), wing shape (Palsson and Gibson 2004), and heart rate (Nikoh et al. 2004).

A concern with the above studies is their use of inbred strains of Drosophila raised under laboratory conditions. Flies in nature are clearly not inbred, and inbreeding can alter both genetic and phenotypic variation (Whitlock and Fowler 1999), and furthermore we understand very little about how differences between laboratory and natural environments might affect phenotype. Hence, effects identified in laboratory association studies may not always translate well to effects in nature. In this case, laboratory studies may tell us little about the characteristics of the evolutionarily relevant segregating polymorphisms that contribute to standing phenotypic variation. Two recent studies suggest that replicating laboratory associations in nature may not be straightforward. We attempted to replicate a highly significant laboratory bristle number association (Robin et al. 2002) in two large wild-caught population samples of Drosophila melanogaster, but were unable to find any evidence that the site contributed to bristle number variation in nature (Macdonald and Long 2004). Second, Dworkin et al. (2005) report a replication in nature of a strong laboratory wing shape quantitative trait nucleotide (QTN) initially identified by Palsson and Gibson (2004). Nevertheless, overall wing shape variation differed between the laboratory-reared lines and the natural sample, suggesting that wing shape in the two groups may not be completely comparable.

To overcome concerns about the relevance of laboratory-identified genetic factors to standing variation in nature, an obvious approach is to initially carry out association studies in natural populations. However, human genetic studies have shown that this approach is also fraught with difficulty, and replication of significant associations in follow-up studies is not guaranteed (e.g., Ioannidis et al. 2001; Lohmueller et al. 2003; Freedman et al. 2005). Several hypotheses have been put forward to explain the lack of replicability in human disease-gene association studies, including unrecognized population structure (Freedman et al. 2004; Marchini et al. 2004) and ethnic heterogeneity in the genetic architecture of disease. However, in many cases it appears that human genetic studies are underpowered to detect small effects, as sample sizes must be very large to detect subtle-effect QTN (Long and Langley 1999; Altshuler et al. 2000). A distinct advantage of Drosophila then is that extremely large cohorts can be easily sampled from nature, and the potential problem of unrecognized population structure minimized by collecting from a single location. However, these advantages must be tempered by the observation that Drosophila exhibits high levels of polymorphism, and linkage disequilibrium (LD) extends only a short distance relative to that in humans. So while it is possible to achieve very high resolution, to attain full coverage a very large number of single-nucleotide polymorphisms (SNPs) must be genotyped. Given the current expense of genotyping many sites in a large panel of individuals, researchers must focus on well-known candidate gene regions for the trait of interest.

Fortunately, the Drosophila system is sufficiently well studied that excellent candidate genes exist for many traits, and the model quantitative trait of bristle number is particularly attractive. There is a large set of viable candidate genes for bristle number (Mackay 1995), including many members of the Notch signaling pathway that control neural cell fate and the pattern and spacing of adult mechanosensory bristles (reviewed by Jan and Jan 1994; Artavanis-Tsakonas et al. 1999; Lai 2004). Many years of thorough investigation have yielded a wealth of knowledge on the development of bristles, including the molecular functions and interactions of the key players in the Notch pathway. Quantitative genetic work has further validated some of the candidate genes, including scabrous (Lai et al. 1994), Delta (Long et al. 1998), hairy (Robin et al. 2002), and the achaete-scute complex (Mackay and Langley 1990; Long et al. 2000).

In this study we focus on the well-known Enhancer of split complex [E(spl)-C], which harbors 12 transcription units, 11 of which are involved in various aspects of neural cell fate determination and act at the end of the Notch signaling pathway as effectors of the Notch signal. Several quantitative genetic studies have implicated genes of the E(spl)-C in the control of bristle number (Long et al. 1995; Nuzhdin et al. 1999; Dilda and Mackay 2002; Norga et al. 2003). However, the majority of interest in this locus as a candidate gene harboring variants of subtle effect contributing to bristle number variation comes from developmental biology work. E(spl)-C is arguably the best functionally annotated gene region in Drosophila, and an array of binding sites for cis-regulatory transcription factors have been identified, and a set of 3′-UTR regulatory elements is also known (Tietze et al. 1992; Kramatschek and Campos-Ortega 1994; Eastman et al. 1997; Leviten et al. 1997; Lai et al. 1998; Nellesen et al. 1999; Lai et al. 2000a,b; Lai 2002). The latter has been shown to negatively regulate transcript abundance, mediated by the formation of RNA duplexes with micro-RNAs, and to elicit changes in adult bristles (Lai and Posakony 1997, 1998; Lai et al. 2005).

We have previously examined nucleotide diversity at the E(spl)-C within and between species of Drosophila and identified regions of the locus that are visible to various selective forces (Macdonald and Long 2005). Identified regions include those showing evidence of population structure, positive selection (selective sweeps), and conservation between diverged species. Polymorphisms in regions that are visible to selection are likely to be functional. We have good evidence that E(spl)-C genes influence adult Drosophila bristle patterning, and the action of stabilizing selection on bristle number is well documented (Linney et al. 1971; Nuzhdin et al. 1995; García-Dorado and González 1996). Thus, a reasonable hypothesis is that the group of sites in regions visible to selection should be enriched for bristle number QTN. Together with SNPs in functionally annotated domains, SNPs in regions identified by these in silico annotation approaches are good candidates for bristle number QTN.

Here, we report the results of a large-scale association study for bristle number variation at the E(spl)-C locus. We successfully genotype 203 polymorphisms, including 167 common sites, across the locus in a single large sample of ∼2000 D. melanogaster individuals and test each site for an association with the two bristle traits, sternopleural and abdominal bristle number. None of the single-marker association tests show a significant effect of genotype after even liberal correction for multiple testing. We demonstrate that this result is unlikely to be due to insufficient marker density or power and that a QTN contributing 1–2% to total phenotypic variation could have been detected if present.

MATERIALS AND METHODS

Fly population and phenotyping:

A sample of 2000 D. melanogaster (1000 males and 1000 females) was collected in 2001 from a single locality in Napa Valley, California. This sample corresponds to the “nv2001” population described in Macdonald and Long (2004). For each fly two phenotypic measurements were taken: sternopleural bristle number (SBN) is the sum of the number of macro- and microchaetae on the left and right sternopleural plates, and abdominal bristle number (ABN) is the number of microchaetae on the most posterior sternite, corresponding to segment six of females and segment five of males.

Polymorphism identification and genotyping:

The complete sequence of the E(spl)-C was obtained for 16 third-chromosome extraction strains of D. melanogaster (GenBank accession nos. AY779906–AY779921), where the natural chromosome was derived from Napa Valley, California, and made homozygous against a balancer chromosome. See Macdonald and Long (2005) for a description of the sequencing strategy.

Biallelic polymorphisms were identified from a 47,677-bp alignment of the 16 E(spl)-C alleles (corresponding to positions 21,820,334–21,867,640 of the 3R D. melanogaster Release 4.1 genome sequence), and a subset, including both SNPs and simple insertion/deletion polymorphisms, was selected for genotyping in the large cohort of flies. Polymorphisms for genotyping were selected using a complex heuristic involving the site frequency, the level of LD with other sites, and the location of the site with respect to known functional elements or regions identified as visible to selection (see Macdonald and Long 2005). In all, 278 polymorphisms were chosen for genotyping. Genomic DNA was individually extracted from each of the 2000 flies, and for each individual the entire ∼47-kb E(spl)-C locus was PCR amplified in 20 overlapping 2- to 3-kb amplicons. These PCR products were used as a template to genotype the selected polymorphisms. A single SNP was genotyped using fluorescence polarization (Chen et al. 1999), and the remaining 277 sites were genotyped using a system based on the oligonucleotide ligation assay (Landegren et al. 1988), described fully in Genissel et al. (2004) and by Macdonald et al. (2005).

Population and quantitative genetic data analysis:

Unless otherwise stated all analyses were performed using custom scripts written for the statistical programming language R (www.R-project.org).

Linkage disequilibrium:

LD was calculated between polymorphisms both within the haploid E(spl)-C resequencing data and within the large diploid cohort. For the haploid data LD between sites was estimated using R², and the null hypothesis of linkage equilibrium was tested using a χ²-test (Hartl and Clark 1997, pp.101–103). The diploid genotyping data are unphased, so gametic frequencies cannot be easily inferred as the double heterozygote classes are indistinguishable. Instead, for every pair of sites gametic frequencies were estimated using a log-likelihood EM algorithm assuming random mating, such that the genotypic frequencies are the products of the gametic frequencies (Weir 1996, p. 76). The maximum-likelihood estimates of the gametic frequencies were then used to calculate R² and D′.

Population recombination rate:

The population recombination rate, ρ (or 4Nc, four times the effective population size times the probability of a recombination event per gamete per generation) per base pair for the E(spl)-C locus was estimated from 167 frequent (>5% minor allele frequency) diploid genotyped sites using the program MAXDIP (http://genapps.uchicago.edu/labweb/index.html), which generates a maximum-composite-likelihood estimate of ρ (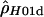)in the presence of gene conversion (Hudson 2001; Frisse et al. 2001; Wall et al. 2003). Ten entirely random samples of 49 individuals were extracted from the cohort of 2000 individuals, and the value of ρ per base pair was estimated for each. We used an initial estimate of ρ = 0.01, assumed values of f = 0, 1, …, 6, where f is the gene conversion rate parameter, defined as the ratio f = g/r (where g is the probability per generation that a gamete has a gene conversion tract, and r is the probability of a recombination event per gamete per generation), and a mean gene conversion tract length of 352 bp (Hilliker et al. 1994). Sites were used for the calculation only when they had >5% minor allele frequency within the sample of 49 individuals. For each sample we also estimated variation in ρ across E(spl)-C in a sliding-window framework, using the program RECSLIDER (Wall et al. 2003; http://genapps.uchicago.edu/labweb/index.html), with an initial value of ρ = 0.01 and a window of 20 segregating sites.

Tests of association:

For each polymorphism, various single-marker tests of association were performed. In all cases these models assume that the effects at the tested marker are not dependent on other markers; i.e., the effects are additive over loci. For each of the four sex/trait combinations (male SBN, male ABN, female SBN, and female ABN) both additive and arbitrary dominance effect ANOVA models were applied. The additive model is Y_ij = μ + G_i + ε_ij, where Y_ij is the bristle number of the jth individual for the ith genotype, G_i is the fixed effect of genotype (i = −1, 0, +1), μ is the grand mean, and ε_ij is the normally distributed error. This model corresponds to a regression of the phenotypic data on the number of major alleles present in each individual and provides an estimate of the effect, a, of an allelic substitution. The power of the additive model to detect QTN was tested using a Monte Carlo simulation with N = 1000 and minor allele frequencies between 0.05 and 0.5, as described in the Figure 2 legend in Macdonald and Long (2004). Irrespective of the allele frequency at the site, there is >90% power to detect a site contributing 1–2% to the total phenotypic variation in bristle number. The arbitrary dominance model is Y_ijk = μ + G_i + D_j + ε_ijk, with variables as for the additive model with the addition of the fixed-effect variable D_j, representing the dominance deviation (j = 0 for homozygotes and 1 for heterozygotes). The F-ratio statistic of the arbitrary dominance model is mathematically equivalent to a one-way ANOVA with three levels and provides estimates of a and the dominance deviation, d. Also, sexes were pooled, and for each trait the following factorial genotype-by-sex ANOVA model was applied, Y_ijk = μ + G_i + S_j + (G × S)_ij + ε_ijk. The variables are as described for the additive model above, with the inclusion of the fixed effect of sex, S_j, and the genotype-by-sex interaction, (G × S)_ij. This model provides estimates of a, the effect of sex, s, and an estimate of the genotype-by-sex interaction, a × s. Type II sums of squares were used for the genotype-by-sex model (R uses type I sums of squares by default), applied using the ANOVA function available in the car R package (http://cran.r-project.org/). For every single-marker test we ensured that each genotypic class (GG, Gg, and gg) was represented by at least 10 individuals, such that some tests compared just the two most frequent genotypic classes (GG and Gg), and for the rarest polymorphisms association tests were not performed.

Figure 2.

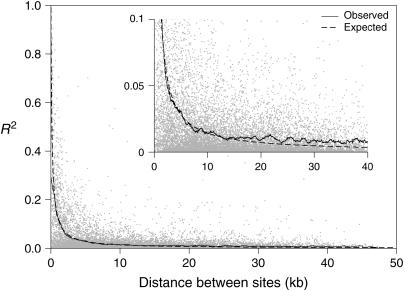
Decay of linkage disequilibrium with distance in the Drosophila melanogaster Enhancer of split gene complex. Each point is the R²-value, calculated from 2000 individuals, between a pair of sites from a set of 167 frequent (>5% minor allele frequency) sites in Enhancer of split. The solid line represents a smoothed curve through the raw data using the ksmooth function in the statistical programming language R (www.R-project.org). The dashed line is the expected value of R² calculated using the formula 1/(1 + 4Nc) (Hill and Robertson 1968), where 4Nc = ρ, the population recombination rate per base pair. A value of ρ = 0.0069 was estimated from the genotyping data, assuming the gene conversion parameter, f = 1 (see materials and methods and Table 1). The inset plot is an expanded version of the bottom portion of the full plot.

To account for multiple testing and to control the type I error rate such that the probability of a false positive over all tests is ≤0.05, for each of the 10 ANOVA models applied to the data we performed a permutation test (Churchill and Doerge 1994). For each model, 1000 permuted data sets were generated, where the bristle count data are randomly permuted with respect to the multilocus genotype of the individuals (for the genotype-by-sex interaction model, phenotypes were permuted within sex). After testing all sites the smallest P-value is extracted from each permuted data set. The smallest P-value from the real nonpermuted data is considered significant at P < 0.05 if it is in the lower 5% of the distribution of 1000 permuted values. Controlling the type I error rate in this fashion provides strict control over the number of false positives. A less conservative form of multiple-testing correction is provided by the false discovery rate (FDR) as measured by the q-value (Storey 2002; Storey and Tibshirani 2003). If q-values ≤0.05 are taken as significant, there is an FDR of 5% among the significant associations, meaning that 5% of the significant associations are false positives.

We also examined the degree to which epistatic interactions among pairs of polymorphisms in the E(spl)-C may influence bristle number. For each sex/trait combination we carried out a one-way ANOVA with nine levels, corresponding to the nine genotypic classes possible with two loci in diploids. The formula for this model is identical to the single-marker additive model described above, except that rather than being a regressor, here G is the fixed effect of a two-locus genotype and is represented by a nine-level factor. We carried out a similar analysis in a sex-pooled data set, including sex as a fully crossed factor in the ANOVA and using type II sums of squares. The formula for this model is the same as that for the single-marker genotype-by-sex model discussed above, but again G is a nine-level factor. We note that the sums of squares, and hence the P-values associated with our epistatic models, are equivalent to those obtained from more sophisticated models having nine orthogonal regressors (L. M. McIntyre, personal communication), which estimate the traditional quantitative genetics parameters (i.e., μ, a₁, a₂, d₁, d₂, a₁ × a₂, a₁ × d₂, d₁ × a₂, and d₁ × d₂; Zeng et al. 2005). Thus, we test only for the presence of epistasis. Parameter estimates could be obtained using more advanced models, but would likely be of value only if generated in a second independent data set (Beavis 1994).

Finally, our experimental design permitted a test of the effect of transposable element (TE) insertions on bristle number variation. Multiple genotyping assays were developed within each of 20 2- to 3-kb PCR amplicons across the E(spl)-C. A TE insertion within a PCR amplicon would knock out the single TE-harboring allele, render the genotype for each site within the amplicon a homozygote, and generate a homozygous amplicon haplotype (HAH). HAH individuals may harbor a TE (or actually be a homozygote for every SNP in the amplicon), while those showing at least one heterozygous site (non-HAH individuals) cannot harbor a TE. Comparing bristle number between these two classes is then a weak test for the effect of TE insertions. Within each amplicon, individuals with fewer than five polymorphisms assigned a genotype were ignored, while the remaining individuals were categorized as non-HAH if at least one of the assigned genotypes is a heterozygote and (A) HAH if all assigned genotypes are homozygous or (B) HAH if all assigned genotypes are homozygous, but not all show the major homozygous allelic state. For each amplicon (aside from amplicon 19 for which fewer than five sites were genotyped), for tests A and B, and for each trait/sex combination we examined the effect of TE insertion on bristle number in a one-way ANOVA: Y_ij = μ + T_i + ε_ij, where Y_ij is the bristle number of the jth individual for the ith state of the amplicon, and T_i is the fixed effect of a homozygous amplicon (i = 0 for non-HAH and 1 for HAH). Also, we pooled the sexes and tested the effect of TE insertion on each bristle number phenotype, using a fully factorial ANOVA model: Y_ijk = μ + T_i + S_j + (T × S)_ij + ε_ijk, where the notation is the same as that in the one-way ANOVA above with the inclusion of the fixed effect of sex, S, and the amplicon state-by-sex interaction term. For this factorial ANOVA statistics were evaluated using type II sums of squares.

RESULTS

Genotype and phenotype data:

The E(spl)-C in D. melanogaster is a ∼47-kb locus on the third chromosome harboring 12 genes. We previously resequenced 16 alleles for the entire region (Macdonald and Long 2005) and identified 1027 biallelic polymorphisms, 550 of which are nonsingletons. Genotyping assays were designed for 278 of the polymorphisms. Generally sites selected for genotyping were nonsingletons, and as far as was possible we attempted to genotype sites such that each had low LD with other genotyped sites. Polymorphisms were also selected if they were present in or were close to known upstream regulatory domains, were nonsynonymous, or were in intergenic sequence conserved between D. melanogaster and D. pseudoobscura (Macdonald and Long 2005).

Of the 278 genotyping assays developed, 228 converted to working assays; i.e., three (or two, in the case of rare polymorphisms) genotype clusters could be resolved. Of these, 203 polymorphisms were retained following a posteriori quality control. First, we have demonstrated that oligonucleotide ligation assay-based genotyping can be sensitive to segregating sites in the binding regions of the genotyping oligos, but that problems can be controlled using degenerate nucleotides in the oligos (Macdonald et al. 2005). Twelve genotyped sites showed a SNP within the oligo-binding regions that was not controlled for in the design of the assay and showed deviation from Hardy-Weinberg equilibrium (HWE) at P < 0.05. These 12 sites were removed. Second, large sample sizes should allow subtle deviation from HWE to be recognized (Weir 1996). We supported this by showing that while a set of SNPs genotyped in a large cohort may show more sites deviating from HWE than expected by chance, random small subsamples from the cohort do not (Macdonald et al. 2005). However, deviation from HWE can be an indicator of low genotyping assay quality (Hosking et al. 2004). Thus, we removed an additional 13 sites for which >20% of 1000 random samples of 96 individuals showed deviation from HWE at P < 0.05. Of the remaining 203 polymorphisms, 191 are SNPs and 12 are insertion/deletion events. Hereafter, for simplicity we collectively refer to the genotyped polymorphisms as SNPs.

The 203 E(spl)-C SNPs were genotyped in a single large cohort of 2000 D. melanogaster individuals, each of which had been phenotyped for SBN and ABN. These bristle traits exhibit normal distributions (c.f. Genissel et al. 2004) with means (variance) of 16.7 (4.67), 17.3 (4.80), 15.7 (5.50), and 18.2 (7.63) for male and female SBN and for male and female ABN, respectively. The cohort was sampled directly from nature, and since the sibling species D. melanogaster and D. simulans occupy the same broad ecological niche, and the females are difficult to distinguish phenotypically, we sought to ensure that the flies used for association mapping were only D. melanogaster. We accomplished this by genotyping along with the cohort a number of known D. simulans individuals and prior to analysis clustered all individuals on the basis of the multilocus genotype using the hclust function in the statistical programming language R (www.R-project.org). Eight individuals from the cohort clustered with D. simulans and were removed for all subsequent analyses.

Linkage disequilibrium across Enhancer of split:

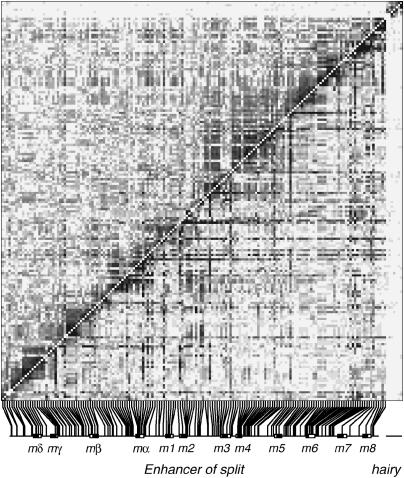
Using the SNPs genotyped in the panel of 2000 D. melanogaster, we calculated LD between all pairs of sites, and Figure 1 shows the pairwise LD for the 167 frequent (>5% minor allele frequency) polymorphisms in E(spl)-C and seven frequent sites in the hairy locus (Macdonald and Long 2004). The very large sample size should ensure that these estimates of LD are subject to relatively little sampling error, and in general the two LD measures used, R² and D′, appear to show a similar pattern. It is immediately apparent that E(spl)-C and hairy are in linkage equilibrium. There is no long-range LD between the loci [between SNPs in hairy and SNPs in E(spl)-C mean R² = 0.00056], which is expected as the loci reside ∼60 cM apart on the third chromosome of D. melanogaster. This observation is consistent with our large cohort being a sample from a single random-mating population, as population structure would be manifest as excess between-locus LD (Nei and Li 1973). Cryptic population structure can lead to spurious positive association mapping results (Freedman et al. 2004; Marchini et al. 2004), and its absence considerably simplifies the interpretation of association mapping data.

Figure 1.

Extent of linkage disequilibrium across the Enhancer of split gene complex in Drosophila melanogaster. The pairwise LD among a set of 167 frequent (>5% minor allele frequency) sites in Enhancer of split and 7 frequent sites upstream of the hairy gene, calculated from 2000 diploid individuals, is represented as shaded blocks (dark, high LD; light, low LD). D′ is shown below the diagonal (values from 0 to 1 are split into 10 equal bins), and R² is shown above the diagonal (values split into 10 bins defined by 1, ). The site positions in the Enhancer of split locus are shown below the plot, with the 12 genes labeled (solid boxes, exons; open boxes, untranslated regions).

Figure 1 also shows that, as expected, LD falls off with distance. To examine the nature of the decay of LD with distance in E(spl)-C more quantitatively, we plotted the value of R², the correlation coefficient associated with pairs of sites, between all pairs of frequent sites against the distance between the sites (Figure 2). The smoothed best-fit line through the points quite clearly shows that LD drops precipitously with distance, and indeed 199/210 (95%) site pairs with R² > 0.3 are within 2.5 kb of one another. This is fairly typical of previous work in Drosophila (Miyashita et al. 1993; Long et al. 1998; Langley et al. 2000).

The expectation of R² is 1/(1 + 4Nc) (Hill and Robertson 1968), where 4Nc = ρ, the population recombination rate. We estimated the value of ρ at E(spl)-C, assuming various contributions of gene conversion, using 167 frequent genotyped SNPs for 10 sets of 49 individuals randomly sampled from the cohort of 2000 flies (it is computationally infeasible to estimate ρ from the entire cohort). Table 1 shows the mean value of ρ over the 10 samples for each assumed value of the gene conversion rate parameter f, equal to the ratio of gene conversion to crossing over. It is important to include gene conversion, as it may contribute substantially to the overall rate of genetic exchange between homologous chromosomes at intralocus physical distances (Andolfatto and Nordborg 1998). Using the mean values for ρ we generated the expected distribution of R² with distance. In Figure 2 we plot the curve most closely aligned with the best-fit line through the observed data, which is associated with ρ = 0.0069, assuming f = 1; i.e., gene conversion and crossing-over events are equally likely. Although little is known about rates of gene conversion for multicellular eukaryotes, a value of f = 1 is not inconsistent with previous measures for Drosophila (Finnerty 1976; Hilliker and Chovnick 1981). The expected decay of R² with distance fits very well with the observed data in Figure 2, at least up to ∼15 kb, above which the observed level of LD seems marginally higher than expected. This can also be seen in Figure 1, where more LD is between sites separated by >40 kb than between unlinked sites: mean R² = 0.0064 between sites >40 kb in E(spl)-C, while the expected level is <1/(1 + 0.0069 × 40000) = 0.0036.

TABLE 1.

Estimated values of the population recombination rate, ρ, per base pair for Enhancer of split

fa	Mean ρ/bpb	SD ρ/bpb
0	0.0097	0.00118
1	0.0069	0.00068
2	0.0056	0.00053
3	0.0047	0.00044
4	0.0042	0.00038
5	0.0038	0.00036
6	0.0034	0.00033

^aThe gene conversion rate parameter, defined as the ratio of gene conversion to crossing over.

^bThe mean and standard deviation (SD) population recombination parameter, ρ, given various assumed levels of f. ρ was estimated (using the program MAXDIP) for 10 random samples of 49 individuals from the large cohort of 2000 Drosophila melanogaster, using 167 frequent sites (>5% minor allele frequency) across Enhancer of split.

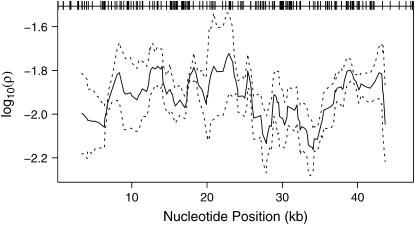
The relatively high density of common SNPs genotyped across E(spl)-C allowed us to examine variation in ρ across E(spl)-C in a sliding-window framework (Figure 3). The plot shows the mean value of ρ for each window of 20 segregating sites for 10 random samples of 49 individuals, showing that while there are some differences in the estimate of ρ across replicate samples, generally the estimates converge to a very similar pattern. There is also some heterogeneity in ρ across the E(spl)-C, with some notable peaks and troughs in the recombination rate. However, unlike in humans where hotspots of recombination result in estimates of recombination varying by four orders of magnitude (McVean et al. 2004), recombination rates appear relatively constant across E(spl)-C.

Figure 3.

Recombination rate across the Enhancer of split complex in Drosophila melanogaster. The population recombination rate, ρ, per base pair was estimated for 10 sets of 49 individuals randomly sampled from a large cohort of 2000 individuals, using 167 frequent sites (>5% minor allele frequency). The program RECSLIDER was used to estimate ρ in a sliding-window framework using a window size of 20 segregating sites and an initial estimate of ρ = 0.01, assuming no gene conversion. The solid line represents the mean value of ρ across the 10 samples for each window, and the dashed lines show the upper and lower 95% confidence intervals on the mean calculated from the 10 population samples. Tickmarks at the top of the plot show the positions of the 167 frequent polymorphisms.

Saturation genotyping of Enhancer of split:

The alignment of 16 resequenced E(spl)-C alleles is 47,677 bp long and encompasses 550 frequent sites (where the minor allele is seen in >1/16 chromosomes), of which we successfully genotyped 167 (30.4%). With such a selective genotyping approach it is important to assess the likelihood of missing a QTN if one truly exists, i.e., the degree to which the region is saturated with markers. One approach is to count the number of SNPs genotyped across E(spl)-C given its recombinational size. Using the estimate of the per base pair population recombination rate, ρ = 0.0069 from above, one 4Nc unit is equal to 1/0.0069 = 145 bp, and the size of the E(spl)-C in units of 4Nc is 47,677 × 0.0069 ≈ 329. Since we genotyped 167 frequent sites across E(spl)-C (with an average distance of 285 bp between them), we succeeded in genotyping roughly one site every two 4Nc across E(spl)-C.

Another criterion with which to assess how well we have covered E(spl)-C with SNPs is the degree to which SNPs in likely functional regions are in LD with genotyped markers. This is because the set of SNPs present in a priori candidate functional regions is presumably more likely to harbor QTN than is a randomly selected subset of SNPs. For each frequent ungenotyped SNP, we calculated the maximum R²-value between it and all genotyped SNPs situated within 3 kb in the sequenced sample of 16 alleles. R² is the natural measure of LD for this purpose as population genetics theory shows that the phenotypic variation attributable to a marker can be estimated as the product of the LD between the QTN and the marker and the variance attributable to the QTN (Hill and Robertson 1968). More formally, 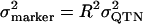(Lai et al. 1994, footnote 24; Long et al. 1998). The 3-kb distance threshold ensured that sites far apart showing strong LD in the 16 resequenced alleles were not used, as it is unlikely that such strong long-range LD would be replicated in the large cohort (see Figures 1 and 2). The significance of the maximum LD value for each ungenotyped SNP was calculated using a χ²-test. If this test was significant at P < 0.005, the ungenotyped SNP was said be in strong LD with a genotyped site. Since the χ²-statistic is numerically equivalent to R²N, where N is the number of sequenced alleles (Hartl and Clark 1997, p. 103), our definition of strong LD implies an R² > 0.5. Figure 4 shows that of the 383 common sites in E(spl)-C that we did not genotype, just 33 (8.6%) are not in strong LD with a genotyped SNP. We were even more successful genotyping SNPs in potentially functional regions, defined as SNPs within transcribed DNA, SNPs in/near annotated upstream regulatory elements, and SNPs in sequence conserved between D. melanogaster and D. pseudoobscura (conserved sequence was assessed using a BLAST approach, detailed in Macdonald and Long 2005). For these common potentially functional variants, 72/76 (95%) were in strong LD with a genotyped SNP. The approach described suggests that we achieve good coverage of potentially functional SNPs, and taken together with the fact that we are genotyping at least one site per two 4Nc, the E(spl)-C locus is very close to being typed to saturation such that causal SNPs are likely to be detected.

Figure 4.

Saturation genotyping of frequent sites in the Enhancer of split complex. Resequencing 16 Drosophila melanogaster alleles for the complete Enhancer of split locus revealed 550 frequent polymorphisms, where the minor allele was seen in at least 2/16 alleles, and 167 of these were genotyped in a large cohort for association mapping. The positions of the 167 typed sites are shown in black relative to the structure of the locus (solid boxes, exons; open boxes, untranslated regions). The remaining 383 not typed sites are categorized as exonic (both synonymous and nonsynonymous), UTR (in either the 3′- or 5′-untranslated regions), upstream regulatory (present within an annotated regulatory element or the 10 bp flanking each side of the element), conserved intergenic (present in intergenic, nonregulatory sequence conserved between D. melanogaster and D. pseudoobscura; Macdonald and Long 2005), or nonconserved intergenic. Each not typed site is color coded to reflect the level of LD with a typed site [green, in strong LD with a genotyped site (χ²-test, P < 0.005) within 3 kb; red, not in LD with a genotyped site]. The values on the right of the plot show, for each category of not typed site (from left to right), the number of ungenotyped sites not in LD with a genotyped site, the number of ungenotyped sites, and the percentage of ungenotyped sites in LD with a genotyped site.

Single-marker associations between bristle number variation and genotype at Enhancer of split:

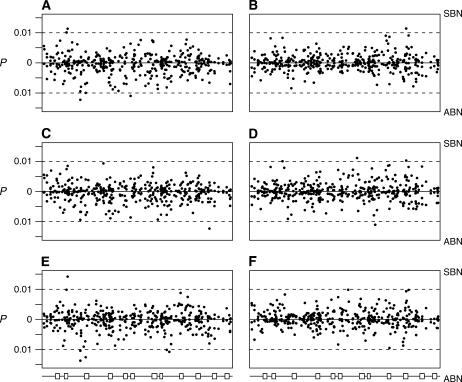
Two hundred three polymorphisms were genotyped, with 195 and 196 SNPs being sufficiently frequent within males and females, respectively, for association tests to be carried out. Figure 5 shows the P-values for the single-marker tests of association with bristle number. It is immediately apparent that for the additive and arbitrary dominance models (Figure 5, A–D), no site for any of the four sex/trait combinations is obviously associated with bristle number. At the 5% level, no test survives the Bonferroni-corrected threshold of P = 0.00026, and no test survives a permutation testing procedure (Churchill and Doerge 1994) or the less strict false discovery rate threshold (Storey 2002; Storey and Tibshirani 2003). Over all four sex/trait combinations the single-marker tests under an additive model reveal just five sites below an arbitrary threshold of P < 0.01, and five sites are significant at P < 0.01 in the arbitrary dominance model. Table 2 details these marginal associations. These nine sites (SNP A39349C is significant in both the additive and the arbitrary dominance models for female SBN) do not show any obvious similarities, other than that they all have frequencies >10%: five of the sites are SNPs and four are simple insertion/deletion polymorphisms, they are not physically clustered, and they are located in different functional regions (one is a synonymous change, two are located in 3′-UTRs, five are located in nonconserved intergenic sequence, and one is in conserved intergenic sequence). Also, each of the nine sites is significant at 1% for a single sex/trait combination only (male SBN, two sites; female SBN, three sites; male ABN, three sites; and female ABN, one site). It is notable that of the five marginal associations for the arbitrary dominance model, two sites show almost complete dominance (in8017del and in42049del), and two show strong overdominance (T26864A and G31458A).

Figure 5.

Single-marker tests for association between bristle number variation and polymorphisms in the Enhancer of split complex in Drosophila melanogaster. (A) Male additive model, (B) female additive model, (C) male dominance model, (D) female dominance model. (A–D) Each point represents the P-value (on a −log₁₀ scale) of a single-marker ANOVA test for association with sternopleural bristle number (SBN, above the x-axis) or abdominal bristle number (ABN, below the x-axis), under either additive or arbitrary dominance models separately for males and females. (E–F) Sex model: Each point is the P-value for the genotype term (E) or the genotype-by-sex term (F) from a single-marker genotype-by-sex interaction ANOVA model with either SBN or ABN. The dashed lines delimit sites showing marginal significance at P ≤ 0.01. Open boxes at the bottom represent the 12 transcription units at Enhancer of split.

TABLE 2.

Results of marginally significant single-marker association tests under the additive and arbitrary dominance ANOVA models

Sitea	Locationb	MAFc	Sex	Trait	Nd	Fd	Pd	a (SE a)e	d (SE d)f
Additive model
A5891C	mγ silent	0.37	M	SBN	838	6.74	0.0096	−0.28 (0.11)	NA
G6121T	mγ 3′-UTR	0.28	M	SBN	848	7.74	0.0055	−0.32 (0.11)	NA
del9384in	Intergenic NC	0.32	M	ABN	915	8.56	0.0035	−0.34 (0.12)	NA
in22062del	Intergenic NC	0.24	M	ABN	890	7.46	0.0064	−0.34 (0.13)	NA
A39349C	m6 3′-UTR	0.23	F	SBN	986	7.78	0.0054	−0.33 (0.12)	NA
Arbitrary dominance model
in8017del	Intergenic NC	0.20	F	SBN	984	4.67	0.0096	0.57 (0.19)	0.45 (0.23)
T26864A	Intergenic NC	0.42	F	SBN	932	5.15	0.0060	−0.05 (0.11)	−0.47 (0.15)
G31458A	Intergenic NC	0.23	F	ABN	946	5.12	0.0062	−0.45 (0.19)	−0.75 (0.24)
A39349C	m6 3′-UTR	0.23	F	SBN	986	4.76	0.0087	−0.18 (0.16)	0.26 (0.20)
in42049del	Intergenic CON	0.11	M	ABN	946	5.72	0.0034	0.85 (0.25)	0.83 (0.30)

NA, not applicable.

^aThe name of the site is given as its position in the 47,677-bp alignment of 16 E(spl)-C alleles, prefixed by the major allele at the site and suffixed by the minor allele.

^bThe location of the site in the E(spl)-C: silent, a synonymous change; UTR, in an untranslated region; intergenic NC, nonconserved intergenic sequence; intergenic CON, conserved intergenic sequence.

^cMinor allele frequency.

^dThe sample size (N) used in the ANOVA and the resulting F-statistic (F) and P-value (P).

^eThe additive effect of the site (a) and its standard error (SE a), where a is the effect on bristle number of substituting a common allele for a rare allele (i.e., aa to Aa or Aa to AA).

^fThe dominance effect of the site (d) and its standard error (SE d), where d is the effect of the heterozygote.

For each bristle trait, every site was also tested in an ANOVA model including sex, genotype, and the genotype-by-sex interaction. Figure 5, E and F, shows the P-values for the genotype and genotype-by-sex interaction terms, respectively, for SBN and ABN. These plots show that there are no SNPs with significant genotype-by-sex effects at P < 0.01, but that one site for SBN and five sites for ABN show genotype effects significant at the 1% level (Table 3). As for the sex-specific models tested above, no site survives any form of multiple-testing correction. Two of the six polymorphisms that are marginally significant for genotype over both sexes were already identified using the additive or arbitrary dominance models, and the remaining four are all SNPs above 29% frequency, of which three reside in nonconserved intergenic regions while one is in a 3′-UTR.

TABLE 3.

Results of marginally significant single-marker association tests under the genotype-by-sex ANOVA model

					Genotype term			Genotype-by-sex term
Sitea	Locationb	MAFc	Trait	Nd	Fd	Pd	a (SE a)e	Fd	Pd	a × s (SE a × s)f
G6121T	mγ 3′-UTR	0.28	SBN	1760	10.19	0.0014	−0.32 (0.12)	0.46	0.4962	0.11 (0.16)
T9366A	Intergenic NC	0.30	ABN	1836	7.03	0.0081	−0.29 (0.13)	0.30	0.5822	0.10 (0.18)
del9384in	Intergenic NC	0.32	ABN	1858	9.79	0.0018	−0.34 (0.13)	0.44	0.5072	0.12 (0.18)
T10738G	mβ 3′-UTR	0.35	ABN	1797	8.80	0.0030	−0.31 (0.13)	0.12	0.7273	0.07 (0.19)
G31243T	Intergenic NC	0.29	ABN	1880	6.79	0.0092	−0.27 (0.13)	0.09	0.7618	0.06 (0.18)
A31914G	Intergenic NC	0.45	ABN	1893	7.30	0.0070	−0.18 (0.12)	0.21	0.6451	−0.08 (0.17)

^a–eSee Table 2 legend.

^fThe genotype-by-sex effect of the site (a × s) and its standard error (SE a × s).

No evidence for an excess of very subtle-effect variants affecting bristle number:

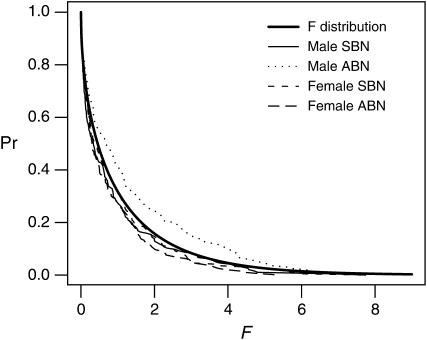
Despite the lack of highly significant associations in the single-marker tests, it is of interest to examine whether the distribution of F-ratio statistics obtained in our analyses conforms to the expected null F-distribution. Figure 6 shows the cumulative proportion of additive model association tests that yield various F-statistics compared to a theoretical F_1,1000-distribution. Collectively, the association tests for male ABN show slightly more moderate-value F-statistics than expected, and a one-sided Kolmogorov-Smirnov (K-S) test confirms that the difference is significant (K-S test D = 0.11, P = 0.0089). However, if we repeat this K-S test for the set of F-statistics obtained from each of 1000 permuted data sets, the observed K-S P-value is not in the lower 5% of the P-values from the permuted data. We speculate that LD between genotyped markers can result in a distribution of F-statistics that falsely indicates a slight excess of “moderately” significant associations.

Figure 6.

Cumulative distribution of F-ratio statistics under a single-marker additive model for sites in Enhancer of split. The distributions of 195 (for males) or 196 (for females) observed F-statistics from single-marker tests of association under an additive model are shown for each of the four sex/trait combinations (SBN, sternopleural bristle number; ABN, abdominal bristle number). The expected F-distribution for F_1,1000 (thick solid line) is also presented for comparison.

A test for mutation-selection balance:

Under mutation-selection balance, rare alleles should generally have deleterious phenotypic consequences. Dworkin et al. (2003) have suggested that a weak test of this hypothesis is to ask whether >50% of association tests show the rare allele to be associated, regardless of statistical significance, with a phenotypic change toward the mutant phenotype. Since the wild-type function of genes in the E(spl)-C is to repress neural development, the Dworkin et al. (2003) sign test would predict that under mutation-selection balance, rare alleles would increase bristle number. For the additive model for each sex/trait combination, the proportion of sites where the rare allele increases bristle number was tested against 50% using a Binomial test: male SBN, 91/195 (P = 0.993); female SBN, 100/196 (P = 0.415); male ABN, 118/195 (P = 0.002); and female ABN, 110/196 (P = 0.050). These results show that the rarer allele is significantly more likely to increase male ABN. However, the sign test assumes that each association test is independent, so the appropriate way to examine the significance of the deviation from 50% is by a permutation test (such a test was not employed in Dworkin et al. 2003). The permutation test showed that for a deviation from 50% to be significant at 5% for male ABN, >124/195 sites must show the rare allele associated with an increase in bristle number. We conclude that there is no evidence for rarer alleles being generally associated with increases in bristle number.

Testing for the effect of transposable element insertions:

Individually rare TE insertions have been shown to contribute as a class to variation in bristle number in laboratory studies (Mackay and Langley 1990; Long et al. 2000). As a by-product of our genotyping assay design we were able to implement a test of the effect of TE inserts at E(spl)-C on bristle number. Multiple SNPs were genotyped within each of 20 overlapping long amplicons across E(spl)-C. If an individual has a TE insertion within an amplicon, the allele harboring the TE will fail to amplify and only the non-TE-containing allele will be genotyped, resulting in a homozygous genotype for every SNP in the amplicon. We call such an event a HAH and note that a HAH could be the result of a TE insertion, or in a large sample such as ours HAH may represent a normal diploid genotype. As a result, any statistical tests comparing HAH and non-HAH individuals will tend to be conservative, because although all non-HAH individuals are free of TE insertions, only a proportion of the HAH individuals are likely to harbor a TE. We carried out two tests to assess the impact of TE insertions on bristle number variation. Test A compares all HAH individuals to all non-HAH individuals, whereas test B compares HAH individuals, excluding those whose haplotype consists entirely of the major allele at each SNP, to all non-HAH individuals. The principle behind test B is that major HAH individuals may not be particularly uncommon even in the absence of TE insertions, especially when a modest number of SNPs are genotyped, and the SNPs show LD. In contrast, HAH individuals having at least one minor homozygous site in their haplotype are much more likely to be associated with the presence of a TE insertion. The number of HAH individuals in test B may be much lower than the number of individuals in test A if the sites in the amplicon are in LD, or if the sites are generally rare.

ANOVA tests of association between individuals putatively harboring TE insertions and variation in SBN and ABN were carried out within each sex and over sexes in a model with sex as a fully crossed factor. The majority of the PCR amplicons show little detectable effect of TE insertion (data not shown), but six of the amplicons show at least one test significant at P < 0.05 (Table 4), although none are significant after Bonferroni correction for multiple testing. Across all 19 amplicons and all four sex/trait combinations, the numbers of tests significant at the 5% (1%) level are 4/76 (1/76) and 5/76 (2/76), for the type A and the type B tests, respectively. In all cases this is more than expected by chance. Three of the 6 significant amplicons (11, 16, and 17) are consistent with the notion that TE insertions increase bristle number, as do loss-of-function mutations in E(spl)-C genes, while the other 3 amplicons (8, 9, and 12) imply that TE insertions decrease bristle number.

TABLE 4.

Selected tests for the effect of transposable element insertions on bristle number

		Males				Females				Both sexesd
Amplicona	Testb	N (HAH)c	N (non-HAH)c	SBN Fc	ABN Fc	N (HAH)c	N (non-HAH)c	SBN Fc	ABN Fc	SBN Fc	ABN Fc
8	A	153	704	1.45	4.51*	180	799	0.58	0.01	0.06	1.86
9	A	202	709	1.01	8.15**	212	768	0.56	0.44	0.02	5.42*
9	B	177	709	0.48	8.39**	186	768	0.43	0.02	0.00	3.80
11	B	94	686	2.75	0.22	102	657	6.10*	0.32	8.66**	0.02
12	B	54	830	0.00	4.05*	59	882	0.01	0.59	0.01	0.46
16	A	185	674	6.04*	0.99	223	754	0.60	0.23	4.94*	0.98
16	B	5	674	2.13	4.06*	3	754	0.01	0.01	1.19	1.88
17	A	113	780	4.53*	0.06	96	894	1.89	0.19	0.35	0.03
17	B	81	780	7.21**	1.34	58	894	0.03	0.52	3.66	1.70

*Significant at 0.01 ≤ P < 0.05, **significant at P < 0.01. SBN, sternopleural bristle number, ABN, abdominal bristle number.

For each type of test (A or B), amplicons are presented only when at least one of the tests is significant at P < 0.05.

^aAmplicons across the Enhancer of split complex.

^bWithin each amplicon, considering only individuals with more than four sites assigned a genotype, putatively TE-containing (homozygous amplicon haplotype, HAH) individuals and non-TE individuals (non-HAH) are compared. A, an individual is HAH if no site shows a heterozygous genotype; otherwise, the individual is considered non-HAH. B, an individual is HAH if no site shows a heterozygous genotype, but is completely ignored if all sites show the major allele homozygote; otherwise, the individual is considered non-HAH. See materials and methods and Results for details.

^cThe number (N) of HAH and non-HAH individuals per amplicon and the F-statistic from an ANOVA on phenotype.

^dFor the factorial genotype-by-sex model, the F-statistic from the genotype term is presented. The number of individuals for each pooled-sex test is simply the sum of the number of individuals used for each of the single-sex tests.

It is useful to estimate the proportion of HAH individuals expected to harbor a TE insertion, as if the true proportion is low, the HAH test we describe is very conservative. Kaminker et al. (2002) reported that the D. melanogaster genome sequence shows an average of 13.46 TE insertions per megabase. Thus, for a 2.5-kb amplicon, a sample of 1800 alleles (i.e., 900 diploid flies, similar to the number of individuals tested for each sex) should harbor ∼60 TE inserts on average. Across the tested amplicons, the mean number of individuals we define as HAH is ∼174 for the single-sex tests. Thus, on average we might expect one-third of these individuals to truly harbor a TE, although without independent confirmation the number may be much lower (or higher). This suggests that the HAH test we propose, while conservative, is likely useful to identify amplicons in which TE insertions have phenotypic effects.

Epistatic interactions between SNPs in Enhancer of split:

Despite the number of possible pairwise comparisons, and the conservative correction for multiple testing that examining epistasis implies, the power of methods that look for statistical interaction between sites can be high in some circumstances (Marchini et al. 2005). Tests for epistasis were conducted between all pairs of sites in E(spl)-C (20,503 separate tests), both for each of the four sex/trait combinations and for the two bristle traits including sex as a fully crossed factor. No test survived the highly conservative Bonferroni correction of 0.05/20,503 or the more liberal FDR procedure. Despite no tests for epistasis achieving statistical significance, 7, 11, 5, 6, 13, and 11 tests show P-values <0.0005 for male ABN, female ABN, ABN over sexes, male SBN, female SBN, and SBN over sexes, respectively (∼10 in each category would expected by chance alone). It will be of interest to determine if any in this set of potentially interacting pairs replicate in future independent studies.

DISCUSSION

Linkage disequilibrium:

Knowledge of the extent and distribution of LD is fundamental for mapping genetic factors contributing to phenotypic variation. The density of markers required to uncover causal sites is critically dependent on the local level of LD (Kruglyak 1999). In Drosophila, LD falls rapidly with physical distance (Miyashita et al. 1993; Long et al. 1998), even within regions of low crossing over such as the telomeric region of the X chromosome (Langley et al. 2000). Genotyping a large number of common polymorphisms in a very large panel of 2000 D. melanogaster allowed us to generate extremely robust estimates of LD, subject to little sampling variance, across the 47-kb E(spl)-C. We confirm previous observations that LD falls off rapidly with distance in Drosophila and also show that the unlinked E(spl)-C and hairy loci are, as expected, in linkage equilibrium. We do not observe any signature of LD “blocks” as has been reported for humans (Gabriel et al. 2002).

The level of LD generally follows expectation, although there is a very slight excess of long-range intralocus LD (∼15–50 kb). Our data are from a sample of D. melanogaster collected in North America, populations thought to have recently expanded since their colonization by sub-Saharan African populations (David and Capy 1988; Lachaise et al. 1988). That such a demographic change could have increased levels of intralocus LD is supported by the observation that flies from Zimbabwe show levels of LD in line with expectations, unlike previous studies of non-African flies that show an excess of LD (compare Andolfatto and Wall 2003 and Andolfatto and Przeworski 2000). It seems unlikely that these demographic changes completely explain our observation of a slight excess of long-range intralocus LD, however, because one might expect that any demographic influence on the pattern of LD between sites >15 kb apart would have even more pronounced effects on closely linked sites, yet these appear to neatly follow expectation (Figure 2). The expected level of LD is generated using the estimated value of ρ, the population recombination rate, and it is conceivable that the assumptions on which this estimate is based are not supported. ρ was estimated under a constant population size model (Hudson 2001), which may not be appropriate for our North American sample of Drosophila, and we assumed levels of gene conversion and gene conversion tract lengths, which while within the range of the limited data available, may not be appropriate for the E(spl)-C locus. Furthermore, we demonstrate some heterogeneity in ρ across the E(spl)-C, so we may not expect a single average ρ-value to properly fit all the data. As genotyping large panels of flies for large genomic regions becomes more routine, it will be possible to compare patterns of LD among loci and among populations, and this may help inform the models under which the expected level of LD for Drosophila is estimated.

Saturation genotyping to identify QTN:

An important determinant of the ability to detect sites contributing to complex trait variation is the expected level of LD between the actual causal site (or QTN) and the set of genotyped markers, which may not include the QTN. Population genetics theory shows that the phenotypic variation attributable to a marker can be estimated as the product of the LD (as measured by R²) between the QTN and the marker and the variance attributable to the QTN (Hill and Robertson 1968; Lai et al. 1994; Long et al. 1998). Hence, if the actual causal site is included within the set of markers genotyped, the power of association mapping can be high (Risch and Merikangas 1996; Long and Langley 1999). If the causal site is not genotyped, the power to detect it is dependent on genotyping markers at a sufficiently high density to ensure that one of the markers is in strong LD with the QTN. Over the complete E(spl)-C locus we genotyped around one in three of the common sites and at least one common SNP for every two 4Nc across the region. 4Nc is an estimate of the number of recombination events that have occurred in the region in the history of the sample. A density of one site per 4Nc implies that most markers are in LD with at least one other, so one or more markers are likely to be in LD with a QTN (Long et al. 1998; Long and Langley 1999).

The E(spl)-C is arguably the most well-annotated gene region in Drosophila. The region encompasses a large number of annotated binding sites for cis-regulatory transcription factors and micro-RNAs (Tietze et al. 1992; Kramatschek and Campos-Ortega 1994; Eastman et al. 1997; Lai and Posakony 1997, 1998; Leviten et al. 1997; Lai et al. 1998, 2000a,b, 2005; Nellesen et al. 1999; Lai 2002) and harbors a number of areas showing indications of past natural selection (Macdonald and Long 2005). This extensive annotation allowed us to design SNP genotyping assays for sites that are most likely to be functional, and we genotyped by LD virtually every common SNP in functional regions (upstream transcription factor binding sites, exons, UTRs, micro-RNA target sites, and conserved noncoding sequence).

The combination of our large sample size and high SNP density gives us confidence that if an intermediate-frequency QTN contributing > ∼2% to bristle number resides within the E(spl)-C locus we are likely to detect it. Nevertheless, there are some important caveats. Our assessment of the number of ungenotyped SNPs that are in LD with a genotyped SNP is dependent on the set of 16 resequenced chromosomes and the large cohort having the same underlying LD pattern. This may not be unreasonable as the chromosomes sequenced were derived from flies collected at the same location as the cohort. Of greater concern is that even if the LD structure is identical, because of sampling, estimated LD values from the resequenced data set may not be a good predictor of LD values in the large cohort. It is also clear that even sites that are closely linked in the large cohort can show low levels of LD (see Figure 2). A common ungenotyped QTN in linkage equilibrium with all other sites in E(spl)-C would remain undetected, as by definition it would give a test of association independent from all others. Palsson and Gibson (2004) use this reasoning to promote a whole-gene resequencing association mapping approach, as the single SNP in association with wing shape in their study may not have been utilized in a selective-genotyping study. However, we note that full-gene sequencing of large panels of outbred diploid flies is not a viable experimental approach. Segregating insertion/deletion polymorphisms in noncoding regions make sequence data collection difficult in Drosophila, and the costs associated with full resequencing of 2000 individuals for 50 kb (i.e., 100 Mb) would be prohibitive.

The ability to saturate a region with genotyped SNPs is also dependent on producing working genotyping assays. Many SNPs that it would be desirable to genotype are unlikely to work well with a given genotyping technology, or assays simply fail for unknown reasons. This is the case for the four SNPs in potentially functional regions that are missed by LD (Figure 4): genotyping assays were attempted, but did not yield high-quality genotype data. The benefit of high-throughput biology is that one can always compensate for apparently stochastic assay failure by genotyping more SNPs, but a distinct problem is that cleanup of a data set for a few desirable, yet recalcitrant SNPs may be almost as time-consuming as the initial genotyping push. In the human disease-gene mapping literature, there is currently a focus on the best way to identify “tagging” SNPs that capture the majority of common haplotype variation in humans with the fewest SNPs (e.g., Johnson et al. 2001; Gabriel et al. 2002). It is of note that the consequences of some level of stochastic assay failure leading to a reduced, nonoptimal set of tag SNPs are generally not explored.

Individual Enhancer of split polymorphisms contribute little to bristle number variation:

We investigated whether any of 203 polymorphisms in E(spl)-C show an effect on bristle number variation in a natural—wild-caught—population of D. melanogaster. However, despite saturating the locus with SNPs, no site considered alone showed a significant (additive over loci) effect on either bristle trait. The large cohort size implies that we have power to detect sites contributing 1–2% to the total variation for bristle number (Long and Langley 1999; Macdonald and Long 2004). For a SNP with a minor allele frequency of 0.25, this corresponds to an effect of a = (0.02 × V_P/2pq)^1/2 = 0.5 bristles, where the total phenotypic variance for bristle number, V_P = 5 (Falconer and Mackay 1996). Thus, irrespective of heritability there are no sites with effects >0.5 bristles segregating at E(spl)-C in our cohort, so we do not lack power to detect a subtle effect if present. The absence of QTN at E(spl)-C is perhaps a surprising result: genes of the E(spl)-C have been considered very good bristle number candidate genes, in part because of suggestive quantitative genetic work (Long et al. 1995; Nuzhdin et al. 1999; Dilda and Mackay 2002; Norga et al. 2003), but mainly due to a substantial number of developmental biology studies showing the role of the genes in neurogenesis. The locus is additionally highly annotated with respect to functional domains (enhancer regions and micro-RNA binding sites) and potentially functional domains (conserved noncoding sequence and regions showing population structure). Yet no site within or linked to these regions shows a significant main effect on bristle number variation. We emphasize the implicit assumption in the single-marker tests we apply that there is additivity over loci, such that the effect at each tested site is not dependent on the alleles present at other loci.

Given the relatively short extent of LD in Drosophila, we opted to perform single-marker tests of association for each site, which are powerful tests of association when the QTN is of moderate effect and of intermediate frequency (Risch and Merikangas 1996; Long and Langley 1999). A plethora of haplotype-based association mapping methods are now available, and these analyses are promoted as the best method to identify sites contributing to disease risk in human populations (Gibbs et al. 2003). The utility of haplotypes is expected to be highest when they are biologically or evolutionarily defined, for instance, when there are clear haplotype blocks defined by hotspots of recombination, and the SNPs within the haplotype have a common evolutionary history. Our data do not show a block-like LD pattern (Figure 1), and such a pattern is unlikely to be true of any Drosophila locus. As an alternative to biologically defined haplotypes, one can use naïve haplotypes, defined arbitrarily as all pairs of sites, all triplets, all quadruplets, and so on. In simulation studies the advantage of such an approach over single-marker tests to detect QTN is equivocal (Long and Langley 1999), unless the QTN is rare, when these arbitrary haplotypes can show greater power (Lin et al. 2004). Furthermore, the above simulation studies assume that haplotypes are known, whereas in practice for studies such as ours haplotypes would be inferred statistically from diploid genotypes, a process that is subject to error (Stephens and Donnelly 2003). The effect of haplotype estimation error on haplotype-based association mapping remains unexplored.

A handful of sites, over the tested single-marker models, show marginally significant genotype main effects but do not survive correction for multiple testing. These sites are not clustered with respect to position along the E(spl)-C or similar in terms of their location relative to functionally annotated elements. Given the number of tests performed, it is likely that these sites are truly not significant. However, it is possible that a subset of them are real, very subtle-effect QTN or are in LD with ungenotyped QTN, such that the effect at the marker represents the effect at the QTN “diluted” by the level of LD between the sites. This hypothesis can be tested by genotyping the sites in a second, similarly large cohort of flies, preferably sampled from the same location as our current cohort to control for any heterogeneity in the genetic architecture of bristle number across populations. If the SNPs marginally associated in the current study are true small-effect QTN, or linked to such sites, effects should be replicable across samples. Regardless of the results of replication studies, data from the current study suggest that, at least for the E(spl)-C genes, detailed molecular dissection and sequence analysis may not be helpful in predicting which polymorphisms influence standing phenotypic variation. Our data may further suggest that putative candidate genes, often identified as those harboring mutants of large effect, may not always harbor DNA variants of more subtle effect. Further study is needed to clarify the generality of this observation.

A potential concern with our approach is the use of a large cohort of flies sampled directly from nature. The environmental conditions experienced by these flies are not controlled, and measured allelic effects represent a weighted average over environments. Thus, to the extent that a genotypic effect is influenced by environmental conditions, our ability to detect it might be diminished. Furthermore, our natural cohort of Drosophila is essentially a single “snapshot” of the population (and species) as a whole, sampled over a fairly narrow spatial/temporal window. It is possible that biologically significant associations exist for bristle number at the E(spl)-C, but that such QTN contribute significantly to standing variation only under conditions other than those experienced by the flies we collected.

Using five nutritional/temperature environments Geiger-Thornsberry and Mackay (2002) identified significant genotype-by-environment interaction (GEI) acting upon two SNPs in the Delta gene that influence bristle number. Therefore, it is at least plausible that GEI can influence the outcome of association studies carried out in natural cohorts. Unfortunately the magnitude of GEI for individual QTN is unclear, and it is difficult to say with any degree of confidence whether GEI contributed to our failure to detect QTN at the E(spl)-C. If GEI makes a substantial contribution to phenotypic variation it may be particularly difficult to extrapolate from laboratory studies to nature, as laboratory environments may be very different from natural conditions from the standpoint of the organism under study. It remains an important question to determine the extent of GEI in nature for bristle number as well as other traits.

Rare variants and bristle number variation:

Our experiment was designed to assess the contribution of common polymorphisms to variation in bristle number, as screening just 16 alleles for polymorphisms will not consistently identify sites at which the minor allele is rare in the population. If mutation-selection balance plays a role in the maintenance of variation for bristle number in nature, we expect that several individually rare mutations, each of large effect, contribute to standing variation. Dworkin et al. (2003) recently proposed a weak test for mutation-selection balance and found a significant result for sites in the gene Egfr and cryptic variation for photoreceptor determination. Although the test proposed by Dworkin et al. (2003) is significant for male abdominal bristle number in the current study, it does not survive an additional permutation test that controls for the nonindependence of markers. However, we note that unlike the Dworkin et al. (2003) study >80% of the sites we genotyped were frequent and perhaps not expected to show a signature of mutation-selection balance.

Transposable element insertions:

Previous work on the quantitative genetics of bristle number has shown that TE insertions can contribute to bristle number variation (Mackay and Langley 1990; Long et al. 2000). A feature of our genotyping approach allowed us to categorize each individual as potentially harboring a TE, or definitely not harboring a TE, for each of the overlapping PCR amplicons spanning the E(spl)-C. Thus, for each amplicon we could perform a test of the effect of TE insertions, as a class, on bristle number. In general, we expect that TE insertions should act as loss-of-function mutations and in E(spl)-C genes should cause an increase in bristle number. Some of the amplicons we examined show effects on bristle number variation consistent with TE insertions, and in most cases the observed effects appear to be sex or trait specific. The test we have developed to detect the effect of TE insertions is conservative, as within the set of individuals showing a genotype consistent with the presence of TE, there will be number of individuals that do not actually harbor a TE. On the basis of data presented in Kaminker et al. (2002), we estimate that on average around one-third of the individuals with genotypes consistent with a TE actually have one, suggesting that the test we propose is useful to detect the effect of TE insertions on phenotype, although conservative. Since many of the current generation of high-throughput genotyping technologies work directly from genomic DNA or use small multiplexed PCR amplicons, they are unable to detect TE insertions in the manner that we have. Thus, it is possible that future studies in humans and model organisms will ignore phenotypic variation attributable to TE insertion events as a class.

Epistatic interactions between sites in Enhancer of split influence bristle number:

Increasing empirical evidence suggests that interactions between loci may contribute to variation in complex traits (e.g., Mackay 2001). However, the number of potential testable interactions is generally believed to undermine any attempt to identify epistatic interactions. Marchini et al. (2005) recently showed that, for a range of models defining particular interlocus interactions, even after correcting for multiple tests, epistasis could be reliably detected. We found no pair of sites in E(spl)-C showing a significant epistatic interaction. However, because of the extreme statistical correction required with 20,503 tests (a P-value must be <2.4 × 10⁻⁶ to attain significance at the 5% level after Bonferroni correction), even nontrivial epistasis might be difficult to detect in some circumstances. Thus, as for the marginally significant single-marker tests described above, replication of our work in a second sample of Drosophila is the only way to determine whether the effect of epistasis on standing bristle number variation in nature is important.

Prospectus:

The Drosophila community has enjoyed considerable success using association studies to dissect a variety of complex traits. Typically, such studies are carried out using panels of inbred lines or natural chromosomes substituted into a standardized isogenic background. This strategy has the advantage that candidate genes can be resequenced in all lines, a technique unavailable in outbred Drosophila due to the number of segregating insertion/deletion polymorphisms. Complete resequencing allows all QTN in the sequenced region to be directly identified, rather than being picked up by LD as in a selective-genotyping approach. Laboratory studies are valuable as they implicate genes as being involved in the genetic control of the character under study. Nevertheless, it is important to extend the results of laboratory work to natural populations. If variants associated with phenotype in the laboratory have no effect in natural populations, they are invisible to natural selection in nature or subject to extensive environmental modulation. Clearly, in terms of understanding the forces that generate and maintain phenotypic variation in morphological characters, it is important to both confirm associations seen in a laboratory setting in natural populations and identify de novo associations in nature, as these may not be observed in laboratory experiments. The study reported here is the first large-scale association study of a region that a priori was a strong candidate to harbor sites contributing to variation in bristle number. The lack of significant single-marker associations despite near-saturation genotyping of SNPs throughout the region, and sufficient sample sizes to detect even subtle-effect QTN, highlights the potential difficulties of carrying out association studies in natural outbred populations. The large number of tests performed may limit our ability to detect epistasis between SNPs, and the hypothesis that pairs of sites may contribute to standing variation in bristle number via epistatic interaction rather than main effects remains to be confirmed. Additional work is needed if we are to understand the complex forces that maintain phenotypic variation for traits under stabilizing selection in natural populations.

Given that more sensitive and powerful methods of association mapping are being developed at an accelerating rate, others may be able to tease apart subtle effects that we were unable to observe in our data, using methodologies that are currently unavailable or computationally impractical. Furthermore, large-scale experimental data sets such as ours may be valuable to researchers developing analytical methods able to cope with “real-world” genotyping data. As such, we have made the data available from our website (http://cstern.bio.uci.edu/pubs.htm) and as supplemental material on the Genetics website (http://www.genetics.org/supplemental).