Combining the Meiosis Gibbs Sampler With the Random Walk Approach for Linkage and Association Studies With a General Complex Pedigree and Multimarker Loci

Abstract

A linkage analysis for finding inheritance states and haplotype configurations is an essential process for linkage and association mapping. The linkage analysis is routinely based upon observed pedigree information and marker genotypes for individuals in the pedigree. It is not feasible for exact methods to use all such information for a large complex pedigree especially when there are many missing genotypic data. Proposed Markov chain Monte Carlo approaches such as a single-site Gibbs sampler or the meiosis Gibbs sampler are able to handle a complex pedigree with sparse genotypic data; however, they often have reducibility problems, causing biased estimates. We present a combined method, applying the random walk approach to the reducible sites in the meiosis sampler. Therefore, one can efficiently obtain reliable estimates such as identity-by-descent coefficients between individuals based on inheritance states or haplotype configurations, and a wider range of data can be used for mapping of quantitative trait loci within a reasonable time.

A linkage analysis can find patterns of inheritance states, genotype configurations, or haplotype configurations. These latent variables are essential for linkage mapping and association mapping. In linkage mapping, for example, the coefficients sharing founder genes through segregation in a recorded pedigree can be estimated on the basis of the inheritance states [i.e., pedigree-based identity-by-descent (IBD) probabilities]. In association mapping, the coefficients sharing the genes from a common ancestor beyond the recorded pedigree can be estimated on the basis of the haplotype configurations [i.e., linkage disequilibrium (LD)-based IBD probabilities].

The linkage analysis is routinely based upon observed pedigree information and marker genotypes for individuals in the pedigree. This could cause difficulties in general pedigrees as genotype probabilities are hard to derive when pedigrees are complex, especially when there are many missing genotypic data. Exact methods for linkage analysis such as pedigree peeling (Elston and Stewart 1971; Cannings et al. 1978) or chromosome peeling (Lander and Green 1987) increase exponentially in computational complexity with the number of markers or the number of pedigree members. In addition, having a number of individuals with missing genotypic data severely affects the computational task in deriving such probabilities.

Markov chain Monte Carlo (MCMC) algorithms are an alternative and flexible method to estimate genotype probabilities. In early MCMC, genotypic configurations or segregation indicators as latent variables are updated at each site, which makes it possible to deal with a large proportion of missing genotypic data in a complex general pedigree (Lange and Matthysse 1989; Sheehan et al. 1989; Thompson 1994), although reducible sites often occur in complex pedigree structures and mixing problems also appear in using multiple marker loci (Thompson and Heath 1999; Cannings and Sheehan 2002). By updating segregation indicators jointly for all marker loci in a single meiosis, the meiosis Gibbs sampler (Thompson and Heath 1999) greatly improves mixing of the Markov chain. However, noncommunicating classes are generated when founder allelic types are determined by direct or indirect observations, which makes the chain reducible (Thompson and Heath 1999; Heath 2003). The random walk approach suggested by Sobel and Lange (1996) remedied the reducibility problems by taking multiple moves of the random walk that allow the chain to pass through illegal configurations of segregation indicators on its way between legal configurations of segregation indicators. However, illegal or less likely configurations are often proposed, which are mostly rejected by a Metropolis mechanism; therefore, the computational efficiency of the random walk approach is much less than that of the meiosis Gibbs sampler, where updated variables are always accepted.

It is desirable to combine the merits from both the random walk approach and the meiosis Gibbs sampler. The meiosis sampler is used for all sites where updated variables are always accepted; therefore, the variables are more frequently updated at the same time (computational efficiency is high if there is no reducibility problem). If there are noncommunicating classes, the random walk approach is applied. Combining these two approaches should give a higher computational efficiency than the random walk approach alone. In addition to that, joint updates of segregation indicators for all marker loci help mixing and therefore improve accuracy. On the other hand, reducibility problems in the meiosis sampler alone can be remedied with the random walk approach. This study proposes a combined sampler and investigates its performance.

MATERIALS AND METHODS

Distribution of segregation states conditional on marker data and pedigree:

One realization of segregation states (S) in a pedigree can be expressed in an M × L matrix whose elements are 0 or 1. If the gene in the 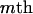meiosis at the 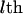locus receives the paternal parental allele, the segregation indicator 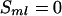, and 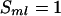for the maternal parental allele. The maximum number of possible configurations for S is 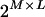when none of the pedigree members is genotyped. The probability of S given observed marker data is

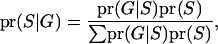(1)

where G represents the observed marker data, pr(S) is the prior probability of the segregation indicators, Pr(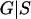) is the probability of the observed marker data given S, and the denominator is summed over the probabilities of all possible configurations of S. Since the computation of the denominator is infeasible in general pedigrees, a MCMC approach is required to obtain the posterior distribution of the segregation indicators.

Likelihood estimation:

The likelihood for observed marker data given one configuration of segregation indicators is a function of all recombinations in every meiosis and of the sum of all genotype configurations of founders, which are consistent with the segregation indicators,

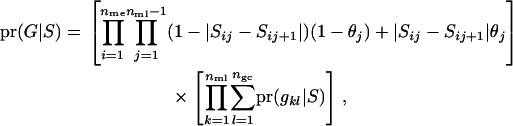(2)

where n_me, n_ml, and n_gc are the numbers of meioses, marker loci, and founder genotype configurations, respectively. 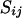is the segregation indicator for the ith meiosis at the jth locus, 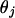is the recombination rate between markers j and j + 1, and g is a genotype configuration for founders. Note that since nonfounders' genotypes are totally dependent on founders' genotypes and the segregation indicators, there is no need to consider their genotype configurations in (2). The computation of the first term in (2) is the function of all recombinations given S and is therefore relatively straightforward. The second term is the sum of all genotype configurations for founders given the segregation indicators. It involves allele assignments to founder genes consistent with S (see Sobel and Lange 1996; Bureau 2001).

Updating schemes for segregation indicators:

In a MCMC method, updated variables for segregation indicators are proposed on the basis of an approximate distribution and the decision of acceptance for the updated variables is made by the Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970), which gives the correct equilibrium distribution of segregation indicators. In a Gibbs sampler (a special case of MCMC), updated variables are always accepted because they are sampled on the basis of the correct distribution.

Meiosis Gibbs sampler:

This algorithm makes joint updates for the inheritance at linked loci for one individual at a time (e.g., by order of age). For example, for the 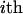individual, segregation indicators at all loci can be sampled using a forward-backward algorithm (Thompson and Heath 1999), according to all possible segregation states for the ith individual, conditional on the segregation indicators for other individuals (see appendix a). Joint updates for each individual result in better mixing properties and the process is much more reliable than that of a single-site Gibbs sampler (Thompson and Heath 1999). Because of joint updates without rejection, the method is more computationally efficient than other MCMC methods where proposed variables are often rejected. However, when founders' genotypes are constrained, some sites can be reducible where new variables are never updated.

Random walk approach with a Metropolis mechanism:

Updated variables for segregation indicators are a series of sequential movements in which the magnitude and direction of each move are determined by chance. To apply this approach to inheritance states, transition rules (see appendix b) were introduced by Lange and Matthysse (1989) and developed as more suitable for segregation indicators by Sobel and Lange (1996). Taking multiple transitions at each update, the Markov chain can move through illegal configurations of segregation indicators on its way to other legal configurations. This makes reducible sites have new variables and results in no or few noncommunicating classes in the Markov chain. The new updated variables are either accepted or rejected by the Metropolis probability a (Metropolis et al. 1953):

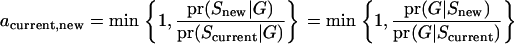(3)

Method combining the meiosis sampler and random walk approach:

It is desirable to use the advantageous factors from each method, i.e., the computational efficiency and higher mixing property from the meiosis sampler and the irreducibility from the random walk approach. For this purpose, the meiosis sampler is first applied to all loci for every individual. During the meiosis sampler, it is possible to detect potential reducible sites. On the basis of transition probabilities, if the current state for the ith individual at the jth locus does not update to any other states, 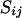is treated as a reducible site. After a cycle of the meiosis sampler, a random walk is carried out for segregation indicators, proposing different variables in every move. As noted earlier, the size and direction of each move are randomly determined. If proposed variables include any reducible sites that were never updated in the meiosis sampler, proposed variables are accepted as new variables with a Metropolis acceptance probability (3). If proposed variables do not include any reducible sites, a new set of variables is proposed without updating because nonreducible sites are already updated in the meiosis sampler. After enough moves of the random walk (e.g., number of moves ∼ number of meioses × number of markers), all reducible sites have an equal chance to be updated and they can have new variables.

Initial legal configuration for the Markov chain:

A MCMC approach requires a starting configuration, consistent with observed marker data. The genotype elimination through inheritance constraint (GEIC) algorithm (Henshall et al. 2001) is suitable for finding a legal configuration of segregation indicators at a single locus. After this algorithm finds a legal configuration for each locus independently, the MCMC mechanism in the combined method obtains the desired conditional distribution, taking into account the linkage between markers and the relationships between individuals.

Simulation study:

A population size of 100 was simulated for 10 biallelic or multiallelic marker loci for 100 generations before pedigree recording. In each generation, the number of male and female parents was 50 and their alleles were transmitted to descendants on the basis of Mendelian segregation using the gene-dropping method (MacCluer et al. 1986). Parents were randomly mated with a total of two offspring for each of 50 mating pairs. In the multiallelic marker model (e.g., microsatellites), the number of alleles assumed in each marker locus was 4 and base allele frequencies were all at 0.25. In the biallelic marker model (e.g., SNP), the number of alleles was 2 and starting allele frequencies were 0.5. The marker alleles were mutated at rates of 4 × 10⁻⁴ per generation in multiallelic markers (Dallas 1992; Weber and Wong 1993; Ellegren 1995) and 2.5 × 10⁻⁸ per generation in biallelic markers (Nachman and Crowell 2000). A mutated locus was switched between the two existing alleles for biallelic markers whereas a new allele was added for multiallelic markers. This simulation model ensured that the population would have an equilibrium distribution of alleles in all loci after 100 generations. Note that pedigree information is not available for these 100 generations.

At generation 101, a population of size N_e was simulated for t generations with pedigree recording. In each generation, the number of male and female parents was N_e/2 and they were randomly mated with a total of two offspring for each of N_e/2 mating pairs. Therefore, the recorded pedigree had complex relationships between animals with a value of t > 2.

The efficiency of three algorithms was investigated with complete or incomplete genotypic data, i.e., the random walk approach, the meiosis sampler, and the combined method. In complete genotypic data, genotypes were available for all pedigreed individuals. In incomplete genotypic data, genotypes were available for progeny in the last generation (ancestral and parental genotypes were all missing but their relationships were used).

IBD probabilities were estimated on the basis of true haplotypes or sampled haplotypes, using the random walk approach (RA), the meiosis Gibbs sampler (MS), and the combined method (RAMS). IBD probabilities were also estimated using MCMC linkage software “SimWalk2” (Sobel and Lange 1996). SimWalk2 implements the same random walk approach as in RA; however, the most likely segregation state is found by a simulated annealing and used as a starting legal configuration for the Markov chain while RA, MS, and RAMS use any legal segregation configuration. Therefore, SimWalk2 takes much more computing time than other methods. To check the accuracy of estimating IBD probabilities, correlation between true and estimated IBD probabilities for progeny in the last generation was calculated at the middle point of each marker interval and averaged over all positions. The mean and standard error of correlations over 10 replicates were plotted against the time spent for sampling segregation indicators. Therefore, in each analysis, 90 sets of IBD probabilities were estimated (9 sets of IBD probabilities within a replicate).

To investigate robustness to alternative family structures, unequal numbers of male and female parents with a larger number of progeny were simulated for the recorded pedigree. Furthermore, to illustrate our proposed method with a real data set, we considered an existing pedigree and genotypic data of four half-sib families with a back pedigree spanning approximately four to five generations. Four sires were related through back pedigree, and most dams were unrelated among themselves and to the sires except ∼50 dams that were related to each other and to the sires. Base animals were assumed unrelated. The number of individuals in this pedigree was 1252. Each sire was mated to ∼100–200 dams and had an average of ∼143 offspring. The offspring were genotyped for 13 microsatellites positioned at 10-cM intervals on average. However, there were missing genotypes: some offspring were genotyped for <13 markers and ancestors were not genotyped at all. The proportion of missing genotypes at all marker loci in the whole pedigree is 73%. Since the true IBD probabilities were not known for the real data set, it was not feasible to determine the accuracy of each sampler. Therefore, we simulated genotypes at all marker loci for all individuals in the real pedigree, according to real data; e.g., the pedigree, the marker distance and order, and the structure and proportion of missing genotypes were the same. Given simulated data but on the basis of a real data structure, estimated IBD probabilities using different samplers were compared to true IBD probabilities.

RESULTS

Pedigree spanning three generations:

A population with N_e = 20 was simulated for three generations with 10 multiallelic markers at 10-cM intervals. The kinship coefficient between parents in the last generation averaged over replicates was 2%.

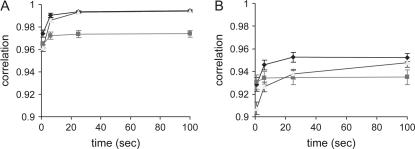
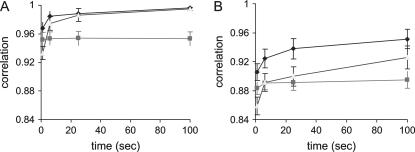
Figure 1A shows correlations between true IBD probabilities and those estimated using RAMS, RA, and MS when genotypes are available for all pedigreed animals. The correlation (i.e., the accuracy of IBD estimates) for RAMS converged slightly more quickly to a stable value than that for RA. After 20 sec, the accuracy is similar between RAMS and RA (0.995 and 0.994). The accuracy for MS is always lower than that for RAMS or RA. The numbers of rounds after 100 sec real time are 800, 670,000, and 1700 for RAMS, RA, and MS, respectively. Note that 1 round for RA is one move of the random walk, which involves a few individuals and loci at any limited number of sites while 1 round for RAMS and MS updates all sites (after each round RAMS operates an additional move of the random walk).

Figure 1.

Correlation between true IBD probabilities and estimated IBD probabilities using the combined method (RAMS), the random walk approach (RA), and the meiosis sampler (MS) with a pedigree spanning three generations (N_e = 20). In complete genotypes (A), all individuals are genotyped and the numbers of sampling rounds at 100 sec are 800 for RAMS, 670,000 for RA, and 1700 for MS. In incomplete genotypes (B), only individuals in the last generation are genotyped and the numbers of sampling rounds at 100 sec are 2500 for RAMS, 1,600,000 for RA, and 6300 for MS. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

Figure 1B shows the accuracy of each method for the same situation except that genotypes are available only for progeny in the last generation (ancestral genotypes are all missing). In this situation, the accuracy of RAMS is much quicker to reach a stable value than that of RA; i.e., RAMS reaches a stable value at 25 sec (0.952), which RA can reach at 100 sec (0.948), indicating that RAMS is approximately four times quicker. The accuracy of MS is higher than that of RA until 20 sec; however, it is not improved afterward. The numbers of rounds performed after 100 sec real time are 2500, 1,600,000, and 6300 for RAMS, RA, and MS, respectively. It should be noted that empirical standard errors (SEs) of these estimated correlations are very low (see SE bars in figures and SEs in Table 1).

TABLE 1.

Comparison of RAMS, SimWalk2, and MS

	Accuracya	SEb	Time (sec)	No. of rounds
Three generations with complete genotypic data
RAMS	0.995	0.001	100	770
SimWalk2c	0.974	0.004	>1,800	>19,200,000
MS	0.974	0.003	100	1,480
Three generations with incomplete genotypic data
RAMS	0.952	0.004	100	2,480
SimWalk2	0.938	0.004	>1,200	>19,200,000
MS	0.935	0.006	100	6,330
Five generations with complete genotypic data
RAMS	0.988	0.002	300	660
SimWalk2	0.974	0.003	>4,200	>32,000,000
MS	0.95	0.005	300	1,600
Five generations with incomplete genotypic data
RAMS	0.91	0.009	300	5,000
SimWalk2	0.899	0.008	>2,400	>32,000,000
MS	0.88	0.013	300	9,372

Data are from random mating of 10 males and females with 20 progeny per generation.

^aCorrelation between true and estimated IBD probabilities.

^bStandard error of mean accuracy based on 10 replicates.

^cSimWalk2 carried out a simulated annealing for approximately half of the sampling rounds.

More complex pedigree:

A population with N_e = 20 was simulated for five generations with 10 multiallelic markers at 10-cM intervals. The kinship coefficient between parents in the last generation averaged over replicates was 7%.

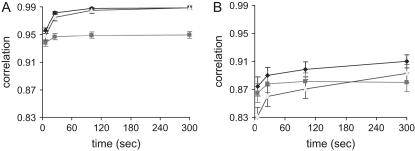
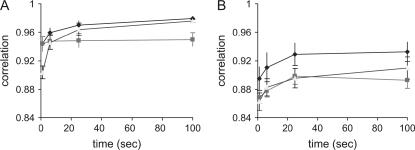
With a more complex pedigree and complete genotypic data (Figure 2A), it is clear that the accuracy of RA is slow to reach the same stable value as that of RAMS. Similar accuracies are shown at 300 sec (0.988 and 0.989 for RAMS and RA). The accuracy of MS is always lower than those of the other methods. The numbers of rounds at 300 sec are 600, 1,140,000, and 1500 for RAMS, RA, and MS, respectively.

Figure 2.

Correlation between true IBD probabilities and estimated IBD probabilities using RAMS, RA, and MS with a pedigree spanning five generations (N_e = 20). In complete genotypic data (A), the numbers of sampling rounds at 300 sec are 600 for RAMS, 1,140,000 for RA, and 1500 for MS. In incomplete genotypic data (B), the numbers of sampling rounds at 300 sec are 5100 for RAMS, 4,800,000 for RA, and 9300 for MS. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

In Figure 2B, the accuracies show that the combined method is much more efficient than either the random walk approach or the meiosis sampler alone when using incomplete genotypes (genotypes are available only for progeny in the last generation). The accuracy of RAMS is reasonably high at 300 sec (0.91). However, the accuracy of RA is lower and it takes longer to reach the same value: 0.893 at 300 sec for RA and 0.89 at 25 sec for RAMS. Although the accuracy of MS is higher than that of RA until 200 sec, it does not increase thereafter. The numbers of rounds at 300 sec are 5100, 4,800,000, and 9300 for RAMS, RA, and MS, respectively.

Compared to a pedigree of three generations, accuracies are slower to reach a stable value in a pedigree spanning five generations. This is probably due to the fact that the state space of the Markov chain becomes larger with a more complex pedigree. After reaching a stable value, the accuracy for RAMS in a pedigree of three generations is similar to that in a pedigree of five generations with complete genotypic data (0.995 and 0.989); however, they are quite different with incomplete genotypic data (0.952 and 0.910). This is because the amount of missing ancestral genotypic data is larger in a pedigree spanning five generations (four generations missing) than in a pedigree spanning three generations (two generations missing).

Alternative family structures:

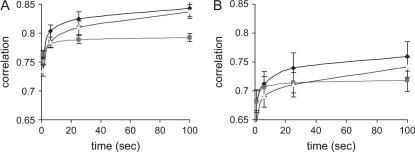
When a much smaller effective size is used with an unequal number of male and female parents and a larger family size for three generations with genotyping only on the last, the accuracy for all methods decreased (Figure 3). When there are five sires and 10 dams with 10 random-mating pairs of five offspring producing a total of 50 progeny in each generation, the accuracy for RAMS is 0.843 at 100 sec. Note that the kinship coefficient between parents in the last generation is 4%. When the number of sires and dams is two and 10 with 50 progeny in each generation, the accuracy for RAMS is 0.76 at 100 sec. The kinship coefficient in this case is 8%. Although overall accuracy is low in such extreme cases, the combined method still performs better than any other method alone.

Figure 3.

Correlation between true IBD probabilities and estimated IBD probabilities using RAMS, RA, and MS with alternative family structure. In (A) alternative family structure A, the numbers of sires and dams are 5 and 10 with 50 progeny produced in each generation, and the numbers of sampling rounds at 100 sec are 600 for RAMS, 890,000 for RA, and 1200 for MS. In (B) alternative family structure B, the numbers of sires and dams are 2 and 10 with 50 progeny produced in each generation, and the numbers of sampling rounds at 100 sec are 1000 for RAMS, 1,080,000 for RA, and 2000 for MS. In both cases, the pedigree spans three generations with genotyping only in the last generation. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

Using a larger pedigree:

A relatively large pedigree where N_e = 100 for five generations (total number of individuals is 500) was further investigated only for the combined method. The kinship coefficient between 100 parents in the last generation was 1.6%.

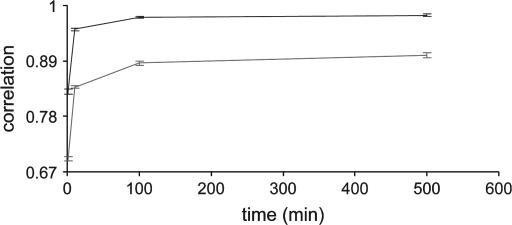
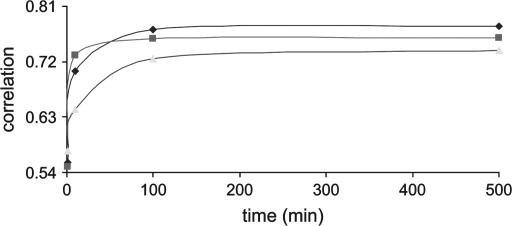
Figure 4 shows that when genotypes are available for all animals, the correlation between true and estimated IBD probabilities rapidly increases to 0.952 over the first 10 min and then gradually increases (0.976 at 100 min) to finally stabilize (0.98 at 500 min). Each sampling round took ∼1 min. With incomplete genotypic data, the correlation is also reasonably high although overall values are low compared to those based on complete genotypic data. The correlation substantially increases in the first 10 min (0.838) and then gradually increases (0.886 at 100 min) until it reaches a stable level (0.902 at 500 min). Analysis with incomplete genotypes took ∼5 sec per round.

Figure 4.

Correlation between true IBD probabilities and estimated IBD probabilities using the combined method when N_e = 100 is simulated for five generations (500 individuals are used for analysis). Ten multiallelic markers are positioned at 10-cM intervals. The numbers of sampling rounds at 500 min are 500 for complete genotypic data and 6000 for incomplete genotypic data. Solid line, complete genotypes; shaded line, incomplete genotypes.

The accuracy of the combined method with complete genotypic data using a larger pedigree is similar to that using a smaller pedigree (N_e = 20 for five generations), reaching stable values of 0.988 and 0.98 for the small and large pedigrees, respectively. With incomplete genotypic data, the accuracies are 0.91 and 0.902 for smaller and larger pedigrees, respectively. This suggests that the combined method should be able to handle much larger pedigrees. The accuracy of the random walk approach alone did not reach the same value as that in the combined method after 500 min for complete and incomplete data (result not shown).

Simulation based on real data:

The accuracy of RAMS, MS, and RA for analyzing a real pedigree with simulated genotypes is shown in Figure 5. The accuracy of MS rapidly increases in the first 10 min (0.731) while that of RAMS is lower (0.704) and that of RA is much lower (0.642). The accuracy of RAMS and RA keeps increasing, whereas that of MS hardly improves (0.773 for RAMS, 0.725 for RA, and 0.757 for MS at 100 min). Ultimately, RAMS and MS have reached a stable value and RA is slightly improving (0.778 for RAMS, 0.759 for MS, and 0.738 for RA at 500 min). Again, the accuracy of RAMS is higher than that of MS and much quicker to converge than that of RA, which is still increasing after 500 min. Overall accuracy is relatively low compared to that of simpler designs (e.g., Figures 1 and 2). This is probably because the pedigree structure in the real data is more complex and larger.

Figure 5.

Correlation between true IBD probabilities and estimated IBD probabilities between all individuals using RAMS, MS, and RA with a real pedigree spanning approximately five generations with simulated genotypes. The number of pedigree members is 1252 and the offspring (n = 571) in the last generation are genotyped for 13 microsatellites (there are missing genotypes among them). The numbers of sampling rounds at 500 min are ∼460 for RAMS, 4,600,000 for RA, and 650 for MS. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

Denser marker spacing:

When 10 multiallelic markers are positioned at 1-cM intervals, similar results are obtained. RAMS converges more quickly than RA or MS in data with both complete and incomplete genotypes (Figure 6). The accuracy of RAMS at 100 sec is very similar to that with a marker spacing of 10 cM (0.996 with complete genotypes and 0.951 with incomplete genotypes). The accuracy of MS and RA at 100 sec is generally lower than that with a marker spacing of 10 cM (0.953 with complete and 0.895 with incomplete genotypes for MS and 0.995 with complete and 0.926 with incomplete genotypes for RA). This indicates that the combined method is also a suitable tool for denser marker spacing.

Figure 6.

Accuracy of RAMS, RA, and MS using a pedigree spanning three generations with complete genotypic data (A) or incomplete genotypic data (B) and with multiallelic markers positioned at 1-cM intervals. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

When 10 biallelic markers are positioned at 1-cM intervals, the accuracy of RAMS is slightly lower than that with multiallelic markers, yet it is reasonably high after reaching a stable value (0.981 with complete and 0.932 with incomplete genotypes). Interestingly, the accuracy of MS with biallelic markers is equivalent to that with multiallelic markers in spite of a smaller marker information content (0.95 and 0.892 for complete and incomplete genotypic data). This is probably due to the fact that with only two alleles for each marker, reducibility is less of a problem in the meiosis sampler. The accuracy of RA with biallelic markers is lower than that with multiallelic markers (Figure 7).

Figure 7.

Accuracy of RAMS, RA, and MS using a pedigree spanning three generations with complete genotypic data (A) or incomplete genotypic data (B) and with biallelic markers positioned at 1-cM intervals. Solid diamond, RAMS; solid box, MS; shaded triangle, RA.

Comparison with a standard linkage software SimWalk2:

Table 1 shows the accuracies for the combined method, SimWalk2, and the meiosis sampler when the values of IBD probabilities are stabilized. The direct comparison among the methods in the same time span was not attempted since it is not feasible to control the time exactly for estimation in SimWalk2. Instead, we set a high enough number of sampling rounds for SimWalk2, which could surface all possible states on the basis of the posterior distribution after such a long MCMC. This shows that the combined method can give a reasonably high accuracy compared with that of SimWalk2 or the meiosis sampler.

Computational efficiency and size of pedigree or number of markers:

The time spent for one sampling round was measured for different effective population sizes with a pedigree spanning five generations and 10 multiallelic markers. The time increase with a larger effective size is not exponential although it is also not linear. When the effective population sizes are 20, 40, 80, and 160, the times (seconds) are 0.45, 3.33, 26.48, and 204.07 with complete genotypic data and 0.06, 0.3, 2.05, and 12.68 with incomplete genotypic data. Therefore, it is possible for the combined method to handle a relatively large pedigree (n > 1000). The computational efficiency with incomplete genotypic data is much better than that with complete genotypic data. This is because the computation of 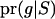in Equation 2 can deal efficiently with ungenotyped animals without any extra computation. Note that genotypes are generally not available for ancestors in real situations for which the RAMS can be suitable. The time spent for one sampling round increases with a larger number of markers, but again, it is not exponential. When the numbers of markers are 10, 20, 40, and 80, the times (seconds) are 0.45, 1.52, 5.36, and 20.18 with complete genotypic data and 0.06, 0.18, 0.72, and 3 with incomplete genotypic data (effective size is 20). This shows that the combined method presented here is suitable for analyses of a large number of markers.

DISCUSSION

The combined method could remedy the reducibility problems in the meiosis Gibbs sampler and is computationally more efficient than the random walk approach. Therefore, more reliable estimates can be efficiently obtained within a shorter time. This makes it possible to use more abundant resources for QTL mapping such as back pedigree information, which is often ignored due to computational complexity. In addition, the combined method is suitable for a larger number of markers with denser spacing, which are necessary for fine mapping of QTL.

A lower accuracy of MS is due to the reducibility problem. If founder allelic types are constrained in a Markov chain, reducibility would occur (Sobel and Lange 1996; Thompson and Heath 1999). The proportion of reducible sites is higher for complete genotypic data (17 and 22% for three and five generations of pedigree) because founders are genotyped and therefore constrained. With incomplete genotypic data, the proportion of reducible sites decreases (3 and 1% for three and five generations of pedigree). This explains that the accuracy of MS is never higher than that of RA with complete genotypic data, whereas with incomplete genotypic data the performance of MS is better than that of RA initially and converges quickly although the accuracy of MS is lower than that of RA after more sampling rounds. The lower accuracy of the meiosis sampler is due to the fact that the reducible sites never update new variables; therefore, the Markov chain can never reach certain inheritance states. Combining it with the random walk approach makes it possible for the reducible sites to update new variables, which makes the Markov chain pass through all inheritance states.

The combined method is much more efficient to quickly reach a reasonable accuracy compared to the random walk approach alone, especially with incomplete genotypic data where state space is wider than that of complete genotypic data. This is probably due to the fact that not all updated variables are accepted in each sampling round in the random walk approach whereas updated variables for nonreducible sites are always accepted in the combined method. If the proportion of nonreducible sites increases, the computational efficiency for the combined method also increases.

It is shown that the estimated IBD probabilities are close to the true ones. The two different algorithms integrate well and help improve mixing in the Markov chain, which results in reasonably accurate estimates with general pedigrees. However, there still can be reducibility problems in some cases, e.g., a combination of complex deep back pedigree and large half-sib families. If information from the back pedigree and from one of the half-sib families is somehow contradictory, the Markov chain would stay in a limited state space for a long period. The current random walk approach simultaneously considers at most three generations and is more favorable for full-sib families (see Sobel and Lange 1996) than for half-sib families. This may partially explain the low accuracy of RA in the real pedigree (Figure 5). Although RAMS can improve this situation (the accuracy of RAMS is higher than that of RA or MS), it is desirable to extend and modify the random walk to make it suitable for large half-sib families.

With incomplete genotypes, only the last generation is genotyped and ancestors are missing. In this situation, the accuracy of IBD probabilities between animals in the last generation is reasonably high (>0.9). It is interesting to investigate the accuracy of IBD estimates with a random pattern and different percentage of missing information. Table 2 shows the accuracy of IBD probabilities between all individuals and those between only genotyped individuals with different proportions of missing genotypes (genotyped individuals are randomly selected in the pedigree). When 60% of animals are not genotyped, the accuracy of estimated IBD probabilities between all animals is relatively low (0.85); however, that between genotyped animals is reasonably high (0.95). When the proportion of missing genotypes is <40%, the accuracy between all individuals is >0.9. This shows that the estimated IBD probabilities between genotyped individuals can give high accuracy even with a small proportion of known genotypes, whereas those between all individuals need a relatively high proportion of known genotypes.

TABLE 2.

Accuracy of RAMS for different proportions of missing genotypes

	Proportions of missing genotypes
	0.6	0.4	0.2	0
Accuracy of all animals	0.854	0.896	0.938	0.981
SEa	0.005	0.003	0.006	0.005
Accuracy of genotyped animals	0.948	0.949	0.963	0.981
SE	0.006	0.004	0.005	0.005

Data are from a pedigree spanning five generations with effective size of 20. The combined sampler is used for 100 sec.

^aStandard error over 10 replicates.

Given reasonably high correlations between true and predicted IBD estimates, it is expected that the mapping resolution with estimated IBD probabilities can be equivalent to that with true ones. However, the relationship between the accuracy of IBD estimates and mapping resolution has not been empirically studied. Moreover, the usefulness of phenotypes for ungenotyped animals was not empirically demonstrated. Further study is required to investigate whether phenotypes of ungenotyped animals help to improve the accuracy of QTL mapping.

We estimated the correlation between true and estimated IBD probabilities along with the time spent for sampling segregation indicators and noted that the curve reached a stable value (convergence). For example, using a pedigree spanning five generations with effective size of 100, the number of sampling rounds required for convergence is a few hundred with complete genotypic data and a few thousand with incomplete genotypic data. A larger and more complex pedigree in real situations will require a larger number of sampling rounds and a diagnostic test for convergence is desirable. Convergence can be assessed by comparison of mean values between different parts of the chain (Geweke 1992) or by analysis of variance between and within the multiple chains with widely different starting points (Gelman and Rubin 1992). Further work is warranted to integrate such convergence criteria in the proposed method to automatically stop the chain when reliable estimates are obtained.

Association studies require reconstructed haplotypes that utilize linkage disequilibrium information. Haploytype reconstruction is an analog of finding inheritance states; therefore, the present method can be comfortably integrated in association studies (see Lee and Van der Werf 2005). The present method would not attempt to find the most likely haplotype configurations, but rather would continuously sample haplotype configurations on the basis of the posterior distribution. The MCMC sampling approach that considers all possible sets of haplotypes would be more accurate than using only one optimal set of haplotypes based on maximum likelihood (Morris et al. 2004).

The locus Gibbs sampler implemented in LOKI (Heath 1997) can be an efficient tool to find inheritance states and estimate IBD probabilities (only) if the pedigree can be peeled for at least one locus. However, it is often impossible to peel even for a single locus with a complex pedigree with many missing genotypes (e.g., the real pedigree in this study). The Elston-Stewart Iterative Peeling (ESIP) (Fernandez et al. 2001, 2002) is more flexible for this problem because it uses iterative peeling. However, the ESIP with multiple markers has not been examined. Fernandez et al. (2002) reported that the ESIP for sampling genotypes jointly at multiple loci might be inefficient. They suggested that sampling genotypes at one locus conditional on other loci (which is exactly what LOKI does) could be a better strategy. However, this would cause a horizontal dependence.

It has been infeasible to use all available information for a large complex pedigree with sparse genotypic data, which is a common case in real populations. For example, one may not be able to use the relationships between ungenotyped ancestors due to computational complexity. Unless LD information is fully utilized from highly dense markers, these relationships generally contain useful information (Lee and Van der Werf 2005). The meiosis Gibbs sampler is robust to a complex pedigree with many missing genotypic data; however, reducibility problems often occur. By applying the random walk approach to the reducible sites in the meiosis sampler, the present method could remedy the reducibility problems. In addition, combining two very different samplers makes the chain more thoroughly explore all possible configurations, which always gives higher accuracy than the use of either method alone. The proposed method allows use of a wider range of data for mapping of QTL and can give more reliable estimates within real time.

APPENDIX A: FORWARD-BACKWARD ALGORITHM IN THE MEIOSIS SAMPLER

Joint updates for sampling segregation indicators of all genes at linked loci in a single meiosis were introduced by Thompson and Heath (1999). Following their method, we describe how to jointly sample the latent variables at linked loci in a single individual.

Forward working:

In forward working, the cumulative probability (Q) for the segregation indicator 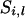is computed, conditional on inheritance of all individuals at marker loci up to and including marker locus l except the ith individual itself, which is updated at the current stage. The working order is from the first marker to the last marker (1−L),

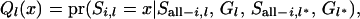(A1)

where 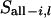= all segregation indicators at locus l except the ith individual, 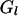is the observed marker data at locus l, 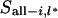is all segregation indicators from locus 1 to locus l − 1 except the ith individual, and 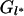is the observed marker data from locus 1 to l − 1. For 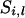= x, there are four possible inheritance states. The first is the paternal and maternal gamete being transmitted from the paternal allele of the father and the mother (x = 1), the second is the paternal gamete being the paternal gene of the father and the maternal gamete being the maternal gene of the mother (x = 2), the third is the paternal gamete being the maternal gene of the father and the maternal gamete being the paternal gene of the mother (x = 3), and the last is the paternal and maternal gamete being the maternal gene of the father and mother (x = 4).

The right-hand side in (A1) can be divided into two parts as

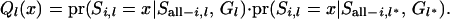(A2)

The first part in the right-hand side in (A2) can be obtained, using Bayes' theorem:

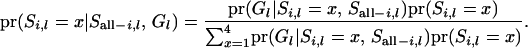(A3)

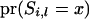is a prior probability with a value of 0.25; therefore, (A3) can be simplified as

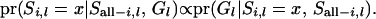(A4)

The second part of the right-hand side in (A2) can be computed using the cumulative probability of the previous locus and recombination rate between locus l and the previous locus l − 1:

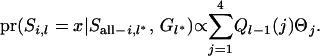(A5)

If x = j then 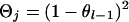. If x = 1 and j = 2 or 3, x = 2 and j = 1 or 4, x = 3 and j = 1 or 4, or x = 4 and j = 2 or 3, then 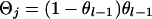. If x = 1 and j = 4, x = 2 and j = 3, x = 3 and j = 2, or x = 4 and j = 1, then 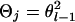, where 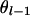is the recombination rate between the locus l and l − 1. Note that the right-hand side in (A5) for the first marker locus is negligible (= 1) without previous marker information.

From (A1), (A4), and (A5),

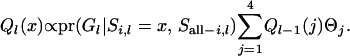(A6)

The estimation of the term 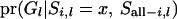is explained in Sobel and Lange (1996) or in Bureau (2001). When forward working is completed, we have the cumulative probability of the segregation indicator for the last locus (L), which takes into account all possible segregation states for the ith individual at locus l, conditional on all observed marker data and segregation states for all other members and other loci; that is,

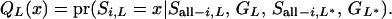(A7)

Therefore, 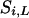can be sampled from this posterior distribution.

Backward sampling:

In backward sampling, the segregation indicator 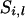is sampled conditional on the already sampled marker locus (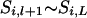) and using the cumulative probability for locus l that was computed in the forward working. The sampling order is the second last locus to the first locus [(L − 1) − 1]

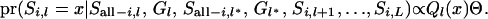(A8)

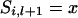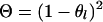If then . If 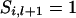and x = 2 or 3, 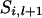= 2 and x = 1 or 4, 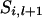= 3 and x = 1 or 4, or 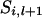= 4 and x = 2 or 3, then 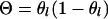. If 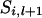= 1 and x = 4, 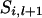= 2 and x = 3, 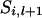= 3 and x = 2, or 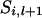= 4 and x = 1, then .

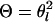APPENDIX B: TRANSITION RULE FOR A RANDOM WALK

Following Sobel and Lange (1996), we describe how to integrate a random walk to segregation indicators.

Basic transition rule (T₀):

An arbitrary single meiosis at a single locus is randomly chosen and the segregation indicator for the site is switched.

The first composite transition rule (T₁):

An arbitrary single individual at a locus is randomly chosen and 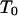is applied to the meioses of all progeny descended from the chosen individual.

The second composite transition rules (T_2a and T_2b):

An arbitrary couple at a locus is randomly chosen and 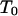is applied to the meioses for each progeny of the couple if the meioses (for progeny) have different segregation indicators (which is for 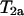) or if the meioses have the same segregation indicator (which is for 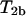). And then 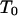is applied to the meioses of all grand progeny descended from the chosen couple.

The number of transitions per sampling round is randomly determined with a geometric distribution with mean of 2 (i.e., n_t with probability 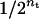, where n_t is the number of transitions). For each transition in a sampling round, one of the transition rules is randomly chosen and carried out. Therefore, multiple moves of the random walk in each sampling round are carried out. Note that the symmetry of the proposal transition matrix and the reversibility of the Markov chain were already proven by Sobel and Lange (1996).

In the combined method, the situation is slightly different in that the random walk approach is applied only to the reducible sites (in the meiosis sampler). In this case, the proposal distribution is also symmetrical. The number of transitions k of a step is chosen with probability pr(k) and a particular transition rule (r) and pivots (p) are chosen with probability pr(r, p). The transitions generate the transformation group, that is,

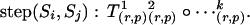When one of the transitions includes a reducible site, the proposal probability of the step (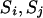) is .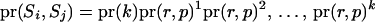

When none of the transitions includes a reducible site, the proposal probability of the step (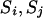) is pr(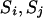) = 0.

Consider the inverse process,

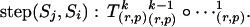The number of transitions k of a step is chosen with the same probability pr(k) in the step (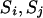) and a particular transition rule and pivots are also chosen with the same probability pr(r, p) in the step (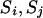) (Sobel and Lange 1996).

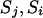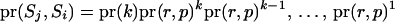When one of the transitions includes a reducible site, the proposal probability of the step () is . When none of the transitions includes a reducible site, the proposal probability of the step (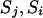) is 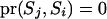. Therefore, whether a reducible site is included or not, the proposal distribution is always symmetrical; i.e., .

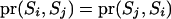The nonreducible sites that are not proposed and not updated in the process of the random walk approach are always updated in the meiosis Gibbs sampler according to the posterior distribution.