Fine Mapping and Physical Characterization of Two Linked Quantitative Trait Loci Affecting Milk Fat Yield in Dairy Cattle on BTA26

Abstract

Previously, a highly significant QTL affecting fat yield and protein yield and mapped to the bovine BTA26 chromosome has been reported to segregate in the French Holstein cattle population. To confirm and refine the location of this QTL, the original detection experiment was extended by adding 12 new families and genotyping 25 additional microsatellite markers (including 11 newly developed markers). Data were then analyzed by an approach combining both linkage and linkage disequilibrium information, making it possible to identify two linked QTL separated by 20 cM corresponding to ∼29 Mb. The presence of a QTL affecting protein yield was confirmed but its position was found to be more telomeric than the two QTLunderlying fat yield. Each identified QTL affecting milk fat yield was physically mapped within a segment estimated to be <500 kb. Two strong functional candidate genes involved, respectively, in fatty acid metabolism and membrane permeability were found to be localized within this segment while other functional candidate genes were discarded. A haplotype comprising the favorable allele at each QTL position appears to be overrepresented in the artificial insemination bull population.

SINCE the first experiment reported 10 years ago (Georges et al. 1995), several genomewide scans for QTL have given primary localizations of numerous QTL affecting production, health, or conformational traits in dairy cattle (Khatkar et al. 2004). Depending on the assumed effective size of the population, between 50 and 100 segregating genes are expected to affect the variation of a given quantitative trait (Hayes and Goddard 2001). However, identification of the corresponding underlying causal mutations is hampered by the small effect of the QTL on the trait considered. Recently, the development of both dense genetic maps (Barendse et al. 1997; Kappes et al. 1997; Ihara et al. 2004) associated with high-throughput genotyping techniques and new models for the analysis of data have improved fine-mapping techniques greatly. Indeed, methodologies were proposed to combine linkage analysis (LA) and linkage disequilibrium (LD) mapping information on the basis of either variance component (Meuwissen and Goddard 2000) or likelihood models (Farnir et al. 2002). These strategies exploit residual LD existing in the bovine population (Farnir et al. 2000) and have demonstrated their efficiency by greatly reducing the interval of location for some QTL (Meuwissen et al. 2002; Olsen et al. 2005). Furthermore, they recently contributed to the characterization of a causal mutation in the DGAT1 gene (Grisart et al. 2002, 2004) and of two other putative causal mutations, respectively, in the GHR gene (Blott et al. 2003) and the OPN gene (Schnabel et al. 2005). All these mutations are associated with a strong effect on milk production traits.

In parallel, knowledge on the bovine genome has benefited greatly from structural genetics studies. Detailed human/bovine comparative maps have been developed (Hayes 1995; Band et al. 2000; Hayes et al. 2003), increasing the possibility of exploiting the genome sequence and the growing functional characterization of reference species such as man (Lander et al. 2001), rat (Gibbs et al. 2004), or mouse (Waterston et al. 2002). These data provide new insights to unravel the genetic determinism involved in the variation of some traits of breeding interest (Andersson and Georges 2004). More recently, a first-generation physical map of the bovine genome was released (Schibler et al. 2004), opening the way toward the whole bovine genome sequence planned to be assembled at the beginning of 2006.

In this study, most of the available positional cloning tools in cattle were applied for the fine mapping and the physical characterization of a highly significant QTL affecting milk fat yield on bovine chromosome 26 (BTA26). This QTL was originally described to segregate in the French Holstein dairy population (Boichard et al. 2003) and was confirmed later in a combined analysis associating French and German families (Bennewitz et al. 2003). According to the results from a recently published high-resolution comparative map between BTA26 and human chromosome 10 (HSA10) (Gautier et al. 2003), 14 publicly available microsatellite markers and 11 newly developed microsatellite markers were genotyped in the families of the original design extended by the addition of new families originating from the marker-assisted selection (MAS) program initiated in 2000 in France (Boichard et al. 2002). These new data were then analyzed using a methodology combining LA and LD to identify the most likely QTL marker interval. A detailed physical and comparative map of the corresponding interval was then constructed.

MATERIALS AND METHODS

Animal material:

Only Holstein families were included in this analysis since it was known that no BTA26 QTL affecting milk production traits segregates in families of the two other breeds (Montbéliarde and Normande) included in the initial QTL detection protocol (Boichard et al. 2003) or MAS program (Boichard et al. 2002). Thus, the resulting design consisted of a classical granddaughter design with 21 half-sib families: 9 from the original QTL program and 12 from the MAS program. As shown in Table 1, 1510 half-sib progeny were tested—on average 72 (ranging from 20 to 182) per family—and some families were strongly related, as some sons appeared also as sires in the design.

TABLE 1.

Family structure of the granddaughter design used in the study

Sire	Origin	Birth date	Father	No. of sons
1200	MAS program	1990	2010a	46
1351	MAS program	1982	3538	20
2010	QTL program	1983	3538	64
3517	QTL program	1981	3538	66
3518	QTL program	1983	3538	67
3519	QTL program	1984	3538	55
3532	MAS program	1982	3538	36
3533	MAS program	1982	3538	67
3534	MAS program	1981	3538	24
3535	MAS program	1986	42
3536	MAS program	1991	44
3537	MAS program	1973	43
3538	MAS program	1974	27
3539	QTL program	1979	131
3540	QTL program	1980	169
3541	QTL program	1981	84
3542	QTL program	1983	182
3543	QTL program	1985	134
3544	MAS program	1986	3539	97
3545	MAS program	1986	3539	54
3546	MAS program	1989	a	58
				Total 1510

Each half-sib family is named by the name of the sire. Size (number of progeny-tested sons) and origin (families from the initial design-named QTL program and families originating from the MAS program) are also indicated. The name of the father of the sire is indicated when it is included as a sire in the granddaughter design.

^aSire 3538 is a grandfather (maternal or paternal) of the corresponding sons.

Daughter yield deviation (DYD) for the five milk production traits (milk yield, fat yield, protein yield, fat percentage, and protein percentage) and corresponding reliabilities originated from the routinely performed bull genetic evaluations. Effective numbers of daughters were computed from the reliabilities assuming heritabilities of 0.3 and 0.5 for yield and percentage traits, respectively (Boichard et al. 2003). All bull DNAs were available from the previously mentioned studies.

Genotyping data:

Previously available genotyping data:

Before the beginning of the study, genotypes for four microsatellite markers (ABS12, BMS907, INRA081, and IDVGA59) were available (Boichard et al. 2003). Nevertheless, ABS12 and IDVGA59 were genotyped only on the sons from the nine families of the original QTL program, which explains the lower number of genotyped sons (see Table 2).

TABLE 2.

Characteristics of the microsatellite markers from BTA26 used in this study

Marker name	Accession no.	Allelle	Heterozygous sires	Genotyped half-sibs	Informative meioses
ABS12	6	6	948 (62%)	550
BES26_1	CR792711	8	11	1419 (93%)	661
BM188	9	15	1504 (99%)	784
BMS332	9	17	1490 (98%)	846
BMS907	4	12	1455 (96%)	630
BZ840628	BZ840628	7	11	1450 (96%)	475
CSKB74	7	16	1428 (94%)	699
FASMC2	8	5	901 (59%)	72
HAUT27	9	19	1447 (95%)	1182
HEL11	10	15	1484 (98%)	606
IDVGA59	8	4	922 (61%)	309
INRA081	7	16	1501 (99%)	785
INRA272	6	5	1501 (99%)	198
INRArrmg310	AY609062	5	3	1396 (92%)	114
INRArrmg311	AY609063	8	16	1359 (90%)	723
INRArrmg313	AY609065	8	14	1081 (71%)	877
INRArrmg314	AY609066	9	13	1335 (88%)	553
INRArrmg315	AY609067	4	4	1414 (93%)	181
INRArrmg317	AY609069	2	3	1155 (76%)	83
INRArrmg318	AY609070	10	14	1179 (78%)	859
INRArrmg322	AY609073	7	15	1279 (84%)	635
INRArrmg324	AY609074	8	18	1087 (71%)	545
MAF36	4	13	1332 (88%)	467
NOR6	10	18	1398 (92%)	1100
RM26	10	13	1478 (97%)	795
RME011	4	15	1501 (99%)	835
RME40	13	19	1496 (99%)	1300
TGLA429	6	17	1498 (99%)	1029
URB8		14	16	1469 (97%)	819

Microsatellite marker selection and production:

According to the primary localization results and mapping information available for BTA26 (Gautier et al. 2003), 19 microsatellite markers from the public database (http://dga.jouy.inra.fr/cgi-bin/lgbc/main.pl?BASE=cattle) were selected. Since the number of markers in the linkage map of the centromeric region of BTA26, which corresponded to the most likely QTL region, was too low, we decided to selectively isolate new microsatellite markers in this region from 37 bacterial artificial chromosomes (BACs) containing at least one of the following 18 genes: AW289352, MBL2, MINPP1, LIPF, ACTA2, CH25H, LIPA, RI58, PPP1R3C, KIAA0940, KNSL1, IDE, HHEX, LGI1, PDE6C, CYP2C19, SH3D5, PDLIM1, and PYCS, these genes mapping to the region of interest (Gautier et al. 2003). Some of these genes also represented functional candidate genes. The INRA BAC library was PCR screened as previously described (Eggen et al. 2001) for the gene PRKG1, using primers deriving from the sequence Y08961 (PRKG1F, GCTCCAGGAGAAGATCGAGGA and PRKG1R, GCTGAGATCCTGGATGTCAAA). Although this gene could not be mapped directly on the BTA26 radiation hybrid (RH) map due to strong sequence similarities among bovine primers and hamster genomic sequences, comparative mapping results indicate that it represents a good candidate to refine the boundaries between the two blocks of conserved synteny called HB4 and HB5 in one of our previous publications (Gautier et al. 2003). Two additional INRA BAC clones (bI0054A11 and bI0735C02) were thus added to the 37 previously selected ones.

Microsatellite sequence isolation from these 39 bovine BAC clones was performed according to standard procedures (Vaiman et al. 1994). The protocol was slightly improved to increase the yield. Briefly, BAC clone DNA was extracted by mini-preparation in 96-well plates using a modified alkaline lysis procedure (Schibler et al. 2004). Pools of three to four BAC DNA (300–500 ng each) were mixed, digested to completion with Sau3A (Promega, Madison, WI), and cloned in a dephosphorylated pGEM4Z vector (Promega). Sublibraries were then organized in 96-well plates and individual clones were spotted onto a 22 × 22-cm membrane at a medium density (Amersham, Arlington Heights, IL). Arrays were then screened using (TG)₁₀ and (TC)₁₀ ³²P-radiolabeled oligonucleotides and DNA of positive clones was extracted for sequencing with an ABI377 sequencer (ABI Prism) according to standard procedures. Of the 32 microsatellite sequences obtained, 16 either contained repetitive sequences or were too short to design suitable primers; they were thus discarded from further analysis (our unpublished data). PCR primers were designed for the 16 remaining and first tested to screen the BAC library (Eggen et al. 2001) to identify or confirm the BAC clone(s) from which the microsatellite markers were isolated.

Three additional microsatellite markers (BZ840628, BES26_1, and CC471573) were produced in silico from BAC end sequences available in the public domain. The chosen BACs were selected according to the first draft of the physical map of the bovine genome (Schibler et al. 2004) and their expected positions were checked before genotyping by radiation hybrid mapping on the BTA26 RH map using standard mapping procedures (Gautier et al. 2003).

Finally, 42 microsatellite markers were considered in this study (23 publicly available and 19 newly developed), of which 13 were not included in the analysis (see below). The remaining 29 markers are described in Table 2.

Genotyping procedure:

The genotyping procedure consisted of a multiplex fluorescent PCR amplification with one fluorescent end-labeled primer (MWG-Biotech). According to the fluorochrome dye and the PCR product length, the 38 microsatellites were assembled into five groups. For each group, one or two multiplex PCRs were performed and resulting PCR products pooled before migration. Multiplex PCR conditions were set up by adjusting the final concentration of marker primers after several successive testing experiments performed on calibrated bovine DNA (20 ng/μl) as template. PCR reactions were performed using the Multiplex PCR kit (QIAGEN, Valencia, CA) and according to the QIAGEN recommendations on a PTC-100 thermocycler (MJ Research, Watertown, MA) in a 10-μl final volume. Samples were preheated for 5 min at 94° and subjected to 35 cycles of 94° for 20 sec, 55° for 30 sec, and 72° for 30 sec and then to a final extension step of 5 min at 72°. During the setup process, PCR products were run on a 377 ABI sequencer and raw data were analyzed with the Genotyper software (ABI Prism). PCR products from further genotyping were first purified on Sephadex G50 before running on a MegaBACE 96 capillaries sequencer (Molecular Dynamics, Sunnyvale, CA). Raw data were then analyzed using Genetic Profiler v1.5 (Molecular Dynamics). Three markers, ARO25, INRA320 (AY609072), and INRA325 (AY609075), were discarded during the setting up of the multiplex PCR conditions for technical reasons (nonspecific cross products in PCR amplification). Final conditions for the multiplex genotyping of the 35 remaining markers are available upon request.

Linkage map construction:

Marker order and map distances were estimated using the CRIMAP 2.4 software (Green et al. 1990). First, the marker order was challenged against that of the comprehensive RH map of BTA26 (Gautier et al. 2003), using the FLIPS option with a five-marker window to obtain the most likely order given our data set. The CHROMPIC option was subsequently used to identify unlikely double crossovers, which were considered as missing genotypes (0.2% of the genotypes). Final map distances were computed on the basis of Haldane's mapping function.

QTL mapping statistical analysis:

LA:

LA was performed using a classical regression interval analysis (Haley and Knott 1992), using the web-based version of the software QTL express (Seaton et al. 2002), with both a one-QTL and a two-QTL model computed every centimorgan along the chromosome. During this step, marker informativity at each position along the chromosome was also computed as the mean (1 − 2p_ij)², where p_ij is the probability for son j of inheriting from sire i one arbitrarily defined chromosome segment at the position considered (Seaton et al. 2002). Analyzed data correspond for each trait of interest to twice the so-called DYD of the bulls (Boichard et al. 2003) weighted by their respective reliabilities. A 95% chromosomewise significance threshold was computed on the basis of 10,000 permutations and a confidence interval was estimated using the bootstrapping option on 10,000 iterations. The heterozygous status of the different sires was established on the basis of the t-test value at the position considered. To evaluate the status at positions other than the maximum peak one, a subset of the data set surrounding the position of interest was used.

The variance component-based LA was performed using a similar model to that detailed in the next section except that base haplotypes were considered unrelated (Meuwissen et al. 2002). The fraction of the total additive genetic variance explained by the QTL was estimated as 2σ_h²/(2σ_h² + σ_u²), where σ_h² and σ_u² correspond, respectively, to the variance component associated with the haplotype effect and the additive polygenic effect (see below).

Combined linkage disequilibrium and linkage analysis:

Fine mapping of the QTL was performed using the same approach previously described (Meuwissen et al. 2002). Briefly, it consists of a variance component mapping method (Hoeschele et al. 1997), which is extended to take into account information provided by residual LD in the population. The procedure consists of three successive steps:

• Construction of maternally and paternally inherited marker haplotypes for each recorded individual (Windig and Meuwissen 2004).

• Computation of the matrix H_p of identity-by-descent (IBD) probabilities among pairs of base haplotypes at each putative QTL position p (typically the midpoint of each marker bracket), as previously described (Meuwissen and Goddard 2001). The G_p matrix of IBD probabilities of all haplotype pairs at position p is then deduced from the H_p matrix and from known pedigree information (Fernando and Grossman 1989). When the IBD probability of a haplotype pair was >0.95 at a given position, they were considered identical.

• Calculation of the likelihood of the data at each position p following the mixed model: y = μ1 + Z_qh + Z_au + e, where y is the vector of DYD records, μ is the overall mean, h is a vector of random haplotype effects, u is a vector of random additive polygenic effects resulting from the combined effect of background genes, e is a random sampling error, and Z_q and Z_a are incidence matrices. The variance matrices Var(u), Var(h), and Var(e) are, respectively, Var(u) = Aσ_u² with A being the additive genetic relationship matrix based on the pedigree of the bulls, Var(h) = G_pσ_h², and Var(e) = Rσ_e², where R is a diagonal matrix with n_j⁻¹ on the diagonals (n_j being the effective number of daughters of bull j). The variance components of the random effects σ_u², σ_h², and σ_e² and the likelihood L_p of the above model were estimated by the ASREML package (Gilmour et al. 2000) at each position p. The log-likelihood ratio test LRT = −2(log(L₀) − log(L_p)) is then computed, where L₀ corresponds to the likelihood of the null hypothesis model that assumes Var(h) = 0. This test statistic is approximately chi-square distributed with 1 d.f. (Olsen et al. 2004). As above, the fraction of the total genetic variance explained by the QTL was estimated as 2σ_h²/(2σ_h² + σ_u²), where σ_h² and σ_u² correspond, respectively, to the variance component associated with the haplotype effect and the additive polygenic effect.

A two-QTL model linkage disequilibrium and linkage analysis:

To confirm and test the presence of two QTL affecting the trait of interest, a two-QTL model was used to perform linkage disequilibrium and linkage analysis (LDLA). The records were thus modeled by: y = μ1 + Z_q1h₁ + Z_q2h₂ + Z_au + e, where y, μ, u, e, and 1 are as defined above, and h₁ and h₂ are vectors of random QTL effects for the two brackets (1 and 2) analyzed simultaneously. Z_q1 and Z_q2 are the corresponding incidence matrices. As defined previously, Var(u) = Aσ_u², Var(h₁) = G₁σ_h1², Var(h₂) = G₂σ_h2², and Var(e) = Rσ_e². The variance components of the random effects σ_u², σ_h1², σ_h2², and σ_e² and the likelihood L_pq of the above model were estimated by the ASREML package (Gilmour et al. 2000) at each P × (P − 1)/2 pair of positions p and q (P being the total number of brackets). Two kinds of log-likelihood-ratio tests were then computed:

• The two-QTL hypothesis vs. the no-QTL hypothesis: LRT = −2(log(L₀) − log(L_pq)), where L₀ corresponds to the likelihood of the null hypothesis model that assumes Var(h₁) = Var(h₂) = 0. This test statistic is approximately chi-square distributed with 2 d.f.

• The two-QTL hypothesis vs. the one-QTL hypothesis: LRT = −2(log(L_p) − log(L_pq))] and LRT = −2(log(L_q) − log(L_pq)), where L_p (respectively L_q) corresponds to the likelihood of the model that assumes Var(h₂) = 0 [respectively Var(h₁) = 0]. This test statistic is approximately chi-square distributed with 1 d.f.

The fraction of the total genetic variance explained by the QTL at position p was estimated as 2σ_h1²/(2σ_h1² + 2σ_h2² + σ_u²), where σ_h1², σ_h2², and σ_u² correspond to the variance component associated with the two haplotype effects at marker bracket positions p and q and the additive polygenic effect, respectively. The heterozygous status of an individual at marker bracket position p was estimated by testing the difference between its paternal and maternal alleles. The test was thus performed using the two-effect estimates difference (D_h = h_mat − h_pat) and its prediction error variance [PEV = C_ii + C_jj − 2C_ij, where C_kl corresponds to the element (k, l) of the inverse of the mixed-model equation of the haplotype effect], each of the terms of the equation being provided by ASREML. Under the null hypothesis, the statistic N = D_h/PEV^0.5 follows a T-distribution with n = n_pat + n_mat − 2 d.f. (n_pat and n_mat correspond to the number of times the paternally or maternally inherited haplotype is observed, respectively). For most sires (n_pat + n_mat) is large enough to assume that N is approximately standard normally distributed under the null hypothesis.

Physical map construction:

As mentioned previously, all the microsatellite markers considered in this study were screened for in the INRA BAC library (Eggen et al. 2001). Together with previous physical and comparative map information for BTA26 (Gautier et al. 2003; Schibler et al. 2004), these data allowed us to anchor each marker into the INRA first-generation bovine physical map (http://locus.jouy.inra.fr/fpc/cattle). This map is further anchored on the international physical map, which serves as a basis for the genome sequencing consortium (http://www.bcgsc.ca/lab/mapping/bovine), using international BAC clones included in both maps and a precise estimate of the location of the INRA contig and of some of their markers on the international physical map. To refine and confirm the bovine-human comparative map, some of the bovine BAC end sequences (BES) from international (Larkin et al. 2003) and INRA BAC clones (out of the 30,000 recently produced and submitted to GenBank) in the region were aligned against the HSA10 Build35 sequence assembly (http://genome.ucsc.edu/), using the BLAST alignment tool (Altschul et al. 1997). Repetitive sequences were masked and only those alignments producing hits >80 bp long with at least 85% of overall sequence similarity were considered as significant.

RESULTS

Construction of a high-density integrated genetic and physical map of the BTA26 chromosome:

Linkage map construction:

Genotypes for 39 microsatellite markers were available to build a medium-density BTA26 genetic map. Among these, 4 were previously genotyped and 35 were genotyped for the purpose of this study. Six markers had to be discarded during the analysis of raw genotype data because of technical difficulties [BMS4505, INRA319 (AY609071), INRA316 (AY609068), INRA327 (AY609077), and TGLA22] or inheritance inconsistencies due to the segregation of a null allele [INRA312 (AY609064)]. Similarly, no polymorphism was observed in our families for INRA326 (AY609076), CC471573, BM7226, and FASMC1, confirming for this latter marker the low heterozygosity level reported previously (http://www.marc.usda.gov/genome/genome.html).

Finally, 29 markers were considered to build the genetic map, displaying on average 645 informative meioses, from 72 for FASMC2 to 1300 for RME040 (Table 2). Respectively, 6 and 16 markers (Figure 1A, underlined ) were in common with the 8-marker IBRP97 map (Barendse et al. 1997) and the updated 63-marker MARC map (Ihara et al. 2004). Distances and orders were in perfect agreement especially when comparing with the high-density MARC map. In addition, as shown below, the order is supported by independent results from both RH and physical maps.

Figure 1.

(A) The BTA26 linkage map constructed in this study. (B) The map is anchored to the BTA26 physical map and (C) to the HSA10 genome sequence assembly. (D) The previous BTA26 RH map is also given. See text for details.

Integration of linkage and physical maps (Figure 1B):

As previously described (Gautier et al. 2003), almost all the markers from the BTA26 RH map (Figure 1D) were screened for in the INRA BAC library and thus anchored to the INRA physical map (Schibler et al. 2004). The resulting first draft of the BTA26 physical map was estimated to cover ∼70% of the total length of the chromosome. As shown in Figure 1B, the 29 microsatellite markers of the linkage map belong to 13 different INRA contigs (each containing from 1 to 5 markers). Further details for each of these contigs are accessible online (http://locus.jouy.inra.fr/fpc/cattle/). For the four contigs containing >2 markers, physical data confirm the linkage map marker order. Similarly, five (674, 4967, 676, 670, and 151), three (679, 1617, and 680), and two (153 and 684) consecutive INRA contigs are respectively anchored to contig 13420, contig 1154, and contig 10397 from the international physical map (http://www.bcgsc.ca/lab/mapping/bovine).

Integration of linkage and improved comparative map (Figure 1C):

Two blocks of conserved synteny between BTA26 and HSA10 have been previously described (Gautier et al. 2003). Inside each group, only a few discrepancies in the conservation of the gene order remained but they can be attributed to the resolution limit of the RH map (Schibler et al. 2004). In this study, each of the 11 contigs from the integrated BTA26 linkage and physical map were precisely anchored to HSA10, using significant BLAST alignments of bovine BES (Figure 1C and http://locus.jouy.inra.fr/fpc/cattle/), consequently confirming previous results. Additionally, assignment of PRKG1 to BTA26 by linkage mapping of INRA310 allowed us to refine the boundary between the two blocks of conserved synteny to a region <100 kb formed by two overlapping BAC clones inside INRA contig 676 (Figure 1C). As a result, the integrated map strongly supports an overall gene content and order conservation inside each of the two blocks of conserved synteny between BTA26 and HSA10. This provides additional support for the marker order in our BTA26 linkage map and its coverage appears to provide a good marker density with no gap exceeding 6 Mb as estimated on the HSA10 genome map (Figure 1C).

QTL mapping results:

Linkage analysis:

Regression LA on the extended design confirmed the existence of the QTL affecting fat yield (P < 0.001) and protein yield (P < 0.001) (Figure 2). No significant QTL was detected for the three other milk production traits considered: milk yield, fat percentage, and protein percentage, with an F-value profile never >1.5 along the chromosome. According to the t-test performed at the peak position (14 cM on the map), seven sires (2010, 3517, 3518, 3538, 3539, 3542, and 3544) were heterozygous for the QTL affecting fat yield. The F-value profile for the protein yield trait appears very different, with a very flat peak (position 64 cM) at the end of the chromosome where the informativity is weaker due to a lower marker density. Five sires were found to be heterozygous, among which only three (3518, 3538, and 3539) are in common with the previous one. Although the 95% bootstrap confidence intervals are overlapping for the two traits (covering almost the entire chromosome for protein yield), our results suggest the segregation of different QTL affecting protein and fat yield. LDLA results confirmed this hypothesis (see below). We then focused on fat yield and its QTL in the first part of the chromosome where we developed and used a dense marker map. In the following, only fat yield results are presented.

Figure 2.

Linkage analysis results from regression LA. The number of bootstrap samples and the informativity have been rescaled.

For the fat yield trait, qualitative observations of paternal individual contributions (data not shown) as well as the overall “double-peak” shape (one peak arising at position 14 cM, F-value = 2.75, and the other at position 36 cM, F-value = 2.67) of the QTL location curve seem to indicate the segregation of at least two linked QTL for the trait. Moreover, the two most important contributions to the 90% bootstrap interval, which spans a region from position 9 to 68 cM on the map, are located at the two corresponding peaks (Figure 2).

We thus performed a two-QTL regression analysis. The maximum F-value statistics for the models of two QTL vs. no QTL (42 and 1510 − 42 = 1478 d.f.) and two QTL vs. one QTL (42 and 21 d.f.) = 2.27 (P_2vs.0 < 8.3 × 10⁻⁶) and 1.75 (P_2vs.1 < 0.084), respectively. On the two-QTL regression model F-value contour plot curve along the two-dimensional map surface, the surface harboring an F-value superior to an arbitrarily chosen threshold 2.1 was found to cover regions from position 10 to 14 cM for the first fitted QTL (corresponding to the peak value under a one-QTL model) and 33–39 cM and 44–79 cM for the second fitted QTL (the highest F-value being for two QTL located at positions 15 and 68 cM). However, position results should be considered with care because of lack of informativity at the end of the chromosome (see above) and modest resolution of the regression model. Thus, the hypothesis of at least two segregating QTL seems likely.

A variance component LA using linkage information alone (i.e., using LD within the known pedigree) was also performed (Figure 3) and provided an estimate of the QTL effect considered here as the proportion of the total additive genetic variance explained. The curve was found to be slightly different since the two-peak shape was less clear than previously, the first peak being smaller than the second one. Nevertheless, this analysis seems also to agree with the hypothesis of the segregation of two QTL. The QTL variance as estimated over the entire chromosome was found to explain on average 12.8% (from 8.9 to 17.3) of the total additive genetic variance.

Figure 3.

LDLA results and comparison with results from variance component linkage analysis alone. The two-QTL LDLA model 1 (respectively, 2) LRT curve plots the test of the LDLA model fitting the two-QTL bracket effect against the model fitting one QTL at the [BMS907/INRA311] (respectively, [BES26_1/HAUT27]) marker bracket.

LDLA fine-mapping results:

LDLA mapping results support the hypothesis of the segregation of two QTL underlying fat yield as mentioned earlier. Indeed, two peaks of approximately the same size were found for the marker brackets [BMS907/INRA311] and [BES26_1-HAUT27] (Figure 3). Their respective positions (spanning from position 10.0 to 12.5 cM for [BMS907/INRA311] and from position 31.3 to 34.3 cM for [BES26_1-HAUT27]) are in agreement with the results from LA described above.

To test this hypothesis of two segregating QTL, we performed a two-QTL model LDLA (Figure 4). The maximum LRT (LRT = 26.22) value in two dimensions was obtained for the position fitting haplotype effects for both the [BMS907/INRA311] and [BES26_1/HAUT27] brackets. As shown in Figure 3, the likelihood-ratio test of the LDLA model fitting two QTL (at positions [BMS907/INRA311] and [BES26_1/HAUT27]) against the one-QTL model including only the effect of the [BMS907/INRA311] haplotype is 7.28 (P < 0.007). Similarly, against the one-QTL model fitting only the effect of the [BES26_1/HAUT27] haplotype, the LRT = 7.68 (P < 0.006).

Figure 4.

Two-QTL LDLA results for milk fat yield. LRT values (two-QTL segregating against no-QTL segregating) are plotted in two dimensions corresponding to each possible pair of marker bracket effects.

LDLA mapping results for the protein yield trait gave the last marker bracket [TGLA429/MAF36] as the most likely, in agreement with results from LA alone. This also adds credit to the hypothesis of different QTL acting on fat yield and protein yield rather than one or several QTL with a pleiotropic effect. Nevertheless, we cannot exclude a possible pleiotropic effect on fat yield for the QTL affecting protein yield, which may cause the segregation of a third QTL for the trait of interest. However, the marker density in this region was too low to appropriately test this hypothesis and propose a fine characterization of this QTL.

Haplotype effect:

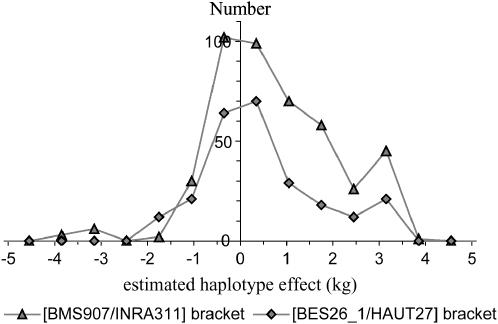
Following LDLA results, the [BMS907/INRA311] and the [BES26_1/HAUT27] marker brackets were found to explain, respectively, 1.8 and 2.5% of the total fat yield additive genetic variance under the two-QTL model. Under the one-QTL LDLA, these estimates were 4.34 and 2.50%, which might indicate the cosegregation of a haplotype carrying alleles of similar effect at the two QTL positions (see below). For the [BMS907/INRA311] and the [BES26_1/HAUT27] marker brackets, respectively, 442 and 247 different identity-by-descent haplotypes were found to segregate in the pedigree. The two corresponding distributions appear approximately bimodal (Figure 5), thus suggesting a biallelic effect for each of the QTL positions, with one favorable allele (increasing fat yield). However, for the [BMS907/INRA311] marker bracket effect distribution, ∼10 IBD haplotypes seem to have a clear decreasing effect. Some clustering procedures might help to confirm this trend.

Figure 5.

Haplotype effect distributions for the two most likely marker brackets.

For each of the corresponding IBD haplotypes, the allelic combination was built when possible. In the case of the [BMS907/INRA311] bracket, an allelic combination (1_2_1) at the marker BMS907-INRA311-INRA314 (this latter marker being added because it is very close to INRA311) was found to be clearly associated with an increasing haplotype effect. Similarly, most of the favorable marker bracket effects pertain to IBD haplotypes carrying the allelic combination 1_3 for marker bracket [BES26_1/HAUT27].

Haplotype analysis among the sires:

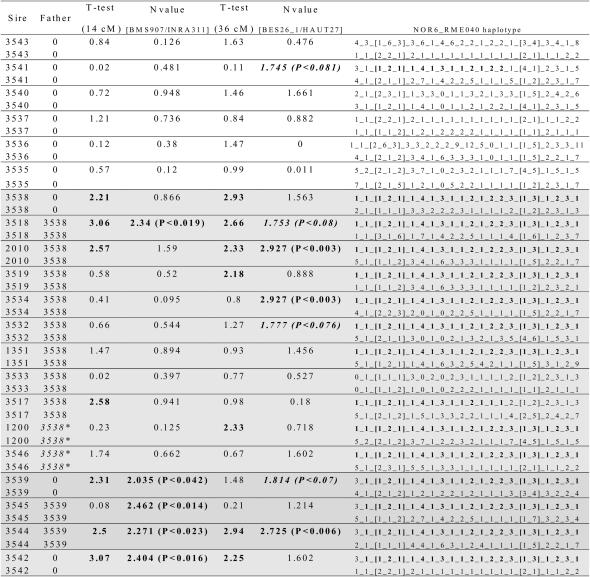
Interestingly, 5 sires (2010, 3518, 3538, 3542, and 3544) found to be heterozygous after regression LA (see above) at the two QTL positions share a common haplotype from marker NOR6 to RME040 (Figure 6). Among the 16 other sires, 8 (1200, 1351, 3519, 3532, 3534, 3539, 3545, and 3546) also share this haplotype. Nevertheless, 5 are homozygous at the two QTL positions (1351, 3532, 3534, 3545, and 3546), 2 (1200 and 3519) are heterozygous only at the second position, and 1 (3539) only at the first position according to the t-test (Figure 6). These sires may have inherited a favorable allele from their dam. For instance, sire 1351 has inherited at the first QTL position a haplotype identical by state to the haplotype of interest and containing in particular the allelic combination 1_2_1 (see above). However, some sires, such as 3532 and 3534, have inherited a maternal haplotype harboring an effect significantly different from the paternal one (respectively, P < 0.076 and P < 0.003) at the second position analyzed. Thus, their homozygous status declared after regression LA could originate from lack of power of the t-test (particularly because of their small family size). More generally, status at the two QTL positions appears to be broadly concordant from both regression LA and N-value test statistics. Differences may be attributed to a greater power of the LDLA (because the clustering process is equivalent to an increased family size). Moreover, their close location makes it difficult to discriminate status at the two QTL positions from the t-test derived from regression, whereas LDLA succeeds in a better disentangling of the two linked QTL by accounting for many more recombination events.

Figure 6.

Haplotypes segregating among the 21 sires of the granddaughter design. The father (or grandfather, when followed by an asterisk) is also mentioned when it is included as a sire in the granddaughter design. The N-value (see materials and methods) is given for the two most likely QTL marker bracket positions. Numbers in boldface and boldface italic type correspond to sires heterozygous at the corresponding position according to the N-statistic at a 5 and 10% significant threshold, respectively. Similarly the t-tests from regression LA are reported for the two peak positions (see text). Finally, the two haplotypes spanning the 30-cM interval containing the two QTL are included. Positions of the markers are indicated with brackets. The common haplotype supposed to carry the two favorable alleles for the two QTL is shown in boldface type.

Together with the estimate of the marker bracket effects at the two corresponding QTL positions, the results strongly suggest that the haplotypes mentioned above (Figure 6) carry the two favorable alleles. Therefore, as expected, sire 3517 having inherited from 3538 a recombinant haplotype between the two QTL positions was estimated to be heterozygous at the first position and homozygous at the second. The widespread presence of this large haplotype among the different sires might be explained by a strong positive selection acting on it because of an overall favorable effect on fat yield, since all these sires were also widely used as artificial insemination (AI) bulls. Moreover, a positive correlation of 0.3 between the haplotype effect at the two QTL positions was observed among the individual haplotypes of the sons and of 0.2 when considering only maternally inherited haplotypes.

A physical map of the two QTL:

As shown in Figure 1, we assigned the marker bracket [BMS907-INRA311] to the BAC contig 676. According to the anchorage of this contig on the HSA10 orthologous region and the overall conservation of the region (Gautier et al. 2003), the size of the interval was estimated to be ∼700 kb. This contig is also anchored to the international contig 13420, which has an estimated size of 3079 kb. On the basis of the relative positions of BACs mapped to both INRA and international contigs and flanking the marker of interest (see materials and methods), the size of the bracket was found to be ∼250 kb on the bovine physical map.

Similarly, as shown in Figure 1, the INRA BAC contigs containing HAUT27 (680) and BES26_1 (1617) were anchored on the HSA10 orthologous region. They are also both integrated in the INRA contig 679 (containing BMS332) and the INRA contig 1909 anchored on a unique international contig (1730) with an estimated size of 1148 kb. According to the comparative map results, the marker bracket [BES26_1/HAUT27] was estimated to cover an orthologous region of <1 Mb on the HSA10 chromosome. As above, the size of the bracket was found to be ∼300 kb on the bovine physical map.

DISCUSSION

A highly significant QTL affecting milk production traits including milk yield, protein yield, and fat yield in Holstein dairy cattle mapping to BTA26 was reported in several studies (Plante et al. 2001; Bennewitz et al. 2003; Boichard et al. 2003). However, the location of the QTL remained very imprecise. In an attempt to refine its location, 25 additional microsatellite markers, including 11 newly developed ones, were genotyped in the French QTL detection granddaughter design. The original granddaughter design corresponded to nine Holstein families and was further extended by 12 families originating from the French MAS program (Boichard et al. 2002). As a first step, a dense linkage map of chromosome BTA26 was constructed and anchored to the INRA bovine physical map (Schibler et al. 2004). LA with a classical one-QTL regression model confirmed the existence of the QTL affecting fat yield at a very high significance level (P < 0.001) but suggested the segregation of two linked QTL. Analysis of the data using a two-QTL regression model supported this hypothesis. A QTL affecting protein yield was also detected but the location of this QTL appeared to be more telomeric than the previous ones. No significant QTL on BTA26 chromosome was found for milk yield, fat percentage, or protein percentage. While not expected, the existence of QTL significant only for fat and protein yields and not for milk yield (which is negatively correlated) or percentages has already been observed (Boichard et al. 2003) and is difficult to explain before the complete molecular characterization of the QTL. Indeed, this allows a more precise estimation of the effect of the QTL on each correlated trait (a significant QTL for a given trait might be nonsignificant for a highly correlated trait but still have an effect on it).

We further focused mainly on the milk fat yield trait. To refine the position of the QTL and confirm the hypothesis of the segregation of two linked QTL, we used a combined LDLA approach that has already proved to be powerful by taking advantage of the structure of the livestock population (Grisart et al. 2002; Meuwissen et al. 2002; Blott et al. 2003). Two approaches (one-QTL and two-QTL models) were applied to our data set. First, the locations of the QTL affecting fat yield and the QTL affecting protein yield were clearly separated, disagreeing with the hypothesis of the existence of a QTL with a pleiotropic effect (Bennewitz et al. 2003). Second, the existence of two QTL affecting milk fat yield was confirmed by both the one-QTL and the two-QTL model LDLAs. The most likely location of these two QTL was refined to two marker brackets, [BMS907-INRA311] and [BES26_1/HAUT27], separated from each other by a distance of 20 cM. Their respective sizes were estimated at 700 and 300 kb. According to comparative map results, the physical distance separating these two QTL covers ∼29 Mb on the HSA10 conserved region.

Interestingly, among the sires of the granddaughter design, most of them also used as AI bulls, a long haplotype containing the two favorable alleles at the two QTL positions was found to be overrepresented. This might be the consequence of selection acting positively on this favorable combination. This is particularly notable when observing the offspring of sire 3538. Historically, this bull is one of the most-used AI bulls in France. Among its 10 closely related descendants (eight sons, 1351, 2010, 3517, 3518, 3519, 3532, 3533, and 3534; and two grandsons, 1200, a son of 2010, and 3546 from the maternal side) included as sires in the granddaughter design, 8 carry the full haplotype, 1 a recombinant haplotype, and only 1 the other haplotype. This also holds true when observing the two sons of sire 3539, which inherited the same favorable haplotype. The close relationship among most families is inherent to the granddaughter design since it uses populations from production farms (Weller et al. 1990). As a result, a bias is introduced in the regression LA, which assumed all families to be independent. Nevertheless, this bias seems relatively weak since variance components LA, which take into account relationships among sires, gave similar results.

One of the main advantages of LDLA over LA is that it uses historical recombinations, the information of which is carried mainly by maternal haplotypes. Since only one generation of recombination is analyzed in LA and since the two QTL are 20 cM apart, <20% of the sons are expected to be recombinants between the two positions (and <4% double recombinants). This explains the lack of resolution of the two-QTL regression model even if the meiosis could be traced almost with certainty (in our case 15 markers are mapped between the two positions). This results in lack of precision when estimating the status of the sires at the two QTL positions. This tendency is more pronounced as the family size decreases, thus making discrimination of the effect of the two QTL more difficult. LDLA, even with a one-QTL model, appeared to be far less sensitive to the segregation of linked QTL because of the large number of different and informative maternal haplotypes. The estimation of the QTL effect (respectively 1.8 and 2.5% of the total genetic variance) was still slightly overestimated using a one-QTL model compared to the two-QTL model for LDLA.

Several genes involved in lipid metabolism or catabolism pathways are located on BTA26, as revealed by direct mapping or suggested by comparative mapping (Gautier et al. 2003). They all were a priori strong functional candidate genes. Among these, from the centromere to the telomere we can quote LIPF (gastric lipase), LIPA (lipase A, cholesterol esterase), SCD (stearyl co-A desaturase), or GPAM (glycerol-3-phosphate acyltransferase, mitochondrial). For the last three, microsatellite markers close to each of these genes (respectively, INRA318, INRA272, and RME011), were included and genotyped and thus could be excluded as positional candidate genes. In contrast, INRA311 is a microsatellite marker developed from a BAC containing the LIPF gene. Whereas no clear effect of any of the INRA311 alleles on fat yield was established (data not shown), this gene appears to represent a strong positional and functional candidate gene. One of its alleles, if associated to a putative mutation inside this gene, could be frequent in the population. This is suggested by the high population frequency of allele “2” belonging to the allelic combination associated with the favorable IBD haplotype at the marker bracket.

The most likely position of the second QTL was found to be located in the marker bracket [BES26_1/HAUT27]. The comparative map showed that the orthologous regions on HSA10, RNO01, and MMU19 were strongly conserved among the three species and measured ∼1 Mb. As revealed by human genome sequence data (http://genome.ucsc.edu/), this region contains only one characterized gene (namely SORCS1), which does not represent a clear functional candidate gene. However, in both mouse and rat orthologous regions, an additional gene is described, the insulin 1 precursor (INS1). This gene is a strong functional candidate gene since insulin is known to accelerate glycolysis and glycogen synthesis in liver and additionally to increase cell permeability to fatty acids. However, the presence of a similar functional short sequence mapping to the corresponding bovine genome orthologous region needs to be confirmed and potential bovine polymorphisms need to be analyzed.