Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2006 Feb;172(2):1165–1177. doi: 10.1534/genetics.105.044586

Association Mapping of Kernel Size and Milling Quality in Wheat (Triticum aestivum L.) Cultivars

Flavio Breseghello *,†, Mark E Sorrells *,1
PMCID: PMC1456215  PMID: 16079235

Abstract

Association mapping is a method for detection of gene effects based on linkage disequilibrium (LD) that complements QTL analysis in the development of tools for molecular plant breeding. In this study, association mapping was performed on a selected sample of 95 cultivars of soft winter wheat. Population structure was estimated on the basis of 36 unlinked simple-sequence repeat (SSR) markers. The extent of LD was estimated on chromosomes 2D and part of 5A, relative to the LD observed among unlinked markers. Consistent LD on chromosome 2D was <1 cM, whereas in the centromeric region of 5A, LD extended for ∼5 cM. Association of 62 SSR loci on chromosomes 2D, 5A, and 5B with kernel morphology and milling quality was analyzed through a mixed-effects model, where subpopulation was considered as a random factor and the marker tested was considered as a fixed factor. Permutations were used to adjust the threshold of significance for multiple testing within chromosomes. In agreement with previous QTL analysis, significant markers for kernel size were detected on the three chromosomes tested, and alleles potentially useful for selection were identified. Our results demonstrated that association mapping could complement and enhance previous QTL information for marker-assisted selection.

THE basic objective of association mapping (AM) studies is to detect correlations between genotypes and phenotypes in a sample of individuals on the basis of linkage disequilibrium (LD) (Zondervan and Cardon 2004). In the study of genetics of complex diseases in humans, AM offers the important advantage of sampling unrelated individuals in the population, as compared to other experimental designs that require sampling within families (Risch 2000). In contrast to humans, plants can be manipulated to develop large experimental populations with desirable characteristics for genetic mapping, so in principle use of the association approach might not seem as appealing as it is in humans.

However, sampling unrelated genotypes presents a number of advantages for the development of tools for marker-assisted selection in plant breeding (Jannink et al. 2001). First, the experimental population can be a representative sample of the population to which inference is desired. Examples are a core collection from a gene bank, varieties representing the elite germplasm of a breeding program or inbred lines representing a synthetic outcrossing population. In this way, information derived from the experiments should be readily applicable to crop improvement. Second, AM can be more efficient in the use of resources. A group of unrelated individuals normally presents variation for many phenotypic aspects; thus several traits can be studied in the same population using the same genotypic data. A higher proportion of molecular markers are likely to be polymorphic, providing better genome coverage than any biparental map. Furthermore, if elite lines are used for study, multi-year and multi-location phenotypic data may be available at no additional cost (Rafalski 2002).

Notwithstanding, AM has higher probabilities of type I and type II errors than biparental QTL analysis. Type I error, or false positives, can arise from unaccounted subdivisions in the sample, referred to as population structure (Pritchard et al. 2000a). The presence of related subgroups in the sample could create covariances among individuals that, if not included explicitly in the model, generate bias in the estimates of allele effects (Kennedy et al. 1992). Increased type II error rate, or reduced power of AM compared to biparental QTL analysis, is attributable to at least three factors: (i) lower correlation between markers and genes due to the decay of LD; (ii) unbalanced design resulting from the presence of alleles at different frequencies; and (iii) a serious multiple-testing problem, aggravated by the relative independence among testing positions, compared to populations with greater LD, which results in extremely strict genome-wise significance thresholds (Carlson et al. 2004). For these reasons, AM will probably have limited application in the detection of rare variants or genes that are variable between populations, but are nearly fixed within subpopulations.

Population structure is a consequence of departures from random mating in the sampling population that result in some individuals being more closely related than others. Population structure conflicts with the assumption of independent errors in ordinary least-squares estimation of allele effects (Kennedy et al. 1992). Some authors avoided this problem by conducting the analysis within subpopulations (Garris et al. 2003; Simko et al. 2004), but this option implies a reduced power of detection. Kennedy et al. (1992) showed that in the presence of inbreeding or selection, the effect of other genomic regions on the trait could create a bias in the significance test for specific loci, resulting in a higher-than-declared type I error rate. These authors proposed that those “polygenic effects” could be accommodated as random factors in a mixed model, where the candidate locus is a fixed factor.

Polygenic effects can be predicted by quantitative genetics theory through the estimation of genetic variance components and individual relatedness, which in turn can be derived from known pedigrees (Kennedy et al. 1992; Simko et al. 2004) or based on molecular marker data (Lynch and Ritland 1999; Ritland 2000). A Bayesian approach for inference of population structure based on unlinked markers was implemented in the computer program Structure (Pritchard et al. 2000a). This program assigns individuals to subpopulations, and that assignment is considered in testing associations of markers with dichotomous traits, like many human diseases (Pritchard et al. 2000b). This method was extended for the analysis of quantitative traits by using the matrix of population assignments and the quantitative trait as predictors in a logistic regression model, where the dependent variable was a binary genetic polymorphism (Thornsberry et al. 2001).

Methods and examples are needed for association analysis between quantitative traits and multi-allelic markers, while accounting for the effect of population structure. This study is an example of such cases. We analyzed the association of simple-sequence repeat (SSR) markers with kernel size and milling quality in a collection of modern cultivars of soft winter wheat from the wheat region of the eastern United States, accounting for population structure as a random factor in a mixed-effects model.

MATERIALS AND METHODS

Plant material:

A population of 149 cultivars of soft winter wheat (Triticum aestivum L.) that had been evaluated for milling quality at the USDA–ARS Soft Wheat Quality Laboratory (SWQL) at Wooster, Ohio, was genotyped with 18 unlinked SSR markers. On the basis of those results, the sample was reduced to 95 cultivars by discarding very similar entries (≥15 identical alleles), creating a “normalized” panel used for further analyses. Three of the selected cultivars were released in the 1980s, 53 in the 1990s, and 39 in the 2000s. The selected cultivars belong to 35 seed companies or research institutions and were representative of the variability of the current elite soft winter wheat germplasm in the eastern United States.

Phenotypic data—kernel size:

Samples for evaluation of kernel size and shape were obtained from field experiments conducted in Wooster, Ohio (OH), and Ithaca, New York (NY). The samples from OH were from seed-multiplication fields harvested in 2002 and 2003. Thirty-six lines were grown in 2002 and 83 in 2003, with 24 lines in common between years. Trait values for OH were the least-squares means over years, obtained by SAS PROC GLM (SAS Institute, Cary, NC). Data from NY were arithmetic means of two replicates of a field experiment in a randomized complete block design harvested in 2004. Six typical spikes were selected from each plot and threshed in bulk, and 24 kernels were visually selected as representative of normal, fully developed kernels of each cultivar. These kernels were weighed and photographed, and the images were analyzed in the program ImageJ (http://rsb.info.nih.gov/ij). Kernel morphology traits were: kernel weight (KW) in milligrams; area of the projection of the kernel (AREA) in square millimeters; and kernel length (LEN) and kernel width (WID) in millimeters. Analysis of variance was done over locations and within locations. In OH, years were treated as replicates. Estimates of heritability were computed on the basis of results from NY, which were approximately balanced, by the formula h2 = [(MSC − MSE)/2]/MST, where MSC, MSE, and MST are the mean squares of cultivars, error, and total, respectively.

Milling quality data:

Milling quality data are the means of a variable number of years of standard evaluation at the SWQL (Andrews and Gaines 2002). Sixty-four cultivars were evaluated once, 13 cultivars twice, 6 cultivars three times, and 12 cultivars were tested four or more times. The cultivar “Caldwell” was the laboratory standard and was tested 83 times. Significance of the variance among cultivar means was confirmed (P < 0.0001) by testing against the residual variance of the replicated data [F* = Var(Y)/MSE with d.f.1 = 94, d.f.2 = 150, where Var(Y) is the variance of the phenotypic means of cultivars and MSE is the mean square error of the ANOVA of replicated data, according to the model y = cultivar + year]. A sample of 500 g of air-aspirated grains was milled in a modified Allis-Chalmers mill, generating the following traits (Yamazaki and Andrews 1977): flour yield (FY), endosperm separation index (ESI), friability (FRIA) and break-flour yield (BFY). A composite milling score (MS) was derived (L. Andrews and C. Gaines, unpublished results) as MS = 100 − 3.7(80 − FY) + 2.8(6 − ESI) − 3.3(32 − FRIA).

Genotypic data:

DNA was extracted from individual plants at Cornell University, using a mini-extraction protocol based on β-mercaptoethanol. SSR markers were selected and synthesized according to information available in the GrainGenes database (Matthews et al. 2003; http://wheat.pw.usda.gov/GG2). Markers producing a single band and assigned to a unique wheat chromosome in previous mapping studies were selected when available. In the cases of markers that produced more than one band, each band was scored independently as a different locus, provided that the size ranges were clearly separated. In those cases, and when a marker was mapped to different chromosomes in previous reports, the marker was tested on nullisomic-tetrasomic stocks (Sears 1966), along with the cultivar Chinese Spring and four random cultivars. Markers selected from chromosomes 5A or 5B were tested on N5AT5D, N5BT5D, and N5DT5B, while markers selected from 2D were tested on N2AT2B, N2BT2D, and N2DT2A. Loci that failed to confirm their chromosome positions by this method were used as unlinked markers.

Most of the marker positions within chromosomes were based on the consensus map Ta-SSR-2004 (Somers et al. 2004). The loci Xbarc297-2D, Xbarc219-2D, Xbarc303-5A, and Xbarc308-5B were positioned by comparison with the Wheat Composite 2004 map (http://rye.pw.usda.gov/cmap). A total of 93 SSR loci were detected by 88 markers, including 31 BARC (Song et al. 2005), 30 WMS (Röder et al. 1998), 18 WMC (Gupta et al. 2002), 8 CFA/CFD markers (Guyomarc'h et al. 2002), and the EST-SSR KSUM244 (Yu et al. 2004). Alleles were identified as A#, where # indicates the approximate fragment size.

The 18 markers used for sample selection were analyzed using a three-primer system (Schuelke 2000), including a universal M13 oligonucleotide (TGTAAAACGACGGCCAGT) labeled with one of the fluorescent dyes 6-FAM, VIC, NED, and PET, a special forward primer composed by the concatenation of the M13 oligonucleotide and the specific forward primer, and the normal reverse primer. Sizing of the fragments was done in an ABI3730 sequencer (Applied Biosystems, Foster City, CA) and results were analyzed in GeneMapper V3.0. Other markers were analyzed by PCR followed by polyacrylamide gel electrophoresis. PCR reactions were prepared according to Röder et al. (1998). PCR runs were 40 cycles of 45 sec at 94°, 45 sec at the annealing temperature, 90 sec at 72°, plus a 10-min final extension at 72°. In the three-primer system, PCR runs were 30 cycles as described above, plus 10 cycles with an annealing temperature of 53° (adapted from Schuelke 2000).

Statistical analysis:

Allele diversity:

All cultivars were treated as pure lines. A small proportion of heterozygosity was observed, and the following criteria were used to define the working allele. If the two bands had different intensities, then the stronger band was scored; if the two bands had similar intensities, then the more common allele was retained. If neither method could be applied, it was considered as missing data. Marker alleles with less than five counts in the population were bulked with missing data and null alleles. This group was treated as missing data for population structure and LD analysis and as a null allele for AM. The effective number of alleles was computed on the basis of common alleles as 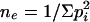Inline graphic (Hartl and Clark 1997). The estimate ne represents the number of equally frequent alleles that would result in the same probability observed of randomly drawing two different alleles from the population. It is a measure of variability at the locus that takes into account both allele number and frequency.

Population structure:

Thirty-six unlinked or distantly linked marker loci (hereafter referred to as “unlinked”), distributed over all the wheat chromosomes except 3A and 6D, were used for assessment of population structure. The program Structure (Pritchard et al. 2000a) was used to test the hypotheses for one to six subpopulations, without admixture and with correlated allele frequencies (Falush et al. 2003), burn-in phase of 105 iterations, and a sampling phase of 2 × 105 replicates. Cultivars were discretely assigned to the subpopulation for which the probability was >0.5. The degree of differentiation of each subpopulation was measured by a modified FST parameter (Falush et al. 2003). The program Genetix (Belkhir et al. 1996–2004; http://univ-montp2.fr/∼genetix) was used to compute an overall FST (Weir and Cockerham 1984) and to conduct multiple correspondence analysis, with three dimensions, according to the algorithm of Benzécri (1973).

To verify whether the number of unlinked loci used for estimation of population structure was sufficient, Structure was run with reduced numbers of markers to observe the decay in the confidence with which cultivars were assigned to subpopulations. Four set sizes—12, 18, 24, and 30 markers—were used, with 10 sets randomly drawn, without replacement, for each set size. Additionally, the full set of 36 markers was used in 10 runs. All the program options were the same as in the actual analysis, and the number of subpopulations was kept constantly equal to four. For each run, the number of lines assigned to one of the four subpopulations with probability P > 0.50, P > 0.70, and P > 0.90 was tabulated, and a rate of success in assigning lines to subpopulations was computed for each combination of sample size and probability level.

Linkage disequilibrium:

The program Tassel (http://www.maizegenetics.net) was used to estimate the LD parameter r2 among loci and the comparison-wise significance was computed by 1000 permutations. LD was estimated separately for unlinked loci and for loci on the same chromosome (unlinked r2 and syntenic r2, respectively). Syntenic r2 was plotted against map distance on chromosomes 2D and 5A and a smooth line was drawn by second-degree loess (Cleveland 1979) using the statistical program R (http://www.r-project.org). A critical value of r2, as an evidence of linkage, was derived from the distribution of the unlinked r2. Unlinked-r2 estimates were square root transformed to approximate a normally distributed random variable; then the parametric 95th percentile of that distribution was taken as a population-specific critical value of r2, beyond which LD was likely to be caused by genetic linkage. The intersection of the loess curve fit to syntenic r2 with this baseline was considered as the estimate of the extent of LD in the chromosome.

Association analysis:

Association between markers and traits was tested using a linear mixed-effects model, where the marker being tested was considered as a fixed-effects factor and subpopulation was considered as a random-effects factor (Kennedy et al. 1992). The lme function (Pinheiro and Bates 2000) of the program R was used to fit the model through restricted maximum likelihood. Significance of associations between loci and traits was based on an F-test, at a level αc corresponding to α corrected for multiple testing. Corrected significance levels αc were computed by 1000 permutations within a chromosome. Combinations of significant markers (αc < 0.05) were tested as two-marker models against single-marker models by a likelihood-ratio test (Pinheiro and Bates 2000).

RESULTS

Ninety-five contemporary soft winter wheat cultivars were genotyped for 93 SSR loci on 19 chromosomes. Thirty-six unlinked loci were used for population structure assessment. AM was analyzed for 62 markers with 33 on chromosome 2D, 20 on 5A and 9 on 5B. Markers on 2D were approximately evenly spaced, whereas most markers on 5A were located near the centromere. Five markers on 5B were clustered on the long chromosome arm. The identification of the cultivars and markers used is in supplemental Tables 1 and 2 at http://www.genetics.org/supplemental/. The complete data set is available in the GrainGenes database (http://wheat.pw.usda.gov/GG2).

Marker polymorphism:

The total number of alleles varied from 2 to 10, with an average of 4.81 alleles per locus. The number of common alleles (occurring in five or more cultivars) varied from 2 to 7, with an average of 3.67. Effective allele numbers varied from 1.16 to 6.47, with an average of 2.80. The mean frequency of missing data was 7.73%, or 10.62% when pooled with rare alleles. In addition to the 93 informative loci, the following primer sets were tested and found to be monomorphic in our population: BARC1135, BARC1158, BARC1174, CFD160, KSUM26, KSUM73, KSUM232, WMC470, WMS249, and WMS382.

Population structure:

Four subpopulations captured the relevant subdivisions of the sample. Although the posterior probability of the data did not peak in the range of one to six subpopulations, beyond four the increase was nonsignificant, and more lines became split between two or more subpopulations. The four subpopulations (S1–S4) included 19, 32, 13, and 31 cultivars, which had an FST equal to 0.337, 0.111, 0.295, and 0.064, respectively. FST across subpopulations was 0.188, indicating moderate differentiation.

Multiple correspondence analysis (MCA) was conducted to visualize the relative dispersion of the subpopulations in a three-dimensional space. Figure 1 shows projections of the MCA cloud on two orthogonal planes, with different symbols identifying each subpopulation according to the classification from Structure. The cloud was continuous, with four protrusions approximately corresponding to the four subpopulations. In agreement with FST estimates, subpopulations S1 and S3 were less dispersed than S2 and S4.

Figure 1.

Figure 1.

Open in a new tab

Orthogonal projections of the cloud of points representing the genetic distance among varieties, based on 36 unlinked SSR markers analyzed by multiple correspondence analysis. Subpopulations S1–S4 were inferred in Structure.

It was not possible to identify origin-related causes for the subpopulations observed. The only clear relationships between origin and subpopulations were that all nine cultivars from Pioneer Hi-Bred classified as S2, and all four Canadian cultivars were placed in S4. Nevertheless, those subpopulations had the most variation, and those cultivars were not similar enough to be discarded in the initial selection.

When population subdivision was inferred on the basis of <36 markers, the confidence (probability P) with which cultivars were assigned to subpopulations was reduced (Table 1). According to the resampling experiment conducted, if P > 0.50 is accepted as the criterion for assigning lines to subpopulations, as done in this study, as few as 18 markers would be sufficient to allocate almost all cultivars, but if a higher confidence of assignment were required, >36 markers would be needed. Some cultivars were more difficult to classify than others, and it was observed that those cultivars in most cases were located near the center of the cloud of points defined by MCA (results not shown). From this experiment, we concluded that the number of unlinked markers used was sufficient to capture the relevant groupings in the sample, such that they could be used as random factors in the mixed-model analysis. However, it is possible that a portion of the polygenic effect remained unaccounted, which could slightly inflate the rate of false positives.

TABLE 1.

Percentage of cultivars assigned to a subpopulation with probability P, based on different numbers of unlinked markers

No. of unlinked markers
Probability 12 18 24 30 36
P > 0.50 60.5 96.8 97.2 98.6 100
P > 0.70 34.6 78.5 83.8 88.6 92.4
P > 0.90 23.6 59.6 62.2 77.4 87.6
Open in a new tab

Linkage disequilibrium:

When the initial set of 149 cultivars was genotyped, the LD parameter r2 was significant for most of the pairwise comparisons among a set of 18 unlinked SSR loci, but was mostly nonsignificant in the normalized sample of 95 cultivars, after exclusion of very similar or identical genotypes (Figure 2). In the selected sample, pairwise r2 estimates among 36 loci (630 estimates) varied from 0.000 to 0.133, with a median of 0.022. The 95th percentile of the distribution of those estimates was used as a population-specific threshold for this parameter as an evidence of linkage. By this approach, it was estimated that values of r2 > 0.065 were probably due to genetic linkage.

Figure 2.

Figure 2.

Open in a new tab

Effect of selection of cultivars on LD. Solid, dark shading, and light shading indicate comparison-wise P < 0.0001, P < 0.001, P < 0.01, respectively, for r2 estimates among 18 unlinked SSR markers on 149 varieties (above diagonal) and 95 selected varieties (below diagonal).

The pattern of syntenic LD was studied in chromosomes 2D and 5A. On 2D, 33 markers covered most of the chromosome with intervals of 0–15 cM in the consensus map. Pairwise estimates of r2 varied from 0.000 to 0.551, with a median of 0.028. Although 65 of the estimates were above the baseline of 0.065 and 15 were above the maximum r2 among unlinked markers, a loess curve fitted on the r2 estimates did not reach the baseline (Figure 3), indicating that the marker density was not sufficient to detect consistent LD. Those results indicated that LD for chromosome 2D in this population decayed below the centimorgan scale. The consensus map used had a resolution of 1 cM, and consequently a point estimate could not be made. Most comparison-wise significant r2 estimates on 2D were observed toward the ends of the chromosome, whereas in the centromeric region seven markers within 4 cM (positions 63–67 cM, Figure 4) exhibited inconsistent LD.

Figure 3.

Figure 3.

Open in a new tab

Estimates of r2 vs. linkage distance on chromosomes 2D and 5A. Horizontal straight lines indicate the 95th percentile of the distribution of unlinked r2. Curves were fit by second-degree loess. Axis scales are different for each plot.

Figure 4.

Figure 4.

Open in a new tab

Consensus map of loci tested on chromosome 2D and 5A. Underlined loci were positioned by comparison with the Wheat Composite 2004 map. (*) and (**) indicate loci associated with kernel traits at αc = 0.05 and αc = 0.01, respectively. In the triangles, black, dark shading, and light shading indicate comparison-wise significance of r2 at P < 0.0001, P < 0.001, P < 0.01, respectively.

Twenty markers were tested on chromosome 5A, 14 of them in the centromeric region. Pairwise r2 estimates varied from 0.000 to 0.909, with a median of 0.053. Considering the baseline of 0.065, the extent of LD in this part of chromosome 5A was ∼5 cM (Figure 3). This extensive LD is due to an LD block observed in the centromeric region of 5A, including 11 loci within 6 cM (positions 53–59 cM, Figure 4). At distances >5 cM most of the pairwise LD estimates were within the distribution of unlinked r2. Significant r2 estimates observed >20 cM were due to Xgwm154-5A, which was in LD with the centromeric region, although it is positioned 19 cM away from Xbarc197-5A at the end of the LD block. The break in LD at Xbarc186-5A may have been caused by the low polymorphism of this locus (effective allele no. 1.46).

Phenotypic data:

Kernel morphology was evaluated in NY and OH, whereas milling quality was evaluated in OH for a variable number of years (Table 2). Break-flour yield required transformation [log(x)] to achieve normality. Kernel size was larger in NY than in OH, probably because of more favorable weather conditions in the NY environment. According to the intraclass correlation coefficient, population structure accounted for >20% of the phenotypic variation of kernel area and weight and >30% of the variation in kernel length. Kernel width and milling traits were less affected by population subdivisions.

TABLE 2.

Summary statistics of kernel morphology and milling quality traits

Trait Location Unit Mean Standard deviation Minimum Maximum P-value of normality testa Intraclass correlation coefficientb
KW NY mg 53.53 4.171 44.98 64.95 0.213 0.288
OH mg 43.07 3.871 35.39 52.45 0.255 0.218
AREA NY mm2 21.23 1.269 18.38 25.24 0.334 0.271
OH mm2 17.73 1.194 15.24 20.32 0.394 0.252
LEN NY mm 7.038 0.329 6.186 7.807 0.983 0.305
OH mm 6.628 0.350 5.794 7.383 0.267 0.351
WID NY mm 3.838 0.101 3.618 4.161 0.051 0.114
OH mm 3.403 0.100 3.191 3.672 0.854 0.039
MS OH % 68.54 11.69 39.32 97.81 0.855 0.046
FY OH % 77.22 1.135 74.35 80.03 0.992 0.027
FRIA OH % 28.70 1.342 25.10 31.87 0.193 0.105
ESI OH % 9.632 1.314 6.63 13.10 0.693 0.001
BFYc OH % 31.57 3.882 24.50 42.20 0.605 0.005
Open in a new tab
a

Shapiro–Wilk test.

b

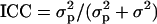Inline graphic, where 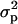Inline graphic is the variance among subpopulations and σ2 is the residual variance (Neter et al. 1996).

c

Analyzed as log-transformed data.

The results of the analysis of variance of kernel size traits (Table 3) confirmed that location had a large effect on kernel size, whereas the interaction location × cultivar was small. ANOVA within locations indicated that differences among cultivars were highly significant in both environments, compared to the interaction cultivar × replicate (within-location error). Kernel weight, area, length, and width had heritabilities of 0.73, 0.77, 0.82, and 0.55, respectively, indicating that there was more error in the evaluation of kernel width than the other kernel morphology traits.

TABLE 3.

Mean squares of the analysis of variance of kernel size measurements in two locations

Source of variation d.f. Weight Area Length Width
ANOVA over locations
Location 1 7289.7** 906.7** 12.49** 14.09**
Replicate/Location 2 10.61 15.14** 0.258** 0.248**
Cultivar 94 47.04** 4.406** 0.337** 0.027**
Location × Cultivar 94 4.366 0.445** 0.022* 0.005
Error 109 4.034 0.266 0.015 0.004
r2 of the model 0.965 0.980 0.967 0.975
ANOVA per location
Replicate/NY 1 17.79 10.74** 0.023 0.265**
Cultivar/NY 94 32.37** 3.031** 0.206** 0.020**
Error 86 4.588 0.300 0.017 0.004
r2 of the model/NY 0.886 0.920 0.930 0.847
Replicate/OH 1 3.427 19.54** 0.492** 0.231**
Cultivar/OH 94 19.04** 1.821** 0.153** 0.012**
Error 23 1.959 0.136 0.006 0.003
r2 of the model/OH 0.975 0.984 0.991 0.957
Open in a new tab

*, ** indicate significance at the probability levels of 0.05 and 0.01, respectively.

The cultivars used in this study represented a broad variation in milling quality. Correlations between kernel morphology and milling quality were low (Table 4). The few significant correlations indicated that larger kernels tended to be associated with a superior milling score, higher flour yield and friability, and lower endosperm separation index. Kernel length was more correlated with milling traits than kernel width.

TABLE 4.

Pearson correlation coefficients between kernel morphology and milling quality traits

Trait Location Milling score Flour yield Endosperm separation index Friability Break- flour yield
KW NY 0.180 0.187 −0.177 0.151 −0.148
OH 0.226* 0.232* −0.207* 0.205* −0.126
AREA NY 0.204* 0.187 −0.194 0.201 −0.117
OH 0.172 0.151 −0.139 0.195 −0.010
LEN NY 0.219* 0.188 −0.190 0.243* −0.133
OH 0.178 0.141 −0.140 0.219* −0.021
WID NY 0.069 0.087 −0.098 0.019 −0.038
OH 0.076 0.096 −0.066 0.055 −0.005
Open in a new tab
*

indicates significance at the probability level 0.05.

Association mapping:

The hypothesis of association of SSR markers with kernel traits in the presence of population structure was tested through a mixed-effects linear model. Significance thresholds corrected for multiple testing within chromosomes were approximately proportional to the reciprocals of the number of markers tested in each chromosome. Consequently, the power of the hypothesis tests was highest in 5B, intermediate in 5A, and lowest on 2D.

Significant markers were detected in the three chromosomes tested (Table 5). Kernel width was associated with the locus Xwmc111-2D in both NY and OH and with Xgwm30-2D in NY only. A two-marker model including both loci was significantly (P = 0.0002) more informative for KW in NY than either marker separately, indicating that the information from those markers is not redundant. The locus Xgwm539-2D was associated with kernel length in NY, and possibly in OH, although in this location it did not achieve the corrected threshold.

TABLE 5.

Comparison-wise P-values of association of SSR loci with kernel morphology traits

Locus
KW
AREA
LEN
WID
Chromosome cM Name NY OH NY OH NY OH NY OH
2D 7 Xcfd56 0.069 0.160 0.012 0.119 0.076 0.031 0.000** 0.252
11 Xwmc111 0.005 0.020 0.005 0.108 0.003* 0.107 0.000** 0.000***
23 Xgwm261 0.145 0.016 0.019 0.009 0.027 0.009 0.058 0.001**
28 Xwmc112 0.012 0.057 0.047 0.120 0.480 0.367 0.001** 0.024
64 Xgwm30 0.081 0.862 0.053 0.848 0.312 0.820 0.000*** 0.212
91 Xgwm539 0.042 0.038 0.030 0.039 0.001** 0.005 0.290 0.334
5A 55 Xcfa2250 0.021 0.007 0.044 0.014 0.014 0.002** 0.637 0.649
55 Xwmc150b 0.002** 0.003* 0.003* 0.005* 0.009 0.002** 0.093 0.429
56 Xbarc117 0.009 0.002** 0.021 0.005 0.118 0.022 0.044 0.039
60 Xbarc141 0.631 0.037 0.232 0.024 0.038 0.002** 0.852 0.863
5B 48 Xcfa2121b 0.785 0.053 0.525 0.039 0.289 0.245 0.290 0.005**
66 Xbarc89 0.651 0.110 0.791 0.118 0.518 0.159 0.003** 0.070
129 Xbarc308 0.041 0.000*** 0.117 0.000*** 0.461 0.001*** 0.049 0.005**
134 Xbarc232 0.016 0.001*** 0.005* 0.003** 0.064 0.002** 0.090 0.551
Open in a new tab

Only markers significant at the multiple testing-corrected significance level αc = 0.05 for at least one trait are shown. *, **, *** indicate significance at αc = 0.10, 0.05, and 0.01, respectively.

Six loci in the LD block near the centromere of 5A were associated with kernel area, length, and weight, but not with kernel width. The most significant locus in this region was Xwmc150b-5A, and no other locus within the LD block could add significant information, according to the likelihood-ratio test. However, a model including Xwmc150b-5A and Xbarc141-5A was significantly (P = 0.0002) better than either marker alone.

On the long arm of chromosome 5B, Xbarc308 was strongly associated with kernel area, length, and weight in OH, but had no significant effect in NY. The marker Xbarc232 showed similar associations; however, it added no significant information to Xbarc308 in a two-marker model, indicating that both markers are probably in LD with the same QTL. The markers Xbarc308-5B and Xwmc150b-5A were simultaneously significant (P = 0.0075) for kernel length, as expected from markers located in different chromosomes.

Allele effects were estimated in comparison to the “null allele” (missing plus rare alleles) for each locus. Five cultivars with the allele A174 at Xgwm539-2D produced significantly shorter kernels than lines carrying other alleles. Kernels of 45 lines with A270 at Xwmc150b-5A were longer, on average, than those of 41 lines with A248. At Xbarc308-5B, lines carrying A278 produced significantly longer kernels than lines with A280, but only in OH. Greater kernel width was associated with A246 at Xwmc111-2D (14 cultivars) and with A217 at Xgwm30-2D (24 cultivars), especially in NY. The allele A221 at Xgwm30-2D was associated with opposite effects for kernel width in each environment. Associations with kernel weight were similar to those observed for kernel length. For those traits, the locus Xwmc150b-5A had approximately the same effect in both environments, whereas Xbarc308-5B had a more pronounced effect in OH than in NY (Figure 5).

Figure 5.

Figure 5.

Open in a new tab

Phenotypic effect of marker alleles at loci significantly associated with kernel length, width, and weight in NY and OH.

Milling traits had fewer significant associations than kernel morphology (Table 6). Only weak associations (αc < 0.10) were detected on chromosome 2D. The locus Xcfa2250-5A was associated with friability and with kernel length, which could explain part of the correlation between those traits. Xbarc142-5B was moderately associated with break-flour yield, which is a parameter of kernel texture. The locus Xbarc232-5B showed the most significant associations with milling traits, including milling score, endosperm separation index, and friability. This locus was significantly associated with kernel size in OH. Although Xbarc308-5B was similarly associated with kernel size, it had no influence on milling quality.

TABLE 6.

Comparison-wise P-values of association of SSR loci with milling quality traits

Chromosome cM Locus Milling score Flour yield Endosperm separation index Friability Break-flour yield
2D 23 Xgwm261 0.008 0.052 0.019 0.003* 0.523
2D 41 Xgwm484 0.022 0.039 0.003* 0.130 0.886
2D 85 Xwmc181 0.003* 0.003* 0.007 0.006 0.607
5A 55 Xcfa2250 0.010 0.029 0.047 0.002** 0.081
5B 130 Xbarc142 0.616 0.877 0.763 0.325 0.009*
5B 134 Xbarc232 0.002** 0.005* 0.002** 0.003** 0.199
Open in a new tab

Only markers significant at the multiple-test corrected significance level αc = 0.10 for at least one trait are shown. *, ** indicate significance at αc = 0.10 and 0.05, respectively.

DISCUSSION

We applied AM in wheat for identification of genetic markers associated with kernel morphology and milling quality. The experimental material was representative of the current elite breeding pool of soft winter wheat in the eastern United States. The presence of closely related individuals in the sample violates the assumptions of the algorithm of Structure (Pritchard and Wen 2003) and inflates LD among unlinked loci; therefore, a preselection of cultivars was necessary. Exclusion of closely similar entries (“normalization”) provided near independence among unlinked loci, so that significant correlations could be interpreted as evidence of genetic linkage. This result showed that the level of LD observed is highly dependent on the sampling scheme.

Consensus maps were needed for our study, because in this type of population, locus position could not be inferred from segregation analysis. Although consensus maps inherently contain errors in marker order and linkage distance, the pattern of LD detected was relatively coherent with consensus marker positions (Somers et al. 2004). The hexaploid nature of the wheat genome introduced an additional difficulty for AM compared to other crops with less complex genomes. A number of markers amplified multiple bands or had been mapped to multiple chromosomes in previous studies. Those markers required testing on special genetic stocks to confirm chromosome assignment. Because of the narrow genetic base sampled, we did not expect amplification of different homoeologous loci in different cultivars, but this might be a reason for some concern in studies involving wide genetic variability in wheat.

SSR allele diversity:

Even though our sample was restricted to elite soft wheat, the level of polymorphism detected was relatively high, with as many as 10 putative alleles detected at some loci and an average of 4.8 alleles per locus. A similar number of alleles was found for 60 hexaploid wheat cultivars from Eastern Europe, genotyped at 42 SSR loci (Stachel et al. 2000). Other estimates of mean allele number per locus from previous studies using SSR markers on more diverse germplasm were: 5.6 alleles at 70 loci on 58 durum cultivars of diverse geographical origins, including old cultivars (Maccaferri et al. 2003); 10.5 alleles at 19 loci on 502 European hexaploid wheat varieties (Röder et al. 2002); and 18.1 alleles at 26 loci on 998 accessions of hexaploid wheat from the IPK gene bank in Germany (Huang et al. 2002). Therefore, the SSR allele diversity found in our sample was approximately half of the total diversity found in European wheat elite germplasm, or a quarter of the diversity found in a wheat germplasm repository.

Our estimates of SSR allele diversity in wheat were comparable to estimates reported for other grasses, when the sampling breadth is considered. Lu et al. (2005) found, on average, 5.15 alleles per locus within a group of 136 elite japonica rice cultivars, or 6.57 alleles if nine indica varieties were included. In a more diverse panel, composed of 236 rice varieties of indica and japonica types, an average of 11.9 alleles was detected at 60 SSR loci (Xu et al. 2005). In 198 accessions of African cultivated rice (Oryza glaberrima Steud.), Semon et al. (2005) reported an average of 9.4 alleles on 93 SSR loci. A panel of 102 maize inbred lines of both temperate and tropical origins comprised on average 6.85 alleles per SSR locus at 47 loci selected for high polymorphism (Remington et al. 2001).

The sample size used in our study is relatively large compared to previous LD studies in plants (Tenaillon 2001; Nordborg et al. 2002; Zhu et al. 2003). However, there is justification for using even larger sample sizes in future AM studies. Most loci presented one or more alleles with fewer than five occurrences, which were pooled with missing data. A larger sample size would both increase detection power and allow the quantification of the effect of more alleles that, although still at low frequency, would have enough counts to be used in their own identity for association analysis.

The effective allele number was relatively close to the number of common alleles, indicating that in most cases none of the alleles was highly predominant. This was in part attributed to the normalization of the sample. The reduction of the imbalance in the data through previous selection of the sample was beneficial to the association analysis; however, allele frequencies in the normalized sample are not directly representative of the actual frequencies in the population.

Linkage disequilibrium:

Previous studies considered the extent of LD as the genetic or physical distance taken for a decay of r2 to an arbitrary value, normally 0.10 (Remington et al. 2001; Nordborg et al. 2002; Palaisa et al. 2003). We propose that the extent of useful LD should be defined in comparison to the LD observed among unlinked loci in the sample, which we demonstrated to be highly dependent on the sampling scheme. The 95th percentile of the distribution of unlinked-r2 estimates sets a sample-specific critical value, which we call “baseline LD,” and the point where the line defined by the regression of syntenic LD intersects this baseline defines the extent of LD attributable to linkage. We recognized that unlinked-LD estimates were not independent and this could skew its distribution, but this should not pose a significant problem if a sufficiently large number of unlinked markers are used. The primary advantage of this method is that the unlinked-LD distribution incorporates the effects of population structure and selection in the experimental material.

Two contrasting LD levels were detected in this study: ∼5 cM in the centromeric region of 5A and <1 cM on average on chromosome 2D. In either case, LD in soft wheat measured in this study was far higher than LD found in maize, which decayed to r2 = 0.10 at a distance of ∼1 kb (Remington et al. 2001; Tenaillon 2001; Palaisa et al. 2003). For comparison, considering the wheat genome physical size as 16 Gb (Aragumuganathan and Earle 1991) and the total length of the genetic map of 2569 cM (Somers et al. 2004), 1 cM in the scale used in this study corresponded on average to >6000 kb.

Probably the most important cause for this difference of more than three orders of magnitude in LD estimates is the mating system, which is outcrossing in maize, while wheat is almost completely self-pollinating. Inbreeding drives lineages to homozygosity and renders recombinations ineffective in breaking down LD. Another likely cause is the narrow elite germplasm sampled in our study, as opposed to samples planned to represent worldwide variation. In agreement with that, in 36 U. S. elite maize inbreds, Ching et al. (2002) found no significant LD decay within genes. Finally, Slatkin (1994) demonstrated that multi-allelic markers are more likely to give significant LD estimates. Hence, comparison of LD estimates between studies using SSR markers and studies using biallelic SNPs may include a bias. This could partially explain why Remington et al. (2001) found proportionally higher estimates of LD at long distances between SSR markers than at short distances between SNPs.

In a panel of 20 diverse genotypes of the selfing species Arabidopsis thaliana, LD was estimated to decay to r2 = 0.10 within ∼250 kb in the region of the FRI gene (Nordborg et al. 2002). This physical distance represents ∼1 cM in Arabidopsis, which is comparable to our results for chromosome 2D. In the genomic region of the resistance gene xa5 in rice, r2 > 0.10 persisted at >100 kb (Garris et al. 2003). Sorghum may represent an intermediate situation between selfing species and maize in terms of LD level (Hamblin et al. 2004). High LD at distances up to 10 cM was found among AFLP loci in barley cultivars (Kraakman et al. 2004); however, those results are not directly comparable with ours, because of the normalization done in our sample, which drastically reduced overall LD.

Some hypotheses can be presented to explain the buildup of the LD block on 5A. A possible explanation is that recombination is less frequent around the centromere (Jones et al. 2002). However, according to the consensus map, the centromere is adjacent to the LD block (between Xgwm304 and Xbarc141), rather than embedded in it. Additionally, no similar LD block was detected in the centromeric region of 2D. Another possible cause for the extensive LD in 5A could be artificial selection in the breeding programs, which could account for the apparent reduction in allele diversity in that region (supplemental Table 2 at http://www.genetics.org/supplemental/). Reduction of genetic variability was observed in the region of the Y1 gene in maize, which has been strongly selected for the yellow endosperm characteristic (Palaisa et al. 2004). One of the highest LD estimates reported in the literature was found in Dutch dairy cattle (Farnir et al. 2000), where r2 was >0.10 even for unlinked loci. Elite cattle are known to be subject to extreme selection pressure. Yet another possible explanation for the LD block on 5A would be the loss of variability during domestication, in which case the LD block should exist in other wheat classes as well. An important domestication-related QTL that affected grain weight, grain number per spike, plant height, heading date, and yield per plant has been detected in this region (Peng et al. 2003).

The two levels of LD identified in our study point to contrasting scenarios for AM. If LD blocks like the one observed in 5A were common, a scan with marker intervals of 5 cM would have a reasonable chance of detecting major QTL at a coarse resolution. However, if the level of LD observed on 2D proves to be more representative of the genome, more than one marker per centimorgan would be needed to achieve a reasonable power of detection. This scenario would be favorable for fine mapping of QTL within previously defined confidence intervals. Furthermore, the extent of LD over the wheat genome is likely to be specific to the type of population studied.

Association mapping:

We focused on chromosomes 2D and 5A/5B because of previous evidence of QTL for kernel size on those linkage groups (F. Breseghello and M. E. Sorrells, unpublished results). Several loci on those chromosomes were significant at the comparison-wise level. However, permutation analysis showed that low P-values were frequently obtained by chance, resulting in very strict thresholds. We defined independent thresholds for each chromosome, since chromosomes had been selected on the basis of previous, independent data. In this way, QTL information helped to improve the power of AM.

We detected significant association of kernel width in both environments with Xwmc111 and in OH with Xgwm261 (Table 5), 12 cM apart on the short arm of 2D. Dholakia et al. (2003) detected a QTL for kernel size in bread wheat near Xgwm261. Our population did not allow a precise location of this QTL because LD was relatively high in this genomic region (Figure 4).

The loci Xgwm30, Xwmc18, and Xgwm515a are located within 1 cM of the centromere of 2D. Xgwm30 was associated with kernel width in NY at high significance; Xwmc18 was near the most important QTL for kernel cross section in the mapping population AC Reed × Grandin (F. Breseghello and M. E. Sorrells, unpublished results) and Xgwm515 has been related to kernel weight (Dholakia et al. 2003). The association of kernel width with Xgwm30 and not with other closely linked markers can be interpreted as improved resolution of AM compared to QTL analysis. However, other factors related to marker and gene allele frequencies and initial LD in the breeding population could explain those results as well.

Pleiotropic effects of major genes could alter the pattern of association of quantitative traits with molecular markers. Coventry et al. (2003) showed that kernel size QTL in barley were frequently collocated with developmental genes. Known genes that possibly could have indirect effects on kernel size include (but are not limited to): Rht8 (reduced height) and Ppd1 (response to photoperiod) on chromosome 2D, and on 5A, B1 (awnedness inhibitor), Rht12 (reduced height), and Vrn1 (response to vernalization) (McIntosh et al. 1995). The three genes on 5A are located near the end of the long arm (Wheat Composite 2004 map, GrainGenes, http://wheat.pw.usda.gov/GG2) in a region not covered by this study.

In this study we found significant associations between kernel traits and SSR markers in elite wheat germplasm, while controlling false positives potentially deriving from population structure and multiple testing. From these results, a simple but essential step of confirmation would be required for individual cultivars involved in crosses before marker-assisted selection can be applied to the progeny: e.g., F2 plants could be genotyped and F3 progeny could be phenotyped to confirm the effect associated with the marker locus. Confirmation is necessary because the marker alleles are correlated with, but not entirely predictive of, the gene alleles. This study demonstrated that association mapping in elite germplasm can enhance the information from QTL studies toward the implementation of marker-assisted selection.

Acknowledgments

We thank the USDA Soft Wheat Quality Laboratory in Wooster, Ohio, for the wheat milling quality data. We thank the studentship granted to F. Breseghello by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (Brazil). Financial support was also provided by the U.S. Department of Agriculture (USDA) Hatch Project 149419.

References

  1. Andrews, L., and C. Gaines, 2002. Quality Characteristics of Soft Wheat Cultivars. USDA-ARS Soft Winter Wheat Quality Laboratory, Wooster, OH.
  2. Aragumuganathan, K., and E. D. Earle, 1991. Nuclear DNA content of some important plant species. Plant Mol. Biol. Rep. 9: 208. [Google Scholar]
  3. Belkhir, K., P. Borsa, L. Chikhi, N. Raufaste and F. Bonhomme, 1996–2004. GENETIX 4.05, logiciel sous Windows pour la génétique des populations. Université de Montpellier II, Montpellier, France.
  4. Benzécri, J. P., 1973. L'Analyse des Données: T. 2, L'Analyse des correspondances. Dunod, Paris.
  5. Carlson, C. S., M. A. Eberle, L. Kruglyak and D. A. Nickerson, 2004. Mapping complex disease loci in whole-genome association studies. Nature 429: 446–452. [DOI] [PubMed] [Google Scholar]
  6. Ching, A., K. S. Caldwell, M. Jung, M. Dolan, O. S. Smith et al., 2002. SNP frequency, haplotype structure and linkage disequilibrium in elite maize inbred lines. BMC Genet. 3: 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cleveland, W. S., 1979. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 74: 829–836. [Google Scholar]
  8. Coventry, S. J., A. R. Barr, J. K. Eglinton and G. K. McDonald, 2003. The determinants and genome locations influencing grain weight and size in barley (Hordeum vulgare L.). Aust. J. Agric. Res. 54: 1103–1115. [Google Scholar]
  9. Dholakia, B. B., J. S. S. Ammiraju, H. Singh, M. D. Lagu, M. S. Roder et al., 2003. Molecular marker analysis of kernel size and shape in bread wheat. Plant Breed. 122: 392–395. [Google Scholar]
  10. Falush, D., M. Stephens and J. K. Pritchard, 2003. Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Farnir, F., W. Coppieters, J. J. Arranz, P. Berzi, N. Cambisano et al., 2000. Extensive genome-wide linkage disequilibrium in cattle. Genome Res. 10: 220–227. [DOI] [PubMed] [Google Scholar]
  12. Garris, A. J., S. R. McCouch and S. Kresovich, 2003. Population structure and its effect on haplotype diversity and linkage disequilibrium surrounding the xa5 locus of rice (Oryza sativa L.). Genetics 165: 759–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gupta, P. K., H. S. Balyan, K. J. Edwards, P. Isaac, V. Korzun et al., 2002. Genetic mapping of 66 new microsatellite (SSR) loci in bread wheat. Theor. Appl. Genet. 105: 413–422. [DOI] [PubMed] [Google Scholar]
  14. Guyomarc'h, H., P. Sourdille, G. Charmet, K. Edwards and M. Bernard, 2002. Characterization of polymorphic microsatellite markers from Aegilops tauschii and transferability to the D-genome of bread wheat. Theor. Appl. Genet. 104: 1164–1172. [DOI] [PubMed] [Google Scholar]
  15. Hamblin, M. T., S. E. Mitchell, G. M. White, J. Gallego, R. Kukatla et al., 2004. Comparative population genetics of the Panicoid grasses: sequence polymorphism, linkage disequilibrium and selection in a diverse sample of Sorghum bicolor. Genetics 167: 471–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hartl, D., and A. Clark, 1997. Principles of Population Genetics. Sinauer Associates, Sunderland, MA.
  17. Huang, X. Q., A. Borner, M. S. Röder and M. W. Ganal, 2002. Assessing genetic diversity of wheat (Triticum aestivum L.) germplasm using microsatellite markers. Theor. Appl. Genet. 105: 699–707. [DOI] [PubMed] [Google Scholar]
  18. Jannink, J. L., M. Bink and R. C. Jansen, 2001. Using complex plant pedigrees to map valuable genes. Trends Plant Sci. 6: 337–342. [DOI] [PubMed] [Google Scholar]
  19. Jones, L. E., K. Rybka and A. J. Lukaszewski, 2002. The effect of a deficiency and a deletion on recombination in chromosome 1BL in wheat. Theor. Appl. Genet. 104: 1204–1208. [DOI] [PubMed] [Google Scholar]
  20. Kennedy, B. W., M. Quinton and J. A. M. Vanarendonk, 1992. Estimation of effects of single genes on quantitative traits. J. Anim. Sci. 70: 2000–2012. [DOI] [PubMed] [Google Scholar]
  21. Kraakman, A. T. W., R. E. Niks, P. Van den Berg, P. Stam and F. A. Van Eeuwijk, 2004. Linkage disequilibrium mapping of yield and yield stability in modern spring barley cultivars. Genetics 168: 435–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Lu, H., M. A. Redus, J. R. Coburn, J. N. Rutger, S. R. McCouch et al., 2005. Population structure and breeding patterns of 145 US rice cultivars based on SSR marker analysis. Crop Sci. 45: 66–76. [Google Scholar]
  23. Lynch, M., and K. Ritland, 1999. Estimation of pairwise relatedness with molecular markers. Genetics 152: 1753–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Maccaferri, M., M. C. Sanguineti, P. Donini and R. Tuberosa, 2003. Microsatellite analysis reveals a progressive widening of the genetic basis in the elite durum wheat germplasm. Theor. Appl. Genet. 107: 783–797. [DOI] [PubMed] [Google Scholar]
  25. Matthews, D. E., V. L. Carollo, G. R. Lazo and O. D. Anderson, 2003. GrainGenes, the genome database for small-grain crops. Nucleic Acids Res. 31: 183–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. McIntosh, R. A., G. E. Hart and M. D. Gale, 1995. Catalogue of gene symbols for wheat, pp. 1333–1500 in Proceedings of the 8th International Wheat Genetics Symposium, edited by Z. S. Li and Z. Y. Xin. China Agricultural Scientech Press, Beijing.
  27. Neter, J., M. H. Kutner, C. J. Nachtshein and W. Wasserman, 1996. Applied Linear Statistical Models. McGraw-Hill, New York.
  28. Nordborg, M., J. O. Borevitz, J. Bergelson, C. C. Berry, J. Chory et al., 2002. The extent of linkage disequilibrium in Arabidopsis thaliana. Nat. Genet. 30: 190–193. [DOI] [PubMed] [Google Scholar]
  29. Palaisa, K. A., M. Morgante, M. Williams and A. Rafalski, 2003. Contrasting effects of selection on sequence diversity and linkage disequilibrium at two phytoene synthase loci. Plant Cell 15: 1795–1806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Palaisa, K., M. Morgante, S. Tingey and A. Rafalski, 2004. Long-range patterns of diversity and linkage disequilibrium surrounding the maize Y1 gene are indicative of an asymmetric selective sweep. Proc. Natl. Acad. Sci. USA 101: 9885–9890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Peng, J., Y. Ronin, T. Fahima, M. S. Roder, Y. Li et al., 2003. Domestication quantitative trait loci in Triticum dicoccoides, the progenitor of wheat. Proc. Natl. Acad. Sci. USA 100: 2489–2494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Pinheiro, J. C., and D. M. Bates, 2000. Mixed-Effects Models in S and S-PLUS. Springer, New York.
  33. Pritchard, J. K., and W. Wen, 2003. Documentation for Structure Software, Version 2. Department of Human Genetics, University of Chicago, Chicago.
  34. Pritchard, J. K., M. Stephens and P. Donnelly, 2000. a Inference of population structure using multilocus genotype data. Genetics 155: 945–959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Pritchard, J. K., M. Stephens, N. A. Rosenberg and P. Donnelly, 2000. b Association mapping in structured populations. Am. J. Hum. Genet. 67: 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Rafalski, J. A., 2002. Novel genetic mapping tools in plants: SNPs and LD-based approaches. Plant Sci. 162: 329–333. [Google Scholar]
  37. Remington, D. L., J. M. Thornsberry, Y. Matsuoka, L. M. Wilson, S. R. Whitt et al., 2001. Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98: 11479–11484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Risch, N. J., 2000. Searching for genetic determinants in the new millennium. Nature 405: 847–856. [DOI] [PubMed] [Google Scholar]
  39. Ritland, K., 2000. Marker-inferred relatedness as a tool for detecting heritability in nature. Mol. Ecol. 9: 1195–1204. [DOI] [PubMed] [Google Scholar]
  40. Röder, M. S., V. Korzun, K. Wendehake, J. Plaschke, M. H. Tixier et al., 1998. A microsatellite map of wheat. Genetics 149: 2007–2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Röder, M. S., K. Wendehake, V. Korzun, G. Bredemeijer, D. Laborie et al., 2002. Construction and analysis of a microsatellite-based database of European wheat varieties. Theor. Appl. Genet. 106: 67–73. [DOI] [PubMed] [Google Scholar]
  42. Schuelke, M., 2000. An economic method for the fluorescent labeling of PCR products. Nat. Biotechnol. 18: 233–234. [DOI] [PubMed] [Google Scholar]
  43. Sears, E. R., 1966. Nullisomic-tetrasomic combinations in hexaploid wheat, pp. 29–45 in Chromosome Manipulation and Plant Genetics, edited by R. Riley and K. R. Lewis. Oliver & Boyd, Edinburgh.
  44. Semon, M., R. Nielsen, M. P. Jones and S. R. McCouch, 2005. The population structure of African cultivated rice Oryza glaberrima (Steud.): evidence for elevated levels of linkage disequilibrium caused by admixture with O. sativa and ecological adaptation. Genetics 169: 1639–1647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Simko, I., S. Costanzo, K. G. Haynes, B. J. Christ and R. W. Jones, 2004. Linkage disequilibrium mapping of a Verticillium dahliae resistance quantitative trait locus in tetraploid potato (Solanum tuberosum) through a candidate gene approach. Theor. Appl. Genet. 108: 217–224. [DOI] [PubMed] [Google Scholar]
  46. Slatkin, M., 1994. Linkage disequilibrium in growing and stable populations. Genetics 137: 331–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Somers, D. J., P. Isaac and K. Edwards, 2004. A high-density microsatellite consensus map for bread wheat (Triticum aestivum L.). Theor. Appl. Genet. 109: 1105–1114. [DOI] [PubMed] [Google Scholar]
  48. Song, Q. J., J. R. Shi, S. Singh, E. W. Fickus, J. M. Costa et al., 2005. Development and mapping of microsatellite (SSR) markers in wheat. Theor. Appl. Genet. 110: 550–560. [DOI] [PubMed] [Google Scholar]
  49. Stachel, M., T. Lelley, H. Grausgruber and J. Vollmann, 2000. Application of microsatellites in wheat (Triticum aestivum L.) for studying genetic differentiation caused by selection for adaptation and use. Theor. Appl. Genet. 100: 242–248. [Google Scholar]
  50. Tenaillon, M. I., 2001. Patterns of DNA sequence polymorphism along chromosome 1 of maize (Zea mays ssp. mays L.). Proc. Natl. Acad. Sci. USA 98: 9161–9166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Thornsberry, J. M., M. M. Goodman, J. Doebley, S. Kresovich, D. Nielsen et al., 2001. Dwarf8 polymorphisms associate with variation in flowering time. Nat. Genet. 28: 286–289. [DOI] [PubMed] [Google Scholar]
  52. Weir, B. S., and C. C. Cockerham, 1984. Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370. [DOI] [PubMed] [Google Scholar]
  53. Xu, Y., H. Beachell and S. R. McCouch, 2005. A marker-based approach to broadening the genetic base of rice in the USA. Crop Sci. 44: 1947–1959. [Google Scholar]
  54. Yamazaki, W. T., and L. C. Andrews, 1977. Experimental milling of soft wheat cultivars and breeding lines. Cereal Chem. 59: 41–45. [Google Scholar]
  55. Yu, J. K., M. La Rota, R. V. Kantety and M. E. Sorrells, 2004. EST derived SSR markers for comparative mapping in wheat and rice. Mol. Genet. Genomics 271: 742–751. [DOI] [PubMed] [Google Scholar]
  56. Zhu, Y. L., Q. J. Song, D. L. Hyten, C. P. Van Tassell, L. K. Matukumalli et al., 2003. Single-nucleotide polymorphisms in soybean. Genetics 163: 1123–1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zondervan, K. T., and L. R. Cardon, 2004. The complex interplay among factors that influence allelic association. Nat. Rev. Genet. 5: 89–100. [DOI] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES