Abstract
In 1990, Frank Wright introduced a method for measuring synonymous codon usage bias in a gene by estimation of the “effective number of codons,” Nc. Several attempts have been made recently to improve Wright's estimate of Nc, but the methods that work in cases where a gene encodes a protein not containing all amino acids with degenerate codons have not been tested against each other. In this article I derive five new estimators of Nc and test them together with the two published estimators, using resampling under rigorous testing conditions. Estimation of codon homozygosity, F, turns out to be a key to the estimation of Nc. F can be estimated in two closely related ways, corresponding to sampling with or without replacement, the latter being what Wright used. The Nc methods that are based on sampling without replacement showed much better accuracy at short gene lengths than those based on sampling with replacement, indicating that Wright's homozygosity method is superior. Surprisingly, the methods based on sampling with replacement displayed a superior correlation with mRNA levels in Escherichia coli.
NONRANDOM usage of synonymous codons is a phenomenon that has been studied in a wide range of life forms. Often, the biased usage of synonymous codons is caused by translational selection; i.e., highly expressed genes tend to have a set of codons corresponding to the more abundant tRNA species (Ikemura 1981, 1985; Gouy and Gautier 1982). The study of this phenomenon relies on quantification of the codon usage bias, and for this purpose several one-dimensional statistics have been proposed (reviewed by Comeron and Aguade 1998). Frank Wright introduced an intuitive measure of codon in 1990, termed the “effective number of codons” (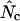 ) used in a gene. The idea is simple: one assigns to a gene a number between 20 and 61 that tells to what degree the entire genetic code is used. A value of 20 indicates that just one codon is used for each amino acid (extreme bias), while a value of 61 indicates that all codons are used equally (no bias). To calculate
) used in a gene. The idea is simple: one assigns to a gene a number between 20 and 61 that tells to what degree the entire genetic code is used. A value of 20 indicates that just one codon is used for each amino acid (extreme bias), while a value of 61 indicates that all codons are used equally (no bias). To calculate  for a gene, one needs to have knowledge about the codon “homozygosity” (
for a gene, one needs to have knowledge about the codon “homozygosity” ( , explained in the appendix) for individual amino acids. For individual amino acids
, explained in the appendix) for individual amino acids. For individual amino acids 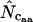 is given by
is given by 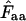 −1. Wright's formula was
−1. Wright's formula was
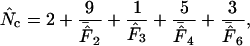 |
(1) |
where  denotes the average homozygosity for the class with i synonymous codons. The coefficients 9, 1, 5, and 3 come from the number of amino acids belonging to the different classes. Since exactly one codon is used by methionine and tryptophan, they have by definition always one effective codon each, so two are added without further calculation. Note that there is averaging involved in this formula; some genes encode proteins in which not all amino acids are present (or present in such low counts that calculation is problematic, see later), and in such cases the
denotes the average homozygosity for the class with i synonymous codons. The coefficients 9, 1, 5, and 3 come from the number of amino acids belonging to the different classes. Since exactly one codon is used by methionine and tryptophan, they have by definition always one effective codon each, so two are added without further calculation. Note that there is averaging involved in this formula; some genes encode proteins in which not all amino acids are present (or present in such low counts that calculation is problematic, see later), and in such cases the 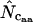 needs to be appropriately approximated. In Wright's original method, the problem of missing amino acids was solved by assuming that the
needs to be appropriately approximated. In Wright's original method, the problem of missing amino acids was solved by assuming that the 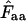 -value of the missing amino acid is equal to the mean of the
-value of the missing amino acid is equal to the mean of the 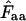 -values of the other amino acids belonging to the same degeneracy class. For example, if in a gene we have alanine and glycine codons missing, it is assumed that their
-values of the other amino acids belonging to the same degeneracy class. For example, if in a gene we have alanine and glycine codons missing, it is assumed that their  -values are equal to the mean of the
-values are equal to the mean of the  -values for proline, threonine, and valine, giving an
-values for proline, threonine, and valine, giving an 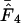 that is based on three values. Recently, it was shown that in Escherichia coli there is a poor correlation between the
that is based on three values. Recently, it was shown that in Escherichia coli there is a poor correlation between the  -values within a degeneracy class, so using the average of the
-values within a degeneracy class, so using the average of the  -values generally gives a rather poor estimate (Fuglsang 2004). In the same work it was illustrated how this type of averaging may lead to a systematic underestimation of
-values generally gives a rather poor estimate (Fuglsang 2004). In the same work it was illustrated how this type of averaging may lead to a systematic underestimation of  ; this happens when there is “bias discrepancy,” which was qualitatively defined as the phenomenon of observing a strong bias for one amino acid while observing weak bias for another amino acid having the same degeneracy. That work ended up in a proposal about adding individual
; this happens when there is “bias discrepancy,” which was qualitatively defined as the phenomenon of observing a strong bias for one amino acid while observing weak bias for another amino acid having the same degeneracy. That work ended up in a proposal about adding individual  -values, yielding an estimator called
-values, yielding an estimator called 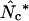 , and a simulation study suggested this to be a safe choice in long genes. Marashi and Najafabadi (2004) pointed out a potential weakness in the methodology since there is a chance that the individual
, and a simulation study suggested this to be a safe choice in long genes. Marashi and Najafabadi (2004) pointed out a potential weakness in the methodology since there is a chance that the individual 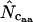 -values exceed the degeneracy. This has to do with the way
-values exceed the degeneracy. This has to do with the way  is calculated. I here refer the reader to the appendix, in which I have described the two methods for
is calculated. I here refer the reader to the appendix, in which I have described the two methods for  calculation. Wright's way of calculating
calculation. Wright's way of calculating  (A2) can be viewed as involving sampling without replacement, while an alternative formula (A1) can be viewed as involving sampling with replacement. The latter was then proposed to be useful in an estimator called
(A2) can be viewed as involving sampling without replacement, while an alternative formula (A1) can be viewed as involving sampling with replacement. The latter was then proposed to be useful in an estimator called  (Fuglsang 2005), which also was based on addition of all individual
(Fuglsang 2005), which also was based on addition of all individual  -values. Although this estimator would converge toward the “true” Nc value with increasing gene lengths, the problem of missing amino acids was not solved, as Banerjee et al. (2005) pointed out. They therefore suggested an estimator that combined Wright's way of averaging within degeneracy classes with the
-values. Although this estimator would converge toward the “true” Nc value with increasing gene lengths, the problem of missing amino acids was not solved, as Banerjee et al. (2005) pointed out. They therefore suggested an estimator that combined Wright's way of averaging within degeneracy classes with the  -calculation based on sampling with replacement, but they did not test their idea in a controlled experiment.
-calculation based on sampling with replacement, but they did not test their idea in a controlled experiment.
As mentioned earlier averaging is associated with a systemic error if there is bias discrepancy, and since this is apparently often the case (see Fuglsang 2005), I believe there is a need for an estimator that is resistant to bias discrepancy, preferably one that is also capable of handling missing amino acids.
The purpose of this article is to suggest such estimators. I introduce some new ideas about how to handle the problem of missing amino acids, giving rise to five new estimators. The best way to test the behavior of such bias estimates is to test them under conditions that can be fully controlled. This can be achieved by simulation/resampling (Wright 1990; Comeron and Aguade 1998; Fuglsang 2004, 2005). Here, all of the six methods that allow estimation of Nc when amino acids are missing (or present in too low an amount to allow calculation of 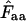 ) are tested by resampling. Finally, in a recent article a surprisingly good correlation was observed between
) are tested by resampling. Finally, in a recent article a surprisingly good correlation was observed between  and mRNA levels in E. coli. The new estimates are tested in a similar fashion for their correlation with mRNA levels in E. coli. It should be noted here that
and mRNA levels in E. coli. The new estimates are tested in a similar fashion for their correlation with mRNA levels in E. coli. It should be noted here that  and
and  will not receive any focus in this article, since these methods require that no amino acids are missing.
will not receive any focus in this article, since these methods require that no amino acids are missing.
To avoid too much further confusion and word clutter, all estimators tested in this work are given unique subscripts, and Wright's estimator in the following is referred to as  while the method of Banerjee et al. (2005) is referred to as
while the method of Banerjee et al. (2005) is referred to as 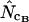 .
.
MATERIALS AND METHODS
Derivation of an N̂c based on degeneracy usage:
We might want to incorporate as much knowledge about codon bias as possible in estimates for codon bias for missing amino acids. Let us consider the degree by which the codons for a given amino acid represent full usage of all synonymous alternatives. In the following this is referred to as “degeneracy usage” (DU). If only one codon is used then DU is 0.0 (zero percent, synonymous alternatives are not used at all), but if all degenerate codons are used equally DU will be 1.0 (100% usage of the synonymous alternatives).
The general formula for estimating DU is
 |
(2) |
where Degaa is the degeneracy. Note the caret symbol:  is an estimate. A
is an estimate. A  -value can be obtained for all amino acids for which
-value can be obtained for all amino acids for which 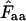 and thereby
and thereby 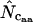 can be calculated. The average of the
can be calculated. The average of the  -values (
-values (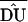 ) can then be used to estimate a
) can then be used to estimate a  -value for each missing amino acid, by rearranging Equation 2. Thus, for all amino acids other than methionine and tryptophan (for which we by definition set
-value for each missing amino acid, by rearranging Equation 2. Thus, for all amino acids other than methionine and tryptophan (for which we by definition set 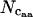 = 1), we have
= 1), we have
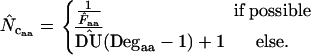 |
(3) |
From this we will always be able to summarize an  :
:
 |
(4) |
In other words, the  -value for missing amino acids is approximated through knowledge of the average codon bias. In principle this resembles the original method by Wright, but in contrast to his method the knowledge about bias for as many amino acids as possible is included in each estimate. As an advantage we can in principle calculate the estimate for genes as short as one codon (apart from the start and stop codons, provided that the codon encodes a degenerate amino acid). Note that Equation 2 has two different implementations, depending on the method used to measure
-value for missing amino acids is approximated through knowledge of the average codon bias. In principle this resembles the original method by Wright, but in contrast to his method the knowledge about bias for as many amino acids as possible is included in each estimate. As an advantage we can in principle calculate the estimate for genes as short as one codon (apart from the start and stop codons, provided that the codon encodes a degenerate amino acid). Note that Equation 2 has two different implementations, depending on the method used to measure  . In the following, when Equation A1 is used to estimate the homozygosity, the estimate is referred to as
. In the following, when Equation A1 is used to estimate the homozygosity, the estimate is referred to as  , and when Equation A2 is used the estimate is referred to as
, and when Equation A2 is used the estimate is referred to as  .
.
Derivation of an N̂c based on relative homozygosity:
Quite similarly to the method listed above we can define a relative homozygosity estimate; we note that, in theory, 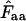 is a value between 1/Degaa and 1.0. We can normalize this by
is a value between 1/Degaa and 1.0. We can normalize this by
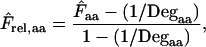 |
(5) |
which has a value between 0 and 1 across all amino acids in all degeneracy classes. We can use this normalization to obtain an average relative homozygosity estimate  . On the basis of this average we get
. On the basis of this average we get
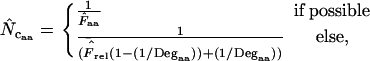 |
(6) |
and this also allows us to make an 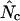 by summation. In the following, when Equation A1 is used to calculate the homozygosity, the estimate is referred to as
by summation. In the following, when Equation A1 is used to calculate the homozygosity, the estimate is referred to as 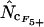 , and when Equation A2 is used the estimate is referred to as
, and when Equation A2 is used the estimate is referred to as 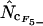 .
.
Derivation of an N̂c based on error-correction of N̂cW:
As shown previously (Fuglsang 2004) there is a methodological weakness built into  because it averages the
because it averages the  -values in degeneracy classes. This adds some systematic error, ɛ, in the estimator, and we might be capable of estimating this by using a little trick. Formally we can write
-values in degeneracy classes. This adds some systematic error, ɛ, in the estimator, and we might be capable of estimating this by using a little trick. Formally we can write
 |
where ɛ is a function of the gene.
In the previous report (Fuglsang 2004) an example was given that showed when and how 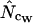 would be exactly 4.5 off for lengths going toward infinity. As is demonstrated in the following section,
would be exactly 4.5 off for lengths going toward infinity. As is demonstrated in the following section,  , (and others) converges toward the true Nc with increasing length. When we have a gene in which we estimate
, (and others) converges toward the true Nc with increasing length. When we have a gene in which we estimate  using whichever method, we could assume that the true codon probabilities correspond to those actually observed in the gene at hand and calculate
using whichever method, we could assume that the true codon probabilities correspond to those actually observed in the gene at hand and calculate 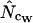 and
and  at infinite length with the actual codon probabilities. The difference is an estimate of the error that is caused by the averaging for
at infinite length with the actual codon probabilities. The difference is an estimate of the error that is caused by the averaging for  :
:
 |
(7) |
Here the ∞ subscript has been added to indicate the infinite length. In practice, it is easily approximated just by multiplying all codon counts with a large integer (e.g., 1,000,000, which typically puts the uncertainty on fifth decimal) and calculating 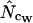 on the resulting counts. Note that at infinite length we expect that (A2) and (A1) reach the same value, as do
on the resulting counts. Note that at infinite length we expect that (A2) and (A1) reach the same value, as do 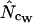 and
and 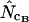 . Also
. Also 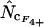 ,
,  ,
,  , and
, and  approach similar values, so Equation 7 can be written in many ways. Note also that
approach similar values, so Equation 7 can be written in many ways. Note also that  equals
equals  . The estimator calculated as
. The estimator calculated as 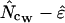 is referred to as
is referred to as  in the following.
in the following.
Simulation:
To test accuracy and precision of 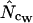 ,
, 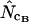 ,
,  ,
,  ,
, 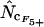 ,
,  , and
, and 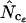 (all summarized in Table 1) simulation was used. Genes were initially simulated using the same amino acid composition as Wright originally used and with various sets of codon frequencies, corresponding to no bias (true Nc = 61.0), weak bias (true Nc = 53.0), medium bias (true Nc = 40.5), and strong bias (true Nc = 29.0). Furthermore, for the medium bias (true Nc = 40.5) two different sets of codon frequencies were used: one corresponding to no bias discrepancy and one corresponding to bias discrepancy as explained in a previous article (Fuglsang 2004). The simulated gene lengths (measured in codons) were: 50, 60, 70, 80, 90, 100, 110, 120, 130, 150, 200, 300, 500, 900, 1250, and 2000. This range of values was chosen on the basis of the distribution of lengths in E. coli (see Figure 1), but since the chance that amino acids are missing increases with shorter gene lengths, it was decided to go as low as 50 codons length. Each combination of bias and gene length was resampled 10,000 times as in the article by Comeron and Aguade (1998) and average and standard deviations of the estimates were recorded. Finally, as is explained further in results and discussion and as shown previously (Fuglsang 2004), the choice of codon frequencies and possibly also amino acid usage employed in the simulation experiment will heavily influence the accuracy of the estimator. For that reason, the simulations were also carried out with sets of codon and amino acid frequencies actually observed in selected genes from the genome of E. coli K12 genes (GenBank accession no. NC_000913).
(all summarized in Table 1) simulation was used. Genes were initially simulated using the same amino acid composition as Wright originally used and with various sets of codon frequencies, corresponding to no bias (true Nc = 61.0), weak bias (true Nc = 53.0), medium bias (true Nc = 40.5), and strong bias (true Nc = 29.0). Furthermore, for the medium bias (true Nc = 40.5) two different sets of codon frequencies were used: one corresponding to no bias discrepancy and one corresponding to bias discrepancy as explained in a previous article (Fuglsang 2004). The simulated gene lengths (measured in codons) were: 50, 60, 70, 80, 90, 100, 110, 120, 130, 150, 200, 300, 500, 900, 1250, and 2000. This range of values was chosen on the basis of the distribution of lengths in E. coli (see Figure 1), but since the chance that amino acids are missing increases with shorter gene lengths, it was decided to go as low as 50 codons length. Each combination of bias and gene length was resampled 10,000 times as in the article by Comeron and Aguade (1998) and average and standard deviations of the estimates were recorded. Finally, as is explained further in results and discussion and as shown previously (Fuglsang 2004), the choice of codon frequencies and possibly also amino acid usage employed in the simulation experiment will heavily influence the accuracy of the estimator. For that reason, the simulations were also carried out with sets of codon and amino acid frequencies actually observed in selected genes from the genome of E. coli K12 genes (GenBank accession no. NC_000913).
TABLE 1.
The different types of 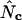 and their calculation
and their calculation
Estimate of 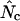 , formula , formula |
 -formula -formula |
Reference | Comment |
|---|---|---|---|
 |
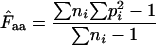 |
Wright (1990) | Requires that at least one 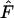 -value can be calculated for degeneracy classes 2, 4, and 6. -value can be calculated for degeneracy classes 2, 4, and 6. |
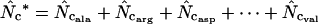 |
 |
Fuglsang (2004) | Requires that the 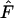 -value can be calculated for all amino acids. -value can be calculated for all amino acids. |
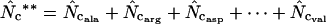 |
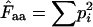 |
Fuglsang (2005) | Requires that the  -value can be calculated for all amino acids. -value can be calculated for all amino acids. |
 |
 |
Banerjee et al. (2005) | Requires that at least one  -value can be calculated for degeneracy classes 2, 4, and 6. -value can be calculated for degeneracy classes 2, 4, and 6. |
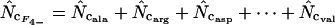 |
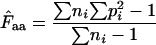 |
This article | Can always be calculated. |
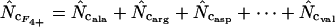 |
 |
This article | Can always be calculated. |
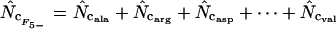 |
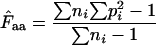 |
This article | Can always be calculated. |
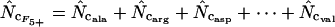 |
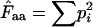 |
This article | Can always be calculated. |
 |
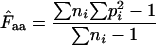 |
This article | Requires that at least one  -value can be calculated for degeneracy classes 2, 4, and 6. -value can be calculated for degeneracy classes 2, 4, and 6. |
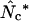 and
and  are outside the scope of this article.
are outside the scope of this article.
Figure 1.
Length distribution of genes in E. coli. The histogram was generated with a bin width of 10. The insert is the same histogram with a logarithmic axis.
Correlation with expression levels:
The correlation of different  's with mRNA levels obtained from E. coli grown in a rich medium was tested with nonparametric correlation analysis as described previously (Goetz and Fuglsang 2005). The raw expression data were from Bernstein et al. (2002).
's with mRNA levels obtained from E. coli grown in a rich medium was tested with nonparametric correlation analysis as described previously (Goetz and Fuglsang 2005). The raw expression data were from Bernstein et al. (2002).
RESULTS AND DISCUSSION
The type of homozygosity estimation is a key to both accuracy and precision:
Figure 2 shows the results of the simulations using a true Nc of 40.5 (medium bias) and without bias discrepancy. All estimates converge toward the true Nc with increasing length, and this also holds true for other levels of true Nc (data not shown).  and
and 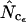 appear to be the methods most independent of length. There is a noteworthy difference in standard deviations: methods using homozygosity based on sampling with replacement (
appear to be the methods most independent of length. There is a noteworthy difference in standard deviations: methods using homozygosity based on sampling with replacement (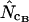 ,
, 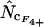 , and
, and  ) have lower standard deviations than those based on sampling without replacement (
) have lower standard deviations than those based on sampling without replacement ( ,
, 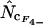 ,
,  , and
, and  ). The pattern is the same at the other levels of bias, i.e., true Nc = 29, 53, and 61 (data not shown). When a regimen with bias discrepancy is used (Figure 3) the situation is slightly different:
). The pattern is the same at the other levels of bias, i.e., true Nc = 29, 53, and 61 (data not shown). When a regimen with bias discrepancy is used (Figure 3) the situation is slightly different: 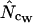 and
and 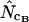 converge toward the wrong value of 36.0 (for an explanation of this phenomenon, see Fuglsang 2004), while the other estimates approach the correct value. Again, methods using homozygosity based on sampling with replacement (
converge toward the wrong value of 36.0 (for an explanation of this phenomenon, see Fuglsang 2004), while the other estimates approach the correct value. Again, methods using homozygosity based on sampling with replacement (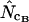 ,
, 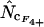 , and
, and  ) have lower standard deviations than those based on sampling without replacement (
) have lower standard deviations than those based on sampling without replacement (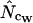 ,
,  ,
, 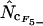 , and
, and 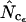 ). These results illustrate that bias discrepancy is a serious problem for
). These results illustrate that bias discrepancy is a serious problem for  and
and  , and, equally important, that the outcome of a simulation study is highly dependent on the conditions used for the simulation. There are an infinite number of ways to implement a true Nc of 40.5, and Figure 2 shows an implementation that favors all the Nc estimates, while Figure 3 shows an implementation that clearly favors methods that do not average homozygosities within degeneracy classes. The crucial part of this type of experiment is thereby not so much the bias—the true Nc—but rather the way a particular bias level has been implemented.
, and, equally important, that the outcome of a simulation study is highly dependent on the conditions used for the simulation. There are an infinite number of ways to implement a true Nc of 40.5, and Figure 2 shows an implementation that favors all the Nc estimates, while Figure 3 shows an implementation that clearly favors methods that do not average homozygosities within degeneracy classes. The crucial part of this type of experiment is thereby not so much the bias—the true Nc—but rather the way a particular bias level has been implemented.
Figure 2.
Average (left) and standard deviation (right) of the estimated Nc, at a “true” Nc of 40.5 (dashed line) without bias discrepancy. Symbols: ▪,  □,
□, 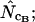 •,
•, 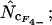 ○,
○,  ♦,
♦,  ⋄,
⋄, 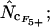 and ×,
and ×,  . Note that the horizontal axis is logarithmic. The methods based on calculation of
. Note that the horizontal axis is logarithmic. The methods based on calculation of  without replacement (solid symbols) show the highest standard deviations, and all converge toward the true Nc of 40.5 with increasing length.
without replacement (solid symbols) show the highest standard deviations, and all converge toward the true Nc of 40.5 with increasing length.
Figure 3.
Average (left) and standard deviation (right) of the estimated Nc, at a “true” Nc of 40.5 (dashed line) with bias discrepancy. Symbols: ▪, 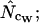 □,
□, 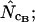 •,
•, 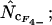 ○,
○,  ♦,
♦, 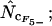 ⋄,
⋄,  and ×,
and ×, 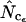 . Note that the horizontal axis is logarithmic. The methods based on calculation of
. Note that the horizontal axis is logarithmic. The methods based on calculation of  without replacement (solid symbols) show the highest standard deviations (right), and the methods based on averaging of
without replacement (solid symbols) show the highest standard deviations (right), and the methods based on averaging of 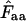 within degeneracy classes (
within degeneracy classes (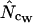 and
and 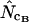 ) converge toward the wrong value of 36 (left).
) converge toward the wrong value of 36 (left).
Are both simulations relevant or realistic? This is fundamentally very difficult to answer because true Nc is never known for genes found in nature. The poor correlation between intraclass  -values that was observed in a previous study (Fuglsang 2004) seems to suggest that bias is seldom uniform within classes. To get closer to an answer to the question, a series of experiments were performed, in which the codon and amino acid frequencies precisely reflect those observed in individual E. coli genes for which all 61 codons are present at least once. In such cases we have a known true Nc for a simulation experiment on the basis of the observed codon and amino acid frequencies of actually observed genes (but the reader should not misinterpret this as having knowledge about true Nc for any actual gene).
-values that was observed in a previous study (Fuglsang 2004) seems to suggest that bias is seldom uniform within classes. To get closer to an answer to the question, a series of experiments were performed, in which the codon and amino acid frequencies precisely reflect those observed in individual E. coli genes for which all 61 codons are present at least once. In such cases we have a known true Nc for a simulation experiment on the basis of the observed codon and amino acid frequencies of actually observed genes (but the reader should not misinterpret this as having knowledge about true Nc for any actual gene).
Figure 4 shows an example of such a simulation with realistic (that is, actually observed) codon and amino acid frequencies. The data for the figure have been made on the basis of the gabP gene of E. coli. Note that 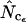 is superior here in terms of accuracy. Experiments of this type reveal that, generally, estimators that are based on Equation A2 for homozygosity calculation seem to reach a maximum at a length of some 100–300 codons, and that
is superior here in terms of accuracy. Experiments of this type reveal that, generally, estimators that are based on Equation A2 for homozygosity calculation seem to reach a maximum at a length of some 100–300 codons, and that 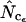 is generally most accurate, except for lengths just around the maximum where
is generally most accurate, except for lengths just around the maximum where 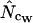 is sometimes (depending on the actual codon frequencies) more accurate. This especially seems to be the case when
is sometimes (depending on the actual codon frequencies) more accurate. This especially seems to be the case when  < −1.5. This clearly emphasizes how important the effect of bias discrepancy, or
< −1.5. This clearly emphasizes how important the effect of bias discrepancy, or  , is for this type of study. A histogram of the estimated errors,
, is for this type of study. A histogram of the estimated errors,  , for the genome of E. coli K12 is given in Figure 5. The median
, for the genome of E. coli K12 is given in Figure 5. The median  is −1.7. My interpretation is that bias discrepancy is a realistic phenomenon that should not be disregarded because it leads to a systematic accuracy error for
is −1.7. My interpretation is that bias discrepancy is a realistic phenomenon that should not be disregarded because it leads to a systematic accuracy error for  and
and 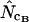 and because it seems to be more of a rule than an exception (Fuglsang 2004). As Figure 4 (and to a lesser extent also Figures 2 and 3) suggests, correcting
and because it seems to be more of a rule than an exception (Fuglsang 2004). As Figure 4 (and to a lesser extent also Figures 2 and 3) suggests, correcting 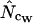 with
with  gives a superior estimate in many cases. Only at very short gene lengths (lengths ∼50–60 codons) can
gives a superior estimate in many cases. Only at very short gene lengths (lengths ∼50–60 codons) can  or
or 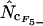 be superior to
be superior to 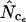 , but at this point a clear recommendation about when this is the case cannot be given. As indicated in Figure 1, gene lengths of 50–60 codons do occur in the genome of E. coli but must be considered exceptional. Generally, I therefore recommend
, but at this point a clear recommendation about when this is the case cannot be given. As indicated in Figure 1, gene lengths of 50–60 codons do occur in the genome of E. coli but must be considered exceptional. Generally, I therefore recommend  as the best overall bias estimator. In reduced genomes, such as that of Mycoplasma genitalium (0.6 Mb) or intracellular parasitic bacteria, genes are often shorter than their counterparts (orthologs) in E. coli and other bacteria with larger genomes. Figures 2–4 suggest that in such cases there could very well be relatively more genes for which
as the best overall bias estimator. In reduced genomes, such as that of Mycoplasma genitalium (0.6 Mb) or intracellular parasitic bacteria, genes are often shorter than their counterparts (orthologs) in E. coli and other bacteria with larger genomes. Figures 2–4 suggest that in such cases there could very well be relatively more genes for which 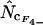 and
and  are more accurate than
are more accurate than 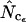 . There is therefore plenty of room for improvement of
. There is therefore plenty of room for improvement of  . It seems an obvious future objective to characterize better the relationships between length, accuracy, and
. It seems an obvious future objective to characterize better the relationships between length, accuracy, and  .
.
Figure 4.
Average (left) and standard deviation (right) of the estimated Nc, using the codon and amino acid composition of gabP from E. coli as reference for the simulation (“true” Nc = 47.2). Symbols: ▪,  □,
□, 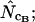 •,
•, 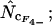 ○,
○, 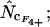 ♦,
♦,  ⋄,
⋄, 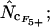 and ×,
and ×, 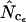 . Note that the horizontal axis is logarithmic. The methods based on calculation of
. Note that the horizontal axis is logarithmic. The methods based on calculation of 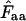 without replacement (solid symbols) show the highest standard deviations (right), and the methods based on averaging of
without replacement (solid symbols) show the highest standard deviations (right), and the methods based on averaging of 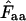 within degeneracy classes (
within degeneracy classes ( and
and 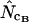 ) converge toward the wrong value of 45.5 (left). Finally,
) converge toward the wrong value of 45.5 (left). Finally, 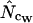 and
and 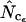 show the best length independence.
show the best length independence.
Figure 5.
Histogram of ɛ̂-values from the genome of E. coli K12. Bin width was 0.05.
The least accurate estimates show better correlations with mRNA levels:
In Table 2, the correlation coefficients are given for the  's and mRNA levels in E. coli grown in a rich medium (expression data from Bernstein et al. 2002). Interestingly, Table 2 demonstrates that there is a considerable correlation with the
's and mRNA levels in E. coli grown in a rich medium (expression data from Bernstein et al. 2002). Interestingly, Table 2 demonstrates that there is a considerable correlation with the 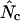 's that are based on Equation A1 for codon homozygosity (
's that are based on Equation A1 for codon homozygosity (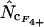 ,
, 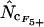 , and
, and  rs ∼ 0.39), whereas those that are based on Equation A2 display much lower correlation (
rs ∼ 0.39), whereas those that are based on Equation A2 display much lower correlation ( ,
,  ,
,  , and
, and  rs ≤ 0.27). For comparison, the correlation coefficient of the codon adaptation index (CAI) with the mRNA levels is 0.43 (Goetz and Fuglsang 2005). CAI is a frequently used indicator of “expressivity” but is species dependent in that the calculation is based on knowledge of codons used in genes that are highly expressed (Sharp and Li 1987). The different
rs ≤ 0.27). For comparison, the correlation coefficient of the codon adaptation index (CAI) with the mRNA levels is 0.43 (Goetz and Fuglsang 2005). CAI is a frequently used indicator of “expressivity” but is species dependent in that the calculation is based on knowledge of codons used in genes that are highly expressed (Sharp and Li 1987). The different 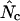 's are not dependent on such knowledge. Previously it was shown only that
's are not dependent on such knowledge. Previously it was shown only that  had a fair correlation (rs = 0.39) with mRNA levels in E. coli (Goetz and Fuglsang 2005). This bias indicator is also based on Equation A1, but relies on
had a fair correlation (rs = 0.39) with mRNA levels in E. coli (Goetz and Fuglsang 2005). This bias indicator is also based on Equation A1, but relies on  being calculated for all 18 degenerate amino acids. Of course, some degree of correlation must be anticipated between CAI and the different
being calculated for all 18 degenerate amino acids. Of course, some degree of correlation must be anticipated between CAI and the different  's. A CAI of 1.0 should always give an
's. A CAI of 1.0 should always give an 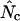 of 20, but apart from that the relationship is not well characterized for any species. Although the bias measures based on Equation A1 are not the most accurate, their existence is certainly justified by the correlation they display with mRNA levels in E. coli. It needs to be mentioned that there is a known correlation between length and codon bias in E. coli (Eyre-Walker 1996). The correlation coefficient for length and mRNA levels used in Table 2 is rs = −0.2697 (P < 0.0001). If length imposes a constraint on codon usage then that could in principle account for some of the correlation between codon bias and expression. The cause-consequence relationships that exist between length, codon bias, and expression are not well understood, however. Moreover, given that the estimates for codon bias have larger variances for low gene lengths, and that this might also be the case with the estimates of mRNA level, random sampling effects in these areas could very well have an influence on the correlations given in Table 2.
of 20, but apart from that the relationship is not well characterized for any species. Although the bias measures based on Equation A1 are not the most accurate, their existence is certainly justified by the correlation they display with mRNA levels in E. coli. It needs to be mentioned that there is a known correlation between length and codon bias in E. coli (Eyre-Walker 1996). The correlation coefficient for length and mRNA levels used in Table 2 is rs = −0.2697 (P < 0.0001). If length imposes a constraint on codon usage then that could in principle account for some of the correlation between codon bias and expression. The cause-consequence relationships that exist between length, codon bias, and expression are not well understood, however. Moreover, given that the estimates for codon bias have larger variances for low gene lengths, and that this might also be the case with the estimates of mRNA level, random sampling effects in these areas could very well have an influence on the correlations given in Table 2.
TABLE 2.
Correlation of the different bias measures with mRNA levels in E. coli grown in rich medium
| Codon bias estimate | Correlation with mRNA levelsa in E. coli |
|---|---|
 |
rs = −0.2198b |
 |
rs = −0.3947 |
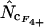 |
rs = −0.3939 |
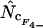 |
rs = −0.2245 |
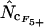 |
rs = −0.3936 |
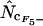 |
rs = −0.2371 |
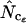 |
rs = −0.2637 |
Interestingly, methods based on Equation A1 for calculation of  display far better correlation coefficients than methods based on Equation A2.
display far better correlation coefficients than methods based on Equation A2.
Expression data are from Bernstein et al. (2002).
Data are from Goetz and Fuglsang (2005).
Concluding remarks
In conclusion, this study has shown that  's based on Equation A1 are less accurate than those based on Equation A2, which was Wright's original suggestion. Wright's idea about homozygosity (Equation A2) is therefore definitively better than the method I suggested (Equation A1).
's based on Equation A1 are less accurate than those based on Equation A2, which was Wright's original suggestion. Wright's idea about homozygosity (Equation A2) is therefore definitively better than the method I suggested (Equation A1).  was generally the best performer in terms of accuracy in simulation studies where the codon and amino acid frequencies were identical to frequencies actually observed in E. coli genes. On the other hand,
was generally the best performer in terms of accuracy in simulation studies where the codon and amino acid frequencies were identical to frequencies actually observed in E. coli genes. On the other hand,  's based on Equation A1 generally have lower standard deviations in simulation studies. They also display a better correlation with mRNA levels in E. coli. The amount of available literature in this field is limited, and there is plenty of opportunity for improvements.
's based on Equation A1 generally have lower standard deviations in simulation studies. They also display a better correlation with mRNA levels in E. coli. The amount of available literature in this field is limited, and there is plenty of opportunity for improvements.
APPENDIX: EXPLANATION OF CODON HOMOZYGOSITY (F)
A basis in population genetics:
Consider an infinitely large population, in which we have X different alleles for a given trait and where one zygote carries one allele. The individual frequencies of the alleles/zygotes are p1, p2, p3, … , pk. Let us then calculate the chance F that two randomly picked zygotes carry the same allele:
 |
(A1) |
If the two zygotes give rise to offspring, F is the chance that it will be homozygotic for the given allele. Conversely, 1/F tells the average number of times we can pick two random zygotes before they have identical alleles. That is the effective number of alleles.
Sampling with replacement:
With the codons in a gene, we use this calculation to get an estimate for codon homozygosity,  , although the direct interpretation then becomes somewhat obscure. A fair way of viewing
, although the direct interpretation then becomes somewhat obscure. A fair way of viewing  is to understand it as the estimated probability that two codons picked at random from the codon pool (consisting of the codons encoding the amino acid in question) are identical. Equation A1 is obviously applicable to a situation in which there is replacement between the two codons picked: the first codon is put back into the codon pool before sampling the second codon. This is the method proposed in Fuglsang (2005).
is to understand it as the estimated probability that two codons picked at random from the codon pool (consisting of the codons encoding the amino acid in question) are identical. Equation A1 is obviously applicable to a situation in which there is replacement between the two codons picked: the first codon is put back into the codon pool before sampling the second codon. This is the method proposed in Fuglsang (2005).
Sampling without replacement, Wright's method:
If we sample without replacement, we have to take into consideration that on sampling number two there is one less of the type picked in the first sample. Our F-estimate becomes
 |
(A2) |
This equation is what Wright used in his original calculation. Obviously, if there is only one codon for a particular amino acid in the gene (and the amino acid is not Trp or Met), or, more generally, if each synonymous codon is present exactly one or zero times then obviously there is zero probability of sampling two such codons, meaning that the effective number of codons cannot be estimated. Finally we note that Equation A2 becomes Equation A1 as the population size (codons in total) goes toward infinity.
It cannot be emphasized enough that the choice of method is a matter of empery, first because it makes little sense to think of codons as mating entities and second because 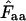 and
and  are estimates of the codon bias in a codon population that is represented by a gene; the gene is not the codon population itself. The caret symbol (∧) is used to indicate that it is an estimate, and consequently we have to discriminate carefully between Wright's concepts of “true” Nc (Wright's original wording) and
are estimates of the codon bias in a codon population that is represented by a gene; the gene is not the codon population itself. The caret symbol (∧) is used to indicate that it is an estimate, and consequently we have to discriminate carefully between Wright's concepts of “true” Nc (Wright's original wording) and  . True Nc and Faa are entities we usually have no way of knowing, while
. True Nc and Faa are entities we usually have no way of knowing, while 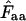 and thereby
and thereby  and subsequently
and subsequently 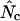 are values we estimate through measurements of the codon population in a gene. In a simulation experiment we can fully control the true F-values, and thus the true Nc, by fixing the codon probabilities, and test how the resulting
are values we estimate through measurements of the codon population in a gene. In a simulation experiment we can fully control the true F-values, and thus the true Nc, by fixing the codon probabilities, and test how the resulting  behaves.
behaves.
References
- Banerjee, T., S. K. Gupta and T. C. Ghosh, 2005. Towards a resolution on the inherent methodological weakness of the “effective number of codons used by a gene.” Biochem. Biophys. Res. Commun. 330: 1015–1018. [DOI] [PubMed] [Google Scholar]
- Bernstein, J. A., A. B. Khodursky, P. H. Lin, S. Lin-Chao and S. N. Cohen, 2002. Global analysis of mRNA decay and abundance in Escherichia coli at single-gene resolution using two-color fluorescent DNA microarrays. Proc. Natl. Acad. Sci. USA 99: 9697–9702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comeron, J. M., and M. Aguade, 1998. An evaluation of measures of synonymous codon usage bias. J. Mol. Evol. 47: 268–274. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker, A., 1996. Synonymous codon usage bias is related to gene length in Escherichia coli: Selection for translational accuracy? Mol. Biol. Evol. 13: 864–872. [DOI] [PubMed] [Google Scholar]
- Fuglsang, A., 2004. The ‘effective number of codons’ revisited. Biochem. Biophys. Res. Commun. 317: 957–964. [DOI] [PubMed] [Google Scholar]
- Fuglsang, A., 2005. On the methodological weakness of ‘the effective number of codons’: a reply to Marashi and Najafabadi. Biochem. Biophys. Res. Commun. 327: 1–3. [DOI] [PubMed] [Google Scholar]
- Goetz, R. M., and A. Fuglsang, 2005. Correlation of codon bias measures with mRNA levels: analysis of transcriptome data from Escherichia coli. Biochem. Biophys. Res. Commun. 327: 4–7. [DOI] [PubMed] [Google Scholar]
- Gouy, M., and C. Gautier, 1982. Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res. 10: 7055–7074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikemura, T., 1981. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes. J. Mol. Biol. 146: 1–21. [DOI] [PubMed] [Google Scholar]
- Ikemura, T., 1985. Codon usage and tRNA content in unicellular and multicellular organisms. Mol. Biol. Evol. 2: 13–34. [DOI] [PubMed] [Google Scholar]
- Marashi, S.-A., and H. S. Najafabadi, 2004. How reliable re-adjustment is: correspondence regarding A. Fuglsang, “the effective number of codons revisited.” Biochem. Biophys. Res. Commun. 324: 1–2. [DOI] [PubMed] [Google Scholar]
- Sharp, P. M., and W.-H. Li, 1987. The codon adaptation index—a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 15: 1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, F., 1990. The ‘effective number of codons’ used in a gene. Gene 87: 23–29. [DOI] [PubMed] [Google Scholar]







