Transcriptional Reprogramming and Backup Between Duplicate Genes: Is It a Genomewide Phenomenon?

Abstract

Deleting a duplicate gene often results in a less severe phenotype than deleting a singleton gene, a phenomenon commonly attributed to functional compensation among duplicates. However, duplicate genes rapidly diverge in expression patterns after duplication, making functional compensation less probable for ancient duplicates. Case studies suggested that a gene may provide compensation by altering its expression upon removal of its duplicate copy. On the basis of this observation and a genomic analysis, it was recently proposed that transcriptional reprogramming and backup among duplicates is a genomewide phenomenon in the yeast Saccharomyces cerevisiae. Here we reanalyze the yeast data and show that the high dispensability of duplicate genes with low expression similarity is a consequence of expression similarity and gene dispensability, each being correlated with a third factor, the number of protein interactions per gene. There is little evidence supporting widespread functional compensation of divergently expressed duplicate genes by transcriptional reprogramming.

GENE duplication is the primary source of new genes (Ohno 1970; Zhang 2003). Consequently, there are many duplicate genes in virtually every genome examined (Zhang 2003). It is often observed that deleting a duplicate gene results in a less severe phenotype than deleting a singleton gene (Gu et al. 2003; Kamath et al. 2003; Conant and Wagner 2004), a phenomenon commonly attributed to functional compensation among duplicates (Conant and Wagner 2004; Gu et al. 2003; Kamath et al. 2003). Conceivably, this compensation relies on a similar expression pattern between duplicates. Indeed, Kafri et al. (2005) recently showed in the yeast Saccharomyces cerevisiae that among relatively young duplicates (with synonymous nucleotide distance d_S < 1), the probability that a gene is dispensable declines as the mean expression similarity (MES) between the duplicate pair decreases, where MES is measured under 40 different conditions. But surprisingly, among ancient duplicates (d_S > 1), which constitute >90% of all yeast duplicates, the probability that a gene is dispensable increases when MES falls from 1 to ∼0.2. Kafri et al. (2005) proposed an interesting idea that these ancient duplicates have acquired an expression reprogramming ability that allows normally differentially expressed duplicates to provide compensation when needed. Because gene expression diverges rapidly between duplicates (Gu et al. 2002; Makova and Li 2003), their hypothesis may explain why deleting an anciently duplicated gene still causes a smaller phenotypic effect than deleting a singleton gene (Gu et al. 2003; Conant and Wagner 2004). In Kafri et al.'s hypothesis, the ability of young duplicates to compensate one another is due to a shared expression inherited from their common ancestor. This ability diminishes quickly with evolutionary time, but the ability to compensate is regained long after duplication by acquisition of transcriptional reprogramming. This regaining of compensation is improbable, because to acquire the relevant expression reprogramming capability, a duplicate gene has to be able to recognize its sister copy even after substantial changes at both expression and sequence levels. Here we provide an alternative explanation to Kafri et al.'s observation, which is not based on expression reprogramming.

DATA AND METHODS

The yeast data used by Kafri et al. (2005) were downloaded from http://longitude.weizmann.ac.il/backupcircuits/. Of 2216 duplicate gene pairs, 1551 pairs had fitness information for both copies and were used in our analyses. As in the analysis of Kafri et al. (2005), a gene may be involved in more than one gene pair. In fact, the data set is highly redundant; on average each gene appeared ∼2.3 times. We computed d_S between duplicate genes using PAML with default parameters (Yang 1997). Those pairs with d_S < 1 were regarded as recent duplicates (116 pairs), and the rest were regarded as ancient duplicates (1435 pairs). We used the yeast protein–protein interaction data compiled in our recent article (He and Zhang 2005). Briefly, we merged the data annotated in the Munich Information Center for Protein Sequences (ftp://ftpmips.gsf.de/yeast/PPI) and the high-confidence subset of the data recently compiled (von Mering et al. 2002). After excluding self-interactions and interactions involving mitochondrial genes, a nonredundant protein interaction data set containing 9316 pairwise interactions among 4292 genes was derived. We obtained the yeast stable protein complex data set from Saccharomyces Genome Database (ftp://genome-ftp.stanford.edu/pub/yeast/data_download/literature_curation/go_protein_complex_slim.tab), which contains 188 complexes comprising 1226 genes. The mean number of protein interaction partners per protein is substantially higher for proteins involved in stable protein complexes (6.77 ± 0.33) than for other proteins (3.61 ± 0.14) (Mann-Whitney U-test, P < 0.0001). To be more conservative, we included proteins with at least one partner in the above comparison.

In the sliding-window analyses presented in Figure 1, we excluded three duplicate pairs (YER081W/YIL074C, YJR091C/YPR042C, and YKL068W/YMR047C) because of the presence of genes with extremely high numbers of protein interaction partners (94 for YER081W, 289 for YJR091C, and 128 for YMR047C) that would inappropriately influence the calculation of the mean number of partners in a window. We used the same strategy as in Kafri et al. (2005) when computing the probability that a gene is dispensable for Figure 2. Specifically, each gene was considered only once in the computation of gene dispensability in each bin.

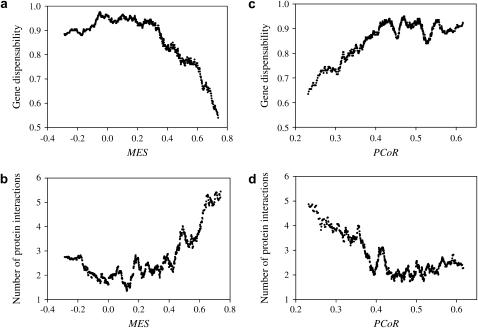
Figure 1.

Covariation with the number of protein interaction partners per gene explains the correlation between the MES or PCoR and gene dispensability. In a and b, duplicate gene pairs are sorted by MES, and the average MES and average gene dispensability are computed for a window size of 100 duplicate pairs, with the sliding window moving every gene pair. In c and d, duplicate genes are sorted by PCoR. A total of 1432 pairs of yeast duplicate genes with d_S > 1 are analyzed here.

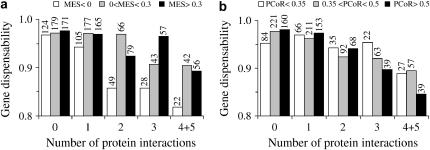
Figure 2.

No consistent relationships exist (a) between the MES and gene dispensability or (b) between PCoR and gene dispensability among the yeast duplicate genes with d_S > 1, when the number of protein interaction partners per gene is controlled for. Genes involved in stable protein complexes are excluded. We first separate genes according to the number of protein interactions and then compute the average gene dispensability for genes with a given number of protein interactions in three MSE or PCoR ranges. The number of genes used is indicated for each bin.

RESULTS AND DISCUSSION

Most proteins execute their functions through interacting with other proteins. Known as the centrality–lethality relationship, proteins involved in more protein–protein interactions tend to be indispensable (Jeong et al. 2001; Hahn and Kern 2005). For two reasons we suspect that, on average, ancient duplicates with high MES have more protein interaction partners than do ancient duplicates with low MES, thus generating a negative correlation between MES and gene dispensability. First, members of the same or related stable protein complexes are expected to show high MES due to transcriptional coregulation and these genes also tend to have more protein interaction partners (see data and methods). Second, housekeeping genes are constantly expressed and therefore should have high MES among themselves. They may also engage in more protein interactions because of their involvement in many cellular processes. We thus hypothesize that the negative correlation between MSE and gene dispensability for ancient duplicates (Kafri et al. 2005) is due to the covariation of these two parameters with the number of protein interactions.

By a sliding-window analysis, we first reproduced the relationship between MES and gene dispensability (Figure 1a) reported by Kafri et al. (2005). Using the same window size and step length, we generated the relationship between MES and the number of protein interactions (Figure 1b). In strong support of our hypothesis, the relationship between MES and the number of protein interactions almost perfectly complements that between MES and gene dispensability. Kafri et al. (2005) also randomly paired genes and found that the relationship between MES and gene dispensability disappeared after random pairing. This is expected if the correlation between gene dispensability and MES is due to (i) the correlation between the number of protein interactions and gene dispensability and (ii) the correlation between the number of protein interactions and MES, because correlation ii should disappear when genes are randomly paired. As a consequence, the correlation between gene dispensability and MES disappears after random gene pairing.

It should be noted that although the numbers of protein interactions used in the above analysis may differ from the true values due to errors in high-throughput genomic studies and/or imperfect data interpretation (e.g., the matrix or spoke strategy in transforming protein complex information to binary interaction information; see Bader and Hogue 2002), the observation of a strong negative correlation between the number of protein interactions and gene dispensability (Jeong et al. 2001) suggests that the estimated number of protein interactions, or at least its relative value, is biologically meaningful. Note that this negative correlation between the number of protein interactions and gene dispensability exists for both singleton genes and duplicate genes (X. He and J. Zhang, unpublished results). Hence, the almost perfect complementation between the relationship of MES and gene dispensability and that of MES and the number of protein interactions strongly suggests the role of the number of protein interactions in causing the unexpected correlation between MES and gene dispensability among ancient duplicates. Kafri et al. (2005) also examined the standard deviation of the correlation in expression response between duplicates under 40 conditions and termed it partial coregulation (PCoR). However, PCoR is highly correlated with MES (Pearson's correlation coefficient = −0.52, P < 10⁻⁹⁸). As expected, we found that the relationship between PCoR and the number of protein interactions closely complements that between PCoR and gene dispensability (Figure 1, c and d).

We next examined whether the relationship between MES and gene dispensability observed by Kafri et al. (2005) disappears when the number of protein interactions is controlled for. We also removed genes involved in stable protein complexes, because they tend to be similarly regulated and could have lower gene dispensability than those not involved in stable complexes even with the same number of protein interactions, due to the importance of dosage balance among components of stable complexes (Papp et al. 2003; Yang et al. 2003). If the expression reprogramming hypothesis (Kafri et al. 2005) is correct, the relationship between MES and gene dispensability should not change after the number of protein interactions is controlled for. But in fact, there are no consistent relationships between MES and gene dispensability among genes of different numbers of protein interactions (Figure 2a). Furthermore, the variation in gene dispensability at different MESs is diminutive for any given number of protein interactions (Figure 2a). A similar result is obtained between PCoR and gene dispensability (Figure 2b). Thus, MES and PCoR are uncorrelated with gene dispensability among ancient duplicates when the number of protein interactions is controlled for. Note that because the number of duplicate genes having a given number (N) of protein interactions is too small when N > 5 (e.g., 30 for N = 6), we limited our analysis to genes with N ≤ 5, which constitutes ∼92% of all genes in our data. Lumping several bins together (e.g., N = 6–10) effectively removes the control and is not appropriate. Because the duplicate gene pairs used are not independent of each other (see data and methods), the effect of the number of protein interactions cannot be statistically measured by a partial correlation analysis.

Our reanalysis of the yeast data suggests that the primary cause of the unexpected correlation between MES and gene dispensability among ancient duplicates is those duplicate pairs for which both proteins are involved in the same or related protein complexes. These duplicate genes tend to have similar expression (i.e., high MES) by coregulation, but low gene dispensability because of the relative importance of protein complexes. Why do such genes affect the relationship between MES and gene dispensability when d_S > 1, but not when d_S < 1? We think that when d_S > 1, it is rare for a duplicate pair to have high MES unless they participate in the same or related protein complexes. To verify this conjecture, we separated ancient duplicate pairs into two groups on the basis of their involvement in protein complexes. Only 6.9% of complex-free duplicate pairs have MES > 0.6, while the number is 25.1% for complex-involving duplicates (χ² = 75, P < 10⁻¹⁷). When d_S < 1, many duplicates can have high MES without the involvement in protein complexes; their high MES is inherited from the common ancestor and has yet to be lost in evolution. In fact, 40.3% of complex-free young duplicates have MES > 0.6, in comparison to only 6.9% among complex-free old duplicates (χ² = 89, P < 10⁻²⁰). In summary, our results show that the primary observation supporting the extraordinary evolutionary hypothesis of transcriptional reprogramming and backup among duplicates (Kafri et al. 2005) was mainly due to a confounding factor unrelated to transcriptional reprogramming. In other words, there is no clear evidence suggesting that the reprogramming hypothesis is true at the genomewide level, although it may work in a few genes (Kafri et al. 2005).

One of the interesting observations of Kafri et al. (2005) is the relatively high prevalence of documented cases of synthetic lethality in paralogous pairs with low MES and high PCoR (Kafri et al. 2005, Figure 5). However, this was based on a casual observation without systematic statistical comparisons. Most importantly, they failed to show that the presumable compensation among synthetic lethal genes is caused by transcriptional reprogramming. In fact, a recent study of synthetic lethal genes of S. cerevisiae showed that transcriptional reprogramming of a gene in responding to the deletion of its synthetic lethal partner is rare in general and virtually absent among duplicates (Wong and Roth 2005).

One may ask if transcriptional reprogramming is not the mechanism, What would be the mechanism of functional compensation among ancient duplicates? We stress that it is important to distinguish between two distinct questions: (1) Is there prevalent functional compensation among duplicates? and (2) If there is, what is the molecular mechanism? Although the observation of a lower fitness effect caused by deleting a duplicate, rather than a singleton, gene is commonly attributed to functional compensation, there are other possible explanations. For example, intrinsically less important genes may have a higher duplicability than more important genes, a trend recently found in yeasts (He and Zhang 2006). If this trend is as strong as has been suggested, no functional compensation is necessary to explain the gene deletion results (He and Zhang 2006). From a mechanistic point of view, although it is possible that functional compensation among young duplicates occurs frequently due to similar expressions and functions, compensation among ancient duplicates may be quite rare. Even if functional compensation does occur among ancient duplicates with low MES, it may not require transcriptional reprogramming. The reason is that low MES simply means that a duplicate pair shows different responses to given conditions, but does not mean that their expression patterns are mutually exclusive. We can imagine a scenario by which compensation could work for those low MES paralogs without transcriptional reprogramming. For example, A and B are a pair of duplicate genes. A has a high-low-high-low temporal expression pattern from phase M to phase G₂ in the cell cycle, while B is constitutively expressed with a constant expression level. Thus, A and B will show low MES. When A is deleted, B can most likely compensate A without reprogramming, because B is always expressed. This scenario is more parsimonious than transcriptional reprogramming in explaining functional compensation among ancient duplicates. It is possible that the overlapping expression of genes A and B is retained by certain constraints. For instance, B may perform another function that requires constitutive expression. These considerations notwithstanding, we caution that genomewide studies of possible functional compensations among duplicate genes and the underlying molecular mechanisms have just begun (Wagner 2000); more analyses are needed to fully address these important questions.