Abstract
A linkage disequilibrium-based method for fine mapping quantitative trait loci (QTL) has been described that uses similarity between individuals' marker haplotypes to determine if QTL alleles are identical by descent (IBD) to model covariances among individuals' QTL alleles for a mixed linear model. Mapping accuracy with this method was found to be sensitive to the number of linked markers that was included in the haplotype when fitting the model at a putative position of the QTL. The objective of this study was to determine the optimal haplotype structure for this IBD-based method for fine mapping a QTL in a previously identified QTL region. Haplotypes consisting of 1, 2, 4, 6, or all 10 available markers were fit as a “sliding window” across the QTL region under ideal and nonideal simulated population conditions. It was found that using haplotypes of 4 or 6 markers as a sliding “window” resulted in the greatest mapping accuracy under nearly all conditions, although the true IBD state at a putative QTL position was most accurately predicted by IBD probabilities obtained using all markers. Using 4 or 6 markers resulted in greater discrimination of IBD probabilities between positions while maintaining sufficient accuracy of IBD probabilities to detect the QTL. Fitting IBD probabilities on the basis of a single marker resulted in the worst mapping accuracy under all conditions because it resulted in poor accuracy of IBD probabilities. In conclusion, for fine mapping using IBD methods, marker information must be used in a manner that results in sensitivity of IBD probabilities to the putative position of the QTL while maintaining sufficient accuracy of IBD probabilities to detect the QTL. Contrary to expectation, use of haplotypes of 4–6 markers to derive IBD probabilities, rather than all available markers, best fits these criteria. Thus for populations similar to those simulated here, optimal mapping accuracy for this IBD-based fine-mapping method is obtained with a haplotype structure including a subset of all available markers.
WITH the identification of numerous quantitative trait loci (QTL) regions in economically important livestock species, the focus has now shifted to fine mapping these QTL as the next step toward identifying genes underlying complex traits. Methods that utilize historical recombination information on the basis of linkage disequilibrium (LD) allow fine mapping using existing outbred populations instead of experimental mapping populations. These methods are becoming popular for QTL fine mapping in livestock, where the creation of mapping populations such as advanced intercrossed lines (Darvasi and Soller 1995) is expensive and time consuming.
Meuwissen and Goddard (2000) proposed a haplotype-based method to fine map QTL, using a mixed linear model that models covariances between individuals at a putative QTL on the basis of similarity of their marker haplotypes. Individuals with similar marker haplotypes are likely to share QTL alleles that are identical by descent (IBD) and so will have a higher covariance. Farnir et al. (2002) stated that exploiting LD is one of the most promising strategies for increasing map resolution and recognized the IBD method of Meuwissen and Goddard (2000) as an example of such work.
The IBD method of Meuwissen and Goddard (2000) has subsequently been extended to include linkage information by both Meuwissen et al. (2002) and Blott et al. (2003). Recently, Olsen et al. (2004) utilized the combined linkage and LD mapping method of Meuwissen et al. (2002) to fine map QTL for milk production traits in dairy cattle. Thus, the IBD method is becoming widely used for fine mapping QTL in livestock, especially in combination with linkage information, because it fits with the established framework in animal breeding of performing genetic analysis of outbred populations using mixed linear models.
It is not clear, however, whether the IBD method of Meuwissen and Goddard (2000) is optimal for fine mapping QTL. Grapes et al. (2004) showed that regression on a single, biallelic marker had similar or greater mapping precision than the IBD method under various population structures. Grapes et al. (2004) observed that IBD probabilities derived using all markers in the QTL region, using the gene drop method described by Meuwissen and Goddard (2000), were not sensitive to the putative position of the QTL, such that probabilities at adjoining QTL positions (i.e., marker brackets) were similar across a 10-locus marker region. This similarity in IBD probabilities limits mapping precision. Thus, when using the IBD method, considering all available markers simultaneously to derive IBD probabilities may not be optimal for fine mapping.
Although it defies expectation that using all available information is not optimal, the same phenomenon has been observed for other LD-based QTL fine-mapping methods. Zhang et al. (2003) found that mapping precision for a variance components analysis (Abecasis et al. 2000) of marker association with immunoglobulin E levels was similar when using single markers compared to using haplotypes of three, four or five markers. Additionally, Abdallah et al. (2004) showed that a haplotype of two markers resulted in more precise estimates of QTL position than a haplotype of six markers for an LD-based maximum-likelihood method that is a generalization of the method of Terwilliger (1995). While neither of these two analyses utilizes the IBD method directly, they are examples of LD-based fine-mapping methods that are also sensitive to haplotype structure. Thus it may be that obtaining the highest mapping accuracy by using fewer markers in a haplotype is a general property of LD-based fine-mapping methods.
The objective of this study was to further explore the impact of haplotype structure on the IBD-based LD mapping method of Meuwissen and Goddard (2000) and to determine the optimal haplotype size for the IBD method of fine mapping. In this work, haplotype size refers to the number of markers in the haplotype, which is used as a sliding “window” across a previously identified QTL region containing 10 total markers. Although Meuwissen and Goddard (2000) showed that the IBD method is quite robust to departures from assumptions about population history when all available markers are considered in the haplotype, these assumptions may affect mapping precision when a smaller haplotype is considered. Thus the impact of alternate population structures on the optimal haplotype size of the IBD method was evaluated also.
METHODS
Population simulations:
Following Meuwissen and Goddard (2000), it was assumed that a previous linkage analysis had mapped a QTL to a region of 2.25–9 cM, and 10 biallelic markers were available in that region. Thus in all simulations, individuals were generated with 10 evenly spaced, biallelic markers, with a QTL centered between 2 adjacent markers, and with a trait phenotypic value.
Default scenario:
The IBD method of Meuwissen and Goddard (2000) is based upon modeling the covariance between individuals under the following assumptions: (1) each marker locus has two alleles with equal frequencies in the founder population, (2) variation in a QTL is due to a mutation that occurred 100 generations ago, and (3) effective population size was 100 during the last 100 generations. Data in the default scenario were generated under these assumptions with the QTL placed in the middle of the 10-marker haplotype. It was assumed known which markers were maternally and paternally inherited so that marker haplotypes could be constructed.
Phenotypic values for individuals in the final generation were generated similar to those in Meuwissen and Goddard (2000). In all simulated populations, except for a crossbred population that is described later, QTL alleles were uniquely numbered in the founders. So with an effective population size of 100, the initial frequency of each QTL allele was 0.005. In all simulations, including the crossbred population, one QTL allele with a frequency >0.1 in the final generation was randomly selected to be the mutant allele. This mutant allele was given an additive genetic value of 1, and the value of all other QTL alleles was set to 0. The phenotypic value for each individual in the final generation was calculated by summing the QTL allele effects with a random error sampled from a standard normal distribution.
Alternative scenarios:
To test robustness of the method to population history assumptions, six alternative scenarios were created that differed from the default for one or more conditions. In the first scenario, two breeds with divergent allele frequencies for two QTL alleles were crossed (see Table 1). After crossing, the population was randomly mated for 1, 5, 10, 20, or 100 generation(s). In the second scenario, the QTL was placed at a noncentral position in the haplotype. In the third scenario, marker allele frequencies were assigned at random in the founder generation within a range of 0.2–0.8. In the fourth scenario, a “worst-case scenario” was created that incorporated all three alternative conditions listed above. In the fifth scenario, effective population size was 50 or 200, instead of the default size of 100. In the last scenario, size of the QTL effect was decreased from 1 to 0.5. Details of all population parameters are summarized in Table 1.
TABLE 1.
Parameters for default and alternative simulated populations
| Default population | |
| Effective population size | 100 |
| No. of generations of random mating since QTL mutation occurred | 100 |
| No. of markers genotyped | 10 |
| No. of alleles per marker in founder population | 2 |
| Initial marker/QTL allele frequencies in founder population | 0.5/0.005 |
| Distance (cM) between adjacent markers | 1, 0.5, 0.25 |
| Position of QTL | Halfway between markers 5 and 6 |
| Additive effect of QTL allele mutation | 1 |
| Residual standard deviation | 1 |
| No. of individuals (records) in final generation | 100 |
| Two-breed cross | |
| No. of generations of random mating following the initial cross | 1, 5, 10, 20, 100 |
| Initial marker/QTL allele frequencies in founder population | |
| Breed 1 | 0.5/0.1, 0.9 |
| Breed 2 | 0.5/0.9, 0.1 |
| Distance (cM) between adjacent markers | 1 |
| Noncentral QTL position | |
| Distance (cM) between adjacent markers | 1 |
| Position of QTL | Halfway between markers 3 and 4 |
| Random founder allele frequencies | |
| Initial marker/QTL allele frequencies in founder population | 0.2–0.8/0.005 |
| Distance (cM) between adjacent markers | 1 |
| Worst-case scenario | |
| No. of generations of random mating following the initial cross | 10 |
| Initial marker/QTL allele frequencies in founder population | |
| Breed 1 | 0.2–0.8/0.1, 0.9 |
| Breed 2 | 0.2–0.8/0.9, 0.1 |
| Distance (cM) between adjacent markers | 1 |
| Position of QTL | Halfway between markers 3 and 4 |
| Alternative effective population size | |
| Effective population size | 50, 200 |
| Distance (cM) between adjacent markers | 1 |
| Smaller QTL effect | |
| Distance (cM) between adjacent markers | 1 |
| Additive effect of QTL allele mutation | 0.5 |
Parameters for alternative populations are the same as the default except for those specified here.
Maximum-likelihood estimation:
For haplotypes with one, two, four, or six markers, phenotypic data of the final generation for a single trait were modeled as
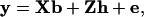 |
(1) |
where y is a vector of phenotypic values, b is a vector of fixed effects, which here reduces to the overall mean, X is the incidence matrix for b, which reduces to a vector of ones, h is the vector of random haplotype effects, Z is the incidence matrix for h, and e is the vector of residuals. The variance–covariance matrix of residuals is 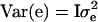 , where I is the identity matrix. The variance of the vector of haplotype effects is
, where I is the identity matrix. The variance of the vector of haplotype effects is 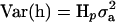 , where Hp contains the IBD probabilities for the QTL at position p. For a haplotype containing 10 markers, there are 1028 possible haplotypes, requiring Z and h to be large. So for 10 markers, phenotypic data were analyzed by an equivalent model as described in Grapes et al. (2004), which fits the genotypic effect as random.
, where Hp contains the IBD probabilities for the QTL at position p. For a haplotype containing 10 markers, there are 1028 possible haplotypes, requiring Z and h to be large. So for 10 markers, phenotypic data were analyzed by an equivalent model as described in Grapes et al. (2004), which fits the genotypic effect as random.
The IBD probabilities for the QTL based on marker haplotypes with 1, 2, 4, or 6 markers were calculated using the analytical method of Meuwissen and Goddard (2001). The IBD probabilities for the QTL based on a 10-marker haplotype were available from a previous study (Grapes et al. 2004), which used the gene drop method. Meuwissen and Goddard (2001) showed that the analytical and the gene drop methods give nearly identical results. All IBD probabilities were calculated assuming population history conditions of the default scenario for each position that the QTL could take within the haplotype window. These positions were the center of each marker bracket within the haplotype window.
Under multivariate normality, the residual log-likelihood for the model given by Equation 1 is
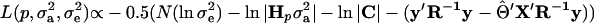 |
(2) |
(Searle 1979), where N is the number of phenotypic observations, C is the coefficient matrix of the mixed-model equations, y is the vector of phenotypic values, 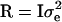 , and
, and 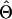 is the vector of solutions to the mixed-model equations. For every putative QTL position, p, in the haplotype window, the log-likelihood was maximized with respect to the variance components
is the vector of solutions to the mixed-model equations. For every putative QTL position, p, in the haplotype window, the log-likelihood was maximized with respect to the variance components 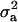 and
and 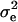 . When all 10 markers were used as the haplotype, the residual log-likelihood was obtained as described in Grapes et al. (2004). When one marker was used as the haplotype window, the QTL position was estimated at the marker locus, but for all other haplotype sizes, the QTL position was estimated at the center of a marker bracket. With haplotype windows of 4 or 6 markers, likelihoods were calculated multiple times for most marker brackets as a result of sliding the window across the 10-marker region. For these marker brackets, the highest likelihood was kept. Regardless of the haplotype size considered, the position with the highest log-likelihood overall was the estimated position of the QTL. Each scenario was replicated 1000 times for each marker haplotype window size.
. When all 10 markers were used as the haplotype, the residual log-likelihood was obtained as described in Grapes et al. (2004). When one marker was used as the haplotype window, the QTL position was estimated at the marker locus, but for all other haplotype sizes, the QTL position was estimated at the center of a marker bracket. With haplotype windows of 4 or 6 markers, likelihoods were calculated multiple times for most marker brackets as a result of sliding the window across the 10-marker region. For these marker brackets, the highest likelihood was kept. Regardless of the haplotype size considered, the position with the highest log-likelihood overall was the estimated position of the QTL. Each scenario was replicated 1000 times for each marker haplotype window size.
Comparison of methods:
To evaluate the ability of the IBD method to estimate the QTL position using marker haplotypes of various sizes, absolute differences between the estimated and true QTL positions were obtained for each replicate of a scenario as 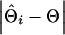 , where
, where 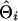 and
and 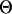 are the estimated and true QTL positions in centimorgans for replicate i. Bias of estimates of QTL position was estimated by
are the estimated and true QTL positions in centimorgans for replicate i. Bias of estimates of QTL position was estimated by 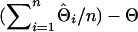 , where n is the number of replicates performed. Absolute differences for all replicates of a simulation were analyzed using ANOVA (JMP ver. 5.0; SAS Institute, Cary, NC) with haplotype size fitted as a fixed effect. Although absolute differences are not normally distributed, ANOVA is known to be robust when the sample size is large, as in this study. The least-squares mean of the absolute differences (LSMD) was obtained for each haplotype size and was used as a measure of a method's ability to estimate the position of the QTL. A method with a smaller LSMD is preferable. Also, to demonstrate the accuracy of the IBD method using different haplotype sizes, the percentage of position estimates that were in the correct marker bracket or in a flanking marker bracket was determined for each haplotype size.
, where n is the number of replicates performed. Absolute differences for all replicates of a simulation were analyzed using ANOVA (JMP ver. 5.0; SAS Institute, Cary, NC) with haplotype size fitted as a fixed effect. Although absolute differences are not normally distributed, ANOVA is known to be robust when the sample size is large, as in this study. The least-squares mean of the absolute differences (LSMD) was obtained for each haplotype size and was used as a measure of a method's ability to estimate the position of the QTL. A method with a smaller LSMD is preferable. Also, to demonstrate the accuracy of the IBD method using different haplotype sizes, the percentage of position estimates that were in the correct marker bracket or in a flanking marker bracket was determined for each haplotype size.
RESULTS
Comparison under the default scenario:
After 100 generations of random mating, marker informativeness was similar across the chromosomal region. The polymorphism information content (Botstein et al. 1980) of each marker, averaged across 1000 replicates of the default simulation, ranged from 0.23 to 0.25 for all marker spacings, which is 61–67% of the maximum for biallelic markers. Also, across 1000 replicates of the default scenario, the probability of a marker locus being fixed ranged from 0.13 to 0.16 regardless of marker spacing. Thus, variability of marker informativeness likely had little impact on mapping accuracy.
The IBD method was used to fine map a QTL using haplotype windows of 1, 2, 4, 6, or 10 markers. The average LSMD across haplotype sizes was 1.32 cM when marker spacing was 1 cM (Table 2). At this marker spacing, an average estimate deviated from the true QTL position by <2 markers or marker brackets, regardless of haplotype size. Mapping resolution increased proportionately as marker spacing decreased; average LSMD across haplotype sizes was 1.32, 0.69, and 0.39 cM for marker spacings of 1, 0.5, and 0.25 cM, respectively. Bias of QTL position estimates was close to zero (−0.4–0.1 cM) for all haplotype sizes under the default conditions. A bias of zero was expected because the QTL was positioned in the center of the chromosomal region.
TABLE 2.
Least-squares mean absolute difference (centimorgans) and percentage of QTL position estimates at or flanking the QTL obtained by the IBD method using different haplotype sizes under the default scenario
| No. of markers used in IBD method
|
|||||
|---|---|---|---|---|---|
| Marker spacing (cM) | 1 | 2 | 4 | 6 | 10 |
| 1 | 1.46a | 1.32b,c | 1.25c,d | 1.20d | 1.36a,b |
| 65.4% | 67.2% | 68.9% | 66.2% | ||
| 0.5 | 0.76a | 0.70b | 0.63c | 0.70b | 0.68b,c |
| 62.9% | 66.9% | 61.3% | 65.8% | ||
| 0.25 | 0.44a | 0.38b | 0.34c | 0.40b | 0.40b |
| 58.3% | 61.2% | 52.5% | 57.8% | ||
The mean absolute difference of the QTL position estimate from its true position for the IBD mapping method used in populations created under the default scenario is shown. The QTL is located in the center of the 10-marker haplotype. The percentage of position estimates at or flanking the true QTL position is given for each haplotype size except for one marker. For a given marker spacing, least-squares means with different superscripts (a, b, c, d) are significantly different (P < 0.05).
Depending on marker spacing, a haplotype window of 4 or 6 markers resulted in the greatest mapping precision (Table 2). When markers were 1 cM apart, a haplotype of 6 markers had the smallest LSMD, but it was not significantly different from the LSMD of a haplotype with 4 markers (Table 2). When markers were 0.5 cM apart, a 4-marker haplotype had the smallest LSMD, but it was not significantly different from a haplotype with all 10 markers. However, when marker spacing was reduced to 0.25 cM, the LSMD for the 4-marker haplotype was significantly smaller than the LSMD for any other haplotype size. Interestingly, LSMD was largest when 1 marker was fitted regardless of marker spacing (Table 2).
As expected, the probability of the QTL being mapped to its true marker bracket or a flanking one was inversely related to the LSMD of a haplotype size (Table 2). With a 1-cM marker spacing, the percentage of position estimates in or flanking the correct marker bracket was highest for a six-marker haplotype, which had the lowest LSMD. For 0.5- and 0.25-cM marker spacings, the percentage was highest for a four-marker haplotype, which had the lowest LSMD for these two-marker spacings. When fitting one marker, the QTL position is estimated at a marker locus, while the true QTL position is always centered between two markers. Thus, it is not fair to compare the position estimates from a one-marker haplotype to those of the other haplotype sizes, and the one-marker position estimates are not shown for any scenario.
Two-breed cross followed by random mating:
Two breeds were simulated, each of effective size 100, that had the same two QTL alleles but at different frequencies (see Table 1). The number of generations of random mating that occurred after the initial cross of the two breeds ranged from 1 to 100. Marker spacing was 1 cM and the QTL was at the center of the 10-marker haplotype (Table 3).
TABLE 3.
Least-squares mean absolute difference (centimorgans) and percentage of QTL position estimates at or flanking the QTL obtained from the IBD method using different haplotype sizes with 1-cM marker spacing in a two-breed cross followed by random mating
| Generations of random mating
|
No. of markers used in IBD method
|
||||
|---|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 10 | |
| 100 | 2.53a | 2.17b | 2.02c | 1.99c | 2.28b |
| 36.7% | 40.9% | 41.3% | 36.2% | ||
| 20 | 2.30a | 2.09b | 1.96c | 1.91c | 2.01b,c |
| 38.2% | 43.4% | 44.6% | 42.8% | ||
| 10 | 2.35a | 2.16b | 2.04b | 2.10b | 2.08b |
| 35.8% | 38.3% | 38.9% | 39.2% | ||
| 5 | 2.43a | 2.25b | 2.07c | 2.07c | 2.22b |
| 31.8% | 36.7% | 38.3% | 36.7% | ||
| 1 | 2.52a | 2.30b,c | 2.21c | 2.18c | 2.40b |
| 31.8% | 34.9% | 34.8% | 31.1% | ||
The mean absolute difference of the QTL position estimate from its true position for the IBD mapping method used in populations created under the crossbred scenario is shown. The position of the QTL is the center of the 10-marker haplotype, and the effective population size is 100. The percentage of position estimates at or flanking the true QTL position is given for each haplotype size except for 1 marker. For a given number of generations, least-squares means with different superscripts (a, b, c) are significantly different (P < 0.05).
Mapping precision was negatively affected by the introduction of population admixture for all haplotype sizes. Even when 100 generations of random mating followed the cross, the LSMDs were all higher than in the default scenario (Tables 2 and 3). Bias remained small, though, ranging from −0.19 to 0.15 cM. As the number of generations of random mating decreased, LSMD tended to increase for all haplotype sizes. However, when the number of generations decreased from 100 to 20, LSMD decreased for all haplotype sizes. This may be due to the fact that there were initially only two QTL alleles in this population, and after 100 generations of mating, the QTL alleles attained extreme frequencies. In 36% of the replicates with 100 generations of random mating following the cross, QTL allele frequencies were >0.85 or between 0.15 and 0.1, compared to 2% of the replicates with 20 generations of random mating, resulting in lower mapping resolution. The QTL allele frequencies never became extreme following 1 or 5 generations of random mating and became extreme for only 0.4% of replicates with 10 generations of random mating.
Regardless of the number of generations of random mating that followed the cross, haplotypes with four and six markers had numerically smaller LSMDs than other haplotype sizes (Table 3). The LSMDs of 4- and 6-marker haplotypes were significantly smaller than the LSMD for a haplotype of 10 markers when 1, 5, or 100 generations of random mating followed the cross (Table 3). Also, similar to the default, use of 1 marker consistently resulted in significantly larger LSMD than any other haplotype size.
Here, the percentage of estimates in or flanking the correct marker bracket did not always follow the LSMD of a method, in contrast to what was seen in the default scenario. With 20 and 100 generations of random mating following the cross, the percentage of estimates in or flanking the correct marker bracket was highest for the haplotype size with the smallest LSMD (Table 3). But for 10, 5, and 1 generations this was not the case, although the percentages were very similar between the haplotype sizes with the smallest LSMDs (Table 3). For example, with 5 generations of random mating, the LSMD was the same for four and six markers (2.07 cM), but the six-marker haplotype had a larger percentage of estimates in or flanking the correct marker bracket (38.3%) than the four-marker haplotype (36.7%, Table 3).
Noncentral QTL position:
In this scenario, the QTL was positioned halfway between markers three and four instead of at its central position between markers five and six as in the default scenario. Results for each haplotype size with marker spacing of 1 cM are presented in Table 4.
TABLE 4.
Least-squares mean absolute difference (centimorgans), bias (centimorgans), and percentage of QTL position estimates at or flanking the QTL obtained from the IBD method using different haplotype sizes in six alternate scenarios with 1-cM marker spacing
| No. of markers used in IBD method
|
||||||
|---|---|---|---|---|---|---|
| Alternate scenario | 1 | 2 | 4 | 6 | 10 | |
| Noncentral QTL position | LSMD | 1.53a | 1.33b,c | 1.19d | 1.23c,d | 1.38b |
| Bias | 0.62 | 0.60 | 0.53 | 0.52 | 0.51 | |
| 69.5% | 71.5% | 71.1% | 66.8% | |||
| Random founder allele frequencies | LSMD | 1.57a | 1.36b | 1.32b | 1.33b | 1.36b |
| Bias | 0.016 | 0.003 | −0.034 | 0.038 | −0.025 | |
| 63.9% | 64.2% | 64% | 63.9% | |||
| “Worst-case” scenario | LSMD | 2.67a | 2.61a,b | 2.38c | 2.38c | 2.45b,c |
| Bias | 1.75 | 1.91 | 1.60 | 1.55 | 1.56 | |
| 35.0% | 37.9% | 37.2% | 36.8% | |||
| Effective population size = 50 | LSMD | 1.91a | 1.66b | 1.53c | 1.64b,c | 1.68b |
| Bias | −0.182 | −0.034 | −0.013 | 0.172 | 0.004 | |
| 56.6% | 60.0% | 54.9% | 56.7% | |||
| Effective population size = 200 | LSMD | 1.44a | 1.18b | 1.15b | 1.09b | 1.17b |
| Bias | 0.017 | −0.009 | −0.107 | −0.029 | −0.075 | |
| 70.0% | 71.8% | 72.3% | 70.9% | |||
| Smaller QTL effect | LSMD | 1.83a | 1.76a | 1.55b | 1.60b | 1.80a |
| Bias | −0.016 | −0.083 | −0.056 | −0.086 | −0.024 | |
| 51.6% | 56.6% | 54.8% | 49.2% | |||
The mean absolute difference of the QTL position estimate from its true position and bias for the IBD mapping method used in populations created under six alternate scenarios with 1-cM marker spacing are shown. The percentage of position estimates at or flanking the true QTL position is given for each haplotype size except for one marker. For a given alternate scenario, least-squares means with different superscripts (a, b, c, d) are significantly different (P < 0.05).
The LSMDs for nearly all haplotype sizes increased when the QTL was positioned toward the beginning of the chromosomal region instead of at the center (Tables 2 and 4). Use of a haplotype with 2 markers was least affected by a noncentral QTL, as its LSMD increased by only 0.01 cM, while use of a single marker was most affected, with an increase in LSMD of 0.07 cM (Tables 2 and 4). Interestingly, the LSMD for a 4-marker haplotype decreased by 0.06 cM as compared to the default, while the LSMD for 6- and 10-marker haplotypes increased slightly (0.03 and 0.02 cM, respectively) (Tables 2 and 4). While the LSMD of the 4-marker haplotype was not significantly different from that of 6 markers under this alternate scenario, it was numerically the smallest for all haplotype sizes and also had the largest percentage of position estimates in or flanking the correct marker bracket, as expected.
Bias was observed in all cases, due to the noncentral position of the QTL. Although the four-marker haplotype had the smallest LSMD, its bias was intermediate (Table 4). Also, as the size of the haplotype increased, bias consistently decreased.
Variable marker allele frequencies:
In all previous scenarios, initial frequency of marker alleles was 0.5. Here marker allele frequencies in the founders were randomly assigned a value between 0.2 and 0.8 for each marker locus. The LSMDs, bias, and percentage of position estimates in or flanking the correct marker bracket for each haplotype size, for a marker spacing of 1 cM, are in Table 4.
For this scenario, haplotype size was a determining factor in the effect of variable marker allele frequencies on LSMD. The LSMDs for all haplotype sizes increased as compared to the default, except for a 10-marker haplotype (Tables 2 and 4). The LSMDs of haplotypes with 1 and 6 markers increased by >0.1 cM, while LSMDs of haplotypes with 2 and 4 markers increased by ∼0.5 cM with variable marker allele frequencies. Although LSMD increased in nearly all cases, the bias for all haplotype sizes remained close to zero, ranging from 0.038 to −0.034 cM (Table 4). Comparing haplotype sizes, the 4-marker haplotype had numerically the smallest LSMD and the largest percentage of position estimates at or near the true QTL, followed closely by 6 markers, but the LSMDs of both were not significantly different from that of 2 or 10-marker haplotypes. This result differs from the default scenario, in which both 4 and 6 markers were significantly better than using all 10 markers (Table 2). So, it appears that sensitivity of the IBD method to marker allele frequencies depends on the size of the haplotype that is considered.
Worst-case scenario:
The previous alternative scenarios differed from the default by only one condition. Here, several conditions were changed from the default scenario to create a worst-case scenario. First, the two breeds described previously were crossed, followed by 10 generations of random mating. Second, the QTL was positioned between marker loci three and four. Third, marker frequencies of the founders were set at random, as described previously.
The LSMD of all methods increased drastically for this worst-case scenario compared to the default (Tables 2 and 4). The average LSMD increased from 1.32 cM under the default scenario to 2.50 cM. Biases also increased markedly, from a range of −0.04 to 0.1 cM in the default, to a range of 1.55 to 1.91 cM in the worst-case scenario (Table 4). Direction of the bias was toward the center of the chromosome for all haplotype sizes. The large bias and near doubling of LSMD when compared to the default are unique to this alternative scenario. However, when comparing LSMD across haplotype sizes, the ranking of haplotype sizes was not unique. Here haplotypes of sizes 4 and 6 had the smallest LSMDs and also the highest percentage of position estimates in or flanking the correct marker bracket, although not significantly different from a haplotype size of 10 (Table 4). Again, using one marker resulted in the largest LSMD, although it was not significantly different from the LSMD for two markers.
Alternative effective population size and smaller QTL effect:
To test the general power of the IBD method with different haplotype sizes, the effective population size and the size of the QTL allele effect were changed from the default scenario (Table 1). With effective population size reduced to 50, the LSMD increased for each haplotype size as compared to the default (Tables 2 and 4). However, a haplotype size of four once again had smaller LSMD than other haplotype sizes, although it was not significantly different from the LSMD of a haplotype of six markers. The four-marker haplotype also had the largest number of position estimates in or flanking the correct marker bracket. When effective population size was increased to 200 individuals, the LSMD decreased for each haplotype size, compared to the default (Tables 2 and 4). The LSMD for the one-locus haplotype was significantly worse than the LSMDs for the other haplotype sizes, which were not significantly different from each other (Table 4). However, the six-marker haplotype did have the numerically smallest LSMD and largest percentage of position estimates in or flanking the correct marker bracket.
When the QTL effect was reduced by half, the LSMD increased for each haplotype size, compared to the default (Tables 2 and 4). In this case, haplotypes with four and six markers were significantly better than the three other haplotype sizes, which were all similar (Table 4). The four- and six-marker haplotypes also estimated the QTL to its true position or a flanking marker bracket the most frequently. In these alternative scenarios involving effective population size and QTL effect, bias remained close to zero as expected (Table 4).
DISCUSSION
Identification of optimal haplotype structure:
Fine-mapping methods that utilize LD information in outbred populations provide a means to map QTL at high resolution without having to sacrifice time and expenses to develop a mapping population. For this reason, and its relative ease of use, the IBD method of Meuwissen and Goddard (2000) and its extension to include linkage information (Meuwissen et al. 2002) have become the basis for many QTL fine-mapping studies conducted in livestock (e.g., Blott et al. 2003; Olsen et al. 2004). However, it has been shown here that additional mapping precision could be obtained with the IBD method if marker information is used in a selective manner to estimate IBD probabilities at any given position. By comparing mapping precision of the IBD method using various haplotype sizes, an apparent optimal haplotype size of four or six markers was identified for the populations simulated here. In scenarios that both adhered to assumptions about the population history for derivation of IBD probabilities and violated those assumptions, using a haplotype of four or six markers resulted in the greatest mapping resolution, as evaluated by LSMD, although differences were not always significant. However, in every scenario simulated here except one (crossbred with 10 generations of random mating), the four- and six-marker haplotypes most frequently estimated the QTL position in or flanking the correct marker bracket. Thus, the optimal haplotype structure requires a subset of markers to be used at any given position rather than all available markers.
The reduced accuracy of QTL position estimates when using all markers compared to a subset of markers is counterintuitive to the general notion that use of more information should result in better estimates. To explore this unexpected result further, we investigated several possible explanations, including the effects of the number of markers in the chromosomal region and differences in the number of times that the QTL position is tested (each position is tested only once with a 10-marker haplotype but central positions, including the QTL position, are tested multiple times with smaller haplotype window sizes). First, chromosomal regions of 4 and 6 markers with 1-cM spacing were tested in 1000 replications of the default population, using a haplotype of all markers against haplotypes containing a subset of available markers. With 4 and 6 markers in the chromosomal region, the mapping accuracy using all available markers was significantly worse (P < 0.05) than that of haplotypes containing a subset of available markers (results not shown). So, even for chromosomal regions containing different numbers of markers, fitting all markers as the haplotype resulted in consistently worse mapping accuracy compared to fitting a subset of markers. Second, the effect of multiple testing of the QTL position was evaluated by simulation of a 14-marker region, which resulted in equally frequent evaluations of the QTL position (five times) for haplotype windows of 10 and 6 markers and fewer (three times) for a haplotype window of 4 markers. The difference in mapping accuracy between the haplotype sizes was not affected compared to results from the 10-marker region; the 4- and 6-marker haplotypes had significantly greater mapping accuracy than the 10-marker haplotype (results not shown, P < 0.05). This demonstrates that the 4- and 6-marker haplotypes have no advantage over the 10-marker haplotype due to multiple testing of the true QTL position.
Correlation of IBD probabilities:
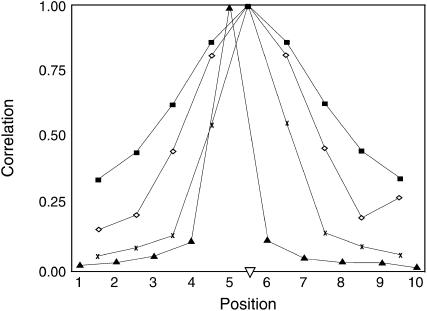
Mapping precision of the IBD method is driven by the degree of change in likelihood across the QTL region, i.e., by the sensitivity of the likelihood to the putative QTL position. This sensitivity is determined by the correlation between estimated IBD probabilities at adjacent positions across the QTL region. If this correlation is high, IBD probabilities at adjacent positions are similar and the likelihood will change very little, causing the likelihood curve to be flat. To demonstrate the impact of haplotype size used to compute IBD probabilities on the relationship between IBD probabilities for adjacent marker brackets, correlations between IBD probabilities at the true QTL position (center of the 10-locus marker region) and IBD probabilities at flanking marker brackets were obtained across 1000 replicates of the default scenario. Resulting correlations were highest (∼0.86) when IBD probabilities were based on all 10 markers and lowest (∼0.12) when only 1 marker was used (Figure 1). Thus, the true QTL position is best distinguished from its surrounding positions by fitting only one marker. With only one marker fitted as the haplotype, there is no overlap in marker information when moving from one putative QTL position to the next. In contrast, when fitting all 10 markers in the haplotype, the same set of markers is considered for every putative QTL position. Also, when fitting 10 markers there are cases where different haplotype states have similar or identical IBD probabilities associated with them; however, there are only two possible IBD probabilities that can be assigned to a QTL position when 1 marker is fit. The high correlation between IBD probabilities results in high correlations between the estimated covariance of a pair of individuals for different QTL positions, which results in similar likelihoods across positions. This makes it more difficult to distinguish between QTL positions and obtain accurate position estimates.
Figure 1.
The correlation between IBD probabilities for the true QTL position and all other putative QTL positions estimated using haplotypes of 1, 2, 4, or 10 markers. With a haplotype size of 1, the true QTL position was at position 5. Results are based on 1000 replicates of the default scenario with a marker spacing of 1 cM. (▴) IBD-1, (x) IBD-2, (⋄) IBD-4, (▪) IBD-10, (∇) QTL position.
Effects of power and sensitivity of IBD probabilities on mapping precision:
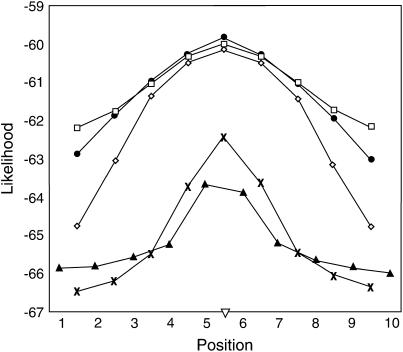
The effect of correlations among IBD probabilities at adjacent positions on shape of the likelihood curve is illustrated in Figure 2, which contains the average likelihood for each marker bracket across 1000 replicates of the default scenario for all haplotype sizes. For the 10-marker haplotype, there is not much difference in the average likelihood between the true QTL position and the outermost positions (Figure 2), indicating decreased mapping precision. The shape of the average likelihood curve of the six-marker haplotype size is similar to that of the 10-marker haplotype, although it is slightly more peaked (Figure 2). Comparing the likelihood curve for 10 markers to that of 2 markers in Figure 2, the average likelihood is much lower for 2 markers than for 10- or 6-marker haplotypes, but the former has a much greater difference between the likelihood at the true QTL position and that at the outermost positions. Thus, a 2-marker haplotype is more discriminating with regard to QTL position.
Figure 2.
The log-likelihood for each putative QTL position averaged across 1000 replicates of the default scenario with marker spacing of 1 cM. (▴) IBD-1, (x) IBD-2, (⋄) IBD-4, (•) IBD-6, (□) IBD-10, (∇) QTL position.
If fitting less marker information at each position allows greater discrimination between putative QTL positions due to decreased correlation of IBD probabilities, then, by extrapolation, using a single marker to estimate IBD probabilities should result in greatest mapping accuracy. This is, however, not what was observed in the simulations presented here (Tables 2–4). Instead, mapping accuracy was worst when using 1 marker, which demonstrates that the ability to map a QTL is also affected by the ability of the method to detect the QTL, i.e., by power. This can be discerned from the scenarios that simulated a smaller QTL effect and different effective population sizes (Table 4). As expected, when effective population size was increased to 200, thus increasing power, mapping accuracy was similar for nearly all haplotype sizes (Table 4). However, when power was reduced either by decreasing effective population size or by decreasing the size of the QTL effect, mapping accuracy was greatest for 4- and 6-marker haplotypes (Table 4). Thus, it appears that a balance is required, such that the marker haplotype window must provide enough information to detect the QTL but also sufficient discrimination between IBD probabilities at different positions, as the window is moved across the region, such that an accurate position estimate can be obtained. The nature of the relationship between these two factors can also be seen in Figure 2. The average likelihood across the chromosomal region is high when all 10 markers are fitted as the haplotype, indicating that using all markers results in high power to detect the QTL. However, using all markers does not allow for discrimination between positions, reducing accuracy. By considering the relationship between detection and discrimination of the QTL position and then examining Figure 2, it seems that a 4-marker haplotype is most favorable among the haplotype sizes considered here. The use of 4 markers provides enough information such that the average value of the likelihood is high, nearly identical to that of 6- and 10-marker haplotypes at the true QTL position, and also results in the greatest difference between the likelihood at the true QTL position and that at the outermost positions compared to all other haplotype sizes. Although the results presented in Tables 2–4 show that haplotypes of size 4 and 6 performed similarly, it may be that a 4-marker haplotype is optimal for fine mapping using the IBD method, especially when markers are closely spaced.
Comparison to regression-based fine mapping:
For populations similar to those considered here, Grapes et al. (2004) showed that regression on a single marker was as effective for fine mapping QTL as the IBD method using all 10 markers. Since fitting all available markers at each position is not optimal for the IBD method, it is worth comparing the IBD method using optimal haplotype sizes of 4 and 6 markers to the regression method. For the regression method, the number of markers genotyped was doubled from 10 to 20 because the regression method does not require haplotype information and, therefore, does not require the genotype of parents (Grapes et al. 2004). Also, results from regression on a two-locus haplotype (HAP) were included in the comparison with the IBD method, as Grapes et al. (2004) showed that HAP using 10 markers had similar accuracy as IBD with 10 markers. Under the default scenario, mapping accuracies of 4- and 6-marker haplotypes using the IBD method and regression on a single marker with 20 markers genotyped (SL-20) were not significantly different at 1 and 0.5 cM marker spacing (Table 5). However, HAP with 10 total markers in the region performed significantly worse than any other method when marker spacing was 1 or 0.5 cM (Table 5). When marker spacing was smallest, the IBD method using a 4-marker haplotype was significantly better than IBD with a 6-marker haplotype as well as the HAP and SL-20 methods (Table 5).
TABLE 5.
Least-squares mean absolute difference (centimorgans) of QTL position estimates obtained by regression-based methods and by the IBD method using different haplotype sizes under the default scenario
| Regression-based methods
|
IBD method: no. of markers used
|
|||
|---|---|---|---|---|
| Marker spacing (cM) | SL-20 | HAP | 4 | 6 |
| 1 | 1.14a | 1.35b | 1.25a | 1.20a |
| 0.5 | 0.63a | 0.71b | 0.63a | 0.70a |
| 0.25 | 0.38a | 0.40b | 0.34c | 0.40a |
The mean absolute difference of the QTL position estimate from its true position for the IBD mapping method and regression-based methods (SL-20, regression on a single marker with 20 markers in the chromosomal region; HAP, regression on a two-locus haplotype with 10 markers in the chromosomal region) used in populations created under the default scenario is shown. The QTL is located in the center of the chromosomal region. For a given marker spacing, least-squares means with different superscripts (a, b, c) are significantly different (P < 0.05).
When compared under many of the alternative scenarios described here (crossbred, noncentral QTL, variable marker allele frequencies, worst-case scenario), mapping precision of SL-20 was similar to that using the IBD method with a 4 or 6-marker haplotype except for two cases. In the crossbred population, both 4 and 6-marker haplotypes were significantly better than SL-20 when one and five generations of random mating followed the cross (data not shown). However, with variable marker allele frequencies, SL-20 had significantly greatest mapping precision (data not shown). So, SL-20 remained comparable to the IBD method, even when the more favorable haplotype sizes of 4 and 6 markers were considered and under different population conditions, except with very dense marker spacing.
It is also worth comparing the IBD method using 1 marker to single-marker regression when 10 markers are available (SL-10), as they used similar information for mapping. These methods use the same information but differ in the way the effects are modeled. The IBD method models the haplotype effect as random, and SL models the allelic effect of the marker as fixed. Comparing the methods under the default scenario and the alternative scenarios used for comparison of SL-20 and the IBD method, the mapping precisions of SL-10 and IBD with a single marker were usually not significantly different (data not shown). However, in both the crossbred population including 100 generations of random mating and the population having variable marker allele frequencies, SL-10 had significantly higher mapping precision (data not shown). Thus, the way in which information was modeled had little impact on mapping precision when a single marker was used. Once again, SL was comparable to the IBD method.
Optimal methods for fine mapping:
Of the methods examined here and in Grapes et al. (2004), fitting a 4-marker haplotype in the IBD method and SL-20 were the optimal methods for fine mapping a previously identified QTL. There is an advantage to using SL-20, though, as it does not require knowledge of haplotypes. However, if the IBD method is used for fine mapping, it would be preferable to fit a smaller haplotype instead of all available markers in the region. As seen here, using a haplotype with 4 or 6 markers as a sliding window across the region resulted in the greatest mapping accuracy compared to that of the other haplotype sizes tested. Regardless of the number of markers fit in the QTL region, though, greatest mapping accuracy was always obtained when fewer than all available markers were fit. Future fine-mapping studies utilizing the IBD method should consider testing subsets of all available markers to identify the haplotype size that results in a likelihood curve with properties similar to that of the 4-marker haplotype in this work, i.e., greatest difference between the highest likelihood (the QTL position estimate) and the lowest likelihoods at distant positions. As the IBD method is widely used for fine mapping QTL in livestock, especially in combination with linkage information, further research is important to determine if using smaller haplotype windows can improve the accuracy of the method with combined linkage and LD information. It is also important to determine if this phenomenon of obtaining higher or similar mapping precision by fitting less than all information, which has now been observed for three LD-based fine-mapping methods (Zhang et al. 2003; Abdallah et al. 2004; this work), is a property of all LD-based fine-mapping methods.
Accuracy of genetic prediction:
Although using 10 markers was not favorable for discriminating between QTL positions, IBD probabilities were most accurate when all markers were considered, i.e., when the correlation between the true IBD state of two QTL and the IBD probabilities obtained given the individuals' marker haplotype information was highest: 0.52 when 10 markers were used, 0.5 when 4 markers were used, and 0.34 when 1 marker was used. Interestingly, the higher accuracy of IBD probabilities based on 10 marker loci did not result in more accurate estimates of the genetic value of an individual compared to other haplotype sizes. In fact, at the true QTL position, the correlation between individuals' true genetic value and the best linear unbiased predictor (BLUP) (Henderson 1973) of the genetic value was the same (∼0.36) for haplotype sizes with 4 and 10 markers, but lowest for a haplotype size of 1 (∼0.27). Thus, although IBD probabilities were most accurate when all marker information was considered, this greater accuracy had little effect on the accuracy of BLUP estimates in this population and in QTL parameters.
Acknowledgments
The authors thank Dan Nettleton for his comments and contribution to this work, as well as the reviewers for their comments. This work was supported in part by funding from the U.S. Department of Agriculture-National Research Initiative, from Sygen International, from Monsanto Co., and from the Iowa Agriculture and Home Economics Experiment Station and by Hatch Act and State of Iowa funds. Laura Grapes was supported by a U.S. Department of Agriculture National Needs fellowship in quantitative and molecular genetics.
References
- Abdallah, J. M., B. Mangin, B. Goffinet, C. Cierco-Ayrolles and M. Perez-Enciso, 2004. A comparison between methods for linkage disequilibrium fine mapping of quantitative trait loci. Genet. Res. 83: 41–47. [DOI] [PubMed] [Google Scholar]
- Abecasis, G. R., L. R. Cardon and W. O. C. Cookson, 2000. A general test of association for quantitative traits in nuclear families. Am. J. Hum. Genet. 66: 279–292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blott, S., J. Kim, S. Moisio, A. Schmidt-Küntzel, A. Cornet et al., 2003. Molecular dissection of a quantitative trait locus: a phenylalanine-to-tyrosine substitution in the transmembrane domain of the bovine growth hormone receptor is associated with a major effect on milk yield and composition. Genetics 163: 253–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botstein, D., R. L. White, M. Skolnick and R. W. Davis, 1980. Construction of a genetic linkage map in man using restriction fragment length polymorphisms. Am. J. Hum. Genet. 32: 314–331. [PMC free article] [PubMed] [Google Scholar]
- Darvasi, A., and M. Soller, 1995. Advanced intercross lines, an experimental population for fine genetic mapping. Genetics 3: 1199–1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farnir, F., B. Grisart, W. Coppieters, J. Riquet, P. Berzi et al., 2002. Simultaneous mining of linkage and linkage disequilibrium to fine map quantitative trait loci in outbred half-sib pedigrees: revisiting the location of a quantitative trait locus with major effect on milk production on bovine chromosome 14. Genetics 161: 275–287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grapes, L., J. C. M. Dekkers, M. F. Rothschild and R. L. Fernando, 2004. Comparing linkage disequilibrium-based methods for fine mapping quantitative trait loci. Genetics 166: 1561–1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson, C. R., 1973. Sire evaluation and genetic trends, pp. 10–41 in Proceedings of the Animal Breeding and Genetics Symposium in Honor of J. L. Lush. American Society for Animal Science, Blackburgh, Champaign, IL.
- Meuwissen, T. H. E., and M. E. Goddard, 2000. Fine mapping of quantitative trait loci using linkage disequilibria with closely linked markers. Genetics 155: 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., and M. E. Goddard, 2001. Prediction of identity by descent probabilities from marker-haplotypes. Genet. Sel. Evol. 33: 605–634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuwissen, T. H. E., A. Karlsen, S. Lien, I. Olsaker and M. E. Goddard, 2002. Fine mapping of a quantitative trait locus for twinning rate using combined linkage and linkage disequilibrium mapping. Genetics 161: 373–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen, H. G., S. Lien, M. Svendsen, H. Nilsen, A. Roseth et al., 2004. Fine mapping milk production QTL on BTA6 by combined linkage and linkage disequilibrium analysis. J. Dairy Sci. 87: 690–698. [DOI] [PubMed] [Google Scholar]
- Searle, S. R., 1979. Notes on Variance Component Estimation: A Detailed Account of Maximum Likelihood and Kindred Methodology. Biometrics Unit, Cornell University, Ithaca, NY.
- Terwilliger, J. D., 1995. A powerful likelihood method for the analysis of linkage disequilibrium between trait loci and one or more polymorphic marker loci. Am. J. Hum. Genet. 56: 777–787. [PMC free article] [PubMed] [Google Scholar]
- Zhang, Y., N. I. Leaves, G. G. Anderson, C. P. Ponting, J. Broxholme et al., 2003. Positional cloning of a quantitative trait locus on chromosome 13q14 that influences immunoglobulin E levels and asthma. Nat. Genet. 34: 181–186. [DOI] [PubMed] [Google Scholar]