The Effects of Genotype-Dependent Recombination, and Transmission Asymmetry, on Linkage Disequilibrium

Abstract

A recent sperm-typing study by Jeffreys and Neumann suggested that recombination rates in different individuals at the DNA2 recombination hotspot appeared to be highly dependent on their genotype at a particular A/G SNP, FG11. Specifically, individuals who carried at least one copy of the A allele at this SNP exhibited rates of crossover considerably higher than those of individuals with no copies. Further, recombinant sperm from heterozygous individuals showed a preferential tendency to carry the G allele. We consider the effects of these phenomena on patterns of linkage disequilibrium and find them to be more subtle than might have been expected. In particular, our analysis suggests that, perhaps surprisingly, patterns of LD among chromosomes carrying the “hot” allele (in this case, A) will typically be similar to those among chromosomes carrying the “cold” allele (G).

MOUNTING evidence exists, both from sperm-typing experiments (Jeffreys et al. 2001) and from patterns of linkage disequilibrium (Crawford et al. 2004; McVean et al. 2004), for considerable fine-scale variation in recombination rates across the human genome. In particular, a substantial proportion of all recombination appears to occur in narrow (∼1- to 2-kb) regions termed recombination “hotspots.” However, the factors affecting the locations and intensities of these hotspots remain largely a mystery. One possible clue comes from observations in sperm-typing experiments at the DNA2 hotspot (Jeffreys and Neumann 2002), where the intensity of the hotspot in different individuals appeared to be highly dependent on their genotype at a particular SNP, FG11, near the center of the hotspot. Individuals homozygous at FG11 for the wild-type allele (AA) or heterozygous (AG) had, on average, recombination rates ∼20 times higher than those of other (GG) individuals. Furthermore, recombinant sperm from heterozygous individuals showed a preferential tendency (68–87%) to carry the G, rather than the A, allele, apparently due to biased gene conversion of markers within the hotspot. These observations can be explained by the double-strand break repair model of recombinations developed for yeast (Szostak et al. 1983), with crossover being initiated at a greater rate on chromosomes bearing the A allele (which we term the “hot” allele) than on those bearing the G (“cold”) allele (Jeffreys and Neumann 2002).

Naively, one might expect that the presence of a SNP, such as FG11, where crossovers are initialized at considerably higher rates on chromosomes carrying the hot allele than on those carrying the cold allele, might lead to quite different patterns of linkage disequilibrium (LD) among sampled haplotypes carrying the different alleles. Specifically, one might expect chromosomes carrying the hot allele to have experienced considerably more recombination in their recent ancestry, and that as a result the breakdown of LD across the SNP might be greater among these chromosomes than among chromosomes carrying the cold allele. In fact, as we demonstrate below, this is not necessarily the case: under many plausible scenarios there will be little difference in patterns of LD among the two groups, and in some cases chromosomes carrying the cold allele could actually have experienced more recombination!

This unexpected result is important for two reasons. First, it suggests that, unfortunately, in most cases it will be difficult to use patterns of LD to identify sites such as FG11 with allele-specific effects on recombination initiation and that sperm-typing experiments will remain the preferred approach to identifying such sites, despite the associated technical challenges. Second, and more positively, it means that ignoring the existence of such sites in analyses of patterns of LD (as is currently routine) should cause fewer problems than might have been expected. For example, there is considerable current interest in trying to detect signatures of selection in the human genome, and one tool for doing this is to identify regions that exhibit unusual patterns of LD (Sabeti et al. 2002; Tishkoff et al. 2003). It will be of particular interest to scan the HapMap data for such signals. But Jeffreys and Neumann's work raises the possibility that the nature of recombination itself could produce such signals. In particular, one might intuitively expect that cold alleles that seldom initiate crossover would lead to unusually long common haplotypes, which might mistakenly be interpreted as the result of a recent (or ongoing) selective sweep. Our work shows that this explanation is considerably less plausible than it initially appears, thus diminishing the concern that sites such as FG11 could be a serious complicating factor in detecting selection from genomewide data.

METHODS AND RESULTS

To set up our calculation we introduce some notation. Suppose that in a population (which we assume is in Hardy–Weinberg equilibrium) there is a single SNP whose genotype affects crossover initiation and that the two alleles (hot, H, and cold, C) have population allele frequencies f_H and f_C. Assume that the probability of a recombination occurring just either side of this SNP in a transmission from an individual is r_CC, r_HC, or r_HH, depending on the individual's genotype (CC, HC, or HH) at this SNP. To model the biased gene conversion observed by Jeffreys and Neumann (2002), suppose that recombinant molecules from heterozygous (HC) individuals carry the C allele with probability q_C.

We now compare the expected amount of recombination experienced in the previous generation by haplotypes currently carrying the C vs. H alleles. We do this by computing the ratio p_C:p_H, where p_C (respectively p_H) is the proportion of chromosomes carrying the cold (respectively hot) allele that are the result of a recombination in the previous generation. To simplify this computation we make the assumption that the frequencies of the two alleles in the current generation are the same as those in the previous generation. There are two reasons that this assumption will not hold exactly in practice. The first is drift, but this will have a negligible effect over a single generation provided the population is sufficiently large. The second is the biased gene conversion, but this will also produce negligible change in allele frequencies provided that r_HC ≪ 1. To see this note that, if the frequency of the cold allele in the current generation is f_C then, ignoring drift, its frequency in the next generation is f_C′ = f_C² + 2f_Cf_H(r_HCq_C + 0.5(1 − r_HC)) = f_C(1 + f_Hr_HC(2q_C − 1)), which is ≈f_C if r_HC ≪ 1. In practice we expect r_HC ≪ 1 as recombination, even in hotspots, is relatively rare (e.g., at FG11 r_HC ≈ 1/28,000).

Having made this simplifying assumption, application of elementary rules for conditional probability gives

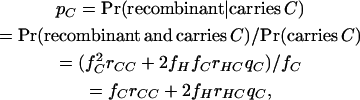and similarly

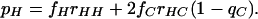To consider some concrete cases:

1. If q_C = 1, corresponding to “extreme” bias in the gene conversion, and r_CC is negligible compared with r_HC and r_HH, then p_C:p_H = 2r_HC:r_HH, independent of the allele frequencies. Thus if r_HH = r_HC (which is consistent with Jeffreys and Neumann's observations) then lineages currently carrying the cold allele will have experienced more recombination than lineages carrying the hot allele! If r_HH = 2r_HC, which might also be considered plausible, then the two types will have experienced the same amounts of recombination.

2. If we use parameters roughly based on observations at FG11 in DNA2, r_CC = r_HC/20 = r_HH/20, q_C = 0.8, f_C = 0.52, and f_H = 0.48, then p_C:p_H = 1:0.87, and so cold lineages will have experienced very slightly more recombination in the previous generation.

3. If f_H is small then it is possible that p_C could be considerably smaller than p_H. For example, if f_H = 0.05, r_CC is negligible compared with r_HC, r_HC = r_HH, and q_C = 0.8, then p_C:p_H = 1:5.4.

Note that the value of the ratio in this last scenario is somewhat sensitive to exactly how negligible r_CC is compared with r_HC and r_HH. For example, if instead of being entirely negligible, r_CC is smaller by a factor of 20 (r_CC = r_HC/20 = r_HH/20), then p_C:p_H = 1:3.4. It is also sensitive to the value of q_C. For example, if q_C = 0.9 instead of 0.8 then p_C:p_H = 1:2.7. The most extreme case would occur if r_CC is entirely negligible compared with r_HC and r_HH, and q_C ≪ 1. This seems unlikely if, as appears to be the case, the biased gene conversion is a direct consequence of the hot strand initiating recombination more frequently (since in that case the smaller r_CC is compared with r_HC the closer q_C would be expected to be to 1). Nevertheless, the case where f_H is small seems the most plausible scenario under which the ratio p_C:p_H could become extreme (very large or small). In principle, the ratio could also become extreme if the bias in gene conversion were in the opposite direction, strongly in favor of the hot allele (q_C ≈ 0), or if the recombination rates in heterozygotes were considerably smaller than those in hot-allele homozygotes (r_HC ≪ r_HH). The former of these (q_C ≈ 0) seems unlikely, since it appears inconsistent with the current double-strand break model for recombination. The latter, while not the case at FG11, is perhaps more plausible and could presumably lead to more extensive LD on haplotypes carrying the cold allele.

This final caveat notwithstanding, the initial calculations above suggest that typically there will be little detectable difference between patterns of LD among chromosomes carrying the hot vs. cold alleles. For example, current methods for identifying hotspots from LD data (Crawford et al. 2004; McVean et al. 2004) have limited power for hotspots that experience recombination at <10 times that of the surrounding sequence. Although the problems are different, and perhaps difficult to compare, this suggests to us that distinguishing between alleles that experience rates of recombination that differ by only a factor of 2 will be difficult. However, care is needed, since the calculations deal only with transmissions from the previous generation, whereas patterns of LD will depend on recombinations experienced on ancestral lineages back many generations. Since p_C:p_H can depend on the frequency of the hot and cold alleles, and these vary over time, it remains possible that differences will be greater than predicted on the basis of current allele frequencies. In particular, if the cold allele were the ancestral type (which is not the case at FG11) then the hot allele frequency will decrease to zero at some point in the past, in which case, as noted above, p_C could have been much smaller than p_H in the past. On the other hand, patterns of LD among hot- and cold-bearing chromosomes would be expected to differ considerably only if p_H ≫ p_C over many generations.

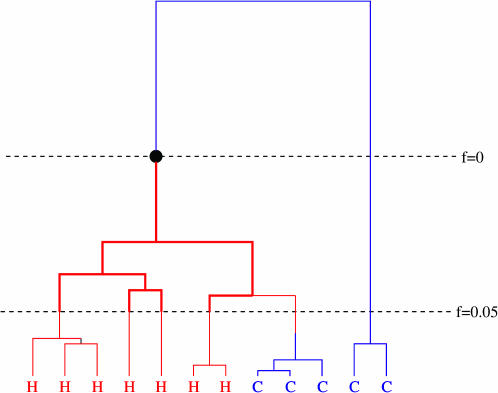
To examine this possibility in more detail it is helpful to consider the genealogy of a sample of chromosomes bearing hot and cold alleles. Consider a site S just downstream of the hot/cold SNP, and assume for simplicity that all recombination that initiated at the hot/cold SNP occurs between the hot/cold SNP and S (a similar argument can be made to deal with recombinations that occur just upstream of the SNP). Figure 1 illustrates a possible genealogy at S. The reason for focusing on the genealogy at S is that the breakdown in LD just downstream of the hot/cold SNP will be affected by recombinations that occur in chromosomes that are ancestral at S or in other words by recombinations that occur on this genealogy. In Figure 1, each ancestral lineage is color coded according to whether the corresponding ancestor carries the hot or cold allele, so at the bottom of the figure the colors represent the hot/cold status of sampled haplotypes. We argue that the amount of recombination expected to occur on the genealogy of the sampled cold haplotypes is similar to the amount expected to occur on the genealogy of the hot haplotypes and that therefore, all other things being equal, the breakdown in LD just downstream of the hot/cold SNP will not differ greatly between the two types.

Figure 1.

Genealogy of a sample of chromosomes carrying hot alleles (H) and cold alleles (C). Time runs backward from bottom to top. The black circle represents the mutation (C to H) that created the SNP. The horizontal dashed lines indicate the times at which the hot allele is at frequencies 0.05 and 0. The thick solid lines indicate the genealogy G referred to in the text.

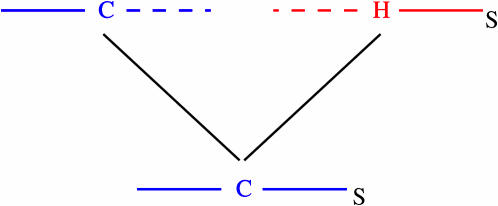
Our first observation is that, due to recombination between the hot/cold SNP and S, ancestors of current cold-bearing chromosomes may themselves have carried the hot allele, and vice versa, which will tend to deplete any distinction between the two types. In Figure 1 this appears as a sudden change in the color of an ancestral chromosome, from blue to red (going backward in time). For added clarity a transmission event that may have caused this change is illustrated in Figure 2. Due to biased gene conversion it will be more common for ancestors of cold-bearing chromosomes to carry the hot allele, as illustrated in the figures, than for ancestors of hot-bearing chromosomes to carry the cold allele.

Figure 2.

Illustration of how, due to recombination, an ancestral lineage at S may change from being a cold-bearing chromosome to a hot-bearing chromosome. Each horizontal line represents a chromosome, with the chromosome at the bottom being the result of a recombination between the two chromosomes at the top. DNA that is transmitted to the bottom chromosome is shown as solid lines and nontransmitted DNA as dashed lines. Genetic material is color coded red or blue according to whether it is on a chromosome carrying a hot or a cold allele. If one traces back the ancestry of the SNP S, it changes from being on a cold-bearing chromosome to being on a hot-bearing chromosome.

However, even without this effect we argue that the amount of recombination expected to occur on the genealogy of the sampled cold haplotypes will typically be similar to the amount expected to occur on the genealogy of the hot haplotypes. Although the ratio p_C:p_H is changing continuously over time, to simplify the discussion assume that it is negligibly different from 1 until f_H first drops below 0.05, at which point it becomes considerably different (because p_C becomes small). Thus, in the portion of the genealogy between the horizontal dotted lines in Figure 1, the cold lineages experience recombination at a rate substantially lower than the hot lineages. However, this will have an observable effect on patterns of LD only if there are several recombinations on the hot lineages during this period. Let G denote the subgenealogy that consists of ancestors of those sampled chromosomes that carry the hot allele, during this period (Figure 1, thick solid lines), and L denote its total length (in number of meioses). The expected number of recombinations will depend on both the recombination rates (r_HH, r_HC) and the distribution of L, which in turn depends on the number of extant hot lineages (m, say) at the bottom of G. (In Figure 1, m = 4.) If we make the “worst-case” assumption, that all the m ancestral hot lineages remain hot all the way back to the time of the mutation that created the H allele, then, conditional on f_H = 0.05, and on m, the genealogy G has the same distribution as the genealogy of a random sample of m chromosomes that carry a variant at frequency 0.05. This distribution has been studied extensively for both neutral and selected variants (Griffiths and Tavaré 1998; Wiuf and Donnelly 1999; Stephens 2000; Wiuf 2001; Stephens and Donnelly 2003). It turns out that the expected length of G is bigger under neutrality than under either positive or negative selection (Wiuf 2001; Stephens and Donnelly 2003) and that even under neutrality the expected length is rather small. For example, even if m = 100 the expected length of G is only ∼26,000 meioses (computed using simulation as in Stephens and Donnelly 2003) for a constant-sized random-mating population of 10,000 diploid individuals. [Although human populations are neither constant sized nor randomly mating, this simple model appears to fit African data fairly well (Frisse et al. 2001) and is often used as a guide to what might be expected for a worldwide sample of humans; if we accounted for the bottleneck apparently experienced by Europeans the expected number of meioses would be smaller.] At many hotspots one would expect few recombination events in this many meioses [e.g., among those carrying the hot allele at FG11 the average rate of crossover in the hotspot was ∼1/28,000 meioses (Jeffreys and Neumann 2002)]. Furthermore, as Jeffreys and Neumann (2002) point out, the biased gene conversion at sites such as FG11 will result in selection against the hot allele, reducing the expected length of G.

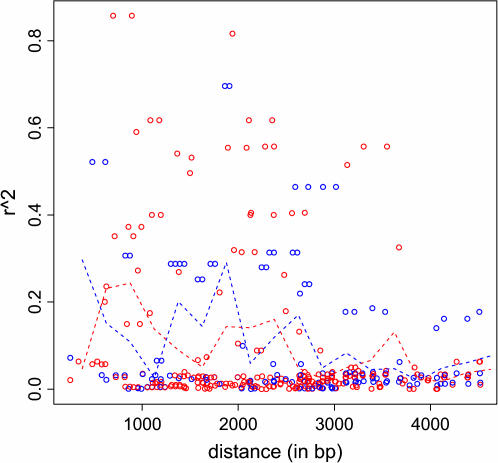
The only real data available to test the predictions of our calculations are the data from Jeffreys and Neumann (2002), which consist of SNP genotypes for 100 Caucasians in the region surrounding FG11 in the DNA2 hotspot. We estimated haplotypes for 33 SNPs in a 4.5-kb region surrounding this hotspot using PHASE v. 2.1 (Stephens et al. 2001; Stephens and Scheet 2005). (We restricted the analysis to only 4.5 kb to avoid the neighboring DNA1 and DNA3 hotspots.) Figure 3 compares the breakdown in LD (r²) across this hotspot, among haplotypes carrying the hot vs. cold alleles. Consistent with our calculations, the plot shows no clear systematic difference between the breakdowns in LD in the two groups, and if one did not know which group corresponded to which allele it would be difficult to deduce this from the plot. Similar plots using |D′| to measure LD instead of r² also show no clear systematic difference. However, these observations provide only limited support for our findings. Not only is this just one example, but also it is unclear how best to assess differences in patterns of LD among the two groups. It is possible that there are differences that cannot be discerned by visual inspection of plots of pairwise LD (such as Figure 3), but that could be detected by more sophisticated (currently undeveloped) methods. This factor also makes it slightly tricky to evaluate our conclusions through simulation studies.

Figure 3.

Graph of squared correlation coefficient, r², against distance. Each circle corresponds to a pair of SNPs that spans the FG11 SNP (i.e., each pair contains a SNP on either side of FG11). The red circles show r² computed using only chromosomes carrying the “hot” allele, and blue circles show r² computed using only chromosomes carrying the “cold” allele. The dashed lines show average r²-values for each group in nonoverlapping 250-bp windows, plotted at the midpoint of each window.

In summary, it seems that striking differences in the rates of crossover among genotypes at SNPs such as FG11 will have a more subtle effect on patterns of LD than one might naively have expected. In particular it seems that, in most cases, chromosomes carrying the cold allele at such SNPs will show similar decay of LD to those carrying the hot allele. One possible exception to this is if only individuals homozygous for the hot allele experience elevated recombination rates, although this is not the case at FG11 and it remains unclear whether this ever occurs in practice. Consequently, the existence of haplotype-dependent recombination should not be invoked as an explanation for unusual patterns of LD without careful consideration. Unfortunately, our results also suggest that it may be challenging to use differences in patterns of LD among chromosomes carrying different alleles to identify SNPs such as FG11 and even harder to identify which allele is hot and which is cold on the basis of LD alone. Of course, LD data may nevertheless be helpful in identifying sites that affect crossover initiation, since such sites will likely be near the center of hotspots, and patterns of LD are informative for hotspot location.