Abstract
Whole-genome profiling of gene expression in a segregating population has the potential to identify the regulatory consequences of natural allelic variation. Costs of such studies are high and require that resources—microarrays and population—are used as efficiently as possible. We show that current studies can be improved significantly by a new design for two-color microarrays. Our “distant pair design” profiles twice as many individuals as there are arrays, cohybridizes individuals with dissimilar genomes, gives more weight to known regulatory loci if wished, and therewith maximizes the power for decomposing expression variation into regulatory factors. It can also exploit a large population (larger than twice the number of available microarrays) as a useful resource to select the most dissimilar pairs of individuals from. Our approach identifies more regulatory factors than alternative strategies do in computer simulations for realistic genome sizes, and similar promising results are obtained in an application on Arabidopsis thaliana. Our results will aid the design and analysis of future studies on gene expression and will help to shed more light on gene regulatory networks.
THE combined study of gene expression and molecular marker data was proposed in 2001 as a novel strategy for the analysis of regulatory networks (Jansen and Nap 2001). The strategy has attracted attention both conceptually (Darvasi 2003; Kraft and Horvath 2003; Jansen and Nap 2004) and practically in a number of real-life applications in yeast, mouse, rat, maize, and human (Brem et al. 2002; Yvert et al. 2003; Schadt et al. 2003, 2005; Morley et al. 2004; Bystrykh et al. 2005; Chesler et al. 2005; Hubner et al. 2005). The genetics of gene expression have been studied in 40 and 86 haploid yeast segregants (Brem et al. 2002; Yvert et al. 2003), 111 F2 mice (Schadt et al. 2003), 30 or 34 recombinant inbred mice (Bystrykh et al. 2005; Chesler et al. 2005), 76 F3 maize lines (Schadt et al. 2003, 2005), 56 and 94 human familial individuals (Schadt et al. 2003; Morley et al. 2004), and 30 recombinant inbred rats (Hubner et al. 2005), by using the common reference design in two-color microarrays (Brem et al. 2002; Yvert et al. 2003; Schadt et al. 2003) or by using single-color microarrays (Morley et al. 2004; Bystrykh et al. 2005; Chesler et al. 2005; Hubner et al. 2005). Despite the remarkable results obtained in these initial studies, it is noted that the power of differential expression analysis is still limited because of the relatively small population sizes. It would be much better to profile several hundred individuals (Churchill et al. 2004), but then the costs may become prohibitive and require that resources—microarrays and population—are used as efficiently as possible. Can we generate more informative data with two-color microarrays than with single-color microarrays? Two-color microarrays can provide twice as much data as single-color microarrays, at least in principle. Is there any room for improving on the well-known common reference and loop designs for two-color arrays where samples are compared to a common reference sample or to each other in a loop order (Churchill 2002; Jansen 2003b)? Ratio-based analysis minimizes the risk of bias as a result of spot or array effect (Wit and McClure 2004); signal-based analysis obtains information about genotype effects also from the differences between spots (Wolfinger et al. 2001). Which method of data analysis should one prefer? We develop answers to all of the questions posed. Particularly, we demonstrate that a new strategy for two-color microarrays, coined the “distant pair design,” and analysis can outperform alternative strategies. The structure of this article is as follows. First we focus on two-color microarrays and we argue that standard methods for design and analysis of expression data can be applied but that we should be able to do much better by fine tuning to the genetics. Then we elaborate on the computational details underlying these arguments, and we show how to design and analyze an improved ratio-based strategy. Next we report results from a real study with Arabidopsis thaliana and results from computer simulations, evaluating the power of alternative strategies for different sizes of genome and population. Thereafter we compare ratio-based to signal-based analysis and two-color to single-color microarrays. Finally we summarize and discuss the consequences for experimental planning of a genetic study of gene expression.
MATERIALS AND METHODS
Recombinant inbred lines:
To illustrate the design issues involved, we consider expression profiling a population of recombinant inbred lines (RILs). RILs are homozygous individuals, which result from repeated self–self mating or sibling mating, starting from an F1 of two homozygous parents, carrying alleles of type A and type B, respectively. The genome of a RIL is therefore a mosaic of the “founder” genomes, which can be viewed with the aid of molecular markers (Figure 1). The aim of a “genetical genomics” experiment is to test along the genome for differences in average expression between the individuals carrying genetic variant A and those carrying B. In this way quantitative trait loci (QTL) underlying expression variation can be mapped and classified as cis-acting (if gene and QTL colocalize) and trans-acting (no colocalization).
Figure 1.
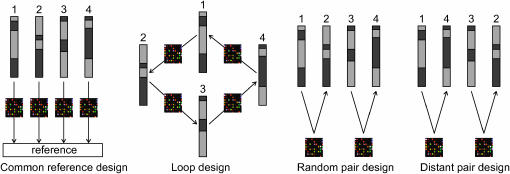
Illustration of four alternative experimental designs. The hypothetical compositions of four genetically different homozygous individuals are shown, each individual carrying different mixtures of two founder genomes (dark and light shading). Four alternative designs to pair samples with two-color microarrays are indicated: the common reference design (all samples are compared to the same reference), the loop design (pairs of samples are made in loop order), the random design (samples are randomly paired), and the distant pair design (samples with dissimilar genomes are paired).
Alternative experimental designs for two-color microarrays:
Now assume that funding allows buying or making n two-color microarray slides. Per microarray two samples can be compared by using a red and a green dye label (the red label for one sample, the green for the other one), so that 2n samples can be profiled in total. The idea of the so-called common reference design is to compare all samples to one and the same reference: each of the n RILs is profiled once, and half of the microarray resource goes into the reference—not an ideal situation (Figure 1). In a more attractive alternative, the loop design, the first RIL cohybridizes with a second RIL on one array, this second RIL with a third RIL on a second array, and so on. This way n RILs can be profiled, not just once as in the common reference design, but twice—a serious improvement in the use of microarray resources (Figure 1). On second thought, however, one is not interested in comparing the first RIL to the second one or any other pair of RILs: there is no real need to loop RILs. Moreover, technical replicates should not be used in place of biological replicates (Speed 2003; Wit and McClure 2004). One could equally well use a random pair design, where the first RIL is compared to a randomly chosen second RIL, a third RIL to a fourth RIL, and so on, so that in total 2n genetically different RILs can be profiled (Figure 1). In each direct comparison between RIL i and RIL j with red and green dye, respectively, there are four possible combinations at a given marker: A/B (RIL i carries allele A, RIL j carries allele B), B/A (RIL i carries allele B, RIL j carries A), and A/A or B/B (they carry the same alleles). These four combinations occur with equal probability in a random pair design. We are primarily interested in detecting differential expression between A and B; thus A/B and B/A are of interest, and A/A and B/B are not. Having realized this, a natural next step is to improve the random pair design in a way that the number of A/B and B/A comparisons is maximized, preferably in equal ratio to balance red and green dye (Dobbin et al. 2005a,b), and with minimal extra variation of total numbers of A/B and B/A across the different markers. We therefore propose to cohybridize RILs that show to be genetically distant according to their molecular marker fingerprints, and we coin our design the distant pair design (Figure 1). The optimal design—a design with as many informative A/B and B/A comparisons as possible—is generated using a statistical optimization technique called simulated annealing; the data generated according to this design can be analyzed for significant differential allele expression A/B and B/A, using a method of QTL mapping (see the next sections for details).
Quantitative trait locus analysis of gene expression variation:
A gene's expression variation may be caused by genetic variation at a regulatory locus (in cis if the gene and regulator coincide, in trans otherwise): the expression level of the gene under study may be high (low) when the regulator locus has genotype A (B) or vice versa. We can observe two types of ratio: the informative A/B and B/A and the relatively uninformative A/A and B/B. The expression ratios of the latter type should be close to unity (zero on log scale), unless there is dye bias. This can be translated into a mathematical model 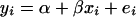 , where yi is the gene's log ratio at the ith microarray (i = 1, … , n); α is the gene-specific differential effect between dyes Cy3 and Cy5 (characterized as consistent across samples in Dobbin et al. 2005b); β is the effect of differential allele expression between A and B at a regulatory locus (or nearby marker) under study; and xi takes the following values: 1 for A/B, −1 for B/A, and 0 for A/A and B/B. In matrix form
, where yi is the gene's log ratio at the ith microarray (i = 1, … , n); α is the gene-specific differential effect between dyes Cy3 and Cy5 (characterized as consistent across samples in Dobbin et al. 2005b); β is the effect of differential allele expression between A and B at a regulatory locus (or nearby marker) under study; and xi takes the following values: 1 for A/B, −1 for B/A, and 0 for A/A and B/B. In matrix form 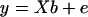 , where
, where 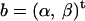 . All standard analysis of variance theory applies; e.g., the estimate of b is
. All standard analysis of variance theory applies; e.g., the estimate of b is 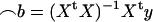 , the variance–covariance matrix of
, the variance–covariance matrix of 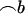 is
is 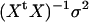 , and the test for differential allele expression follows an F-distribution (null hypothesis β = 0 vs. alternative hypothesis β ≠ 0). The ratios A/B and B/A are converted into differences log(A/B) − log(B/A) = 2{log(A) − log(B)} and used for estimating β and calculating the genotype mean squares in the numerator of the F-test. All four ratios A/B, B/A, A/A, and B/B are used for calculating the error mean squares in the denominator of the F-test. The model can be regarded as a ratio-based modification of the standard QTL model; missing or incomplete marker data can be handled likewise (Jansen 2003a; Sen et al. 2005). The model can also be extended, e.g.,
, and the test for differential allele expression follows an F-distribution (null hypothesis β = 0 vs. alternative hypothesis β ≠ 0). The ratios A/B and B/A are converted into differences log(A/B) − log(B/A) = 2{log(A) − log(B)} and used for estimating β and calculating the genotype mean squares in the numerator of the F-test. All four ratios A/B, B/A, A/A, and B/B are used for calculating the error mean squares in the denominator of the F-test. The model can be regarded as a ratio-based modification of the standard QTL model; missing or incomplete marker data can be handled likewise (Jansen 2003a; Sen et al. 2005). The model can also be extended, e.g., 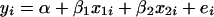 , to dissect the expression variation into the effects of two or more different regulatory loci or QTL on the genome. In a full genome scan, differential allele expression is tested at all (combinations of) markers along the genome to detect one or multiple QTL.
, to dissect the expression variation into the effects of two or more different regulatory loci or QTL on the genome. In a full genome scan, differential allele expression is tested at all (combinations of) markers along the genome to detect one or multiple QTL.
Finding the optimal design:
We define a distant pair design to be optimal for a given marker if it minimizes the sum of the variances of 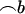 . This is equivalent to minimizing the sum of the diagonal elements (the trace) of the matrix
. This is equivalent to minimizing the sum of the diagonal elements (the trace) of the matrix 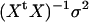 . In our model
. In our model  ; this reduces to finding the minimum of
; this reduces to finding the minimum of  . Note that this favors a design with large
. Note that this favors a design with large  and small
and small  . Here
. Here 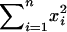 represents the total number of informative A/B and B/A comparisons (which should be large), and
represents the total number of informative A/B and B/A comparisons (which should be large), and 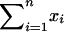 represents the difference between the number of A/B comparisons and the number of B/A comparisons (which should be small, i.e., dyes should be well balanced).
represents the difference between the number of A/B comparisons and the number of B/A comparisons (which should be small, i.e., dyes should be well balanced).
We define a distant pair design to be optimal over all markers if the sum over all markers of the variances of 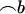 is minimized. We denote this sum by S hereafter. It reads
is minimized. We denote this sum by S hereafter. It reads 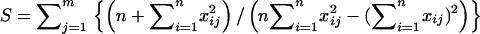 , where j refers to the jth marker (j = 1, … , m).
, where j refers to the jth marker (j = 1, … , m).
We used a technique called simulated annealing to find a design that is optimal or close to optimal (Kirkpatrick et al. 1983; Wit and McClure 2004). The search was iterative and at any particular iteration step compared the current design with a slightly modified version: samples of two randomly chosen pairs {a, b} and {c, d} in the current design were randomly repaired in the new one. Or elements in a randomly chosen pair {a, b} were replaced by one or two samples randomly drawn from the unused part of a larger resource population (selective phenotyping). The new design was accepted if it was better (has a lower value of S) than the old one. It is useful also to accept worse designs with a certain probability to be able to move away from “locally optimal” designs. This probability was 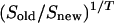 , where T was a tuning parameter that was slowly lowered to zero during the iterative process. One can start from any arbitrary design, but starting at a good initial design can clearly save a lot of computational time. We used a simple heuristic approach to select a reasonable design to be used as a starting point for the simulated annealing procedure: we iteratively selected distant pairs without replacement (starting with a random RIL, selecting a second and distant RIL, randomly taking a third RIL, and so on), taking dye balance into account.
, where T was a tuning parameter that was slowly lowered to zero during the iterative process. One can start from any arbitrary design, but starting at a good initial design can clearly save a lot of computational time. We used a simple heuristic approach to select a reasonable design to be used as a starting point for the simulated annealing procedure: we iteratively selected distant pairs without replacement (starting with a random RIL, selecting a second and distant RIL, randomly taking a third RIL, and so on), taking dye balance into account.
Arabidopsis experiment:
The Arabidopsis RIL population consists of 159 individuals from a cross of Landsberg erecta (Ler) and Cape Verde Islands (Cvi) (Alonso-Blanco et al. 1998). The individuals were paired using a core set of 99 markers, evenly spread over the five chromosomes. Samples were expression profiled using 80 two-color microarrays [QIAGEN–Operon (Valencia, CA/Alameda, CA) Arabidopsis genome oligo set Version 2.10.2]. Data were corrected for background and dye effect and normalized within and between arrays according to methods described in Yang et al. (2001). We analyzed the normalized data in two ways: ratio based (described above) and signal based (described below).
The simulation study:
To better understand the relative performance of alternative experimental designs, we mimicked the above Arabidopsis experiment in a computer simulation, assuming availability of 160 RILs and a genome size of 500 cM. We also simulated experiments with larger genome sizes. The two-color data were simulated in a number of steps. First, marker genotypes of 160 RILs were generated for a genome of a given size (500, 1000, 2000, and 4000 cM, with chromosomes of size 100 cM, each chromosome carrying 21 equidistant markers). Then, assuming availability of 80 two-color microarrays, 80 hybridization combinations were selected using the loop design (loop), the random pair design (ranPair), the distant pair design (disPair), and the common reference design (comRef with 80 arrays). The latter design was also generated for 160 two-color microarrays (comRef with 160 arrays). Finally, hybridization signals were simulated for all pairs of RILs. The hybridization signal sij for a RIL at a given spot on the ith microarray (i = 1, … , n) with the jth dye (j = 1, 2) was simulated using the model log(sij) = m + Gij + Bij + T1i + T2ij, where m is the overall mean, Gij is the genotype effect, Bij is the biological sampling error, T1i is the common technical error for observations at the same spot, and T2ij is the remaining technical error. The model was also used to simulate single-color microarray data (let j take only the value 1).
Genotype effect was simulated for a single quantitative trait locus (QTL) located at 35 cM on the first chromosome and with allele substitution effect of 0.15 (+0.15 for those RIL homozygous A at the QTL and −0.15 for those homozygous B, median QTL effect in the Arabidopsis experiment, explaining 6.4% of the phenotypic variance).
Errors were randomly and independently drawn from normal distributions. Biological sampling error was generated with standard deviation 0.2, technical error T1i with standard deviation 0.5, and technical error T2ij per hybridization with standard deviation 0.2 (levels of noise as observed in the Arabidopsis experiment). In the common reference design, one biological reference sample with one and the same genotype effect and biological sampling error in all hybridizations (Gi2 ≡ G2, Bi2 ≡ B2) was used (i.e., no biological replication, just “pure” technical replication). In the loop design we used Bij ≡ Bi′j′ for the observations on the same RIL (again just pure technical replication).
We simulated 80 two-color microarrays to 80 or 160 single-color microarrays, assuming that the two technologies would both suffer from the same sources of technical noise T1i and T2ij at different levels: up to four times less noise (in terms of variance) in single-color arrays than in two-color microarrays.
Analysis of simulated data:
Ratio-based analysis of common reference data was standard: for each array we calculated the expression ratios yi = log(si1) − log(si2) between a RIL and the common reference and then compared at each marker the ratios from the RILs carrying the A allele to those carrying the B allele using a standard F-test. Ratio-based analysis of data from the other designs requires some further elaboration. First we calculated log ratios yi = log(si1/si2) = log(si1) − log(si2) = m + Gi1 + Bi1 + T11 + T2i1 − (m + Gi2 + Bi2 + T12 + T2i2) = Gi1 − Gi2 + Bi1 − Bi2 + T2i1 − T2i2 for the ith pair of cohybridized RILs. Note that this eliminates the T1i error. Then we translated this into the ratio-based model 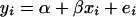 that we have developed above. Here, the xi depends on the RIL's genotypes Gi1 and Gi2 at the marker under study: xi = 1 for A/B, 0 for A/A or B/B, and −1 for B/A. The ei's represent the composite error Bi1 − Bi2 plus T2i1 − T2i2 and these ei's are independent in the random and distant pair designs, but not in the loop design.
that we have developed above. Here, the xi depends on the RIL's genotypes Gi1 and Gi2 at the marker under study: xi = 1 for A/B, 0 for A/A or B/B, and −1 for B/A. The ei's represent the composite error Bi1 − Bi2 plus T2i1 − T2i2 and these ei's are independent in the random and distant pair designs, but not in the loop design.
Alternatively, the signal-based model log(sij) = m + Gij + Bij + T1i + T2ij can be used as the starting point for a signal-based analysis of two-color microarray data. We treated the error components Bij, T1i, and T2ij as random (Wolfinger et al. 2001). The two error components Bij and T2ij are confounded in the random pair and distant pair designs (but not in the loop design) and in these cases the model used in the analysis reduces to log(sij) = m + Gij + T1i + eij, where eij represents the composite errors Bij and T2ij. We used this signal-based model also to analyze our Arabidopsis data. The loop design can be analyzed by using the full model log(sij) = m + Gij + Bij + T1i + T2ij, where Bij ≡ Bi′j′ for observations on the same RIL.
The signal-based model log(sij) = m + Gij + Bij + T1i + T2ij can also be used to analyze single-color microarray data (j takes only the value 1). However, in this case the three error components Bij, T1i, and T2ij are confounded and the model used for analysis reduces to log(sij) = m + Gij + eij, where eij represents the composite error terms Bij, T1i, and T2ij.
For all designs and methods of analysis, differential expression was tested at each marker using the F-test, and in all simulations the minimum P-value along the first chromosome was stored and its distribution over 10,000 runs per simulation setting was plotted [as −log10(P)].
RESULTS
Case study on Arabidopsis:
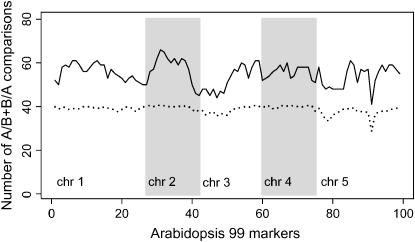
We designed the experiment for a recent study of genetical genomics in A. thaliana. The Arabidopsis RIL population contains 159 individuals. In a random pair design, one would expect half the cohybridizations to give informative ratios A/B or B/A: 40 in the Arabidopsis study. The distant pair approach increased the number to on average 55 (exceeding average values of 40 under the random pair design; Figure 2). Thus, our strategy of pairing distant genotypes led to a significant increase of informative A/B and B/A cohybridizations over the random pair design. We analyzed our Arabidopsis data with the QTL approach. A total of 2829 and 3011 of 24,065 expressed genes showed significant QTL at P < 10−5 in the ratio-based and signal-based analyses, respectively, with strong overlap between the two sets.
Figure 2.
The distant pair design for Arabidopsis. A real-life case study demonstrated the increase in the number of informative comparisons A/B and B/A in the distant pair design as compared to the random pair design. The solid line indicates the numbers of A/B and B/A cohybridizations in the distant pair design. The dotted line indicates the numbers of A/B and B/A cohybridizations at each genome position averaged over 1000 different realizations of the random pair design.
Simulation study—mimicking Arabidopsis genome size:
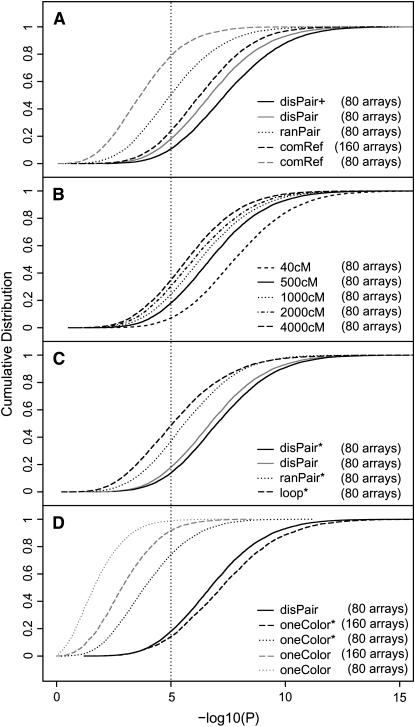
We performed a computer simulation study with 160 RILs and a genome consisting of five chromosomes of 100 cM each, i.e., comparable to our real-life Arabidopsis experiment. Figure 3A shows that the distant pair design (solid line) outperforms both the random pair design (dotted line) and the common reference design (dashed line) with 80 arrays (1.6 and 3.9 times more QTL detected using threshold P = 10−5, respectively). The difference in power between the random pair design and the distant pair design can be explained by the increased number of informative comparisons A/B and B/A in the latter design. The difference in power between these two designs and the common reference design can be explained by the fact that both the random pair design and the distant pair design allow for direct comparison of A to B in the cohybridizations A/B and B/A, while this comparison is indirect (calculated via the reference R) in the common reference design with cohybridizations A/R and B/R (the technical error from the reference R adds noise to the comparison of A to B). The common reference design with 160 arrays had more power than the common reference design with 80 arrays, because the first design provided twice as many data points as the latter. However, the common reference design with 160 arrays gave results slightly worse than the distant pair design with 80 arrays, whereas the costs for arraying were twice as high for the first method as for the second.
Figure 3.
Power of alternative experimental designs. (A) Mimicking the Arabidopsis genome size: comparison of the distant pair design (disPair), random pair design (ranPair), and the common reference design (comRef) for two-color microarrays. Plus (+) indicates selective phenotyping. (B) Mimicking other genome sizes: comparison of the distant pair design for different genome sizes. (C) Ratio-based vs. signal-based analysis: comparison of ratio-based and signal-based analysis of data generated using the loop design (loop), the random pair design (ranPair), or the distant pair design (disPair). The asterisk (*) indicates signal-based analysis. (D) One-color vs. two-color microarrays: comparison of the distant pair design (disPair) for 80 two-color microarrays and a standard design for one-color microarrays (oneColor) with 80 or 160 arrays under equal or different levels of technical noise. The asterisk (*) indicates that technical variance is four times lower for the one-color platform than for the two-color platform.
Can we do better if a larger population (say, 1000 RILs) is available but no more than 80 microarrays? Selective phenotyping has been suggested as a strategy to increase the power (e.g., Jin et al. 2004). Our optimization strategy actually selected the best 80 pairs from the population to maximize the number of informative A/B and B/A comparisons. The computer simulation demonstrated that the number of A/B and B/A comparisons can be increased to 66 and that power was increased likewise (Figure 3A, disPair+).
Simulation study—mimicking other genome sizes:
It is more likely to find distant pairs for organisms with small genomes (e.g., Arabidopsis) than for ones with large genomes (e.g., human). Nevertheless, as shown in Figure 3B, distant pairing is still advantageous for genomes of larger sizes. In all cases the number of desired hybridizations A/B and B/A exceeded the value of 40, which can be obtained on average in a random pair design. The genomewide average number of desired A/B and B/A hybridizations was 47 (49, 53, 58) for a genome size of 4000 (2000, 1000, 500) cM, respectively.
It may not always be the purpose of the researcher to give equal weight to all regions of the genome: emphasis may be on one or more regions on the genome known to carry genes (or QTL) of particular interest. For example, with special interest on two unlinked regions of 20 cM, the researcher can increase the power for differential analysis enormously by using markers only in these two regions in the distant pairing algorithm (Figure 3B, 40 cM in total). The number of A/B and B/A comparisons in the two 20-cM regions increased to 72, close to the upper limit of 80.
Simulation study—the alternatives:
Figure 3C shows that ratio-based and signal-based analyses of the simulated data for the distant pair design are almost equally powerful, the latter performing slightly better by obtaining additional information about genotype effect from the A/A and B/B observations. Figure 3C also shows that the distant pair design outperforms the loop design and the random pair design in signal-based analysis. Figure 3D shows that a distant pair design with 80 two-color microarrays is slightly worse than a straightforward design with 160 single-color microarrays if the technical sources are up to four times noisier (in terms of variance) in the two-color platform than in the one-color platform.
DISCUSSION
A good experimental strategy provides better interpretable and more reliable results at the same or lower costs than alternative strategies do. Central to any gene expression study is the choice of a microarray platform, for which there are various two-color and single-color technologies as options. At first sight two-color microarray technologies have two clear advantages over single-color ones. First, two-color microarrays can generate twice as much hybridization data as single-color ones for the same number of microarrays. Second, two-color microarrays can cohybridize deliberately selected pairs of samples and therefore offer greater flexibility in experimental design than single-color microarrays do. In this article we investigated how to optimize the experimental design for two-color microarrays in genetic studies on gene expression and compared the alternative experimental designs for two-color microarrays to the straightforward design for single-color microarrays.
Common reference and loop designs are currently the most frequently used experimental designs for two-color microarrays, but they do not exploit the full power of genetic studies. We developed an alternative design, the distant pair design, in which individuals with dissimilar genetic (marker) fingerprints are paired together on the same microarray. The principles underlying the distant pair design are: first, direct comparisons between target samples are better than indirect ones via reference samples; second, comparisons between individuals carrying different alleles at many genes are informative, whereas comparisons between individuals carrying identical alleles at many genes are less informative and should be avoided; and third, profiling more genetically different individuals (2n instead of n using the two colors for different RILs without technical replication) increases the number of recombinant points in the study, which may lead to higher power and better resolution in QTL analysis. Our new experimental design and analysis method was outlined for a RIL population, but the three principles of our strategy apply equally well to any other type of population (e.g., F2 or pedigree) in many organisms (including the human) and the method of minimizing the summed variances of parameter estimates is generally applicable (e.g., to find the optimal design for detecting dominance, epistasis, or interaction between QTL and environment). In particular cases the power of the method can be increased even further—we studied two such cases. First, one or a few genome regions may be of major interest if they are known to contain important regulatory loci or genes for phenotypic traits and it is possible to increase or maximize the power for assessing differential expression caused by these loci by giving more weight to markers in these regions (e.g., spanning 40 cM) than to the remaining markers (elsewhere in the genome) in the algorithm for finding distant pairs. Second, a large fingerprinted population (say of size 1000) can serve as a useful resource to select the most distant pairs of individuals from (say 80 pairs only), therewith reducing the number of arrays used without sacrificing too much power. Other strategies of selective phenotyping have been described earlier. For example, Jin et al. (2004) noted that selecting for equal and higher proportions of genotypes A and B would optimize power in a common reference design. We simulated the approach by Jin et al. and noted an increase in power but not to the extent obtained by the distant pair design (the Jin et al. power curve was almost equal to that of the random pair design in Figure 3A; only the curve of the latter design is shown). Note that the approach by Jin et al. works only in the case of profiling a subset of a large population, whereas our new strategy optimizes power no matter whether a population is profiled in part or as a whole. Jannink (2005) provided an interesting suggestion related to selective phenotyping. He noted that some progeny result from gametes with a greater number of recombination events than others and that such progeny can be more useful for QTL mapping than others. This idea can be incorporated into our approach simply by adding an extra term to the optimization criteria to favor selection of genotypes with a larger number of recombination events.
In the analysis of two-color microarray data one can calculate ratios between signals of the cohybridized samples at the same spot. Such a “within spots” analysis minimizes the risk of bias as a result of spot or array effects (Wit and McClure 2004). Alternatively, one can also consider and analyze the individual signals by treating the spot or array effect of cohybridized samples as random (Wolfinger et al. 2001). This analysis has the potential to obtain additional information about genotype effects from the A/A and B/B observations, which can further increase the power of QTL detection. However, distributional assumptions are questionable and bias is risked (Kerr 2003; Wit and McClure 2004). Of course, in our simulations distributional assumptions are known to be correct and therefore there is no risk of bias. For two-color microarrays we recommend using the distant pair design and checking, after the experiment has been performed, how the ratio- and signal-based methods of analysis compare.
We have shown that current studies can be improved significantly by a new design for two-color microarrays. But suppose that one also has the option to buy single-color microarrays. Which technology should one go for? Two-color arrays produce twice as many data as single-color arrays. Both systems suffer from various sources of noise, which may be common or specific for different technology platforms. Our simulations demonstrated that a distant pair design with 80 two-color microarrays can outperform a design with 160 one-color microarrays even if the two-color platform is substantially noisier than the one-color platform. Nevertheless, sources and levels of noise will differ between microarray platforms and even within platforms between laboratories, and only a careful case-to-case evaluation can guarantee the best return on investments.
We conclude that our complete integration of microarrays and genetic analysis—at the level of experimental planning and computational analysis—offers greatly improved perspectives for dissecting the complexity of gene expression regulation. Our results will aid the design and analysis of future genetic studies on gene expression and help researchers in making a choice between two-color and single-color platforms. As in other experimental sciences, the success of a genetic study on gene expression is based a great deal on the experimental planning and analysis.
Acknowledgments
We thank J. P. Nap, M. Koornneef, I. R. Terpstra, A. F. J. M. van den Ackerveken, J. J. B. Keurentjes, J. E. Kammenga, and two anonymous reviewers for stimulating discussions. We also thank D. J. de Koning and C. S. Haley for valuable comments on an earlier draft of this manuscript. J. F. was supported by Netherlands Organization for Scientific Research-Genomics grant 050-10-029.
References
- Alonso-Blanco, C., A. J. Peeters, M. Koornneef, C. Lister, C. Dean et al., 1998. Development of an AFLP based linkage map of Ler, Col and Cvi Arabidopsis thaliana ecotypes and construction of a Ler/Cvi recombinant inbred line population. Plant J. 14: 259–271. [DOI] [PubMed] [Google Scholar]
- Brem, R. B., G. Yvert, R. Clinton and L. Kruglyak, 2002. Genetic dissection of transcriptional regulation in budding yeast. Science 296: 752–755. [DOI] [PubMed] [Google Scholar]
- Bystrykh, L., E. Weersing, B. Dontje, S. Sutton, M. T. Pletcher et al., 2005. Uncovering regulatory pathways that affect hematopoietic stem cell function using ‘genetical genomics’. Nat. Genet. 37: 225–232. [DOI] [PubMed] [Google Scholar]
- Chesler, E. J., L. Lu, S. Shou, Y. Qu, J. Gu et al., 2005. Complex trait analysis of gene expression uncovers polygenic and pleiotropic networks that modulate nervous system function. Nat. Genet. 37: 233–242. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., 2002. Fundamentals of experimental design for cDNA microarrays. Nat. Genet. 32(Suppl): 490–495. [DOI] [PubMed] [Google Scholar]
- Churchill, G. A., D. C. Airey, H. Allayee, J. M. Angel, A. D. Attie et al., 2004. The Collaborative Cross, a community resource for the genetic analysis of complex traits. Nat. Genet. 36: 1133–1137. [DOI] [PubMed] [Google Scholar]
- Darvasi, A., 2003. Genomics: gene expression meets genetics. Nature 422: 269–270. [DOI] [PubMed] [Google Scholar]
- Dobbin, K. K., J. J. Shih and R. M. Simon, 2005. a Comment on ‘Evaluation of the gene-specific dye bias in cDNA microarray experiments.’ Bioinformatics 21: 2803–2804. [DOI] [PubMed] [Google Scholar]
- Dobbin, K. K., E. S. Kawasaki, D. W. Petersen and R. M. Simon, 2005. b Characterizing dye bias in microarray experiments. Bioinformatics 21: 2430–2437. [DOI] [PubMed] [Google Scholar]
- Hubner, N., C. A. Wallace, H. Zimdahl, E. Petretto, H. Schulz et al., 2005. Integrated transcriptional profiling and linkage analysis for identification of genes underlying disease. Nat. Genet. 37: 243–253. [DOI] [PubMed] [Google Scholar]
- Jannink, J. L., 2005. Selective phenotyping to accurately map quantitative trait loci. Crop Sci. 45: 901–908. [Google Scholar]
- Jansen, R. C., 2003. a Quantitative trait loci in inbred lines, pp. 445–476 in Handbook of Statistical Genetics, edited by D. J. Balding, M. Bishop and C. Cannings. John Wiley & Sons, Chichester, UK.
- Jansen, R. C., 2003. b Studying complex biological systems using multifactorial perturbation. Nat. Rev. Genet. 4: 145–151. [DOI] [PubMed] [Google Scholar]
- Jansen, R. C., and J. P. Nap, 2001. Genetical genomics: the added value from segregation. Trends Genet. 17: 388–391. [DOI] [PubMed] [Google Scholar]
- Jansen, R. C., and J. P. Nap, 2004. Regulating gene expression: surprises still in store. Trends Genet. 20: 223–225. [DOI] [PubMed] [Google Scholar]
- Jin, C., H. Lan, A. D. Attie, G. A. Churchill, D. Bulutuglo et al., 2004. Selective phenotyping for increased efficiency in genetic mapping studies. Genetics 168: 2285–2293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr, M. K., 2003. Design considerations for efficient and effective microarray studies. Biometrics 59: 822–828. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, Jr., S., C. D. Galatt and M. P. Vechi, 1983. Optimization by simulated annealing. Science 220: 671–680. [DOI] [PubMed] [Google Scholar]
- Kraft, P., and S. Horvath, 2003. The genetics of gene expression and gene mapping. Trends Biotechnol. 21: 377–378. [DOI] [PubMed] [Google Scholar]
- Morley, M., C. M. Molony, T. M. Weber, J. L. Devlin, K. G. Ewens et al., 2004. Genetic analysis of genome-wide variation in human gene expression. Nature 430: 743–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schadt, E. E., S. A. Monks, T. A. Drake, A. J. Lusis, N. Che et al., 2003. Genetics of gene expression surveyed in maize, mouse and man. Nature 422: 297–302. [DOI] [PubMed] [Google Scholar]
- Schadt, E. E., J. Lamb, X. Yang, J. Zhu, S. Edwards et al., 2005. An integrative genomics approach to infer causal associations between gene expression and disease. Nat. Genet. 37: 710–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sen, S., J. M. Satagopan and G. A. Churchill, 2005. Quantitative trait locus study design from an information perspective. Genetics 170: 447–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speed, T., 2003. Statistical Analysis of Gene Expression Microarray Data. Chapman & Hall/CRC Press, Boca Raton, FL.
- Wit, E., and J. McClure, 2004. Statistics for Microarrays: Design, Analysis and Inference. John Wiley & Sons, Chichester, UK.
- Wolfinger, R. D., G. Gibson, E. D. Wolfinger, L. Bennett, H. Hamadeh et al., 2001. Assessing gene significance from cDNA microarray expression data via mixed models. J. Comput. Biol. 8: 625–637. [DOI] [PubMed] [Google Scholar]
- Yang, Y. H., S. Dudoit, P. Luu and T. P. Speed, 2001. Normalization for cDNA microarray data, pp. 141–152 in Microarrays: Optimal Technologies and Informatics, edited by M. L. Bittner, Y. Chen, A. N. Dorsel and E. R. Dougherty. Society for Optical Engineering, San Jose, CA.
- Yvert, G., R. B. Brem, J. Whittle, J. M. Akey, E. Foss et al., 2003. Trans-acting regulatory variation in Saccharomyces cerevisiae and the role of transcription factors. Nat. Genet. 35: 57–64. [DOI] [PubMed] [Google Scholar]