Abstract
The conventional model of adaptation in asexual populations implies sequential fixation of new beneficial mutations via rare selective sweeps that purge all variation and preserve the clonal genotype. However, in large populations multiple beneficial mutations may co-occur, causing competition among them, a phenomenon called “clonal interference.” Clonal interference is thus expected to lead to longer fixation times and larger fitness effects of mutations that ultimately become fixed, as well as to a genetically more diverse population. Here, we study the significance of clonal interference in populations consisting of mixtures of differently marked wild-type and mutator strains of Escherichia coli that adapt to a minimal-glucose environment for 400 generations. We monitored marker frequencies during evolution and measured the competitive fitness of random clones from each marker state after evolution. The results demonstrate the presence of multiple beneficial mutations in these populations and slower and more erratic invasion of mutants than expected by the conventional model, showing the signature of clonal interference. We found that a consequence of clonal interference is that fitness estimates derived from invasion trajectories were less than half the magnitude of direct estimates from competition experiments, thus revealing fundamental problems with this fitness measure. These results force a reevaluation of the conventional model of periodic selection for asexual microbes.
THE conventional model of adaptation in asexual populations posits that rare high fitness clones become sequentially fixed via relatively rapid selective sweeps alternated by periods during which the population waits for the next beneficial mutation to arise. This model of “periodic selection” (Atwood et al. 1951a) enjoys a certain amount of empirical support and underlies much of the current theory of adaptation based on the convenient assumption of “strong-selection, weak-mutation” (Orr 2005). Early experiments with microbes that led to the original description of periodic selection showed erratic “sawtooth” dynamics in the frequency of neutral mutations and were interpreted as resulting from the sequential occurrence of beneficial mutations sweeping through the population to fixation (Novick and Szilard 1950; Atwood et al. 1951a,b). Later work confirmed these earlier findings (Paquin and Adams 1983) and emphasized that a consequence of the sequential selective sweeps is the continual purging of all genetic and phenotypic variation, leading to the preservation of the wild type (Koch 1974; Levin 1981).
However, under some conditions (e.g., large populations, high mutation rates, novel environmental conditions) beneficial mutations may be sufficiently common that they co-occur in the population. In the absence of recombination, this may lead to competition between separate clones that each carry different beneficial mutations, a phenomenon called “clonal interference” (Gerrish and Lenski 1998). Theoretical work has shown that clonal interference leads to increased fitness effects and longer fixation times of those beneficial mutations that ultimately win the competition (Gerrish and Lenski 1998; Gerrish 2001; Rozen et al. 2002; Wilke 2004). Empirical evidence of clonal interference has begun to accumulate over recent years (Lenski et al. 1991; de Visser et al. 1999; Miralles et al. 1999; Yedid and Bell 2001; Rozen et al. 2002; Shaver et al. 2002; Colegrave 2002), showing its potential significance for adaptation of asexual populations. However, most of the available evidence of clonal interference is inferential and indirect support is scarce.
Here we aim to find more direct evidence of clonal interference by studying the invasion of new beneficial mutations in evolving populations of Escherichia coli. Similar to the classical study by Chao and Cox (1983), we allowed mixtures of two strains with different mutation rates (mut+ and mutS) at varying ratios to adapt to novel conditions for 400 generations while monitoring their ratio using a fixed neutral marker. A problem with earlier studies of short-term adaptation (Novick and Szilard 1950; Atwood et al. 1951a,b; Paquin and Adams 1983; Imhof and Schlötterer 2001) is that they depend on a spontaneous marker from which it is hard to derive precise frequency estimates of the invading beneficial mutant. After evolution, we isolated clones from both marked subpopulations and measured their fitness in competition with the common ancestor. Two earlier studies reported results from these experiments, one on the distribution of fitness effects of fixed beneficial mutations in the wild-type clones (Rozen et al. 2002) and the other on the effect of population size and mutation rate on the fitness effects of fixed mutations (de Visser and Rozen 2005); both studies found results consistent with the clonal interference model. In this study, we compare the fitness of clones from these populations with the frequency trajectories of invading subpopulations. The results provide three lines of support for the significance of clonal interference in these adapting populations. First, in many populations we find that clones from both marked subpopulations increased fitness, indicating the presence of multiple coexisting beneficial mutations. Second, the time-averaged rate of mutant invasion is much lower than that predicted if only the invading mutants are present in the population. Third, the invasion trajectories of beneficial mutants are more erratic than expected from isolated selective sweeps. We also find that fitness estimates of evolved clones derived from the invasion trajectories are less than half the direct estimates from competition experiments, showing fundamental problems with the former estimates. We discuss the implications of our results for the conventional model of adaptation in asexual populations.
MATERIALS AND METHODS
Strains, media, and culture conditions:
The E. coli B strains used in this study were derived from REL606 (Lenski et al. 1991). This strain is unable to utilize arabinose and is DNA repair proficient (Ara−mut+). From this strain, two other strains were derived: one repair-proficient strain that is able to utilize arabinose (Ara+mut+, REL607) and a strain with a deficient methyl-directed mismatch-repair function, also able to utilize arabinose (Ara+mutS, REL7571; de Visser et al. 1999). Fluctuation tests (Luria and Delbrück 1943) using four different selectable phenotypes have shown that the mutation rate of Ara+mutS was ∼33-fold higher than that of both repair-proficient strains (de Visser et al. 1999). These strains had no previous history in the evolutionary environment used in this study, i.e., static test tubes (at 37°) containing 10 ml of Davis minimal broth supplemented with 2 × 10−6 g thiamine hydrochloride and 0.025 g glucose/liter (DM25). Glucose is the component that limits growth in this medium, allowing ∼5 × 107 cells/ml in stationary phase. The daily 100-fold dilutions during transfer of the populations to fresh medium allow ∼6.64 cell generations/day; under these conditions, the effective population size, Ne, is ∼3.3 × 107 (Lenski et al. 1991).
The frequency of the two strains in each mixture (see below) was estimated on two different media: tetrazolium arabinose (TA) plates, allowing growth and color distinction of strains with both Ara markers, and minimal arabinose (MA) plates, i.e., DM broth in which glucose is replaced by arabinose at 4 mg/ml, which allowed growth of the Ara+ strain only.
Experimental evolution:
Luria broth cultures, started from freezer stocks of Ara−mut+, Ara+mut+, and Ara+mutS, were plated on TA to pick individual colonies as ancestors for the 60 mixed populations. Sixty colonies of strain Ara−mut+ and 30 each of Ara+mut+ and Ara+mutS were used to inoculate DM25 cultures. After 1 day, these 60 cultures were again transferred to fresh DM25 via a 100-fold dilution to ensure physiological acclimation; these cultures were used the next day to initiate the mixed populations. Thus, each ancestral clone experienced ∼35 generations [= ln(5 × 1010)/ln(2)], of which some 15 generations were in the evolutionary environment (DM25) prior to the inoculation of the mixed populations. Six replicate populations of each strain/ratio combination were started with 100-fold dilution by mixing the two competitors at the following ratios: 100:1, 10:1, 1:1, 1:10, and 1:100 for Ara+mut+:Ara−mut+ and 1:1, 1:10, 1:100, 1:1,000, and 1:10,000 for Ara+mutS:Ara−mut+, respectively. This range of ratios was chosen to present approximately similar opportunities for both strains to produce beneficial mutations. The ancestral clones and samples from the evolving populations were stored at −80° at every 100-generation interval by mixing 1 ml of each culture with 0.2 ml 80% glycerol. For the first 7 days of evolution, samples of all 60 populations were plated daily on TA (for Ara+ frequencies >0.01) or MA (for Ara+ frequencies ≤0.01) to estimate the relative densities of Ara+ and Ara− subpopulations. Thereafter, populations were monitored by plating samples every other day. From each population sample frozen at 400 generations, a single Ara+ and Ara− clone was isolated and stored at −80. If at 400 generations one competitor was at an undetectably low frequency, that clone was isolated from generation 200 or 300.
Fitness assays:
Competition experiments were performed as described in Lenski et al. (1991). To estimate fitness of the derived clones relative to their ancestor, complete blocks of 180 2-day (∼13.3 generations) competitions were performed (i) between all derived clones and the ancestral freezer stock of Ara−mut+ or Ara+mut+ (Ara+mutS-derived clones were competed against Ara−mut+ as well, giving 120 competitions total) and (ii) between the two derived clones of the same population as an internal control (60 competitions total). Blocks were replicated threefold (360 competitions total). If <50 colonies total or <15 colonies of one competitor were scored, then that competition was discarded and repeated. In a separate block, majority clones of those populations from which no minority clone could be isolated at generation 400 were isolated from population samples at generation 400 and assayed against the reciprocally marked ancestor. A block of 180 competitions between the two ancestral clones of each population was run for 6 days (∼40 generations) with threefold replication to check for the presence of mutations that existed prior to the initiation of the experimental populations. Finally, 28 clones from combinations with fitness deviating from unity (see supplementary information at http://www.genetics.org/supplemental/) were assayed against freezer-stock samples carrying the alternative Ara marker in one block of 2-day competitions with threefold replication; this was done to determine which ancestral clone carried a mutation.
Regression analysis of marker trajectories:
The trajectory describing the frequencies of the two marked subpopulations over time reflects the invasion of a subpopulation due to hitchhiking with beneficial mutations. The slope of the change of the ln marker ratio has been used to estimate the fitness difference of the invading relative to the declining subpopulation. The slope then reflects the selection rate constant, rij (with unit d−1; Dykhuizen and Hartl 1983) from which the dimensionless selection coefficient, Sij, can be calculated as Sij = rij /m, where m is the Malthusian parameter (also with unit d−1, Lenski et al. 1991). Because we diluted the populations 100-fold each day, m = 4.6 d−1 [= ln(100)] if growth is continuous and 6.64 d−1 [= log2(100)] if growth is in discrete cell generations. We will use m = 4.6 d−1 to obtain a “high-end” estimate of Sij from rij. Since ln(a) = 2.3 log10 (a), Sij can thus be estimated from the linear slope of the log10-transformed marker ratio as Sij = 0.5 × slope.
Because many frequency trajectories showed more than one consistent change of the marker ratio, we used a linear step model to estimate the slope of each detectable transition. We fitted the following step model to the trajectory of the log-marker ratio of each population using the Square-Newton and Quasi-Newton routines of Systat (Wilkinson 1999): log (Ara+/Ara−) = C0 + a1*t (if t > T1) + a2*t (if t > T2) + a3*t (if t > T3), where C0 is the initial ratio of the two strains, a1–a3 are the chronological slopes reflecting linear changes of this ratio, and T1–T3 are the times at which a change of the ratio starts. Models including more than three steps did not converge or did not significantly improve the fit in any of the populations after correcting for multiple testing (see below). We began by fitting a single-slope model, after which we added slopes as long as the associated loss of 2 d.f. resulted in a significantly (P < 0.05) better fit according to a partial F-test (Kleinbaum and Kupper 1978). In a few cases where adding one step did not improve the fit but visual inspection suggested more steps, two steps were added at once and the improved fit involving the loss of 4 d.f. was tested. Since this procedure resulted in 86 partial F-tests for all populations together, we applied a serial Bonferroni correction (Rice 1989) to reduce the number of false-positive steps. The fit of all models to the data was checked by eye.
RESULTS
Ancestral clones carrying mutations:
Because we are interested in the invasion of de novo beneficial mutations, we first sought to exclude populations that were started with ancestral clones carrying a mutation. Two analyses were conducted to detect ancestral clones that had fixed a mutation. We first competed the two original clones of each mixture against one another. Cases with relative fitness deviating from unity with two-tailed P < 0.10 were further screened for the presence of mutations. (A conservative P-value was used to reduce the number of false negatives.) Of the 60 pairs, 14 showed evidence for ancestral clones with unequal fitness (Table 1). Each of the 28 clones was then competed against the “parent” ancestral clone with opposite Ara marker (that clone from which the ancestral clones were derived). Of the 28 clones, 7 had a fitness deviating from unity relative to the parent clone (Table 1). As a second method, we examined the slope of the regression of the marker ratio against time during the first 6 days (∼40 generations) for the suspect 14 populations, because some trajectories showed an immediate and consistent change of the marker ratio without a lag period. Where results from competition experiments and regression were consistent in sign and either or both tests were significant, clones were considered to have carried a mutation prior to experimental mixture. Using these criteria, 5 of the 30 ancestral mutS clones and 2 of the 90 ancestral mut+ clones had a mutation (see Table 1). The mutator background generated significantly more mutations than the wild-type background, as expected (χ2 = 8.55, d.f. = 1, P < 0.01). Two of the seven mutations appeared to be beneficial. The seven populations founded with clones already carrying a mutation were excluded from further analyses.
TABLE 1.
Fitness of ancestral clones of populations where their fitness relative to one another deviates from 1
| Relative fitness, W
|
Regression Ara+/Ara− trajectory (day 0–6)
|
||||||
|---|---|---|---|---|---|---|---|
| Ara+/Ara− | Log (Ara+/Ara−) | Population | Ara+vs. Ara−clone | Ara+ clone vs.Ara− ancestor | Ara− clone vs. Ara+ ancestor | Slope,generation−1 | P-value |
| mut+/mut+ | 2 | 1 | 0.9886* | 0.9928 | 0.9726 | −0.01738 | 0.1265 |
| mut+/mut+ | −1 | 2 | 0.9838* | 0.9754 | 1.0082*a | −0.00271 | 0.0517 |
| mutS/mut+ | 0 | 1 | 0.9933* | 0.9725 | 0.9681 | 0.00074 | 0.7823 |
| mutS/mut+ | 0 | 4 | 0.9534** | 0.9298* | 0.9875 | −0.01627 | 0.0026 |
| mutS/mut+ | −1 | 1 | 0.9751* | 0.9544* | 0.9756 | −0.01011 | 0.0136 |
| mutS/mut+ | −1 | 2 | 1.0140*** | 1.0039 | 0.9883 | 0.00288 | 0.5244 |
| mutS/mut+ | −1 | 4 | 1.0279** | 1.0308* | 0.9796 | 0.01035 | 0.0296 |
| mutS/mut+ | −1 | 6 | 1.0288* | 1.0209* | 0.9764 | 0.00667 | 0.0051 |
| mutS/mut+ | −2 | 3 | 0.9923 | 0.9745** | 0.9689 | 0.00392 | 0.5295 |
| mutS/mut+ | −3 | 1 | 0.9677** | 0.9529 | 0.9954 | −0.01175 | 0.0194 |
| mutS/mut+ | −3 | 4 | 1.0280** | 1.0142 | 0.9651*** | 0.02108 | 0.0891 |
| mutS/mut+ | −3 | 6 | 1.0063* | 0.9825 | 0.9950 | 0.00858 | 0.3708 |
| mutS/mut+ | −4 | 5 | 1.0101* | 0.9890 | 1.0011 | −0.00361 | 0.3470 |
| mutS/mut+ | −4 | 6 | 1.0076* | 0.9963 | 0.9805 | −0.00136 | 0.7475 |
Significant negative values indicate deleterious mutations and positive values indicate beneficial mutations in the ancestral background of the subpopulation involved. Asterisks (*) indicate significant deviations from W = 1 on the basis of a two-tailed t-test with d.f. = 2: *P < 0.05, **P < 0.01, ***P < 0.001. The single fitness value in italics is significant at the 0.05 level after correcting for multiple testing (Rice 1989). Underlining indicates those ancestral clones for which competition and regression results consistently indicate the presence of a mutation.
aAlthough the t-test suggests that the Ara− subpopulation started with a beneficial mutation, both the more extreme (negative) deviation from unity of the Ara+ ancestor (which is not significant due to low statistical power, given only three replicate fitness values) and the presumed much higher rate of deleterious relative to beneficial mutations makes this interpretation ambiguous.
Marker trajectories:
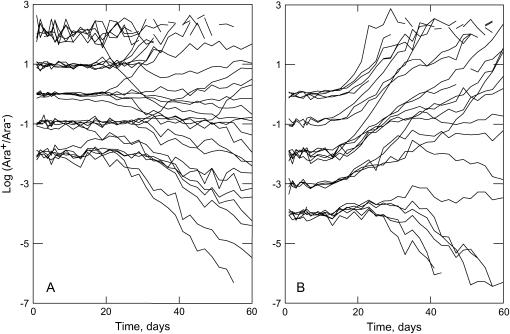
Figure 1 shows the trajectories of log (Ara+/Ara−) of the 53 populations that remained after censoring for ancestral clones carrying a mutation. Consistent with the results of Chao and Cox (1983), subpopulation invasion is frequency dependent: at frequencies >0.5 the Ara+ subpopulation invades most mut+/mut+ populations (Fisher's exact probability that such a threshold is absent is 3.2 × 10−4), while this is true for frequencies >∼5 × 10−4 in most mutS/mut+ populations (P = 8.1 × 10−4). However, two features of these trajectories are fundamentally different from the results of Chao and Cox (1983): (i) some trajectories show the invasion of subpopulations from frequencies below and decline from frequencies above these thresholds and (ii) many trajectories show erratic dynamics, where periods of steady invasion of a subpopulation are alternated by periods of decline. Both differences are consistent with the stochastic nature of the hitchhiking process, which depends on the chance occurrence of beneficial mutations in both subpopulations. Moreover, the erratic marker dynamics suggest that beneficial mutations in both marker backgrounds interfere with each other's spread.
Figure 1.
Trajectories of log10 (Ara+/Ara−) ratios of all 53 populations that were not founded by ancestral clones that already contained a fixed mutation. (A) mut+Ara+/mut+Ara− populations. (B) mutSAra+/mut+Ara− populations.
Fitness of clones from both subpopulations:
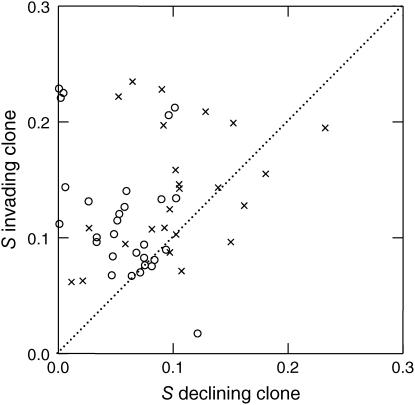
Clonal interference would be directly demonstrated by the finding of multiple beneficial mutations that are simultaneously present in the population. We tested this by measuring the fitness of random clones from both marked subpopulations isolated after 400 generations: one clone from the subpopulation that was invading and one from the subpopulation in decline, where invasion and decline are defined by their net frequency change during evolution. Figure 2 shows the fitness improvement of these clones at the end of evolution for all 53 populations. Two things are apparent from this figure. First, clones from invading subpopulations evolved larger fitness benefits than clones from declining subpopulations: 11.9% vs. 5.7% (t = 5.19, d.f. = 56, P < 0.0001) for the mut+/mut+ populations and 14.1% vs. 10.0% (t = 2.59, d.f. = 46, P < 0.01) for the mutS/mut+ populations, respectively. Second, most populations contained beneficial mutations in both the invading and the declining subpopulations, which is confirmed by two statistical tests. First, the average fitness improvement of clones from both marked subpopulations is significant at the P < 10−7 level for mut+/mut+ and mutS/mut+ alike. Second, when the three replicate fitness estimates are used to test the fitness improvement of individual clones, 34 of the 53 populations (∼64%) showed significant fitness improvement of both differently marked clones using one-tailed t-tests with P < 0.05. Despite the inherent low statistical power due to performing so many tests, each with low replication, a P-value of 0.05 for each clone tested leads to less than one expected false-positive population with fitness improvement of both its clones (53 × 0.052 = 0.13).
Figure 2.
Average fitness improvement (S) over 400 generations of a single clone from both the invading and the declining subpopulation (containing different Ara markers) of all 53 populations of Figure 1 measured in competition against the ancestor. The dotted line is the line of equality. Circles indicate mut+Ara+/mut+Ara− and crosses for mutSAra+/mut+Ara− populations.
Of 15 populations from which one subpopulation was lost after 400 generations, we also measured the fitness of clones isolated at 200 or 300 generations. None of the 5 populations with clones from 200 generations, but 9 of the 10 populations with clones from 300 generations showed significant fitness improvements in both differently marked clones (using one-tailed P < 0.05). The fact that we found more than one beneficial mutation in the majority of the populations by screening only two randomly isolated clones strongly suggests that all populations contained multiple beneficial mutations after 300 generations.
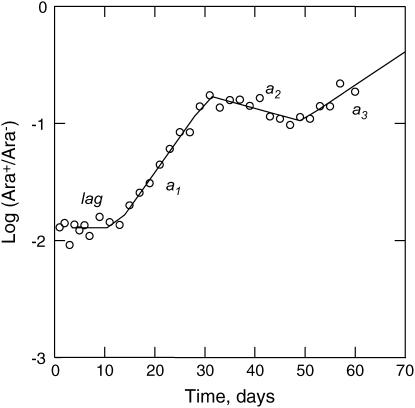
Regression analysis of marker trajectories:
We next used the marker trajectories to test further predictions of the clonal interference model. Figure 3 shows an example of an invasion trajectory that highlights common features of many trajectories: a lag period before one subpopulation invades, followed by one or more seemingly linear changes (a1, a2, and a3). We estimated lag period and slopes by fitting a stepwise linear regression model to the trajectory of each population that was not founded by clones carrying mutations nor limited by our ability to detect steps (the Ara+mut+/Ara−mut+ populations started at a 100:1 ratio). Additional slopes were accepted only if they significantly improved the fit of the model using a combined P < 0.05 criterion for all tests (see materials and methods). In this way we detected 96 slopes in 47 populations (see supplemental Figure S1 and supplemental Table S1 at http://www.genetics.org/supplemental/). Below, the estimates of lag and slope are used to test two further predictions of the clonal interference model concerning the rate of invasion of beneficial mutants and the timescale at which clonal interference is manifest in the marker trajectories.
Figure 3.
Trajectory of log10 (Ara+/Ara−) vs. time and best-fitting linear step model (see text) of a representative (mutSAra+/mut+Ara−) population that shows the typical features of many trajectories. These include a lag period, followed by one or more seemingly linear slopes of the change of log10 (Ara+/Ara−) over time (a1, a2, and a3).
Invasion rate of beneficial mutations:
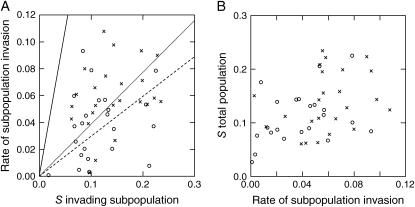
The simultaneous presence of multiple beneficial mutations is expected to extend the fixation time of those mutations that will ultimately become fixed (Gerrish and Lenski 1998) and thus to slow down the invasion of a random beneficial mutation. We tested this by comparing the observed rate of subpopulation invasion of the 47 populations with the expected rate of invasion in the absence of clonal interference, i.e., assuming that only the invading beneficial mutation was present in the population. The observed rate of subpopulation invasion was calculated by dividing the difference in log-marker ratio between the end of the lag period and day 60 by the number of days elapsed between these time points; the expected time-averaged invasion rate equals twice the selection coefficient of the invading clone. Figure 4A shows that the observed time-averaged rate of invasion is much lower than this expectation for both the mut+/mut+ (coefficient = 0.290, 95% confidence limits 0.198 and 0.382) and the mutS/mut+ populations (coefficient = 0.384, 95% limits 0.307 and 0.462). If indeed clonal interference is the cause of the slow rate of mutant invasion, fitness improvement of the entire population (i.e., the average fitness improvement of both marked clones weighted by their final frequency) should be independent of the rate of subpopulation invasion. This prediction is again supported by the data (Figure 4B) for both the mut+/mut+ (F1,21 = 2.53, P = 0.126) and the mutS/mut+ populations (F1,22 = 1.82, P = 0.190). Therefore, the most likely cause of the discrepancy between observed and expected rate of mutant invasion is interference between invading and other beneficial mutations.
Figure 4.
(A) Time-averaged rate of subpopulation invasion (see text) vs. fitness improvement (S) over 400 generations of a clone from the invading subpopulation for the 47 populations that allowed regression analysis. The straight line gives the expected relationship between fitness effect of invading mutation and rate of invasion, given that the invading mutation is the only one present in the population; the dotted and dashed lines give the observed relationships for mut+/mut+ (circles) and mutS/mut+ populations (crosses), respectively. (B) Fitness improvement (S) of the total population vs. time-averaged rate of subpopulation invasion. No significant relationship is apparent for either strain combination (symbols as in A).
Interpretation of marker trajectories:
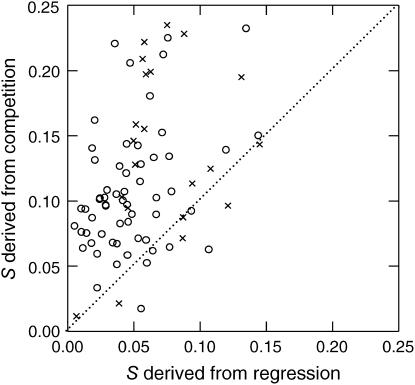
While multiple slopes apparent in the marker trajectories presumably reflect interference between multiple beneficial mutations, one particular interpretation of these seemingly linear slopes is that they reflect the invasion of single beneficial mutations after they are fixed in their subpopulation (Chao and Cox 1983; Dykhuizen and Hartl 1983; Imhof and Schlötterer 2001). If this interpretation is correct, fitness of invading mutants can be estimated from these slopes, where the selection coefficient equals 0.5 × the change of log (Ara+/Ara−)/day (see materials and methods). Fitness improvement after 400 generations is then derived from the selection coefficient corresponding to the last change in slope caused by a mutant from that subpopulation. Following this interpretation, the three slopes apparent in Figure 3 reflect interference among three beneficial mutations, where the selection coefficients (s) of the first, second, and third mutation equal a1/2, [a2 − a1]/2, and s1 + [a3 − a2]/2, respectively, and the latter two are the expected final fitness improvement of the Ara− and Ara+ subpopulations. Figure 5 shows that fitness improvement derived from slopes is on average only ∼43% as high as fitness improvement derived from direct competition experiments against the ancestor (paired t-test: t = 11.45, d.f. = 93, P < 0.0001), despite the overall positive correlation between these two fitness measures (r = 0.392, n = 81, P = 0.00030). Therefore, our data provide no support for the interpretation that these slopes reflect the fitness consequences of single beneficial mutations after they have fixed in their subpopulation.
Figure 5.
Fitness improvement (S) of subpopulations derived from competition experiments of evolved clones against the ancestor vs. fitness improvement derived from the slopes of the log (Ara+/Ara−) trajectories. The analysis was done for both subpopulations of the 47 populations that allowed regression analysis. The dashed line is the line of equality; circles indicate mut+, and crosses indicate mutS subpopulations.
DISCUSSION
We studied the dynamics of invasion of de novo beneficial mutations in evolving populations of E. coli using fitness estimates of evolved clones from competition experiments and the marker trajectories of coevolving subpopulations. We found ample direct evidence of clonal interference in these populations on the basis of three observations. First, we found different coexisting beneficial mutations in the majority of the populations by 300 generations, even though we screened only one clone per marked subpopulation. Second, the time-averaged rate of invasion of the beneficial mutant spawned by the invading subpopulation was much lower than predicted if these mutants were the only ones present. Third, the trajectories of the marker frequencies were more erratic, with periods of steady subpopulation invasion alternated by periods of decline, than predicted by rare selective sweeps isolated in time. In addition, we found increased fitness effects of mutations with increases of the population size or mutation rate, consistent with the predictions of clonal interference, which we reported elsewhere (de Visser and Rozen 2005).
A possible alternative explanation for the observed presence of multiple beneficial mutants in the evolving populations is that negative frequency-dependent interactions cause their stable coexistence (Levin 1981). We did not specifically test the frequency dependence of the fitness of the evolved clones, but we did run control competitions between the evolved clones from the corresponding subpopulations directly against each other (see materials and methods). In the case of frequency-dependent interactions, we would expect the fitness of evolved clones measured in competition against their ancestor not to correspond well to fitness estimates derived from direct competitions among the evolved clones (de Visser and Lenski 2002). Instead, we found a highly significant positive correlation between these two fitness measures (r = 0.760, n = 58, P < 0.0001). Clonal interference thus remains the most plausible explanation for the observed presence of multiple beneficial mutations in many populations.
The support for clonal interference found in this study adds to the accumulating evidence from other recent studies. One study using asexual digital organisms found similar direct evidence that multiple beneficial mutants coexisted in the population (Yedid and Bell 2001). Other studies using bacteria or viruses showed evidence for clonal interference based on more inferential evidence, including the predicted trajectory of mean fitness (Lenski et al. 1991), the relationship between fitness effects of beneficial mutations and population size (Miralles et al. 1999), the diminishing returns relationship between the rate of adaptation and the mutation supply rate (de Visser et al. 1999; Miralles et al. 1999), the population-size-dependent acceleration of adaptation with recombination (Colegrave 2002), and the rate of mutator invasion (Shaver et al. 2002). These combined results indicate the failure of the conventional model of sequential periodic selection of single beneficial mutations (Novick and Szilard 1950; Atwood et al. 1951a,b), as well as the assumption of “strong selection and weak mutation” used in much of the current theory of adaptation (Orr 2005) for asexual microbes.
Other studies reported results that seemed consistent with the conventional model of adaptation by rare periodic selection events. For instance, Chao and Cox (1983) reported monotonic, rather than erratic, invasion of subpopulations in their chemostats. The authors mention plateaus where the ratio of both subpopulations leveled in some chemostats, but suggest differences in wall growth between subpopulations as a possible explanation. Wall growth could not have played a role in our study, which used fresh serially diluted batch cultures every day. Studies monitoring changes in the frequency of spontaneous neutral mutations in evolving microbial populations often interpreted observed sawtooth-like dynamics as evidence for sequential substitutions of beneficial mutations that are consistent with the conventional model (Novick and Szilard 1950; Atwood et al. 1951a,b; Paquin and Adams 1983; Imhof and Schlötterer 2001). However, these studies could not distinguish between mutations increasing to near or to absolute fixation. Indeed, the observed frequencies of the changes in marker frequency are often inconsistent with absolute fixation. For instance, chemostat populations of Saccharomyces cerevisiae showed shifts in marker frequency on average every 40 generations (Johnston and McKay 1977; Paquin and Adams 1983), a frequency inconsistent with fixation of mutants with fitness benefit in the range observed (∼10%) in these populations of size 109–1010. Instead, although the exact explanation remains unclear (see below), these marker trajectories more likely reflect clonal interference between mutants that sequentially increase in frequency but never take over the entire population (see Adams 2004).
A surprising finding of our study was that fitness estimates of evolved clones derived from the slopes of the marker trajectories were less than half those derived from direct competition experiments with the ancestor. Two explanations seem most likely for this discrepancy. First, slopes in invasion trajectories may reflect the fitness difference among beneficial mutants fixed within their subpopulation, but our ability to detect slope changes was limited by insufficient sampling or measurement error. Second, slopes do not reflect fitness consequences of beneficial mutants fixed within their subpopulations, but rather of beneficial mutants that are at varying frequency due to differences in the timing of their occurrence (Hegreness et al. 2006). On the basis of our data we are unable to distinguish between these two, non-mutually exclusive alternatives. However, sampling of a larger number of clones from more time points may help resolve these possibilities.
Irrespective of the precise explanation for the observed discrepancy between direct and indirect fitness estimates, our results have important implications for studies using marker trajectories to estimate fitness changes (e.g., Chao and Cox 1983; Dykhuizen and Hartl 1983; Imhof and Schlötterer 2001). At best, these studies were likely to have underestimated the true fitness improvements of beneficial mutants, especially in cases where clonal interference is expected to be abundant, such as in large populations, those with high mutation rates, or in populations that invade new niches where the fraction of beneficial mutations might be larger. Thus, estimates of mutational fitness effects from such studies should be interpreted with caution.
While we think that interference between mutants containing a single different beneficial mutation is involved in the erratic dynamics of the marker trajectories, we cannot rule out that some mutants accumulated more than a single beneficial mutation. This could be particularly the case for 14 of the 53 populations, where we detected more than one slope change caused by the same subpopulation. In these cases, the second slope (in two subpopulations three slopes were detected) may reflect interference between a later big-effect and an earlier smaller-effect beneficial mutation (dubbed a “leap frog”; Gerrish and Lenski 1998) or the later invasion of a double mutant. We cannot distinguish between these two possibilities on the basis of our data. However, simulation experiments of the mut+/mut+ populations have shown that in 100 trials not a single invading mutant had accumulated more than one beneficial mutation (Rozen et al. 2002). Thus, double mutants remain a possibility in the mutS/mut+ populations, but are unlikely for the mut+/mut+ populations.
Finally, our results have at least two implications for the understanding of adaptation in asexual microbes. First, the slower invasion of new beneficial mutations caused by clonal interference implies that genetic variation is allowed to build up for longer periods before it is purged. We have shown that this is the case for variation that may contribute to adaptation (see Figure 2). Possibly, this increased standing genetic variation enhances the population's long-term survival in the face of environmental changes (Boles et al. 2004). Second, our results are relevant for the invasion of mutator mutants, because their invasion depends on opportunities to hitchhike with beneficial mutations under conditions where clonal interference is abundant: large asexual populations (Sniegowski et al. 1997, 2000; Taddei et al. 1997; Tenaillon et al. 1999; Tanaka et al. 2003). Consistent with the findings of Shaver et al. (2002), we found that hitchhiking of mutators may take much longer than expected from a single selective sweep.
Acknowledgments
We thank Richard Lenski in whose lab these experiments were done; Philip Gerrish for discussing the role of clonal interference over the years; and Noam Shoresh, Fons Debets, Rolf Hoekstra, and two anonymous reviewers for comments and discussion. This work was supported by a fellowship from the Netherlands Organization of Scientific Research to J.A.G.M.dV. and grants from the National Science Foundation to D.E.R. (Postdoctoral Fellowship in Microbial Ecology) and R. E. Lenski.
References
- Adams, J., 2004. Microbial evolution in laboratory environments. Res. Microbiol. 155: 311–318. [DOI] [PubMed] [Google Scholar]
- Atwood, K. C., L. K. Schneider and F. J. Ryan, 1951. a Periodic selection in Escherichia coli. Proc. Natl. Acad. Sci. USA 37: 146–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atwood, K. C., L. K. Schneider and F. J. Ryan, 1951. b Selective mechanisms in bacteria. Cold Spring Harbor Symp. Quant. Biol. 16: 345–355. [DOI] [PubMed] [Google Scholar]
- Boles, B. R., M. Thoendel and P. K. Singh, 2004. Self-generated diversity produces “insurance effects” in biofilm communities. Proc. Natl. Acad. Sci. USA 101: 16630–16635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao, L., and E. C. Cox, 1983. Competition between high and low mutating strains of Escherichia coli. Evolution 37: 125–134. [DOI] [PubMed] [Google Scholar]
- Colegrave, N., 2002. Sex releases the speed limit on evolution. Nature 420: 664–666. [DOI] [PubMed] [Google Scholar]
- de Visser, J. A. G. M., and R. E. Lenski, 2002. Long-term experimental evolution in Escherichia coli. XI. Rejection of non-transitive interactions as cause of declining rate of adaptation. BMC Evol. Biol. 2: 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser, J. A. G. M., and D. E. Rozen, 2005. Limits of adaptation in asexual populations. J. Evol. Biol. 18: 779–788. [DOI] [PubMed] [Google Scholar]
- de Visser, J. A. G. M., C. W. Zeyl, P. J. Gerrish, J. L. Blanchard and R. E. Lenski, 1999. Diminishing returns from mutation supply rate in asexual populations. Science 283: 404–406. [DOI] [PubMed] [Google Scholar]
- Dykhuizen, D. E., and D. L. Hartl, 1983. Selection in chemostats. Microbiol. Rev. 47: 150–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrish, P. J., 2001. The rhythm of microbial adaptation. Nature 413: 299–302. [DOI] [PubMed] [Google Scholar]
- Gerrish, P. J., and R. E. Lenski, 1998. The fate of competing beneficial mutations in an asexual population. Genetica 102/103: 127–144. [PubMed] [Google Scholar]
- Hegreness, M., N. Shoresh, D. Hartl and R. Kishony, 2006. An equivalence principle for the incorporation of favorable mutations in asexual populations. Science 17: 1615–1617. [DOI] [PubMed] [Google Scholar]
- Imhof, M., and C. Schlötterer, 2001. Fitness effects of advantageous mutations in evolving Escherichia coli populations. Proc. Natl. Acad. Sci. USA 98: 1113–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston, J. R., and A. McKay, 1977. Population variation in chemostat cultures of Saccharomyces cerevisiae. FEMS Lett. 2: 313–316. [Google Scholar]
- Kleinbaum, D. G., and L. L. Kupper, 1978. Applied Regression Analysis and Other Multivariate Methods. Duxbury, North Scituate, MA.
- Koch, A. L., 1974. The pertinence of the periodic selection phenomenon to prokaryote evolution. Genetics 77: 127–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenski, R. E., M. R. Rose, S. C. Simpson and S. C. Tadler, 1991. Long-term experimental evolution in Escherichia coli. I. Adaptation and divergence during 2,000 generations. Am. Nat. 138: 1315–1341. [Google Scholar]
- Levin, B. R., 1981. Periodic selection, infectious gene exchange and the genetic structure of E. coli populations. Genetics 99: 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luria, S. E., and M. Delbrück, 1943. Mutations of bacteria from virus sensitivity to virus resistance. Genetics 28: 491–511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miralles, R., P. J. Gerrish, A. Moya and S. F. Elena, 1999. Clonal interference and the evolution of RNA viruses. Science 285: 1745–1747. [DOI] [PubMed] [Google Scholar]
- Novick, A., and L. Szilard, 1950. Experiments with the chemostat on spontaneous mutations of bacteria. Proc. Natl. Acad. Sci. USA 36: 708–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr, H. A., 2005. The genetic theory of adaptation: a brief history. Nat. Rev. Genet. 6: 119–127. [DOI] [PubMed] [Google Scholar]
- Paquin, C. E., and J. Adams, 1983. Frequency of fixation of adaptive mutations is higher in diploid than in haploid populations. Nature 302: 495–500. [DOI] [PubMed] [Google Scholar]
- Rice, W. R., 1989. Analyzing tables of statistical tests. Evolution 43: 223–225. [DOI] [PubMed] [Google Scholar]
- Rozen, D. E., J. A. G. M. de Visser and P. J. Gerrish, 2002. Fitness effects of fixed beneficial mutations in microbial populations. Curr. Biol. 12: 1040–1045. [DOI] [PubMed] [Google Scholar]
- Shaver, A. C., P. G. Dombrowski, J. Y. Sweeney, T. Treis, R. M. Zappala et al., 2002. Fitness evolution and the rise of mutator alleles in experimental Escherichia coli populations. Genetics 162: 557–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sniegowski, P. D., P. J. Gerrish and R. E. Lenski, 1997. Evolution of high mutation rates in experimental populations of E. coli. Nature 387: 703–705. [DOI] [PubMed] [Google Scholar]
- Sniegowski, P. D., P. J. Gerrish, T. Johnson and A. Shaver, 2000. The evolution of mutation rates: separating causes from consequences. BioEssays 22: 1057–1066. [DOI] [PubMed] [Google Scholar]
- Taddei, F., M. Radman, J. Maynard-Smith, B. Toupance, P. H. Gouyon et al., 1997. Role of mutator alleles in adaptive evolution. Nature 387: 700–702. [DOI] [PubMed] [Google Scholar]
- Tanaka, M. M., C. T. Bergstrom and B. R. Levin, 2003. The evolution of mutator genes in bacterial populations: the roles of environmental change and timing. Genetics 164: 843–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon, O., B. Toupance, H. Le Ganard, F. Taddei and B. Godelle, 1999. Mutators, population size, adaptive landscape and the adaptation of asexual populations of bacteria. Genetics 152: 485–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke, C. O., 2004. The speed of adaptation in large asexual populations. Genetics 167: 2045–2053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkinson, L., 1999. SYSTAT: The System for Statistics. SYSTAT, Evanston, IL.
- Yedid, G., and G. Bell, 2001. Microevolution in an electronic microcosm. Am. Nat. 157: 465–487. [DOI] [PubMed] [Google Scholar]