Haplotype Diversity in 11 Candidate Genes Across Four Populations

Abstract

Analysis of haplotypes based on multiple single-nucleotide polymorphisms (SNP) is becoming common for both candidate gene and fine-mapping studies. Before embarking on studies of haplotypes from genetically distinct populations, however, it is important to consider variation both in linkage disequilibrium (LD) and in haplotype frequencies within and across populations, as both vary. Such diversity will influence the choice of “tagging” SNPs for candidate gene or whole-genome association studies because some markers will not be polymorphic in all samples and some haplotypes will be poorly represented or completely absent. Here we analyze 11 genes, originally chosen as candidate genes for oral clefts, where multiple markers were genotyped on individuals from four populations. Estimated haplotype frequencies, measures of pairwise LD, and genetic diversity were computed for 135 European-Americans, 57 Chinese-Singaporeans, 45 Malay-Singaporeans, and 46 Indian-Singaporeans. Patterns of pairwise LD were compared across these four populations and haplotype frequencies were used to assess genetic variation. Although these populations are fairly similar in allele frequencies and overall patterns of LD, both haplotype frequencies and genetic diversity varied significantly across populations. Such haplotype diversity has implications for designing studies of association involving samples from genetically distinct populations.

SINGLE-NUCLEOTIDE polymorphism (SNP) markers are extremely common throughout the genome and provide very dense maps over small chromosomal regions. Individual genes often include multiple SNPs in coding regions, introns, and surrounding regions, so using haplotypes of several SNPs should provide greater statistical power to detect causal genes for complex traits in either conventional case-control or family-based study designs (Schork et al. 2000; Morris and Kaplan 2002). Haplotypes can convey more information about an unobserved causal variant by identifying it uniquely or by identifying related haplotypes that are overrepresented among cases. The disadvantages of haplotype analysis are: (1) the large numbers of possible haplotypes, which often create problems with sparse data even in large samples, and (2) differences in haplotype frequencies across genetically distinct populations. Genetically distinct populations may differ in both the extent of linkage disequilibrium (LD) and their haplotype frequencies, which add a source of heterogeneity to tests of association between cases and controls rather than improving the statistical efficiency of such tests. Genetic diversity must be taken into account when planning haplotype-based studies where samples are drawn from several populations.

We have developed an international, multicenter study to identify genes controlling risk of oral clefts including sites in Maryland, Singapore, Taiwan, and China. Our study design involves large-scale screening of candidate genes using haplotype-based approaches in family-based tests of association. Emerging statistical methods for haplotypes hold the promise of improving statistical power (Schork et al. 2000), but the concern about different population ancestries becomes a greater problem for analysis of haplotypes where the number of different categories can increase dramatically. Using samples from genetically distinct populations will require more care in estimating haplotype frequencies and in selecting SNPs for genotyping, especially if “tagging” SNPs are desired to minimize genotyping effort. Thompson et al. (2003) showed that relatively small samples of individuals can be genotyped for all known SNPs in a region and used to select a subset of markers that will identify or “tag” common haplotypes within a homogeneous population. Whenever the haplotype frequencies vary across populations, selection of tagging SNPs must be tailored to each population. This initial analysis of four samples of unrelated subjects from distinct populations provides the opportunity to estimate genetic distance and variability both within and between populations. Such information partially reflects the historical relationships among these populations.

Patterns of pairwise LD over the human genome are now beginning to emerge (Tiret et al. 2002; Crawford et al. 2004). While pairwise LD generally varies inversely with physical distance between two markers, this is far from uniform within genes or even larger chromosomal regions. Variation in LD is a function of the history of human populations, and reflects the combined forces of drift, admixture, and selection over evolutionary time (Wang et al. 2002; Zhang et al. 2003). Different populations show different patterns of pairwise LD, and this is reflected in different haplotype frequencies. Furthermore, the diversity of haplotypes for a given set of SNPs in a sample reflects both the size of the sample (the number of chromosomes or individuals) and the underlying population structure from which the sample was drawn. Variability in estimated haplotype frequencies across populations will in turn influence the available information about the structure of haplotype blocks and their boundaries. Here we present an analysis on 11 candidate genes, where at least three SNPs were available for analysis in all four populations. We contrast measures of pairwise LD and estimated haplotype frequencies, as well as haplotype diversity among four samples of unrelated individuals [European-Americans (EA) from Maryland, Chinese-Singaporeans (CS), Indian-Singaporeans (IS), and Malay-Singaporeans (MS)], and illustrate some of the limitations in using haplotype-based strategies in studies of candidate genes involving several genetically distinct populations.

MATERIALS AND METHODS

Population samples:

Four populations were sampled. These samples included 135 unrelated EA parents of probands with an isolated nonsyndromic oral cleft who were recruited as part of an ongoing study in Maryland (Beaty et al. 1997, 2001). In addition, DNA from anonymous cord blood samples was extracted from 57 ethnic CS, 45 ethnic MS, and 46 ethnic IS neonates born in Singapore between 1999 and 2003. All Singapore samples were classified by the reported ethnic group of the infant's mother. To assure anonymity of these samples, exact birth dates were removed, but gender and ethnic group information were retained, and approximately equal numbers of males and females were included.

SNP markers:

SNPs for each candidate gene were originally identified through sequencing a small number of parents of infants with an oral cleft from our Maryland study, which would preferentially select EA polymorphic variants. Thus, it is not surprising that some of these SNPs were polymorphic only in the EA group, with one or more of the Singapore groups having only one allele. SNPs were genotyped using the highly multiplexed bead array assay (Oliphant et al. 2002). Genotyping occurred in two rounds, first on the EA samples and subsequently on the three Singapore samples. Analysis of genotype data on duplicated samples showed a very low rate of errors among 15 controls with three to six duplicate samples each: the mean inconsistency rate was 0.3% (ranging from 0.0 to 1.2%) among all duplicated samples, yielding an average agreement in genotypes among duplicates of 99.7%. Each marker was tested for deviation from Hardy-Weinberg equilibrium separately within each population, and observed levels of heterozygosity were calculated for each marker. Supplementary Table S1 (http://www.genetics.org/supplemental/) contains a listing of SNPs used here, and information on novel SNPs has been deposited into dbSNP (http://www.ncbi.nlm.nih.gov/SNP/).

Haplotype frequencies:

Haplotype frequencies for each pair of SNPs and for all SNPs within a gene were estimated within each population using the expectation-maximization (EM) algorithm. Pairwise LD was calculated using both D′ and r², using the SNPEM program (Fallin et al. 2001) and Haploview (http://www.broad.mit.edu/mpg/haploview/index.phy). Measures of haplotype diversity were based on these estimated haplotype frequencies as 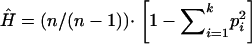for k haplotypes each with frequency p_i and total chromosome count n (Nei 1987). This measure of gene diversity is analogous to the heterozygosity at a single locus and attains its maximum when haplotypes observed in the sample occur at equal frequencies. The number of different haplotypes in each population reflects this haplotype diversity; however, this is colored by available sample sizes as smaller samples are less likely to include rare haplotypes. To understand whether the observed number of unique haplotypes was different among populations, we first calculated the number of expected haplotypes for each population sample on the basis of frequencies from our largest sample and standardized this to the actual size of each group for comparison as shown in Equation 8 from Chakraborty et al. (1988).

Measure of population variability:

Analysis of molecular variance (AMOVA) was used to test for heterogeneity within and among populations on the basis of estimated haplotype frequencies (Excoffier et al. 1992). This approach (as implemented in the Arlequin package) is similar to a traditional analysis of variance of haplotype frequencies, but considers the number of site differences among observed haplotypes. Here, we simply defined four populations (EA, CS, MS, and IS) and estimated the variance within and among populations. In the AMOVA, the variance among populations is analogous to Wright's fixation index (F_ST) and the statistical significance of either the variance among populations or the F_ST itself was evaluated by permuting haplotypes over all four populations (Excoffier 2003). In addition, pairwise F_ST statistics based on haplotype frequencies were used to contrast these four populations (EA, CS, MS, and IS). Again, the statistical significance of these measures of genetic distances was approximated by permuting haplotypes between each member of the pair, and the proportion of permutations giving an F_ST equal to or greater than the observed F_ST served as an empirical P-value.

RESULTS

From an original list of 27 candidate genes, 11 genes had three or more polymorphic SNPs available for haplotype analysis. Table 1 shows the number of SNPs available for each gene, the mean and range of observed SNP heterozygosity seen in each sample, the number of inferred haplotypes for each sample, and a measure of haplotype diversity. Some SNPs showed modest levels of heterozygosity, but at least one SNP in each gene approached the theoretical maximum heterozygosity of 50%. While the maximum expected heterozygosity is 50% under Hardy-Weinberg, some markers had estimates slightly above this value simply due to sampling variation. However, none of these SNP markers showed significant deviation from Hardy-Weinberg equilibrium.

TABLE 1.

SNPs in candidate genes examined in four populations

		Heterozygosity
Gene (no. SNPs; kb covered)	Population	Mean	Range	No. haplotypes	Gene diversity (%)
BMP4 (8; 8.32)	EA	0.393	(0.074, 0.452)	17	76.4 ± 1.70
CS	0.422	(0.085, 0.504)	7	68.7 ± 2.97
MS	0.434	(0.131, 0.505)	12	81.3 ± 2.80
IS	0.428	(0.106, 0.503)	10	81.3 ± 2.32
EGF (6; 29.65)	EA	0.412	(0.156, 0.489)	11	55.5 ± 2.62
CS	0.387	(0.101, 0.503)	6	74.7 ± 1.86
MS	0.400	(0.126, 0.493)	8	76.7 ± 2.37
IS	0.411	(0.123, 0.505)	7	72.7 ± 2.90
FGFR2 (8; 49.72)	EA	0.344	(0.119, 0.511)	16	81.8 ± 1.33
CS	0.202	(0.053, 0.502)	10	74.6 ± 2.76
MS	0.199	(0.045, 0.501)	9	69.6 ± 3.58
IS	0.279	(0.022, 0.493)	9	80.4 ± 1.95
NEDD9 (5; 68.14)	EA	0.403	(0.244, 0.526)	10	84.3 ± 0.87
CS	0.219	(0.018, 0.460)	7	65.4 ± 3.80
MS	0.253	(0.022, 0.497)	7	76.6 ± 2.30
IS	0.290	(0.123, 0.486)	10	73.4 ± 4.16
MMP13 (6; 12.43)	EA	0.344	(0.111, 0.437)	8	58.4 ± 2.70
CS	0.405	(0.068, 0.497)	5	71.2 ± 2.10
MS	0.386	(0.022, 0.503)	5	66.0 ± 3.05
IS	0.417	(0.161, 0.505)	6	68.7 ± 2.66
EDN1 (3; 5.15)	EA	0.420	(0.368, 0.500)	5	65.4 ± 1.48
CS	0.428	(0.400, 0.470)	4	52.5 ± 3.91
MS	0.466	(0.441, 0.493)	5	58.1 ± 3.82
IS	0.493	(0.477, 0.502)	4	56.8 ± 3.01
GABRB3 (4; 3.03)	EA	0.434	(0.371, 0.499)	6	60.6 ± 2.13
CS	0.369	(0.247, 0.442)	5	50.7 ± 5.08
MS	0.399	(0.296, 0.470)	4	55.3 ± 5.04
IS	0.482	(0.468, 0.497)	4	65.7 ± 1.92
GPC1 (4; 1.21)	EA	0.427	(0.391, 0.484)	10	77.9 ± 0.93
CS	0.380	(0.203, 0.455)	6	51.6 ± 4.69
MS	0.365	(0.167, 0.481)	5	60.3 ± 5.11
IS	0.479	(0.471, 0.490)	4	66.6 ± 1.94
ZNF509 (3; 2.77)	EA	0.440	(0.407, 0.502)	3	61.8 ± 1.60
CS	0.392	(0.335, 0.422)	3	63.1 ± 2.29
MS	0.363	(0.324, 0.442)	3	63.5 ± 2.43
IS	0.308	(0.213, 0.497)	3	60.5 ± 2.29
LYAR (4; 2.08)	EA	0.418	(0.404, 0.424)	5	44.1 ± 2.38
CS	0.476	(0.429, 0.492)	4	66.8 ± 1.40
MS	0.452	(0.337, 0.490)	3	57.5 ± 4.03
IS	0.351	(0.179, 0.410)	3	43.8 ± 5.44
RBP1-RBP2 (3; 76.33)	EA	0.402	(0.308, 0.490)	7	61.7 ± 2.79
CS	0.237	(0.132, 0.404)	5	51.3 ± 4.38
MS	0.326	(0.250, 0.406)	5	54.0 ± 5.17
	IS	0.382	(0.245, 0.499)	6	66.6 ± 3.85

EA, European-American (2n = 270); CS, Chinese-Singaporean (2n = 114); MS, Malay-Singaporean (2n = 90); IS, Indian-Singaporean (2n = 92).

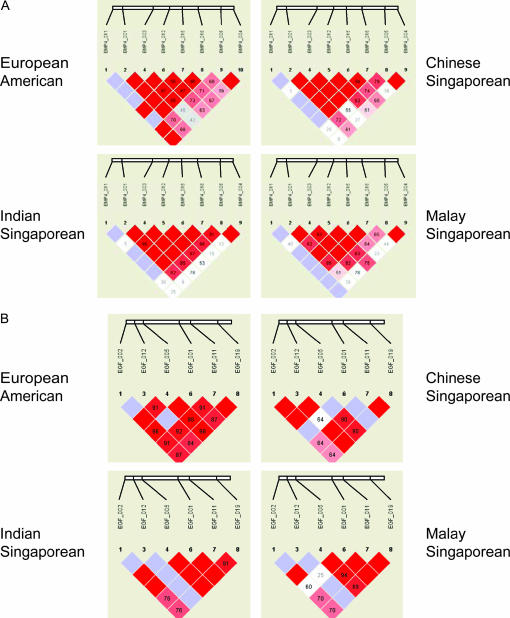
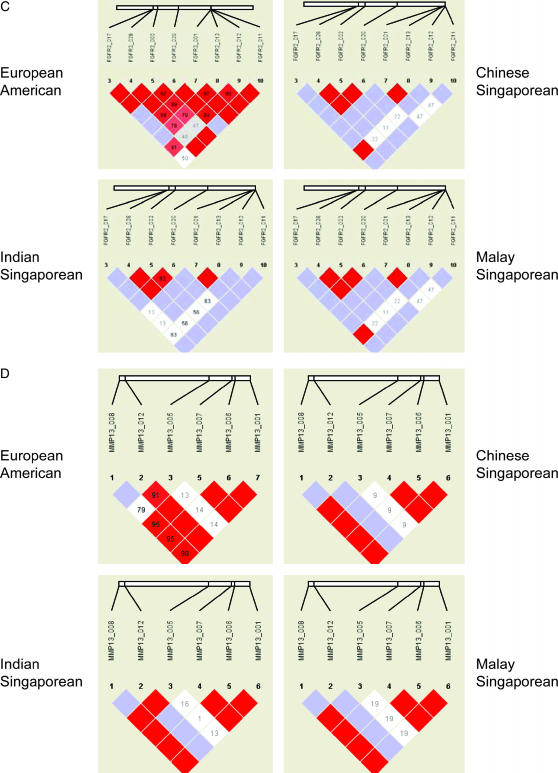
Measures of pairwise LD (both D′ and r²) were calculated for all pairs of SNPs in each gene. To consider patterns of LD, we examined the four genes with at least six SNPs (BMP4, MMP13, EGF, and FGFR2) across each sample (EA, CS, IS, and MS). All SNPs were considered in this analysis, ignoring any suggested block structure (Figure 1). While there was some variability in the estimated magnitude of LD, the overall patterns were similar across all four populations. Samples from Singapore showed higher pairwise LD in general, with more redundancy between SNPs (several had r² = 1, indicating perfect correlation). While pairwise LD varied slightly across populations, overall the block structure appears roughly similar in all four samples (see Figure 1). Some algorithms for selecting blocking boundaries require specification of some cutoff based on LD, so variation across populations in measures of LD and their statistical significance would create some variability in the haplotype blocks. Depending on exactly how their boundaries were defined, haplotype blocks could show considerable variability.

Figure 1.

Pairwise linkage disequilibrium (LD) in candidate genes with six or more SNPs in four populations (European-Americans, Chinese-Singaporeans, Malay-Singaporeans, and Indian-Singaporeans) as generated by Haploview. (A) BMP4, (B) EGF, (C) FGFR2, (D) MMP13.

In part, this variability in LD could also be a function of sample size, since the three Singaporean groups (CS, IS, and MS) were smaller than the EA group. Using the method of Chakraborty et al. (1988) to compute the expected numbers of haplotypes observed in each of these three smaller groups gave no suggestion that the observed differences in haplotype number or diversity could be explained solely by sample size (data not shown).

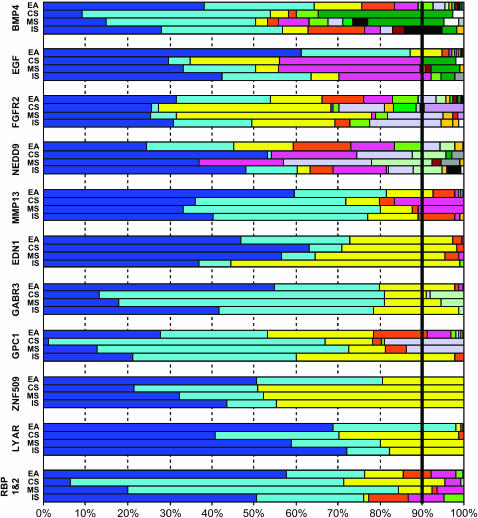
Figure 2 displays the estimated frequencies of each inferred haplotype present in these four samples for these 11 candidate genes with at least three SNPs. In this figure, the order of the haplotypes was set by their relative frequency in the largest sample (here EA), and haplotypes in the other three samples are presented in this same order. For example, the most common haplotype for BMP4 in the EA group was relatively rare in the CS and MS groups, but was more common in the IS group. See supplementary Table S2 (http://www.genetics.org/supplemental/) for estimated frequencies of each haplotype in the four populations, with the order as in Figure 2. The total number of inferred haplotypes for a specified set of SNPs in a sample partly reflects its sample size, with larger samples more likely to include rarer haplotypes. Thus it is not surprising that the largest sample (EA, with 2n = 270 chromosomes) generally had more unique haplotypes, but many of these haplotypes were uncommon (<5%). The three Singaporean groups (CS, MS, and IS) typically had fewer uniquely inferred haplotypes, although this could not be attributed solely to their smaller sample sizes. The thick vertical line in Figure 2 denotes the 90% mark for all inferred haplotypes for all samples. Again using BMP4 as an example, 5 distinct haplotypes (among the 17 present) in the EA group accounted for >90% of all 270 chromosomes. For this same gene, 8 distinct haplotypes (among 10) accounted for >90% of the 92 chromosomes found in the IS sample. These patterns are also reflected in the haplotype diversity levels shown in Table 1. Whenever a small number of haplotypes represents a larger proportion of a sample, there is less genetic diversity. For example, the LYAR gene showed that only 2 or 3 haplotypes accounted for >90% of the sampled chromosomes in all four populations and had correspondingly smaller measures of genetic diversity in Table 1. While this measure of gene diversity varied considerably across these four populations (EA, CS, MS, and IS), there was no clear pattern of major differences in Table 1, and none of these four populations can be considered “restricted” in their genetic diversity. From Figure 2, it is also apparent that the Singapore samples can have diversity equal to or greaterer than that of the EA sample for some candidate genes (e.g., BMP4 and MMP13).

Figure 2.

Haplotype frequencies in samples from four populations ordered by their frequency in the largest sample (EA). Patterns represent different haplotypes from all SNPs in each candidate gene [see Table 1 for number of SNPs and unique haplotypes; see supplementary Table S2 (http://www.genetics.org/supplemental/) for estimated haplotype frequencies in each population].

As with nearly all studies of human populations, most of the variance in haplotype frequencies for these 11 genes occurred within populations. Although all of these 11 genes showed statistically significant differences in haplotype frequency among the four populations (empirical P-values were uniformly <0.001 for all 11 genes), these differences across populations accounted only for a minority of the observed variance in haplotype frequencies (Table 2). The percentage of variation among populations from the AMOVA ranged from 5.32% for MMP13 (based on six SNPs) to 28.78% for RBP1 and RBP2 (based on only three SNPs). This percentage of variance in haplotype frequency attributable to differences among populations can be viewed as a multilocus fixation index (F_ST) statistic and serves as a measure of genetic distance (Degioanni and Darlu 1994). Pairwise comparisons of these four populations showed considerable variation in these F_ST values (see Table 2). For some genes, the differences between the CS and MS groups were not statistically significant (6 of the 11 genes showed nonsignificant empirical P-values and none showed empirical P-values <0.01). The EA and IS groups showed only marginally significant differences for 3 of the 11 genes (BMP4, FGFR2, and GABR3). This suggests that the CS and MS groups are genetically similar, while the IS and EA groups are somewhat similar.

TABLE 2.

Within and among variance components from analysis of molecular variance (AMOVA) and pairwise F_ST statistics for four populations (European-Americans, Chinese-Singaporeans, Malay-Singaporeans, and Indian-Singaporeans)

	% variance from AMOVA	Pairwise FST statistics (above diagonal) and empirical P-values (below diagonal)
Gene		EA	CS	MS	IS
BMP4	Among 6.60	EA —	0.12945	0.05770	0.00930
CS 0.000	—	0.01596	0.09612
Within 93.40	MS 0.000	0.034	—	0.02874
IS 0.060	0.000	0.056	—
EGF	Among 9.98	EA —	0.18053	0.13410	0.05851
CS 0.000	—	0.01774	0.04434
Within 90.20	MS 0.000	0.039	—	0.00646
IS 0.003	0.000	0.168	—
FGFR2	Among 6.0	EA —	0.08821	0.09547	0.01237
CS 0.000	—	0.00159	0.05206
Within 94.8	MS 0.000	0.297	—	0.04908
IS 0.019	0.000	0.001	—
NEDD9	Among 6.49	EA —	0.10181	0.07922	0.04523
CS 0.000	—	0.01837	0.01285
Within 93.51	MS 0.000	0.032	—	0.03262
IS 0.000	0.051	0.004	—
MMP13	Among 5.32	EA —	0.07009	0.10047	0.04170
CS 0.000	—	0.00152	0.01189
Within 94.68	MS 0.000	0.298	—	0.01248
IS 0.001	0.078	0.089	—
EDN1	Among 5.47	EA —	0.04023	0.02859	0.08968
CS 0.003	—	−0.00439	0.10821
Within 94.53	MS 0.006	0.539	—	0.06626
IS 0.000	0.000	0.002	—
GABRB3	Among 14.48	EA —	0.24156	0.19277	0.02012
CS 0.000	—	−0.00402	0.13631
Within 85.52	MS 0.000	0.585	—	0.08946
IS 0.020	0.000	0.000	—
GPC1	Among 10.86	EA —	0.17407	0.11068	0.02849
CS 0.000	—	0.00965	0.15061
Within 89.14	MS 0.000	0.114	—	0.09969
IS 0.002	0.000	0.000	—
ZNF509	Among 7.69	EA —	0.12002	0.08557	0.07030
CS 0.000	—	0.00763	0.05504
Within 92.31	MS 0.000	0.171	—	0.00526
IS 0.000	0.003	0.229	—
LYAR	Among 17.96	EA —	0.12324	0.04557	0.33967
CS 0.000	—	0.02557	0.21712
Within 82.04	MS 0.004	0.026	—	0.31871
IS 0.000	0.000	0.000	—
RBP1-RBP2	Among 28.78	EA —	0.28566	0.34333	0.33249
CS 0.000	—	0.03299	0.26551
Within 71.22	MS 0.000	0.013	—	0.17355
		IS 0.000	0.000	0.000	—

DISCUSSION

Our goal here is to describe SNP and haplotype frequencies for a number of candidate genes in samples of unrelated individuals drawn from four genetically distinct populations. If different populations have the same or similar patterns of pairwise LD, it will be relatively easy to identify the minimum number of SNPs that tag the most common haplotypes, termed “tagging SNPs,” and to use these to test for association under either case-control or family-based study designs. However, whenever haplotype frequencies vary considerably across populations, it becomes more difficult to predict which SNPs will identify enough of the existing haplotypes in all subpopulations to ensure adequate coverage (Evans and Cardon 2005), and the chance of spurious findings due to confounding increases in tests of association. Of course, factors such as sample size become important when estimating haplotype frequencies, but the key determinant of differences remains the underlying level of haplotype diversity and LD across populations. Recently, several groups have demonstrated that there can be substantial variability in LD patterns across ethnic/racial groups even within individual genes (Bonnen et al. 2002; Shifman et al. 2003). Bonnen et al. (2002) showed how patterns of LD can differ substantially in comparable physical regions around candidate genes (∼100–200 kb each), using equal-sized samples of European-Americans, African-Americans, Asian-Americans, and Hispanic-Americans. For some genes, there was virtually complete LD over the entire region in all groups, while regions around other genes showed substantial variation in LD. These four subgroups also showed evidence of substantial genetic diversity as measured by Wright's fixation index, F_ST. Shifman et al. (2003) examined 90 individuals (180 chromosomes) from three subgroups: European-Americans, African-Americans, and Ashkenazi Jews (of Eastern European descent), which represent outbred, admixed, and restricted genetic populations, respectively. Evidence of significant genetic diversity among these three populations was reflected in the haplotype diversity and in differences in LD “useful” for association studies. African-Americans had lower levels of LD and greater haplotype diversity than did European-Americans, which in turn had greater diversity than did Ashkenazi Jews, a genetically restricted population with a historical bottleneck. Recently, Hinds et al. (2005) examined 1.5 million SNPs from 71 individuals of European, African, and Han Chinese descent and observed consistent differences in patterns of LD, haplotype diversity, and haplotype frequency among populations.

For the 11 candidate genes examined here, the overall pattern of LD among these four populations was similar, although the statistical significance of measures of LD (especially D′) varied considerably. However, in an analysis of molecular variance, differences in haplotype frequencies among these four populations were always statistically significant, accounting for 4–28% of the total variance. These differences are sufficient to warrant caution when trying to identify tagging SNPs for either individual genes or haplotype blocks. This is especially true if the known SNPs were initially identified in only one subpopulation, and haplotype blocks were then defined in that subpopulation alone before tagging SNPs were selected. Thompson et al. (2003) suggested that modest numbers of subjects (as few as 25) can reliably identify tagging SNPs, and we suggest that this be done separately in each genetic subpopulation when multicenter studies are being conducted.