Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2005 Sep;171(1):279–289. doi: 10.1534/genetics.104.035915

Balancing Selection in the Wild: Testing Population Genetics Theory of Self-Incompatibility in the Rare Species Brassica insularis

Sylvain Glémin *,1, Thierry Gaude †, Marie-Laure Guillemin ‡, Mathieu Lourmas §, Isabelle Olivieri **, Agnès Mignot **
PMCID: PMC1456519  PMID: 15944365

Abstract

Self-incompatibility (SI) systems are widespread mechanisms that prevent self-fertilization in angiosperms. They are generally encoded by one genome region containing several multiallelic genes, usually called the S-locus. They involve a recognition step between the pollen and the pistil component and pollen is rejected when it shares alleles with the pistil. The direct consequence is that rare alleles are favored, such that the S-alleles are subject to negative frequency-dependent selection. Several theoretical articles have predicted the specific patterns of polymorphism, compared to neutral loci, expected for such genes under balancing selection. For instance, many more alleles should be maintained and populations should be less differentiated than for neutral loci. However, empirical tests of these predictions in natural populations have remained scarce. Here, we compare the genetic structure at the S-locus and microsatellite markers for five natural populations of the rare species Brassica insularis. As in other Brassica species, B. insularis has a sporophytic SI system for which molecular markers are available. Our results match well the theoretical predictions and constitute the first general comparison of S-allele and neutral polymorphism.

HOMOMORPHIC self-incompatibility (SI) systems are widespread physiological mechanisms preventing self-fertilization in Angiosperms by controlling pollen germination or pollen tube growth (De Nettancourt 2001). Pollen and pistil are incompatible when they both express identical alleles. The recognition involves specificity molecules usually encoded by one genome region containing several multiallelic genes (De Nettancourt 2001). In gametophytic (GSI) systems, the pollen phenotype is encoded by its own haploid genome, whereas in sporophytic (SSI) systems, the pollen phenotype is determined by the sporophyte (diploid pollen parent) and can involve dominance interactions among alleles. For instance, two classes of alleles are known in Brassica oleracea (Nasrallah 1991). Class I alleles are dominant over the class II alleles in the pollen, while alleles within class I and class II are mutually codominant. In the pistil, all alleles are codominant. This scheme is also found in B. campestris, with the exception that alleles occur in three dominance levels in the pollen and a few alleles are recessive in the stigma (Hatakeyama et al. 1998). At the molecular level, the SSI system of the Brassicaceae is among the best known (for a recent review see Hiscock and McInnis 2003). Both pistil and pollen genes have been identified (Schopfer et al. 1999; Takayama et al. 2000). In this system, recognition proceeds through receptor-ligand interaction between S-locus cysteine-rich protein (SCR), a small hypervariable ligand peptide, and S-locus receptor kinase (SRK), a transmembrane receptor with an intracellular kinase domain (Kachroo et al. 2001).

SI evolutionary properties have also long aroused the population geneticist's interest because selection pressures are known a priori. Compatible crosses require distinct alleles so that the population-level rare alleles are favored and numerous alleles are expected to be maintained by negative frequency-dependent selection (for a review see Lawrence 2000). In single populations, Wright's (1939) pioneering work, synthesized by Yokoyama and Nei (1979), showed that, in GSI systems, the high number of S-alleles maintained in a population depends greatly on the effective population size, but very little on the mutation rate. In SSI systems, dominance relationships break down the symmetry relationships among alleles and lead to differential allele behaviors and dynamics, according to their dominance levels (Schierup et al. 1997; Uyenoyama 2000). Recessive alleles are expected to be less numerous, but maintained at higher frequencies than dominant ones (Uyenoyama 2000). However, the general relationship between the number of S-alleles and the population size is conserved (Schierup et al. 1997). A higher number of alleles than for neutral markers and a positive correlation with the population size are thus expected for the S-locus.

In subdivided populations, interactions between balancing selection and population structure shape the distribution of S-alleles, sometimes in nontrivial ways. Contrary to what happens for neutral markers, Schierup (1998) showed in a simulation study that subdivision does not greatly affect the number of alleles in the whole population. This result was confirmed by Muirhead (2001), who provided analytical solutions for the case of symmetrical balancing selection (GSI and the MHC locus): when migration is above some threshold, a locus under balancing selection behaves as in a panmictic population. Intermediate migration rates tend to deplete the total number of alleles compared to a single large population. The number of alleles increases with subdivision, as in a neutral case, only when migration is very low. This nontrivial pattern can be explained because balancing selection is expected to increase the effective migration rates as rare migrant alleles are favored (Schierup et al. 2000). Consequently alleles tend to be shared by several subpopulations, so that the total number of alleles is not inflated as would be the case for a neutral locus. In addition, subpopulations are expected to be less differentiated (lower FST values) compared to neutral markers, for both GSI and SSI systems (Schierup et al. 2000).

Although such theoretical studies have now provided a coherent set of predictions, empirical tests of these predictions in natural populations have remained scarce. The effect of population structure on genes under balancing selection has been investigated for the MHC system, for instance, in bighorn sheep (Boyce et al. 1997), in Atlantic salmon (Landry and Bernatchez 2001), and in island fox (Aguilar et al. 2004). Unexpectedly, in several cases, FST values at MHC loci were as high as or even higher than FST at neutral loci (for a short compilation see Muirhead 2001). These results could be explained by the fact that different demes experience different selective environments, locally favoring certain subsets of alleles (Muirhead 2001). Since selection is expected to be driven by mating type, not by environmental factors, departure from theoretical expectation is less likely for the SI system (unless spatially heterogeneous selection pressures operate on linked loci). Recently Brennan et al. (2003) inferred population structure from the autocorrelation pattern within a single population of Senecio squalidus at four allozyme markers and six S-alleles identified by diallele crosses. They found no population structure either for the S-locus or for the allozyme loci. However, local population structure within a population may not be a relevant level for testing the effect of balancing selection, as the theoretical studies do not deal with continuous populations. Cases with strong population differentiation should offer better conditions for comparing the pattern of the two kinds of loci. To our knowledge, no study has yet compared the diversity pattern for S-alleles and neutral markers among populations that are clearly distinct.

In this article we investigate the effect of balancing selection on the number and distribution of S-alleles in natural populations of the rare and endangered species B. insularis. We compared the population genetic structure of five natural populations of the species for 11 microsatellite markers and for the S-locus, using an antibody-based approach to detect S-alleles. Here, we focus mainly on the test of population genetics theoretical predictions. Other results on the mating system of this rare species and their consequences for its conservation will be discussed elsewhere.

MATERIALS AND METHODS

Biological material, characteristics of the populations, and sampling protocol:

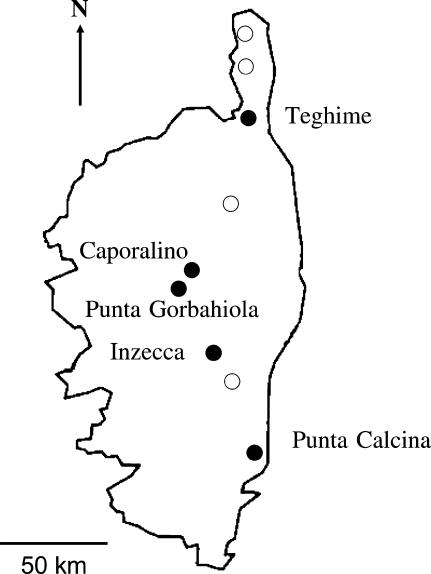
B. insularis is a rare Mediterranean wild species of the B. oleracea group (with 2n = 18 chromosomes). Its distribution is restricted to small, isolated populations in Corsica (9 known populations), Sardinia (15–17 ), Tunisia (5), Algeria (1), and in Pantelleria island, near Sicily (1) (Snogerup et al. 1990). It inhabits primarily limestone or schist cliffs at elevations of 300–1000 m. It is a short-lived perennial species with insect pollination and flowers between March and May. As in other Brassica sp., there is a sporophytic self-incompatibility system; however, individuals vary in self-incompatibility level. In a survey of ∼30 individuals, one plant was found fully compatible, four had a low compatibility level, and eight were mostly incompatible except in some tests (S. Glémin and A. Mignot, unpublished data). We studied five Corsican populations distributed from north to southeast (Figure 1): Teghime, Caporalino, Punta Gorbaghiola, Inzecca, and Punta Calcina. Flowering rates were estimated in most populations in 2000 and 2001 and in 1999 for the Caporalino population. Population sizes were estimated by direct count in the two smallest populations (Punta Calcina and Punta Gorbaghiola). In the other populations, sizes were estimated by extrapolation from the flowering rate estimated in quadrants and the total number of flowering plants counted by eye. Population sizes ranged from 80 to 2500 individuals (Table 1). These populations are geographically isolated and highly and significantly differentiated for allozyme markers (Hurtrez-Bousses 1996; Petit et al. 2001). The range of population sizes and the quite high population structure offer appropriate conditions to detect differences in behavior between S-alleles and neutral alleles.

Figure 1.

Figure 1.

Open in a new tab

Distribution of the five Corsican populations of Brassica insularis studied. Open circles indicate other known populations, not studied here.

TABLE 1.

Characteristics of the populations and the samples

Populations Population size % of flowering No. of flowering plants Sample size for microsatellites Sample size for S allelesc
Teghime 2000 17a 340 71 22/28
Caporalino 1500 27b 405 39 0/55
Inzecca 500 55a 275 40 35/39
Punta Gorbaghiol 300 70a 210 40 37/24
Punta Calcina 80 56a 45 41 29/4
Open in a new tab
a

2000–2001.

b

1999.

c

Natural populations/CBNMP.

Samples for genotyping microsatellite markers were collected in the natural populations in 1999 and 2000. Samples for S-locus genotyping were also collected in the same population in 2000 and/or in individuals issued from seeds collected in the same populations in 1992 and grown at the Conservatoire Botanique National Méditerranéen de Porquerolles (CBNMP), on Porquerolles Island (Table 1). Some populations include local patches a few tens or hundreds of meters distant from each other (Teghime, at least four; Caporalino, at least two; Punta Gorbaghiola, two; Inzecca, two or three; and Punta Calcina, one). As sampling among local patches was not equivalent for the two types of markers, local population structure was not fully studied (see below).

Microsatellite makers:

We used 11 microsatellite loci, 10 developed in B. oleracea [38A, 59A, and 26A from Szewc-McFaden et al. 1996 and 10-B01, 10-B06, 10-D08, 10-E06, 10F07, 11-H09, and 12-D02 from the United Kingdom CropNet Brassica Database (http://ukcrop.net/perl/ace/search/BrassicaDB?class=Microsatellite)] and one in Arabidopsis thaliana (AT129; Bell and Ecker 1994). DNA was extracted using the method of Doyle and Doyle (1987). The amplifications were carried out in a total volume of 15 μl, containing the PCR buffer Eurogentec [750 mm of Tris HCl pH 8.8, 200 mm of (NH4)2SO4, 0.1% Tween 20]; 10 ng of genomic DNA; 1 unit of Taq DNA polymerase; 75 μmol of each dNTP; and 400 nmol of each forward and reverse primer labeled with γ-33P and 0.5 mmol (11-H09), 1 mmol (38A, 10-B06, 10-D08, 10-E06, 10-F07, and 12 D-02), or 2 mmol (AT129, 59A, and 26A) of MgCl2. PCR amplifications were carried out on a Mastercycler Eppendorf thermocycler with a standard program (2 min at 94°; 30 cycles of 30 sec at 94°, 30 sec at the Tl of each locus, 50 sec at 72°; and 2 min at 72°) or a “touchdown” program for loci (10-B06, 10-D08, 10-E06, 10-F07, 11-H09, and 12-D02) that did not amplify with the standard program. The sizes of amplified fragments were determined by radiography after migration on 8% acrylamide-bisabrylamide/TBE gels for loci <300 bp and on 8% acrylamide-bisabrylamide/TTE gels for the other loci. The exact sizes of the fragments were determined using the puc 19 sequence (EMBL no. L09137) as a reference.

Biochemical characterization of S-alleles:

In Brassica species, the genes involved in SI recognition are known (Nasrallah 1991; Schopfer et al. 1999; Takasaki et al. 2000) and the genomic structure of the S-locus has been intensively studied (e.g., Suzuki et al. 1999; Casselman et al. 2000). Rather than through time-consuming phenotypic tests, S-alleles can thus be directly characterized by sequencing or by using molecular or biochemical markers. Here, we used a biochemical method developed on B. oleracea by Gaude et al. (1991). It allows the fast characterization of alleles of the soluble S-locus glycoprotein (SLG) protein and it has been used to characterize SLG polymorphism in Brassica crop collections (Ruffio-Châble et al. 1997, 1999). SLG is not the stigmatic determinant of SI (Takasaki et al. 2000). However, SLG is highly polymorphic and tightly linked to SRK and SCR, forming a haplotype structure (Sato et al. 2002). However, there is no direct estimation of the magnitude of linkage disequilibrium between SLG and SRK or SCR and recombination seems to have occurred in the evolutionary history of S-alleles (Awadalla and Charlesworth 1999; Sato et al. 2002). Despite this limitation, at the scale of our study, SLG polymorphism should give a rough prediction of S-allele polymorphism.

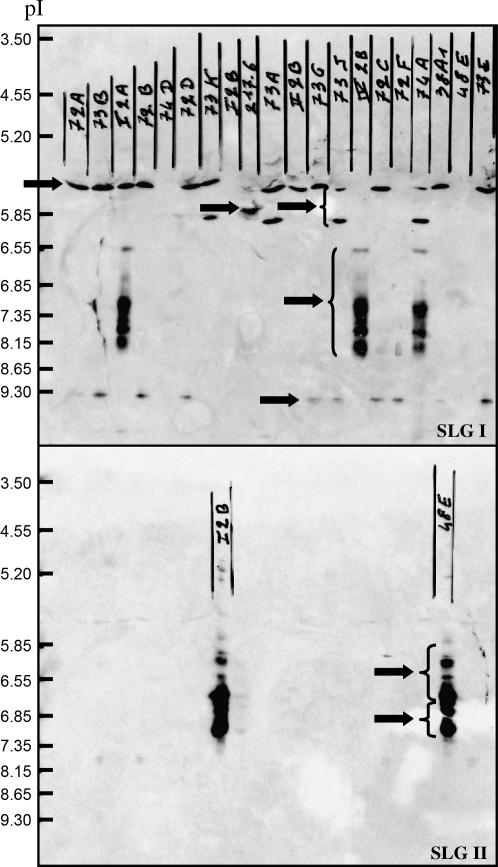
For each plant, 5–10 stigmas were sampled from young unpollinated flowers after anthesis and quickly frozen in liquid nitrogen. Proteins were extracted, separated on isoelectric focusing (IEF) gels, and electrotransferred onto nitrocellulose membranes as previously described (Gaude et al. 1991). SLG proteins were detected by protein blots using two antibodies: a polyclonal serum raised in rabbit and specific for class I proteins (hereafter, anti-class I antibody) and a monoclonal mouse antibody specific for class II proteins (hereafter, anti-class II antibody). These antibodies were raised against synthetic peptides corresponding to the N termini of SLGs of classes I and II, respectively (Gaude et al. 1993, 1995). S-alleles were determined by identifying bands detected by the two antibodies (an example is given in Figure 2). Because of possible multiple glycosylation patterns on the same SLG, one allele can yield several bands (see Figure 2). Comparison of several individuals sharing alleles is thus sometimes required to identify alleles unambiguously.

Figure 2.

Figure 2.

Open in a new tab

Genotyping of individuals by IEF and Western blotting. The Western blot membrane was first immunostained with the anti-class I antibody (up) and then with the anti-class II antibody (down). Isoelectric point (pI) markers are indicated on the left. Each arrow corresponds to one allele (five class I and two class II in all). Because of possible multiple glycosylation patterns on the same SLG, one allele can correspond to several bands. The occurrence of two class II alleles and not only one has been verified on other blots.

Phenotypic tests:

When possible, we performed phenotypic tests to confirm the dominance relationship among alleles, assumed on the basis of antibodies classification. SI was tested using both seed set and assessment of pollen tube growth. Pollinations were performed on young emasculated buds shortly after anthesis. For the seed set method, 10 flowers were used for each cross and 6 flowers for the pollen tube growth method. For the pollen tube growth method, styles were fixed in FAA buffer (glacial acetic acid, 10%; 40% formalin, 10%; 70% alcohol, 80%) after 24 hr. After washing they were placed in a “Z stain” (1% aniline-blue, 10%; detergent, 10%; 0.2 m K3PO4, 70%; 1 m NaOH, 10%) at 65° for 40 min to 1 hr, depending on the style size. Aniline blue was then added and the styles were observed with a fluorescent photonic microscope.

Data analysis:

Genetic diversity and population structure for microsatellite markers:

We used the Genepop software (Raymond and Roussset 1995) to estimate the mean number of alleles per locus, the expected heterozygosity (He), and the fixation index (FIS) for each population. To compare the relative effective population size of the five populations studied, we also estimated the parameter θ = 4Neμ. As we were interested in a rough and relative assessment of the population sizes, the detailed mutation model of the microsatellite loci was not crucial to our purpose. We thus chose to estimate θ from the expected heterozygozity (He) under the stepwise mutation model (SMM) (Kimura and Ohta 1978), 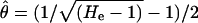Inline graphic, as microsatellites are supposed to evolve mostly according to this model or to derived models (Ellegren 2004). θ was estimated as the mean of the θi estimated for each locus. Population genetic structure was analyzed by estimating global FST and FST between all population pairs. FST values were tested by exact tests implemented in the Genepop software. To compare FST for microsatellites to that of the S-locus, we bootstrapped FST over the 11 microsatellites, so as to provide a confidence interval of overall “neutral” FST.

Estimation of numbers of S-alleles: dealing with undetected alleles:

Because the S-allele genotyping method cannot detect all alleles, we cannot obtain the actual number of alleles in our samples, so uncertainty of typing must be taken into account. This is the main problem of our approach. However, other methods, such as PCR-based methods, also have to cope with undetected alleles (Mable et al. 2003). In previous studies of B. oleracea (Ruffio-Châble et al. 1999), undetected alleles were found. Those studied in detail were found to be class I alleles (Ruffio-Châble and Gaude 2001; T. Gaude and I. Fobis-Loisy, unpublished data). Among class II haplotypes, only S2 was shown to exhibit variable levels of SLG protein expression (Miège et al. 2001) and up to now no new class II allele among undetected alleles. We thus chose to assume that all missing alleles in B. insularis were also class I alleles. Individuals in which only one class I allele was detected were assumed to carry another unknown class I allele. Two kinds of individuals present uncertainties: (i) individuals with no detected allele (“white pattern” in Ruffio-Châble et al. 1999) either can carry two undetected class I alleles or may indicate experimental problems (such as poorly conserved stigmas or too low a concentration of SLGs in the extract) and (ii) individuals with only one class II allele detected can be homozygous for that allele or heterozygous with an unknown class I allele. In B. oleracea, some class I alleles are also detected using the anti-class II antibody (V. Ruffio-Châble and T. Gaude, unpublished data). We treated as “true” class II alleles those that were, at the same time, detected by the anti-class II antibody and shown as recessive in the pollen and codominant in the stigma by phenotypic tests. Alleles detected as class II on the basis of antibody, but without phenotypic confirmation, were considered “ambiguous.”

For each population separately, and for all five taken together, we estimated the numbers of missing alleles by assuming they had the same mean frequency as the mean frequency of class I alleles detected (on the basis of the theoretical prediction that all class I alleles should have the same frequency). Given the sample size, N, the mean frequency of detected class I alleles, fI, and the number of gene copies carrying a missing allele, m, we estimated the number of missing alleles as 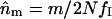Inline graphic. Estimation of the number of missing alleles depends on the assumptions made for points i and ii above. We estimated nm for three cases that are summarized in Figure 3. At one extreme, all white pattern individuals were assumed to be due to experimental errors and all individuals with only one class II or ambiguous allele were assumed to be class II homozygotes (Figure 3, thick solid lines). At the other extreme, all white pattern individuals were assumed to be heterozygotes for two missing class I alleles, and all individuals with only one class II allele were assumed to be heterozygotes with a missing class I allele; ambiguous alleles are considered as class I alleles (Figure 3, dashed lines). In the intermediate case, the number of white pattern individuals was limited to 10% of the sample, as found in Ruffio-Châble et al. (1999), and only 20% of the individuals with one class II allele were assumed to be heterozygous; ambiguous alleles were considered as class I alleles (Figure 3, dashed lines, * indicates the attribution with a given percentage). Other possibilities might occur, for instance, the presence of a class I homozygote due to leaky SI reaction, but they should not affect the results greatly. We chose not to consider them to simplify the analyses. For each population and for each estimation method we computed the repeatability of the study, 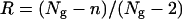Inline graphic, where Ng is the number of genes copies sampled and n is the number of S-alleles determined from the sample (Campbell and Lawrence 1981). Here, the 2 corresponds to the minimum number of alleles that must exist in a population: one class I and one class II. Because of the different assumptions used and the complexity of the SI system in Brassica (two dominance classes), no extrapolation to the total number of alleles in the population is given.

Figure 3.

Figure 3.

Open in a new tab

Rules of attribution of the IEF profiles observed for the four possible genotypes. Ii, class I allele; IIk, class II allele; Am, ambiguous allele; ?, no detection. Thin lines, unambiguous attributions, identical under the three assumptions. Thick solid lines, lowest estimates. Dashed lines, highest and intermediate estimates. These two assumptions differ for attributions indicated by the asterisk (see main text).

Tests of the theoretical predictions:

We analyzed the S-locus data to test the predictions about the effect of population size on the number of S-alleles and of population structure on the distribution of these alleles. Whenever possible, we also took the dominance classes into account. When predictions were available only for symmetrical systems (such as MHC or GSI) we analyzed separately the dominant and recessive alleles, assuming symmetrical equivalence within each class.

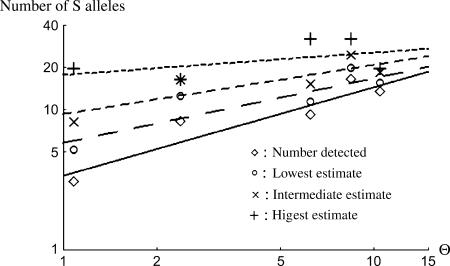
For GSI, an approximate Log-Log linear relationship is expected between the population effective size and the number of S-alleles (Richman and Kohn 1996). For SSI, despite the dominance hierarchy, simulation results revealed a similar relationship (Schierup et al. 1997). To test this prediction we tested for the correlation between Log θ and the Log of the number of S-alleles (Figure 4). We also used nonparametric correlations.

Figure 4.

Figure 4.

Open in a new tab

Number of S-alleles detected and estimated (three estimates) as a function of θ estimated under the SMM hypothesis. Diamonds, number detected; circles, lowest estimate; crosses, intermediate estimate; plus signs, highest estimate. The four regression lines are also given, bottom to top, from the detected number to the highest estimate.

Whatever the dominance relationships, FST at a locus under balancing selection should be lower than that at a neutral locus. To compare with microsatellites, FST at the S-locus was computed using Genepop software, treating the missing alleles as missing data. Here, only two cases were envisaged: individuals with only one class II allele were all declared as heterozygotes with a missing class I allele or all declared as homozygotes. FST at the S-locus was checked against the confidence interval for the neutral markers (see above). Muirhead (2001) suggested that FST is not the best statistic for revealing population differentiation under balancing selection. In the case of symmetrical balancing selection, she showed that the distribution of the number of alleles present in k populations (the “sharing distribution”) is better, because it depends only on the ratio, m/u, of the migration rate to the origination rate of new alleles. We computed this distribution and fitted our data to Muirhead's model by minimizing the sum of the squared error between the expected and the observed distribution (see appendix). We excluded nonambiguous class II alleles and assumed that the others are selectively equivalent. Finally, Schierup (1998) showed that the magnitude of migration can greatly affect both within- and among-population frequency spectra of S-alleles. We thus computed both. As recessive alleles should be maintained at higher frequencies than dominant ones, and as the existing theoretical results concern only GSI, we distinguished the spectra of both classes of alleles separately. As described above for computing FST, individuals with only one class II allele were all declared as heterozygotes with a missing class I allele or all as homozygotes.

RESULTS

Neutral diversity and population structure:

The five populations range from Punta Calcina, the least polymorphic, to Teghime, the most variable (see Table 2). The mean number of alleles per microsatellite locus ranges from 2.55 to 7.27 and the heterozygozity from 0.22 to 0.63. The estimated θ ranges from 1.08 to 10.48. Both the mean number of alleles per locus and θ correlate well with the numbers of flowering plants (respectively, rPearson = 0.95, P = 0.014, and rPearson = 0.89, P = 0.044).

TABLE 2.

Summary of genetic diversity parameters for the five populations studied

Populations Proportion of polymorphic loci Mean no. of alleles per locus He FIS θSMM
Teghime 1.00 7.27 0.58 0.217* 10.48
Caporalino 1.00 6.55 0.63 0.158* 8.43
Inzecca 1.00 5.27 0.48 −0.003 6.25
Punta Gorbaghiola 0.91 4.91 0.50 0.147* 2.38
Punta Calcina 0.45 2.55 0.22 0.045 1.08
Open in a new tab
*

P < 0.0001.

FST among the five populations is quite high (0.28, 95% C.I. 0.22–0.35), and pairwise values are between 0.12 and 0.57. Three populations, Caporalino, Teghime, and Punta Gorbaghiola show quite high and significant FIS values. This could be due to partial selfing as some individuals are partially compatible (tested for the Caporalino and Teghime populations; S. Glémin and A. Mignot, unpublished data). However, quite high levels of selfing are required to explain such FIS values. In a self-incompatible species such a result can be attributed also to local spatial structure (Wahlund effect; Wahlund 1928). This possibility was supported by estimating FST among the local patches within each population. FST values among local patches were indeed significant, especially for Teghime, which shows strong substructure, with at least four patches having pairwise FST from 0.064 to 0.19. These patches are located only a few hundreds meters from each other. The same kind of spatial structure, albeit less marked, was found in the other populations (not shown). Null alleles may also account for the observed high FIS values and would be a more parsimonious interpretation.

Number and distribution of S-alleles:

Estimation of the number of S-alleles:

In the entire sample, we detected 18 alleles with the anti-class I antibody and 6 using the anti-class II one. The number of alleles detected ranges from only 3 alleles in the Punta Calcina population to 16 alleles in the Caporalino population (Table 3). The number of missing alleles varied widely among the populations. In Punta Calcina, we detected at least one allele for each individual, but in Inzecca 32 individuals could not be genotyped. We suspect that this is due not only to missing alleles but also to experimental problems (see materials and methods). Some plants with few to numerous abnormal styles were found in this population in Corsica and 7 out of 19 plants grown in the botanical garden were of this type. We found a large number of class II alleles compared to theoretical predictions (Uyenoyama 2000) and to what was found in B. oleracea and B. rapa, in which only 3 class II alleles and 1 class II allele are known, respectively (Kusaba et al. 1997). However, our phenotypic tests show that only 2 of the alleles detected by the anti-class II antibody were actually shown to be recessive in pollen and codominant in stigma. Moreover, these alleles were the most frequent, as in other Brassica species and as theoretically predicted (Uyenoyama 2000). The four remaining alleles are therefore noted as ambiguous (see materials and methods). The distribution among the five populations of all possible kinds of genotypes under this classification is given in Table 3.

TABLE 3.

Genotypes and number of S-alleles detected and estimated in the five populations

Populations
Teghime
Caporalino
Inzecca
Punta Gorbaghiola
Punta Calcina
Total
No. of plants: 50 55 74 61 33 273
Alleles detected
Class I 8 11 5 6 2 18
Class II 2 2 2 2 1 2
Ambiguous 3 3 2 0 0 4
Genotypes
?/? 7 12 32 6 0 57
I/? 13 9 7 25 3 57
II/? 2 10 15 18 29 74
Ambiguous/? 2 2 10 0 0 14
I/I 18 8 0 2 0 28
II/II 2 5 0 0 0 7
I/II 1 2 6 10 1 20
I/ambiguous 3 6 3 0 0 12
II/ambiguous 0 1 1 0 0 2
Ambiguous/ambiguous 2 0 0 0 0 2
Estimation of the no. of S-alleles
Lowest 15 19 11 12 5 31
R 0.85 0.80 0.89 0.91 0.95 0.93
Intermediate 18 24 15 16 8 41
R 0.83 0.77 0.86 0.89 0.91 0.92
Highest 19 31 31 16 19 56
R 0.83 0.73 0.80 0.88 0.73 0.90
Open in a new tab

Intermediate estimates assume 10% of ?/? individuals, 20% of II/? heterozygotes, and that ambiguous alleles are class I alleles. R is the repeatability index (see main text). ?, “white pattern.”

For all the estimates of allele numbers (given in Table 3), the repeatability (R) is high (between 0.73 and 0.95). This may suggest a good survey of S-allele diversity but could also result from the presence of few class II alleles in high frequency (see Punta Calcina, for instance). The repeatability statistics should thus be viewed with caution in such sporophytic systems. Depending on which assumptions were made (see materials and methods), the range of estimates could be very large. For the Inzecca and Punta Calcina populations, great uncertainty exists (high frequency of white patterns or II/? genotypes). Whereas the lowest and the intermediate estimates are strongly correlated (rPearson = 0.99, P = 0.0006), and both are correlated with the number of alleles detected (rPearson = 0.99, P = 0.0021 and rPearson = 0.97, P = 0.006, respectively), the highest estimate gives results that seems somewhat aberrant. For example, in the Punta Calcina population, the number of S-alleles number is increased from 3 detected to 19 estimated if we assume no class II homozygotes.

We found a positive and significant correlation between θ and the number of S-alleles detected (rPearson = 0.93, P = 0.021; rSpearman = 0.90, P = 0.037) and a marginally significant correlation between θ and the lowest estimate (rPearson = 0.87, P = 0.053; rSpearman = 0.80, P = 0.104) or the intermediate one (rPearson = 0.85, P = 0.068; rSpearman = 0.80, P = 0.104). With the highest estimate, the correlation is not significant (rPearson = 0.53, P = 0.36; rSpearman = 0.30, P = 0.61).

Distribution of S-alleles among populations: FST and frequency spectrum:

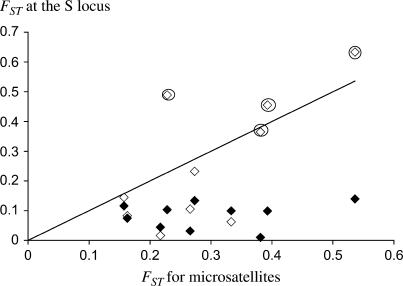
To compare the S-allele and neutral structures, we estimated FST at the S-locus. With the genotype II/? treated as having a missing allele or as homozygotes, the results were very similar, except that some pairwise FST values involving the population Punta Calcina were very high (up to 0.63, see Figure 5). Excluding Punta Calcina, the overall FST is 0.088 or 0.12 under the two different assumptions, respectively, compared with 0.23 for the microsatellites (Punta Calcina excluded; 0.28 when Punta Calcina is included). The S-locus FST value is outside the confidence interval for the neutral FST (0.17–0.31; 0.22–0.35 when Punta Calcina is included). Figure 5 plots pairwise S-locus FST vs. neutral FST. Whichever estimate was used, values of FST at the S-locus are lower than the neutral FST value except for three pairs involving Punta Calcina when all II/? genotypes were assumed to be homozygotes.

Figure 5.

Figure 5.

Open in a new tab

Pairwise FST at the S-locus as a function of the FST for microsatellites. The solid line indicates equality. FST's at the S-locus were computed assuming no class II homozygotes (solid diamonds) or that all II/? profiles were homozygous (open diamonds). The circled diamonds correspond to FST pairs involving Punta Calcina.

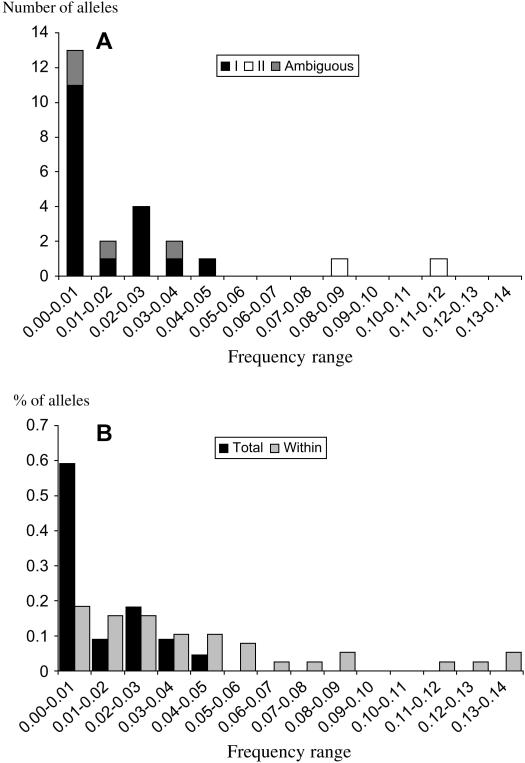
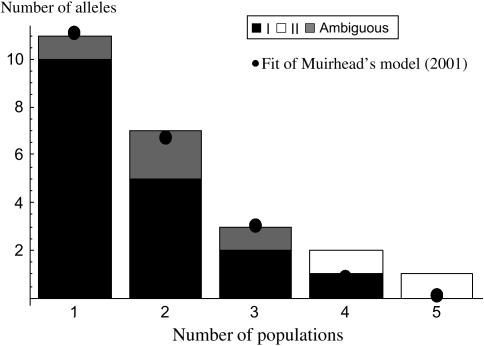
In addition to FST values, we studied the frequency distributions of S-alleles within and among populations. Figure 6A presents the frequency spectrum of the S-alleles over the whole set of populations, for class I, class II, and ambiguous alleles. The two class II alleles show much higher frequencies than the class I or ambiguous alleles, both of which behave similarly. Figure 6B compares the frequency spectrum over the whole populations (as in Figure 6A) and the mean frequency spectrum within each population, excluding class II alleles and pooling class I and ambiguous alleles. Both within and across populations, ambiguous alleles have a frequency similar to that of class I alleles and lower than that of class II alleles. Figure 7 shows the sharing distribution of the number of alleles present in k populations (Muirhead 2001). Except for class II alleles present in four and five populations, respectively, the distribution is skewed toward private alleles present in only one population. This is confirmed by fitting Muirhead's model with a ratio m/u = 1.5, suggesting very restricted migration. Here we stress that, contrary to the estimates from FST, m is the demographic migration rate, not the effective rate taking into account selective advantage of rare migrants (Schierup et al. 2000). However, because the two class II alleles are not equivalent to the others and are excluded from the analysis, the frequencies of the alleles do not sum to one, and a bias toward private alleles is expected. This result should thus be viewed with caution.

Figure 6.

Figure 6.

Open in a new tab

Frequency spectrum of the S-alleles (A) across all the populations and (B) within a population. In B, the two class II alleles are excluded and the ambiguous alleles are pooled with the class I alleles. The frequency spectrum is given here in percentage and not in absolute number of alleles because it is the mean over the five populations.

Figure 7.

Figure 7.

Open in a new tab

“Sharing distribution” of the S-alleles that is the number of alleles present in k populations. The solid circle corresponds to the fit of Muirhead's (2001) model (see the main text).

DISCUSSION

Testing the predictions of population genetics theory of SI:

Number of S-alleles and population size:

Whichever the assumptions we made to assign genotypes (see above), the total estimated numbers of S-alleles were quite high, at least 30, and comparable to other SI systems studied (for review see Lawrence 2000). The five populations we studied have a wide range of population sizes (from ∼80 to ∼2500), and their values are positively and significantly correlated with estimated θ-values, as predicted. Because the Log-Log linear relationship we fitted (see Figure 4) is an approximation of the more complex relationship between the number of S-alleles and the population size in the SSI system, this result should be taken with some caution. However, nonparametric correlations are of the same order.

Genetic structure at the S-locus:

Our microsatellite analysis confirms the strong differentiation among the five populations (mean FST = 0.28, pairwise FST ranging from 0.12 to 0.57), already found with isozyme markers (Hurtrez-Bousses 1996). In agreement with their restricted geographic range and geographical isolation, the populations are also genetically isolated. As predicted, FST at the S-locus is smaller than neutral FST. Excluding the population Punta Calcina (which we discuss later), we found that FST for the S-locus was about half that for microsatellites. Lower differentiation at the S-locus can be explained by a higher effective migration rate for alleles under balancing selection, because rare migrants will be more successful than expected under neutrality (see Schierup et al. 2000). FST at the S-locus is also weakly sensitive to the relative migration rate indicated by the microsatellite analysis and falls mostly in the range 0–0.1, as suggested by simulation results of Schierup et al. (2000; see their Figure 1). This contrasts with results on the MHC (discussed in Muirhead 2001). To explain the pattern observed in several studies on the MHC, Muirhead (2001) invoked additional selection pressure for subsets of alleles in different local populations, due to different environmental pressures (for example, parasites). Unless pleiotropic effects of S-genes or linked loci are involved in local adaptation, SI systems are thus more likely to match theoretical expectations involving a simple form of balancing selection.

We also studied the distribution of S-alleles within and among the populations. For the special case of the Brassica system, no predictions of the frequency spectrum with balancing selection and population subdivision are available. Schierup (1998) performed simulations for the gametophytic case, assuming high, intermediate, and low migration rates. Because of S-allele assay uncertainties and because of the peculiarity of Brassica systems, direct comparison cannot be made easily. However, the skewed total frequency spectrum and the rather flat within-population spectrum (Figure 6B) can hardly fit the pattern Schierup obtained with high migration rates. The observed sharing distribution with numerous private alleles (Figure 7) also fits the theoretical prediction assuming a very low migration/mutation rate ratio (1.5). Assuming a low mutation rate of the order of 10−6 or 10−5 and population size of the order of 100 or 1000 would lead to very low Nm, so that complete differentiation at neutral loci should be observed. Because of the class II alleles in high frequency, class I alleles are less frequent and probably less widespread than alleles in GSI systems, as assumed in Muirhead's (2001) model. This should reduce the fitted m/u ratio and explain the discrepancy between the FST and sharing distribution analyses. Despite these cautions, our data globally fit the theoretical predictions of the impact of balancing selection on population structure, assuming a low migration rate.

Impact of local substructure:

In three populations we found significant FIS (Table 2), suggesting Wahlund effects due to within-population structure, the presence of null alleles, or (less probably) partial selfing. The two latter explanations should have little influence on the interpretation of the results on S-alleles. However, further substructure might affect our conclusions. Local subdivision should increase the local effective population size. This could increase the neutral diversity but has little effect on the number of S-alleles in each population, which is insensitive to local subdivision, unless migration among local subpopulations is very small (Schierup 1998; Muirhead 2001). By increasing local effective population size, local subdivision should reduce differentiation among populations both for neutral markers and for S-alleles, particularly the former. The significant difference in FST values observed for the two different kinds of genes is thus conservative. However, additional theoretical work should examine hierarchical population structure.

Consequences of dominance relationships:

In B. oleracea, S-alleles fall into two classes, I and II, with class II alleles being recessive to class I alleles in pollen and codominant in stigma. Uyenoyama (2000) analyzed theoretically this special case of the Brassica SSI system. As predicted, numerous class I alleles in low frequencies and few class II alleles in higher frequencies are observed in Brassica crops accessions (Ruffio-Châble et al. 1997, 1999), but no such data exist in natural populations. We found up to 18 class I alleles and 2 class II alleles. In the entire population, the class I alleles have frequencies <5%, whereas the frequencies of the two class II alleles are ∼8 and 11% (higher if we assume that some homozygotes occur; see Figure 6A). Within populations, there is at least one frequent class II allele in all populations except in Teghime, where the three most frequent alleles are class I. The two class II alleles are present in all populations except in Punta Calcina (see Figure 7), where only one is present in high frequency (between 45 and 90%, depending on the assumptions about homozygotes). In agreement with the theoretical prediction, there are numerous class I alleles at low frequency and at least two more widespread class II alleles. Uyenoyama (2000) predicted that class II alleles are more prone to stochastic loss than class I alleles, except when only one class II allele exists. She suggested that the evolutionary persistent state should be a state with one class II allele and many class I's. However, she considered only a single (isolated) population. In subdivided populations, local exclusion of class II alleles could be overwhelmed by migration, maintaining polymorphism for such an allelic class. But such a case remains to be modeled.

Finally, we found four ambiguous alleles: they are detected by the anti-class II antibody but are as rare as class I alleles (see Figures 5A and 6), and we do not have any evidence of their dominance category. We exclude that such multiplicity of class II detection might result from the reaction with other members of the S-gene family. Indeed, it is well documented that, among stigmatic proteins, antibodies detect only SLG and a few soluble SRK proteins (Gaude et al. 1993, 1995; Giranton et al. 1995), which were not detected here (weak specific labeling). Cross-labeling, that is, anti-class II antibody detecting class I alleles, was found in some Brassica cultivars (V. Ruffio-Châble and T. Gaude, unpublished data) and may also occur in B. insularis. If they are actually class I alleles, our results match experimental results in B. oleracea and the theoretical predictions on the number and distribution of class I and class II alleles. If they are class II alleles, our results suggest that B. insularis differs from other Brassica species. We also consider that all undetected alleles belong to class I. If some are actually class II alleles, this might also partly contradict the theoretical expectations. To provide a definitive answer, phenotypic dominance tests and sequencing of ambiguous and undetected alleles will be necessary.

The case of Punta Calcina:

In small populations, only a low number of S-alleles can be maintained, and mate availability can be reduced (Byers and Meagher 1992; Vekemans et al. 1998). This has been invoked to explain the reduced fecundity in small endangered populations of self-incompatible plants (for example, Les et al. 1991; Aspinwall and Christian 1992; Demauro 1993; Byers 1995). We found a quite high number of S-alleles in all populations except the smallest, Punta Calcina. This population is likely to be threatened by low mate availability, because only three alleles were detected, one reaching very high frequency (between 45 and 90% depending on the assumptions about homozygotes; see Table 3). The high frequency of this class II allele explains the high pairwise FST values between Punta Calcina and the other populations.

Such a high frequency is difficult to explain, because selection should reduce it. Although Uyenoyama's (2000) model can predict high frequency of a unique class II allele having few class I alleles, our genotype frequencies (under any of our estimation hypotheses) cannot match her predictions (numerical computations not shown). One can propose several explanations. First, the class II allele could have reached a high frequency by chance, after a recent bottleneck. However, the microsatellite data show no signature of such an event (tested using the software Bottleneck; Cornuet and Luikart 1996). Second, in B. oleracea, class II alleles are associated with weaker SI reaction. Partially compatible alleles should be favored in populations experiencing low mate availability. We found some plants with weak or variable compatibility level but there is no association with the class of alleles they carry (S. Glémin and A. Mignot, unpublished data). Moreover, the few individuals from Punta Calcina available at the CBNMP (and carrying the class II allele only) seem to be strongly incompatible. Further, we did not find any deviation from Hardy-Weinberg expectation (FIS = 0.045, NS; see Table 2) that could result from partial selfing of a weakly compatible plant. Finally, even in a small population inbreeding depression might also prevent the spread of such compatible alleles (Glémin et al. 2001), and we effectively found quite high inbreeding depression in two populations (Caporalino and Teghime) of this species (S. Glémin and A. Mignot, unpublished data). A final explanation for the high frequency of the class II allele in the Punta Calcina population could be that it is favored by segregation distortion, as was found in A. lyrata, where the pollen carrying the most frequent and recessive allele seems to be selectively favored (Bechsgaard et al. 2004). This hypothesis remains to be tested, and additional work will be necessary to understand the pattern of S-alleles found in this population.

Acknowledgments

We are grateful to M. Virevaire for help at the Conservatoire Botanique National Méditerranéen de Porquerolles; to C. Petit and S. Maurice for their help during field sampling; to D. Costich, F. Justy, L. Vimond, and E. Paignon for their technical help on microsatellites genotyping; to A.-M. Thierry for helpful advice on biochemical methods; and to A. Cesaro for advice on the Aniline-blue method. We also thank V. Ruffio and C. Miège for helpful discussion for interpreting biochemical data; X. Vekemans and V. Castric for numerous discussions on SI and their comments on the article; and D. Charlesworth, M. Schierup, and M. Slatkin for helpful comments on the article. This work was supported by a contract from the Bureau des Ressources Génétiques to A. Mignot, a contract from the Centre National de la Recherche Scientifique to I. Olivieri (“Impact des biotechnologies dans les agro-écosystèmes”), and by the scientific council of the Montpellier II University. This is publication ISEM 2005-23 of the Institut des Sciences de l'Evolution.

APPENDIX

The sharing distribution can be computed by iterating Equation 6, using conditions given by Equation 7 in Muirhead (2001). Given hk, the number of S-alleles present in k populations, the hk verify

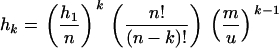graphic file with name M4.gif (A1)

and

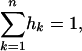graphic file with name M5.gif (A2)

where n is the total number of populations, m is the migration rate, and u is the mutation rate that gives new S-alleles. Given a ratio m/u and replacing the hk in Equation A.2 we can numerically compute the sharing distribution (using the function NSolve in the Mathematica software; Wolfram 1996). To fit the model to our data, we compute the sum-of-squares error, 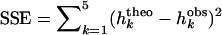Inline graphic, for different m/u ratios and choose the ratio that minimizes SSE. Values of m/u from 0.01 to 10 were tested.

References

  1. Aguilar, A., G. Roemer, S. Debenham, M. Binns, D. Garcelon et al., 2004. High MHC diversity maintained by balancing selection in an otherwise genetically monomorphic mammal. Proc. Natl. Acad. Sci. USA 101: 3490–3494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Aspinwall, N., and T. Christian, 1992. Pollination biology, seed production, and population structure in queen-of-the-prairie, Filipendula rubra (Rosaceae) at Botkin fen, Missouri. Am. J. Bot. 79: 488–494. [Google Scholar]
  3. Awadalla, P., and D. Charlesworth, 1999. Recombination and selection at Brassica self-incompatibility loci. Genetics 152: 413–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bechsgaard, J., T. Bataillon and M. H. Schierup, 2004. Uneven segregation of sporophytic self-incompatibility alleles in Arabidopsis lyrata. J. Evol. Biol. 17: 554–561. [DOI] [PubMed] [Google Scholar]
  5. Bell, C. J., and J. R. Ecker, 1994. Assignment of 30 microsatellite loci to the linkage map of Arabidopsis. Genomics 19: 137–144. [DOI] [PubMed] [Google Scholar]
  6. Boyce, W. M., P. W. Hedrick, N. E. Muggli-Cockett, S. Kalinowski, M. C. Penedo et al., 1997. Genetic variation of major histocompatibility complex and microsatellite loci: a comparison in bighorn sheep. Genetics 145: 421–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brennan, A. C., S. A. Harris and S. J. Hiscock, 2003. Population genetics of sporophytic self-incompatibility in Senecio squalidus L. (Asteraceae) II: a spatial autocorrelation approach to determining mating behaviour in the presence of low S allele diversity. Heredity 91: 502–509. [DOI] [PubMed] [Google Scholar]
  8. Byers, D. L., 1995. Pollen quantity and quality as explanations for low seed set in small populations exemplified by Eupatorium (Asteraceae). Am. J. Bot. 82: 1000–1006. [Google Scholar]
  9. Byers, D. L., and T. R. Meagher, 1992. Mate availability in small populations of plant species with homomorphic sporophytic self-incompatibility. Heredity 68: 353–359. [Google Scholar]
  10. Campbell, J. M., and M. J. Lawrence, 1981. The population genetics of the self-incompatibility polymorphism in Papaver rhoeas. I. The number and distribution of S-alleles in families from three localities. Heredity 46: 69–79. [Google Scholar]
  11. Casselman, A. L., J. Vrebalov, J. A. Conner, A. Singhal, J. Giovannoni et al., 2000. Determining the physical limits of the Brassica S locus by recombination analysis. Plant Cell 12: 23–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cornuet, J. M., and G. Luikart, 1996. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 144: 2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. De Nettancourt, D., 2001. Incompatibility and Incongruity in Wild and Cultivated Plants. Springer, Berlin.
  14. Demauro, M. M., 1993. Relationship of breeding system to rarity in the Lakeside Daisy (Hymenoxys acaulis var. glabra). Conserv. Biol. 7: 542–550. [Google Scholar]
  15. Doyle, J. J., and J. L. Doyle, 1987. A rapid DNA isolation procedure for small quantities of fresh leaf tissue. Phytochem. Bull. 19: 11–15. [Google Scholar]
  16. Ellegren, H., 2004. Microsatellites: simple sequences with complex evolution. Nat. Rev. Genet. 5: 435–445. [DOI] [PubMed] [Google Scholar]
  17. Gaude, T., L. Denoroy and C. Dumas, 1991. Use of a fast protein electrophoretic purification procedure for N-terminal sequence analysis to identity S-locus related proteins in stigmas of Brassica oleracea. Electrophoresis 12: 646–653. [DOI] [PubMed] [Google Scholar]
  18. Gaude, T., A. Friry, P. Heizmann, C. Mariac, M. Rougier et al., 1993. Expression of a self-incompatibility gene in a self-compatible line of Brassica oleracea. Plant Cell 5: 75–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gaude, T., M. Rougier, P. Heizmann, D. J. Ockendon and C. Dumas, 1995. Expression level of the SLG gene is not correlated with the self-incompatibility phenotype in the class II S haplotypes of Brassica oleracea. Plant Mol. Biol. 27: 1003–1014. [DOI] [PubMed] [Google Scholar]
  20. Giranton, J. L., M. J. Ariza, C. Dumas, J. M. Cock and T. Gaude, 1995. The S locus receptor kinase gene encodes a soluble glycoprotein corresponding to the SKR extracellular domain in Brassica oleracea. Plant J. 8: 827–834. [DOI] [PubMed] [Google Scholar]
  21. Glémin, S., T. Bataillon, J. Ronfort, A. Mignot and I. Olivieri, 2001. Inbreeding depression in small populations of self-incompatible plants. Genetics 159: 1217–1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hatakeyama, K., M. Watanabe, T. Takasaki, K. Ojima and K. Hinata, 1998. Dominance relationships between S-alleles in self-incompatible Brassica campestris L. Heredity 80: 241–247. [Google Scholar]
  23. Hiscock, S. J., and S. M. McInnis, 2003. Pollen recognition and rejection during the sporophytic self-incompatibility response: Brassica and beyond. Trends Plant Sci. 8: 606–613. [DOI] [PubMed] [Google Scholar]
  24. Hurtrez-Bousses, S., 1996. Genetic differentiation among natural populations of the rare Corsican endemic Brassica insularis Moris: implications for conservation guidelines. Biol. Conserv. 76: 25–30. [Google Scholar]
  25. Kachroo, A., C. R. Schopfer, M. E. Nasrallah and J. B. Nasrallah, 2001. Allele-specific receptor-ligand interactions in Brassica self-incompatibility. Science 293: 1824–1826. [DOI] [PubMed] [Google Scholar]
  26. Kimura, M., and T. Ohta, 1978. Stepwise mutation model and distribution of allelic frequencies in a finite population. Proc. Natl. Acad. Sci. USA 75: 2868–2872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kusaba, M., T. Nishio, Y. Satta, K. Hinata and D. Ockendon, 1997. Striking sequence similarity in inter- and intra-specific comparisons of class I SLG alleles from Brassica oleracea and Brassica campestris: implications for the evolution and recognition mechanism. Proc. Natl. Acad. Sci. USA 94: 7673–7678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Landry, C., and L. Bernatchez, 2001. Comparative analysis of population structure across environments and geographical scales at major histocompatibility complex and microsatellite loci in Atlantic salmon (Salmo salar). Mol. Ecol. 10: 2525–2539. [DOI] [PubMed] [Google Scholar]
  29. Lawrence, M. J., 2000. Population genetics of the homomorphic self-incompatibility polymorphisms in flowering plants. Ann. Bot. 85 (Suppl. A): 221–226. [Google Scholar]
  30. Les, D. H., J. A. Reinartz and E. J. Esselman, 1991. Genetic consequences of rarity in Aster furcatus (Asteraceae), a threatened, self-incompatible plant. Evolution 45: 1641–1650. [DOI] [PubMed] [Google Scholar]
  31. Mable, B. K., M. H. Schierup and D. Charlesworth, 2003. Estimating the number, frequency, and dominance of S-alleles in a natural population of Arabidopsis lyrata (Brassicaceae) with sporophytic control of self-incompatibility. Heredity 90: 422–431. [DOI] [PubMed] [Google Scholar]
  32. Miège, C., V. Ruffio-Chable, M. H. Schierup, D. Cabrillac, C. Dumas et al., 2001. Intrahaplotype polymorphism at the Brassica S locus. Genetics 159: 811–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Muirhead, C. A., 2001. Consequences of population structure on genes under balancing selection. Evolution 55: 1532–1541. [DOI] [PubMed] [Google Scholar]
  34. Nasrallah, M. E., 1991. The molecular basis for sexual incompatibility, pp. 130–152 in Developmental Regulation of Plant Gene Expression, edited by D. Grierson. Blackie & Son, Glasgow, UK.
  35. Petit, C., H. Fréville, A. Mignot, B. Colas, E. Imbert et al., 2001. Gene flow and local adaptation in two endemic plant species. Biol. Conserv. 100: 21–34. [Google Scholar]
  36. Raymond, M., and F. Roussset, 1995. Genepop (version 1.2), a population genetics software for exact tests and ecumenicism. J. Hered. 86: 248–249. [Google Scholar]
  37. Richman, A. D., and J. R. Kohn, 1996. Learning from rejection: the evolutionary biology of single-locus incompatibility. Trends Ecol. Evol. 11: 497–502. [DOI] [PubMed] [Google Scholar]
  38. Ruffio-Châble, V., and T. Gaude, 2001. S-haplotype polymorphism in Brassica oleracea. Acta Hortic. 546: 257–261. [Google Scholar]
  39. Ruffio-Châble, V., Y. Hervé, C. Dumas and T. Gaude, 1997. Distribution of S-haplotypes and its relationship with self-incompatibility in Brassica oleracea. Part 1. In inbred lines of cauliflower (B. olearacea var ‘botrytis’). Theor. Appl. Genet. 94: 338–346. [Google Scholar]
  40. Ruffio-Châble, V., J. P. Le Saint and T. Gaude, 1999. Distribution of S-haplotypes and its relationship with self-incompatibility in Brassica oleracea. 2. In varieties of broccoli and romanesco. Theor. Appl. Genet. 98: 541–550. [Google Scholar]
  41. Sato, K., T. Nishio, R. Kimura, M. Kusaba, T. Suzuki et al., 2002. Coevolution of the S-locus genes SRK, SLG and SP11/SCR in Brassica oleracea and B. rapa. Genetics 162: 931–940. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Schierup, M. H., 1998. The number of self-incompatibility alleles in a finite, subdivided population. Genetics 149: 1153–1162. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schierup, M. H., X. Vekemans and F. B. Christiansen, 1997. Evolutionary dynamics of sporophytic self-incompatibility alleles in plants. Genetics 147: 835–846. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Schierup, M. H., X. Vekemans and D. Charlesworth, 2000. The effect of subdivision on variation at multi-allelic loci under balancing selection. Genet. Res. 76: 51–62. [DOI] [PubMed] [Google Scholar]
  45. Schopfer, C. R., M. E. Nasrallah and J. B. Nasrallah, 1999. The male determinant of self-incompatibility in Brassica. Science 286: 1697–1700. [DOI] [PubMed] [Google Scholar]
  46. Snogerup, S., M. Gustafsson and R. v. Bothmer, 1990. Brassica sect. Brassica (Brassicaceae). I. Taxonomy and variation. Willdenowia 19: 271–365. [Google Scholar]
  47. Suzuki, G., N. Kai, T. Hirose, K. Fukui, T. Nishio et al., 1999. Genomic organization of the S locus: identification and characterization of genes in SLG/SRK region of S(9) haplotype of Brassica campestris (syn. rapa). Genetics 153: 391–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Szewc-McFaden, A. K., S. Kresovich, S. M. Bliek, S. E. Mitchell and J. R. McFerron, 1996. Identification of polymorphic, conserved simple-sequence repeats (SSRs) in cultivated Brassica species. Theor. Appl. Genet. 93: 534–538. [DOI] [PubMed] [Google Scholar]
  49. Takasaki, T., K. Hatakeyama, G. Suzuki, M. Watanabe, A. Isogai et al., 2000. The S receptor kinase determines self-incompatibility in Brassica stigma. Nature 403: 913–916. [DOI] [PubMed] [Google Scholar]
  50. Takayama, S., H. Shiba, M. Iwano, H. Shimosato, F. S. Che et al., 2000. The pollen determinant of self-incompatibility in Brassica campestris. Proc. Natl. Acad. Sci. USA 97: 1920–1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Uyenoyama, M. K., 2000. Evolutionary dynamics of self-incompatibility alleles in Brassica. Genetics 156: 351–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Vekemans, X., M. H. Schierup and F. B. Christiansen, 1998. Mate availability and fecundity selection in multi-allelic self-incompatibility systems in plants. Evolution 52: 19–29. [DOI] [PubMed] [Google Scholar]
  53. Wahlund, S., 1928. Zuzammensetzung von populationen und korrelationserscheinungen vom standpunkt dervererbungslehre aus betrachtet. Hereditas 11: 65–66. [Google Scholar]
  54. Wolfram, S., 1996. The Mathematica Book. Cambridge University Press, Cambridge, UK.
  55. Wright, S., 1939. The distribution of self-sterility alleles in populations. Genetics 24: 538–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Yokoyama, S., and M. Nei, 1979. Population dynamics of sex-determining alleles in honey bees and self-incompatibility alleles in plants. Genetics 91: 609–626. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES