Estimating the Time to the Whole-Genome Duplication and the Duration of Concerted Evolution via Gene Conversion in Yeast

Abstract

A maximum-likelihood (ML) method is developed to estimate the duration of concerted evolution and the time to the whole-genome duplication (WGD) event in baker's yeast (Saccharomyces cerevisiae). The models with concerted evolution fit the data significantly better than the molecular clock model, indicating a crucial role of concerted evolution via gene conversion after gene duplication in yeast. Our ML estimate of the time to the WGD is nearly identical to the time to the speciation event between S. cerevisiae and Kluyveromyces waltii, suggesting that the WGD occurred in very early stages after speciation or the WGD might have been involved in the speciation event.

NONINDEPENDENT evolution of a multigene family is called concerted evolution (Ohta 1980; Zimmer et al. 1980; Arnheim 1983). The nucleotide divergences among copy members are likely very low during concerted evolution. Interlocus gene conversion has been thought to be the most important mechanism for the homogenization of genetic variation between duplicated genes (or small multigene families), although unequal crossing over should play a significant role in middle-size to large multigene families (reviewed in Ohta 1983; Li 1997). Many duplicated genes in various species exhibit clear evidence for gene conversion (see Innan 2003a and references therein), but a number of unresolved questions remain. For example, How long does concerted evolution last? How often does it occur? What is the evolutionary significance? Very little information is available to answer these questions (Gao and Innan 2004; Teshima and Innan 2004).

With concerted evolution, the behavior of the level of divergence between duplicated genes (d) does not follow the standard molecular clock model (Zuckerkandl and Pauling 1965). Teshima and Innan (2004) demonstrated that the process has three phases [see Teshima and Innan's (2004) Figure 4]. Phase I is the time until d reaches its equilibrium value, d₀. In phase II d fluctuates around d₀, and d increases again in phase III. Phase II represents the time of concerted evolution. The termination of concerted evolution occurs by either mutation or selection. Since interlocus gene conversion results from a nonreciprocal recombination between paralogous regions, the rate of gene conversion may have a positive correlation with the possibility of the pairing of the paralogous regions during meiosis. Large-size insertions or deletions may terminate concerted evolution because they might work as a barrier against the pairing of paralogs. The accumulation of point mutations could also have a similar effect (Walsh 1987; Teshima and Innan 2004) if the divergence between the paralogous regions suppresses gene conversion. Thus, the duration of concerted evolution depends primarily on the mutation and gene conversion rates, although other factors including the tract length of gene conversion also play important roles (Teshima and Innan 2004).

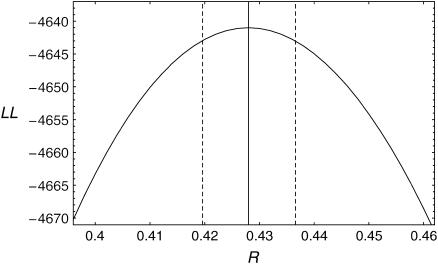
Figure 4.

The log-likelihood curve as a function of R under model I. The maximum-likelihood estimate of R is represented by the vertical solid line. The 95% C.I. is represented by the two dashed lines.

Additionally, selection could also work as a mechanism to terminate concerted evolution. Suppose that a new mutation with a novel function is fixed in one of the duplicated genes while the other keeps the original function (i.e., neofunctionalization). If the state where the two copies have different functions is favored, this state can be maintained by strong selection even under the pressure of homogenization by gene conversion (Innan 2003b). An interesting example is seen in the RHD and RHCE loci in humans. Clear evidence for frequent gene conversion is observed in most of the coding regions of this pair of genes, and the divergence between them is low. On the other hand, ∼10 nonsynonymous nucleotide differences (and a few synonymous ones) are fixed in exon 7 of the two genes, thereby creating a high peak of divergence. It is hypothesized that strong positive selection is operating to keep the amino acid differences in exon 7, and the termination of the concerted evolution might be about to occur in this region (Innan 2003b).

The time of concerted evolution can be considered as the waiting time for a termination event by either selection or neutral mutations; therefore the time length could be approximated by an exponential distribution,

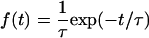(1)

(Teshima and Innan 2004), where τ is the expected length of concerted evolution. This article utilizes this equation to estimate the duration of concerted evolution on a genomic scale. Baker's yeast, Saccharomyces cerevisiae, is used as a model species to take advantage of the fact that the yeast genome has experienced a whole-genome duplication (WGD) (Wolfe and Shields 1997; Dietrich et al. 2004; Kellis et al. 2004). Recently, Kellis et al. (2004) reported the genome sequence of Kluyveromyces waltii, which has diverged from the ancestral lineage of S. cerevisiae before the WGD event. They found that each region of K. waltii is mapped to two regions of S. cerevisiae. Although one copy of most duplicated gene pairs is lost after the WGD, the present S. cerevisiae genome has at least ∼450 pairs of genes originating from the WGD (Kellis et al. 2004). The DNA sequence data of these pairs from the WGD are used to estimate τ together with the time to the WGD event.

MODEL AND THEORY

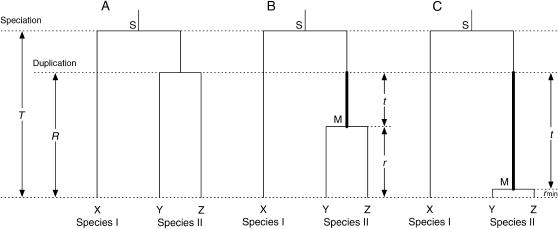
Consider two species, I and II. Suppose that species II has experienced a gene duplication event after the speciation with species I. The three genes, one in species I and two in species II, are denoted by X, Y, and Z, respectively, as illustrated in Figure 1A. Let T be the time to the speciation event (represented by S in Figure 1), and R be the time to the duplication event in units of 2T. Without concerted evolution, the divergence between the two paralogs of species II reflects the time to the duplication and the gene tree should be similar to Figure 1A. In other words, the time to the most recent common ancestor (MRCA) of the paralogs is R. However, if the duplicated pair have undergone concerted evolution, their divergence is expected to be smaller than the prediction under the molecular clock model as illustrated in Figure 1, B and C. M represents the MRCA of the duplicates, and t is the time of concerted evolution (in units of 2T), which is between the duplication event and M. The time length between M and present, represented by r (in units of 2T), contributes to the nucleotide divergence between Y and Z. In Figure 1B, concerted evolution is terminated some time ago, so that Y and Z have a relatively long divergence time. Figure 1C illustrates a case where concerted evolution is ongoing. Note that, in this case, r may not be zero because the sequences of Y and Z are not always identical under concerted evolution. r_min represents the time to MRCA when Y and Z are under concerted evolution, which is mainly determined by the gene conversion rate (Ohta 1982; Innan 2002, 2003a).

Figure 1.

Illustration of gene trees after gene duplication. Thick lines represent the time of concerted evolution. See text for details.

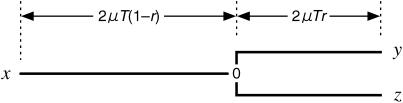
The evolutionary history of the three genes, X, Y, and Z, is summarized by a simple relationship as shown in Figure 2, regardless of how long concerted evolution continues. Focus on a particular nucleotide site, at which x, y, and z represent the nucleotides at the site on X, Y, and Z, respectively. Mutations occur at a constant rate μ per site. A simple two-allele model is considered first. Let 0 be the nucleotide at M, say “G,” and 1 be the other three nucleotides (“A,” “T,” and “C”). Under the Jukes-Cantor model (Jukes and Cantor 1969), the probability that x = 0 is

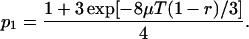(2)

Likewise, the probability that y = 0 is given by

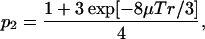(3)

which is identical to the probability that z = 0. Then, it is straightforward to obtain the joint probability for x, y, and z as summarized in Table 1. There are eight possible allelic states, (000), (001), (010), (100), (011), (101), (110), and (111), where the three numbers represent x, y, and z. For example, the probability that x = y = z = 0 is 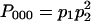, where the subscript of P represents the allelic state.

Figure 2.

The evolutionary relationship among three homologous sites, x, y, and z.

TABLE 1.

Probabilities of allelic states

Allelic state	Probability
Two-allele model
000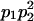
001 and 010	p1p2(1 − p2)
100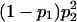
101 and 110	(1 − p1)p2(1 − p2)
011	p1(1 − p2)2
111	(1 − p1)(1 − p2)2
Four-allele model
AAA (x = y = z)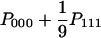
BAA (x ≠ y = z)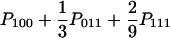
ABA (x = z ≠ y)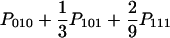
AAB (x = y ≠ z)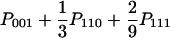
ABC (x ≠ y ≠ z)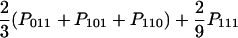

The model is extended to a four-allele model, in which x, y, and z could be one of the four alleles, A, T, G, and C. Let P_AAA be the probability that x = y = z. P_AAA is given by 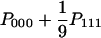because the three nucleotides can be the same with probability 1/9 when x = y = z = 1. In a similar way, we have the probabilities for the other four states, P_BAA, P_ABA, P_AAB, and P_ABC as shown in Table 1.

Suppose that there are L nucleotides in a focal gene, and let l_AAA, l_BAA, l_ABA, l_AAB, and l_ABC be the number of nucleotides of the five allelic states. When P_BAA, P_ABA, P_AAB, and 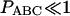, the joint probability of l_AAA, l_BAA, l_ABA, l_AAB, and l_ABC is given by a function of r and m = 2μT,

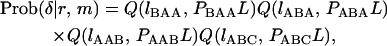(4)

where δ = (l_AAA, l_BAA, l_ABA, l_AAB, l_ABC) and Q(l, s) is the Poisson probability to observe l when its expectation is s:

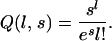(5)

This approximation works well because we use conserved regions such that the proportion of variable sites is ∼10% (see below).

Although (4) involves the mutation rate (m) that is unknown, it is possible to estimate m from the divergence between (X and Y) or (X and Z). Let d_y and d_z be the numbers of nucleotide differences between (X and Y) and (X and Z), respectively. A point estimate of m is easily obtained by the Jukes-Cantor equation:

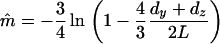(6)

It is also possible to obtain the mutation rate as a probability density distribution, which is given by

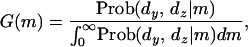(7)

where

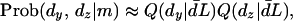(8)

and

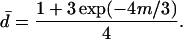(9)

Then, the unconditional probability of δ given r can be obtained from (4) by replacing m with a point estimate given by (6) or by averaging Prob(δ|r, m) weighted by G(m):

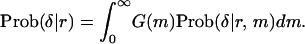(10)

Equation 10 is used in the following analysis although almost identical results are obtained by (4) with a point estimate of m from (6).

MAXIMUM LIKELIHOOD

Data:

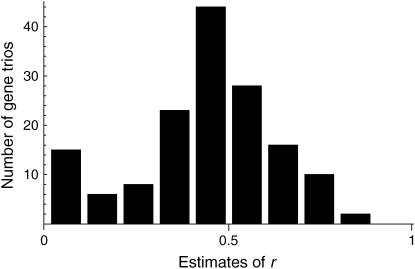
Using Equation 10, we develop a maximum-likelihood (ML) method to estimate the time to the WGD and the duration of concerted evolution in yeast. We use the DNA sequence data for the ∼450 pairs of genes from the WGD in S. cerevisiae plus their orthologs in K. waltii (Kellis et al. 2004). The aligned sequences of the 450 trios were downloaded from http://www.nature.com/nature/journal/v428/n6983/extref/nature02424-s1.htm, and well-aligned regions were extracted (i.e., >90% identity at the first and second positions of the codon). Third positions are not used because the speciation event is so old that nucleotide substitutions at the third positions are almost saturated. The advantage of using the first and second positions is that the effect of multiple mutations at a single site is small, because the first and second positions are more conserved. At the first position, ∼95% of nucleotide changes result in amino acid changes and 100% for the second position. For each of the trios, we count the numbers of the five types of sites, δ = (l_AAA, l_BAA, l_ABA, l_AAB, l_ABC), at the first and second positions of the codon in the well-aligned regions. In the following analysis, we use the data of n = 329 trios, for which >50 bp of the well-aligned regions (i.e., 25 codons) are available. For each trio, r is roughly estimated as 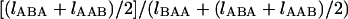, and the distribution is shown in Figure 3. Although the major peak is ∼0.5, there is another peak for very low r, which might reflect genes that have experienced extensive concerted evolution.

Figure 3.

The distribution of estimates of r from 152 gene trios for which l_BAA + (l_ABA + l_AAB)/2 ≥ 20.

The drawback in using the first and second positions of the codon is that they are sensitive to selective pressure, which varies across genes. However, this variation may not cause a serious bias in the theory described above because R is estimated on the basis of the ratio of the divergence from M to X to that from M to Y and Z. In other words, the variation in the substitution rates among genes is allowed (see Equation 7).

If we assume a constant rate of substitution over time, R can be between r_min and 0.5. However, if the selective pressure is relaxed after gene duplication (Ohno 1970; Lynch and Conery 2000), the substitution rate may be higher on the lineage leading to species II than on the lineage leading to species I. If so, R could exceed 0.5. We examine this possibility using the Debaryomyces hansenii genome (Lépingle et al. 2000) as an outgroup of S. cerevisiae and K. waltii. For each of the analyzed trios, their orthologous gene in D. hansenii is identified by BLAST (Altschul et al. 1997). The four amino acid sequences are aligned by CLUSTALW (Thompson et al. 1997) and reverse transcribed into nucleotide sequences. Then, the substitution rates from S to X and from S to Y and Z are estimated from well-aligned regions. Because the two estimates are roughly the same, we find no evidence for such acceleration of the substitution rate on the lineage leading to Y and Z (see discussion). Therefore, in the following maximum-likelihood analysis, we investigated R up to 0.5, unless otherwise noted. It is also possible that the acceleration of substitution rate occurs on one of the duplicated copies, for example, under the scenario of neofunctionalization (Ohno 1970). This problem is also discussed in the discussion.

Model I:

First, we consider a model with no concerted evolution as a null model. The evolutionary relationship for all trios follows Figure 1A. Under this model, it is straightforward to obtain an ML estimate of the time to the WGD, R. The log-likelihood of the data given R is given by

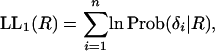(11)

where Prob(δ|R) is from (10).

Model II:

Model II allows concerted evolution. The duration of concerted evolution is approximated by an exponential distribution with mean τ (see Equation 1). τ is assumed to be constant for all duplicated genes. Under this model, the probability density distribution of r is given by

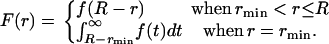(12)

Then, the probability to observe δ is given by a function of R and τ,

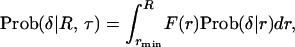(13)

and the log-likelihood of the data is given by

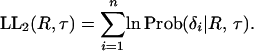(14)

Model III:

This model relaxes the assumption of a constant τ for all genes. It is assumed that τ follows a Gamma function with mean = τ_ave and SD = kτ_ave, which is denoted by Γ(τ|τ_ave, k). Then, the probability to observe δ is given by a function of R, τ_ave, and k,

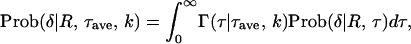(15)

and the log-likelihood of the data given R, τ_ave, and k is

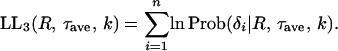(16)

RESULTS

Using the data from 329 trios, the maximum-likelihood analysis is performed. We assume r_min is known. r_min represents the time to the most recent common ancestor of the duplicated genes when they are under concerted evolution; therefore r_min is very small. We assume r_min = 0.01 in the following analysis, but the effect of this assumption is negligible. Almost identical results are obtained for r_min = 0.002 (results not shown). We calculate the likelihood numerically under the three models, I, II, and III. Numerical calculation of likelihood is carried out for R and τ (τ_ave) with intervals 0.002 and 0.01, respectively. For k, the likelihood is calculated with an interval of 0.01 when k < 0.1 and with an interval of 0.1 when k ≥ 0.1.

Model I:

The time to the WGD (R) is estimated without concerted evolution. Figure 4 shows the log-likelihood curve as a function of R. We obtain the maximum-likelihood estimate of R = 0.428 (95% C.I. = 0.420–0.436) with the maximum log-likelihood MLL₁ = −4641.01.

Model II:

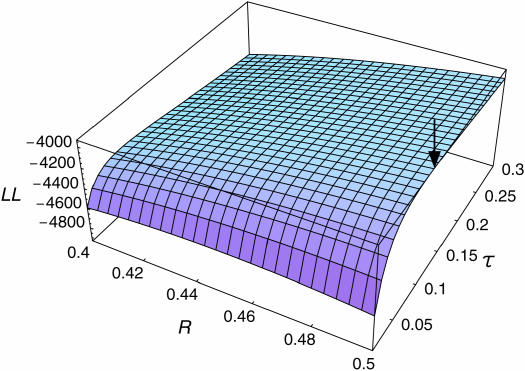
The time to the WGD (R) and the duration of concerted evolution (τ) are simultaneously estimated under the model with concerted evolution. When the rate of substitution is constant over time, R should be a variable between r_min and 0.5 (Figure 5). Under this assumption, we have the maximum-likelihood estimate of R = 0.5 (95% C.I. = 0.498–0.5) with 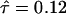(95% C.I. = 0.10–0.13). The maximum log-likelihood is MLL₂ = −3934.82, which is significantly larger than MLL₁ (likelihood-ratio test: P ≈ 0), indicating that model II with concerted evolution provides a much better explanation of the observation than model I. It is suggested that concerted evolution via gene conversion plays a crucial role after genome duplication in yeast.

Figure 5.

The log-likelihood surface as a function of R and τ under model II. The maximum-likelihood estimate is shown by the arrow.

The assumption of a constant rate of nucleotide substitution over time may not hold if the selective pressure is relaxed shortly after gene duplication (Ohno 1970; Lynch and Conery 2000). Although this may not be the case for our data, the assumption can be easily relaxed by investigating the likelihood up to R_max. For example, if R_max = 0.6 is set, we find that maximum log-likelihood MLL₂ = −3786.62 is obtained at R = 0.6 and τ = 0.18 (Table 2). With a more unrealistic setting (R_max = 1), we find the best fit to the data when R = 0.696 and 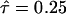with MLL₂ = −3753.41. It is indicated that for any value of R_max the data fit model II significantly better than model I.

TABLE 2.

Summary of ML analysis

Model	No. of parameters	MLL
I	1	−4641.01
Rmax = 0.5
II	2	−3934.82
III	3	−3859.44
Rmax = 0.6
II	2	−3786.62
III	3	−3777.23
Rmax = 1
II	2	−3753.41
III	3	−3753.41

Model III:

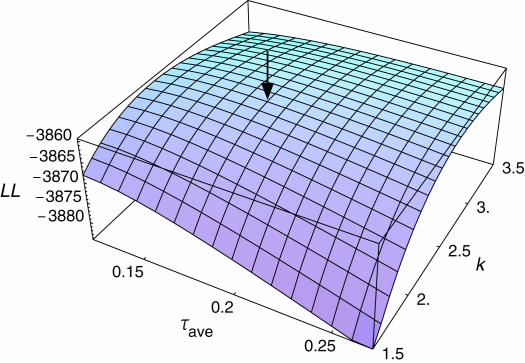
Model III incorporates the variation in τ assuming τ follows a gamma distribution (Figure 6). For R_max = 0.5 the maximum-likelihood estimates are R = 0.5 (95% C.I. = 0.498–0.5), τ = 0.18 (95% C.I. = 0.11–0.27), and k = 2.4 (95% C.I. = 2.0–3.0) with the maximum log-likelihood MLL₃ = −3859.44. MLL₃ is significantly larger than MLL₂ (likelihood-ratio test: P ≈ 0), indicating that the data fit model III significantly better than model II. Similar results are obtained for R_max = 0.6, but maximum likelihoods for models II and III are nearly identical when R_max = 1 (Table 2).

Figure 6.

The log-likelihood surface as a function of τ_ave and k under model III. R is fixed to be 0.5. The maximum-likelihood estimate is shown by the arrow.

DISCUSSION

A maximum-likelihood method is developed to estimate the duration of concerted evolution and the time to the WGD event of yeast. The method utilizes the theoretical results by Teshima and Innan (2004), who demonstrated that the time of concerted evolution approximately follows an exponential distribution. Estimation of the duration of concerted evolution is extremely difficult when we do not know the date of the duplication event. To overcome this problem, we use many duplicated genes that appeared at the same time (i.e., whole-genome duplication). Yeast is one of the ideal species to apply to this method to because of the availability of the genome sequences of S. cerevisiae (Gofieau et al. 1996) and its relatives (e.g., Kellis et al. 2004).

The application of our ML method demonstrates a crucial role of concerted evolution via gene conversion after gene duplication in yeast because the models with concerted evolution (models II and III) fit the data significantly better than the null molecular clock model (model I). It is also shown that the time to the WGD is underestimated under the molecular clock model. In models II and III, the ML estimate of R is 0.5, suggesting that the WGD occurred in very early stages after speciation with K. waltii or the WGD might have been involved in the speciation event.

When the expected duration of concerted evolution (τ) is assumed to be constant (model II), the ML estimate of τ is 0.12. If we assume that the WGD event occurred ∼100–150 million years ago, τ is 24–36 million years. Gao and Innan (2004) have estimated τ to be ∼25–86 million years from different methods, in which the time of concerted evolution in S. cerevisiae is considered directly on the species tree of S. cerevisiae and its six relatives. Our estimate is roughly in agreement with that of Gao and Innan (2004).

Model III incorporates the variation in τ in model II. Model III is more realistic because τ depends on many parameters (Teshima and Innan 2004), which may not be constant over the genome. Selection is one of the most important factors to cause variation in τ among genes. For example, selection could work such that a larger amount of a gene product is favored (Kondrashov and Koonin 2004), which is likely for ribosomal and histone genes. For such genes, τ might be larger than other genes. In fact, the ∼450 yeast genes pairs identified by Kellis et al. (2004) include many ribosomal and histone genes. We find that model III explains the data significantly better than model II. The ML estimate of SD of τ is 2.4 × τ_ave, indicating that τ is very variable.

There are several limitations in our model. First, we assume a constant evolutionary rate over time, but it could fluctuate by the changes of selective pressure. For example, Lynch and Conery (2000) suggested that selective pressure might be relaxed shortly after gene duplication. This possibility was somehow incorporated by investigating the likelihood up to R_max (>0.5). However, we found that R_max may not be 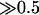. We modified the ML equation to estimate R_max using the D. hansenii sequence as an outgroup, and it turned out that the ML estimate of R_max is 0.49. Another possible scenario is that selective pressure could be relaxed on only one of the duplicated genes, for example, under a neofunctionalization model. Ohno (1970) describes this process such that a redundant copy created by duplication could be “freed” from selective pressure. Since it is very difficult to incorporate this effect into our system, as a proxy, we repeated the same analysis after excluding 63 trios, for which the evolutionary rates on the lineages leading to the two yeast duplicates are significantly different (Tajima 1992). Note that this treatment may not be very fair because the trios excluded are biased toward those with higher r because of the statistical power. Nevertheless, very similar results are obtained.

Second, we assume a Gamma distribution to take into account the variation in the expected duration of concerted evolution, τ. Unfortunately, almost no prior information on this distribution is available. Many factors determine τ, including mutation, gene conversion, recombination rate, and selection. Therefore, our Gamma approximation might oversimplify the situation.

This study demonstrates a significant role of concerted evolution after gene duplication on a genomic scale in yeast. We have successfully estimated the duration of concerted evolution via gene conversion in yeast duplicated genes, indicating that gene conversion is a very important mechanism in the evolution of duplicated genes. The results suggest the importance of the analysis of duplicated genes incorporating the effect of gene conversion rather than simple analysis based on the molecular clock model. As discussed in Teshima and Innan (2004) and Gao and Innan (2004), molecular clock-based analysis causes a bias when the effect of gene conversion is not negligible. Examples of genome-wide analysis of duplicated genes with the molecular clock model include estimation of the age distribution of duplicated genes (Gu et al. 2002; McLysaght et al. 2002) and estimation of the rates of gene duplication and loss (Lynch and Conery 2000). Together with recent evidence for frequent gene conversion in various species (see Innan 2003a and references therein), such analysis should be understood carefully, especially when applied to gene conversion-rich species such as yeast. The extent of interlocus gene conversion on a genomic scale in other organisms is an open question. The development of theories that incorporate gene conversion is also needed to better understand the evolution of duplicated genes.