Using Progenitor Strain Information to Identify Quantitative Trait Nucleotides in Outbred Mice

Abstract

We have developed a fast and economical strategy for dissecting the genetic architecture of quantitative trait loci at a molecular level. The method uses two pieces of information: mapping data from crosses that involve more than two inbred strains and sequence variants in the progenitor strains within the interval containing a quantitative trait locus (QTL). By testing whether the strain distribution pattern in the progenitor strains is consistent with the observed genetic effect of the QTL we can assign a probability that any sequence variant is a quantitative trait nucleotide (QTN). It is not necessary to genotype the animals except at a skeleton of markers; the genotypes at all other polymorphisms are estimated by a multipoint analysis. We apply the method to a 4.8-Mb region on mouse chromosome 1 that contains a QTL influencing anxiety segregating in a heterogeneous stock and show that, under the assumption that a single QTN is present and lies in a region conserved between the human and mouse genomes, it is possible to reduce the number of variants likely to be the quantitative trait nucleotide from many thousands to <20.

ALTHOUGH it is straightforward to map quantitative trait loci (QTL) in animal models such as rodents [>100 that influence behavioral variation alone have been identified (Flint 2003)], finding the quantitative trait nucleotides (QTN) that give rise to a QTL continues to be difficult and expensive; cheaper and quicker ways of moving from QTL to QTN are needed. Unfortunately the genetic architecture of quantitative traits is complex (Mackay 2001). Studies in yeast (Steinmetz et al. 2002) and Drosophila (Anholt et al. 2003) reveal interactions between sex, environment, and genotype and show that no single variant within a locus may be sufficient to explain phenotypic variation. The individual contribution from each locus is usually small, and the responsible sequence variants may lie within noncoding regions (Allen et al. 2003; Helms et al. 2003; Tokuhiro et al. 2003; Ueda et al. 2003; Van Laere et al. 2003; Zhang et al. 2003).

The availability of complete genome sequences and dense single-nucleotide polymorphism (SNP) maps opens up novel approaches to QTN identification (Lander et al. 2001; Sachidanandam et al. 2001; Wade et al. 2002; Waterston et al. 2002). Surveys of genetic variation in the mouse indicate that sequence differences between inbred strains are not randomly distributed across the genome. Wade and colleagues argue that 95% of genetic variation lies in one-third of the mouse genome and suggest that focusing on SNP dense regions of the genome will accelerate QTL searches (Wade et al. 2002).

Sequence differences between inbred strains have long been used to map QTL in panels of recombinant inbred lines (see http://www.webqtl.org). The key idea is that allelic distribution across the panel at a locus is characterized by its strain distribution pattern (SDP): a QTL must be contained in a locus where the SDP correlates with the phenotypic distribution across the panel. More recently, Hitzemann and colleagues have shown that when QTL have been mapped in different combinations of inbred strain crosses, allelic variation among the strains can be combined with mapping data to narrow the region containing the functional variant (Hitzemann et al. 2002). Further, it should be possible to exploit the SDP of multiple inbred strains for QTL mapping in silico (Grupe et al. 2001).

Here, rather than map QTL, we show how to use SDPs to identify candidate QTN. We present a novel approach that combines the high-resolution mapping potential of genetically heterogeneous stock (HS) of mice with the sequence information available from the HS progenitor strains (Talbot et al. 1999; Mott et al. 2000). Our approach differs from that of other methods that use SDP information (for example, Hitzemann et al. 2002; Grupe et al. 2001), in that it incorporates the probabilistic ancestral haplotype reconstruction analysis developed for the analysis of HS populations.

As a test case, we analyzed a QTL that contributes to <10% of the phenotypic variance in a number of behavioral tests of anxiety in the mouse (Turri et al. 2001a,b). The small-effect size is typical for a behavioral QTL and for many other phenotypes too (Flint 2003). The QTL has been mapped to a 4.8-Mb region near position 143 Mb on chromosome 1 in HS mice that are derived from eight inbred progenitor strains, A/J, AKR, BALB/c, C3H, C57BL/6, DBA/2, I, and RIII (McClearn et al. 1970). We screened the region for sequence variants and identified 1720 (including 1325 SNPs) of an estimated total of 15,000 (Yalcin et al. 2004a). All the diallelic variants fall into 19 SDPs, none of which form a simple haplotype block structure. These SDP complexities suggest that a way to test that each variant is a QTN is by combining QTL mapping data in HS animals (Talbot et al. 1999) with the SDPs of HS progenitor strains (Yalcin et al. 2004a) and thus avoiding the need to genotype every polymorphism. The problem this article addresses is equivalent to the hidden SNP problem in human genetics (Evans et al. 2004). However, our solution differs in that we can make use of the known haplotype structure of mouse inbred strains.

MATERIALS AND METHODS

Heterogeneous stock mice:

We used the same mice and phenotype as described in Talbot et al. (1999). The stock is maintained by breeding from 40 pairs and at the time of the experiment reported here mice were at generation 58 at which point the expected average length of unrecombined chromosome is <2 cM, in agreement with experimental observation (Talbot et al. 1999). Open-field activity was measured in 751 heterogeneous stock mice for 5 min in a white plastic 60-cm arena. Defecation was measured by recording the number of fecal boli produced in the open field during the 5-min test period. The phenotype we use, EMO, is the difference between the standardized scores for activity and defecation.

SNP genotyping:

SNP genotyping was performed using the MassExtend system (Sequenom). Extension and amplification primers were designed using SpectroDesigner. Oligonucleotides were synthesized at Metabion (Martinsried, Germany). PCR was carried out with Hotstar Taq obtained from QIAGEN (Düsseldorf, Germany). A 5-μl PCR contained 2.5 ng of genomic DNA, 0.2 units of HotStar Taq, 5 pmol forward and reverse primers, 2 mm of each dNTP, 1× HotStar Taq PCR buffer as supplied by the enzyme manufacturer [contains 1.5 mm MgCl₂, Tris-Cl, KCl, (NH₄)₂SO₄ pH 8.7], and 25 mm MgCl₂ (QIAGEN). The temperature profile consisted of an initial enzyme activation performed at 95° for 15 min, followed by 45 cycles of 94° for 20 sec, 56° for 30 sec, 72° for 60 sec, and a final incubation at 72° for 3 min.

PCR products were treated with shrimp alkaline phosphatase (Sequenom) for 20 min at 37° to remove excess dNTPs. A thermosequenase (Sequenom) was used for the base extension reactions (94° for 2 min, followed by 94° for 5 sec, 52° for 5 sec, and 72° for 5 sec for 55 cycles).

Unincorporated nucleotides were removed from extension products using SpectroClean resin. A few nanoliters of sample was then arrayed onto a 384 SpectroChip by a SpectroPoint robot. Chips were read in the Bruker Biflex III Mass Spectrometer system and data analyzed on SpectroTyper. Genotypes were automatically uploaded into a custom database.

DNA sequencing:

Genomic DNA was amplified in a 50-μl PCR reaction using oligonucleotides synthesized at MWG (Ebersberg, Germany): 100 ng DNA, 0.2 units Gold Taq,10 pmol forward and reverse primers, 8 mm of each dNTP, 1× PCR buffer, and 25 mm MgCl₂. The PCR was run using the following conditions: 95° for 15 min (×1), 95° for 30 sec, 62° for 30 sec at −0.5°/cycle, 72° for 60 sec (×13), 95° for 30 sec, 58° for 30 sec, 72° for 55 sec (×29), and 72° for 7 min (×1). PCR products were purified on a 96-well Millipore purification plate and resuspended in 30 μl of H₂O. Two sequencing reactions were prepared for each DNA sample, one with the forward primer and one with the reverse primer. PCR reagents were removed from solution by an ethanol precipitation in the presence of sodium acetate. All sequencing reactions were analyzed on an ABI3700 sequencer and edited using CONSED software (Gordon et al. 1998).

Sequence variant information:

We used the data set of 1720 variants described in Yalcin et al. (2004a), obtained by resequencing 580 kb of the 4.8-Mb region in each of the eight HS founders. We used DNA from the following eight strains as representative of the founders of the HS: A/J, AKR, BALB/cJ, C3H/HeJ, C57BL/6J, DBA/2J, I/LnJ, and RIII/DmmobJ (hereafter referred to as A/J, AKR, BALB/c, C3H, C57BL/6, DBA/2, I, and RIII). Details of the sequencing strategy are given in Yalcin et al. (2004a); in brief, we resequenced all exons, including at least 1 kb of flanking sequence, all conserved noncoding regions (defined as regions of >70% similarity over ≥100 bp in a comparison between mouse and human sequence), and finally a random selection of 1- to 2-kb segments, at intervals of ∼10 kb. The mean distance between sampled sequences was 8.2 kb.

Marker selection:

We selected a set of SNPs for genotyping the HS animals on the basis of the informativeness of the haplotypes of the eight HS founder strains. The method was originally developed for tagging SNPs in humans (Ackerman et al. 2003). Briefly, the method works on a moving window of SNPs, prioritizing the SNPs in each window by their ability to account for an entropy-based measure of diversity between the founder haplotypes. Each SNP is scored by summing its contributions in all the windows that overlap the SNP. Then the SNPs are ranked across the region by sorting their scores, and the top SNPs are chosen for genotyping. For a detailed explanation the reader is referred to http://www.well.ox.ac.uk/rmott/SNPS.

Testing for a QTL:

The test for a QTL is an extension of the treatment in Mott et al. (2000). A skeleton of markers is genotyped in the HS over a region containing a QTL. The markers must be spaced close enough that on average more than one marker will be present between any two historical recombinants that have accumulated in the HS. We also genotype the progenitor strains with the same markers.

We consider, on both chromosomes, each interval L between genotyped markers in an HS individual i. Because the genotype data provide only incomplete information, the strain origins of each interval are not known with certainty. We use a dynamic-programming algorithm (Mott et al. 2000) to infer the probability F_Li(s, t) of descent from founder strains s, t, where s and t can be any of the progenitors (and may be identical).

If the interval L (the interval between two genotyped markers) contains a QTL, then the expected trait value for an individual with ancestral strains s, t within the interval will be T(s, t), say, for a general “full” model allowing for interaction between the alleles and including dominance, or T(s) + T(t) if the QTL behaves additively. The expected trait value for the individual i with strain probability distribution F is then

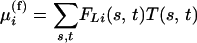(1)

or

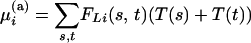(2)

for an additive QTL. The T's are estimated by multiple linear regression of the observed trait values y_i on the probabilities F_Li(s, t). In this instance, the T's are estimated genetic effects from the linear regression model. Under the null hypothesis of no QTL effect, the trait means T(s, t) are the same for all strains s and t. We use analysis of variance to look for significant differences between the strain effects as a test for the presence of a QTL. Furthermore, the additive model (2) is a submodel of the full model (1), so the presence of an interaction within the interval is tested by comparing the models using a partial F-test.

Testing for a QTN within a QTL by merge analysis:

Within the interval (L) we have a series of polymorphisms, determined, for example, by sequence analysis of the progenitor strains, and we test the candidacy of each polymorphism as a QTN. To apply the test of a QTN, the positions and SDPs of all variants are assumed to be known within the interval L. We define p as the sequence polymorphism and we note that p partitions the founder strains into two or more groups, in which all members of a group share the same allele at p; a diallelic SNP will generate two groups. If p is associated with the trait, then merging the founder strains in accordance with p's SDP will retain, or enhance, its statistical significance. However, if the significance level drops markedly, we cannot reject the null hypothesis of no association. We define

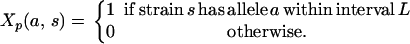The probability that individual i is descended from alleles a, b within interval L at polymorphism p is estimated by

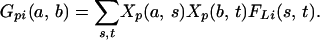The expected trait value for individual i in the merged strains is then

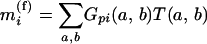(3)

for the full model or

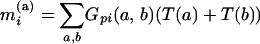(4)

for the additive model. The model for a QTL using the merged strains is a submodel of the corresponding model using the unmerged data: model (3) is a submodel of (1), and (4) is a submodel of (2).

A partial F-test determines whether the fit is significantly different between the models. Although the variance explained by a submodel cannot exceed that of the full model, the partial F-statistic can be more significant in the submodel because of the reduction in the number of degrees of freedom. For example, the test for a diallelic SNP has 1 d.f. in the additive model and 2 d.f. in the full model; by contrast, the full unmerged model (with S = 8 strains) has 35 d.f. [(S(S + 1)/2) − 1 = 35]. Polymorphisms in the same interval that share a SDP behave identically under the test and cannot be distinguished. In this framework, p can be (a) a single polymorphism such as a SNP or microsatellite, (b) a composite of several nearby polymorphisms, or (c) the distinct haplotypes present at a locus, so the test can also be used to investigate and eliminate regions where the haplotype distribution pattern is inconsistent with the phenotype values.

We extended the original C version of HAPPY, which fits only the linear additive model (2), by reimplementing the model-fitting part of the algorithm in the R language (http://www.r-project.org), keeping (for efficiency) the original dynamic-programming engine written in C. The four models and the merge analysis are implemented as R functions in the package. Consequently R's modeling capabilities, including generalized linear models and multivariate analyses, are available in HAPPY (http://www.well.ox.ac.uk/happy).

To see if a single polymorphism could explain all of the genetic variance under a QTL, the effect due to each polymorphism was removed in turn and the merge analysis was repeated across all remaining variants. Writing μ(p) to mean the model for polymorphism p, the fits of the models y_p+q = μ(p) + μ(q) and y_p = μ(p) are compared to test if the effect of fitting polymorphism q after fitting p is significant. The most significant conditional fit for a polymorphism measures how much residual genetic variance is unaccounted.

RESULTS

High-resolution QTL mapping using SNPs:

We began by choosing SNP markers within the 95% confidence interval of a QTL on mouse chromosome 1, corresponding to the 4.8-Mb region described in Yalcin et al. (2004a). QTL mapping information obtained from each marker depends on the marker's SDP: if we use a set of markers with identical SDPs our ability to detect QTL with SDPs different from those of the markers is diminished. Therefore we developed an algorithm that took into account the SDPs of the SNPs to identify a maximally informative set of markers from the 1325 SNPs for which we have SDP data.

We identified 37 SNPs, 3 of which are monomorphic in the HS. Monomorphic markers still provide useful mapping information, since they exclude some haplotype configurations. All 751 animals were genotyped with the 37 SNPs. After inspection for quality and likely genotyping error, we included data from 650 animals to map the anxiety phenotype, using both a full model (testing for dominance) and an additive model.

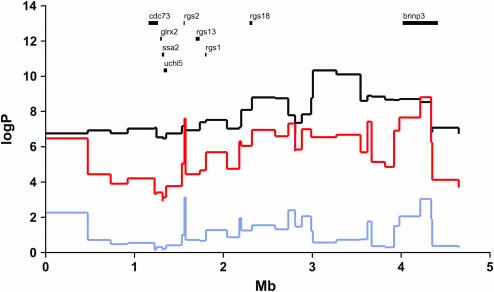
Figure 1 shows log P values within each genotyped marker interval (log P is the negative base-10 logarithm of the analysis-of-variance F-statistic). The fit of the full model is significantly better than that of the additive model (log P > 3.0) at two positions, at 1.7 Mb in the promoter of the rgs2 gene and at 4.3 Mb in an intron of the brinp3 gene. All remaining analyses presented in this article use the full model; the results using the additive model are qualitatively similar. The relative flatness of the log P plot in Figure 1 reflects the fact that markers within the region are in linkage disequilibrium (LD). LD values (measured by D′) are high (>0.8) over many hundreds of kilobases and we cannot expect to obtain additional mapping information by adding more markers.

Figure 1.

Dynamic programming analysis of chromosome 1 QTL. The vertical scale is in log P units and the horizontal scale is in megabases. The position and name of genes are shown above the likelihood curves. Three tests are shown: black, the fit to an additive model; red, the fit to a full model; and purple, the results of a partial F-test comparing additive to full models. A significant difference between full and additive models is shown by the significance of the partial F-test result (purple line) as can be seen at position 1.7 Mb.

QTN analysis:

There may be thousands of polymorphisms to investigate within even a few megabases (Yalcin et al. 2004a). Our aim is to prioritize candidate QTN for functional investigation without further genotyping. The principle behind the test is that, to be a functional candidate, the SDP of a genetic variant must match that of the QTN. As an illustration, consider a cross descended from just three strains in which there is a QTL with two alleles. If strains 1 and 2 carry the decreaser and strain 3 the increaser allele, the SDP of the true QTN is 001 (where 1 is the increaser allele). Now consider sequence variants near the QTN, such that no recombination has occurred between the QTN and the variants. We obtain the SDP of each variant by genotyping the three founder strains. We can eliminate all variants whose SDPs are not 001. This simple scenario demonstrates the power of the approach for evaluating candidate sequence variants.

The SDPs for all common diallelic variants (SNPs and insertion/deletions) across the 4.8-Mb region are shown in Figure 2 by a sequence of digits representing the alleles for the eight founder strains, in the order A/J, AKR, BALB/c, C3H, C57BL/6, DBA, I, RIII. The allele for the first strain A/J is coded as 0. The alleles for the other strains are coded as digits, with the kth strain corresponding to the kth digit in the sequence. For example, a SNP in which the strains A/J, AKR, BALB/c, and RIII have allele C and the remainder allele T has the SDP 00011110 (in this instance “0” indicates “C” and “1” indicates “T”). SDPs with multiallelic markers were included in our analysis [the region we have examined contains 258 microsatellites (Yalcin et al. 2004a)] but the large number of SDPs to which they give rise is not displayed in Figure 2.

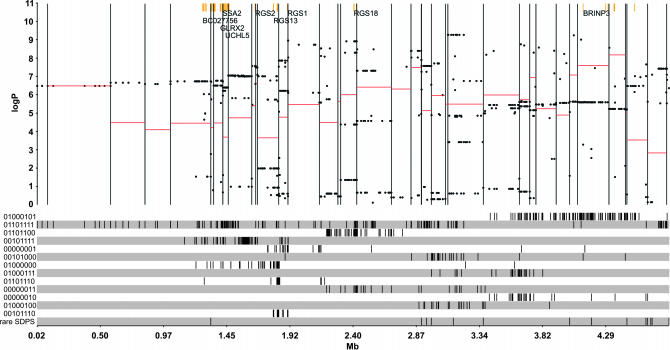
Figure 2.

Quantitative trait nucleotide analysis across a 4.8-Mb QTL on mouse chromosome 1. The horizontal axis is the coordinate in megabases. The top half shows the QTN merge analysis. Yellow bars indicate the positions of the exons of genes in the region. Each gene's name is positioned at the leftmost exon of the gene. The vertical black lines are the positions of genotyped markers; each region between adjacent lines defines a marker interval. The positions and log P significance levels of 1720 sequence variants under a merged strain analysis are indicated by black dots. The unmerged value for the marker interval is shown by a horizontal red line, whose placement is identical to that in Figure 1. The vertical position of a black dot relative to the red line measures the evidence that the variant could be a QTN for the trait. Variants with black dot values <log P 2 are unlikely to be QTN, while variants with very high black dot values could be QTN or share the same strain distribution pattern with a nearby QTN. The gray and white horizontal tracks in the bottom half of the figure show the spatial arrangement of the variants' strain distribution patterns. Each track corresponds to the SDP indicated in the left margin by a string of 0's and 1's representing the alleles for the eight founder strains of the HS, in the order A/J, AKR, BALB/c, C3H, C57BL/6, DBA, I, RIII. Repeat-length polymorphisms are combined into a single track, as are rare variants (all SDPs occurring <10 times). Within each SDP track the vertical black lines give the locations of the variants with that SDP.

Figure 2 shows the full-model merge log P values of all variants as black dots. The unmerged values are the same as those we obtain from the HAPPY QTL analysis, under a full model for the interval that contains the variant [shown as a red line; this is model (2) in materials and methods]. The partial F-test that compares merged and unmerged is not shown for clarity. Variants with the same SDP are not confined to simple haplotype blocks and consequently variants with high-scoring log P values occur throughout most of the region.

The strategy excludes many variants: 493 variants (28%) have a merge log P < 2. However, there is an excess of high-scoring variants: 681 (39%) score >6 (almost all of these either are repeats or have the SDPs 01101111 or 00101111). Even if we include only those variants for which merged and unmerged models are not significantly different (defined as a partial F-test log P < 2), we still retain 542 (31%) variants. Consequently a simple ranking by log P does not reduce the number of variants to a manageable number.

The number of candidate variants can be restricted further by considering only variants in regions of sequence conservation, assuming that all functional variants are within such a sequence. We used sequence similarity between human and mouse, which is likely to be conservative as many regions of sequence similarity will have been maintained by chance since the divergence of primate and rodent lineages (Wade et al. 2002). We examined all variants within expressed sequences and within potentially functional sequence (defined as sequence with >70% similarity to that of human over 100 bp). No variants are predicted to disrupt the reading frame or alter the length of transcripts; none are predicted to have an effect on the protein's function [POLYPHEN (Ramensky et al. 2002) and SIFT programs (Ng and Henikoff 2003)], although we cannot exclude the possibility. There are 614 noncoding variants, with a distribution of merge log P values similar to that of the full set of results: 68% (419) have merge log P > 6. So, while taking into account functional information reduces the number of potential QTN, it still leaves many hundreds of candidates.

The analysis did not exclude any gene, since high- and low-scoring variants are intermixed, with no useful spatial clustering. There are 77 variants with log P values > 8 (5% of the total) covering a 2.2-Mb region; the highest 10% of log P values extend over 2.9 Mb. The uneven pattern is not consistent with a simple haplotype block structure. Figures 2 and 3 show how, even within a single gene, different SDPs coexist.

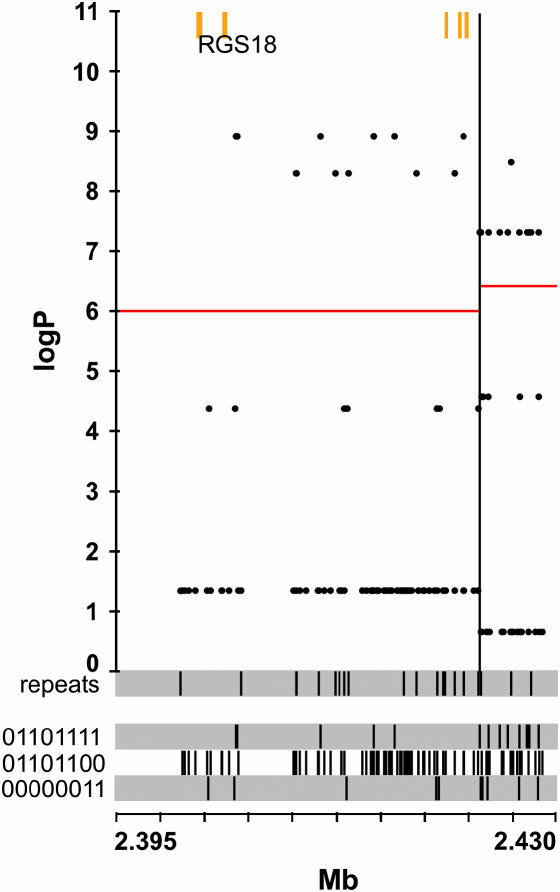
Figure 3.

Merge analysis of 139 variants surrounding the rgs18 gene. See Figure 2 legend for explanation. The SDP track labeled “repeats” gives the positions of all repeat polymorphisms.

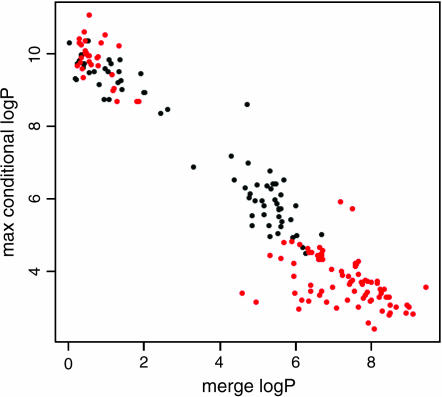
To reduce the number of candidate QTNs further we examined the effects of fitting the model for one variant conditional upon another variant being fitted at the same time. In general, the more significant a variant is, the less significant is the best remaining variant. We found that the sum of the merge log P for a given variant and the maximum conditional merge log P among all the other variants was almost constant and equal to the maximum observed merge log P (Figure 4). This is a consequence of linkage disequilibrium between markers within the region. Figure 4 shows a bimodal distribution of log P scores, with a cluster of nonsignificant values <2 and another cluster of candidates with scores >4. Figure 4 also shows that the SDPs that distinguish between the strains A/J and C57BL/6 (shown in red) constitute almost all of the highest-scoring variants with merge log P > 6; these strains were used to map the QTL in an F₂ intercross (Gershenfeld et al. 1997).

Figure 4.

Conditional merge analysis. Scatter plot of the merge log P is shown for each variant (x-axis) vs. the maximum merge log P (y-axis) for all other variants, conditional on the variant being fitted. Red dots indicate variants with an SDP that distinguishes A/J and C57BL/6 strains, the strain pair used to map the QTL in an F₂ intercross.

If we set a condition that, once the variant is fitted, the remaining best significant fit is <log P 2, 14 variants remain (Table 1), of which 12 are repeats and only 2 are SNPs. With a more relaxed criterion of <log P 3, 65 variants are included. Four variants are significant by a conditional fit criterion and lie within a conserved sequence. All are within introns of the rgs18 gene and are repeats, not SNPs. Figure 3 shows the merge analysis for the region containing rgs18. Of the 139 variants in the region, only 34 (24%) have merge log P values >4, of which 12 (8%) are >9.

TABLE 1.

Conditional merge analysis of variants that could explain all of the genetic variability in the data set

Classification	Position	Merge log P	Max. conditional log P	A/J	AKR	BALB/cJ	C3H	C57BL/6	DBA/2	I	RIII	SDP
NC	2335805	9.10	1.56	CTTT [13]	CTTT [7]	CTTT [7]	CTTT [13]	CTTT [7]	CTTT [7]	CTTT [11]	CTTT [11]	01101122
Intron rgs18	2409307	9.10	1.71	CA [22]	CA [23]	CA [23]	CA [22]	CA [23]	CA [23]	CA [25]	CA [25]	01101122
Intron rgs18	2412379	9.10	1.76	A [12]	A [15]	A [15]	A [12]	A [15]	A [15]	A [11]	A [11]	01101122
Intron rgs18	2418850	9.10	1.79	CA [22]	CA [23]	CA [23]	A [22]	CA [23]	CA [23]	CA [24]	CA [24]	01101122
Intron rgs18	2421868	9.10	1.92	A [13]	A [11]	A [11]	A [13]	A [11]	A [11]	A [14]	A [14]	01101122
NC	3680729	10.05	1.92	CA [22]	CA [14]	CA [21]	CA [22]	CA [21]	CA [14]	CA [14]	CA [14]	01202111
NC	3751958	9.87	1.92	A [9]	A [11]	A [10]	A [9]	A [10]	A [11]	A [9]	A [11]	01202101
NC	3790500	10.04	1.92	CA [16]	CA [24]	CA [17]	CA [16]	CA [17]	CA [24]	CA [16]	CA [24]	01202101
NC	3906262	9.95	1.92	GT [24]	GT [17]	GT [23]	GT [24]	GT [23]	GT [17]	GT [23]	GT [17]	01202121
NC	3949974	9.31	1.92	CT [22]	CT [16]	CT [18]	CT [22]	CT [18]	CT [16]	CT [19]	CT [16]	01202131
NC	3981213	10.04	1.95	CA [21]	CA [22]	CA [20]	CA [21]	CA [20]	CA [22]	CA [21]	CA [22]	01202100
NC	3997269	10.14	1.96	CT [28]	CT [23]	CT [25]	CT [28]	CT [26]	CT [23]	CT [26]	CT [23]	01203131
NC	4053050	9.75	1.97	T	C	C	T	C	C	C	C	01101111
NC	4107860	9.77	1.99	A	G	G	A	G	G	G	G	01101111

Shown are all variants for which the maximum conditional log P of any other variant is <2 (i.e., P-value 0.01). Classification, the context of the variant; NC, not conserved noncoding sequence; Position, location in base pairs of variant from start of 48-Mb region; Merge log P, the log P of the variant; Max conditional log P, the maximum log P across all other variants, conditional upon the first variant being fitted; A/J through RIII columns, the variant's alleles in the eight HS progenitors; SDP, the strain distribution pattern of the variant.

Finally we used simulation to confirm that the method identifies QTN correctly. We retained the LD structure in the data set and performed simulations taking each of the 37 genotyped markers in turn, generating a single, additive, QTL on the basis of the genotypes at the marker. The merge analysis was repeated to see how accurately the simulated QTN was identified. We found that on average the simulated QTN was in the top 3.2% of the log Pvalues with a mean log P difference of 0.46 between the maximum and the log P of the simulated QTN.

DISCUSSION

In this study we investigated whether the mosaic structure of the mouse genome would aid identification of QTN and developed a statistical test that can reject polymorphisms as being QTN. By noting which progenitor strains share the same allele at a locus we can test if it is a QTN, first merging the strains according to that variant's SDP and then comparing the statistical evidence in favor of the presence of a QTL under the merged and unmerged models. We stress that the test does not prove that a variant is a QTN; that requires further functional analysis (for example, see Van Laere et al. 2003; Zhang et al. 2003), but it does eliminate variants.

We applied the method to a 4.8-Mb region in which there are nine genes and ∼15,000 sequence variants, any of which might be a QTN that influences anxiety in the mouse (Yalcin et al. 2004a). Our method excluded two-thirds of candidate QTN, but left hundreds of variants with significant merge log P values. We showed that it is possible to lessen the number of candidates by restricting the analysis to variants in known or putative functional regions. Where additional evidence implicates a particular gene then the number of candidate QTN can be reduced significantly, as shown, for example, in an analysis of the variants surrounding rgs18 (Figure 3).

Finally, we identified those variants that could explain all of the genetic variance in the region. On the assumption that all candidate functional regions have been identified, sequenced, and hence tested within the framework and that only a single QTN is responsible, we were able to reduce the 15,000 variants to 14 putative QTN. Of these variants, 4 lie within regions of conserved sequence (an index of potential function), in introns of a regulator of G-protein signaling (rgs18) (Table 1). It is noteworthy that 12 of the variants were repeats, including all 4 within the rgs18 gene; interestingly, differences in repeat length have been reported to have a quantitative effect on gene expression (Albanese et al. 2001).

Although conditional QTN analysis identifies which variants could account for all the genetic variance, there may be more than one functional candidate. Because of the high LD in the region, the genetic variance could be explained either by a single variant or by at least two working together. While we have substantially reduced the number of candidate QTN, we emphasize that in the absence of sufficient historical recombinants to provide adequate mapping resolution and because high-scoring SDPs are distributed throughout the region, we cannot exclude any gene.

A number of factors could compromise the performance of our method. First, it is possible that there may be other SDPs in the region that are associated with the QTL effect; their presence, if not taken into account, could reduce the power of our analysis. An analysis of the distribution of sequence variants in the region indicated that we had detected >98% of SDPs (Yalcin et al. 2004a) so, at least in this case, it is unlikely that missing SDPs are damaging our method's power.

A second problem for the method is that even when analyzing a small region, we may be dealing with multiple QTN, rather than a single effect. When a merge analysis is performed incorrectly assuming the presence of a single QTN, the results may be misleading: if the additional QTN are on different SDPs, then this should be detectable because no single SDP will perform as well as the unmerged models (1) or (2). However, if they are on the same SDP and are very close together then it will be difficult to distinguish multiple from single effects. The consequence of the latter situation will be the presence of equally ranked SNPs that will remain candidates, as we discuss in the context of rgs2, below. We cannot at the moment say how often merge analyses will have to deal with multiple QTN. While we have restricted our search to a region of <5 Mb, a relatively small region by the standards of most QTL analyses, it is quite possible that it contains multiple QTN.

We have elsewhere shown that rgs2 is a quantitative trait gene for open field behavior, by using a commercial outbred stock of mice called MF1 (Yalcin et al. 2004b). Although the ancestry of MF1 is unknown, MF1 chromosomes can be modeled as a mosaic of standard laboratory strains, i.e., like an HS, and therefore can be analyzed in the same way. However, because the MF1 has built up much more ancestral recombination than the HS, we were able to resolve the QTL analyzed in this article into three smaller QTL, one of which contains rgs2, while the others did not contain any known gene. All 10 variants occurring in or near to rgs2 have the same SDP 00101111 and all have highly significant merge log P values of 7.64, although they are not the most significant. The maximum conditional log P for the rgs2 variants is 4.27, indicating that these variants do not account for all of the genetic variation.

We developed the method for HS mice, but it can be applied to all QTL mapping experiments involving more than two strains where sequence information is available to identify candidate QTN. However, we must point out that we have not undertaken a comprehensive analysis of all the factors that impact on the method's power, which would require a large set of simulations incorporating variations in the number of founder strains, distribution of sequence variants, and position and effect size of the QTL.

When high-resolution SNP maps of many inbred strains become available they will have wide utility. In the simplest case, a merge analysis can then be carried out, in silico, for any QTL mapped in multiple strains. Many phenotypes have already been mapped in multiple strain crosses [for example, obesity (Brockmann and Bevova 2002) and anxiety (Flint 2003)]. The method is also robust in the presence of epistasis, because for a segregating cross if unlinked loci are epistatic we would expect to see all combinations of alleles present in the mapping population. The effect of epistasis is to reduce the genetic variance attributable to each locus individually, but we would still expect to see a concordance between QTN and trait.

The method may have additional applications. Studies of sequence variation in the mouse suggest that commonly used laboratory strains are descended from a few subspecies (Beck et al. 2000; Lindblad-Toh et al. 2000; Wade et al. 2002; Wiltshire et al. 2003). In theory, a large number of inbred strains can be treated as a set of recombinant inbred strains, derived from a small set of progenitors. By combining high-density SNP maps with phenotypic data from the mouse phenome database (http://www.jax.org/phenome), potential QTN can be identified in a merge analysis, although the complexity of the mosaic structure of the mouse genome may limit success (Yalcin et al. 2004a). Merging functional with in silico approaches may be the best strategy for the simultaneous identification of the large numbers of loci underlying complex phenotypes.