Estimation of Preferential Pairing Rates in Second-Generation Autotetraploid Pacific Oysters (Crassostrea gigas)

Abstract

Although previously disregarded, polyploidy, and in particular autopolyploidy, is now believed to have played a prominent role in the evolution of plants and animals. We estimated the rate of preferential pairing in second-generation autotetraploid Pacific oysters from gametic frequencies. We found significant levels of preferential pairing in these recently generated autopolyploids, suggesting that genetic variation in standing populations may play a role in meiotic mechanisms of polyploids derived from these populations.

POLYPLOIDY has played a prominent role in the evolution and domestication of plants and animals (Soltis and Soltis 1999; Furlong and Holland 2004; Mable 2004). Although natural metazoan polyploids are presumed uncommon and many animals show reduced fitness after induced polyploidy (Mable 2004), polyploidization is a critical component of the evolution of some vertebrates, including fish (Schultz 1980; LeComber and Smith 2004) and amphibians (Bogart 1980; Mable 2004), as well as invertebrates such as bivalves (Wang and Guo 2004). In addition, genome duplication is hypothesized to have led to key innovations in vertebrate development (Ohno 1970; Meyer and Schartl 1999; Furlong and Holland 2004).

Patterns of meiosis in polyploids are influenced by their mode of origin (Sybenga 1996). Polyploids resulting from the conjugation of two unrelated genomes (allopolyploids) are expected to show disomic inheritance, with pairs of related chromosomes preferentially pairing. In contrast, polyploids resulting from conjugation of related genomes (autopolyploids) generally show tetrasomic inheritance (random pairing of chromosomes), but may also exhibit disomic inheritance for some chromosomes.

Autopolyploids are also assumed to be rare in nature, although this assumption is being challenged. Use of allozyme markers has revealed an increasing number of natural autopolyploids (Soltis and Soltis 1993), many with tetrasomic inheritance (Soltis and Soltis 1993 and references therein; Maki et al. 1996; Weidema 1996; Fjellstrom et al. 2001). Many of these studies have focused on differentiating between the two extremes, disomic and tetrasomic inheritance (Rieseberg and Doyle 1989; Soltis and Soltis 1989; Maki et al. 1996; Weidema 1996). In reality, patterns of inheritance may be far more complex, as revealed by highly polymorphic molecular markers (Fjellstrom et al. 2001), with divergence between chromosomes leading to a progression from tetrasomic to disomic inheritance at linked loci (Weiss and Maluszynska 2000). Thus, estimating the level of preferential pairing between chromosomes may more accurately capture this dynamic process. Sybenga (1994) introduced the preferential pairing parameter, p (range = 0.0–0.66), to quantify the level of preferential pairing within the genome as estimated from diakinesis/metaphase I configurations. Estimates of preferential pairing for autotetraploid plants range from near complete preferential pairing (p = 0.512) in Hyoscyamus muticus to little preferential pairing (p = 0.077) in Tradescantia (Sybenga 1994).

A general polyploid model for estimating p from genetic data was recently proposed (Wu et al. 2001), paving the way for a more dynamic analysis of genetic data. In addition, the proposed model estimates the frequency of double reduction, a phenomenon unique to autopolyploids. Double reduction results from the passing of two sister chromatids to the same gamete; this requires quadrivalent pairing of the four homologous chromosomes, crossing over of nonsister chromatids, and cosegregation of the sister chromatids (Wu et al. 2001).

Pacific oysters share the ability to undergo successful polyploidization (Allen and Downing 1986; Allen et al. 1989; Guo and Allen 1994a,b; Guo et al. 1996). Triploid Pacific oysters were initially produced by chemical treatment (Stanley et al. 1981) and the production of tetraploid Pacific oysters through similar means followed, but tetraploid lines are now maintained through breeding. Meiotic segregation in tetraploid oysters (4n = 40 chromosomes) is predominately balanced, with 65–75% of progeny receiving 20 chromosomes, and the remaining individuals being aneuploid (Guo and Allen 1997). As bivalents are uncommon, balanced gametes appear to result from the segregation of quadrivalents during metaphase I (Guo and Allen 1997). These lines represent an ideal population in which to examine the patterns of meiosis in autotetraploids shortly after polyploidization. To this end, we estimated double reduction and preferential pairing rates in second-generation tetraploid Pacific oysters (Crassostrea gigas), using the methods of Wu et al. (2001).

To assess levels of genetic diversity in these autotetraploid stocks, we genotyped eight tetraploid males for 40 loci, distributed across seven linkage groups. An average of 34.6 loci were sampled for each individual, with an average of 2.43 alleles per locus (Table 1). In addition, we estimated gametic homozygosity, a tetraploid metric that is directly comparable to diploid homozygosity (Moody et al. 1993). Gametic homozygosity ranged from 26.3 to 54.3% in these tetraploid males, with a mean of 35.5% (Table 1). Analysis of variance of gametic homozygosity and diploid homozygosity of eight F₁ individuals did not indicate significant differences in homozygosity at any of the levels analyzed (Table 1). Thus, these tetraploid lines appear to have levels of gametic homozygosity consistent with their narrow genetic base. As oysters carry a large genetic load (Launey and Hedgecock 2001), inbreeding of hatchery stocks could lead to inbreeding depression unless care is taken to avoid consanguineous matings and to broaden the genetic base of tetraploid lineages.

TABLE 1.

Allelic diversity at 40 microsatellite DNA markers surveyed in eight tetraploid Pacific oysters derived from tetraploid × tetraploid crosses

		Lineagea
A				B
	Parentb:	1	2	3	4	1	2	3	4	Mean
Descriptive statistics
No. loci surveyedc	27	38	39	35	34	37	38	33	34.6
Avg. no. alleles/parentd	2.37	2.49	2.55	1.97	2.52	2.71	2.28	2.55	2.43
Gametic homozygositye	0.358	0.338	0.325	0.543	0.338	0.263	0.389	0.283	0.355

Variable		d.f.	Sum of squares	Mean square	F-value	P
ANOVA resultsf
Ploidy	1	0.512	0.512	1.4	0.45
Lineage	1	0.365	0.365	1.67	0.22
Parent	13	2.844	0.219	1.44	0.13
Residuals		531	80.45	0.152

^aTetraploid males were second-generation-mated tetraploids created from a chemically induced tetraploid founder (see Guo et al. 1996). In 1996, tetraploid founders were created from the eggs of two triploid females and four diploid males. Lineages A and B were then created by crossing the 1996 broodstock; one tetraploid female founder and two male founders were used for lineage A and one female founder and three male founders for lineage B. In 2000, individuals from each lineage were crossed to produce the second-generation-mated tetraploid males used for this experiment. Crosses were performed and animals were reared by Benoit Eudeline at Taylor Resources (Quilcene, WA).

^bFour males from each lineage were crossed with the same diploid female to produce triploid progeny. Progeny were sampled at 11 days postfertilization, killed in 3% chlorine bleach, and stored in 70% ethanol.

^cDNA extraction, PCR amplification, and genotyping were done following the methods of Hubert and Hedgecock (2004) and Li et al. (2003), with the exception of three loci, for which the parents were genotyped using the Beckman (Fullerton, CA) CEQ 2000 automated system.

^dLevels of allelic polymorphism were tallied for each tetraploid parent according to the number of bands in the gel phenotype.

^eTetraploid gametic homozygotic contributions were scored according to Moody et al. (1993), with the following values: 1 for an individual with 1 allele, 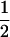for two alleles in a 3:1 ratio, 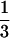for two alleles in a 2:2 ratio, 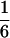for three alleles, and 0 for four alleles. The average of these values across loci gives the average gametic homozygosity. Individuals having two alleles (two-banded phenotypes) were classified genotypically as either 2:2 (i.e., two copies of each allele) or 1:3, on the basis of the relative intensities of the bands.

^fWe tested for differences in homozygosity between the two tetraploid lineages, as well as a set of diploid individuals, using analysis of variance. Diploid homozygosity estimates are from F₁ hybrids (Hedgecock et al. 2004); gametic homozygosity was used as the metric for the tetraploid males, as this measure is directly comparable with diploid homozygosity (Moody et al. 1993). A 16 × 40 data matrix (eight tetraploid and eight diploid parents by loci), with each cell consisting of the representative homozygotic contribution, was used in an analysis of variance. Diploid homozygotic contributions were scored as either a 1 or a 0 (homozygous or heterozygous); tetraploid homozygotic contributions were scored as above. Homozygosity estimates were subjected to nested analysis of variance according to the model, gametic homozygosity = ploidy/lineage/parents, using the statistical package R (http://www.R-project.org).

We then estimated the rates of preferential pairing and double reduction by examining inheritance patterns of microsatellite loci for the triploid progeny of crosses between these eight tetraploid male parents and a single diploid female (see Table 1 for details). Loci at which the male parent had four discernable alleles were genotyped in the progeny of this male, providing, in effect, estimates of gametic frequencies. In total, progeny were genotyped for 12 family-locus cases, with an average of 74.6 progeny genotyped for each case (Table 2). The 12 cases are distributed across six of the parents and four linkage groups (Hubert and Hedgecock 2004). Parents A3 and B4 are polymorphic for four alleles at a single locus each, but these loci could not be scored in the offspring. Allele frequencies did not differ from the expected 1:1:1:1 ratio for any of the families genotyped.

TABLE 2.

Male allele and gametic frequencies observed in triploid offspring of tetraploid males crossed to diploid females

Male/locus	ABa	AC	AD	BC	BD	CD	Diploid	Tetraploid	pb	α	2Δ Lnc	Probability
B1/ucdCgi-194	17	12	9	17	19	13	2	1	0.093	0.051	0.473	0.789
A3/ucdCgi-194	7	11	16	16	15	8	1	0	0.304	0.051	5.84	0.054
A2/ucdCgi-194	19	10	12	7	25	16	0	0	0.295	0	6.21	0.045
B1/ucdCgi-126	13	14	13	11	14	12	1	1	0.061	0.038	0.164	0.921
B1/cmrCgi-1	9	12	16	10	13	21	2	0	0.069	0.037	0.225	0.894
A1/cmrCgi-1	9	14	11	10	9	14	1	0	0.056	0.022	0.120	0.942
B3/ucdCgi-126	8	13	10	8	5	14	1	2	0.063	0.074	0.139	0.932
B2/ucdCgi-197	17	16	10	11	17	15	0	0	0.228	0	3.24	0.197
B2/ucdCgi-156	9	10	16	10	11	10	0	0	0.125	0	0.629	0.730
B4/ucdCgi-14	12	13	11	14	17	15	0	1	0.080	0.018	0.303	0.859
B4/ucdCgi-156	14	7	13	12	21	9	1	0	0.085	0.019	0.327	0.849
B1/ucdCgi-133	15	14	12	7	7	12	0	0	0.135	0	0.765	0.681

^aGametic frequencies were tallied directly from gel phenotypes. Assuming all gametic types are possible, including double reductions and aneuploids, there are 17 possible gametic types, although we expect the majority to be of one of the six two-banded (two-allele) types. Allele frequencies for each locus/family combination were calculated from the observed gametic frequencies and subjected to a chi-square test for goodness of fit to 1:1:1:1.

^b

We estimated the rate of double reduction and preferential pairing (α and p, respectively), using the method of Wu et al. (2001). As chromosomes that preferentially pair at metaphase I will segregate to opposite poles, the maximum estimate of preferential pairing is derived from the lowest-frequency pair of gametes with mutually exclusive alleles. We report estimates for the pair of mutually exclusive gametes with the highest rate of preferential pairing. The crosses reported here are fully informative for the purposes of estimating p and α (i.e., gel phenotype equals genotype); therefore, rather than using the expectation-maximization algorithm approach, we were able to explicitly solve for p and α using the equations derived from those given in Wu et al. (2001, p. 874),

where P_x is allele x. In this model, allele 1 preferentially pairs with allele 2 and allele 3 with allele 4. Substituting the frequency of all homozygous gametes for the final term in the second (or third) equation, we then solved for p.

^c

The likelihood-ratio test was used to determine if the likelihood of the estimated p was significantly >p = 0 (Wu et al. 2001). The likelihood was calculated by summing the product of the vector of expected frequencies given p and α and a 1/0 matrix of gametic types (in our case, the gametic matrix is 10 × n, where n is the number of triploid progeny genotyped). This reduces to

where j and i correspond to one of the four possible alleles, f(P_iP_j) is the expected frequency of the P_iP_j gamete given α and p, and X_nj is the count of P_iP_j gametes. Twice the log-likelihood difference (2Δ Ln) is compared to the chi-square distribution (d.f. = 2) to obtain the probability (P-) value.

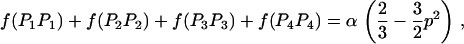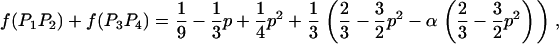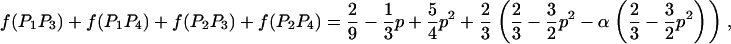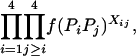Eight of the 12 cases exhibited progeny for which the number of paternally inherited alleles does not equal the expected two alleles (i.e., progeny are either diploid or tetraploid), with frequencies ranging from 0 to 4.9% across cases (average = 1.86%); these cases were nearly evenly divided between diploid progeny (60%) and tetraploid progeny (40%). We estimated the frequency of double reduction, assuming that diploid progeny represent double-reduction events. Frequencies of double reduction ranged from zero to 0.074 (Table 2), with 8 out of 12 cases exhibiting possible double reductions.

Double reduction is a rare phenomenon in wild plants, with few estimates available for comparison (Soltis and Soltis 1989; Maki et al. 1996). Estimates from potato cultivars are generally low, with only 2 of the 11 estimates being significantly greater than zero (Haynes and Douches 1993). Fjellstrom et al. (2001) observed several progeny presumed to be of double-reduction origin, but estimates were not reported. We also observed low levels of double reduction, similar in magnitude to the nonsignificant estimates from potatoes. In addition to diploid progeny, we also observed tetraploid progeny, which are expected only if unequal segregation at metaphase I of meiosis leads to the inheritance of three paternal chromosomes. This result suggests that the diploid progeny we observed are actually aneuploids rather than double reductions. This is supported by the observation that the total numbers of diploid and tetraploid progeny are nearly equal, as would be expected for aneuploidy; in addition, chemically induced tetraploid Pacific oysters have a high rate of aneuploidy (Guo and Allen 1997). Thus, although we cannot differentiate between the two hypotheses at this time, we propose that aneuploidy is a more parsimonious explanation for our observations. We point out that power to observe tetraploid progeny was maximized in our study because we examined only cases in which the parent was segregating for four alleles; in contrast, power to detect aneuploids is reduced when the number of alleles is less than the maximum, as has been the case in previous studies (Haynes and Douches 1993; Fjellstrom et al. 2001).

Preferential pairing rates (p) are low for many of the loci examined (Table 2). Seven of the family-locus cases show only weak levels of preferential pairing (p < 0.1). Two cases showed slightly greater levels of preferential pairing, which are still only 20% of the maximum possible value of two-thirds. In contrast, three cases yield substantial estimates of p ranging from 0.228 to 0.304, or nearly 50% of the maximum. One case (B2/ucdCgi-197) is not significant (P = 0.2, Table 2). The other two cases involve ucdCgi-194, which is on linkage group 1 (Hubert and Hedgecock 2004); A3 shows marginally significant preferential pairing (p = 0.304, P = 0.054) and A2 is significant at the 5% level (p = 0.295, P = 0.045).

Preferential pairing is proportional to the frequency of bivalent formation at metaphase I of meiosis. Bivalent formation results from the inability of divergent chromosomes to form tetravalents and leads to disomic patterns of inheritance at genetic loci on that chromosome. Genetic divergence and structural rearrangements are expected to occur following polyploidization (Soltis and Soltis 1993), although this may occur more readily in allopolyploids, which maintain heterozygosity for ancestral genomes through disomic inheritance. These genomic changes are hypothesized to lead to diploidization, whereby chromosomes behave in a diploid manner and hallmarks of polyploid ancestry are lost. The observation of extensive bivalent formation in advanced generations of autopolyploid Arabidopsis (Weiss and Maluszynska 2000) indicates that this phenomenon is not limited to allopolyploids. Regardless, it is surprising to find high levels of preferential pairing in these second-generation autotetraploid Pacific oysters. This suggests that either there are structural differences between the chromosomes or substantial genetic divergence has occurred at this location on the chromosome; whether these differences emerged within the previous two generations or were present in the founders of these tetraploid lines is not certain. Differences in gene order have been observed among mapping families of diploid Pacific oysters (Hubert and Hedgecock 2004). We hypothesize that the levels of genomic variation in a standing diploid population may have a pronounced effect on chromosome inheritance in polyploids newly derived from that population. In addition, what effect the initial level of disomic inheritance has on the rate of evolution of chromosomal inheritance in polyploids is unknown. Thus, these tetraploid lines present an ideal opportunity to examine the effects of chromosomal and genetic divergence on the rates of evolution of disomic inheritance in autotetraploids.