The Evolution of Plastic Recombination

Abstract

Empirical data suggest that recombination rates may change in response to stress. To study the evolution of plastic recombination, we develop a modifier model using the same theoretical framework used to study conventional (nonplastic) modifiers, thus allowing direct comparison. We examine the evolution of plastic recombination in both haploid and diploid systems. In haploids, a plastic modifier spreads by forming associations with selectively favored alleles. Relative to nonplastic effects, selection on the plastic effects of a modifier is both much stronger and less sensitive to the specifics of the selection regime (e.g., epistasis). In contrast, the evolution of plastic recombination in diploids is much more restricted. Selection on plasticity requires the ability to detect DNA damage or cis-trans effects as may occur through maternal effects on fitness.

BIOLOGISTS have struggled to understand the forces governing the evolution of recombination. Recombination has the positive effect of assembling good genotypes from bad ones but it also has the negative effect of breaking apart favorable genotypes. Because good genotypes become overrepresented as a result of selection, recombination is often undoing the work of selection (Eshel and Feldman 1970). Consequently, reduced recombination is typically favored (Feldman et al. 1997). In deterministic models, increased rates of recombination are favored only under very specific conditions, such as directional selection with epistasis that is both weak and negative (Barton 1995) or selection with fluctuating epistasis (Sasaki and Iwasa 1987; Barton 1995) as may arise under some types of host-parasite coevolution (Peters and Lively 1999; Otto and Nuismer 2004). Models incorporating genetic drift show that stochastic associations among beneficial alleles can select for recombination over a broader range of conditions regarding epistasis (Otto and Barton 2001). Although most theory assumes that alleles modifying recombination rates are invariant in their effect, some recent works have considered “plastic” modifiers (Gessler and Xu 2000; Hadany and Beker 2003b). Analogous to the concept of phenotypic plasticity, we define a recombination modifier as plastic if the rate of recombination caused by that modifier depends on the phenotypic state or condition of the organism in which it is found. For example, a plastic modifier may induce a higher recombination rate when it is found in individuals of poor condition than in individuals of good condition. Hadany and Beker (2003a,b) referred to such modifiers as “fitness-associated recombination” (FAR) modifiers.

A variety of empirical evidence suggests that recombination rates are plastic, with the most common pattern being an increase under stress. For example, there is some evidence that recombination rates in Drosophila melanogaster increase when flies are reared either above or below their optimal temperature (Plough 1917, 1921; Grell 1978), are nutritionally stressed (Neel 1941), or are reared under stressful densities (L. Hadany and M. Siegal, unpublished data). Socially stressed mice have increased recombination rates (Balyaev and Borodin 1982). In yeast, Saccharomyces cerevisiae, meiotic recombination frequencies increase with nutrient stress (Abdullah and Borts 2001). A “cold-resistant” tomato strain has a higher chiasma frequency than a “standard” strain when both are grown under warm conditions but not when both are grown under cold conditions (Zuchenko et al. 1986). Two recent plant studies report increases in recombination in response to parasitic infection (Lucht et al. 2002; Kovalchuck et al. 2003). Further evidence is discussed by Parsons (1988) and Korol et al. (1994). However, a number of these studies also report negative results with respect to certain stresses and/or certain chromosomes (e.g., Plough 1917, 1921), and it is difficult to ascertain how many other studies finding negative results have not been published.

A primary question is when such plasticity is expected to evolve. A recombination modifier is adaptive in the “group” sense if it increases the mean fitness of the group or population. However, the spread of a modifier within a population by selection requires that it be able to spread at the individual level, i.e., beneficial in the “selfish gene” sense (see Feldman et al. 1997 for a discussion of both types of benefits to recombination). Intuitively, if a modifier is plastic in its expression such that it increases recombination only when in individuals in poor condition, then the beneficial effects of recombination might be realized while avoiding the detrimental effects of recombination. Such an allele is not necessarily beneficial to the population as a whole. Rather it benefits itself by assessing whether or not it is currently on a bad haplotype and preferentially recombining away if so. We call this the “abandon-ship” strategy. Explicit theoretical models are needed to quantitatively evaluate the conditions under which plastic recombination is likely to evolve.

Investigating condition-dependent bacterial transformation, Redfield (1988) used computer simulations to study how this related phenomenon influenced mean fitness but she did not explicitly examine the evolution of condition dependence. In their book on recombination, Korol et al. (1994) emphasized the gap in population genetics theory with respect to the evolution of plastic recombination. They presented preliminary simulation results suggesting that plastic recombination could evolve in diploids experiencing fluctuating environments. Using computer simulations, Gessler and Xu (2000) showed that a plastic allele spread to fixation in haploid organisms experiencing recurrent deleterious mutations. Hadany and Beker (2003b) examined several haploid models of plastic recombination. In an analytical model of a haploid organism involving one recombination locus and one fitness locus experiencing recurrent deleterious mutation, plastic recombination evolved whenever selection was stronger than the mutation rate. The form of plasticity favored by selection was one in which the recombination rate was increased in low-fitness genotypes relative to that in high-fitness genotypes (i.e., FAR). With two fitness loci, FAR also produced an advantage in terms of mean fitness (a population-level advantage), by generating associations between beneficial fitness alleles. In multilocus computer simulations of haploid organisms, both genic- and population-level advantages were shown.

Our goals here are twofold. First, we set out to examine the evolution of plastic modifiers using the same framework used by Barton (1995) in his analysis of conventional (nonplastic) modifier theory. Unlike previous models of plastic recombination, this approach allows us to compare directly the importance of a modifier's plastic effects with its nonplastic effects in determining its evolutionary fate. Second, we set out to examine the evolution of plastic recombination in diploids. Much of the recent theory (Gessler and Xu 2000; Hadany and Beker 2003b) has focused on haploid organisms, while most empirical data for plastic recombination come from diploid organisms. Here we build on previous work by examining the evolution of plastic recombination in both haploids and diploids under relatively simple selection regimes.

MODEL AND RESULTS

Genetics and recombination in a haploid model:

We consider an organism having one recombination modifier locus (M) and two fitness loci (A and B), each with two alleles. The three loci are assumed to be arranged in the order MAB with recombination rates of rec_MA between the M and A locus and rec_AB between the A and B locus (we assume no interference). To begin, we consider a haploid model, where individuals mate at random, briefly forming diploids at which point recombination occurs. The amount of recombination depends on the mean recombination rates of each of the two haploids involved. Haploids carrying the m allele induce constant recombination rates of rec_MA[m] = R and rec_AB[m] = r. Haploids carrying the plastic modifier, M, induce recombination rates of

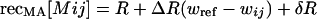and

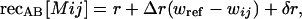where ij represents the alleles carried at the A and B loci. These equations show that, relative to the m allele, the M modifier causes nonplastic changes in recombination (represented by δR and δr terms) as well as plastic changes that are proportional to an individual's fitness (represented by ΔR and Δr terms). The magnitude of the plastic effect depends on the extent to which an individual's fitness or condition differs from some inherent reference point, w_ref. w_ref can be thought of as the condition of an individual below which it exhibits a stress response, which itself might have evolved in response to past environmental conditions. Including both plastic and nonplastic effects of the modifier allows us to compare their relative impact on the dynamics of the modifier. In this haploid model, we assume that fitness (or condition) in the haploid state alters the expression of the modifier gene in a manner that is passed on to the transient diploid state, where recombination rates are affected.

Among individuals carrying the M allele, individuals with low fitness have more recombination than individuals with high fitness when ΔR and Δr are positive. We refer to this form of plasticity as FAR-type plasticity. Conversely, individuals with low fitness have less recombination than individuals with high fitness when ΔR and Δr are negative. We refer to this form of plasticity as anti-FAR-type plasticity.

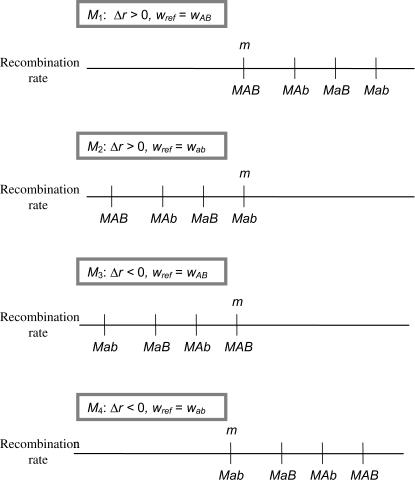
Either type of plasticity can be achieved in different ways depending on the choice of the reference fitness, w_ref (Figure 1). For example, with FAR-type plasticity (ΔR, Δr > 0), the modifier acts by increasing recombination in the less-fit genotypes if w_ref is the fitness of the best genotype (w_max). In contrast, if w_ref is the fitness of the worst genotype (w_min), the modifier acts by reducing recombination in more-fit genotypes. In the former case (w_ref = w_max), FAR results in an incidental increase in the average rate of recombination; in the latter case (w_ref = w_min), FAR results in an incidental decrease in the average rate of recombination. The opposite pattern holds for an anti-FAR allele (ΔR, Δr < 0). If only a single reference genotype was examined, it would be impossible to tell whether selection on a modifier was due to its plastic effects per se or due to the incidental changes in the average recombination rate. However, because the average effect on recombination changes sign depending on the reference genotype, examining the fate of a plastic modifier using different reference genotypes provides a convenient method for identifying the true target of selection (i.e., plasticity or the average rate of recombination). If selection on a modifier is determined primarily by its form of plasticity, then the fate of a plastic modifier should be the same regardless of the reference genotype. Alternatively, if selection on a modifier is determined primarily by its average effect on recombination, then the sign of selection should depend on the reference genotype used.

Figure 1.

Recombination rate of a plastic modifier. The recombination rates of individuals with different haploid genotypes are illustrated. Individuals carrying the m allele always have the baseline level of recombination regardless of the alleles they carry at the fitness loci. Individuals carrying the plastic modifier allele M have a recombination rate that depends on their fitness. We assume that w_ab < w_aB < w_Ab < w_AB. In cases M₁ and M₂ (Δr > 0), individuals with low fitness have more recombination than individuals with high fitness (FAR). The FAR modifier causes an incidental increase in recombination on average when w_ref = w_AB (case M₁) but decreases recombination on average when w_ref = w_ab (case M₂). In cases M₃ and M₄ (Δr < 0), individuals with low fitness have less recombination than individuals with high fitness (anti-FAR). The anti-FAR modifier decreases recombination on average when w_ref = w_AB (M₃) but increases recombination on average when w_ref = w_ab (M₄).

It is important to recognize that the use of w_ref in the preceding equations could be replaced by any arbitrary constant. The use of w_ref is simply a matter of convenience that allows us to easily control whether the modifier's incidental average effect on the rate of recombination is positive or negative. The plasticity in recombination that we model here is conceptually no different from plasticity in any other trait that is sensitive to condition. No special mechanism of determining one's own fitness relative to the population average is required. We note that our model assumes that plastic recombination is a simple linear function of an individual's fitness, but we discuss below the results that might be affected by this assumption.

Haploid selection:

We deterministically model a haploid, semelparous population in which the life cycle proceeds in the following order: selection (on haploid genotypes), syngamy, followed immediately by gametogenesis. The organism has one recombination modifier locus (M) and two fitness loci (A and B), each with two alleles. The M locus is assumed to have no direct effect on fitness, so that an individual's fitness is determined by its “AB” genotype: w_ab = 1, w_Ab = (1 + s_A), w_aB = (1 + s_B), and w_AB = (1 + s_A)(1 + s_B) + ɛ, where ɛ measures epistasis. We assume that the A and B alleles are unconditionally beneficial and that there is no mutation.

At the beginning of a generation the frequency of genotype G (G {MAB, MAb, MaB, Mab, mAB, mAb, maB, mab}) is given by x_G. After selection, the frequency changes to 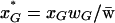, where 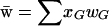is the mean fitness (note that w_G is determined by the AB genotype of G, e.g., w_MAb = w_mAb = w_Ab). The frequency of genotype G among offspring in the next generation is calculated in the usual way: by summing the probability that a given pair of parents produces genotype G across the frequency distribution of all possible haploid mating pairs, accounting for the recombination rate in the diploid produced (not shown).

Our goal is to find an approximate analytical expression for the change in the frequency of the plastic allele (Δp_M). To do so, genotype frequencies are described in terms of the moments of the multilocus allele distribution used by Barton (1995), i.e., the frequencies of the alleles p_M, p_A, and p_B and their statistical associations (i.e., disequilibria) C_MA, C_MB, C_AB, and C_MAB. C_xy measures the two-way linkage disequilibrium between loci x and y as their second central moment (equivalent to the standard gametic-phase linkage disequilibrium); C_MAB measures the three-way disequilibrium among alleles at the M, A, and B loci as their third central moment. Each of the eight genotype frequencies can be described as a function of these moments. For example, x₂ = p_Mp_A(1 − p_B) + (1 − p_B)C_MA − p_AC_MB − p_MC_AB − C_MAB. Describing the x_G in this form, we obtain offspring genotype frequencies (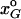) as a function of the moments of the distribution in the previous generation. From the genotypic frequencies among the offspring we can calculate the moments of the distribution in the offspring generation and then determine how these moments have changed as a result of a single bout of selection and sex.

Allele frequency changes depend on the association measures, making the results difficult to interpret. This dependence on the disequilibria is particularly strong for the evolution of the modifier, which has no direct effect on fitness but rather evolves through its associations with directly selected alleles. To interpret Δp_M we need to know what associations develop within the population. We employ a quasi-linkage equilibrium (QLE) assumption to predict these associations (Kimura 1965; Nagylaki 1993; Barton 1995). The QLE assumes that associations among alleles reach a steady state for a given set of allele frequencies faster than the alleles change in frequency. Thus, we can solve for the steady-state associations in terms of allele frequencies, selection coefficients, and recombination rates. Because the rate at which associations approach this steady state depends on recombination whereas the rate at which allele frequencies change depends on selection, the QLE requires that recombination is strong relative to selection (see appendix). Consequently, these analytical results should apply only to cases where the baseline level of recombination is high. Further, we focus only on the evolution of small changes in recombination. Simulations show that these approximations perform reasonably well over a surprisingly broad set of parameters. A Mathematica package deriving the analytical approximations is available upon request.

The analysis below assumes that s_A, s_B, ɛ, δR, and δr are of O(ξ), where ξ is small. Because ΔR and Δr are weighted by fitness differences, the effect of the plastic modifier is also of O(ξ), assuming that ΔR and Δr are O(1). A first-order Taylor series expansion around terms of O(ξ) shows that the alleles at the fitness loci change according to

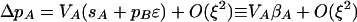(1)

and

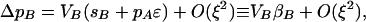(2)

where V_i = p_i(1 − p_i) is the variance at the ith locus (i ∈ {M, A, B}) and selection on the ith locus is defined as β_i ≡ Δp_i/V_i ≈ s_i + p_jɛ, with j referring to the beneficial allele at the other selected locus. To order ξ, Δp_M is zero, indicating that it is driven by the higher-order terms that we consider below.

As we expect the modifier to evolve through its associations with the other loci, it is necessary to consider how these associations develop,

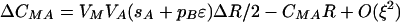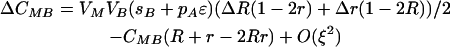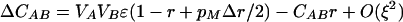and

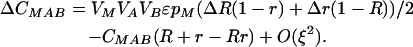By setting each ΔC to zero, dropping terms of O(ξ²), and substituting β_A and β_B where appropriate, we can solve for the QLE values of these associations ,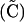

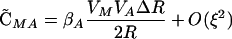(3)

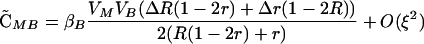(4)

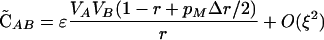(5)

and

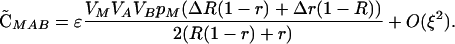(6)

Note that the sign of 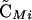is determined by the sign of selection on the ith locus, β_i (i.e., a FAR allele becomes positively associated with the selectively favored allele), and that the sign of 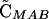is determined by the sign of epistasis, ɛ (i.e., a FAR allele becomes positively associated with the combination of alleles having favorable epistatic interactions). Although all of the associations involving the modifier depend on its plastic effects (ΔR and Δr), none of the associations depend on the nonplastic effects (δR and δr) of the modifier, at least not to leading order.

Using these QLE approximations, we can evaluate Δp_M using a second-order Taylor Series expansion,

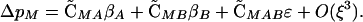(7)

From Equations 3, 4, and 6, all the terms in Equation 7 contain squared selection coefficients. Thus Equation 7 is positive if ΔR, Δr > 0, demonstrating that a FAR allele always increases in frequency. The first two terms show the beneficial effect of the FAR allele in building associations with the A and B alleles, respectively, of the same sign as selection on the alleles. The third term shows the beneficial effect of the FAR allele with respect to building an association with the combination of alleles that has the most favorable epistatic effect. Conversely, Equation 7 indicates that an anti-FAR allele (ΔR, Δr < 0) would decline in frequency. The results (Equations 1–7) are the same regardless of which genotype is used as the reference genotype.

The simulations of Hadany and Beker (2003b) showed that associations between selected loci arise even in the absence of epistasis when recombination is plastic. In contrast, no disequilibrium develops when epistasis is absent in nonplastic models of recombination (Eshel and Feldman 1970). Although Equation 5 indicates that 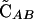= 0 to 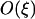when epistasis is absent (ɛ = 0), the next-order term is

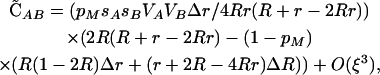which simplifies to 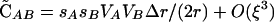when p_M = 1. (For simplicity, we have ignored nonplastic effects of the modifier here.) This confirms the observation of Hadany and Beker that plastic recombination generates a positive association among beneficial alleles at the selected loci, which results in a population-level advantage for plastic recombination when Δr > 0. This disequilibrium produced by plastic recombination is weak, O(ξ²), and is negligible when epistasis is present (as in Equation 5).

In the absence of epistasis, recombination should generate disequilibrium whenever the rate of recombination in unions between intermediate types (Ab and aB) is different from the rate of recombination in unions between extreme types (AB and ab). The disequilibrium generated will be of the same sign as this difference. Because we have modeled plasticity as a linear function of fitness, the sign of this difference, (w_Ab + w_aB)/2 − (w_AB + w_ab)/2, is positive when fitnesses are multiplicative. If plasticity was modeled as a nonlinear function of fitness, it would be possible to observe negative disequilibrium, although here we limit ourselves to only linear models of plasticity.

The analytical results were checked by deterministic computer simulations. The parameter values tested included all combinations of w_ref = w_AB, w_ab; ΔR = Δr = 0.05/(w_AB − w_ab); δR = δr = 0, 0.05, 0.1; R = r = 0.05, 0.25, 0.35; and X = 0.05, 0.5, 0.9, where s_A = s_B = X, and ɛ = −0.5X, 0, +0.5X. The analytical approximations perform very well under the assumptions of the QLE (i.e., selection weak relative to recombination) although they become less accurate when these assumptions are violated. The qualitative conclusion that FAR alleles spread and anti-FAR alleles decline in frequency virtually always held. The only exception occurred when selection was strong, epistasis was positive, and the modifier had large nonplastic effects (i.e., the modifier declined in frequency with s_A = s_B = 0.5 or 0.9, ɛ = s_A/2, δR = δr = 0.1, and w_ref = w_ab).

Barring severe violations of the assumptions, the modifier's nonplastic effects do not contribute to the associations shown in Equations 3–6. Thus, the evolutionary fate of the modifier depends only on its plastic effects to leading order. Nonplastic effects contribute smaller-order terms that have a relatively minor effect on the evolution of the modifier. The contribution of these nonplastic effects is easiest to see by way of comparison with traditional models. Our model is built using the same framework developed by Barton (1995) to study the evolution of nonplastic (conventional) modifiers. Under the assumptions that we used in our analysis of weak directional selection [i.e., s_A, s_B, and ɛ are of O(ξ)], a nonplastic modifier that increases recombination is always negatively selected (epistasis is too strong, in this case, for directional selection to favor recombination). Further, the strength of selection on such a modifier is weak [Δp_M ∼ O(ξ³)] relative to selection on a plastic allele [Δp_M ∼ O(ξ²)]. Only under weak negative epistasis [ɛ < 0 and of O(ξ²)] is a nonplastic modifier that increases recombination favored. Selection on such a modifier [Δp_M ∼ O(ξ⁵)] is three orders weaker than selection on a plastic allele [Δp_M ∼ O(ξ²)]. The two most important conclusions with respect to haploids are that selection on the plasticity of a recombination modifier is much stronger than that on the nonplastic effects of the modifier and that this selection always favors FAR-type plasticity (i.e., more recombination in less-fit individuals and/or less recombination in more-fit individuals).

It is easier to understand the difference between selection on these two types of modifiers by recognizing that any modifier can be selected on the basis of one or both of its two possible effects: (i) its modification of the recombination rate between itself and one or more selected loci and (ii) its modification of the recombination rate among selected loci. Depending on the type of modifier, effect i allows the modifier to directly generate an association with a selected allele (C_MA and/or C_MB). We refer to a modifier's ability to directly generate an association with a selected allele as its “direct effect.” (Note that our use of direct effect is different from the typical usage as the modifier has no effect on the immediate fitness of an organism.) Effect ii of a modifier alters the association between selected loci (C_AB) and, in doing so, indirectly generates an association with a combination of selected alleles (C_MAB). We refer to this as the modifier's “indirect effect.” Selection on a modifier due to this indirect effect is weaker because higher-order associations are involved and would be effective only when summed over many pairs of loci. Further, the indirect effect requires that multiple selected loci be present whereas the direct effect can occur even when there is only a single selected locus.

In the haploid model, which of these effects is acting differs between plastic and non-plastic alleles. At QLE, nonplastic (conventional) modifiers ultimately evolve by altering the disequilibria between selected loci and hence becoming associated with some combinations of alleles over others. In other words, the evolution of a nonplastic modifier is driven by its indirect effect. In contrast, our analysis reveals that the evolution of a plastic modifier is driven by its direct effect. By responding to the fitness of the organism in which it is found, a FAR allele has information about whether it is linked to a good or bad haplotype and thus whether it is advantageous to recombine away from this haplotype. The direct effect of a FAR allele (i.e., directly generating associations with selectively favored alleles) results in an abandon-ship advantage by which we mean the advantage of escaping a low-fitness genotype (metaphorically, a sinking ship). Because a FAR allele can directly generate associations with selected alleles, the abandon-ship advantage can occur even when only a single selected locus is present. Hadany and Beker (2003b) were the first to demonstrate this point by showing that a plastic modifier is expected to reach fixation in a mutation-selection balance model involving a single fitness locus. Our equations confirm this result because Δp_M remains positive in Equation 7 even if one of the two selected loci is fixed (i.e., V_A = 0 or V_B = 0).

Diploid model:

The abandon-ship advantage is a powerful force in haploids driving the evolution of plastic modifiers. However, there is less information available to a plastic modifier in a diploid than in a haploid. Consider a FAR allele that is present in a diploid organism heterozygous for the A locus (A/a). Fitness is the same whether the modifier is linked to the A allele or the a allele, and thus there is no fitness-based information that can be used to increase recombination away from the less-fit allele. Although this verbal reasoning suggests that the abandon-ship advantage of FAR alleles may not be realized in diploids under such general conditions, it is necessary to model the diploid case formally to understand all the forces acting on plastic modifiers.

Relative to the haploid model, the diploid case is considerably more complicated due to the larger number of genotypes and selection parameters needed to describe a completely general model. We focus our attention on what we consider to be the most reasonable cases. The diploid models were built following the same logic as that for the haploid model except that there is a change in the order of events in the life cycle. In diploids, syngamy precedes selection: syngamy, selection on diploid genotypes, followed by gametogenesis. The recombination rate is determined by the mean recombination rate induced by each allele that a diploid individual carries at the modifier locus. Note that we assume obligate sexuality. A future article considers the advantages to plastic modifiers of sexual vs. asexual reproduction (L. Hadany and S. P. Otto, unpublished results).

One selected locus:

In haploids, the abandon-ship mechanism works with a single locus. To begin, we modeled the dynamics of a plastic modifier with a single selected locus. The recombination rate of a diploid individual with genotype G is given by R + ΔR(w_ref − w_G)n + δRn, where n is the number of modifier alleles carried by the individual. Assuming no initial association exists between M and A, no association develops (ΔC_MA = 0), and there is no evolution of the modifier (Δp_M = 0). These results are exact rather than QLE approximations and therefore apply to both strong and weak selection. As the modifier is unable to directly generate an association with the selected locus (ΔC_MA = 0), plastic modifiers in diploids do not have a direct effect, as suggested by our verbal reasoning described above. Consequently, the abandon-ship advantage cannot occur in diploids under the simple and general conditions under which it occurs in the haploid model.

Two selected loci, multiplicative selection:

It is conceivable that some effects of plastic recombination require multiple selected loci. The simplest case to consider is two selected loci with multiplicative selection: w_ab/ab = 1, w_ab/aB = 1 + s_B, w_ab/Ab = 1 + s_A, w_ab/AB = w_Ab/aB = (1 + s_A)(1 + s_B), w_Ab/Ab = (1 + s_A)², w_Ab/AB = (1 + s_A)²(1 + s_B), w_aB/aB = (1 + s_B)², w_aB/AB = (1 + s_A)(1 + s_B)², and w_AB/AB = (1 + s_A)²(1 + s_B)². Assuming that there are no initial disequilibria (i.e., C_MA = C_MB = C_AB = C_MAB = 0), we find that no disequilibria develop (i.e., ΔC_MA = ΔC_MB = ΔC_AB = ΔC_MAB = 0), and there is no change in the frequency of the modifier (Δp_M = 0), regardless of its plastic and nonplastic effects. Again, these results are exact, not approximations. Along with the single-locus findings, these results confirm that there is no direct effect of plastic alleles in diploids. Thus the abandon-ship advantage that strongly favors plasticity in haploids is not acting in diploids under these conditions.

Epistatic selection, no cis-trans effects:

Although plastic modifiers do not have a direct effect in diploids in the above cases, selection might act on a plastic modifier through the way it alters recombination between selected loci (i.e., indirect effects). Such effects, if they occur at all, exist when there is disequilibrium among the selected loci, as arises in response to epistasis. To allow for epistasis (but assuming no cis-trans effects), we modified the multiplicative scheme by changing the fitness of the AB/AB individuals to w_AB/AB = (1 + s_A)²(1 + s_B)² + ɛ. The parameter ɛ describes the deviation from multiplicativity and therefore introduces epistasis. We also assume that fitness is a monotonically increasing function of the number of A and B alleles. To simplify the analysis, we begin by assuming that there are no nonplastic effects (δR = δr = 0). Assuming that s_A, s_B, ɛ are all O(ξ), the QLE associations become

(8)

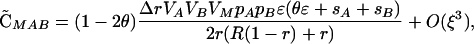(9)

where θ is an indicator variable such that θ = 0 if w_ref = w_min and θ = 1 if w_ref = w_max. 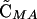and 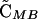= 0 to O(ξ²).

Using these approximations, we find

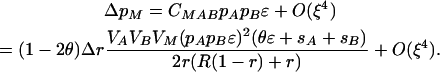(10)

This result shows that the evolutionary fate of the modifier is determined by the sign of the product (1 − 2θ)Δr. [Note the term (θɛ + s_A + s_B) is positive because we assume a monotonic fitness function.] If Δr > 0, then the modifier increases in frequency if w_ref = w_min but decreases if w_ref = w_max. The reverse pattern holds if Δr < 0. Because the results change when the reference genotype changes, it is clear that the fate of the modifier does not result from its plasticity. Rather, selection on the modifier is primarily determined by the modifier's average effect on recombination. Specifically, the modifier spreads only when it causes, on average, a decrease in recombination. This result echoes conventional modifier theory showing that reduced recombination evolves when epistasis is strong [i.e., ɛ of 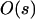; Barton 1995]. We confirmed this result by analyzing a model with only nonplastic effects (δr ≠ 0, δR = ΔR = Δr = 0), which confirmed that only modifiers that decrease recombination spread, at a rate similar to Equation 10, when ɛ, s_A, and s_B are of the same order. Provided the modifier has weak effects, interactions between plastic and nonplastic effects should be negligible, leading us to conclude that decreases in recombination are favored under these assumptions.

In addition to this epistatic fitness regime, we analyzed other models in which epistasis terms (ɛ) were added to the fitness of every genotype having at least one A and one B allele. The results were qualitatively similar. That is, the sign of selection was determined by a modifier's average effect on recombination rather than by its form of plasticity.

Cis-trans effects:

The previous results assume no cis-trans effects on fitness. Cis-trans effects may be of special importance because they provide information about whether a modifier resides in the cis double heterozygote (AB/ab) vs. the trans double heterozygote (Ab/aB). In the former, recombination generates the repulsion gametes (Ab and aB) whereas, in the latter, the coupling gametes are produced (AB and ab). Consequently, it may be beneficial to induce recombination between the selected loci in one type of double heterozygote but not in the other.

With cis-trans effects (w_AB/ab ≠ w_Ab/aB), associations between plastic modifiers and the selected loci arise within a single generation from an initial state of no associations among loci (results not shown), which did not occur in the epistatic regimes considered previously. In particular, nonzero values of C_MAB are generated. Thus, cis-trans effects generate the genetic associations that are necessary for the evolution of plastic recombination. Although cis-trans effects are unlikely to be common, “cis-trans-like” behavior can arise through maternal effects on fitness that are ubiquitous among animals and plants (Mousseau and Fox 1998). We thus proceeded to explore a model of maternal effects. We describe the details of the analysis in the supplementary materials (http://www.genetics.org/supplemental/), and here we report our qualitative findings.

We used deterministic computer simulations to investigate the evolution of modifiers that are sensitive only to the fitness of an individual, but we allowed fitness to depend on the genotypes of both the individual and its mother. The simulations indicated that maternal effects on fitness can generate selection on plasticity. FAR plasticity is favored under most conditions, although anti-FAR can be favored with weak, negative epistasis. The selection on plastic effects is weak such and of the same order as selection on nonplastic effects. Consequently, the evolutionary fate of a modifier is often determined by its average effect on recombination rather than by its form of plasticity. Again, unlike the haploid model, recombination rates did not evolve with only one selected locus. This observation indicates that the evolution of plastic recombination, when it did occur, did not result from the abandon-ship advantage, but rather because of the indirect effects of the modifier on disequilibria among selected loci.

Diploid damage model:

Finally, we consider a diploid model in which the modifier of recombination is able to detect DNA damage. The model is similar to the haploid simulations of Gessler and Xu (2000), although here we consider diploids. When DNA damage occurs, repair enzymes are recruited to the area of damage. It seems plausible that a modifier could detect the same signal that attracts the repair enzymes and thus could respond when DNA damage has occurred nearby. We examined a diploid model with a single fitness locus, A, and a modifier locus, M. The basic framework of the model followed that of Otto (2003), except the modifier affected recombination rather than sex. DNA damage (i.e., mutation) changed the wild-type A allele to its deleterious alternative a. DNA damage occurred at rate μ. If a mutation occurred on the same chromosome as the plastic modifier allele M (i.e., in cis), then recombination was increased by an amount Δr. If the mutation occurred in trans to the M allele, then recombination was not altered. The nonplastic allele, m, did not respond to DNA damage. The fitnesses of individuals carrying zero, one, or two deleterious a alleles were 1, 1 − hs, and 1 − s, respectively. Note that the modifier did not respond to fitness but only to the actual mutation event.

Under these conditions, an association develops between the modifier and the selected locus that at QLE is given by 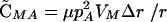. As a result of this association, the modifier evolves,

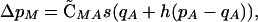(11)

where q_A = 1 − p_A. At mutation-selection balance q_A ≈ μ/hs, this becomes

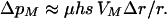(12)

This result indicates that selection on the modifier is quite weak. Selection on the modifier can become stronger by considering a number of linked loci. Yet it is unclear whether a modifier gene could respond to damage in cis across long stretches of DNA. Thus, even the damage model suggests that plastic recombination is difficult to evolve in diploids.

DISCUSSION

Our results show that plastic recombination in haploids readily evolves provided plasticity works such that individuals in poor condition have higher recombination (i.e., FAR-type plasticity). In contrast, plasticity that reduces recombination in individuals of poor condition (i.e., anti-FAR) is selected against. Previous authors (Gessler and Xu 2000; Hadany and Beker 2003b) have reached a similar conclusion using different approaches. Selection for plastic recombination can either increase or decrease the average rate of recombination in the population. If the population initially has no recombination, then the only type of FAR allele that is possible is one that increases recombination in individuals of poor condition, resulting in an overall increase in the average rate of recombination in the population. If the population already recombines at some uniform rate then a second type of FAR allele is possible: a modifier that reduces recombination in individuals of good condition. To leading order, selection is for FAR-type plasticity, not for an increase or decrease in the average recombination rate. The theory of plastic modifiers of recombination in haploids thus makes no prediction about the average rate of recombination, other than it should be >0 and <0.5.

In stark contrast to the haploid case, our analysis reveals that plastic recombination does not readily evolve in diploids. In diploids, selection on a modifier is primarily determined by its average effect on recombination rather than by its form of plasticity. The reason for the difference between the haploid and diploid results becomes clear when we consider the modifier's perspective.

In a haploid organism, a FAR modifier has some information regarding whether it is on a good or bad chromosome on the basis of the fitness of the haploid organism. If it is in a low-fitness organism, it is likely to be on a bad chromosome and thus can gain an advantage by recombining away from that chromosome (i.e., the abandon-ship advantage). In diploids, the fitness of an organism provides a modifier with less information regarding whether it is on a good or bad chromosome. Consider a modifier allele M in the heterozygote A/a. By assessing the organism's fitness (w_A/a) or condition, the modifier could detect that it is in a heterozygote, but it cannot detect if it is on the good chromosome (i.e., MA/ma) or the bad one (i.e., mA/Ma). In the latter case, the modifier would gain an advantage from recombining onto the A chromosome but in the former case it would be disadvantageous to recombine. Consequently, there is no net advantage (or disadvantage) to plastic recombination, and the abandon-ship advantage does not occur in this standard diploid model of selection. Adding more selected loci or epistasis does not alter this conclusion.

In the standard models of selection the plastic allele cannot accrue the abandon-ship advantage because there is no information allowing the plastic modifier to improve its genetic background; i.e., there is no direct effect. For the abandon-ship advantage to work in diploids there must be some mechanism that provides the modifier with information about the haplotype on which it resides. An abandon-ship advantage could occur in diploids if the recombination rate induced by the plastic modifier depends on the fitness of the individual from whom it inherited the plastic allele. For example, the abandon-ship mechanism would work if there were gametic selection and if the effect of the plastic allele depended on the fitness of the gamete, which subsequently altered recombination in the diploid phase.

We emphasize that our models focus exclusively on recombination, not on sex or segregation. The model assumes that organisms are obligately sexual, as they are in many of the empirical examples (flies, mice, and Arabidopsis). In contrast to recombination, diploid models of selection can generate relatively strong selection on plastic modifiers of sex through the abandon-ship advantage (L. Hadany and S. P. Otto, unpublished results), because asexual reproduction causes a modifier to remain associated with all selected alleles within the genome (whether in cis or in trans), while sex allows a modifier to escape from low-fitness genomes.

We did find that selection on plasticity in recombination can arise in diploids for a different reason than the abandon-ship mechanism as long as there is information that can allow a modifier allele to behave differently in cis and trans double heterozygotes (AB/ab vs. Ab/aB). Plasticity is potentially beneficial in this situation because the consequences of recombination in these two genotypes are opposite (producing repulsion vs. coupling gametes). Either cis-trans epistasis or maternal effects on fitness cause fitness differences between the two double heterozygotes, allowing a plastic modifier allele to alter recombination rates to different degrees in these genotypes. Although cis-trans epistasis is unlikely to be common, maternal effects on fitness are ubiquitous. Our simulations show that there is selection on plasticity when such maternal effects occur (supplementary material at http://www.genetics.org/supplemental/). In contrast to the abandon-ship mechanism observed in haploids, plastic alleles in this diploid model are favored because the modifier becomes associated with a beneficial combination of alleles, which requires at least two selected loci. Because the modifier builds an association with a combination of alleles rather than a direct association with individual alleles, selection on plasticity tends to be weak. Consequently, the fate of a plastic modifier is often determined by its incidental effect on the average recombination rate rather than by its plastic effects. Nonetheless, our results show that plastic recombination can evolve in diploids with maternal effects on fitness.

The abandon-ship advantage can be recovered in diploids if the modifier has some way of assessing whether it is on a good or bad chromosome. By detecting and responding to local DNA damage in cis, a plastic modifier can preferentially associate itself with wild-type alleles. However, selection arising on plasticity in this way is very weak unless damage can be detected in cis at a very large number of selected loci.

Our theoretical results suggest that, provided the appropriate variation exists, plastic recombination should readily evolve in haploids. However, the conditions under which it is favored in diploids are considerably more restricted. Curiously, many of the empirical examples of plastic recombination come from diploids (e.g., Plough 1917; Balyaev and Borodin 1982; Lucht et al. 2002; Kovalchuck et al. 2003). Despite the promising haploid results reported by previous authors (Gessler and Xu 2000; Hadany and Beker 2003b) and confirmed here, we are unable to provide strong theoretical support for a selection-based explanation of the empirical data, although maternal effects provide a promising avenue for future empirical research.

It is possible that selection regimes more complicated than those considered here may favor plastic recombination in diploids. Zuchenko and Korol (1985) report simulation results in which plastic modifiers did evolve in diploids experiencing selection involving both overdominance and strong fluctuating epistasis. It is likely that plastic alleles evolve in this situation due to fluctuations in disequilibrium and not due to the abandon-ship advantage. More work on the potential importance of fluctuating selection is needed.

An alternative reason that plastic recombination could evolve is because of the costs of recombination. Such costs might arise from the energetic requirements of the cellular machinery required for recombination and/or because recombination can be mutagenic. In the presence of costs, a plastic modifier allele could always invade a population with uniform recombination if it reduced recombination in those individuals in whom recombination has no effect on the array of offspring produced, for example, among the best homozygous genotypes. On the other hand, costs of being plastic, e.g., costs of assessing and responding to condition, might hinder the evolution of plastic recombination.

Of course, plastic recombination need not be a product of selection. Our diploid analysis does not show selection against plasticity but rather indicates that it is selectively neutral (or very weakly selected). Changes in recombination may be an incidental by-product of a genome under stress. There is some evidence that mutation rates increase under stress (e.g., Hall 1992; Foster 1999; Goho and Bell 2000). Theory suggests that such a phenomenon is unlikely to be adaptive in sexual organisms (Leigh 1970; Sniegowski et al 2000). Condition-dependent changes in recombination rates and mutation rates may simply indicate that genomic processes (e.g., elimination of DNA-damaging agents) are sensitive to an organism's state; organisms experiencing stress might, for example, have higher rates of double-strand breaks as a result of the diversion of resources toward tolerating stress. Even if condition-based sensitivity of genomic processes is wholly nonadaptive, it remains an empirical challenge to more fully document the extent of such sensitivity and a theoretical challenge to understand the evolutionary consequences on the mean fitness of a population (e.g., Redfield 1988; Agrawal 2002; Hadany and Beker 2003a).

APPENDIX: THE RATE AT WHICH DISEQUILIBRIUM APPROACHES ITS STEADY STATE

Here we show that, under the assumptions of the QLE, a disequilibrium approaches its steady-state value at a rate determined only by the average level of recombination, even if disequilibrium is generated by both selection and plastic recombination (i.e., even if recombination rates differ among genotypes). Let C[t] be the disequilibrium at time t, α be the change in disequilibrium caused by selection, and γ be disequilibrium generated by plastic recombination. If the disequilibrium is broken apart by an average recombination rate, r, the disequilibrium after one generation (selection followed by recombination) will be

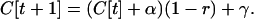(A1)

This equation assumes that the disequilibrium is small so that terms of order C²[t] can be ignored. At QLE,

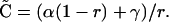(A2)

The deviation of the disequilibrium at time t from its QLE steady-state expectation is

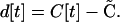(A3)

Assuming no change in the α or γ (in particular, allele frequencies change slowly because selection is weak), the deviation in the following generation becomes

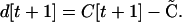(A4)

Using Equation A1, followed by Equation A3, followed by Equation A2 gives

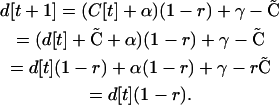(A5)

This result shows that the rate of approach to 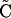is determined by r and does not depend on the forces generating disequilibrium, α and/or γ (selection and/or plastic recombination). In contrast, allele frequencies change at a rate determined by selection. Thus for the QLE approximation to be accurate requires that recombination is strong relative to selection. See Kimura (1965), Nagylaki (1993), and Bürger (2000) for a full treatment of the QLE.