Abstract
The type of interactions among deleterious mutations is considered to be crucial in numerous areas of evolutionary biology, including the evolution of sex and recombination, the evolution of ploidy, the evolution of selfing, and the conservation of small populations. Because the herbicide resistance genes could be viewed as slightly deleterious mutations in the absence of the pesticide selection pressure, the epistatic interactions among three herbicide resistance genes (acetolactate synthase CSR, cellulose synthase IXR1, and auxin-induced AXR1 target genes) were estimated in both the homozygous and the heterozygous states, giving 27 genotype combinations in the model plant Arabidopsis thaliana. By analyzing eight quantitative traits in a segregating population for the three herbicide resistances in the absence of herbicide, we found that most interactions in both the homozygous and the heterozygous states were best explained by multiplicative effects (each additional resistance gene causes a comparable reduction in fitness) rather than by synergistic effects (each additional resistance gene causes a disproportionate fitness reduction). Dominance coefficients of the herbicide resistance cost ranged from partial dominance to underdominance, with a mean dominance coefficient of 0.07. It was suggested that the csr1-1, ixr1-2, and axr1-3 resistance alleles are nearly fully recessive for the fitness cost. More interestingly, the dominance of a specific resistance gene in the absence of herbicide varied according to, first, the presence of the other resistance genes and, second, the quantitative trait analyzed. These results and their implications for multiresistance evolution are discussed in relation to the maintenance of polymorphism at resistance loci in a heterogeneous environment.
THE type of interactions among deleterious mutations is considered to be crucial in numerous areas of evolutionary biology, including the evolution of sex and recombination (Kondrashov 1988; Barton and Charlesworth 1998; Peck and Waxman 2000; Otto and Lenormand 2002), the evolution of ploidy (Perrot et al. 1991), the evolution of selfing (Charlesworth and Charlesworth 1998), and the conservation of small populations (Lande 1994). All these issues relate to the mutation load of a population due to the accumulation of deleterious mutations (Kimura and Maruyama 1966). Sex and recombination can provide an advantage by reducing this load (Kondrashov 1982). The mutational deterministic (MD) hypothesis states that the elimination of deleterious mutations provides an advantage to sex if the interactions among mutations are synergistic, that is, when each additional deleterious mutation leads to a greater decrease in fitness than the previous one (Rivero et al. 2003).
Empirical evidence for synergistic epistasis is rather sparse, however (e.g., de Visser et al. 1997). Elena and Lenski (1997) generated 225 genotypes of Escherichia coli carrying one, two, or three successive mutations and measured their fitness relative to an unmutated competitor. Several combinations of mutations exhibited significant interactions for fitness, but they displayed synergistic epistasis as often as they displayed antagonistic epistasis. Similar results were found in Aspergillus niger (de Visser et al. 1997). Recently, using five chromosomal regions containing visible recessive mutations in Drosophila melanogaster, Whitlock and Bourguet (2000) found that the productivity showed a pattern of strong synergistic epistasis. This pattern was not observed, though, for male mating success. In the same manner, using chemically induced deleterious mutations, Rivero et al. (2003) found that synergistic epistasis occurred for longevity, but not for egg production in the parasitic wasp Nasonia vitripennis. By combing the literature, de Visser and Hoekstra (1998) studied the distribution of a variety of quantitative characters related to fitness in plants. Fitness-related traits show almost exclusively negative skewness, suggesting the existence of synergistic epistasis among deleterious alleles.
Studying the dominance level of deleterious mutations is also crucial to understanding how natural selection may work against the load of deleterious mutations (Muller 1950). In diploid genomes, deleterious mutations tend to be recessive (Wright 1934; Kacser and Burns 1981; Bourguet 1999). A deleterious allele can be masked therefore by the wild-type allele. Masking has long-term costs for populations because the deleterious allele persists for a longer time (Haldane 1937). However, few observations were available to assess the interactions among deleterious mutations in the heterozygous state (Yang et al. 2001; Szafraniec et al. 2003).
To understand how deleterious mutations act together, the type of interactions were tested here among three herbicide resistance mutations in Arabidopsis thaliana in the absence of herbicide, i.e., among deleterious mutations, in both the homozygous and the heterozygous states. Compared to previous studies on the type of interactions among deleterious mutations, the resistance mutations are rather original as (1) they are deleterious in the absence of herbicide and adaptive in the presence of herbicide, and (2) they correspond to actual cases where different genes, providing resistance to the same pesticide or to several pesticides, are concomitantly present in pest populations (Raymond et al. 2001; Sibony and Rubin 2003; Délye et al. 2004).
In this article, we present results from an analysis of eight productivity-related traits in a segregating resistant-susceptible (R/S) population for the three herbicide resistances in the absence of herbicide treatment. Analyzing at least 30 plants for each of the 27 possible genotypes at the three resistance loci, our objectives were (i) to determine the type of interactions among the three resistance genes in both the homozygous and the heterozygous states and (ii) to measure the stability of the dominance level according to the presence of other resistance genes. The results and their implications for multiresistance evolution are discussed.
MATERIALS AND METHODS
Plant materials:
The csr1-1 chlorsulfuron resistance (Bergelson et al. 1996; Purrington and Bergelson 1997, 1999), the ixr1-2 isoxaben resistance (Heim et al. 1989), and the axr1-3 2,4-D resistance (Estelle and Somerville 1987) were used to investigate the type of interactions among deleterious alleles in both the homozygous and the heterozygous states. These resistances were chosen according to three criteria. First, there must be evidence that each resistance mutation induces some fitness penalty. The csr1-1, ixr1-2, and axr1-3 resistances of A. thaliana were isolated by Haughn and Somerville (1986), Heim et al. (1989), and Estelle and Somerville (1987), respectively, from ethyl methanesulfonate (EMS)-mutagenized populations of the wild-type Columbia (Col) ecotype. In a segregating F2 population from a cross between each mutant line (Col genetic background) and the male-sterile-sensitive line NW77 (Ler genetic background), the csr1-1, ixr1-2, and axr1-3 resistances were found to confer a decrease in total seed production of 37, 43, and 78% compared to wild type, respectively (Roux et al. 2004). Second, the resistances must segregate freely from each other for us to study all genotype combinations at the three resistance loci. The CSR, IXR1, and AXR1 resistances genes are located on chromosomes III, V, and I of A. thaliana, respectively, so they should segregate freely from each other. Third, the resistance genes are key metabolism genes involved in the biosynthesis of the branched-chain amino acids isoleucine, valine, and leucine (CSR, Haughn and Somerville 1986); of cellulose synthase (IXR1, Heim et al. 1989); and of hormone auxin (AXR1, Leyser et al. 1993). It could be expected that epistasis would take place between two primary metabolism gene mutations. More, using a QTL approach, recent studies found that epistasis would be a common trend in A. thaliana (Weinig et al. 2003; Juenger et al. 2005; Kroymann and Mitchell-Olds 2005).
The csr1-1 mutant is resistant due to a point mutation resulting in the Pro197-to-Ser amino acid substitution (Haughn et al. 1988), the ixr1-2 mutant is resistant due to a point mutation resulting in the Thr942-to-Ile substitution (Scheible et al. 2001), and the axr1-3 mutant is resistant due to a point mutation resulting in the Cys154-to-Tyr substitution (Leyser et al. 1993). The three resistant mutant lines were provided by the Nottingham Stock Centre.
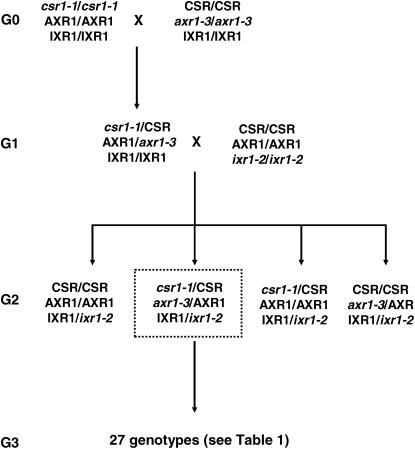
The cross design among the three resistant lines is illustrated in Figure 1. Crossing success was checked by genotyping each resistance allele using an allele-specific PCR method (Roux et al. 2004). A csr1-1 homozygous resistant plant was crossed with an axr1-3 homozygous resistant plant. In this cross, the csr1-1 resistance line was used as the maternal parent. A resulting F1 plant was crossed with an ixr1-2 homozygous resistant plant. In this cross, the F1 plant was used as the maternal parent. Four genotypes (generation 2) were expected from that cross. A resulting triple heterozygous plant, i.e., a heterozygous plant at the three resistance loci, was isolated and selfed to produce the 27 expected genotypes numbered and described in Table 1. This cross design was replicated six times, giving six triple-heterozygous resistant-susceptible (R/S) plants (called the G2 family), each used to originate a segregating family (G3). The EMS origin of the csr1-1, ixr1-2, and axr1-3 lines means that they may carry several mutations other than the ones conferring resistance (Jander et al. 2003). By our crossing protocol, any EMS mutations other than the ones conferring resistance (except those closely linked to the resistance mutations) would contribute equally to the average fitness of each of the 27 genotypes. Because of an expected 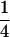 ,
, 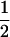 ,
, 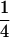 segregation for each resistance gene, the triple-heterozygote RS genotype should be eight times more frequent than any triple-homozygote genotype. The total number of plants to be analyzed was therefore adjusted such that it would exceed 30 for the rarest genotypes.
segregation for each resistance gene, the triple-heterozygote RS genotype should be eight times more frequent than any triple-homozygote genotype. The total number of plants to be analyzed was therefore adjusted such that it would exceed 30 for the rarest genotypes.
Figure 1.
Crossing scheme. For the three resistance genes, susceptible and resistance alleles are indicated in uppercase type and italics, respectively. A csr1-1 homozygous resistant plant was crossed with an axr1-3 homozygous resistant plant. A resulting F1 plant was crossed with an ixr1-2 homozygous resistant plant. Four genotypes (generation 2) were expected from that cross. A resulting triple-heterozygous resistant-susceptible plant, i.e., a heterozygous plant at the three resistance loci, was isolated and selfed to produce the 27 expected genotypes described in Table 1. This cross design was replicated six times.
TABLE 1.
Deleterious effects of the resistance genes for eight quantitative traits
| CSR | IXR | AXR | Genotype | No. of plants | FLOR (±SE) | LEAF (±SE) | CAULIN (±SE) | H1FL (±SE) | HMAX (±SE) | HEADS (±SE) | TOTSIL (±SE) | LEN (±SE) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Col | ||||||||||||
| SS | SS | SS | Control | 83 | 30.4 ± 0.4abcde | 11.7 ± 0.3a | 3.2 ± 0.1b | 55.1 ± 2.7a | 305.3 ± 8.5a | 9.2 ± 0.7 abcd | 1626.5 ± 171.1a | 6.0 ± 0.1a |
| G3 plants (see Figure 1) | ||||||||||||
| SS | SS | SS | 1 | 60 | 30.5 ± 0.6abcde | 10.8 ± 0.5abcdefg | 3.1 ± 0.1b | 51.3 ± 3.6abcde | 266.0 ± 10.4ab | 7.6 ± 0.6bcdef | 1405.6 ± 189.6abc | 6.0 ± 0.2a |
| SS | SS | RS | 2 | 98 | 28.5 ± 0.3fhgi | 9.8 ± 0.2fgh | 3.0 ± 0.1b | 52.5 ± 2.5abcde | 271.7 ± 6.0a | 8.6 ± 0.6abcde | 1466.5 ± 137.3a | 6.1 ± 0.2a |
| SS | SS | RR | 3 | 54 | 26.0 ± 1.5hi | 8.9 ± 0.6gh | 3.8 ± 0.3a | 48.2 ± 3.6abcde | 201.6 ± 13.9c | 10.0 ± 1.0a | 1576.9 ± 256.7a | 2.9 ± 0.2b |
| SS | RS | SS | 4 | 84 | 29.1 ± 0.3efghi | 10.4 ± 0.3abcdefgh | 3.0 ± 0.1b | 45.5 ± 1.8abcdef | 271.0 ± 6.8a | 8.5 ± 0.5abcde | 1442.3 ± 145.7a | 6.2 ± 0.2a |
| SS | RS | RS | 5 | 205 | 29.3 ± 0.3defghi | 10.3 ± 0.2bcdefgh | 3.1 ± 0.1b | 44.8 ± 1.8abcdef | 265.0 ± 6.5ab | 8.3 ± 0.5abcde | 1340.1 ± 111.9ab | 6.2 ± 0.2a |
| SS | RS | RR | 6 | 81 | 26.4 ± 1.2hi | 9.1 ± 0.5gh | 4.1 ± 0.3a | 46.1 ± 3.1abcde | 199.3 ± 10.0c | 9.4 ± 0.8ab | 1376.0 ± 228.9ab | 2.7 ± 0.1bc |
| SS | RR | SS | 7 | 52 | 31.5 ± 0.4ab | 11.2 ± 0.3abcde | 3.2 ± 0.2b | 38.8 ± 2.2ef | 214.4 ± 7.3c | 6.2 ± 0.4efg | 880.8 ± 115.2cdef | 6.1 ± 0.2a |
| SS | RR | RS | 8 | 80 | 31.0 ± 0.3abcd | 11.4 ± 0.2abc | 3.0 ± 0.1b | 39.2 ± 2.0def | 223.6 ± 5.5bc | 6.8 ± 0.4cdefg | 1014.8 ± 91.0abcde | 5.9 ± 0.1a |
| SS | RR | RR | 9 | 35 | 28.6 ± 1.5bcdef | 9.8 ± 0.5bcdefgh | 4.1 ± 0.2a | 35.5 ± 2.9f | 159.3 ± 9.5e | 8.3 ± 0.9abcde | 636.7 ± 93.2f | 2.7 ± 0.2bc |
| RS | SS | SS | 10 | 87 | 29.2 ± 0.4efghi | 10.0 ± 0.3efgh | 2.7 ± 0.1b | 50.6 ± 2.5abcd | 267.8 ± 6.2a | 8.0 ± 0.5abcdef | 1299.9 ± 118.3abc | 6.5 ± 0.1a |
| RS | SS | RS | 11 | 204 | 28.9 ± 0.3efghi | 9.9 ± 0.2efgh | 3.1 ± 0.1b | 52.5 ± 2.3a | 266.1 ± 6.9ab | 7.9 ± 0.3abcde | 1370.9 ± 109.8a | 6.1 ± 0.2a |
| RS | SS | RR | 12 | 83 | 28.2 ± 0.3ghi | 9.7 ± 0.2fgh | 4.6 ± 0.2a | 55.0 ± 2.6a | 211.2 ± 7.4c | 10.2 ± 0.6ab | 1445.4 ± 114.9a | 3.0 ± 0.1bc |
| RS | RS | SS | 13 | 184 | 29.7 ± 0.3bcdefgh | 10.6 ± 0.2abcdefgh | 2.9 ± 0.1b | 49.2 ± 2.4abcde | 270.3 ± 5.3a | 8.0 ± 0.3abcde | 1273.7 ± 75.9ab | 6.3 ± 0.2a |
| RS | RS | RS | 14 | 377 | 29.2 ± 0.2defghi | 10.3 ± 0.1abcdefgh | 3.1 ± 0.1b | 47.0 ± 1.7abcde | 267.1 ± 5.5ab | 7.9 ± 0.3abcde | 1315.8 ± 100.0ab | 6.1 ± 0.1a |
| RS | RS | RR | 15 | 174 | 28.0 ± 0.2hi | 9.7 ± 0.2fgh | 4.6 ± 0.1a | 50.5 ± 1.9abc | 206.3 ± 5.1cd | 9.9 ± 0.5ab | 1401.1 ± 100.5a | 2.9 ± 0.1bc |
| RS | RR | SS | 16 | 94 | 32.0 ± 0.4a | 11.3 ± 0.2abcd | 2.9 ± 0.1b | 38.6 ± 1.9def | 200.8 ± 7.6cd | 6.0 ± 0.4fg | 797.0 ± 73.4def | 5.9 ± 0.1a |
| RS | RR | RS | 17 | 187 | 31.3 ± 0.3abc | 11.0 ± 0.2abcdef | 2.9 ± 0.1b | 39.3 ± 1.5cdef | 211.0 ± 4.8c | 6.5 ± 0.3defg | 895.3 ± 66.3abcdef | 5.8 ± 0.1a |
| RS | RR | RR | 18 | 104 | 28.7 ± 0.9cdefghi | 9.5 ± 0.3fgh | 4.3 ± 0.2a | 42.0 ± 2.2abcdef | 163.8 ± 8.2e | 9.4 ± 0.7abc | 823.2 ± 96.2def | 2.8 ± 0.1bc |
| RR | SS | SS | 19 | 38 | 29.5 ± 0.4defghi | 10.0 ± 0.3efgh | 2.9 ± 0.2b | 52.6 ± 3.4a | 265.0 ± 6.2ab | 7.4 ± 0.6bcdef | 1153.0 ± 107.7abcd | 6.7 ± 0.3a |
| RR | SS | RS | 20 | 96 | 29.1 ± 0.3efghi | 10.1 ± 0.2cdefgh | 3.0 ± 0.1b | 54.5 ± 2.9a | 266.4 ± 7.4ab | 7.7 ± 0.4abcdef | 1277.7 ± 81.6abc | 6.2 ± 0.2a |
| RR | SS | RR | 21 | 45 | 27.9 ± 0.4i | 9.6 ± 0.2gh | 4.3 ± 0.2a | 51.8 ± 2.8ab | 176.4 ± 12.7de | 8.6 ± 0.7abcd | 1126.3 ± 118.6abcd | 2.5 ± 0.2cd |
| RR | RS | SS | 22 | 82 | 29.9 ± 0.4bcdefg | 10.4 ± 0.2abcdefgh | 3.0 ± 0.1b | 49.3 ± 2.7abcde | 266.5 ± 7.5ab | 7.9 ± 0.5abcdef | 1219.7 ± 115.6abcd | 6.6 ± 0.3 a |
| RR | RS | RS | 23 | 182 | 29.9 ± 0.2bcdefg | 10.6 ± 0.2abcdefgh | 3.1 ± 0.1b | 48.1 ± 1.9abcde | 265.5 ± 6.2ab | 7.8 ± 0.3abcdef | 1302.4 ± 115.1abc | 6.1 ± 0.1a |
| RR | RS | RR | 24 | 69 | 27.9 ± 0.3i | 9.4 ± 0.2h | 4.2 ± 0.2a | 46.1 ± 2.6abcdef | 194.7 ± 10.1cde | 10.0 ± 0.7ab | 1356.1 ± 185.8abcd | 2.8 ± 0.1bc |
| RR | RR | SS | 25 | 44 | 31.8 ± 0.4a | 11.3 ± 0.4abcd | 2.8 ± 0.1b | 39.7 ± 2.1bcdef | 214.1 ± 7.4c | 5.5 ± 0.5g | 861.5 ± 108.2bcdef | 6.0 ± 0.2a |
| RR | RR | RS | 26 | 88 | 31.9 ± 0.5a | 11.4 ± 0.3ab | 3.0 ± 0.1b | 40.3 ± 2.6def | 204.0 ± 5.2cd | 6.2 ± 0.5fg | 791.0 ± 68.8def | 5.7 ± 0.2a |
| RR | RR | RR | 27 | 44 | 29.6 ± 0.4cdefghi | 10.0 ± 0.2defgh | 4.4 ± 0.2a | 40.2 ± 2.5ef | 151.3 ± 10.2f | 9.1 ± 0.8abcd | 734.7 ± 101.1ef | 2.5 ± 0.2d |
| Five worldwide ecotypes: | 34.5 | 13.6 | 4.3 | 73.3 | 307.3 | 12.3 | 1669.1 | 5.4 | ||||
For each untransformed quantitative trait, different letters indicate different groups according to the genotypes after the REGWQ multiple-range test at P = 0.05, performed on the within-tray mean values (see materials and methods for description of the test). FLOR, flowering time; LEAF, number of rosettes leaves; CAULIN, number of cauline leaves; H1FL, height from the soil to the first flower at flowering; HMAX, maximum plant height; HEADS, total number of flowering heads; TOTSIL, total silique length (seed production); LEN, mean distance between siliques. FLOR is expressed in number of days after sowing; H1FL, HMAX, TOTSIL, and LEN are expressed in millimeters.
Growth and quantitative traits:
To measure epistatic interactions among the three herbicide resistances, an experiment involving 3744 plants was established. For each G2 family, 552 seeds corresponding to the G3 (see Figure 1) were included. In the experiment, 96 Col SS seeds, 48 Ler SS seeds, and 48 seeds of each mutant Col RR line (csr1-1, ixr1-2, and axr1-3) were also added as external controls of known genotypes. Forty-eight RS seeds of each resistance were also added as a control. These RS seeds were obtained by crossing a mutant Col RR line with a Ler NW77 SS line (Roux et al. 2004). Seeds were sown in 36 trays (44 × 28.5 cm) filled with a commercial soil (Terreau Semis Bouturage Repiquage, Composana, Roche-les-Beaupré, France), and watered twice a week without supplementary nutrients. Each tray consisted of an 8 × 13 array of plants. All 3744 seeds were randomized among plots and grown in the absence of herbicides in the greenhouse in autumn 2003, under natural light supplemented by artificial light to provide a 16-hr photoperiod. The temperature was maintained between 20° and 25°. In each tray, the 104 seeds were regularly spaced 3 cm apart. The experiment stopped after senescence of all plants.
The edges of each tray (46 places) were sown with nine seeds of each Bur-0, En-T, Oy-0, Rld-2, and Ta-0 ecotypes (the remaining place in each tray was sown with seeds of Ler ecotype and was not further considered in our study). Using seeds of these five worldwide ecotypes permitted us to achieve several goals. First, the seeds buffered against possible border effects. Second, although the trays were regularly rotated during the growing period, the highly genetically diverse ecotypes Bur-0, En-T, Oy-0, Rld-2, and Ta-0 (McKhann et al. 2004) allowed us to take into account a general effect of environmental microvariation among trays. In each tray, the plants were then assessed for eight quantitative traits (see below) relative to these five ecotypes used as within-tray internal standard references.
Due to the pattern of epistasis potentially varying with the measured trait (Whitlock and Bourguet 2000; Rivero et al. 2003), we decided to extend the recorded information beyond solely seed production. Roux and Reboud (2005) have shown that some characters (such as plant height) may still induce an ecological cost while they have no direct impact on seed production under optimal experimental conditions. Since >3300 plants (552 seeds × 6 families) were needed to cover the 27 genotypes, the quantitative measures were restricted to the most informative characters. As detailed in Reboud et al. (2004), three criteria were utilized for the choice: high genetic heritability, low sensitivity to environmental conditions, and contribution to fitness (with the lowest possible redundancy between traits). One phenological and three morphological characters were measured during the experiment: flowering time (FLOR), number of rosette leaves (LEAF) and cauline leaves (CAULIN), and height from the soil to the first flower at flowering (H1FL). The four other morphological traits were measured on harvested plants: maximum plant height (HMAX); the total silique length (TOTSIL), a derived trait closely matching the total seed production and corresponding to the multiplication of the mean silique size (measured on the third, fifth, seventh, and ninth siliques on the main stem) by the total number of siliques; the total number of flowering heads (HEADS) measured by summing the number of flowering axes and the number of primary and secondary branches on the primary and secondary axes; and the mean distance between siliques (LEN). This set of variables describes the height and volume occupied by the inflorescence and its degree of ramification and compactness (Reboud et al. 2004). Most of these traits have been shown to have values of heritability >0.2 when analyzed for a worldwide collection of wild-type A. thaliana accessions (McKhann et al. 2004).
Genotyping the resistance status:
DNA was extracted from a section of the first cauline leaf that was cut during the last 3 days of the experiment. Each cauline leaf section was then placed in a microcentrifuge tube containing 50 μl of the extraction buffer described by Saini et al. (1999). The cauline leaf sections were crushed using a mixer mill. Tubes were placed in a water bath at 95° for 6 min, transferred onto ice for 5 min, and vortexed for 15 sec. DNA extracts were kept at −20° prior to PCR analysis.
The single-nucleotide polymorphisms (SNPs) conferring the csr1-1, axr1-3, and ixr1-2 resistances were genotyped by matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometry as described by Sauer et al. (2000). In addition, the genotypes obtained were confirmed by using fluorescence-based technologies: either the Amplifluor technology (Serological Corporation) for the csr1-1 and the axr1-3 resistances or the TaqMan technology (Applied Biosystems, Foster City, CA) for the ixr1-2 resistance.
Statistical analysis:
For each tray and for each quantitative trait, the mean value of each of the 27 expected genotypes (see Figure 1 and Table1) was expressed as the ratio to the mean of the five worldwide ecotypes used as the within-tray reference. The natural logarithm of this ratio is the measure of the log-relative trait of these five worldwide ecotypes. In contrast to untransformed data, this measure of log trait would decline linearly with additional mutations if the trait was determined by a multiplicative interaction among alleles. The log-trait score would decline with negative curvature if there were synergistic epistasis (Elena and Lenski 1997).
The resistances in both the homozygous and heterozygous states were treated as fixed effects. Due to a balanced design with equal numbers of within-tray mean values for each genotype, a Ryan-Einot-Gabriel-Welsch (REGWQ) multiple-range test was performed for each trait using SAS software version 8.1 (Statistical Analysis System; SAS Institute, Cary, NC). This step-down test divides just pairwise differences into possibly overlapping groups; i.e., it groups the genotypes with an identical effect. Means within the same group are not significantly different; those from different groups are significantly different at an assumed level α that depends on the number of comparisons but keeps overall significance at the P = 0.05 level. The susceptible Col control line was also analyzed to test for the presence of EMS mutations other than the ones conferring the resistances. As the csr1-1, ixr1-2, and axr1-3 resistant lines were all generated from the wild-type Col line, each trait of the triple-homozygous susceptible plants (genotype 1) was compared at generation 3 to the trait of the susceptible Col control plants.
The triple SS homozygote genotype 1 was expected to be of highest fitness. To assess the type of epistasis, genotype 1 was therefore used as a reference for the genotypes 2–27 as all genotypes have an identical origin; i.e., plants are issued from the selfing of triple-heterozygous R/S plants. Considering only the homozygous genotypes 1, 3, 7, 9, 19, 21, 25, and 27 (see Table 1), a three-factor full factorial analysis of variance was performed, looking at the effects in the homozygous state on each trait. In the same manner, considering the heterozygous genotypes 1, 2, 4, 5, 10, 11, 13, and 14, a three-factor full factorial analysis of variance was performed, looking at the effects in the heterozygous state on each trait. The size of these effects was estimated using the general linear model (GLM) procedure in SAS. As stated by Whitlock and Bourguet (2000), if the interaction effect is significantly negative, synergistic epistasis occurs. If the effect is significantly positive, antagonistic epistasis occurs. If no effect is detected, gene interaction does not depart from multiplicativity.
To detect an effect of the number of resistances accumulated in the genome on the dominance level of a particular resistance, we focused only on genotypes for which a dominance coefficient could be calculated. For each resistance and trait, we first compared SS, RS, and RR plants in each of the nine genetic backgrounds as determined by the two other resistances (see Table 3) by a GLM procedure. When a genotype effect was detected, the dominance coefficient was calculated on untransformed ratios and was taken as
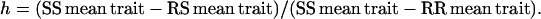 |
TABLE 3.
Dominance level of the csr1-1, ixr1-2, and axr1-3 resistances for each quantitative trait and genetic background
| ixr1-2 | axr1-3 | FLOR | LEAF | CAULIN | H1FL | HMAX | HEADS | TOTSIL | LEN |
|---|---|---|---|---|---|---|---|---|---|
| A. csr1-1 | |||||||||
| SS | SS | — | — | — | — | — | — | — | a0.42 ± 0.14 |
| SS | RS | — | — | — | — | — | — | — | |
| SS | RR | — | — | — | — | a−0.29 ± 0.24a | — | — | b−0.29 ± 0.29a |
| RS | SS | — | — | — | — | — | — | — | — |
| RS | RS | — | — | — | — | — | — | — | — |
| RS | RR | — | — | — | — | — | — | — | — |
| RR | SS | — | — | — | — | — | — | — | — |
| RR | RS | — | — | — | — | b0.50 ± 0.19a | — | 0.33 ± 0.24a | — |
| RR | RR | — | — | — | — | — | — | — | — |
| csr1-1 | axr1-3 | FLOR | LEAF | CAULIN | H1FL | HMAX | HEADS | TOTSIL | LEN |
| B. ixr1-2 | |||||||||
| SS | SS | a−1.53 ± 0.36a | — | — | a0.47 ± 0.15c | a−0.09 ± 0.13bc | a−0.68 ± 0.37b | ab−0.07 ± 0.28bc | — |
| SS | RS | b0.34 ± 0.11a | a0.29 ± 0.12a | — | a0.58 ± 0.13a | a0.14 ± 0.14a | b0.19 ± 0.25a | a0.28 ± 0.25a | — |
| SS | RR | b0.15 ± 0.46 a | — | — | a0.17 ± 0.25a | a0.05 ± 0.24a | — | a0.21 ± 0.24a | — |
| RS | SS | b0.20 ± 0.10ab | a0.47 ± 0.15a | — | a0.12 ± 0.20ab | a−0.03 ± 0.08b | ab−0.01 ± 0.17ab | ab0.05 ± 0.15ab | 0.35 ± 0.32ab |
| RS | RS | b0.15 ± 0.09ab | a0.36 ± 0.13ab | — | a0.42 ± 0.13a | a−0.02 ± 0.10b | ab0.03 ± 0.19ab | ab0.11 ± 0.21ab | — |
| RS | RR | b0.00 ± 0.30a | — | — | a0.35 ± 0.15a | a0.10 ± 0.11a | — | ab0.07 ± 0.16a | — |
| RR | SS | b0.18 ± 0.17a | a0.36 ± 0.17a | — | a0.26 ± 0.21a | a−0.03 ± 0.15a | ab−0.23 ± 0.27a | ab−0.23 ± 0.40a | — |
| RR | RS | b0.27 ± 0.08ab | a0.36 ± 0.13ab | — | a0.45 ± 0.13a | a0.01 ± 0.10ab | ab−0.08 ± 0.24b | ab−0.05 ± 0.24b | — |
| RR | RR | b0.00 ± 0.20ab | — | — | a0.49 ± 0.22a | b−0.73 ± 0.40b | — | b−0.59 ± 0.47b | — |
| csr1-1 | ixr1-2 | FLOR | LEAF | CAULIN | H1FL | HMAX | HEADS | TOTSIL | LEN |
| C. axr1-3 | |||||||||
| SS | SS | a0.44 ± 0.08a | — | bc−0.14 ± 0.14b | — | abc−0.09 ± 0.09b | a0.44 ± 0.26a | — | a−0.04 ± 0.05b |
| SS | RS | b−0.08 ± 0.10a | a0.11 ± 0.13a | ab0.03 ± 0.09a | — | bc0.09 ± 0.09a | — | — | ab0.00 ± 0.05a |
| SS | RR | — | a−0.12 ± 0.17ab | c−0.31 ± 0.14a | — | ab−0.16 ± 0.10ab | ab0.30 ± 0.21b | −0.54 ± 0.37a | abcd0.05 ± 0.03ab |
| RS | SS | — | — | a0.20 ± 0.07a | — | bc0.03 ± 0.12a | ab−0.03 ± 0.14a | — | bcd0.10 ± 0.05a |
| RS | RS | ab0.28 ± 0.12a | a0.31 ± 0.17a | ab0.09 ± 0.05ab | — | bc0.05 ± 0.09ab | b−0.07 ± 0.14b | — | abcd0.06 ± 0.04ab |
| RS | RR | ab0.21 ± 0.09a | a0.15 ± 0.14a | ab0.05 ± 0.06a | — | a−0.28 ± 0.13b | ab0.15 ± 0.09a | — | abc0.02 ± 0.04a |
| RR | SS | ab0.26 ± 0.17a | — | ab0.09 ± 0.06a | — | abc−0.02 ± 0.08a | — | — | cd0.13 ± 0.04a |
| RR | RS | b0.04 ± 0.12a | a−0.13 ± 0.17a | ab0.06 ± 0.07a | — | bc0.01 ± 0.09a | ab−0.01 ± 0.18a | — | d0.14 ± 0.03a |
| RR | RR | b−0.06 ± 0.21a | a−0.09 ± 0.21a | a0.12 ± 0.06a | — | c0.16 ± 0.08a | ab0.18 ± 0.14a | — | abcd0.07 ± 0.05a |
No value indicates no difference among SS, RS, and RR plants. Different superscript letters (a, b, c, d) at the left and right of the values indicate significant Fisher's least-significant-difference grouping at P = 0.05 according to the genetic background and the quantitative trait, respectively. FLOR, flowering time; LEAF, number of rosettes leaves; CAULIN, number of cauline leaves; H1FL, height from the soil to the first flower at flowering; HMAX, maximum plant height; HEADS, total number of flowering heads; TOTSIL, total silique length (seed production); LEN, mean distance between siliques.
Following convention, the resistant allele is dominant for the herbicide resistance cost when h = 1, semidominant when h = 0.5, recessive when h approaches 0, and overdominant and underdominant when h > 1 and <0, respectively. Overdominance and underdominance indicate identical and opposite effects of RS and RR plants compared to SS plants, respectively. For each dominance coefficient, a distribution was generated by calculating a dominance coefficient for each value of the RS data set with their respective SS and RR mean traits. For each resistance and trait, using these generated distributions, dominance coefficients were grouped after a Fisher's least-significant-difference test.
RESULTS
Genotypic frequencies:
For 3312 plants corresponding to generation 3 (552 seeds × 6 families), 2931 plants were successfully genotyped for the three resistances (Table 1).
As expected, the triple-heterozygote RS genotype (genotype 14) was the most frequent genotype with 377 plants while the number of plants for each triple-homozygote genotype ranged from 35 (genotype 9) to 60 (genotype 1). No distortion from Mendelian segregation was detected either when taking into account the 27 genotypes of the G3 (χ2 = 30.05, P = 0.27, d.f. = 26) or for each resistance gene analyzed individually (CSR, χ2 = 3.65, P = 0.16, d.f. = 2; IXR1, χ2 = 1.97, P = 0.37, d.f. = 2; AXR1, χ2 = 4.50, P = 0.11, d.f. = 2). In a previous study (Roux et al. 2004), no distortion from Mendelian segregation was found for the csr1-1 and ixr1-2 resistances but a significant distortion from Mendelian segregation was detected for the axr1-3 resistance.
Deleterious effects of the mutations:
The untransformed quantitative trait estimates for each genotype and the results after REGWQ multiple-range tests are given in Table 1. The results of variance analysis on each quantitative trait in the homozygous and the heterozygous states are shown in Table 2, A and B, respectively.
TABLE 2.
Analysis of variance for effects of alleles on each log-transformed trait
| FLOR
|
LEAF
|
CAULIN
|
H1FL
|
HMAX
|
HEADS
|
TOTSIL
|
LEN
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | Estimate | P | Estimate | P | Estimate | P | Estimate | P | Estimate | P | Estimate | P | Estimate | P | Estimate | P |
| A. Homozygous state | ||||||||||||||||
| csr1-1 | −0.031 | −0.070 | −0.090 | 0.051 | 0.019 | −0.008 | −0.118 | 0.120 | ||||||||
| ixr1-2 | 0.034 | 0.049 | 0.029 | −0.252 | ** | −0.200 | ** | −0.182 | −0.474 | ** | 0.011 | |||||
| axr1-3 | −0.083 | *** | −0.108 | * | 0.273 | *** | 0.051 | −0.193 | * | 0.334 | ** | 0.118 | −0.652 | *** | ||
| csr1-1*ixr1-2 | 0.041 | 0.076 | −0.023 | −0.016 | −0.019 | −0.128 | 0.144 | −0.117 | ||||||||
| csr1-1*axr1-3 | 0.027 | 0.070 | 0.152 | −0.061 | −0.225 | * | −0.173 | −0.172 | −0.322 | ** | ||||||
| ixr1-2*axr1-3 | 0.034 | 0.025 | 0.032 | −0.102 | −0.057 | −0.048 | −0.420 | −0.111 | ||||||||
| csr1-1*ixr1-2*axr1-3 | −0.051 | −0.104 | −0.033 | 0.089 | 0.054 | 0.356 | 0.217 | 0.137 | ||||||||
| B. Heterozygous state | ||||||||||||||||
| csr1-1 | −0.043 | ** | −0.072 | * | −0.136 | ** | 0.017 | 0.028 | 0.053 | −0.030 | 0.091 | * | ||||
| ixr1-2 | −0.045 | ** | −0.022 | −0.003 | −0.077 | 0.038 | 0.135 | 0.075 | 0.032 | |||||||
| axr1-3 | −0.065 | *** | −0.081 | * | −0.028 | 0.059 | 0.042 | 0.138 | 0.105 | 0.033 | ||||||
| csr1-1*ixr1-2 | 0.064 | ** | 0.090 | 0.107 | 0.055 | −0.027 | −0.094 | −0.038 | −0.065 | |||||||
| csr1-1*axr1-3 | 0.057 | * | 0.084 | 0.156 | * | −0.015 | −0.052 | −0.104 | −0.023 | −0.096 | ||||||
| ixr1-2*axr1-3 | 0.074 | ** | 0.070 | 0.031 | −0.076 | −0.066 | −0.168 | −0.169 | −0.022 | |||||||
| csr1-1*ixr1-2*axr1-3 | −0.080 | * | −0.096 | −0.110 | −0.003 | 0.063 | 0.126 | 0.106 | 0.055 | |||||||
If the estimate is significantly negative or positive, synergistic or antagonistic epistasis occurs, respectively. If no effect is detected, gene interaction does not depart from multiplicativity. FLOR, flowering time; LEAF, number of rosettes leaves; CAULIN, number of cauline leaves; H1FL, height from the soil to the first flower at flowering; HMAX, maximum plant height; HEADS, total number of flowering heads; TOTSIL, total silique length (seed production); LEN, mean distance between siliques. *0.05 > P > 0.01, **0.01 > P > 0.001, ***P < 0.001.
For each trait, no significant difference was detected among the triple-homozygous susceptible genotype (genotype 1) and the Col susceptible control line (Table 1). This result indicated the absence of any significant effect of potential EMS mutations other than the ones conferring resistance. If there were cryptic EMS-induced mutations other than the resistance mutations, their phenotypic effects were not detectable in our assays.
Compared to the mean of the five worldwide ecotypes, the 27 genotypes of generation 3 exhibited, in most cases, lower values for each quantitative trait except LEN). No general trend among the quantitative traits was observed when grouping the 27 genotypes (Table 1). The number of significantly different groups ranged from nine for FLOR to two for CAULIN. FLOR seemed thus the most sensitive variable to the presence of the resistance genes studied here.
In the homozygous state, the csr1-1 (genotype 19) resistance has no effect on quantitative traits while the ixr1-2 (genotype 7) and axr1-3 (genotype 3) resistances have a significant effect on one and five quantitative traits, respectively (Table 1). Analyses of variance indicated no effect on quantitative traits for the csr1-1 resistance and an effect on three and six quantitative traits for the ixr1-2 and axr1-3 resistances, respectively (Table 2A). In particular, TOTSIL drops 37% compared to wild type (genotype 1) for the ixr1-2 resistance (genotype 7). This value is consistent with the one estimated by Roux et al. (2004), where the ixr1-2 resistance was found to confer a decrease in TOTSIL of 43%. Although the estimate of the TOTSIL decrease conferred by the csr1-1 resistance (18%, genotype 19 vs. genotype 1) is close to the one found in previous studies (26%; Purrington and Bergelson 1997), this value does not here significantly differ from 0 mainly because of the higher significance level required when adjusted for multiple pairwise comparisons. Surprisingly, the axr1-3 resistance conferred no difference in TOTSIL compared to the wild type; this is in contrast to a previous study by Roux et al. (2004) in which a decrease in TOTSIL of 78% was found to be associated with the axr1-3 resistance in a segregating F2 population from a cross between a Col and a Ler genetic background. This potential effect of genetic background on the expression of a fitness cost associated with axr1-3 resistance is currently under deeper investigation.
In the heterozygous state, no significant effect on quantitative traits was detected for the csr1-1 (genotype 10) and ixr1-2 (genotype 4) resistances while a significant effect on FLOR was detected only for the axr1-3 resistance (Table 1). A significant effect on four, one, and two quantitative traits was detected for the csr1-1, ixr1-2, and axr1-3 resistances, respectively (Table 2B). The few disparities in the results between the two statistical methods come from the level of significance, which is adjusted to the number of performed comparisons for the REGWQ multiple-range tests but not for the GLM procedure.
Epistatic interactions for quantitative traits:
Overall, the analysis of variance on each quantitative trait shows few significant interaction terms in either the homozygous or the heterozygous state (Table 2, A and B, respectively). On average, there was no departure from multiplicative effects among the three resistance genes. In the homozygous state, only 2 of 24 two-way interactions were significant; in each of these two cases the direction of this effect is negative; that is, synergistic epistasis occurred (Table 2A). Both synergisms (affecting either HMAX or LEN) occurred between the csr1-1 and axr1-3 resistances. No three-way interaction was detected. In the heterozygous state, only 4 of 24 two-way interactions were significant; in each of these 4 cases the direction of this effect is positive; that is, antagonistic epistasis occurred (Table 2B). Only the three-way interaction for FLOR was significant; in this case synergistic epistasis occurred (Table 2B).
Dominance of resistance genes:
For each quantitative trait, the effects of the number of resistance genes accumulated in the genome on the dominance of the csr1-1, ixr1-2, and axr1-3 resistances are given in Table 3, A, B, and C, respectively. For each resistance, 72 comparisons (8 traits × 9 genetic backgrounds determined by the two other resistances) among SS, RS, and RR plants were performed. Only 5 genotype effects were detected for the csr1-1 resistance (Table 3A), while 48 genotype effects were detected for both the ixr1-2 and axr1-3 resistances (Table 3, B and C). Five, 48, and 48 dominance coefficients were therefore calculated for the csr1-1, ixr1-2, and axr1-3 resistances, respectively.
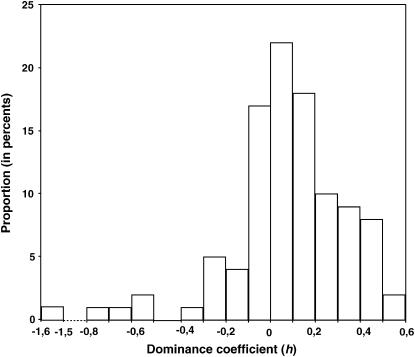
Overall, the dominance for the herbicide resistance cost ranged from partial dominance with a value of 0.58 (H1FL for the ixr1-2 resistance in a csr1-1 SS and axr1-3 RS genetic background) to underdominance with a value of −0.73 (HMAX for the ixr1-2 resistance in a csr1-1 RR and axr1-3 RR genetic background) with an extreme value of −1.53 (FLOR for the ixr1-2 resistance in a csr1-1 SS and axr1-3 SS genetic background). The distribution of the dominance coefficients is illustrated in Figure 2. The mean dominance is 0.07 with a standard error of 0.29, indicating that most mutations are recessive whatever the quantitative trait or the genetic background. In a previous study (Roux et al. 2004), the mean dominance on TOTSIL was found to be 0.05, 0.13, and 0.10 for the csr1-1, ixr1-2, and axr1-3 resistance alleles, respectively.
Figure 2.
Overall distribution of dominance coefficients. The resistant allele is dominant for the fitness cost when h = 1, semidominant when h = 0.5, recessive when h approaches 0, and overdominant and underdominant when h > 1 and <0, respectively.
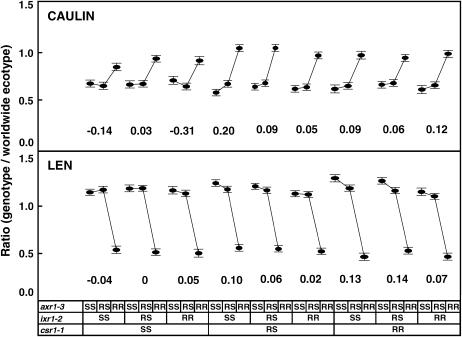
The effect of the quantitative traits on the dominance found for each resistance depends on the genetic background determined by the two other resistances. In a csr1-1 SS and axr1-3 RS genetic background, the dominance of the ixr1-2 resistance was very stable over the different quantitative traits. By contrast, in a csr1-1 RS and ixr1-2 RS genetic background, the dominance for the axr1-3 resistance varied among the different quantitative traits. In parallel, the effect of the genetic background on the dominance depended on the quantitative trait. The dominance of the ixr1-2 resistance did not vary for the LEAF and H1FL traits whatever the genetic background at the two other resistance loci. By contrast, the genetic background greatly affected the dominance of the axr1-3 resistance for the CAULIN and LEN traits (see Figure 3). The general trend that emerges from all these comparisons is that the genetic background had much more effect on the dominance than the type of quantitative trait analyzed.
Figure 3.
Effect of the accumulation of resistance genes on the dominance of the axr1-3 resistance allele for the number of cauline leaves (CAULIN) and mean distance between siliques (LEN) traits. Means and standard errors of the SS, RS, and RR plants for the axr1-3 resistance are grouped according to the genotypes of the ixr1-2 and csr1-1 resistances. Values under each group indicate the dominance coefficient (see Table 3).
DISCUSSION
Epistatic interactions among deleterious alleles:
Quantifying selection coefficients, degree of dominance for the fitness penalty, and direction and intensity of genetic interactions is crucial to understanding how natural selection may work against load of deleterious mutations in general and against resistance stacking (multiresistance) in particular. In our study, in the absence of herbicide, for eight quantitative traits, most interactions between two or three resistance genes in the homozygous state were best explained by multiplicative effects rather than by synergistic effects. Such a pattern was also observed in the heterozygous state. However, no distortion of segregation for any resistance gene was detected in the progeny of selfed triple-heterozygous resistant-susceptible plants while a distortion of segregation in favor of the wild type was described in the progeny of axr1-3 heterozygous resistant-susceptible plants (Roux et al. 2004). The restoration of segregation of the axr1-3 resistance allele in a triple-heterozygous plant could be viewed as a kind of antagonistic epistasis in the heterozygous state among the csr1-1, ixr1-2, and axr1-3 resistance alleles. Since Otto (2003) suggested that the benefits of segregation were more likely than the benefits of recombination to have driven the evolution of sexual reproduction in diploids, the determination of the type of interactions among deleterious mutations in the heterozygous state and the analysis of the meiotic drive would be worth incorporating into further studies.
Several explanations can be advanced for the general observed lack of synergistic epistasis for the eight quantitative traits among the csr1-1, ixr1-2, and axr1-3 resistance genes. First, as argued by de Visser and Hoekstra (1998), the MD hypothesis predicts synergistic epistasis among slightly deleterious mutations, which are thought to be more relevant for evolution than deleterious mutations with large effect. Using a computer model, You and Yin (2002) also suggested that synergistic epistasis may be difficult to distinguish experimentally from nonepistasis because its effects appear to be most pronounced when the effects of mutations on fitness are more challenging to measure. Here, the csr1-1 mutation in the homozygous state has no detectable effect on any quantitative trait analyzed. The two cases of synergism detected in the homozygous state (HMAX and LEN) involved the csr1-1 and axr1-3 mutations. The csr1-1 mutation could therefore be considered as a slightly deleterious mutation. Such a feature was also observed in D. melanogaster (Whitlock and Bourguet 2000) for male mating success. Antagonistic interaction was found between two mutations although no detectable effect was associated with either of the mutations when considered alone. Our inability to detect the deleterious effects of the three resistance genes is thus expected to affect in a conservative way our ability to detect synergistic or antagonistic interactions. In other words, although the experiment involved >2900 genotyped plants, we still lack statistical power in our study to distinguish between synergistic and multiplicative effects. Second, the CSR, IXR1, and AXR1 resistance genes are tissue dependent, meaning that their levels of expression vary between different parts of the plant. The acetolactate synthase encoded by the CSR gene has its peak of activity in reproductive organs (Purrington and Bergelson 1999). The IXR1 gene is mainly expressed in stems (Dhugga 2001), while the AXR1 gene is expressed during many stages of plant growth and development from embryogenesis to senescence (Nagpal et al. 2000). Testing for an interaction between genes for a specific trait could be useless if only one of the two genes is expressed at a time in the quantitative trait. Further investigations on the pattern of expression of the resistance genes are needed to clarify whether the lack of synergistic or antagonistic interactions is not biased by different levels or timings of expression. Third, Rivero et al. (2003) pointed out that deleterious mutations may lead to fitness consequences only in individuals competing for limited resources. Peck and Waxman (2000) demonstrated also that synergistic epistasis may not be detected unless experiments are redesigned to make them much more like in nature. Bergelson and Purrington (2002) showed that the deleterious effects of the csr1-1 resistance were enhanced under competition. Although our experimental protocol was designed to allow competition for available resources and light (plant rosettes overlap each other), it could be relevant to examine how each interaction tested in this study would respond to other stressful conditions such as a change in total plant density. At the opposite, Kishony and Leibler (2003) suggested that environmental stress could also alleviate the average deleterious effects of mutations. Fourth, although a direct measure of several life-history traits may provide information about the underlying components contributing to the fitness cost of a resistance gene, only the measure of changes in resistance allele frequency in untreated populations over several generations allows the estimation of the complete fitness cost (Gilliland et al. 1998). Cumulating slightly synergistic epistasis present in different quantitative traits could result in a detectable synergism at the fitness level. Microevolutionary dynamics in experimental populations could be more sensitive for assessing the type of interactions among deleterious mutations and would also include directly the effects of any meiotic drive.
In a perspective of herbicide resistance management, nonepistasis among resistance alleles in both the homozygous and the heterozygous states would indicate that the decline of multiresistance in an herbicide-free population would be slower than that with a synergism among resistance alleles. However, compared to previous studies on the types of interactions among deleterious mutations, the resistance mutations studied here are rather original as they are deleterious in the absence of herbicide and adaptive in the presence of herbicide. Although Raymond et al. (1989) found that the type of epistasis among resistance alleles depends on the particular physiological mechanisms of resistance, theory on sexual reproduction and recombination (Barton and Charlesworth 1998; Otto and Michalakis 1998) predicted antagonistic epistasis among beneficial alleles and synergistic epistasis among deleterious alleles. Both antagonistic and synergistic epistases could therefore be expected for resistance genes according to the presence or absence of herbicides, respectively. Evolutionary data are required to evaluate how independent epistasis is in a favorable environment (presence of herbicide) compared to that expressed in a less permissive environment (absence of herbicide).
Dominance of deleterious mutations:
As the dominance coefficient (h) is expected to affect the mean fitness of populations, it is an important parameter in models of variation in mating systems and in the evolution of sex and recombination (e.g., Peters et al. 2003). In an overview of the estimate of dominance, Szafraniec et al. (2003) show that alleles with small fitness effects retain approximately one-quarter of their impact on fitness in heterozygotes, suggesting that small mutational effects are only moderately masked by wild-type alleles. Here, the mean coefficient of dominance of the herbicide resistance cost was found to be h = 0.07, a value close to the ones found by Korona (1999) in the yeast Saccharomyces cerevisiae (h = 0.08) and by Peters et al. (2003) in the nematode Caenorhabditis elegans (h ∼ 0.01). This low coefficient suggests a strong masking effect of the susceptible (wild-type) alleles and could be partly explained by the enzymatic function of the CSR, IXR1, and AXR1 genes. In their detailed biochemical theory of dominance, Kacser and Burns (1981) demonstrated that the activity of the wild-type enzymes is usually far in excess of that necessary as a consequence of the kinetic properties of metabolic pathways. For the CSR, AXR1, and IXR1 genes, a single copy of the sensitive allele would confer sufficient enzymatic activity to produce identical phenotypes between RS and SS plants. In the presence of herbicide, the enzymatic activity of RS individuals would thus be out of the “safety margin,” a value used to describe the maximum decrease of the enzyme activity that can be tolerated without affecting the phenotype (Wright 1929). The phenotype of RS plants would depend on the relative activity of the R enzyme vs. the S enzyme and how much S enzyme is left functional in the SS plant after herbicide treatment. Although the predictions of metabolic control theory are well met by the cases where enzyme pathways are involved, Kacser and Burns (1981) do not claim that this theory applies to genes encoding nonenzyme products. In the presence of insecticides, sodium-channel-based resistance in the mosquito Culex pipiens tends to be much closer to recessivity than acetylcholinesterase-based resistance (e.g., Charlesworth 1998). In the absence of herbicides, Roux et al. (2004) observed that deleterious mutations in structural proteins could confer distinct patterns of dominance when compared to deleterious mutations affecting enzymes. Most estimates of the dominance coefficients were obtained for spontaneous or EMS-induced mutations, regardless of the gene function. The hypothesis that the level of dominance may change according to the enzymatic status of the gene product may contribute to the explanation of a lower coefficient of dominance found here compared to other studies.
Our estimate of the mean coefficient of dominance could be difficult to compare to other estimates, however, as the dominance was shown here to depend on both the genetic background and the trait (to a lesser degree). The effect of a deleterious mutation that leads to different dominance coefficients in two traits was reviewed by Keightley and Kacser (1987) and was supported by recent work (Fernández and Lopez-Fanjul 1996; Houle et al. 1997). Two explanations can be advanced for the variation of the dominance among traits. First, Keightley and Kacser (1987) assumed that the cellular environment of a specific gene in different traits must clearly be different due to the tissue-dependence of the expression of other genes. Two traits could be different by sustaining different substrate concentrations and/or different activation or induction of genes. The safety margin for any metabolism may therefore change according to the expression of other genes. The effect of a deleterious mutation could easily lead to different dominance coefficients among traits. Second, as suggested by Roux et al. (2004), physiological requirements are variable within a plant and change over time. As a result, the safety margins for different enzymes are also expected to vary according to the plant tissue and developmental stage requirements. Therefore, two quantitative traits expressed in different parts of the plants or at different times/stages could be differently affected by a resistance allele. As an illustration, for the ixr1-2 resistance, the absence of differentiation among genotypes for the CAULIN trait could mean either that the ixr1-2 mutation has no biological effect on the CAULIN trait or simply that it is not expressed in the CAULIN trait.
Keightley and Kacser (1987) showed that most mutations, especially those affecting an enzyme, have similar dominance relations for the traits they affect pleiotropically. This pattern fits our results, as the dominance among traits varied much less than the dominance levels expressed in varying genetic backgrounds. For most traits, the dominance of the cost for a specific resistance was affected by the genetic background determined by the two other resistances. However, the accumulation of resistance genes does not lead to a unique trend of increase or decrease of the dominance level. For some traits such as LEAF and H1FL for the ixr1-2 resistance and LEAF for the axr1-3 resistance, the absence of a genetic background effect on the dominance of a specific resistance allele could mean either that the two other resistance mutations (csr1-1 and axr1-3) have no biological effect on the dominance of the former resistance allele or that the two other resistance genes are not expressed in the analyzed traits.
Fisher and Meunier (2001) as well as Gergersen et al. (2001) noted that a mutation that affects the level of expression or the enzyme kinetics can lead to cellular disorders with different activation or induction of other genes. As the targets of herbicides involve key metabolism genes, a mutation conferring herbicide resistance might deeply affect the cellular environment for other genes and, thus, change their safety margin. The cellular environment of a specific gene would depend not only on whether other resistance genes are expressed (as described above) but also on the effect of a resistant mutation on the activation or induction of the other genes in the cell. The possible disruption of the cellular environment for other genes could be also advanced as a reason for the variation of the dominance in different genetic backgrounds.
Conclusion:
Mutation load is a cornerstone in evolutionary theories for the evolution of sex, recombination, and ploidy level. Despite its importance, the cases where a full analysis of the joint effect of deleterious mutations can be conducted are scarce. Here, because the favorable herbicide resistance genes behave like slightly deleterious mutations in the absence of the pesticide selection pressure, the epistatic interactions among three deleterious resistance genes were estimated in both the homozygous and the heterozygous states, giving 27 genotype combinations. We analyzed the stability of the dominance with respect either to quantitative traits or to the presence of other resistance genes in the genetic background. Our results give little evidence for synergistic epistasis among deleterious mutations in either the homozygous or the heterozygous state. In addition, the mean dominance coefficient was estimated to be 0.07, suggesting that the csr1-1, ixr1-2, and axr1-3 resistance alleles are nearly fully recessive. More interestingly, the dominance of a specific resistance gene varied according to the quantitative trait studied and the presence of the other resistance genes. Our results highlight that both the presence of synergism among the three resistance genes and the stability of the dominance may depend on the expression of the resistance genes and/or the effect of a resistance on the activation or induction of other genes affecting the quantitative trait studied. In general, this result would mean that deleterious mutations with different spatial and temporal expression within a plant could be much more easily accumulated during an evolutionary process in a plant than deleterious mutations with overlapping expression profiles.
Acknowledgments
Special thanks are given to Joy Bergelson and two anonymous reviewers for their helpful discussions and comments on an earlier version of this manuscript. We are grateful to Aurélie Bérard, Stéphanie Durand, and Geoffray Petitjean for their technical assistance. We also thank H. McKhann for correcting the English. Part of the high-throughput genotyping has been financed by Action incitative programmée Institut National de la Recherche Agronomique (INRA) séquençage végétal et post-séquençage and by projets Santé des Plantes et Environnement INRA. This study was supported by a grant to F.R. from Bayer Crop Sciences.
References
- Barton, N. H., and B. Charlesworth, 1998. Why sex and recombination? Science 281: 1986–1990. [PubMed] [Google Scholar]
- Bergelson, J., and C. B. Purrington, 2002. Factors affecting the spread of resistant Arabidopsis thaliana populations, pp. 17–33 in Genetically Engineered Organism: Assessing Environmental and Human Health Effects, edited by D. B. Letourneau and B. E. Burrows. CRC Press, Cleveland/Boca Raton, FL.
- Bergelson, J., C. B. Purrington, C. J. Palm and J. C. Lopez-Guitierreze, 1996. Costs of resistance: a test using transgenic Arabidopsis thaliana. Proc. R. Soc. Lond. 263: 1659–1663. [DOI] [PubMed] [Google Scholar]
- Bourguet, D., 1999. The evolution of dominance. Heredity 83: 1–4. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1998. The struggle for dominance. Curr. Biol. 8: R502–R504. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., and D. Charlesworth, 1998. Some evolutionary consequences of deleterious mutations. Genetica 102/103: 3–19. [PubMed] [Google Scholar]
- de Visser, J. A. G. M., and R. F. Hoekstra, 1998. Synergistic epistasis between loci affecting fitness: evidence in plants and fungi. Genet. Res. 71: 39–49. [Google Scholar]
- de Visser, J. A. G. M., R. F. Hoekstra and H. van den Ende, 1997. Test of interaction between genetic markers that affect fitness in Aspergillus niger. Evolution 51: 1499–1505. [DOI] [PubMed] [Google Scholar]
- Délye, C., C. Straub, S. Michel and V. Le Corre, 2004. Nucleotide variability at the acetyl coenzyme A carboxylase gene and the signature of herbicide selection in the grass weed Alopecurus myosuroides (Huds.). Mol. Biol. Evol. 21: 884–892. [DOI] [PubMed] [Google Scholar]
- Dhugga, K. S., 2001. Building the wall: genes and enzymes complexes for polysaccharide synthases. Curr. Opin. Plant Biol. 4: 488–493. [DOI] [PubMed] [Google Scholar]
- Elena, S. F., and R. E. Lenski, 1997. Test of synergistic interactions among deleterious mutations in bacteria. Nature 390: 395–398. [DOI] [PubMed] [Google Scholar]
- Estelle, M. A., and C. Somerville, 1987. Auxin-resistant mutants of Arabidopsis with an altered morphology. Mol. Gen. Genet. 206: 200–206. [Google Scholar]
- Fernández, J., and C. Lopez-Fanjul, 1996. Spontaneous mutational variances and covariances for fitness-related traits in Drosophila melanogaster. Genetics 143: 829–837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher, N., and B. Meunier, 2001. Effects of mutations in mitochondrial cytochrome b in yeast and man. Deficiency, compensation and disease. Eur. J. Biochem. 268: 1155–1162. [DOI] [PubMed] [Google Scholar]
- Gilliland, L. U., E. C. McKinney, M. A. Asmussen and R. B. Meagher, 1998. Detection of deleterious genotypes in multigenerational studies. I. Disruptions in individual Arabidopsis actin genes. Genetics 149: 717–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregersen, N., B. S. Andresen, M. J. Corydon, T. J. Corydon, R. K. Olsen et al., 2001. Mutation analysis in mitochondrial fatty acid oxidation defects: exemplified by acyl-CoA dehydrogenase deficiencies, with special focus on genotype-phenotype relationship. Hum. Mutat. 18: 169–189. [DOI] [PubMed] [Google Scholar]
- Haldane, J. B. S., 1937. The effect of variation on fitness. Am. Nat. 72: 337–349. [Google Scholar]
- Haughn, G. W., and C. R. Somerville, 1986. Sulfonylurea-resistant mutants of Arabidopsis thaliana. Mol. Gen. Genet. 204: 430–434. [Google Scholar]
- Haughn, G. W., J. Smith, B. Mazur and C. Somerville, 1988. Transformation with a mutant Arabidopsis acetolactate synthase gene renders tobacco resistant to sulfonylurea herbicides. Mol. Gen. Genet. 211: 266–271. [Google Scholar]
- Heim, D. R., J. L. Roberts, P. D. Pike and I. M. Larrinua, 1989. Mutation of a locus of Arabidopsis thaliana confers resistance to the herbicide isoxaben. Plant Physiol. 90: 146–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle, D., K. A. Hughes, S. Assimacopoulus and B. Charlesworth, 1997. The effects of spontaneous mutation on quantitative traits. II. Dominance of mutations with effects on life-history traits. Genet. Res. 70: 27–34. [DOI] [PubMed] [Google Scholar]
- Jander, G., S. R. Baerson, J. A. Hudak, K. A. Gonzalez, K. J. Gruys et al., 2003. Ethylmethanesulfonate saturation mutagenesis in Arabidopsis to determine frequency of herbicide resistance. Plant Physiol. 131: 139–146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juenger, T. E., S. Sen, K. A. Stowe and E. L. Simms, 2005. Epistasis and genotype-environment interaction for quantitative trait loci affecting flowering time in Arabidopsis thaliana. Genetica 123: 87–105. [DOI] [PubMed] [Google Scholar]
- Kacser, H., and J. A. Burns, 1981. The molecular basis of dominance. Genetics 97: 639–666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., and H. Kacser, 1987. Dominance, pleiotropy and metabolic structure. Genetics 117: 319–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M., and T. Maruyama, 1966. The mutational load with epistatic gene interactions in fitness. Genetics 34: 1337–1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kishony, R., and S. Leibler, 2003. Environmental stresses can alleviate the average deleterious effect of mutations. J. Biol. 2: 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1982. Selection against harmful mutations in large sexual and asexual populations. Genet. Res. 40: 325–332. [DOI] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1988. Deleterious mutations and the evolution of sexual reproduction. Nature 336: 435–440. [DOI] [PubMed] [Google Scholar]
- Korona, R., 1999. Unpredictable fitness transitions between haploid and diploid strains of the genetically loaded yeast Saccharomyces cerevisiae. Genetics 151: 77–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroymann, J., and T. Mitchell-Olds, 2005. Epistasis and balanced polymorphism influencing complex trait variation. Nature 435: 95–98. [DOI] [PubMed] [Google Scholar]
- Lande, R., 1994. Risk of population extinction from fixation of new deleterious mutations. Evolution 48: 1460–1469. [DOI] [PubMed] [Google Scholar]
- Leyser, H. M. O., C. A. Lincoln, C. T Iimpte, D. Lammer, J. Turner et al., 1993. Arabidoposis auxin-resistance gene AXR1 encodes a protein related to ubiquitin-activating enzyme E1. Nature 364: 161–164. [DOI] [PubMed] [Google Scholar]
- McKhann, H. I., C. Camilleri, A. Berard, T. Bataillon, J. L. David et al., 2004. Nested core collections maximizing genetic diversity in Arabidopsis thaliana. Plant J. 38: 193–202. [DOI] [PubMed] [Google Scholar]
- Muller, H. J., 1950. Our load of mutations. Am. J. Hum. Genet. 2: 111–176. [PMC free article] [PubMed] [Google Scholar]
- Nagpal, P., L. N. Walker, J. C. Young, A. Sonawala, C. Timpte et al., 2000. AXR2 encodes a member of the Aux/IAA protein family. Plant Physiol. 123: 563–574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., 2003. The advantage of segregation and the evolution of sex. Genetics 164: 1099–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto, S. P., and T. Lenormand, 2002. Resolving the paradox of sex and recombination. Nat. Rev. Genet. 3: 252–261. [DOI] [PubMed] [Google Scholar]
- Otto, S. P., and Y. Michalakis, 1998. The evolution of recombination in changing environments. Trends Ecol. Evol. 13: 145–151. [DOI] [PubMed] [Google Scholar]
- Peck, J. R., and D. Waxman, 2000. Mutation and sex in a competitive world. Nature 406: 399–404. [DOI] [PubMed] [Google Scholar]
- Perrot, V., S. Richerd and M. Valero, 1991. Transition from haploidy to diploidy. Nature 351: 315–317. [DOI] [PubMed] [Google Scholar]
- Peters, A. D., D. L. Halligan, M. C. Whitlock and P. D. Keightley, 2003. Dominance and overdominance of mildly deleterious induced mutations for fitness traits in Caenorhabditis elegans. Genetics 165: 589–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purrington, C. B., and J. Bergelson, 1997. Fitness consequences of genetically engineered herbicide and antibiotic resistance in Arabidopsis thaliana. Genetics 145: 807–814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purrington, C. B., and J. Bergelson, 1999. Exploring the physiological basis of costs of herbicide resistance in Arabidopsis thaliana. Am. Nat. 154: S82–S91. [DOI] [PubMed] [Google Scholar]
- Raymond, M., D. G. Heckel and J. G. Scott, 1989. Interactions between pesticide genes: model and experiment. Genetics 123: 543–551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond, M., C. Berticat, M. Weill, N. Pasteur and C. Chevillon, 2001. Insecticide resistance in the mosquito Culex pipiens: What have we learned about adaptation? Genetica 112–113: 287–296. [PubMed] [Google Scholar]
- Reboud, X., V. Le Corre, N. Scarcelli, F. Roux, J. L. David et al., 2004. Natural variation among accessions of Arabidopsis thaliana: Beyond the flowering date, what morphological traits are relevant to study adaptation?, pp. 135–142 in Plant Adaptation: Molecular Biology and Ecology, edited by Q. C. Cronk, J. Whitton and I. E. P. Taylor. NRC Research Press, Ottawa, ON, Canada.
- Rivero, A., F. Balloux and S. A. West, 2003. Testing for epistasis between deleterious mutations in a parasitoid wasp. Evolution 57: 1698–1703. [DOI] [PubMed] [Google Scholar]
- Roux, F., and X. Reboud, 2005. Is the cost of herbicide resistance expressed in the breakdown of the relationships between characters? A case study using synthetic-auxin resistant Arabidopsis thaliana mutants. Genet. Res. 85: 101–110. [DOI] [PubMed] [Google Scholar]
- Roux, F., J. Gasquez and X. Reboud, 2004. The dominance of the herbicide resistance cost in several Arabidopsis thaliana mutant lines. Genetics 166: 449–460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saini, H. S., M. Shepherd and R. J. Henry, 1999. Microwave extraction of total genomic DNA from barley grains for use in PCR. J. Inst. Brew. 105: 185–190. [Google Scholar]
- Sauer, S., D. Lechner, K. Berlin, H. Lehrach, J. L. Escary et al., 2000. A novel procedure for efficient genotyping of single nucleotide polymorphisms. Nucleic Acids Res. 28: 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheible, W-R., R. Eshed, T. Richmond, D. Delmer and C. Somerville, 2001. Modifications of cellulose synthase confer resistance to isoxaben and thiazolidinone herbicides in Arabidopsis Ixr1 mutants. Proc. Natl. Acad. Sci. USA 98: 10079–10084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibony, M., and B. Rubin, 2003. The ecological fitness of ALS-resistant Amaranthus retroflexus and multiple-resistant Amaranthus blitoides. Weed Res. 43: 40–47. [Google Scholar]
- Szafraniec, K., D. M. Wlock, P. Sliwa, R. H. Borts and R. Korona, 2003. Small fitness effects and weak genetic interactions between deleterious mutations in heterozygous loci of the yeast Saccharomyces cerevisiae. Genet. Res. 82: 19–31. [DOI] [PubMed] [Google Scholar]
- Weinig, C., L. A. Dorn, N. C. Kane, Z. M. German, S. S. Halldorsdottir et al., 2003. Heterogeneous selection at specific loci in natural environments in Arabidopsis thaliana. Genetics 165: 321–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitlock, M. C., and D. Bourguet, 2000. Factors affecting the genetic load in Drosophila: synergistic epistasis and correlations among fitness components. Evolution 54: 1654–1660. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1929. Fisher's theory of dominance. Am. Nat. 63: 274–279. [Google Scholar]
- Wright, S., 1934. Physiological and evolutionary theories of dominance. Am. Nat. 68: 25–53. [Google Scholar]
- Yang, H.-P., A. Y. Tanikawa, W. A. van Voorhies, J. C. Silva and A. S. Kondrashov, 2001. Whole-genome effects of ethyl methanesulfonate-induced mutation on nine quantitative traits in outbred Drosophila melanogaster. Genetics 157: 1257–1265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You, L., and J. Yin, 2002. Dependence of epistasis on environment and mutation severity as revealed by in silico mutagenesis of phage T7. Genetics 160: 1273–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]