A computerized model for the self—non-self discrimination at the level of the T_h (Th genesis). II. The behavior of the system upon encounter with non-self antigens

Abstract

In the final analysis, the self (S)—non-self (NS) discrimination is regulated by the sufficiency or insufficiency of effector T_h (eT_h) specific for the given antigen. We have described a model (Th genesis) for the origin of eT_h based on an antigen-independent pathway from initial state T_h (iT_h) to eT_h, and on obligatory associative recognition of antigen (ARA) by an iT_h and an eT_h in order for the iT_h to be activated. A computer analysis (referred to as Th genesis) was developed to evaluate this model that is extended here to describe the response to NS antigen. Th genesis fills in the missing element of the two-signal or ARA model for the S—NS discrimination, i.e. the origin of the primer eT_h. The conclusions from this analysis are compared with those of the other models for the origin of eT_h.

Introduction

This paper extends our analysis of a ‘Minimal Model’ (1) for the self (S)—non-self (NS) discrimination (2). Under this model, the S—NS discrimination is determined in the end by the effector T_h (eT_h). The question of the origin of eT_h arises under the Minimal Model in the following way:

1. All cells specifically responsive to antigen are born in an initial state (i-cells) that expresses no effector activity.

2. Upon interaction with antigen via its antigen-specific receptor (Signal[1]), the i-cell differentiates to an anticipatory or a-cell that has two pathways open to it, death or activation to effector. The decision as to which pathway is taken depends on whether or not the a-cell receives a second signal from the eT_h via associative recognition of antigen (ARA). No Signal[2] results in death; delivery of Signal[2] results in activation.

3. As all cells including T_h are born as i-cells, which require Signals([1] + [2]) to be activated, the question arises: where does the ‘primer’ eT_h come from? Clearly, under this model, primer eT_h must arise by a pathway unique to it, referred to here as ‘ Th genesis’.

This pathway must include an antigen-independent step from iT_h → eT_h at a rate slow enough to permit the iT_h →aT_h → death pathway to effectively purge the iT_h anti-S cells. The rate equations and kinetic constants for Th genesis that permit a viable regulation of the S—NS discrimination were derived previously (2). However, the analysis stopped short of a consideration of the behavior of the system when NS antigens are encountered. In order to do this, we must consider the consequence of ARA, which is mediated by what we term the ‘autocatalytic’ step

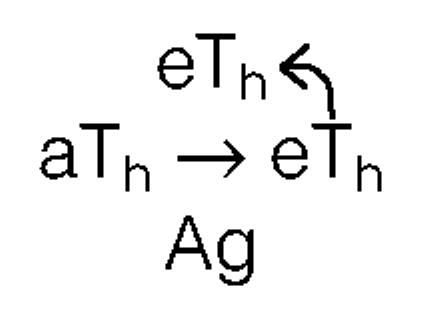and which is initiated by the ‘primer’ eT_h interacting with aT_h on the surface of an antigen-presenting cell (APC).

The pathway of the analysis of Th genesis

Recalling the elements of the model

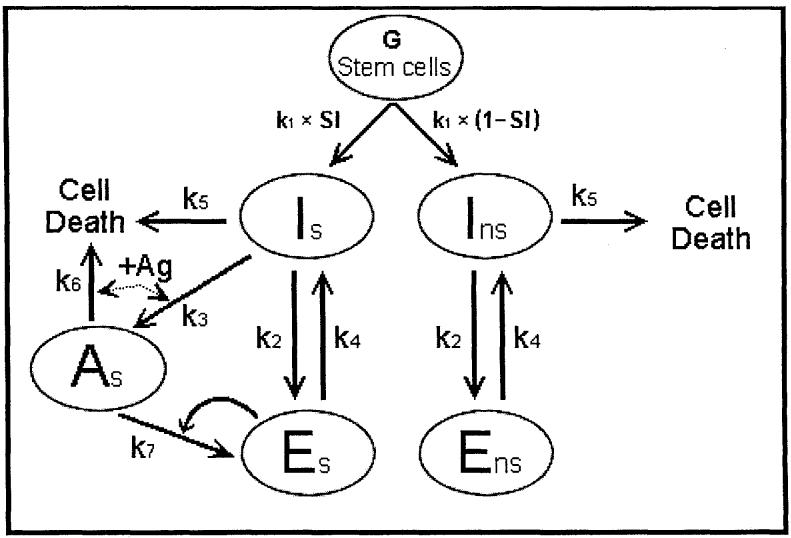
The relationships of the cells in the postulated T_h pathway in the absence of NS antigen are shown in Fig. 1. The previous analysis using rate equations (2) showed that the effective steady-state level of eT_h anti-S (E_s) could be maintained at 10^-2that of eT_h anti-NS (E_ns). This translates into a steady-state level of 0.2 E_s per S peptide (P_s) per T-Protecton (10⁷ cells) and 23 ‘primer’ E_ns per NS peptide (P_ns) per T-Protecton (10⁷ cells). We judged this to be a difference adequate to account for tolerance. However, two questions were left unanswered.

1. Is the steady-state or priming level of E_ns adequate to initiate a sufficiently rapid response to an NS antigen?

2. Given the autocatalytic step, what are the limits to the parameters that would permit a rapid enough response to NS and yet maintain the steady-state level of E_s sufficiently low?

Fig. 1.

The pathway (Th genesis) generating ‘primer’ eT_h in the absence of NS antigen.

While our analysis using rate equations to determine steadystate levels of E_s is adequate because S antigens are always present, it is inadequate for NS antigens, which are transient. This forced another approach, i.e. to model the process using a step-by-step calculation of output as a function of time. The rate equations are evaluated at each transition, the results of which are summed to follow how the system behaves over time. We will refer to this format as the ‘ Th genesis time model’.

The behavior of Th genesis in the presence of NS antigen. The ‘Th genesis time model’ begins by seeding G stem cells that undergo thymic selection and peripheralize with a probability k₁ (equal to the rate constant) to initiate Th genesis. Referring to Fig. 1, the cells are divided into I_s and I_ns by the specificity index (SI), the probability of being anti-S. In the absence of NS antigen, the system reaches a steady state with two components E_s and E_ns of particular interest because the concentration of E_s must be maintained low enough to not be debilitating and primer E_ns must be maintained high enough to initiate a sufficiently rapid immune response to a pathogen. In order to evaluate this, we must set boundary conditions above which E_s/P is defined as debilitating and below which E_ns/P is defined as insufficiently responsive. The values of the rate constants k₁ to k₆ were analyzed previously as being reasonable (2) and this assumption will be reanalyzed here by considering the system in the presence of NS antigen.

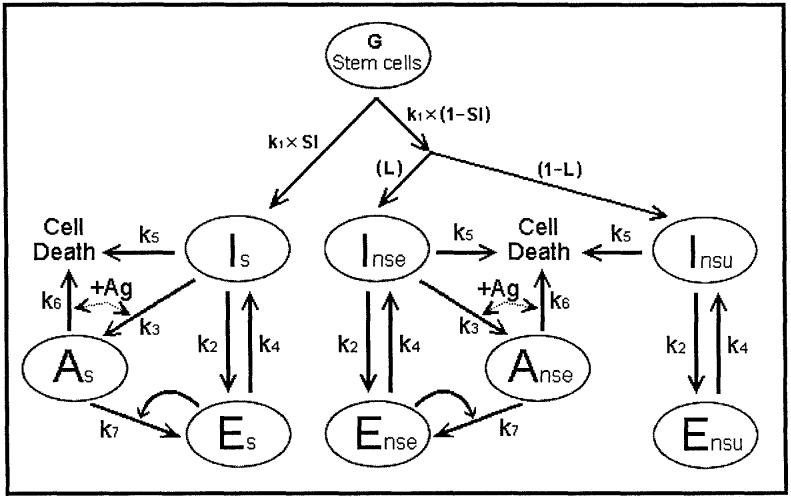
Referring now to Fig. 2, the addition of NS antigen engages a proportion of the repertoire (R) defined as the antigenic load(L). This divides the E_ns population into those cells that are engaged (E_nse) and those that are unengaged (primer E_nsu). These latter are required to initiate the response to a new antigen. The system reaches a steady state, in which two parameters, E_s/P and primer E_nsu/P, will be of interest. When the steady state is attained, NS antigen is added to the system and the time taken to reach various levels of E_nse/P will be examined under a variety of conditions.

Fig. 2.

The pathway after the addition of NS antigen.

Detailing the autocatalytic step. The activation of iT_h (I) on the pathway to effectors (eT_h) is postulated to require an iT_h-APC interaction (Signal[1]) that yields aT_h—APC. The aT_h (A) cannot undergo the antigen-independent step to eT_h (E). The conversion of A to E requires a second signal from an E. This is mediated by an interaction of ARA between A— APC—E permitting the delivery of Signal[2] from E to A. In order to do this, the antigen, defined as a unit of elimination (an eliminon), must be taken up by an APC as a particle or antigen—antibody complex and processed as a unit such that its derivative peptides are expressed on the surface in a ‘signaling patch’. The signal from E toA must be confined to the patch, if ARA is to be mandated (1). Initiating Signal[2] requires the presence of primer E derived by the antigenindependent pathway (Th genesis time model). In sum,

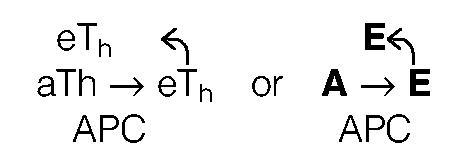described here as the ‘autocatalytic’ step because E, the product, is also the ‘catalyst’.

The problem that arises when analyzing the response to NS antigens

There is at present no unifying theory for the regulation of the magnitude and class of the effector response. Pathogens (NS antigens) infect the host, multiply, are met with an immune response and are ridded. The time course and conditions for this are a bag of variables that behave as singularities: one pathogen—one set of variables. In the case of S antigens, because they are ever present, the system is in a steady state with respect to S. NS antigens are normally ridded, the rules for which are unknown. The treating of NS as unriddable gives a maximum steady-state level of E_nse. This is an interesting number because it also describes the state of the system when tolerance is broken (see Discussion). As evolution is selecting for a response to the limit case, the fastest growing pathogens, it seems reasonable to pose the problem as follows: what is the maximum initial rate of response to NS antigen that still permits an acceptable or minimal steady-state level of response to S antigens?

This requires that we set boundary conditions for the response to S antigen (the autoimmune boundary) and, under these conditions, examine whether the response to NS antigen would be adequate (the immune boundary). Further, we need to consider how the induction of engaged E_nse affects the level of unengaged E_nsu responsible for the response to a new antigen (i.e. the displacement boundary).

Analysis of Th genesis using the time model

Presentation of the analysis

The ‘Th genesis time model’ describes the state of the system as a function of time. It can be accessed on our website (http:// www.cig.salk.edu, click on ‘Th genesis time model’). The system is seeded with iT_h from the thymic output (k₁G, Fig. 2). We begin the analysis in the absence of NS antigen when all components are in a steady state. At this point, our interest will be in the values of E_s/P and E_nsu/P.

The data then will begin with the system in a steady state at time step 1000 when NS antigen is added. We can and will assign real values to each time step to evaluate how reasonable the response is. The initial response, number of time steps to reach 10² and 10³ E_nse/P, will be considered (immune boundary). The effect of the response on E_s/P (autoimmune boundary) and E_nsu/P (displacement boundary) will be evaluated. Beyond this point the computer simulation becomes arbitrary because NS antigen is normally ridded, simulation of which by removing it is of limited heuristic value, but for special purposes (see later) we have added it as an option to our program. Also, the program can be run to consider what happens when NS antigen is not ridded and the response cascades to a steady-state limit. This allows simulation of one pathway to the breaking of tolerance (see Discussion).

The rate constants (k₁ to k₆), the repertoire size (R), the total number of cells in the T-Protecton (T) and the specificity index (SI) were determined previously as reasonable, and will be used as default values (see Fig. 3 or Table 1) to introduce the analysis. The autocatalytic rate constant k₇, the number of divisions of E cells after activation (EDivs) and the number of time steps per division (SEDiv) were added to the previously described program (2) to evaluate the response to NS peptide. The assumption is that, following activation, the E_nse cell divides an average number of times (EDivs). Both EDivs and SEDiv are determined by the operator. For example, at 5 h per time step and 3 time steps per division, the division time would be 15 h.

Fig. 3.

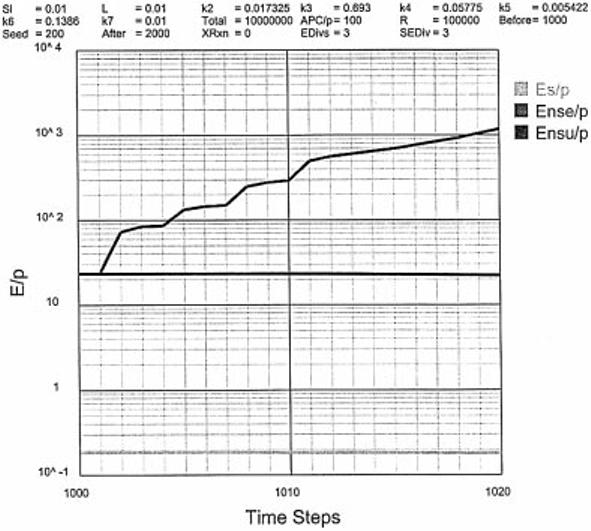
The response to an NS antigenic load as a function of time. The NS antigen is added at time step 1000.

Table 1.

Range of values of parameters that meets boundary conditions starting from default values

	Steps to reach Ense/P equal to
	100	1000
T	7.7 × 106-2 × 107	8.5 × 106-2 × 107
R	5 × 104-1.3 × 105	4.9 × 104-1.2 × 105
T/R	77-200 (the copy number)	85-200
SI	<0.5	<0.5
k7	1.7 × 10-3-8.4 × 10-2	1.7 × 10-3-8.4 × 10-2
APC	24-900	32-950
L	<0.86	<0.076

Boundary conditions: E_s/P ≤ 1, E_nsu/P ≥ 10 and E_nse/P ≥ 10² in ≤5 time steps and E_nse/P ≥ 10³ in ≤20 time steps.

Default values: k₂ = 0.017325, k₃ = 0.693, k₄ = 0.05775, k₅ = 0.005422, k₆ = 0.1385, k₇ 0.01, SI = 0.01, L = 0.01, T = 1 × 10⁷, R = 1 × 10⁵, APC/P = 100, EDivs = 3, SEDivs = 3, k = ln2/t_1/2.

Only the interval between addition of NS antigen (time step 1000) and response reaching E_nse/P = 10³ in ≤20 time steps is being considered above.

The NS antigen is added as an antigenic load (L). L is the proportion of the NS repertoire (R) that is engaged. The system should be able to handle a NS load equal to or greater than the S load (i.e. L≥SI). When SI = L = 1/R the system is responding to a single S and NS peptide.

The boundary conditions

The autoimmune boundary is the level of E_s/P above which a debilitating response to S occurs. A reasonable boundary would be a steady state of ≤ 1 E_s per S peptide per TProtecton (10⁷ cells).

The immune boundary is the level that E_nse/P must reach in a given time if the individual is to be protected against a pathogen. A reasonable boundary would be that ≥ 10² E_nse per NS peptide per T-Protecton must be induced in 1 day if the individual is to be protected from infection. In our analysis we set this boundary at 5 steps using 5 h per step. This results in a 25 h boundary to reach ≥ 100 E_nse/P. Furthermore, we explore a second reasonable boundary, i.e. E_nse/P must reach 1000 in ≤ 20 steps (=100 h) or ∼4 days.

The displacement boundary is the level of E_nsu/P below which the response to a new antigen would be unacceptably compromised. As the total number of cells per T-Protecton (T) is maintained homeostatically, the dividing cells engaged by the antigenic load (L) displace (‘washout’) the unengaged cells, I_nsu and E_nsu. If they are reduced to too low a level, the response to a new antigen would be compromised. A reasonable value for the displacement boundary would be E_nsu/P ≥ 10.

The addition of NS antigen

We begin with a choice of default values that illustrate the system. The time course to the response to an NS antigenic load (L) is shown in Fig. 3. In the absence of NS antigen, a steady-state level of E_s/P = 0.2 and E_nsu/P = 23 is reached, a 10²-fold difference. At time step 1000, a load (L) of NS antigen is added equal to 0.01 and the rate of increase of E_nse/P is graphed. Selecting EDivs = 3 and SEDiv = 3, the number of time steps for E_nse to reach 10² is 4.3 and to reach 10³ is 18.6. Assuming 5 h per time step (i.e. a division time of 15 h), it takes 21.5 h to reach 10² and 93 h to reach 10³ E_nse/P. During this period, E_s/P remains stable at 0.2 and B_nsu/P remains at 23, well within our boundary conditions (i.e. E_s/P ≤ 1, E_nsu/P ≥ 10 and time to reach 10² E_nse/P < 25 h). If the antigenic load (L = 0.01) is not ridded, the system eventually breaches the autoimmune boundary condition, a situation we will deal with later (see Fig. 8).

Fig. 8.

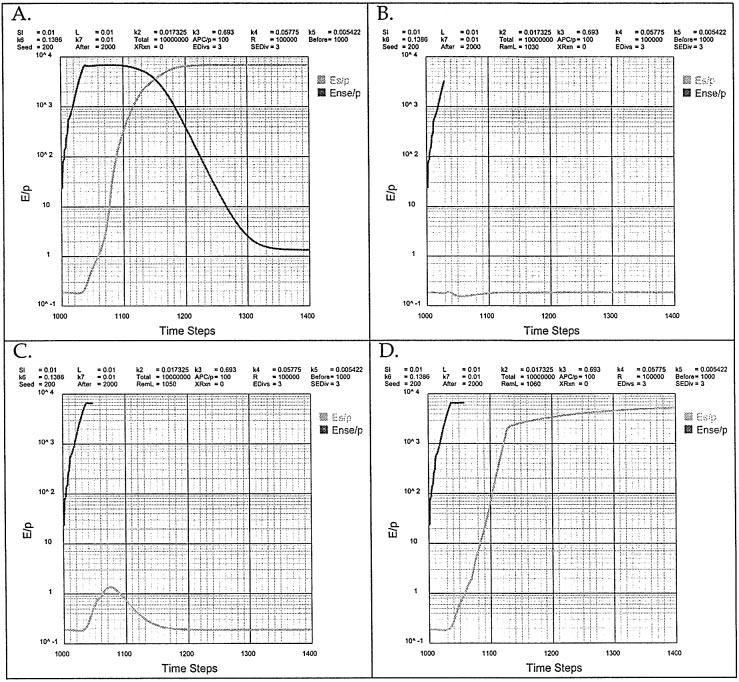
The effect of the removal of NS antigen; simulating the normal response.

The next step is to see how the system behaves as a function of the various parameters. This will be considered with respect to the three boundary conditions.

Figure 4 illustrates the analysis. The values of E_nsu/P and E_s/P are given at the point when E_nse/P reaches 100. Also, the number of steps to reach 100 after the addition of NS antigen is shown.

Fig. 4.

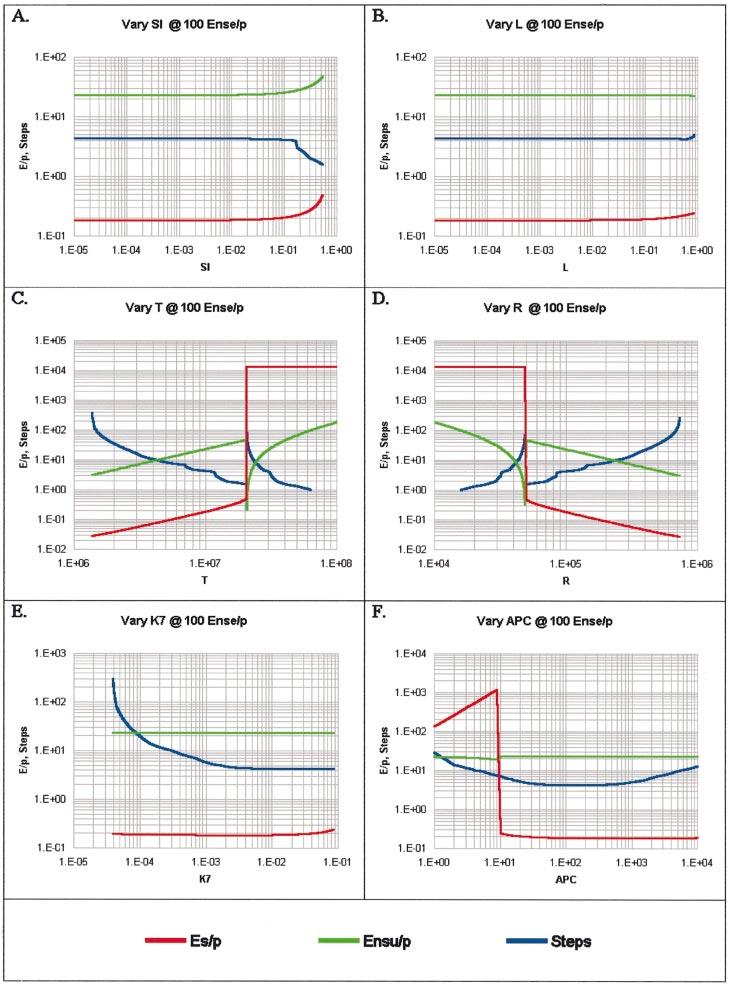
The responses of Th genesis as a function of critical parameters. For default values, see Fig. 3.

As a function of SI, as long as it is <0.1, the E_s/P = 0.2, E_nsu/P = 23 and the number of steps to reach E_nse/P = 100 is 4.3 (Fig. 4A). This is well within our boundary conditions of E_s/P ≤ 1 and E_nsu/P ≥ 10, and, if each time step is 5 h, the E_nse/P reaches 100 in ∼1 day. Values of SI > 0.1 are unrealistic and are ignored. Values of SI < 0.001 are unselectable (2).

Over the entire range of L the values of E_nsu/P and E_s/P are within boundary conditions during the time interval it takes E_nse/P to reach 100 (Fig. 4B). E_nse/P reaches 100 in close to 1 day given 4-5 h per time step.

The relationships as a function of the size of the Protecton (T) and of the repertoire (R) are essentially a reflection of the basic unit of response, the copy number [i.e. the number of cells responsive to a given peptide per Protecton (T)]. The value of T/R (copy number) is only based on recognition of P by a T-Protecton. If restrictive recognition is introduced then the copy number per allele-specific determinant must be considered, but this is not a factor of relevance for Th genesis because the value of E_nse/P is a summation of the number of cells that see a given peptide sequence in any allelic context. The autoimmune boundary, where E_s/P ≤ 1, is satisfied at T < 2 × 10⁷ (Fig. 4C) and symmetrically at R > 5 × 10⁴ (Fig. 4D). At 4.3×10⁶ < T < 2 × 10⁷, E_nsu/P ≥ 10, the displacement boundary is satisfied. Symmetrically at 5 × 10⁴ < R < 2.3 × 10⁵,E_nsu/P ≥ 10. The number of steps to reach E_nse/P = 100 within 5 steps is accomplished at 7.7 × 10⁶ < T < 2 × 10⁷ or 5 ×10⁴ < R < 1.3 × 10⁵, which we take as the immune boundary. In order to meet all three boundaries, 7.7 × 10⁶ < T < 2 ×10⁷ and 5 ×10⁴ < R < 1.3 × 10⁵.

At R = 1 × 10⁵, T > 2 × 10⁷ or at T = 1 × 10⁷, R < 5 × 10⁴,results in a runaway E_s/P response. The reason is that the copy number of E_s/P becomes too high and the autocatalytic activation of I_s → E_s overrides the k₆ pathway to death (Figs 1 and 2). This results in such a large throughput of cells (‘washout’) that there is a sharp increase in the time to reach E_nse/P = 100 breaching the immune boundary and a sharp decrease in E_nsu/P to below the boundary of 10. In sum, evolution had to walk a tightrope. At a copy number of E/P that is too low, it takes too long to respond, and when too high, results in autoimmunity. This, in turn, sets both the size of the Protecton, T ∼ 1 × 10⁷ and the repertoire, R. ∼ 1 ×10⁵.

The autocatalytic rate constant, k₇, must be >1.7 × 10^-3to meet the immune boundary of E_nse/P = 100 in ≤ 5 steps. In the range 1.7 × 10^-3 < k₇ < 8.4 × 10^-2, the boundary conditions of E_nsu/P ≥ 10 and E_s/P ≤ 1 are met (Fig. 4E).

The effect of number of APC presnting a given peptide is dramatic (Fig. 4F). At values of APC per peptide <10, the autoimmune boundary E_s/P ≤ 1 is sharply breached because every E_s is bound as an As—APC—E_s complex undergoing autocatalytic induction. The time to each E_nse/P = 100 is also sharply dependent on the number of APC presenting a peptide. The immune boundary (≤ 5 time steps) is met when 24 < APC < 900. When too few APC present a given peptide the time to reach E_nse/P = 100 is too long, limited by the number of complexes (I_s—APC—E_s) that can form; when too many APC present a given peptide the numbers of E_ns that find themselves on an APC complexed to a corresponding I_ns decreases (see Discussion and Fig. 9).

Fig. 9.

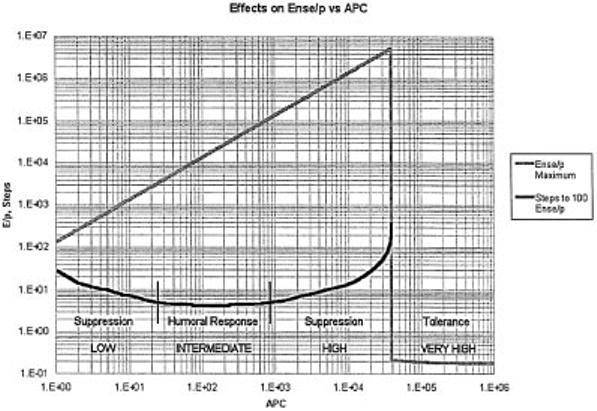
The APC as a determinant of the Mitchison phenomenon. Suppression is dominant (‘positive’) antigen-specific humoral unresponsiveness. Tolerance is recessive (‘negative’) antigenspecific humoral unresponsiveness.

Table 1 summarizes the data in Fig. 4 when E_nse/P = 100, obtained by varying one parameter at a time keeping the other parameters as default values. Any value of SI < 0.1 satisfies the boundary conditions. The ranges within which T (7.7 × 10⁶-2× 10⁷ when R = 1 × 10⁵) and R (5 ×10⁴-1.3×10⁵ when T = 1 × 10⁷) are compatible with the boundary conditions are surprisingly narrow. This translates into a range for the copy number of 77 < T/R < 200. The values of k₇ compatible with the boundaries are quite broad, 1.7 × 10 ^-3 < k₇ < 8.4 × 10 ^-2. The number of APC presenting a given peptide per Protecton (T = 10⁷) is a generally overlooked parameter. To be compatible with our three boundary conditions, it must fall between 24 and 900.

Also in Table 1 is data of a similar analysis to reach 1000 E_nse/P, while maintaining the autoimmune boundary (E_s/P ≤ 1), the immune boundary (E_nse/P ≥ 1000 in ≤ 20 time steps) and the displacement boundary (E_nsu/P ≥ 10). In general, both sets of data have similar values for R, SI and k₇. Under 1000 E_nse/P, however, the minimum Protecton size (T) is increased from 7.7 × 10⁶ to 8.5 × 10⁶, resulting in a corresponding increase in the required copy number from 77 to 85. The range of APC also increased from 24-900 to 32-950 as more A_s—APC—E_s complexes are necessary to have a greater immune response, although the valid range is still broad. At first glance, a load of 0.076 may appear to be small; however, this equates to 1000 E_nse/P for each of 7524 NS peptides [R(1 - SI)L] or collectively 75% of the Protecton. The effect of APC and of L will be dealt with again (see Discussion).

Other views

One of the best ways to appreciate the value of the analysis presented here is to apply the methodology to other models. The competing models for the origin of eT_h have not been formulated in a way that easily permits the type of analysis described here. Several of the competing models are dependent on the presence of antigen to provide attached information (e.g. NS markers like ‘danger’ or ‘pathogenicity’) needed to initiate or prime the formation of eT_h anti-NS. The S antigens are characterized as not having attached to them the additional information needed to induce eT_h. We have argued (3) that a priori considerations render these models unlikely. Nevertheless, analyzing them sharpens the discussion. Common to all of the models [Janeway et al. (4-6), Matzinger et al. (7-9), Fazekas de St Groth (10) and Zinkernagel (11)] is the absence of any role for eT_h in the induction of aT_h to become eT_h. In essence, these models do not finger the eT_h as the critical or final determinant of the S—NS discrimination. Therefore, they allow no distinction to be made between the origin of primer eT_h and the induction of an effective effector level of helpers—they are one and the same event. Bretscher (12), by contrast, postulates a role for eT_h in the induction of iT_h to become eT_h and, consequently, like us has to produce a model for the origin of primer eT_h.

The Matizinger—Janeway models for the induction of eT_h

The two postulates of this class of model are that:

1. All iT_h interacting with APC_t (tolerigenic-only) are deleted (Signal[1]).

2. Those APC_t that have been activated to APC_i (inductiveonly) by interaction with the NS marker [e.g. ‘danger’ (7) or ‘pathogenicity’ (5)], interact with iT_h and induce them to become effectors, eT_h.

As is obvious, the APC_i that provides an antigen-unspecific signal (i.e. co-stimulation) to any iT_h that interacts with it cannot distinguish iT_h anti-S from iT_h anti-NS. Both would be induced to eT_h. Aware of this problem, basically two different solutions were proposed.

First, there is the solution offered by Medzhitov and Janeway (6) that the APC itself makes a S—NS discrimination. They suggest that APC_t when activated to APC_i cease antigen uptake. Therefore, they argue that ‘by becoming nonendocytic after their activation, dendritic cells (APC_i) may be prevented from taking up and presenting S antigens that are not involved in thymic deletion, at the times when they express co-stimulatory signals’. This effectively makes the APC_i responsible for making the S—NS discrimination by virtue of the APC_i being able to present NS, but not S, thereby ignoring iT_h anti-S.

In a similar vein, Fazekas de St Groth (10) proposes that ‘the distinction between foreign and S antigen is a germlin-eencoded property of two subsets of antigen-presenting cell... the lymphoid [LDC] and myeloid [MDC] dendritic cells which induce tolerance and immunity respectively’. This assumption makes it a variant of the Janeway model because it requires that LDC present S antigens only and MDC present NS antigens only. We view as untenable the Janeway—Fazekas assumption that the APC or dendritic cells make a S—NS discrimination.

The Fazekas model differs from the Matzinger model in that the tolerigenic-only APC_t (LDC) and the immunogenic-only APC_i (MDC) are different cell lineages not convertible by NS ‘danger’ from one to the other. The Fazekas model as published (10) leaves unanswered how LDC manage to present exogenous S and not NS or how the MDC manage to present exogenous NS and not S.

Second, Matzinger (7,8) attempts to deal with this problem by introducing a set of assumptions based on the separation of S and NS in ‘space’ (13). The space in question is one where non-activated (tolerigenic-only) APC_t present S only (S—APC_t). Interaction of iT_h anti-S with S—APC_t is postulated to lead to deletion of the cell (Signal[1]). Inducible-only APC_i are activated by NS (the NS marker is ‘danger’) to present both S and NS (S—APC_i—NS). Then, in a key departure from the other emodels, interaction of iT_h anti-S or iT_h anti-NS with S—APC_i—NS results in their differentiation to eT_h anti-S and eT_h anti-NS respectively. There is competition between S—APC_t (tolerigenic-only) and S—APC_i—NS (inducible-only) to regulate the level of eT_h anti-S. The Matzinger proposal can be summarized along the lines that inactivation versus activation of extrathymic iT_h depends on the ratio of S—APC_i—NS/S—APC_t. In the absence of NS antigen this ratio is zero, thus favoring inactivation of the iT_h anti-S. However, in an infected enclave where most S—APC_t would be driven to S—APC_i—NS by ‘danger’, the ratio would be high, favoring induction to eT_h of all iT_h that interact with the S—APC_i—NS. Here the ability to distinguish S from NS decreases.

These three models are compared in Table 2.

Table 2.

A comparison of three variations of a ‘space’ model

Matzinger	Fazekas de St Groth	Janeway
S-APCt (tolerigenic-only)	S-LDC (tolerigenic-only)	S-APCt (tolerigenic-only)
↓ ‘Danger’	+	↓ ‘Pathogenicity’
S-APCi-NS (immunogenic-only)	NS-MDC (immunogenic-only)	NS-APCi (immunogenic-only)
Response to S is a function of the ratio S-APCi-NS/S-APCt	S-NS discrimination is germline encoded	APC presents either S or NS; therefore, response is all or none

The Matzinger model analyzed by the simulator

The Matzinger proposal (7-9) can be reformulated by analogy with the Minimal Model (Fig. 5) so that it can be transformed into the simulation tool. The APC_t that are not activated, only present S. The interaction of I_s with S—APC_t leads to death at a rate k₃. The APC_i are activated, and present both S and NS. Interaction of an i-cell with S—APC_i—NS, whether I_s or I_ns, leads to induction to the e-state, E_s and E_ns, at a rate k₂.

Fig. 5.

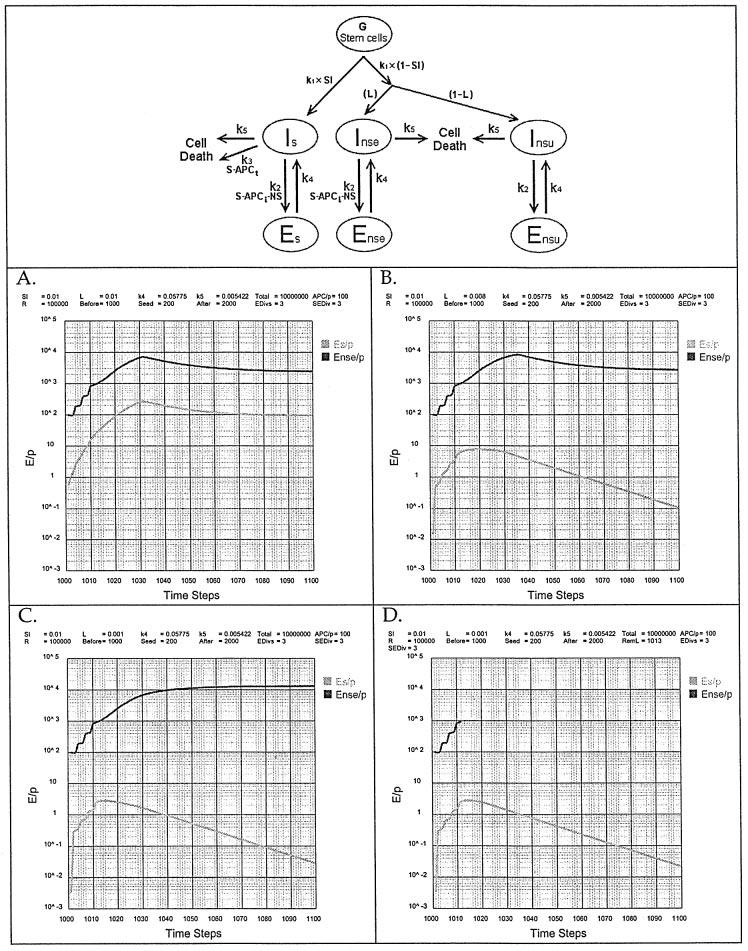
Simulation of the Matzinger ‘space’ model by translation into the Th genesis format.

The anticipatory a-state is not part of this model because ARA is not postulated to be required at the level of induction of eT_h, only at the level of iB and iT_c where an a-state would be required. The rate of antigen-driven inactivation (k₃) must be slow enough (t_1/2 > 5 h, k₃ < 0.1386) to allow the iT_h-APC_i inductive interaction to occur before the irreversible consequences of Signal[1] sets in.

A special subprogram of ‘Th genesis time model’ was written to simulate these conditions (http://www.cig.salk.edu, click on ‘Th genesis Matzinger’).

Prior to the appearance of NS, the Matzinger model would have E_s/P = E_ns/P = 0. The reason is that, under the Matzinger model, there are no immunogenic APC_i in the absence of ‘danger’ (prior to the encounter with NS), only tolerigenic APC_t. As the distributions of P_s are the same for APC_i and APC_t, one can treat the competition between P_si and P_st as a consequence of the ratio APC_i/APC_t. The totality of the P_s repertoire is presented by the total APC population per Protecton (T). The program (Th genesis Matzinger) calculates as a function of steps (time) the induction of E_ns/P and E_s/P. This is illustrated in Fig. 5(A). When L = SI the system breaches the autoimmune boundary of E_s/P ≤ 1. If L is reduced to 0.008 then E_s/P = 9, significantly above the autoimmune boundary (Fig. 5B). Reducing the value of L ≤ 0.001 [i.e. a load of <100 NS peptides (Fig. 5C)] the value of E_s/P = 3, somewhat above the autoimmune boundary. If antigen is removed (RemL = 1013) when E_ns/P reaches 10³, it takes 20 steps (∼100 h) for E_s/P ≤ 1 (Fig. 5D). This might be taken as an acceptable level of autoimmunity, but the inability to handle a load (L) equal to or greater than the S load (SI) is not acceptable. We conclude, therefore, that, in addition to our other arguments (3), the assumption that maintaining the S—NS discrimination by competition between tolerigenic-only APC_t and inductiveonly APC_i is untenable.

In sum, Janeway is telling us that there are two classes of APC, one that is tolerigenic-only, S—APC_t that are not activated and one that is immunogenic-only, NS—APC_i that are activated. Matzinger differs in that the activated immunogenic-only APC_i present both S and NS. Janeway makes the S—NS discrimination a property the APC itself, whereas Matzinger maps the S—NS discrimination onto the ratio of S—APC_i—NS/S—APC_t. Both the Matzinger and Janeway models allow for an everchanging S because a germline selected recognition of an NS marker is postulated. The Fazekas model leaves us with a quandary on this point because in the absence of an NS marker, an everchanging S is indistinguishable from an everchanging NS. Consequently, the Fazekas model requires a non-changing or static S targeted to recognition by LDC that can present all S, but no NS. Until a mechanism that makes this possible is proposed, this has no place to go.

We have argued (1,3,13-15) that germline-selected NS markers like ‘danger’, ‘pathogenicity’ and ‘localization’ cannot regulate in an antigen-specific way, a S—NS discrimination determined by a somatic selection process. As the somatically selected S—NS discrimination of immune systems cannot be based on recognition of a physical or chemical property of antigens that divides them into S or NS as classes and because germline-selected recognitive elements have different specificity profiles from the somatically selected recognitive elements (BCR/TCR), the APC, no matter what germlineselected recognitive property that they are endowed with, cannot determine a somatically selected S—NS discrimination. Were it to be experimentally established that the immune system views the S repertoire of an individual as everchanging, then the Th genesis and ARA models as presented here would be disproven; a static S would make germline selected NS marker models gratuitous.

The Bretscher solution

Bretscher (12) postulates that, around birth, when NS antigens first enter the system, there is a window when iT_h cells are endowed with a ‘basal eT_h activity’. This does not distinguish basal eT_h anti-S from basal eT_h anti-NS. To make this distinction, he argues that ‘the greater number of cells specific for a foreign than a S antigen could allow the foreign but not the S antigen to generate some eT_h cells’. Having generated some eT_h cells anti-NS, then `the continuous presence of an appropriate variety of foreign antigens and spectrum of pT_h (iT_h) cells’ would ‘yield a wider spectrum of eT_h cells...’, a phenomenon referred to as epitope spreading.

This model has been discussed in some detail in a forumtype publication (16). Nevertheless, the small differences between the Bretscher model and Th genesis are worth highlighting.

First, the requirement for ARA is solved differently. Bretscher proposes an elegant solution, i.e. that the B cell acts as an APC for T_h. In this way the peptides derived from a single antigen (anything linked to a given epitope) participate in the aT_h—B—eT_h interaction. While there are a priori limitations to this suggestion, we consider the evidence that B-less or Igdeficient individuals respond normally in the cell-mediated class to show that B cells (if they function in this capacity at all) are not the sole APC for T_h-cells. The APC (non-B) then, must have a mechanism to permit ARA and we suggested the concept of a unit of elimination (antigen—antibody complex, a particle, innate receptor-mediated uptake, etc.) referred to as an eliminon that is processed into a signaling patch [see Discussion (16) and above, ‘Detailing the autocatalytic step’].

Second, the only interpretation of ‘basal activity’ that makes sense is that a proportion of the iT_h population can be converted to eT_h while in the window. This means that the cell population under the Bretscher model prior to the introduction of NS antigen can be treated as similar to that described under Th genesis.

The window during which iTh is converted antigen independently to eT_h is the fundamental difference. When the window closes, the NS antigen-driven population of eT_h must be maintained throughout life by induction in order to prime or initiate responsiveness to any new antigen. This is a recipe for the breaking of tolerance, as ∼10% of NS antigens cross-react with S (share epitopes with S). The antigen-independent pathway keeps this eT_h anti-NS population at a minimum or priming level that acts autocatalytically to initiate induction of aT_h (see Discussion and Fig. 7). Under the Bretscher proposal, eT_h is maintained by immunogenic encounter at an effective effector level. Further, as NS is, in large measure, transient, the composition of the eT_h anti-NS pool will be discontinuously everchanging, leaving holes that affect responsiveness to new antigens. There is no way to maintain the eT_h repertoire complete enough to function at any moment in time to any antigen. We, therefore, do not see how ‘the priming problem may be reduced to understanding the origin of a few eT_h cells neonatally’ because the primary response must be adequate for any antigen throughout life. For every epitope seen by an iT_h anti-NS, there must be an eT_h anti-NS able to activate it by ARA. Interestingly, after the window closes, the eT_h anti-S would become non-existent and iT_h → aT_h → death would be the only pathway for iT_h anti-S. For iT_h anti-S the sole way to divert them to eT_h anti-S would be by response to an NS antigen that shares epitopes with S. If an animal were free of NS antigen for a period after the window closes, it would be forever unresponsive to all eT_h-dependent antigens.

Fig. 7.

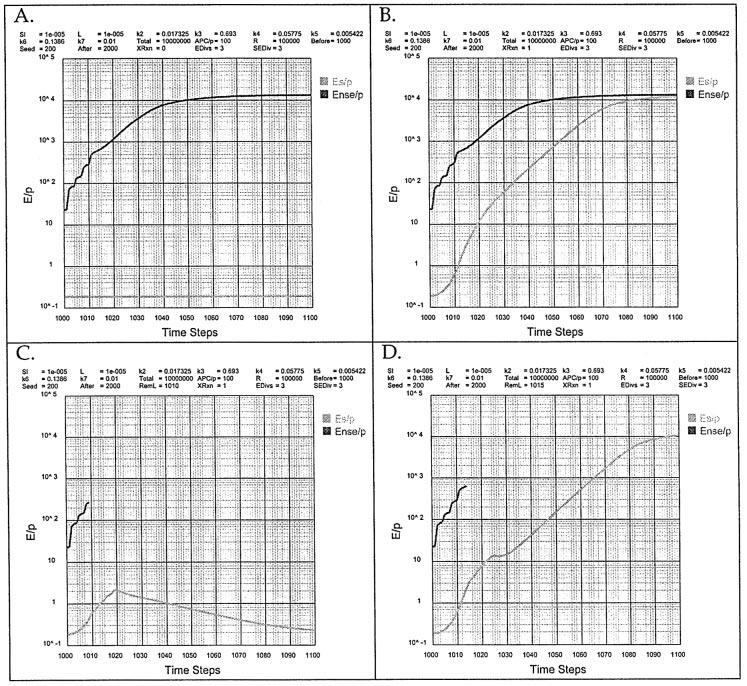
The breaking of tolerance by an NS antigen that shares epitopes with S.

It is possible to transform the Bretscher model into the Th genesis format, but the eT_h pool would no longer be dependent on an open then shut window within which iT_h cells are endowed with basal eT_h activity; rather the window would remain open throughout life. This possible transformation would make the model no longer competing as an alternative to Th genesis because it would eliminate the need to maintain the priming eT_h by immunogenic encounter.

The Zinkernagel solution

Zinkernagel (11) challenges us to unravel the Gordian knot with the stroke of a sword by proposing a disarmingly simple mechanism for the S—NS discrimination. He postulates that iT and iB cells are inducible-only. Upon interaction with antigen, S or NS, they become effectors, eT or eB. These effectors have a short half-life. The distinction then between the induction of anti-S and anti-NS i-cells depends entirely on the initial frequency of the i-cells interacting with a given antigen. If the frequency of anti-NS were sufficiently low, then the effector response would be ineffective and, if anti-S, would be non-debilitating. If the frequency of anti-NS were sufficiently high, then the effector response would be effective and, if anti-S, would be debilitating. T_h are not involved in the S—NS discrimination; they function elsewhere. In fact, Zinkernagel views this simple model as obviating the need to postulate any form of ‘regulatory’ cell, developmental time window, or decision step determining whether a T or B cell should be turned on or off. Interaction with antigen acting as an ‘on’ signal and a short-lived effector is all that is required. Can such a model account for a S—NS discrimination?

The frequency of antigen-unselected or newborn i-cells specific for any given S or NS component (in this case, peptide) is the same. In order for this model to work, a mechanism to decrease the copy number of i-cells specific for a given S antigen and to increase the copy number of i-cells specific for a given NS antigen must operate. This requires a developmental time window during which only S antigens are present. Adding this modification to the Zinkernagel model, then, as i-cells anti-S arise, they undergo exhaustive differentiation to effectors and to death, never attaining a debilitating effector level. As S is prior and persistent, the steady state of induction of anti-S effectors at an ineffective level is maintained. During this period in the absence of NS, anti-NS i-cells accumulate to a sufficiently high steady-state level limited by the size of the repertoire and the Protecton. It seems, therefore, that a developmental time window is unavoidable. The question then is what would be the characteristics of the response when NS is introduced? We will simulate this model using the T_h as an example but the results are generalizable to any cell type. This can be done using the Th genesis time model by setting k₂ = 0, k₄ = 0, k₇ = 0, EDivs = 0 and SEDiv = 0, leaving k₅ = 0.0054, R= 10⁵ and T= 10⁷. The Zinkernagel model is best illustrated using the response to one peptide, S and NS by setting SI = 10^-5and L= 10^-5(i.e. 1/R). The variables then are k₃ and k₆ because the response is essentially independent of any contribution by EDivs and SEDivs. This modification isolates the pathway I → k₃ → A → k₆ → death (Fig. 2), which is equivalent to Zinkernagel's I → k₃ → E → k₆ → death. In other words, A becomes equivalent to E.

Referring to Fig. 6, with k₃ maximized at 0.99 and k₆ = 0.6, E_s/P = 0.9 just within the autoimmune boundary (E_s/P ≤ 1). At values of k₆ < 0.6, the autoimmune boundary is breached (E_s/P > 1). At k₃ = 0.99, the conversion of I to E rapidly reaches a maximum at E_ns/P = 10² in 1 time step and then falls at a rate dependent on k₆. Since k₆ must be ≥ 0.6, the E_ns/P level falls from 10² to a background level of 1 in 8 time steps or at 4-5 h per step, in 32-40 h. If k₃ is reduced, with k₆ = 0.6 then the maximum E_ns/P falls rapidly from 10² to 10¹ at k₃ = 0.1. No condition can be found under which a reasonably sustained response, E_ns/P ≥ 10² and E_s/P ≤ 1 exists. As described then (11), this simple formulation cannot meet the boundary conditions for a viable S—NS discrimination.

Fig. 6.

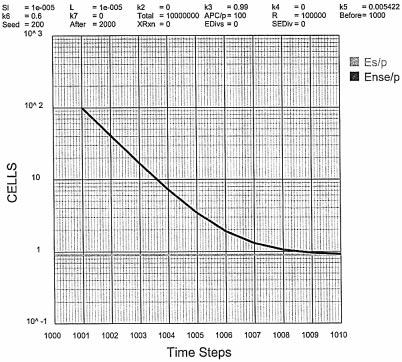
Simulating the Zinkernagel `exhaustive differentiation' model.

Discussion

The role of co-stimulation

We feel impelled to deal with this subject because the phenomenon of co-stimulation is being introduced without justification at the level of the S—NS discrimination. In essence, for the induction of iT_h to eT_h, the role of ‘co-stimulation’ is presented as follows.

Under the Matizinger—Janeway view, co-stimulation solves ‘the primer problem’ by totally rejecting the requirement for ARA at the level of the induction of iT_h. However, since the APC cannot make a S—NS discrimination, the sorting of the T_h repertoire has to be carried out independently, making costimulation irrelevant to the S—NS discrimination (i.e. the sorting of the paratopic repertoire). Under the Bretscher view, ARA is a strict requirement at the level of induction of iT_h and therefore he adds ‘co-stimulation’ as a proliferation signal for aT_h on the pathway to inactivation, in order to solve a ‘scarcity problem’ believed to arise when aT_h are diverted by eT_h to activation. We agree with Bretscher that ARA is a requirement at the level of activation of aT_h and, therefore, we put the phenomenology of co-stimulation at the level of Decision 2, the regulation of the class and magnitude of the effector response, not at the level of Decision 1, the S—NS discrimination. Given Protecton theory, Bretscher's ‘scarcity problem’ needs quantitation as i-state cells are in high enough copy number to be activated without the necessity for a ‘costimulatory’ amplifying step on the pathway to tolerance. The requirement that the anti-S cells be amplified prior to deleting them is a corollary of the necessity to amplify anti-NS cells (putatively scarce) prior to activating them. Without this assumption there would be no evolutionary rationale to amplifying the pool of anti-S cells prior to deleting them.

The term ‘autoimmunity’

There are many ways in which the immune response can be turned self-destructive. Zinkernagel et al. (17) has made a compelling case for immunopathology being at the origin of what is often termed ‘autoimmunity.’ The classical example is a non-cytopathic virus such as LCMV, which would not be detected by outward appearance in mice infected in utero, but if an LCMV carrier is given immune spleen cells, the carrier dies of an overwhelming immune response directed to its own tissues. However, this is easily dismissed as not being ‘autoimmunity’ because we know the virus and the entire history of the phenomenon. If the virus were not known and if an immune response developed by a pathway other than the injection of anti-viral immune cells, then deciding whether this is true autoimmunity or unknown immunopathology is all but impossible.

‘Autoimmunity’ arises in response to a S component in an individual that would normally be unresponsive. Autoimmunity implies the breaking of tolerance. ‘Immunopathology’ arises in response to a NS component in an individual that would be normally responsive. The consequence in both cases is a debilitating effector activity, but the initiation of autoimmunity requires an additional step, i.e. the breaking of tolerance. When the S—NS discrimination mechanism breaks down, as is statistically inevitable, the most likely time would be within the youthful years for a human and it is unlikely to be the slow or chronic relapsing disease that is observed in post-reproductive individuals. It might be well to recall that natural selection is operating to keep the frequency of breakdown of the S—NS discrimination acceptably low, but it only operates prior to the termination of procreation. The term ‘autoimmunity’ has been generally applied to chronic diseases with an onset that is past the reproductive age and when natural selection is no longer operative. Thus, we are reluctant to confuse the kind of selfdestruction that arises from a breakdown of the S—NS discrimination with other pathways that lead to immune selfdestruction.

The S—NS discrimination

In our view, the mechanism of the S—NS discrimination is dependent, in the last analysis, on the sufficiency or insufficiency of effector T_h specific for the antigen. Today, aside from Bretscher (12) with whom we agree, this postulate has little favor. We have argued here and elsewhere (3,13,15,18) that the numerous competing assumptions are untenable. Here we would like to discuss experimental data supporting our view. To our knowledge, there is an absence of evidence opposing it.

The two postulates, an antigen-independent pathway to generate ‘primer’ eT_h anti-NS and obligatory ARA for the activation of the aT_h receiving Signal[1], are what makes the Th genesis model unique.

Is there a hint of an antigen-independent pathway to effector T_h? Lafaille et al. (19) generated a transgenic mouse expressing a single TCR specific for a class II restricting element (RII) and a peptide from myelin basic protein (MBP). This mouse develops an autoimmune encephalitis in 100% of cases in 12 months, 80% of cases in 4.5 months and detectable onset in 1.5 months. As these cells are peripheralized as iT_h anti-MBP without effector activity, what kind of a scenario can be envisaged that induces them to become effectors. The target MBP is in an organ sequestered behind the blood-brain barrier. This suggests the following scenario. The iT_h peripheralize in the absence of MBP and undergo the antigen-independent pathway to produce eT_h anti-MBP. These latter open the blood-brain barrier to iT_h by an effector attack on the endothelial cells of the blood-brain barrier presenting MBP and permit exposure to brain MBP as a NS antigen. This initiates the autocatalytic aT_h-APC-eT_h reaction resulting in an effective immune attack on MBP-expressing glia. It is because the total T_h cell population is specific for MBP that one sees a dramatic onset of disease. This is an experiment that should be repeated with a TCR without anti-‘S’ reactivity (e.g. anti-H-Y in females) and the unselected eT_h levels derived by the antigen-independent pathway measured directly.

Is there any evidence hinting the existence of an aT_h-APC-eT_h interaction? The evidence for an aB-eT_h and an aT_c-APC-eT_h interaction for activation is strong; in fact, unquestioned. However, at the level of the regulatory T_h itself, there are few studies. Bretscher et al. (20,21) were the first to address this question. They showed that ARA by an effector T_h and an aT_dh (dh = delayed hypersensitive) cell was required for the induction of an effective level of delayed hypersensitive effectors. These studies (20,21) were confirmed and extended in a somewhat different context by Zanetti et al. (22) who showed that the aT_h-eT_h interaction occurred on an APC, a detailed proposal for which has been made by den Haan and Bevan (23). Consequently, today we would equate iT_dh with iT_h1 cells, and place the interaction of ARA between iT_h1 and eT_h on an APC. The ‘regulatory’ iT_h that undergo the antigen-independent pathway, as a reasonable guess, are iT_h0.

Under what conditions can tolerance be broken at the Th level? In order to convert an S antigen into an NS antigen, the eT_h anti-S must be induced to a level that makes their production autogenerative. Basically there are two pathways to autoimmunity.

The first and most obvious pathway is the breaking of tolerance by an NS antigen that shares peptides with S. In this case the autoimmunity would be specific for the shared epitope. This can be simulated by Th genesis as follows:

The Th genesis program has as one of its options the analysis of the response to NS antigens that share epitopes (peptides) with self. This option is exercised by answering ‘yes’ to ‘E_nse and A_s interact in linked recognition (k₇)?’. The effect is best illustrated by considering one S antigen and one NS antigen that share a peptide (Fig. 7). In the absence of the cross-reaction (Fig. 7A), the E_nse/P rises to a steady state at ∼10⁴, while the E_s/P remains below the boundary condition at 0.2. If the NS antigen cross-reacts with the S antigen (Fig. 7B) the E_s/P level rises rapidly to the steady-state level of the E_nse/P at 10⁴, clearly an autoimmune state.

Given that NS antigens that share determinants with S are not uncommon, why is autoimmunity not a common event? One reason is that the NS antigen is ridded. This can be simulated in Th genesis by removing the NS antigen. If it is removed at time step RemL = 1010 (Fig. 7C) then the E_s/P rises to a maximum of 2 and falls steadily to background at ≥ 1. This might be viewed as limited, but acceptable, autoimmunity. If the NS antigen is removed at time step RemL = 1015 the E_s/P cascades out of control (Fig. 7D). The timely ridding of NS antigens that cross-react with S is critical.

The second way is the breaking of tolerance by too high an antigenic load that is not riddable. Normally NS antigens are ridded and any debilitating surges in the response to S antigens would be evanescent, and, in large measure, dependent on whether or not the target is self-renewing or not.

Here the autoimmunity will be generalized, visible clinically as directed to the most vulnerable target. No sharing of epitopes with S is required.

Central to the problem of breaking tolerance as well as choice of the autoimmune boundary is the question ‘how many E_s/P are permitted before the autocatalytic reaction (k₇) outcompetes the death pathway (k₆) resulting in autoimmunity?’. We added as an option to the Th genesis time model the effect of artificially adding E_s (option C in the program). This allows a test of how close one is to breaking tolerance under any given set of acceptable conditions. In the absence of an NS load (L = 0) E_s/P > 5 artificially added will cascade the E_s response to a maximum. This is to be compared with an autoimmune boundary of E_s/P ≤ 1.

Another way to illustrate the effect of antigenic load (L) is to consider the standard conditions. Up to this point we have only examined the initial steps of the response to NS antigen when E_s/P ≤ 1 (Fig. 3). Normally the NS antigen is ridded before autoimmunity ensues. This can be simulated by artificially removing the antigen and analyzing the resulting behavior (Fig. 8). The conditions are those used in Fig. 3 where the response is illustrated up to time step 1020 when E_nse/P reaches 10³. Under these conditions if antigen is not ridded, then the autoimmune boundary of E_s/P ≤ 1 is eventually breached (Fig. 8A). If the antigen is removed when E_nse/P = 3000 (time step RemL = 1030), the E_s/P reemains at 0.2, well below the autoimmune boundary (Fig. 8B). Removal of NS antigen when E_nse/P reaches its maximum value of 6000 at time step RemL = 1050 results in an evanescent breach of the autoimmune boundary (Fig. 8C). However, if NS antigen is removed when E_s/P = 1, at time step RemL = 1060, then E_s/P cascades out of control (Fig. 8D).

To put some limits on this pathway to breaking tolerance, at k₇ = 0.003, a minimum value that meets the boundary conditions, L ≤ 0.0016 is the maximum permissible unriddable load; at k₇ = 0.01, L ≤ 0.0008 is the maximum unriddable load. As an example, for housekeeping antigens which are continuously being generated and ridded ( equivalent to unriddable), tolerance at the T_h level would be broken (i.e. E_s/P > 1) at loads >160 immunogenic autogenously generated peptides being presented in a steady state. Further, each peptide must be presented by APC ≤ 10² per T-Protecton. This assumes no antigen-specific feedback controls, which, of course, are likely to exist. ‘Suppression’ is optimally understood in this context (see Discussion and Fig. 9).

Under what conditions can one establish tolerance after the immune system is mature (i.e. in the presence of ‘primer’ eT_h)? establishing tolerance in the embryo is equivalent to maintaining tolerance in the adult. In both cases the i-cells encounter antigen (Signal[1]) in the absence of eT_h. However, establishing tolerance in an adult requires dealing with an effective priming level of eTh specific for the test antigen. Mitchison established the basic phenomenon of low/high zone unresponsiveness separated by intermediate zone responsiveness in adults. Today, we know that at low doses of antigen, suppression of a humoral response is induced (dominant humoral unresponsiveness is not ‘tolerance’); at intermediate doses of antigen, a ‘ridding’ humoral immune response is evoked; at high doses of antigen, suppression is once again induced; and at very high doses negative unresponsiveness (‘tolerance’) can sometimes be established. The first-order guess is that when the effective eT_h level is below a given threshold for a long enough period, the system responds in the cell-mediated class with suppression of humoral responsiveness (24,25). When the eT_h level is ‘zero’, tolerance is the result. The Mitchison phenomena is a property of the ARA on an APC. At low dose, few APC present the antigen and the rate at which aT_h is autocatalytically converted to eT_h is adequate for induction of suppression, but too low for a humoral response. At intermediate dose the APC/P is optimal for an aT_h—APC—eT_h interaction and a humoral response is evoked. At high dose when many APC present antigen, the probability of an iT_h and an eT_h specific for that antigen finding themselves on the same APC is low, once again favoring suppression. As the dose increases to a very high level, the iT_h—APC—eT_h interaction of ARA becomes vanishingly small, resulting in tolerance. To illustrate this we consider 1 NS peptide (L = 1 × 10 ^-5). The dose translates into number of APC presenting a peptide from the experimental NS antigen. Referring to Fig. 9, if no feedback suppression were operative, the maximum steady-state level of E_nse/P increases with number of APC presenting the peptide until at a critical level, APC/P ≥ 4 × 10⁴, the response drops to background (E_nse/P = E_s/P = 0.2), the state of ‘tolerance’. Given this insufficiency of eT_h, all effector classes, suppression included, become unresponsive (‘tolerant’).

Considering now the time steps to reach E_nse/P = 100, in the intermediate range (24 < APC/P < 900) the number of steps to reach Ense/P = 100 is less than 5 (4-5 h per step, ≤1 day). This range permits an optimal humoral response and absence of suppression. The longer it takes for E_nse/P to reach 100, the higher the level of induced suppression. For example, if suppression were maximum when the number of time steps to reach E_nse/P = 100 was ≥ 10 (50 h) then at APC/P < 5 or APC/P > 5 × 10³ no humoral response would be induced. This is lowand high-zone dominant humoral unresponsiveness. When APC/P > 4 × 10⁴ there is a sharp shift from dominant unresponsiveness (regulation of effector class) to recessive unresponsiveness (S—NS discrimination, tolerance). In essence, establishing unresponsiveness in adults is equivalent to a titration of the ‘primer’ E_ns derived from the antigenindependent pathway resulting in different outcomes. The rule is that establishing unresponsiveness in the embryo (insufficiency of eT_h) is antigen dose independent, while in the adult (sufficiency of eT_h) unresponsiveness is antigen dose dependent. Maintenance of unresponsiveness (once an insufficiency of eT_h is established) is antigen dose independent. Of course, the terms, antigen dose dependence and independence only apply above the threshold concentration that is detectable as a signal by the cell.

The take-home lesson is that establishing antigen-specific tolerance in adults without having to create a window of total unresponsiveness (i.e. reinventing an eT_h-deficient embryo) is well nigh impossible given the antigen-independent pathway. The only practical way that comes to mind would be to present the given ligand, RII-P, in a way that does not permit delivery of Signal[2]. This might be accomplished by use of an (RII-P)_n polymer or by presenting RII-P on a cell unable to allow ARA. The iT_h that interact with such a cell would be deleted and the ‘primer’ eT_h would be eliminated by reversion to iT_h, which, in turn, would be purged. Such an obligatorily tolerigenic cell might be a fibroblast or a muscle cell, a non-professional APC, or a professional APC chemically or physically inactivated.

The antigen-independent pathway to produce ‘priming’ levels of eT_h anti-NS has been discussed in various formats since 1983 (26,27). The Th genesis model, as presented here, supercedes all previous versions.

Abbreviations

APC

antigen-presenting cell

ARA

associative recognition of antigen

aT_c

anticipatory cytotoxic T cell

aT_dh

anticipatory delayed hypersensitive T cell

aT_h(A)

(A) Anticipatory T_h

E_ns

Effector T_h anti-non-self

E_nse

Effector T_h anti-non-self engaged by antigen

E_nsu

Effector T_h anti-non-self unengaged by antigen

E_s

Effector T_h anti-self always engaged by self

eT_h(E)

Effector T_h

iT_h(I)

Initial state ‘antigen-responsive’ T_h

LDC

lymphoid dendritic cells

MBP

myelin basic protein

MDC

myeloid dendritic cells

NS

non-self

P

peptide

P_ns

non-self peptide

P_s

self peptide

R

size of paratopic T cell repertoire

RII

class II restricting element encoded by the MHC

S

self

T

total number of cells per T-Protecton

Computer program abbreviations

After

number of time steps to simulate after NS antigen is added

Before

number of time steps to simulate before addition of NS antigen

EDivs

number of divisions of newly induced E_nse

RemL

remove NS antigenic load (L) at indicated time step

SEDivs

number of time steps per division

Seed

number of time steps to grow or seed the simulator from 0 to the total simulation size (T)

Total

T(above); total cells per Protecton

XRxn

NS antigen shares epitopes with S; 0 = no, 1 = yes

Addendum

After this paper had been submitted, an important study appeared (28) that raised questions in the minds of reviewers about the validity of the assumptions upon which the model for the S—NS discrimination analyzed here are based. The referees asked that these assumptions (2,27,29-33) be succinctly restated and commented upon in the light of these new findings.

Some background and the assumptions

The effector response of the adaptive immune system to an antigen involves two different decision steps: (i) The S—NS discrimination, and (ii) the determination of the magnitude and class of the effector response. These two decision steps are characterized in the appended Table 3.

Table 3.

The characteristics of the two decision steps taken by the immune system in response to an antigen

The process	Decision 1 (The sorting of paratopes)	Decision 2 (The determination of effector class)
Is encoded and selected	somatically	in the germline
Is initiated	prior to encounter with NS	after encounter with NS
Is mediated	epitope-by-epitope	antigen-by-antigen
Results in	deletion of anti-S, paratope-by-paratope	a coherent effector response to each epitope linked on the antigen (i.e. ARA)
Operates when there is	an insufficiency of eTh specific for the given antigen	a sufficiency of eTh specific for the given antigen

The S—NS discrimination is the somatically encoded mechanism by which a somatically generated, large and random (with respect to S and NS) repertoire is sorted into anti-S and anti-NS. The anti-S is purged and the residue is defined as anti-NS.

The effector class is determined by a collection of germlineencoded mechanisms that couple the appropriate receptor, Ig or TCR, to the effector function so that it can be both specifically and effectively armed.

The two decisions also differ in that Decision 1 (the sorting of paratopes) is initiated before NS antigens engage the system, whereas Decision 2 (the coupling of paratopes to effector class) is initiated after NS antigens engage the system.

As a consequence, Decision 1 (the sorting of paratopes) operates when S epitopes purge the anti-S repertoire paratope-by-paratope by interactions epitope-by-epitope. By contrast, Decision 2 (the determination of class) involves regulatory mechanisms that operate antigen-by-antigen because the response to each epitope linked on the antigen must be in the same effector class (i.e. coherent). This is what ARA accomplishes. An effector regulatory T cell interacting with one epitope on an antigen tells any cell interacting with any other epitope on that antigen how to respond (3).

essential to the ARA model (27) is the existence of a developmental window during which all S and no NS are present. The antigen-responsive or initial state cells (i-cells) arise during this period in the absence of eT_h. Interaction with S establishes tolerance, while failure to interact allows anti-NS cells to accumulate. This differential behavior, once established, is maintained by the persistence of S and the transience of NS. The developmental window is closed when the antigen-independent pathway is operative and the priming level of eT_h is attained. In essence, it is the insufficiency or sufficiency of eTh that is the Decision 1 maker.

Comments on models

Not every experimental example of unresponsiveness can be extrapolated to the mechanism of Decision 1 (the sorting of paratopes). Unresponsiveness due to Decision 2 (the coupling of paratopes to effector class) reveals nothing about the sorting mechanism (Decision 1).

The sorting of paratopes is a somatically learned process that (i) is based on the behavior of the antigen, not on any physical or chemical property of antigens as classes, S or NS, and (ii) operates to purge anti-S paratopes epitopebyepitope, not antigen-by-antigen (3). The necessity for a somatic learning process based on behavior rules out S (34) and NS marker (4-8) models that posit germline-encoded mechanisms for the sorting of paratopes. The requirement that paratopes be sorted epitope-by-epitope, not antigen-byantigen, rules out regulatory suppressor sorting models (27,35).

This leaves us with ‘space’ models (29) that are in contrast to ‘developmental time’ models (3). The requirement of any mechanism for sorting paratopes based on a ‘tolerigenic-only’ enclave such as thymus is that the cells be born in a milieu where, in the absence of effector eT_h, all S and no NS is presented. It takes an immune attack on one S component or a failure to rid one pathogen to debilitate the animal.

This introduces the thought provoking study by Andersen et al. (28) that describes a mechanism for expressing in the thymic enclave many peripheral tissue-specific antigens but leaves open the question of ‘all S and no NS’. If it were true that all S were appropriately expressed in the thymus, then no mechanism for peripheral tolerance would be necessitated. This, in turn, would obviate the need for helper or suppressor cells in the decision process. Of course, any pathogens that managed to enter or be presented in the enclave would escape detection, a strong selection pressure for such behavior. It is reasonable, then, to assume that thymic negative selection is not all that is required to solve the sorting problem for T cells. The experimental demonstration of one peripheral S antigen that is not expressed in thymus should settle this argument concerning the existence of a peripheral ‘tolerance,’ although there are quite convincing transgenic examples (36).

What does thymic negative selection accomplish?

The Anderson et al. (28) findings present us with this challenge. Aire is a transactivating transcriptional regulator that permits wild-type thymus to express ectopically a unique subset of peripheral tissue-specific ligands. In aire-deficient animals, this family of peripheral tissue-specific ligands is not expressed in thymus, with the result that thymic negative selection of i-cells recognizing them is inoperative. Is, as generally assumed, this failure of thymic negative selection sufficient to explain the resultant autoimmunity?

In order to discuss this, we will consider three categories of S peptides. Category I are S peptides common to thymus and peripheral tissues. Category II are ectopically expressed in thymus, aire-controlled peripheral tissue-specific S peptides. Category III are S peptides that are not expressed in thymus, only in the periphery.

In the absence of thymic negative selection, the copy number of antigen-responsive or initial state i-cells per peptide leaving the thymus, would, on average, be the same for each functionally distinguished peptide, S or NS. The text illustrates this for the T_h and the Andersen et al. study (28) raises once again the question as to whether T cell tolerance is solved by thymic negative selection alone. The effect of aire deletion is on the steady-state level of i-cells specific for a given Category II S peptide that leave the thymus. In wild-type individuals the steady-state level of i-cells per peptide is decreased relative to that of aire-deficient mutants. How then does this translate into autoimmunity, above all one that is eT_h-dependent?

Under NS marker or ‘failsafe’ models, aire deficiency is predicted to have no effect. Given that the aire-controlled antigens are normal S components (i.e. not co-stimulatory or dangerous or pathogenic or inFLammatory or localized in lymph nodes) no autoimmune response is expected in aire-negative animals under the variety of NS marker models discussed in the text. ‘Ignorance’ does not explain autoimmunity. These S antigens should mediate deletion (Signal[1]), not autoimmunity. Under the ARA model initiated by the antigenindependent pathway, autoimmunity, as observed, arises under defined conditions.

Whenever an i-cell encounters antigen (Signal[1]) in the absence of an eT_h-delivered Signal[2], it is deleted. There is no difference between the thymus and the periphery in this regard. Thymus has no eT_h and during the developmental period when there is an insufficiency of eT_h in the periphery, icells interacting with antigen are deleted. The thymically presented peptides (Categories I and II) are always deletional. The uniquely peripheral S peptides (Category III) are deletional during the developmental period before the antigen-independent pathway to eT_h is operational and this unresponsive state is maintained as long as the S peptide persists (2). Any S antigen not expressed in thymus (Category III) must be expressed in the periphery within the developmental time window and persist if the state of tolerance is to be established and maintained. Once the antigen-independent pathway is operative, any putative newly arising S antigen would be indistinguishable from a NS antigen. For this reason, once defined, S never changes during the life of the individual (3).

What then was the selective pressure to gather a subset of peripheral antigens under the control of aire in order to express them ectopically in thymus?

S components are selected upon to function in the physiology of the animal. The immune system is selected upon not to attack these S components. The only mechanism for defining S is its unique presence during the developmental window when there is an absence of eT_h. Any component, the function of which requires that expression be initiated after the window closes, would be treated as NS and destroyed. The only selectable solution, then, was to gather these delayed expression components under one control, aire, and ectopically present them in the thymus which is an eT_h-deficient enclave throughout life. By contrast, the periphery is only eT_h deficient during the developmental window. Expression of the aire-controlled ligands must occur in thymus prior to their presentation in the periphery on APC. The expression of these peripheral components is aire independent in APC which are required for the presentation of not only these Category II S antigens, but also any NS antigens. Autoimmunity in airenegative individuals arises due to the expression and presentation on APC of the aire-regulated peripheral components after the developmental window closes and the antigenindependent pathway is operative. The lack of thymic negative selection against Category II antigens in aire-negative individuals is a necessary but not a sufficient factor driving autoimmunity because the level of i-cells per peptide is the same as that faced by peripheral S antigens not expressed in thymus (Category III). The Category II S antigens must appear in the periphery on APC after the developmental window closes and the antigen-independent pathway is operative. Category III S antigens are present in the periphery when the developmental window is open.

The fact that aire-negative individuals succumb to a specifically targeted autoimmunity (in part antibody-mediated) confirms the a priori argument that no antigen-unspecific, physical or chemical property (‘inflaammation’, ‘danger’, ‘localization, ‘pathogenicity’, etc.) defines S as distinct from NS. The autoimmune response to S in aire-negative individuals is uniquely dependent on the initial expression of Category II components on APC outside of the developmental window. Add to this study (28) the experiments of Lafaille et al. (19) (discussed in text) and of Adams et al. (36), and we have a fairly solid justification for an eT_h-insufficient developmental period that defines S, followed by an eT_h-sufficient period that defines NS. The antigen-independent pathway described here has been proposed to account for this transition from unresponsive to S to responsive uniquely to NS.

One S antigen—one mechanism?

While it is agreed that epitope-by-epitope deletion of a proportion of the anti-S cells occurs in a protected eT_h deficient enclave like thymus where antigen-responsive T cells are born, once peripheralized, it is widely assumed that a variety of other sorting mechanisms are operative. This is to be questioned on the most general of grounds as a solution to the sorting problem (3).

(i) Proposals of multiple different mechanisms dependent on a variety of distinct properties of antigens must face the fact that epitopes are randomly assorted on antigens. This means that each of these NS marker sorting mechanisms (‘danger’, ‘pathogenicity’, ‘localization’, ‘mode of entry’, etc.) must be able to distinguish S from NS epitopes in any antigenic context. Given that a proportion of NS antigens share epitopes with S antigens and APC present both S and NS peptides, the discrimination must be both somatically learned and specific. This is the role of eT_h, the insufficiency or sufficiency of which is a decision mechanism that is antigen specific. Rejecting this singular solution requires that the epitope-specific sorting be accomplished prior to activation (Decision 2) by the NS marker, thereby making the marker irrelevant to Decision 1.

(ii) Multiple mechanisms imply that no one of them is adequate for sorting. Over evolutionary time an adequate mechanism, like Signal[1] deletion, will replace the inadequate mechanism and this one mechanism will then become responsible for sorting. It is not unreasonable then to envisage a single mechanism for Decision 1.

(iii) All of the proposed unique mechanisms (often referred to as ‘failsafe’) are lacking for reasons discussed in the paper; however, importantly, in many cases, they are clearly part of Decision 2, the regulation of effector class and cannot contribute to Decision 1, the sorting of paratopes.

(iv) Consider an individual with two peripheral S components that are not expressed in the thymus, one (Category II) because of the inactivation of aire, the other (Category III) normally. The levels of iT cells per peptide that leave the thymus and are specific for each component are the same, yet one is attacked as if it were NS, and the other is ignored and treated as S. What peripheral or failsafe mechanism would one envisage that would distinguish these two S components? Are any of the proposed peripheral mechanisms alone or in combination (‘co-stimulation’, ‘danger’, ‘pathogenicity’, ‘localization’, ‘mode of entry’, ‘dose’, ‘inflaammation’) explicative? The assumption that there is an expression difference relative to the developmental window, a singular mechanism, is at least testable and, in its wake, will be the need to explain the origin of effector T_h (2)?

Is the two-decision pathway of heuristic value?

Evolution is selecting at the level of the effector output, which must be sufficiently discriminatory or specific to rid the pathogen without debilitating the host. There are many steps between the birth of antigen-responsive cells and the effector output that affect the resultant discrimination by the effector output. The debates are engendered by the use of the term ‘S—NS discrimination' to include any and all steps in the pathway to an effector output whether or not they are antigen specific. While we do not wish to engage in this semantic debate, it should be clear that the failure to delineate Decision 1 from Decision 2 has meaningful consequences. The chances that one will be able to successfully manipulate the immune system in an antigen-specific way (e.g. in treating allergic disorders or autoimmunity) at the level of Decision 1 are poor, while at the level of Decision 2 they are good. Understanding the difference is not just a conceptual exercise.