Switch interactions control energy frustration and multiple flagellar filament structures

Abstract

Bacterial flagellar filament is a macromolecular assembly consisting of a single protein, flagellin. Bacterial swimming is controlled by the conformational transitions of this filament between left- and right-handed supercoils induced by the flagellar motor torque. We present a massive molecular dynamics simulation that was successful in constructing the atomic-level supercoil structures consistent with various experimental data and further in elucidating the detailed underlying molecular mechanisms of the polymorphic supercoiling. We have found that the following three types of interactions are keys to understanding the supercoiling mechanism. “Permanent” interactions are always maintained between subunits in the various supercoil structures. “Sliding” interactions are formed between variable hydrophilic or hydrophobic residue pairs, allowing intersubunit shear without large change in energy. The formation and breakage of “switch” interactions stabilize inter- and intrasubunit interactions, respectively. We conclude that polymorphic supercoiling is due to the energy frustration between them. The transition between supercoils is achieved by a “transform and relax” mechanism: the filament structure is geometrically transformed rapidly and then slowly relaxes to energetically metastable states by rearranging interactions.

The bacterial flagellum is a biological nanomachine for the locomotion of bacteria. The flagellum comprises three parts: the basal body as a rotary motor, the filament as a helical propeller, and the hook as a universal joint that connects the motor with the filament. When the motor rotates in a counterclockwise direction, several flagellar filaments of a left-handed helical structure form a bundle and act as a screw to move the bacteria straight (run). When the motor reverses its rotation, a transition of the filament structure into a right-handed helix is induced, the bundle is untangled, and bacteria change the direction of movement (tumble) (1). The flagellar filament is a tubular supercoil structure consisting of subunits composed of a single protein, flagellin. This structure can be described as stacked helical units, each consisting of 11 subunits, or as 11 circularly arranged protofilaments each forming nearly longitudinal helical arrays of subunits (2). The filament can be transformed into various distinct supercoil forms by changes in chemical environment (3–5), single amino acid mutations (6, 7), or mechanical forces (8, 9). The polymorphic state in the “run” mode is called “normal,” and in the “tumble” mode the state is either in “semicoil, ”“curly I,” or “curly II” (8, 10). From a static point of view, the polymorphism of supercoils is reasonably well understood as a bistable protofilament model (11–14) in which subunit conformation is assumed to be the same within each protofilament, and protofilament conformation including the interactions with neighboring protofilaments is classified into two distinct forms: R-type and L-type. Two aspects, the assumed intrinsic bistable character of the protofilament and geometrical constraints coming from the formation of a tubular structure, result in discrete polymorphic states of the flagellar filament, as characterized by combination of the R- and L-type protofilaments, i.e., normal (2R/9L), semicoil (4R/7L), curly I (5R/6L), and curly II (6R/5L) (15, 16). Although the bistable protofilament model gives a reasonable static and mechanical view of polymorphic supercoiling on the nanoscale, the underlying molecular mechanisms are not yet fully understood.

Here, we present a previously undescribed polymorphic supercoiling mechanism, which was deduced from massive 2.4-million-atom molecular dynamics (MD) simulations for 20 ns. In contrast to the semimacroscopic mechanical bistable protofilament model, we give a microscopic view in which an essential role is played by thermal fluctuations, and these fluctuations in turn are responsible for softness of protein structures (17–19). From the microscopic view we also present a molecular mechanism for transitions between different supercoiled states.

Results and Discussion

Stability of R-Type Straight Filament Models.

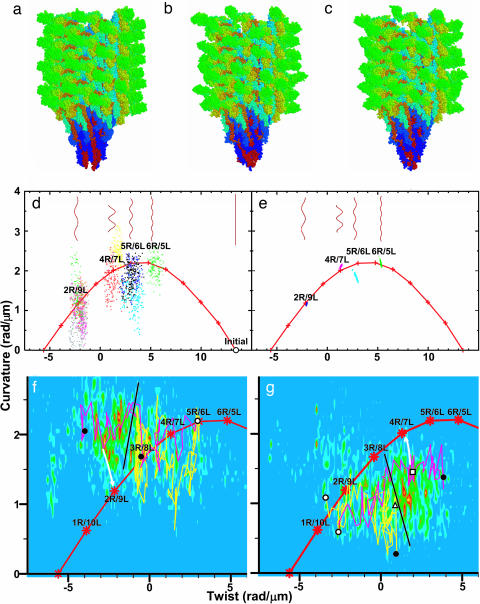
The A449V flagellin mutant from SJW1655 strain of Salmonella typhimurium forms a straight filament, whose protofilaments are all in R-type. Its atomic structure recently was solved by x-ray crystallography for the F41 fragment of flagellin (41 kDa) (20) and by electron cryomicroscopy for the whole filament (21). The simulated system, whose initial atomic coordinates were taken from the latter, contains a short filament consisting of 44 flagellin subunits, i.e., four helical units made of 316,668 atoms (Fig. 1a) and surrounding water molecules and counterions (see Materials and Methods). The R-type straight filaments were also constructed with wild-type (WT) (SJW1103) and G426A mutant (SJW1160) flagellin, which are known to form “normal (2R/9L)” and L-type straight (0R/11L) filaments in the native state, respectively. The helical form of the filaments can be characterized by two parameters, twist and curvature. For each instantaneous structure (snapshot), the local twist and curvature between the two central 11 subunits (elementary helical step hereinafter) were measured (see Materials and Methods). The structure of the A449V filament, which is expected to take the R-type straight form, is actually confined within the vicinity of the initial straight structure during the simulation, while the WT and G426A filaments drifted away from it (see Fig. 5, which is published as supporting information on the PNAS web site). This computational observation of stability and instability in the straight form in the first and latter two cases, respectively, does agree with the expectation from experiments.

Fig. 1.

Simulated models of flagellar filaments and helical parameters of WT filaments in the twist–curvature diagram. (a) Initial structure for simulation. (b and c) Snapshots of normal (b) and semicoil (c) during simulation. (d) Helical parameters of metastable structures of 10 distinct MD trajectories (last 150 ps). Red “+” connected by lines indicates parameters expected from the bistable protofilament model. Long filaments consisting of 10,680 subunits are also shown (see Materials and Methods). (e) Structures of randomly generated long filaments. (f) Results of force–bias MD starting from right- toward left-handed supercoil. Magenta (Movie 1) and yellow (Movie 2) lines represent results obtained for a torque of 5.0 and 2.0 × 10² pN·nm, respectively. Density map shows probability determined from 11 trajectories that reached near 2R/9L or 1R/10L. White circle, initial structure; black circle, final structures; black line, probable position of energy barrier; white arrow, expected relaxation pathway. (g) Same as f but in the opposite direction. The magenta (Movie 3) and yellow (Movie 4) lines represent the results for a torque of 4.0 and 2.0 × 10² pN·nm, respectively. Density map was determined from 34 trajectories that reached near 4R/7L or 5R/6L. White triangle and square, transient structures experimentally observed (9). Figs. 1 a–c, 2b, and 3 were created with rasmol (37).

Finding Polymorphic Supercoil Structures.

Starting from the structure obtained above, a torque was applied by force–bias MD to the filament model composed of WT flagellin to find whether polymorphic supercoil structures exist as energetically metastable states (see Materials and Methods). The torque applied on one end of the filament simulates the torque produced by the motor, and that of the opposite rotation on the other end simulates the reaction as hydrodynamic effect that should come from the connecting long filament. After equilibration without force–bias, the local twist and curvature were found to be clustered into four regions in the twist–curvature space (Fig. 1d). Remarkably, the centers of these clusters corresponded very well to experimentally observed values of normal (2R/9L, Fig. 1b), semicoil (4R/7L, Fig. 1c), curly I (5R/6L), and curly II (6R/5L). Metastable states corresponding to “small amplitude” (1R/10L) and “coil” (3R/8L) were not found, despite careful searching in their vicinities. Interestingly, these two states also were not observed experimentally (10). Observation of these discrete polymorphic states in our simulation indicates that our very short filament model captures the essence of the flagellar filament embodied in the bistable protofilament model. Our filament model even correctly reproduced the absence of experimentally unobservable states (1R/10L and 3R/8L). This finding indicates that our model more faithfully captures the energy profile of the system than the bistable protofilament model.

Distribution of the data shown in Fig. 1d is expected to be larger than those in real system because even a small fluctuation in the elementary step is accumulated and amplified in the long filament. To estimate more realistic fluctuation of the twist and curvature, we assumed that microscopic-state variations along the flagellar filament can be replaced by temporal-state variation of the same elementary helical step observed during the simulation. Models of polymorphic flagellar supercoil structures were generated by repeatedly stacking elementary helical steps belonging to the same cluster in the twist–curvature space (see Materials and Methods). The twist and curvature of the flagellar filament thus generated were measured and are plotted in Fig. 1e. These data agreed remarkably well with the experimental results. Comparison of Fig. 1 d and e showed that, when a tubule is formed from the ensemble of elementary helical steps, the degree of shape variations decreases drastically. This result indicates a “semimacroscopic” character of the tubular filament structure composed of “microscopic” helical steps.

Key Interactions in Supercoiling.

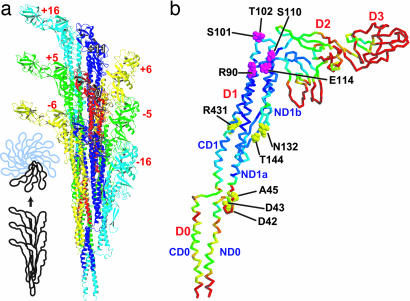
After successfully reproducing various experimental results, we should then ask whether our simulation endorses the bistable protofilament model, and, if yes, determine the basis of the differences between the R- and L-type forms with regard to structure and interaction. In the flagellar filament, a reference subunit numbered 0 makes contact with eight surrounding subunits labeled ±5, ±6, ±11, and ±16 (Fig. 2a). A helical line along subunits −5, 0, and +5 is called 5-start, for example. In this work, we treat the flagellar filament as stacked helical units. The helical unit consisting of 11 subunits is in fact made of two turns of a 1-start helix (see figure 2 of ref. 16). Intersubunit interactions along 5-, 6-, and 16-starts involve those between neighboring protofilaments, whereas interactions along 11-start involve those within each protofilament. Domains D2 and D3 protrude into solvent and have almost no contribution to intersubunit contacts. Domains D0 and D1 make intersubunit contacts and compose the filament core. The level of variation in subunit conformation among different protofilaments is indicated by different colors in Fig. 2b. When locally best-fitted, the upper part of domain D1 was found to be significantly rigid compared with the other regions. Similar tendencies also were seen in the thermal fluctuation of each subunit during the simulations. In addition, the upper part of D1 also was found to be rigid in a 1-ns MD simulation of isolated F41 monomer in solution (results not shown). Therefore, it should be understood that this rigidity originates mainly from the intrinsic nature of the flagellin structure rather than from intersubunit interactions. Although we attempted various classifications, we could not classify the subunits as R- or L-type from a structural view only because the subunit structures show significant variations and fluctuations (for example, see Fig. 6, which is published as supporting information on the PNAS web site).

Fig. 2.

Subunit arrangement in the filament viewed from outside (a) and structural variation of subunits (b). In b, rms differences of C^α atom positions among different protofilaments are shown by colors mapped on the C^α trace; highly flexible regions are in warmer (red) colors. Residues in the CPK model (magenta and yellow) are involved in permanent interactions. a was created with molmol (38).

With regard to interactions, we have performed a systematic analysis of all types of interactions that may be correlated with different filament supercoiled states. No intrasubunit interactions were found to be correlated. Intersubunit interactions are classified into three types: “permanent” (same interacting pair throughout the simulation), “sliding” (same type of interactions, i.e., hydrophilic or hydrophobic, with variable partner), and “others.” Among the others category, those correlated with supercoiled states should be particularly important. We refer to these as “switch” interactions.

In Fig. 2b, all 11-aa residues involved in permanent interactions are shown. Among these residues, R90, S101, T102, S110, and E114, which are situated in the ND1a and ND1b helices in the upper part of D1, were found to make permanent contacts with residues of neighboring subunits of the observed supercoil structures. E114 of subunit 0 maintained a salt bridge with R431 of subunit +5 (Fig. 3). S101 and T102 (not visible in Fig. 3c) were hydrogen-bonded to T144 and N132 of subunit +11, respectively. R90 formed salt bridges with both D42 and D43 in subunit +16. S110 always made hydrophobic contact with A45 of subunit +16. Interestingly, it has been shown experimentally that when N-terminal regions including D42 and D43 were deleted, filaments were severely destabilized (22).

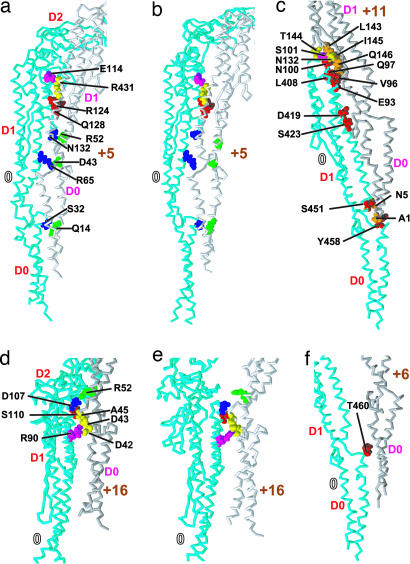
Fig. 3.

Atomic details of intersubunit interactions. Interactions in 5-start in L-type (a) and R-type (b), 11-start (c), 16-start in L-type (d) and R-type (e), and 6-start (f). CPK model: key residues. Those in magenta and yellow are involved in permanent interactions with residues in other subunits; those in red and orange are always involved in sliding interactions; those in blue and green are involved in switch interactions.

The second important intersubunit interactions are sliding interactions (Fig. 3). Hydrophilic sliding interactions are formed between variable hydrophilic residue pairs, and hydrophobic ones are formed between variable hydrophobic residue pairs. S32, R124, Q128 (5-start), T460 (6-start), N5, E93, Q97, N100, Q146, D419, S423, S451, and Y458 (11-start) always made intersubunit hydrophilic interactions, i.e., hydrogen bonds or salt bridges, with variable partners, resulting in small changes in interaction energy among different structures. In 11-start, hydrophobic residues A1, V96, L143, I145, and L408 always made intersubunit hydrophobic interactions. When an N-terminal region involved in the sliding interactions was truncated, flagellin has been known to form an Lt-type straight filament, which was different from both the L- and R-type (23). This result indicates that a loss of sliding interactions leads, in this case, to a malignant supercoiled state.

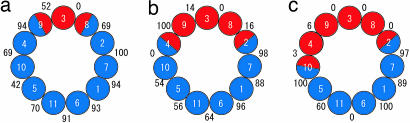
We found the following switch interactions in protofilament interfaces only along 5- and 16-starts (Fig. 3). In 5-start, R65 and N132 residues can form a salt bridge and a hydrogen bond with D43 and R52, respectively. When these interactions were broken, these residues were highly exposed to solvent (compare Fig. 3 a and b). S32, which always maintained (sometimes hydrophobic) contacts with some residues in subunit +5, can form a switch hydrogen bond with Q14. In 16-start, D107 can form a switch salt bridge with R52. The probabilities of these switch interactions to be “on” during the simulation are shown in Fig. 4. Also in Fig. 4, protofilament interfaces were classified into the R- and L-type as required by the bistable protofilament model (see Materials and Methods). We observed a high correlation between the probability and type of protofilament interfaces. Therefore, we conclude that these interactions act as a switch between the two states of protofilament interfaces. Interestingly, the mutation D107E resulting in the L-type straight filament (6, 7) can be explained by strengthening a salt bridge that prefers the L-type form by replacing the aspartic acid (D) side chain with a longer one of glutamic acid (E).

Fig. 4.

Correspondence between the bistable protofilament model and switch interactions in 2R/9L (a), 4R/7L (b), and 5R/6L (c). Colored circles represent 11 protofilaments; L-type (blue) or R-type (red) protofilament interfaces were assigned based on the model. Numbers represent the probability in percentage that at least one of the switch interactions is formed between the pairs of protofilaments consisting of the middle 22 subunits during the simulations.

We have now concluded that the molecular mechanisms behind the bistable character of the protofilament are “on–off” switch interactions between neighboring subunits. Therefore, we can now extend the concept of bistability from the “semimacroscopically” defined one for the protofilament to a “microscopic” one, as defined for each neighboring subunit pair, i.e., R-type for absent switch interactions and L-type for others. As seen in Fig. 4, R- and L-type states microscopically defined for each subunit pair show significant fluctuations behind the bistability semimacroscopically defined by the bistable protofilament model. It should be noted that, although each subunit structure fluctuates significantly, the typical or average L-type subunit structure was slightly more extended along the protofilament than that of R-type (see Fig. 7, which is published as supporting information on the PNAS web site), as expected from experimental data (15, 16).

Supercoiling Mechanism.

The presence of permanent, sliding, and switch interactions suggests the following supercoiling mechanism. Permanent interactions determine the overall architecture of the flagellar filament. In each of the interacting residue pairs, one residue is located in the relatively rigid region in the upper part of domain D1, and the other is located in the more flexible regions, either in the lower part of domain D1 or the “spoke” between domains D1 and D0. This arrangement assures flexibility in intersubunit distances without changing interacting pairs. Permanent interactions are mainly responsible for the geometrical constraints of the tubular structure. Sliding interactions provide a mechanism that allows large flexibility in the intersubunit interface without a large change in interaction energy. A similar mechanism was suggested for the protofilament of the flagellar hook to allow a large variation in the intersubunit distance while maintaining intersubunit contacts to achieve bending flexibility (24). The S101–T144 and T102–N132 residue pairs in 11-start, each having a permanent interaction, act as a pivot for the local rotational motion of the surrounding residues involved in sliding interactions.

Switch interactions play essential roles in locking each protofilament interface to be in either the R- or L-type state. Some experimental results suggest that flagellin monomer tends to be in the R-type conformation if intersubunit interactions are lost (20) or if the constraints to form the native tubular structures are weakened (20, 23). The present MD simulation showed that the formation of switch salt bridges and hydrogen bonds actually drives the subunit to take the L-type conformation in the filament. This result indicates that switch interactions are formed at the expense of intrasubunit interaction energy, leading to coexistence of the R- and L-type protofilaments in the polymorphic supercoil structures. This finding is also consistent with the phase diagram of the supercoil structure vs. pH (3). The flagellar filament isolated from strains SJ670 and SJ25 takes normal form at neutral pH, where the L-type protofilament conformation is preferred because of salt bridge stabilization, and took coil, semicoil, and curly forms at higher or lower pH, where the R-type conformation is favored because of salt bridge destabilization. In the MD simulation of a mutant without switch interactions, the filament structure moved from the normal to the one with more R-type protofilaments (Fig. 5b).

Mechanism of Polymorphic Transition.

Conformational transitions of the filament model from a right- to left-handed supercoil and vice versa were driven by the torque applied on domains D0 and D1 to simulate the torque produced by the rotary motor (see Materials and Methods) as shown in Fig. 1 f and g and also in Movies 1–4, which are published as supporting information on the PNAS web site. Here, the transitions clearly show hysteresis. This hysteresis indicates that the transitions should occur in two steps. The initial step mainly involves twist changes, while roughly maintaining curvature, and accompanying these twist changes, the filament is transformed between right- and left-handed helices. We also observed that a number of switch interactions remained almost constant during the first step. The first step is therefore a geometrical response of the filament helix to external torque. After the first step, the filament structure relaxes slowly into a new metastable state involving changes in switch and other interactions. In this second step, curvature changes while the handedness of the filament is maintained. We designated this two-step mechanism the “transform and relax” mechanism. The supercoil transformations discussed above were observed when a torque of 3.0 × 10² pN·nm or greater was applied. When the torque was insufficient, the filament structure changed as indicated by the yellow trajectories in Fig. 1 f and g, i.e., only to states with no change in helical handedness. These results agree in the order of magnitude with experimental values estimated by Hotani (9): 11 × 10² and 4 × 10² pN·nm in the normal to semicoil transition and vice versa, respectively. The filament model we used in this study is a very short segment, and analysis is focused on the central helical step. This treatment implicitly assumes that an elementary event of supercoil transition does not involve any cooperative motion of numerous helical steps. This assumption is endorsed by the agreement between the experimentally and computationally observed order of magnitude of torque necessary to induce this transition. Interestingly, the transient supercoil structures observed in left- to right-handed supercoil transformations here also have been experimentally observed as transient states (9): the experimentally observed structure shown by the triangle in Fig. 1g was observed computationally when insufficient torque was applied, and that indicated by the square was observed after the transition but before energy relaxation.

To induce the conformational transition of each elementary helical step from normal to semicoil, a torque of 3.0 × 10² pN·nm (= 43 kcal/mol·radian) carries out a work of 0.8 kcal/mol as the step is twisted by 0.018 radian in this process. When supercoil transition from normal to semicoil occurs, six salt bridges are lost per elementally helical step. These losses should be accompanied by a free energy increase of several kcal/mol. Concomitant transformation of two subunits from L- to R-type should be accompanied by a free energy decrease. Balance between these two competing energy terms results in the above free energy difference of 0.8 kcal/mol. This result is a clear example of a very general principle of the molecular mechanisms for biomacromolecular machinery to function. Functions of biological macromolecules are generally performed by transitions between multiple-energy-minimum substates realized in the native or near-native states of the machinery (25, 26). Such multiple energy minima are brought forth by the existence of competing energy terms or frustration. Frustration exists generally behind the molecular function. This characteristic is in clear contrast to protein folding. When a more coarse-grained view of conformation in which the native state is regarded just as “one state” is used, the various energy terms responsible for folding were found to be consistent (27, 28) or minimally frustrated (29).

In the dynamic process of supercoil transition at the molecular level, a certain mechanism of propagating the transition from R- to L-type or vice versa along the protofilament is expected. It is suggested that R52 is a key residue in this propagation along the protofilament. If D107 in subunit 0 forms a salt bridge with R52 in subunit +16, the same R52 is also expected to form hydrogen bonds with N132 in subunit +11 because subunit +16 corresponds to subunit 5 if viewed from subunit +11.

Recently, computer simulations carried out by atomic detailed models (30–33) and by coarse-grained models (34, 35) have given new insights into understanding how biological supramolecules work. In this study, we utilized the former because fine differences in the structure and interactions are essential for detailed understanding of the supercoiling mechanism. However, coarse-gained models also should be constructed to investigate more macroscopic dynamical behaviors of the polymorphic supercoil transition. We believe that multiscale simulation, a combination of atomic model and coarse-grained models, will become a powerful tool in understanding the dynamic behaviors and functional mechanisms of supramolecular systems.

Materials and Methods

MD Starting from R-Type Structure.

MD simulation was performed by using the module sander of the molecular simulation package amber7 (36) with the parm99 force field. As the initial filament model, the atomic model of the R-type straight filament composed of mutant flagellin A449V from strain SJW1655 of S. typhimurium, consisting of 44 flagellin subunits (316,668 atoms), was placed in a periodically repeated rectangular box of 261 × 261 × 381 ų, and the gaps were filled with 689,089 water molecules and 528 chloride ions. Chloride ions were added to neutralize the system. Periodic boundary conditions were used, and nonbonded interactions were calculated by Particle-Mesh Ewald method. For the WT (SJW1103) and L-type (SJW1660, i.e., G426A) filaments, simple amino acid substitutions were carried out for the pertinent side chains. Total numbers of atoms in the A449V, G426A, and WT filaments were 2,384,463, 2,384,331, and 2,384,199, respectively. Periodic boundary conditions were used, and nonbonded interactions were calculated by the Particle-Mesh Ewald method. During the simulations described in this work, the filament was separated from its images by at least 4∼10 layers of water molecules. For each system, a 1.2-ns equilibrium simulation was performed. The first 250-ps simulation was performed with constraints on the initial structure, and the system was equilibrated in an isothermal-isobaric ensemble at 300 K and 1 atm (1 atm = 101.3 kPa).

Construction of Long Filament and Assignment of R- or L-Type of Interface.

For each instantaneous structure observed in the simulation, we focused our attention on relative spatial arrangement (translation and orientation) between the two central 11 subunits (elementary helical step). When this arrangement is repeated many times, a helical structure is generated. Twist and curvature of such a helix is defined as the local twist and curvature of the elementary helical step. If these two parameters fluctuate around those of a theoretically expected supercoil structure deduced by the bistable protofilament model (11–14), e.g., 2R/9L (normal) state, the two shortest protofilament interfaces are assigned to R-type and the other nine protofilament interfaces to L-type.

Generating Various Supercoil Structures.

To generate metastable supercoil structures, force–bias MDs were performed starting from equilibrated structures of the WT at 900 ps. A torque was applied to the two sets of 11 subunits at both ends of the short filament model in opposite directions to twist the filament from right- to left-handed supercoils around the tangential directions of local axes of these subunits defined for each instantaneous structure. Force–bias MDs were carried out for 25∼50 ps and then continued without a torque to equilibrate the system for 50∼250 ps. This process was repeated up to 10 times. In the first four iterations, tangential forces were applied to atoms in domains D0 and D1 of these subunits amounting to a torque of 5.0 × 10² pN·nm. To speed up the equilibration of domains D2 and D3 exposed to solvent, 10.0 × 10² pN·nm was applied to all of the residues in the rest of the iterations.

A total of 37 structures with different supercoil parameters were generated. Equilibrium MD without force bias was initiated from each of these structures. In 18 cases, the filament structures appeared trapped in metastable states relatively quickly. In these cases MDs were extended up to 250 ps. In the other 19 cases where relatively large conformational changes continued, MDs were stopped at ≈50∼200 ps. After 250-ps MD simulations starting from 18 different structures, the filament structures were trapped in metastable states ranging from 1R/10L to 6R/4L: four 1R/10L (small amplitude), two 2R/9L (normal), three 3R/8L (coil), three 4R/7L (semicoil), one 5R/6L (curly I), four 6R/5L (curly II), and one 7R/4L. Simulations were further extended for 200∼400 ps (in total 2.8 ns) starting from 10 selected structures (three 1R/10L, one 2R/9L, two 3R/8L, three 4R/7L, and one 5R/6L). Finally four 2R/9L (normal), two 4R/7L (semicoil), three 5R/6L (curly I), and one 6R/5L (curly II) structures were identified as metastable states. Total simulation time in these processes was 13 ns.

In the real flagellar filament, elementary helical steps along the filament should, of course, microscopically differ from each other. To generate a realistic flagellar filament structure from the result of simulation, elementary helical steps in each cluster in the twist–curvature space are chosen randomly and stacked repeatedly by superimposing the lower 11 subunits of the first elementary helical step to the upper 11 subunits of the second step.

Observation of Supercoil Transition.

Supercoil transitions from right- to left-handed and from left- to right-handed were simulated by using the same force–bias MD described above. For this purpose, a torque ranging from 1.0∼10.0 × 10² pN·nm was applied only to domains D0 and D1. For these simulations, 3.5-ns MD was performed.

Abbreviation

MD

molecular dynamics.