Finite simple groups as expanders

Abstract

We prove that there exist k ∈ ℕ and 0 < ε ∈ ℝ such that every non-abelian finite simple group G, which is not a Suzuki group, has a set of k generators for which the Cayley graph Cay(G; S) is an ε-expander.

Let X be a finite graph and 0 < ε ∈ ℝ. Then X is called an ε-expander if for every subset A of the vertices of X with |A| ≤ (1/2)|X| we have |∂A| ≥ ε|A|, where ∂A denotes the boundary of A, i.e., the vertices of distance 1 from A.

Expander graphs play an important role in computer science and combinatorics, and many efforts has been dedicated to their constructions (cf. ref. 1, the references therein, and ref. 2). Many of these constructions are of Cayley graphs, and in particular various infinite families of finite simple groups have been shown to be expanding families.

A finite group G is called an ε-expander with respect to a generating subset S if the Cayley graph Cay(G; S) is an ε-expander. We will say that an infinite family 𝔊 of groups is a family of expanders if there exists k ∈ ℕ and 0 < ε ∈ ℝ such that every group G ∈ 𝔊 has a subset S of k generators with respect to (w.r.t.) which G is an ε-expander. In this situation we also say that the groups G ∈ 𝔊 are expanders “uniformly.” Until recently all known such families consisting of simple groups were of bounded Lie rank (cf. refs. 1 and 3), a fact that has raised speculation that this is the only possibility (see refs. 4 and 5).

It is easy to see that the diameter of each graph X_i from an expander family {X_i} is most c log|X_i| (where c is a constant). In ref. 6 it was shown that every non-abelian finite simple group has a set S of seven generators for which the Cayley graph Cay(G; S) has a diameter bounded by C log(|G|) for an absolute constant C. It was conjectured there that one can even make all finite simple groups expanders uniformly, although, as observed by Y. Luz (see ref. 4), the generators used in ref. 6 do not give rise to expanders.

The main goal of this note is to announce a proof of almost the whole of this conjecture.

Theorem 1.

There exist k ∈ ℕ and 0 < ε ∈ ℝ such that every non-abelian finite simple group G, which is not a Suzuki group, has a set S of k generators for which Cay(G; S) is an ε-expander.

In fact careful estimates using variations of some of the arguments below yield k < 1,000 and ε > 10⁻¹⁰.

We believe that the above theorem holds also for the Suzuki groups, but our (diverse) methods do not apply to them. What makes them exceptional is the fact that they do not contain copies of SL₂(𝔽_p) or PSL₂(𝔽_p) like all the other finite simple groups (see below for more details).

The proof of Theorem 1 is the accumulation of the works (refs. 7–10 and A.L., unpublished results) in the following chronological order.

In ref. 7 it was proved, extending the work of Shalom (3), that for m ≥ 3 and k ≥ 0 the group SL_m(ℤ[x₁, …, x_k]) has property (τ), i.e., its finite quotients are expanders. It was then further shown in ref. 8 that if R = ℤ〈x₁, …, x_k〉 is a free noncommutative ring, then suitable finite quotients of EL_m(R) are also expanders uniformly, provided m ≥ 3 [where EL_m(R) denotes the subgroup of the multiplicative group of Mat_m(R) generated by the elementary matrices]. This includes, in particular, the groups EL₃(Mat_n(𝔽_q)) ≃ SL_3n(𝔽_q), and thus SL_3n(𝔽_q) are uniformly expanders for all n and for all prime powers q. For every d ≥ 3, the group SL_d(𝔽_q) is a bounded product of copies of SL_3n(𝔽_q) for n = ⌊d/3⌋, which implies (using Lemma 1 below) that the groups {SL_d(𝔽_q) | d ≥ 3, q prime power} form a family of expanders.

It was then shown in ref. 10 that every finite simple classical group of Lie type is a bounded product of copies of SL_d(𝔽_q) and its central quotients. This fact can be combined with the previous results to yield that all classical groups of Lie type of sufficiently high rank are expanders uniformly.

The alternating groups Alt(n) [or equivalently the symmetric groups Sym(n)] for n ≥ 5 are also expanders in a uniform way. This result is proved in ref. 9. The argument here is more involved because Alt(n) contains copies of SL_d(𝔽_q), but it is not boundedly generated by such groups. The proof instead goes by decomposing the regular representation of Alt(n) into two components. On the first component Alt(n) acts as if it is boundedly generated by some copies of powers of SL_d(𝔽_q). On the second component one applies the eigenvalue estimates of ref. 11. The idea of this decomposition comes from work of Roichman (12).

On the other hand, it is shown by A.L. (unpublished results) that the family SL₂(𝔽_q), q a prime power, is also a family of expanders. This result is proved by a combination of Selberg’s Theorem (cf. ref. 1 and Section 4) with the explicit construction of Ramanujan graphs as given in ref. 13. In fact, a similar method (using the theory of Ramanujan complexes cf. ref. 14 and their explicit construction in ref. 13) also gives that the groups SL_d(𝔽_q) for all d ≥ 2 and all prime powers q are expanders uniformly.

The case of SL₂(𝔽_q) is the crucial new case of A.L. (unpublished results). It is further shown there, using some model theoretic results of Hrushovski and Pillay (15), that for a fixed r, all finite simple groups of Lie type and of rank at most r, with the exception of the Suzuki groups, are bounded products of copies of SL₂(𝔽_q)’s. One therefore deduces that the groups of Lie type and rank ≤ r are expanders uniformly. This case exactly complements the results of refs. 8 and 10 and all together gives that all finite simple groups of Lie type, with the possible exception of the Suzuki groups, are expanders uniformly.

By the classification of the finite simple groups (CFSG), every (non-abelian) finite simple group is either alternating or of Lie type or one of finitely many sporadic groups. Thus, Theorem 1 follows from the works described above.

The layout of the current note does not reflect the chronological story. We recall and make in Section 1 some observations regarding the representation theoretic reformulation of the problem. In Section 2 we describe the proof for SL₂, while Sections 3 and 4 give two proofs for the case of SL_d, (d ≥ 3): first, via Ramanujan complexes and second, via EL₃(ℤ〈x₁, …, x_k〉). In Section 5 we use the results for SL_d(𝔽_q) to construct expanding generating sets in all simple groups of Lie type (with the exception of the Suzuki groups). In Section 6 we describe the proof for Alt(n), which is a case of great special interest.

1. A Representation Theoretic Interpretation

As is well known (cf. ref. 1, Chap. 4), the expanding property of Cay(G; S) is equivalent to representation theoretic properties. We need some notation.

The normalized adjacency matrix of a k-regular graph X is defined to be Δ = 1/k·A where A is the adjacency matrix of X. Then all the eigenvalues of Δ are in [−1, 1]. The second largest eigenvalue is denoted λ(X).

Let I(α, G, S) denote the following statement:

For every unitary representation (V, ϕ) of G, every 0 ≠ v ∈ V and every 0 < δ ∈ ℝ, if |ϕ(s)v − v| < δ for each s ∈ S, then |ϕ(g)v − v| < αδ for each g ∈ G (i.e., a vector v which is “S-almost invariant” is also “G-almost invariant”).

Proposition 1 below can be deduced from the proofs of propositions 4.2.4 and 4.2.5 and theorem 4.3.2 of ref. 1, noting that the “nonnormalized spectral gap” λ₁(X) there is equal to k(1 − λ(X)) under our definition.

Proposition 1.

The following hold:

• (i)
  • (a)
    For each α > 0 there is ε > 0 such that a Cayley graph X = Cay(G; S) is an ε-expander if I(α, G, S) holds.
  • (b)
    For each δ > 0 there is α > 0 such that if X = Cay(G, S) is a Cayley graph and λ(X) < 1 − δ then I(α, G; S) holds.
• (ii)Moreover, if k = |S| is bounded then the implications in (i) can be reversed.

We shall repeatedly use the following easy lemma.

Lemma 1 (9).

Let G be a finite group generated by a collection of subgroups {H_i} and let ε₁, δ > 0. Assume that each subgroup H_i is generated by a subset S_i such that |∪_i S_i| ≤ k and that each graph Cay(H_i; S_i) is an ε₁-expander. Moreover, assume that the graph Y = Cay(G; ∪_iH_i) satisfies λ(Y) < 1 − δ.

Then there exists ε > 0 depending on ε₁, δ and k such that the Cayley graph Cay(G; ∪_iS_i) is an ε-expander.

For the proof take any unitary representation (V, ϕ) of G with a ∪_iS_i-almost invariant vector v. Restricting the representation to each H_i we see that v is H_i-almost invariant. The last assumption of Lemma 1 implies that v is then G-almost invariant and by Proposition 1, Cay(G; ∪_iS_i) is an expander.

This lemma implies for example that if G is a bounded product of a bounded number of subgroups H₁, H₂, …, H_ℓ and each H_i is an ε₀-expander (w.r.t. some set of generators S_i), then G is an ε-expander w.r.t. their union S = ∪S_i.

2. The SL₂(𝔽_p^k) Case

In this section we will show, following A.L. (unpublished results), that PSL₂(q) can be made into expanders uniformly for every prime power q = p^α. It is known that:

Fact 1:

The family of groups SL₂(𝔽_p), p prime, w.r.t. the generators

form a family of expanders. For a proof, based on Selberg’s theorem λ₁ ≥ 3/16, see ref. 1, Section 4.

Fact 2:

For a fixed prime p, the groups SL₂(𝔽_p^k), k ∈ ℕ, have a subset S_p of p + 1 generators for which the Cayley graphs X = Cay(SL₂(p^k); S_p) are Ramanujan graphs, i.e., λ(X) ≤ (2$\sqrt{p}$/p+1). This fact means, in particular, that they are ε-expanders with a common expanding factor ε > 0, even if we let both p and k vary. The problem is that the number of generators is unbounded when p → ∞.

The result of Fact 2 was first proved by Morgenstern (16), and it relies on Drinfeld’s solution to the characteristic p Ramanujan conjecture for GL₂. However, for our purpose we need the explicit construction of Ramanujan graphs (as special cases of Ramanujan complexes) as given in ref. 13. In the construction there, a symmetric set of p + 1 generators S′_p for SL₂(𝔽_p^k) is given as the p + 1 conjugates of a fixed element C by a fixed nonsplit torus H of SL₂(𝔽_p), i.e., S′_p = {h⁻¹C^±1h | h ∈ H}. Now

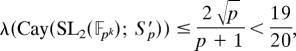therefore these graphs are ε-expanders by Proposition 1, for some ε > 0 independent of k and p. However, the generating sets S′_p are not bounded.

At the same time Cay(SL₂(p); {A, B}) are expanders uniformly by Fact 1. All together, these facts imply that Cay(SL₂(𝔽_p^k); {A, B, C}) are expanders by Lemma 1: Indeed, if (V, ϕ) is a representation of G = SL₂(𝔽_p^k) and v ∈ V is S-almost invariant for the set S = {A, B, C}, then v is SL₂(𝔽_p)-almost invariant and hence is also S′_p-almost invariant, because S′_p ⊂ SL₂(𝔽_p)·C·SL₂(𝔽_p), and hence v is G-almost invariant.

This argument shows that SL₂(𝔽_p^k) are uniformly expanders with three generators.

3. SL_d (𝔽_p^k) via Ramanujan Complexes

One can generalize the proof for SL₂ described in Section 2 to SL_d for every d. We sketch the proof below (details available from A.L. upon request).

Let F = 𝔽_q be the field of order q = p^k, for some prime p. Let E = 𝔽_q^d be the unique field extension of degree d. The natural map E* → GL_d(𝔽_q) given by letting E* act on E by multiplication, induces an isomorphism of

where H is a nonsplit maximal torus of order (q^d − 1)/(q − 1). In ref. 13 it was shown that there exists an ε > 0 such that for a suitable choice of D ∈ SL_d(𝔽_q), the Cayley graphs Cay(SL_d(𝔽_q); S′) are ε-expanders when S′ = {h⁻¹Dh | h ∈ H}. What is really proved there is that the adjacency operator of this Cayley graph is the sum of the first and the last of the d − 1 Hecke operators on the Cayley complex SL_d(𝔽_q), which is a Ramanujan complex, see ref. 14. The eigenvalue bound on these Hecke operators implies that

and in particular these are ε-expanders by Proposition 1.

We mention that the proof here (when d ≥ 3) does not need the full power of the Ramanujan bound. A weaker bound

which is sufficient for our purposes, can be deduced from the infinite dimensional representation theory of the group SL_d(𝔽_q((t))).

Assume now that d is even, d = 2m. Then the map E* GL_d(𝔽_q) described above factors through

which shows that H ≤ SL_d(𝔽_q) is contained in a copy of SL₂(𝔽_q^m).

Take now the expanding generating set {A, B, C} of SL₂(𝔽_q^m) from Section 2 with D to obtain a generating set S of four elements for SL_d(𝔽_q).

We claim that SL_d(𝔽_q) are a family of expanders w.r.t. these four generators. By Lemma 1 again, an S = {A, B, C, D}-almost invariant vector is SL₂(𝔽_q^m)-almost invariant, and then it is H·D·H-almost invariant hence also S′-almost invariant and thus G = SL_d(𝔽_q)-almost invariant as required.

This argument covers the case of even d. For odd d, the group SL_d(𝔽_q) is a product of four copies of SL_d−1(𝔽_q), and we can apply Lemma 1.

4. SL_d(𝔽_p^k) for (d ≥ 3) via EL₃ (R)

A different proof for the case of SL_d has been given in ref. 8 [prior to the proof of A.L. (unpublished results), which is described in Section 3]. This proof builds on the work of Shalom (3), where he gave a new proof of Kazhdan’s result (17) that SL₃(ℤ) has property (T). Shalom’s proof has two ingredients.

Part 1:

The group Λ = SL₂(ℤ) |× ℤ² has a relative Kazhdan property (T) relative to ℤ², i.e., if (V, ϕ) is a unitary representation space of Λ with an almost invariant vector w.r.t. the set of four natural generators, then this vector is ℤ²-almost invariant.

Part 2:

The group Λ is isomorphic to a maximal parabolic subgroup of SL₃(ℤ). Conjugating with the Weyl group gives rise to six obvious embeddings of Λ in SL₃(ℤ). The images of ℤ² in these embeddings (which include all root subgroups) boundedly generate SL₃(ℤ) by a result of Carter and Keller (18).

Parts 1 and 2 together imply that if V is a unitary representation of Γ = SL₃(ℤ) and v ∈ V is an almost invariant vector (w.r.t. some generating set) it will be Γ-almost invariant, and therefore the group Γ has property (T).

A similar argument to Part 1 works also for Λ = SL₂(R₀) |× R₀², when R₀ is the polynomial ring in k variables over ℤ. However, it is not known if the bounded generation of Part 2 holds in this case, which would imply that SL₃(R₀) has property (T). Still, by analyzing the congruence kernel of SL₃(R₀), it is deduced in ref. 7 that Γ = SL₃(R₀) has property (τ), i.e., all of its finite factors are expanders (w.r.t. a fixed set of generators of Γ).

A step further is taken in ref. 8: it is shown there that Part 1 holds even if one takes the noncommutative free ring R = ℤ〈x₁, …, x_k〉, i.e., Λ = EL₂(R) |× R² has property (T) relative to R².

It will be quite surprising if the analogue of the Carter and Keller result holds for Γ = EL₃(R), i.e., if Γ is boundedly generated by its root subgroups. However, this fact holds for many quotients R̄ of R: If R̄ = Mat_n(𝔽_q) or R̄ = Mat_n(𝔽_q)^s for s ≤ qⁿ², then R̄ is an image of ℤ〈x₁, x₂, x₃〉 and EL₃(R̄) is boundedly generated by its elementary matrices in a way that is independent of n, q, and s. This result implies that the groups EL₃(Mat_n(𝔽_q)) = SL_3n(𝔽_q) and EL₃(Mat_n(𝔽_q)^s) = SL_3n(𝔽_q)^s are a family of expanders.

For a general d ≥ 3, one notes again that SL_d(𝔽_q) is a bounded product of a bounded number of copies of SL_3n(𝔽_q) for n = ⌊d/3⌋. We can therefore deduce by Lemma 1 that SL_d(𝔽_q) form a family of expanders for all d ≥ 3 and every prime power q.

One of the advantages of this construction is that it also produces expanders in very large powers of the group SL_d(𝔽_q), which are essential for constructing expanding generating sets in the alternating groups (see Section 6).

5. Simple Groups of Lie Type

The following two theorems show how to reduce the case of finite simple groups of Lie type (minus the Suzuki groups) to the case of SL_d(𝔽_q) described in Sections 2–4.

Theorem 2 (10).

There exists a constant C such that every finite simple group G of classical type is a product of at most C subgroups of G which are quotients of SL_d(𝔽_q) (for some d ≥ 2 and q).

Theorem 3 (A.L., unpublished results).

Given r ∈ ℕ, there exists a constant C(r) with the following property: Suppose G is a finite simple group of Lie type of Lie rank at most r, which is not a Suzuki group. Then G is a product of at most C(r) subgroups each of which is a quotient of SL₂(𝔽_q) for a suitably chosen field 𝔽_q.

As explained in Lemma 1, once a group G is a product of boundedly many groups that are ε-expanders, its Cayley graph is an ε′-expander. So Theorem 1 is now proved for all groups of Lie type except for the Suzuki groups. The reason for the Suzuki groups to be excluded is the fact that they do not contain copies of SL_d(𝔽_q) or PSL_d(𝔽_q) for any d ≥ 2 and prime power q. In fact, the order of a Suzuki group is not divisible by 3, whereas |SL_d(𝔽_q)| is.

The proof of Theorem 2 is based on the fact that an arbitrary connected Dynkin diagram of high rank becomes one of type A_d after a vertex is deleted. In this way we can find a quasisimple quotient G₁ of SL_d+1(𝔽_q) inside G (in fact it is a Levi factor of a suitable parabolic subgroup).

If U (resp. U₁) is a maximal unipotent subgroup of G (resp G₁) then ref. 10 proves that U is a product of at most 14 conjugates of U₁ (using that the positive root system of G parameterizing U is “close” to the root system A_d of U₁). A theorem of Liebeck and Pyber in ref. 19 now gives that G is a product of at most 13 conjugates of U and hence a product of at most 13 × 14 = 182 conjugates of G₁.

A very detailed and laborious analysis of this kind will also lead to a similar proof of Theorem 3 with explicit bounds for C(r), but this is not the way this theorem is proved by A.L. (unpublished results).

Instead, the author there appeals to a model theoretic method developed by Hrushovski and Pillay (15). There, it is shown that “definable” subgroups of GL_n(F) over pseudo-algebraically closed field F are very much like Zariski closed subgroups over algebraically closed field. In particular, if a definable subgroup H is generated by finitely many definable subgroups L₁, …, L_c, then it is a bounded product of them. Now, it follows from the Lang–Weil Theorem that ultraproducts of finite fields are pseudo-algebraically closed (see ref. 20). As elementary statements are true in an ultraproduct if they are true in almost all factors, one can get “bounded results” over finite fields. This scheme is applied to show that all the finite simple groups (except the Suzuki groups) contain “definable” subgroups isomorphic to SL₂(𝔽_q) or PSL₂(𝔽_q) and hence are generated by them in a bounded way (when the rank is bounded).

6. The Alternating Groups

Last but not least is the case of the alternating groups Alt(n). For its special importance, we restate it as follows.

Theorem 4 (9).

There exist l ∈ ℕ and 0 < ε ∈ ℝ such that for every n ∈ ℕ the alternating group Alt(n) has an explicit set of generators S_n of size at most l such that Cay(Alt(n); S_n) is an ε-expander. The same holds also for the symmetric groups Sym(n).

The main idea of the proof in ref. 9 is as follows. Assume first that n = d⁶ and d = 2^3k − 1 for some k. Based on ideas and results from ref. 8 (see Section 4) it is shown first that the Cayley graphs of the groups Δ_k = SL_3k(𝔽₂)^d5 w.r.t. some generating set F_k of size at most 20 are ε₀-expanders for all k and d = 2^3k − 1 (for some fixed ε₀ > 0).

Now, thinking of the set {1, …, n} as the points in a six-dimensional cube of size d, and remembering that SL_3k(𝔽₂) acts transitively on a set of size d (via its defining linear action on 𝔽₂^3k), we can construct six different embeddings π_i of Δ_k into Alt(n), where the image under π_i of each copy of SL_3k(𝔽₂) in Δ_k acts on the points on a line parallel to the ith coordinate axis in the cube. Denote S_n = ∪_iπ_i(F_k) and E = ∪_iπ_i(Δ_k). We will show that the Cayley graphs of Alt(n) with respect to S_n form a family of expanders. Using that F_k is an expanding generating set in Δ_k by Lemma 1 it suffices to show that the existence of an E-almost invariant vector v in any unitary representation V of Alt(n) implies the existence of an Alt(n)-almost invariant vector.

We decompose V as a sum of two representations V₁ ⊕ V₂, where V₁ is the sum of all irreducible representations of Alt(n) in V corresponding to partitions λ ⊢ n, where the first row λ₁ is not too big (less than n − d^5/4) and V₂ contains all others. A similar decomposition is used by Roichman in ref. 12 to show that the Cayley graphs of Alt(n) with respect to conjugacy classes have some expanding properties. We will use two different arguments to show that the projection v₁ of v in V₁ is small and that projection v₂ in V₂ is close to an invariant vector.

Argument 1:

Using the definition of the set E, it is shown that a bounded power of E acts transitively on “nearly all” ordered ℓ-tuples of points in the cube for some ℓ of size approximately d⁵/(3 log d). Also a bounded power of E contains a permutation that acts as ℓ-cycle. Thus, the vector v, and therefore v₁, is almost invariant by nearly all elements in the conjugacy class C_ℓ of ℓ-cycles in Alt(n). Here nearly all means a subset of proportion tending to 1, as k and n tend to infinity. This fact implies that v₁ is almost invariant under the action of the operator

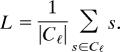The operator L acts as a multiplication by χ_λ(C_ℓ)/χ_λ(id) on the irreducible representation V_λ corresponding to the partition λ, where χ_λ is the character of V_λ. At this point one can appeal to the results of Roichman (11), who studied normalized character values of the symmetric groups. Roichman’s results give that |χ_λ(C_ℓ)/χ_λ(id)| ≪ 1, for any λ ⊢ n, provided that the first row λ₁ is small. Therefore, ‖Lv₁‖ ≪ ‖v₁‖, which together with the almost invariance of v₁ under L, implies that the vector v₁ is short.

Argument 2:

Using that all irreducible representations in V₂ corresponds to partitions with λ₁ ≥ n − d^5/4, one can view the linear span W of the orbit of v₂ in V₂ as part of the induced representation to Alt(n) of the trivial representation of Alt(n − d^5/4). This induced representation has a basis 𝔅, whose elements corresponds to the ordered d^5/4-tuples of points in the cube. The size of the basis 𝔅 is significantly smaller that the size of E, and it can be shown that the random walk on 𝔅 defined by E mixes in just several steps. This fact, together with the almost invariance of v₂ under E, implies that v₂ is close to an invariant vector.

This argument finishes the sketch of the proof for the case Alt(n) for n = (2^3k − 1)⁶ for some k. The case of general n follows from the observation that Alt(n) can be written as a product of a bounded number of copies of Alt(n_k) for n_k = (2^3k − 1)⁶ embedded in Alt(n). By adding any odd permutation to S_n, we see that the symmetric groups Sym(n) also form a family of expanders.

Abbreviation

w.r.t.

with respect to.