Nanoindentation studies of full and empty viral capsids and the effects of capsid protein mutations on elasticity and strength

Abstract

The elastic properties of capsids of the cowpea chlorotic mottle virus have been examined at pH 4.8 by nanoindentation measurements with an atomic force microscope. Studies have been carried out on WT capsids, both empty and containing the RNA genome, and on full capsids of a salt-stable mutant and empty capsids of the subE mutant. Full capsids resisted indentation more than empty capsids, but all of the capsids were highly elastic. There was an initial reversible linear regime that persisted up to indentations varying between 20% and 30% of the diameter and applied forces of 0.6–1.0 nN; it was followed by a steep drop in force that is associated with irreversible deformation. A single point mutation in the capsid protein increased the capsid stiffness. The experiments are compared with calculations by finite element analysis of the deformation of a homogeneous elastic thick shell. These calculations capture the features of the reversible indentation region and allow Young's moduli and relative strengths to be estimated for the empty capsids.

Viral genomes are surrounded and protected by a protein shell, the capsid. X-ray diffraction and cryo-electron microscopy have allowed the structures of viral capsids to be determined to high resolution (1, 2). Many capsids have highly symmetric structures that exhibit icosahedral symmetry; they range in diameter from ≈30 to 100 nm. Capsids are composed of multiple copies of just a few proteins, often only one, which are arranged into pentameric and hexameric structural units called capsomers. The forces between the proteins are typical of those associated with protein secondary and tertiary structures and are therefore weak compared with the covalent bonding in the proteins. Yet it has been shown that the capsids of bacterial viruses such as φ29 and λ, which contain highly stressed DNA genomes, are capable of withstanding internal pressures of tens of atmospheres without rupturing (3–5). It is therefore of interest to investigate the mechanical properties of viral capsids and determine how their strength and elasticity depend on the capsid structure. Atomic force microscopy (AFM) nanoindentation measurements are a convenient method for probing the mechanical properties of biological objects (6–8), and, in a recent article (9), this technique was used to study procapsids of the bacteriophage φ29. Here, we use the same methodology to examine the plant virus CCMV (cowpea chlorotic mottle virus).

The CCMV capsid (Fig. 1) is an icosahedral shell with an outer diameter of 28 nm and an average thickness of 3.8 nm (1). It is made up of 180 copies of a single 190-residue-long protein that are organized into two structural units (capsomers): pentamers and hexamers (10). CCMV capsids consist of 12 pentamers and 20 hexamers [Caspar-Klug triangulation number T = 3 (2)]. Each pentamer is surrounded by six hexamers, and each hexamer is surrounded symmetrically by three pentamers and three hexamers. The CCMV genome is multipartite; it consists of four single-stranded RNAs: RNAs 1 and 2, each ≈3,000 bases long, are packaged separately; RNAs 3 and 4 (2,000 and 1,000 bases, respectively) are packaged together (11). Capsids that contain these different parts of the genome are morphologically indistinguishable (12). Beyond its relative simplicity and symmetric structure, CCMV has a number of properties that make it an appealing target for study. The virus is able to self-assemble in vitro. Under the proper conditions of pH and ionic strength, mixtures of the capsid protein and RNA will spontaneously form infectious viruses, indistinguishable from those obtained from infected plants (11, 12). Moreover, under other conditions, the protein alone can self-assemble into empty capsids that are structurally indistinguishable from full capsids (12). Thus, by comparing the properties of empty and full capsids it is possible to assess the effect of the protein–RNA interaction on capsid elasticity and strength. CCMV capsids can also assemble spontaneously around a wide variety of anionic polymers (13, 14), and this property has raised the possibility of their use as nanocontainers (15).

Fig. 1.

Structure of CCMV capsid from x-ray diffraction studies (1). (Left) “Depth-cued” showing outer surface. (Center and Right) The detailed structure as viewed down a twofold axis (Center) and the cross section of the capsid at the midplane showing the capsid wall (Right).

Because of the broad interest in CCMV, a number of mutants have been obtained in which substitutions and/or deletions of residues in the capsid protein have been performed (15–18), making it possible to explore the effects of the protein primary structure on the mechanical properties. Among them is the salt-stable (ss) mutant, which does not dissociate at pH 7.5 at high ionic strength (i > 1 M) (16). Sequence analysis shows that there is a single substitution of Lys-42 of the capsid protein to arginine. Another mutant, SubE, has the same substitution, but, in addition, the nine basic residues (lysine and arginine) at the N terminus have been replaced by glutamic acid (15). As a result of the charge inversion, RNA cannot be packaged into subE capsids.

Results

The capsids were first imaged in a large field of view (1 × 1 mm or 2 × 2 mm), low resolution (128 pixels per mm), and low maximal force (≤100 pN) to determine their position on the substrate. When the imaging was performed with loads >150–200 pN, there was irreversible deformation of the capsids, and some local damage could be observed.

Under conditions in which there was low thermal drift, both empty and full WT capsids were observed with three distinct shapes: hexagonal, pentagonal, and round (Fig. 2). In a sample of 35 full WT capsids, all measured with the same tip, 15 were distinctly pentagonal (Fig. 2A), 8 round (Fig. 2B), and 12 hexagonal (Fig. 2C). For the 37 empty WT capsids imaged, the corresponding numbers were 19, 9, and 9. The average height of the capsids with pentagonal cross sections was distinctly lower than those with hexagonal and circular cross sections, which were closely similar (Table 1). These differences in shape and height are consistent with the structure of the icosahedral CCMV capsid, which has axes that display two-, three-, and fivefold symmetry. X-ray structural analyses of WT capsids (10) showed that the external diameters along these axes are, respectively, 24.0, 28.6, and 29.1 nm, and image reconstructions showed that capsid cross sections perpendicular to twofold axes appeared pentagonal, and those perpendicular to the three- and fivefold axes appeared, respectively, hexagonal and circular (1). We are therefore able to associate the lower heights with capsids that adsorb onto the substrate at a twofold site and the higher, hexagonal and circular cross-section capsids with those that adsorb onto threefold sites (hexamer faces) and five-fold sites (pentamer faces). For an icosahedron, the numbers of two-, three-, and fivefold sites are in the ratio 30:20:12, and if the adsorption occurs randomly, this distribution would be expected in the capsid images and heights. As shown in Table 1, relative numbers of each type of image and their heights are roughly in accord with this expectation.

Fig. 2.

AFM images of WT capsids. (Upper) Direct images. (Lower) Derivative images obtained from the direct images that show the shapes more clearly. (A) Empty capsid, adsorption on a twofold site. (B) Full capsid, adsorption on a fivefold site. (C) Full capsid, adsorption on a threefold site. The loading forces were ≈100 pN.

Table 1.

Capsid heights, spring constants, and threshold forces

Capsid type	Height, nm			k, N/m	f, nN
	Pentagonal	Hexagonal	Circular
WT
Full	25.4 ± 0.3,*n = 15	27.7 ± 0.2, n = 12	27.5 ± 0.3, n = 8	0.20 ± 0.02, n = 32	0.81 ± 0.04, n = 28
Empty	24.6 ± 0.3, n = 19	28.6 ± 0.3, n = 9	28.7 ± 0.2, n = 9	0.15 ± 0.01, n = 31	0.6 ± 0.04, n = 27
Mutants
Full ss		27.5 ± 0.2, n = 29		0.31 ± 0.02, n = 29	1.06 ± 0.03, n = 29
Empty SubE		28.2 ± 0.2, n = 41		0.19 ± 0.02, n = 41	0.77 ± 0.02, n = 35

*Uncertainty is standard error of the mean.

The AFM images of both the subE and ss mutants do not show such clear distinctions, and the height distributions are unimodal. The average height of the empty SubE capsids was 28.2 ± 0.2 nm (n = 41), and that of the ss mutant was 27.5 ± 0.2 nm (n = 29), essentially indistinguishable from the larger height for the WT capsids.

After individual objects were imaged, indentation measurements were performed. In these measurements, the applied force (measured in V) was obtained as a function of the displacement of the Z-piezo upon which the sample was mounted. The relation between the voltage output and the force was first determined by making force–distance (FZ) measurements on the incompressible substrate surface next to the capsid. The tip was then centered above the capsid, and a series of three to five successive FZ curves was generated, after which the capsid was reimaged, and its height was redetermined. If there was no obvious change, additional FZ curves were obtained on the same capsid.

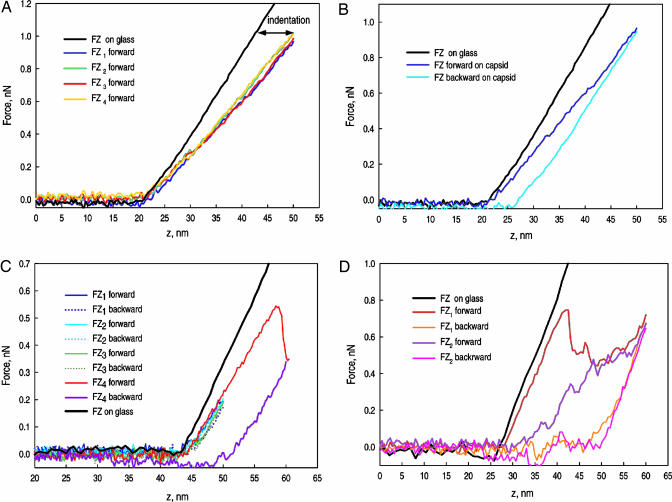
The FZ curves for an empty SubE capsid are shown in Fig. 3A and B. The black curves are the FZ curves performed on the substrate surface next to the capsid; they have been translated to match the contact points. The horizontal differences between this line and successive FZ curves correspond to the extent of indentation of the capsid. At pH 5, all capsids exhibited the same qualitative behavior. In each case there was a linear regime extending to relative indentations ranging from 20% to 30% of the diameter and forces from 0.6 to 1 nN. The curves were highly reproducible, as evidenced by the overlap of the curves for repeated indentations in Fig. 3A. The retraction curves under these conditions show, at most, only a very small hysteresis (Fig. 3B). The resilience, the fraction of the indentation energy returned upon retraction, was >90%. There was no detectable loss in height, and images taken immediately after indentation show no evidence of damage. No significant dependence of the linear behavior on the indentation rate was observed in indentations at rates ranging from 20 to 2,000 nm/s.

Fig. 3.

FZ indentation curves. The force is shown as a function of the distance traveled downward by the cantilever from its initial raised position. (A) Empty SubE capsid in the linear regime. The black curve shows the cantilever on the glass surface; it has been translated to match the contact point of the capsid. Four successive force curves are shown. (B) Empty SubE capsid showing some hysteresis. The dark blue line is the forward curve (indentation), and the light blue one is the backward (retraction) curve. (C) FZ curve for an empty WT capsid showing repeated small indentations followed by a larger indentation beyond the reversible region. The red-blue curve shows the large hysteresis upon retraction. (D) Full WT capsid showing successive indentations beyond the reversible region. All of the capsids examined exhibited the same qualitative behavior.

The linear regime typically ended with a catastrophic drop in the force (Fig. 3C), which occurred for deformations of 20–30% corresponding to ratios of the deformation to the wall thickness of ≈2. The values of the force at which the jump occurred ranged from 0.6 to 1 nN and were slightly sensitive to the indentation rate: an increase of two orders of magnitude in speed resulted in an increase in the extent of the linear regime by ≈10%. The force then increased with further indentation (Fig. 3D), but additional smaller drops often occurred. At high indentations the FZ curve asymptotically approached that of the incompressible surface. Reversibility was lost once the threshold at which the force plummets had been exceeded. In subsequent indentations the linear region became smaller or disappeared, the initial slope tended to decrease, and the force drop was smeared out. Capsids that had been indented beyond the threshold force showed losses in height of up to 10 nm and were deformed. A partial restoration of the height could be observed after relaxation for ≈20 min.

Spring constants for the capsids can be obtained from the slopes of the forward curves in the linear regime. The capsid and cantilever can be considered as two harmonic springs in series. The spring constant k_cap of the capsid is then related to k_eff, the slope of the FZ curve, and k_c, the cantilever spring constant by: k_cap = k_c k_eff (k_c − k_eff)⁻¹. Mean values of the spring constant distributions for each type of capsid are shown in Table 1. The spring constants in successive low-force indentations of a single capsid with the same cantilever differed by <1%; the generally larger spread in values for an array of capsids may represent capsid variability. Unlike the height distributions, the spring constant distributions for the WT capsids were not bimodal, and there were no significant differences in the averages taken separately over the three capsid shapes.

Both the WT and mutant full capsids were more resistant to indention than empty capsids. The onset of the catastrophic drop in the force occurred at essentially the same deformation for all of the capsids. Hence, the forces at the threshold were proportional to the force constants.

If one adopts a continuum model for the capsid as a first approximation, the spring constant can be related to the Young's modulus, E, of the protein shell. The simplest model for the elastic response is to assume the capsid to be an elastic thin spherical shell undergoing small deformations. In that case,

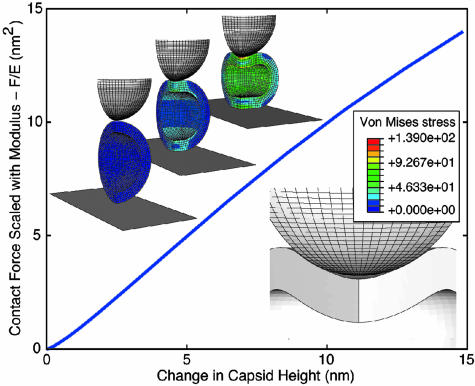
where h is the wall thickness, R is the outer radius, and α is a geometry-dependent proportionality factor (19). For CCMV, however, the thin-shell approximation h/R ≪ 1 is clearly marginal, and, moreover, the deformations that have been investigated are not small. We have therefore gone to the next level of approximation and modeled the capsid as a homogeneous elastic thick shell subject to large deformations. To model the shells, we carried out finite-element analyses with the program abaqus (ABAQUS, Fremont, CA). The calculations allow us to follow the shape of the capsid as it is indented and to determine the local stresses in its wall. The calculated curves all scale with E, so for a fixed tip shape and size the only input parameters are h, R, and the Poisson ratio σ, which we take as 0.4. (The results are rather insensitive to the value of σ.) A typical calculated indentation curve F/E versus tip displacement is shown in Fig. 4 for R = 14.3 nm, h = 3.8 nm, and a spherical tip of radius 14 nm. Fig. 4 shows how the capsid shape changes with indentation, and the color is an indication of the von Mises stress, which is a combination of the principal stresses (20).

Fig. 4.

Calculated dependence of F/E on capsid deformation for R = 14.3 nm, h = 3.8 nm, and s = 0.4. The images above the curve show a one-quarter segment of the capsid at indentations d = 0, 5.6, and 14 nm, and the von Mises stress is indicated by the color. The image below the curve shows the buckling of the capsid away from the tip that is mirrored by a decrease in the slope.

The effect of the thickness of the shell is obvious only at very small indentations d, where the curve is not linear but rises as d^3/2 in accord with the Hertz model (19). The calculated stress distributions suggest that this nonlinear behavior is associated with the radial spread of the stress through the capsid wall as the indentation begins. The tip radius and the shell thickness limit this initial Hertzian regime to the indentation depth at which the shell contact area has spread to about the shell thickness. Beyond this initial region, the curve is linear until the decrease in slope around d = 7–8 nm. At this point, the top of the capsid buckles away from the end of the tip (see Fig. 4). Buckling is found in all of our calculations, which have been performed with a large range of tip diameters and for indentation between flat plates. This behavior is in accord with experiments on macroscopic thin shells (ping-pong balls) compressed between plates, for which a buckling transition was observed at deformations corresponding to 2h (21). Moreover, the slope of the linear region is insensitive to the tip radius. It increases by ≈10% when the tip radius is increased from 7 to 28 nm; an increase from 14 nm to an infinite radius, indentation between two planes, leads to an increase of 25%.

The result, then, of the thick-shell analysis for CCMV is that the thin-shell formula (Eq. 1) holds for indentations ranging from a few percent up to ≈30%, and estimates of the slope of the linear region in Fig. 4 give α = 1. Using this expression with the values h = 3.8 nm and R = 14.3 nm, we find Young's moduli of 140 and 190 MPa for the empty WT and subE capsids, respectively. To the extent that the wall thicknesses are the same for the two capsids, the relative values of the Young's modulus can be expected to be reliable to 10%. The absolute values are more uncertain because there is some arbitrariness in the choice of the capsid dimensions (mainly the shell thickness) and because the calibration of the cantilever spring constant may be uncertain by as much as 10%. These Young's moduli are comparable in magnitude to those of soft plastics such as Teflon (22).

Discussion

The CCMV capsid is clearly not a homogeneous spherical shell. Nevertheless, until the onset of irreversible deformation the response of the capsid to indentation closely resembles that expected for this idealized model, demonstrating that the experiment provides a measure of the average properties of the protein assembly. The higher Young's modulus, and therefore greater strength of the subE mutant, is not unexpected, given that it shares the same point mutation with the more stable ss mutant. The enhanced stability is seen as well in the full mutant capsids, where the ss mutant has a higher spring constant than the WT. Clearly higher forces are required to irreversibly damage both mutants.

The elasticities that we have measured for CCMV can be compared with those reported by Ivanovska et al. (9) for the φ29 procapsid. In that study a bimodal distribution of spring constants was observed, with average values of 0.31 and 0.16 N/m (9). The larger value was attributed to an average over the inhomogeneous shell and the smaller to a locally soft region. In contrast, we see no evidence of a bimodal stiffness distribution for CCMV. Tama and Brooks (23) concluded from a normal mode analysis that the pentamer faces of CCMV were more flexible than the hexamer faces. On the other hand, Hespenheide et al. (24), on the basis of the rigidity percolation method, argue that pentamers are stiffer than hexamers. Our results cannot resolve this contradiction, but measurements made with sharper tips may have a chance of settling it.

To determine the Young's moduli from the ks for φ29, Ivanovska et al. (9) performed a finite element analysis for a point loading force on a homogeneous hollow geodesic ellipsoid. They obtained a Young's modulus for φ29 of 1.8 GPa, an order of magnitude greater than those for CCMV. Because the yield stress is generally proportional to E, the phage should therefore be able to resist much higher internal stresses than CCMV. The force exerted by the DNA in φ29 corresponds to an internal pressure on the order of 60 atm, and a packaging motor is required for assembly (4). In CCMV, which self-assembles, it is highly unlikely that the RNA exerts a large internal pressure, which is consistent with the difference in the Young's moduli.

The positively charged N termini of the capsid protein are known to interact strongly with the RNA, which will enhance the stability of the full capsids. Although the x-ray analysis did not resolve the portion of the RNA within the capsid, Monte Carlo simulations of a coarse-grained model for RNA within a CCMV capsid found that the RNA forms a shell bound to the capsid (25). If one assumes that a protein/RNA composite has a Young's modulus similar to that of the capsid alone, then the difference in the ks between the full and empty capsids could be attributed to a 10% increase in the wall thickness, a value comparable to that found in the simulations.

The qualitative features of the force curves we have measured are very similar to those that have been observed for microtubules by de Pablo et al. (7), who found a linear regime followed by a catastrophic drop in force that arose for indentations >20%. The diameter of the microtubule cylinders and the wall thickness were closely similar to those of CCMV. From an analysis of the indentations accompanying the abrupt drops in force, de Pablo et al. argued that the microtubules could collapse into double or single layers of protein. In the case of CCMV, the minimum after an initial drop in force generally occurs at a indentation of ≈50%, which does not correspond to a flattening that brings the capsid walls in contact. The resolution in the images of the deformed capsids is not sufficiently high to allow us to determine the nature of the capsid failure.

We cannot expect finite element calculations on spherical shells to describe the sharp decline in the force because failure may well be localized at specific sites such as pentamer faces that one might expect to be more weakly bound than hexamer faces. However, we can attempt to use the calculations to provide an estimate of the force at which failure is likely to occur. It is known that the tensile strengths of many materials are 5–10% of their Young's moduli (22). When the stress is not purely uniaxial, this criterion is often expressed in terms of the von Mises stress (20). The finite element calculations showed that at an indentation of 30% the maximum von Mises stress in the capsid is ≈100 MPa, close to half the Young's modulus, and therefore well in excess of the 5–10% rule of thumb. Such relatively high tensile strengths are found for highly elastic materials such as rubber and elastin, which also have low Young's moduli (26).

The success of a continuum elastic model in describing the properties of a protein array may be interpreted as evidence for the fact that the relaxation of the capsomer protein conformations is very slow compared with the rate at which the capsid is indented in our measurements. If the deformation that accompanies the sharp drop in force is associated with changes in the organization of the capsomers and not the result of a complete loss of one or more proteins, then it is possible that the very slow rate at which the deformed capsids regain their height is a measure of this slow relaxation. If this were true, the mechanical properties and response that we obtain would not be those of a capsid that was indented in an equilibrium fashion. It could be argued, for example, that frequency dependence of the elastic constants accounts for the very large difference between the Young's moduli of tubelin microtubules determined from AFM measurements (7, 26) and those obtained from osmotic compression measurements (27), which are four orders of magnitude smaller. On the other hand, estimates of E made from an analysis of thermal fluctuations of a microtubule, an equilibrium measurement, are in good accord with the AFM studies (28), and recent high-indentation measurements on φ29 show that the capsids regain their initial heights within milliseconds.

The AFM measurements and finite-element analysis that we have described have provided detailed insights into the structural properties of protein assemblies. They have revealed that viral capsids are remarkably elastic and that their properties are well represented by a model of a homogeneous elastic thick shell. A single point mutation in a capsid protein has been shown to be able to enhance measurably the mechanical stability of the capsid. A comparison between the properties of CCMV and φ29 capsids has demonstrated that their strengths, as measured by the Young's modulus, can differ by nearly an order of magnitude. This case is consistent with the need of the phage capsid to withstand a high internal pressure. The fact that we are able to distinguish different capsid orientations for both the empty and full WT capsids and not for either of the mutants suggests that the point mutation that the mutants share has an effect on the capsid geometry that has not been noted in cryoelectron microscopy images but might be determined by x-ray crystal analysis.

Materials and Methods

The WT viruses were prepared at the University of California, Los Angeles from infected plants following the procedures described (29). The ss and SubE mutants were kindly provided to us by the group of M. Young and T. Douglas (Montana State University, Bozeman). Solutions of the mutants were studied in virus buffer (0.1 M sodium acetate, pH 4.8/1 mM EDTA) without further treatment.

Empty WT capsids were prepared by disassembly of native virions at high salt concentration (≈1 M) above pH 7. A sample of full CCMV capsids solution (3 ml at 2 mg/ml in virus buffer) was dialyzed overnight at 4°C against disassembly buffer (0.9 M NaCl/0.02 M Tris·HCl, pH 7.4/1 mM DTT/0.5 mM PMSF) in dialysis cassettes with a 3.5-kDa molecular mass cutoff membrane (Pierce Slide-A-Lyser; Fisher Scientific). The mixture of RNA and coat protein was then diluted at least two times against disassembly buffer and centrifuged at 4°C in swinging buckets (Beckman rotor SW41) at 99,000 × g for 25 h. The collected upper supernatant was then concentrated by using a Centriplus YM-3 filter (Millipore polyethersulfone membrane with a nominal molecular weight cutoff of 3,000) by centrifugation at 4°C for 2 h at 3,000 × g. UV measurement of the concentrate shows a spectrum characteristic of a pure protein solution with a maximum at 277 nm. The absorbance ratio A₂₆₀/A₂₈₀ was typically of the order of 0.6–0.7. The concentration of CCMV protein monomers was determined spectroscopically (30): c = 0.2–0.3 mg/ml. The coat protein solution was then dialyzed overnight at 4°C against the reassembly buffer (0.9 M NaCl/0.1 M sodium acetate, pH 4.8/10 mM MgCl₂/0.5 mM PMSF). The reassembled empty WT CCMV capsids were finally dialyzed and stored in buffer (0.1 M sodium acetate, pH 4.8/1 mM MgCl₂/0.5 mM PMSF).

For AFM, virus particles were adsorbed onto microscope coverslips. The circular glass substrates were first cleaned in a saturated solution of KOH in ethanol, then dried in vacuum and made hydrophobic by silanization with 1,1,1,3,3,3-hexamethyldisilazane (C₆H₁₉NSi₂, 99.9% pure; Sigma-Aldrich) vapor. Initial stock solutions (≈1 mg/ml) of each type of CCMV capsid were diluted 100-fold in the corresponding buffer. A 100-μl droplet of viral solution was deposited on the hydrophobic substrate and allowed to stand for 20 min to allow the capsids to adsorb. Another 100 μl of buffer was then added to ensure complete immersion of the cantilever.

All of the imaging and force measurements were performed at the Vrije Universiteit with an atomic force microscope (Nanotec, Madrid) in jumping mode (31). In this mode, imaging is achieved by a succession of FZ measurements executed in several milliseconds in a raster scan fashion. Lateral displacements occur only when the tip is not in contact with the sample, thereby minimizing shear forces. A complete description of the apparatus and the measurement procedures can be found in ref. 9. Silicon nitride, gold-coated cantilevers (Olympus Research, Melville, NY) with nominal spring constants of 0.05 Nm⁻¹, were calibrated by the method described by Sader et al. (32). The four-sided pyramidal-shaped tip radii were 20 nm, so the tip apex could be approximated as a sphere with a diameter of ≈40 nm. Imaging and force measurements were all performed at room temperature in virus buffer at pH 4.8.

Abbreviations

AFM

atomic force microscopy

CCMV

cowpea chlorotic mottle virus

ss

salt stable

FZ

force–distance.