Time, temperature, and load: The flaws of carbon nanotubes

The “mechanics of nanostructures” is of intrinsic and practical interest. An acorn turning into an oak tree can lead one to consider the (often unknown) mechanical forces exerted by, and acting on, nanostructures present in the tree. A mantra of nanotechnology [which may ultimately outpace (1) “natural” evolution] is having “a place for every atom and every atom in its place” (www.foresight.org/nano/whatismm.html). What level of perfection might be achieved considering the known laws of physics and the constraints of chemistry? In principle, there is no limitation to achieving essentially perfect covalent bonding in material structures. With increasing atom number, a size is eventually reached where the defect-free structure is not the most stable (consider the role of entropy) (2), but it may be kinetically stable if there are high barriers to the nucleation of defects. In a recent issue of PNAS, Dumitrica et al. (3) consider carbon nanotubes (CNTs) and, building on prior theoretical work by themselves and others, present the pathways to failure caused by tensile load as a function of time and temperature. Because CNTs can have different chiralities, the issue of the orientation of the CC bonds in the different CNTs is treated and shown to critically influence the ultimate strength, the type of defects that nucleate and how they grow or propagate, and the modeled time to failure (3).

The possibility of having structures entirely free of defects would seem more likely for small structures than large structures, and living organisms routinely achieve such perfection. The remarkable mechanics of biological motors (4, 5) and viral DNA packaging and ejection (6, 7) (as a few examples among many interesting studies) have been probed. Analysis based on continuum mechanics (8) discusses the possibility that evolution has optimized composite materials present in biological systems such as bone or abalone such that they are inherently “flaw-tolerant.” Nanostructures having covalent bonding with (relatively) stiff bonds, in contrast, are not tolerant of, e.g., point defects (a missing atom in the lattice) (9). A single missing atom in a hypothetical CNT of the “(10,10)” type stretching from the surface of the Earth to geostationary orbit (thus containing of order 6 × 10¹⁷ otherwise perfectly bonded atoms) would have a tensile strength ≈80% that of the hypothetical defect-free tube (9). This reduction in strength and “end effects,” such as have been discussed in a review of the ultimate strength and stiffness of polymers (10), are relevant to the strength of the hypothetical space elevator (11). Even if structures such as space elevators could be defect-free by a remarkable future nanotechnology used to construct them and supposing they were composed largely of CNTs, the question of how long before defects arise can be debated in light of the treatment presented by Dumitrica et al. (3), although this advance in treating the time and temperature dependence of CNT strength (3) is not incorporating potentially reactive chemical environments, radiation, including cosmic rays, cycling of thermal or mechanical loads, or other external perturbations present in the real world (and space!).

The synthesis of carbon, boron nitride, and metal dichalcogenide nanotubes (among others), and single-crystal inorganic and metal nanowires (and nanorods, ribbons, plates, platelets, sheets, etc.) enables study of the influence small numbers of atomic-scale defects will have on strength. The ultimate strength has perhaps been measured for a few specimens of microscale whiskers (12) and glass fibers (13). For example, a several-millimeter-long, 0.34-μm-diameter β-Si₃N₄ whisker with strength of 59 GPa might have been defect-free (9, 14, 15). Nanostructures can be created with a very broad range of compositions and can be (apparently) single-crystal throughout (16). But are they free of defects? Measurements of strength, such as of CNTs (17) or WS₂ nanotubes (18), play a role in revealing such defects.

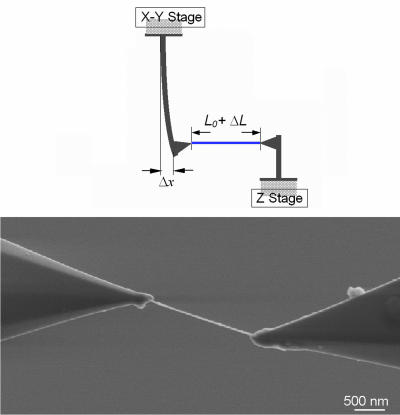
Given this analysis of CNT strengths (3), what challenges remain for both modeling and experiment? The impact of thermal and mechanical load cycling, and during loading of chemical environments differing from vacuum, of photons or electrons or ions, of electromagnetic fields, of simultaneous transport of current, or of other external perturbations can be considered. If one were to accept that the final word has been rendered on the strength of CNTs as a function of time and temperature in vacuum (3), what of the strength of Si or Ge nanowires (19, 20) or nanowires containing heterostructures (thus, “striped”) along the one-dimensional axis (21)? Has the ultimate strength of MoS₂ nanowires really been measured (18)? Experiments are needed for all of the above topics and others and to also further probe the strength of CNTs in vacuum or perhaps under inert gas and as a function of time and temperature. Experimentalists are improving the capabilities for nanostructure fracture mechanics measurements through the fabrication of better testing stages and methods (22–27), but there are significant challenges in configuring the nanostructure of interest on the testing device with appropriate boundary conditions and in having complete knowledge of the detailed geometry and atomic structure before, during, and after application of mechanical load. An example of tensile loading of the outer shell of an arc-grown multiwalled CNT is shown in Fig. 1.

Fig. 1.

The Young’s modulus of the outer CNT shell was determined to be 1,100 ± 110 GPa, its tensile strength was 66 ± 4.4 GPa, and the strain at failure was 6.3 ± 0.5%. The outer shell failed quite close to one of the clamps. The temperature was close to 298 K, and the time to failure was ≈20 min (W. Ding, L. Calabri, K. M. Kohlhaas, X. Chen, and R.S.R., unpublished work; see also ref. 17).

Even with a few atomic-scale defects, the strengths of many nanostructures are many times that of conventional materials. Achieving atomic-scale perfection in bonding might well be critical for other properties (electronic, thermal, etc.), but what about for the mechanical strength? What applications require, e.g., 100 GPa of strength (on a per-weight basis)? What types of composites can exploit 100-GPa strength (28) nanostructures as fillers, or will 30 or 10 GPa suffice? Are there nanoelectromechanical systems where such large strengths (and thus relatively large deformations) will be integral? Just as there has been, and still is, “plenty of room at the bottom” (29) for placing atoms to yield new applications, there are undoubtedly benefits from such high strengths other than affording a larger safety margin for conventional uses.

There are many other fascinating aspects of the mechanics of nanostructures. The possibility of (near) frictionless sliding in neighboring shells in multiwalled CNTs so that low-loss linear (30, 31) or rotational (32) bearings might be achieved has been discussed. The nonlinear dynamics of nanostructures will be very rich because their size suggests smaller damping; as an example, parametric resonances have been observed (33), and the possibility of sensing single molecules through their influence on the mechanical resonance of nanobeams has been recently assessed (34). The assembly of synthetic nanostructures means that understanding the nanoscale mechanics of, e.g., a CNT “yarn” (35) will be critical; there are differences in the mechanical interactions between neighboring CNTs compared with between neighboring metal wires that comprise the cables currently holding up suspension bridges (36). Statics is also relatively unexplored for nanoscale structures. For example, CNTs are not typically cylindrical (do not have a “perfectly circular” cross section, although they typically are depicted in this way); instead they are often deformed by interaction with nearby surfaces (37–40). The importance of interfaces and the effects they will have on virtually all nanostructure mechanics from natural systems, such as the gecko (41, 42), to nanostructures that are human-made, is also relatively unexplored. Indeed, it is fair to say that the field of mechanics of synthetic nanostructures is in its infancy but beginning to flower (3).