Observations on related ecological exponents

Abstract

We observe a relationship among three independently derived power laws in ecology: (i) total number of species versus area, (ii) species frequency versus species length, and (iii) maximal body size versus area. Aside from showing how these historically disparate phenomena are connected, we show how recent empirical results relating the maximal body size of top terrestrial vertebrates to the square root of land area conform to a prior theoretical expectation given by two of the above power laws. Of particular interest is the observation that the exponent relating species length to species frequency suggests a dimension for niche space for terrestrial vertebrate assemblages of D ≈ 3/2. This value, along with power law for maximal body size, versus area, gives rise to the canonical species area exponent z ≈ 1/4.

More often than not in the natural sciences, one variable (e.g., force) is related to another variable (e.g., acceleration) only when it is raised to some power (e.g., 2 in this case). Indeed, the recent proliferation and interest in power laws, allometric scaling relationships, and so-called “scale-free network” phenomena suggest the possibility of some common principles operating in distant theaters of science (1–10).

However enticing this idea may be, the ubiquity of power laws (particularly empirical ones) must certainly be due in large part to the human tendency to seek parsimonious and ready fits to data, with power laws being perhaps the simplest and most forgiving approximation. Additionally, power laws arise naturally when there is explicit reference to the dimension or covering measure of a quantity, such as when one is seeking to normalize, or make comparable, measurements of length and volume. Thus, it is not surprising to find scaling relationships in diverse fields such as astrophysics, particle physics, turbulence theory, computer science, physiology, ecology, geography, etymology, and terrorist networks, to name a few.

On a more concrete level, the diversity of these power laws within a given field suggests that there may be interchangeability among some of them that can be usefully exploited.

Our aim here is to show how three common power laws in ecology are related and to show further how this relationship can lead to an independent verification of a recent and very interesting empirical result that relates the body size of the largest resident terrestrial vertebrates (from the Late Pleistocene to present) to modern Holocene land areas (11). On a more ambitious note, we show that the observed exponent relating species length to species frequency suggests a dimension for niche space for terrestrial vertebrate assemblages between D = 3/2 and D = 2.

The Species-Area Exponent

One of the earliest and most ubiquitous scaling relationships in ecology came from the observation that larger areas contain more species in a surprisingly orderly way. This so-called species- area relationship emerged in the early 20th century as a sampling phenomenon and describes empirically how the number of new species (S_T = total number of species) accumulates as increasingly larger areas (A) are sampled (12–16): S_T = cA^z. Here c is a fitted constant related to the density of species on the landscape.

An interesting fact that is not well appreciated is that the commonly observed value of the exponent, z ≈ 1/4, can be related to the specific form of the underlying canonical lognormal species abundance distribution (14, 15, 17–19). A lower value of z corresponds to more disequitability in the ensemble or a larger variance in log-transformed abundances.

There has been much discussion concerning the underlying reasons for the exponent z and the range of values it can take (e.g., refs. 20–22; for a review of these and other proposed mechanisms, see ref. 23). Values of z for continents are often closer to 1/3, whereas those for islands are typically slightly lower (1/8 to 1/4) (24). This difference in z follows from the fact that equitability in species abundances on islands is often lower than on mainlands (16). For a given number of species (S_T), an underlying lognormal distribution on islands will have a larger variance than the comparable distribution of abundances on mainlands. A recent global estimate of z reported by Smith et al. (25) for phytoplankton spanning 15 orders of magnitude from microcosms to oceans resembles the pattern of small islands and suggests higher disequitability in these assemblages.

What is interesting is that the values for z appear to be constrained in a nonrandom way so that typical values have a relatively narrow range clustered around 1/4 (21). Among many possible ultimate factors [e.g., concerning the distribution of home range sizes, H (26), and dispersal dynamics (27)], this value of the species area exponent (z ≈ 1/4) reflects the proximate constraints that the canonical lognormal distribution places on how the equitability of species abundances varies with species richness. Equitability declines with species richness in the canonical lognormal because it is inversely related to the variance of log abundances, and the variance increases canonically with species richness. Because of this functional connection, it is not surprising that the species-area power law

and the canonical lognormal distribution share in their ubiquity and generality. Both have been observed for more than a half-century and across many different kinds of ecological systems.

The Species-Frequency Versus Species-Length Exponent

Another seemingly unrelated ecological scaling relationship was proposed in the only paper that G. E. Hutchinson and his student Robert MacArthur published together (28). It was based on a theoretical argument about niche dimensionality and species packing and attempts to explain the important but surprisingly undersubscribed question of why there are so many more species of small vertebrates than big ones (at the large end of the length–size spectrum). It is a difficult and rather abstract piece of work, but it presaged later interest in the importance of fractal scaling and home range size (H) for this question in ecology (29).

In a constructed example of their theory as applied to mammals, they suggest that within a given biotope there would be a rapid increase in numbers of species up to modal size, then a slow decline in numbers at the larger sizes, converging asymptotically “to unity.” At the large end, Hutchinson and MacArthur hypothesize that the frequency of species as a function of length S(L) would decline roughly as L⁻² (30). Hutchinson and MacArthur (28) essentially combine the observation that L² α H (their figure 4) with the hypothesis that S(L) α 1/H(L) to derive their prediction that S(L) α L⁻². A 10-fold increase in body size should result in a 100-fold decrease in species numbers.

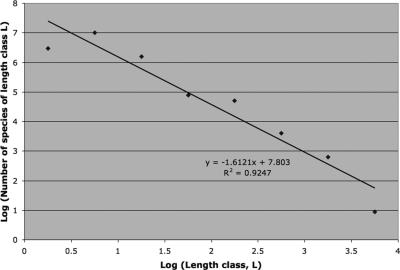
This seemingly off-the-cuff example matches data remarkably well. May (30) constructed a synoptic species-size distribution for terrestrial animals (his figure 12.2) and found a reasonably good qualitative match (drawn by eye), which was surprising considering the inchoate state of the field. If the regression line through the large end of the spectrum is actually computed from this figure, a slope of around −3/2 emerges (Fig. 1), which is not too far off from Hutchinson and MacArthur’s (28) theoretical reckoning. Note that the slope does not change significantly when the leftmost and rightmost points that fall below the line of fit are eliminated. This robustness in slope is confirmed by an analysis of covariance test for the heterogeneity of slopes (P = 0.853).

Fig. 1.

Log length [log(L)] versus log number of species in each length class [log (S(L))] for terrestrial vertebrates. Data are from Fig. 12.7 in ref. 29. The regression line has a slope of approximately −3/2 (y = −1.6121x + 7.803; r² = 0.9267), consistent with scaling implied in Eqs. 1 and 3.

Taking May’s empirical figure for the larger species (essentially vertebrates) in terrestrial animal assemblages, we obtain the power law

for the decline in species frequency as a function of length, L. Thus, at the large end of the body size spectrum, there is an approximate 3/2 power law decline in the number of species of a given body length as a function of body length in vertebrate assemblages. The number of species of size class L (S(L)) falls as L^−3/2.

Body Size Versus Area Exponent

More recently, Burness et al. (11) investigated variation in the maximum body size of top terrestrial herbivores and carnivores, and in particular how the size of the largest animals varies as a function of land area. From data over the past 65,000 years from oceanic islands and continents, they find convincing empirical evidence that the body mass of top species (M_max) increases approximately as the square root of land area (A),

This is a robust approximation for ectothermic herbivores, endothermic herbivores, ectothermic carnivores, and endothermic carnivores. Although the intercept (c₂) for the log–log plots of each of these groups was different, they all had similar slope (≈1/2). A similar relationship was found when body masses of mid- to large-sized mammals are plotted against home range sizes (H), thus replacing A with H and M_max with M in Eq. 3 (31). The substitutability of A and H is suggestive evidence that maximum body size may be constrained by the home ranges that can fit into a given land area.

Interrelationships Among Exponents

Although these three scaling laws are historically unrelated, it is instructive to show that they are functionally related. For example, it is possible to derive relation 3 from relations 1 and 2 simply by observing that 2 implies that the total number of species in the assemblage will vary proportionately with the maximal length of a species in the assemblage (x intercept of Fig. 1) raised to the 3/2 power. This relationship follows because an assemblage with more species corresponds to the line of Fig. 1 (or humped curve in the full distribution) being shifted upward in parallel fashion with the same slope. Thus, S_T α L_max^3/2.

This means that the total number of species will scale as the square root of the maximal body mass found in the assemblage S_T α M_max^1/2. When combined with Eq. 1, this yields relation 3, M_max α A^1/2. Thus, in principle, one could have foreseen the more recent result of Burness et al. (11) from relations suggested 20 years earlier.

Equivalently, Eq. 2 can be shown to follow from 1 and 3. By substituting M_max = c²A^1/2 into S_T = cA^1/4, we get back S_T α M_max^1/2, which in turn becomes S_T α L_max^3/2. From the argument above this implies S(L) α L^−3/2 and so on.

Thus, we have a case of three related exponents where, with any two, one can derive the third. In particular, note that relations 2 and 3 can be used to explain why z ≈ 1/4 and, as such, forms a partial explanation for Preston’s canonical hypothesis (14, 15, 19). We believe that searching for such relations among existing scaling laws is an enlightening exercise and is an accounting that should be done to look for consistencies or, more interestingly, to detect inconsistencies among such exponents.

In this vein, we note that a larger value of the species-area exponent z might have been expected when relations 2 and 3 were invoked to calculate it. This result follows because the data used to estimate relations 2 and 3 were derived from large continental landmasses. Thus, we might have expected to obtain a higher continental value of z to reflect this. For example, holding 3 fixed, a continental value of z = 1/3 implies a length-species exponent of 2. Thus, all else equal, a larger length-species exponent corresponds to a higher value for z, and higher equitability in relative species abundance. Clearly an accounting of interrelationships among scaling laws is an exercise worth doing (8, 9, 10).

The Species-Length Exponent and the Dimensionality of the Niche

Finally, we make a comment about the interpretation of the length-species scaling exponent as a particular dimension of ecological niche space. The motivation for this interpretation comes from fractals, where the dimension of a fractal curve is computed from the slope of a log–log plot of apparent length against the ruler length (sides of a polygonal approximation to the curve): Apparent length decreases as the ruler lengths used are increased (32). Similarly, in Fig. 1, we see that the number of species decreases as body length is increased according to a scaling exponent. The exponent 3/2 can be thought of as the length–species dimension of niche space. It is the dimension that arises from a measure and covering that maps body length into the numbers of species realized in an environment. Number of species is the measure, and body length is the covering element. That is, the length–species dimension is an abstract niche measure that describes how species at the large end of the body size spectrum can be rendered into an environment as a function of body length. It is complementary to other possible measures of niche space, such as the dimension of resource overlaps (33, 34), which, coincidentally, is also between 1 and 2.

Obviously, niche space can be rendered in many ways, with alternative measures and coverings, and each of these may be informative (or not) and have a characteristic dimensionality associated with it. A length–species dimension between 3/2 and 2 conveys a sense of the increasing density or resistance of evolutionary–ecological niche space to being populated by large species. A larger exponent would indicate relatively greater evolutionary potential for successful small-species solutions and relatively greater resistance for multiple large-species solutions. A higher length-species dimension suggests the importance that body size has in structuring the assemblage and implies higher equitability in abundances. A lower exponent would signify a circumstance where body size appears to be less important in structuring the assemblage and where equitability in abundances is lower. The range of values that this exponent can take in different taxa and in different environments should be a topic of future interest.