Weak selection and recent mutational changes influence polymorphic synonymous mutations in humans

Abstract

Recent large-scale genomic and evolutionary studies have revealed the small but detectable signature of weak selection on synonymous mutations during mammalian evolution, likely acting at the level of translational efficacy (i.e., translational selection). To investigate whether weak selection, and translational selection in particular, plays any role in shaping the fate of synonymous mutations that are present today in human populations, we studied genetic variation at the polymorphic level and patterns of evolution in the human lineage after human–chimpanzee separation. We find evidence that neutral mechanisms are influencing the frequency of polymorphic mutations in humans. Our results suggest a recent increase in mutational tendencies toward AT, observed in all isochores, that is responsible for AT mutations segregating at lower frequencies than GC mutations. In all, however, changes in mutational tendencies and other neutral scenarios are not sufficient to explain a difference between synonymous and noncoding mutations or a difference between synonymous mutations potentially advantageous or deleterious under a translational selection model. Furthermore, several estimates of selection intensity on synonymous mutations all suggest a detectable influence of weak selection acting at the level of translational selection. Thus, random genetic drift, recent changes in mutational tendencies, and weak selection influence the fate of synonymous mutations that are present today as polymorphisms. All of these features, neutral and selective, should be taken into account in evolutionary analyses that often assume constancy of mutational tendencies and complete neutrality of synonymous mutations.

In mammals, variation in mutational tendencies across the genome is the major factor influencing nucleotide composition and evolutionary trends, particularly at sites evolving neutrally or under weak selection (1, 2). Synonymous mutations are nucleotide changes in coding sequences that do not cause a change of amino acid, and evolutionary studies in many eukaryotes suggest that they are under weak selection. Indeed, model eukaryotes such as Saccharomyces cerevisiae, Drosophila melanogaster, Arabidopsis thaliana, and Caenorhabditis elegans all show patterns that indicate the action of weak selection on synonymous mutations by favoring translation efficiency (i.e., translational selection) (3–13). Two features characterize the classic model of translational selection: (i) the set of codons preferentially used in highly expressed genes (favored codons) corresponds to the most abundant tRNAs and (ii) the degree of synonymous codon usage bias toward favored codons increases with gene expression (3, 10, 11, 13–17).

For years, evolutionary studies failed to provide evidence for translational selection in humans (11, 18–22). Such inconclusive results were in accord with population genetic theory forecasting that the influence of weak selection decreases in species with smaller population sizes (4, 23–25). That is, the influence of weak selection is predicted to be less noticeable in humans than in species such as Drosophila, yeast, etc. Nevertheless, recent large-scale genomic analyses of gene composition, levels of gene expression, and tissue and isochore effects suggest minor but demonstrable long-term effects of translational selection (26–28). A more recent study that has compared rates of evolution of X-linked and autosomal genes between human and chimpanzees has also detected the influence of weak selection on synonymous mutations (29). The question of whether weak selection, and translational selection in particular, plays any role in shaping the fate of synonymous mutations that are present today as polymorphisms remains open.

Several methods have been proposed to detect and measure present (or recent) selection, taking into account possible differences in mutation rates. Two of the most common approaches are based on the comparison of (i) the frequency of new mutations in a sample (f) and (ii) the ratio of polymorphism to divergence (rpd) between mutation types or functional classes (30). Weakly advantageous mutations are expected to be present at a higher frequency within a population than weakly deleterious mutations, with neutral mutations at intermediary frequencies (30–34). Likewise, advantageous mutations will exhibit a relative excess of fixed differences between species and hence a smaller rpd relative to neutral or deleterious mutations (4, 30). The advantage of comparing allele frequencies or rpd estimates to infer recent selective events is twofold. First, differences in mutation rates between sites or genomic regions will influence the number of polymorphisms and fixed differences between species but not their frequency in a sample or rpd. Second, demographic changes can influence allele frequencies, but they cannot cause a systematic difference between two classes of mutations unless the initial frequencies were already different. Additionally, computer simulation studies have shown that these two approaches are statistically powerful in detecting very small differences in selection coefficients (34, 35). These approaches have been successfully applied to the comparison of synonymous mutations a priori classified as potentially advantageous or deleterious under a translational selection model, detecting and measuring selection coefficients, particularly in Drosophila species (18, 34–40).

Nevertheless, there are two entirely neutral scenarios that can also influence rpd and allele frequencies (f) and, under particular circumstances, generate evolutionary patterns similar to those expected under translational selection (11, 18, 38, 41–48). The first frequency-altering neutral mechanism is a very recent change in mutational tendencies. A recent increase in the GC-to-AT mutation rate (w) will cause an excess of newly derived AT neutral mutations to segregate at lower frequency than mutations at mutation-drift equilibrium, including GC neutral mutations. The second neutral mechanism that can influence mutation-drift expectations is a biased mismatch repair during gene conversion events [biased gene conversion (BGC)] (42, 49). In mammalian cells, mitotic mismatch repair usually favors C:G pairs (43, 50), and analyses from sperm DNA at a recombination hot spot (DNA2) in the MHC region show one G variant overtransmitted in A:G heterozygous sites (47). Thus, if BGC favoring G:C pairs is a general mechanism in human germinal cells, neutral GC mutations would be present at higher frequencies than AT mutations. In sum, a recent increase in w or a BGC mechanism favoring GC are neutral mechanisms that can generate polymorphism patterns resembling those caused by translational selection in species where most favored codons end in G or C, as is the case in Drosophila and humans.

Here, we studied patterns of synonymous variation in humans to investigate the influence of translational selection at the polymorphic level. The distinction between types of mutations according to their expected fitness effect (favored vs. nonfavored by translational selection) instead of mutational (GC vs. AT) class (18, 38, 51, 52), the study of different isochores separately, and the comparison of coding and noncoding sequences allow us to distinguish between selective and mutational factors, including frequency-altering neutral mechanisms.

Results

To look into the current influence of mutational and selective tendencies in humans, we first focused on polymorphic synonymous mutations, using chimpanzee orthologous sequences as an outgroup to infer the ancestral and derived variants (51). We classified derived synonymous mutations based on the set of codons overrepresented and underrepresented in highly expressed genes in humans after taking into account isochore effects (26). Preferred (P) and unpreferred (U) mutations refer to changes from a codon underrepresented (nonfavored codon) to a codon overrepresented (favored codon) and changes from a favored to a nonfavored codon, respectively. Under neutrality, P and U mutations are expected to exhibit equivalent patterns of polymorphism and divergence. Under translational selection, P and U mutations are expected to be advantageous and deleterious, respectively, and to be at mutation–selection–drift (MSD) equilibrium (53, 54). This selective scenario predicts that P mutations will show a smaller ratio of polymorphism to divergence (rpd) and higher allele frequencies (f) than U mutations. For simplicity's sake, we defined synonymous mutations between two nonfavored codons as neutral (N); granted that nonfavored codons might have slight differences in fitness, these differences are predicted to be smaller than those associated with P or U mutations. The translational selection model therefore predicts that N mutations will exhibit intermediate patterns of rpd and f when compared with P and U mutations.

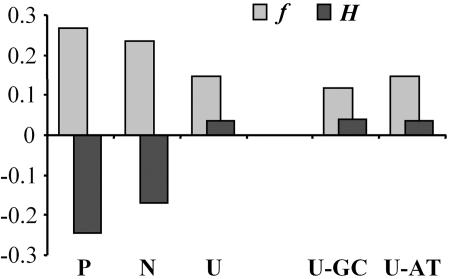
We investigated human variation in 264 genes with a sample size of 90 chromosomes and observed that polymorphic U mutations are more numerous than P mutations (P = 4 × 10⁻⁶). The study of synonymous polymorphisms and fixed mutations in the human lineage after the split from chimpanzee reveals that P mutations show a smaller rpd than U mutations (rpd_P = 0.025 and rpd_U = 0.041; G = 12.9; P = 0.0003), with N mutations showing intermediate rpd (0.032). Despite the fact that P mutations are less abundant, they segregate at a higher frequency in the sample than U mutations (f_P = 0.268 and f_U = 0.146; nonparametric Mann–Whitney U test, P = 0.012), with N mutations showing intermediate frequencies (f_N = 0.236) (see Fig. 1). We also estimated Fay–Wu's H (55), a statistic that compares the observed allele frequencies with those expected under neutrality and is particularly sensitive to high-frequency variants and hence an excellent statistic when studying mutations with potential fitness benefits. (Negative H values indicate frequencies that are higher than expected, and positive values indicate frequencies that are lower than those expected under neutrality.) H estimates of P, N, and U mutations are −0.246, −0.172, and +0.035, respectively (Fig. 1).

Fig. 1.

Frequency (f) and Fay–Wu's H statistic of polymorphic synonymous mutations in humans. P, U, and N mutations define changes from a nonfavored to a favored codon (26), from a favored to a nonfavored codon, and between two nonfavored codons, respectively. U-GC and U-AT describe U mutations that are GC or AT, respectively.

Demographic changes, such as those expected in humans, have little impact on estimates of rpd (56–58), but they are expected to strongly influence the frequency of derived mutations. Therefore, we investigated the statistical significance of the observed differences in frequencies (Δf = 0.122) and H (ΔH = 0.281) between P and U mutations by using coalescent simulations under several plausible scenarios of human demography, including recent population size growth and a possible ancestral bottleneck (59, 60) (see Materials and Methods for details). The results indicate that the observed differences between P and U mutations cannot be explained under a strictly neutral model (Supporting Text and Table 1, which are published as supporting information on the PNAS web site), under nonstationary conditions (P < 0.0001), or under the conservative neutral scenario of constant population size and complete linkage (P = 0.0012 and P = 0.0002 for Δf and ΔH, respectively).

BGC, Changes in Mutational Tendencies, and Isochore Environment.

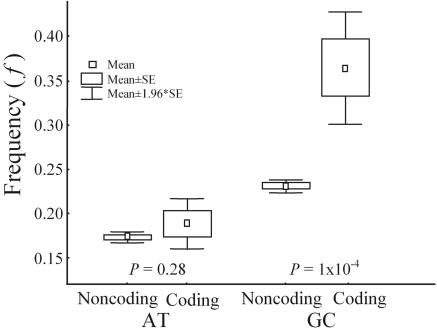
Previous studies of human synonymous variation, based on pooled data from coding and noncoding regions or on a limited number of genes, showed that GC mutations segregate at higher frequency than AT mutations (18, 38, 44). These results could be explained by a BGC mechanism favoring GC, an increase in the GC-to-AT mutational change (w), or translational selection (18, 38, 44). To examine the influence of neutral tendencies on the frequency of derived mutations, we investigated variation in noncoding sequences adjacent to the coding regions used to study synonymous mutations. The analysis of 13,513 noncoding, non-CpG, polymorphic sites shows the same tendency: GC mutations are present at higher frequencies than AT mutations (f_noncod-GC = 0.230 and f_noncod-AT = 0.173; nonparametric Mann–Whitney U test, P < 1 × 10⁻¹²; Fig. 2). This result is evidence that a frequency-altering neutral mechanism, either BGC or a recent change in w, plays a significant role in polymorphic mutations in humans.

Fig. 2.

Frequency (f) of GC and AT derived mutations in noncoding sequences and at synonymous sites in coding sequences. Probabilities are based on the nonparametric Mann–Whitney U test.

To distinguish between these two neutral mechanisms, we then analyzed derived mutations according to their isochore environment. A specific prediction of BGC is that its effect, increasing the frequency of GC mutations, will intensify with recombination rates. In humans, the rate of meiotic recombination is known to be positively associated with isochore GC content (49, 61–64); therefore, BGC forecasts that f_noncod-GC will increase (and f_noncod-AT will decrease) with isochore GC content. In contrast, a recent genome-wide increase in w predicts AT mutations at lower frequencies than GC mutations but no differences across isochores. We observe that the relationship between isochore GC content (and presumably recombination rates) and f_noncod-GC is fairly weak and nonsignificant (nonparametric Spearman R = +0.021; P = 0.084) and that f_noncod-AT does not change (R = −0.005; P > 0.60). These results suggest that the contribution of BGC to current polymorphism is minor and that the nonequilibrium condition observed in noncoding sequences can be explained by a recent increase in w.

To assess whether mutational tendencies alone can fully explain the polymorphic patterns observed at synonymous sites, we compared the frequency of GC and AT mutations in noncoding sequences with those at synonymous sites (irrespective of being P, U, or N). We observe that GC mutations at synonymous sites segregate at a higher frequency than GC mutations at adjacent noncoding sites (nonparametric Mann–Whitney U test, P = 1 × 10⁻⁴; Fig. 2). AT mutations in coding and noncoding sequences segregate at equivalent frequencies (P > 0.20) as expected if both exhibit a reduction in frequency. Because most noncoding mutations are intronic, we can also rule out a possible effect of transcription-associated mutational biases causing a difference between synonymous and noncoding sites.

We then focused on a unique qualitative difference between neutral tendencies and translational selection: Neutral mechanisms will distinguish between GC and AT mutations, whereas translational selection will distinguish between P and U mutations (52). We compared the frequency of U mutations that are also GC mutations (U-GC) to that of P mutations that are GC (P-GC mutations). Mutational biases (BGC or changes in w) predict that U-GC mutations will show the same pattern as P-GC mutations, with U mutations that are AT (U-AT) showing lower frequencies. Conversely, translational selection predicts that the frequency of U-GC mutations will be lower than the frequency of P-GC mutations and similar to that of U-AT mutations.

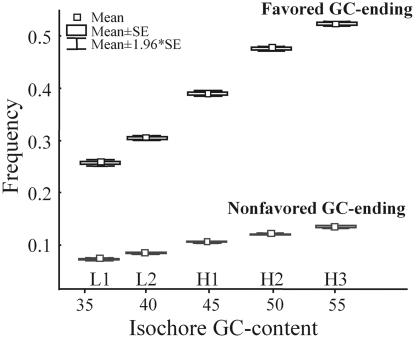
Contrary to neutral expectations, we observe that U-GC mutations (f_U-GC = 0.126) segregate at a lower frequency than P-GC mutations (f_P-GC = 0.265), with U-AT mutations segregating at f_U-AT = 0.162. (Congruently, we also observe H_U-GC = +0.021, H_P-GC = −0.227, and H_U-AT = +0.023.) Under conservative conditions of complete linkage and constant population size (see above), the difference between U-GC and P-GC mutations is significant (P = 0.027 and P = 0.017 based on Δf and ΔH, respectively). Furthermore, this result at the polymorphic level is consistent with the observation that, in all isochores, the frequency of favored codons ending in GC is higher than the frequency of nonfavored codons also ending in GC (Fig. 3).

Fig. 3.

Comparison between the frequency of GC-ending favored and GC-ending nonfavored codons in genes located in different isochores.

Thus, the results reveal two main findings. First, there is a definitive influence of neutral mechanisms on the frequency of extant mutations in humans, causing nonstationary conditions at the polymorphic level. The observed patterns are best explained by a recent genome-wide increase in w that causes AT mutations to segregate at lower frequency than GC mutations across the whole genome. Second, changes in mutational tendencies are not sufficient to explain the high frequency of GC synonymous mutations or the difference between P and U mutations, hence suggesting that weak selection, and translational selection in particular, is also playing a small but measurable role in human polymorphic mutations.

Estimates of Selection Intensity on Synonymous Mutations.

We investigated the magnitude of selection intensity (γ) in terms of the product between the effective population size (N_e) and the selection coefficient (s), with γ = 2N_es. Two common approaches to estimate γ use either the ratio of polymorphism to divergence or the frequency of derived mutations in a sample. Both methods, however, require the use of sequences evolving under complete neutrality to properly gauge mutational and population tendencies. To avoid this often challenging requirement, we can compare evolutionary patterns of two types of mutations that share the same magnitude of selection but with opposite sign (39, 40). Hence, we can estimate γ on synonymous mutations by using P (+s) and U (−s) mutations simultaneously (39, 40): γ based on rpd of P and U mutations [γ_rpd (40)], γ based on the ratio (r) of U-to-P polymorphic mutations [γ_r (39)], or γ based on the difference in frequency of P and U mutations (γ_Δf).

A caveat to all of these methods is that they also assume MSD equilibrium. Therefore, it is critical to recognize the influence that departures from MSD equilibrium (e.g., recent changes in mutational and/or demographic parameters) would impinge on estimates of γ (γ_rpd, γ_r, and γ_Δf) for synonymous mutations. A recent change in mutational tendencies toward an increase in w, as observed in the human lineage, will cause a serious overestimation of γ_r and, to a smaller degree, an underestimation of γ_rpd that will be detectable for many generations (40). Demographic changes, as those accepted in humans, have little impact on estimates of γ_rpd (56–58), but they will influence γ_r and γ_Δf, with a tendency to overestimate γ_r and, more conspicuously, γ_Δf when N_e decreases (40). Finally, another feature that can influence our estimates of selection is the common and simplifying assumption of genic selection (h = 0.5). Williamson et al. (58) have shown that dominance (h > 0.5) or recessivity (h < 0.5) has little influence on estimates of γ_rpd that assume genic selection. Our analyses (Supporting Text and Fig. 6, which are published as supporting information on the PNAS web site) show that variation in h also has a minor effect on γ_r, whereas the assumption of genic selection might bias our estimates of γ_Δf.

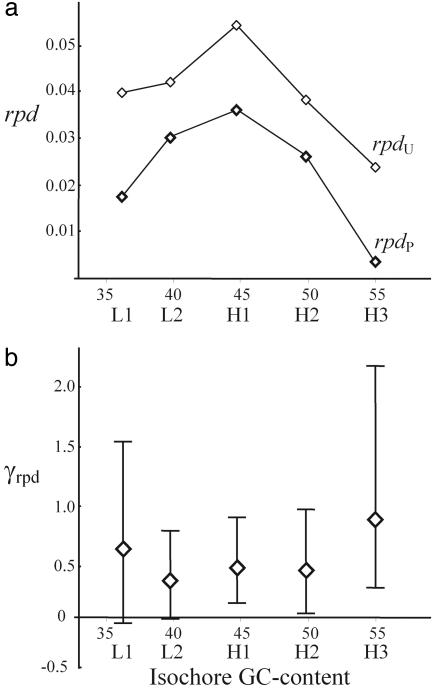
We therefore estimated γ on human synonymous mutations by using the three methodologies (γ_rpd, γ_r, and γ_Δf), taking advantage of the fact that these estimates would exhibit opposite biases under nonequilibrium conditions. The study of rpd across isochores shows that the difference between P and U mutations is not attributable to a single isochore (Fig. 4a). As predicted by translational selection, rpd for P mutations (rpd_P) is always smaller than rpd for U mutations (rpd_U). Fig. 4b shows estimates of γ_rpd and their 95% confidence intervals for each isochore separately to allow for possible differences in γ among isochores in association with variation in recombination rates or mutational tendencies. Our estimates of γ_rpd range between 0.34 and 0.89, and neutrality can be rejected in H1, H2, and H3 isochores, even though γ_rpd is expected to underestimate the true γ under nonequilibrium scenarios. Estimates of γ_r also vary among isochores (0.49, 0.57, 0.40, 0.34, and 1.15 for L1, L2, H1, H2, and H3, respectively), and γ_r is significantly higher than zero (P < 0.05) for genes located in H1, H2, and H3 isochores. Estimates of γ_Δf are influenced by the dominance parameter, ranging between 0.96 and 1.35 when h ≈ 1 and h ≈ 0, respectively.

Fig. 4.

Estimates of the ratio of polymorphism to divergence (rpd) for P (rpd_P) and U (rpd_U) mutations (a) and selection intensity on synonymous mutations based on rpd (γ_rpd) and 95% confidence intervals (b) in different isochores. Estimates of γ_rpd and 95% confidence intervals were obtained by using the mkrpf program (85).

Lastly, we applied a recent maximum-likelihood method that allows estimating γ and dominance parameters simultaneously by using the complete frequency spectrum of derived mutations [γ_s (58)]. We obtain joint maximum-likelihood estimates of γ_s and h (for P mutations) of 0.695 (+0.41 to +0.98) and 0.085 (−0.07 to +0.24), respectively (Fig. 7, which is published as supporting information on the PNAS web site). These results support our previous estimates of selection on synonymous mutations and indicate that P mutations are partially recessive.

Discussion

Nucleotide composition and evolutionary patterns across the human genome are strongly influenced by mutational, neutral trends. Our results suggest a recent increase in mutational tendencies toward AT (w) that causes polymorphic mutations to be at nonequilibrium, beyond the expected influence of demographic changes that affect all neutral mutations similarly. This increase in w is observed in all isochores, and it is a major factor responsible for AT mutations segregating at lower frequencies than GC mutations. However, we do not detect a significant contribution of BGC to current polymorphic patterns based on the study of the frequency of derived mutations at noncoding sites.

To confirm this recent change in w, we studied fixed synonymous mutations in the human lineage after the split from chimpanzee. Indeed, the evolutionary consequences of a change in w, including nonstationarity at the level of mutation frequencies, are expected to persist for many N_e generations (40), and, therefore, an increase in w in the human lineage would be consistent with the results at the polymorphic level. Congruently, we observe a significant reduction of P and synonymous GC in the human lineage (P < 1 × 10⁻⁹ in both cases; Table 2, which is published as supporting information on the PNAS web site). These results cannot be a consequence of using chimpanzee and a distant outgroup (such as mouse), because any systematic bias toward increasing AT and U mutations in the human lineage should be accompanied by an increase in GC and P mutations in the chimpanzee lineage, which is not observed; there is an excess of AT and U mutations also in the chimpanzee lineage (P < 1 × 10⁻⁶ in both cases).

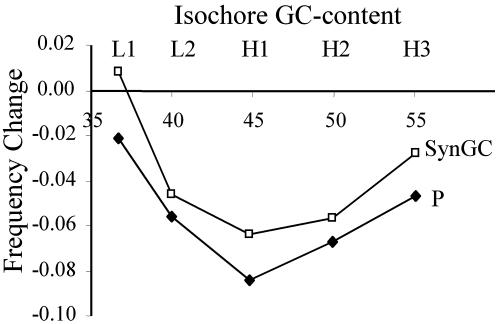
Further, we investigated the theoretical prediction that, after an increase in w, the reduction in P and GC content at synonymous sites will not be constant across the genome but with a maximum change in isochores with intermediate GC content (Supporting Text and Fig. 8, which are published as supporting information on the PNAS web site). In agreement, the change in both P and synonymous GC is mostly caused by genes located in isochores with intermediate-low GC content (Fig. 5). The observed reduction of P and GC content in the human lineage after human–chimpanzee separation could be also explained by a reduction in BGC, and this scenario would be congruent with BGC having a very small effect at the polymorphic level. Contrary to the observations, however, a reduction in BGC forecasts a maximum influence in GC-rich isochores (Fig. 8).

Fig. 5.

Observed change in the frequency of favored codons (P) and synonymous GC content (SynGC) in the human lineage after human–chimpanzee separation. Results are shown for different isochores, using only codons with a single synonymous mutation among the human–chimpanzee–mouse comparison and after removing CpG dinucleotides. Changes are assigned to the human lineage by using chimpanzee and mouse orthologous sequences.

The conclusion that BGC is playing a minor role in the recent history of humans is also consistent with another pattern of synonymous evolution between humans and chimpanzees (29). As indicated, BGC is a neutral mechanism with evolutionary effects that resemble those caused by weak selection (42); it has been put forward that BGC has indistinguishable consequences from those caused by translational selection in species with GC-ending favored codons (65, 66). Yet, theory predicts that BGC can only mimic the effects of weak selection under the assumption of genic selection (42). Lu and Wu (29) showed that synonymous evolution between human and chimpanzees is incompatible with genic selection, and our results at the polymorphic level also suggest nongenic selection. Hence, the rejection of genic selection for synonymous mutations can be used to reject a significant contribution of BGC. Nevertheless, it is important to recognize that our results do not rule out an earlier influence of BGC. Previous studies on ancient mammalian evolution (38, 67) reported a significant decline in GC content, particularly in GC-rich isochores, which fits with predictions after a reduction of BGC (Fig. 8).

In sum, we demonstrated that polymorphic patterns of synonymous mutations cannot be explained by mutational tendencies alone, with a small but detectable influence of weak selection at the level of translational selection favoring P and against U mutations. Thus, random genetic drift, recent changes in mutational tendencies, and weak selection influence the fate of synonymous mutations that are present today as polymorphisms. All of these features should be taken into account in evolutionary analyses as well as in association studies of genetic diseases.

Finally, our results provide further evidence that species with differences in population size of many orders of magnitude (e.g., Drosophila vs. humans) can show related outcomes for weakly selected traits. This observation, and most likely its explanation, is comparable to the “paradox of variation” (68) describing that the amount of genetic variation within species is surprisingly similar among species that differ greatly in census population size (N). Population genetics theory predicts that both the intensity of selection (γ) and the level of polymorphism (θ) will depend on N_e, not N, hence redirecting the paradox to the causes for a discrepancy between N_e and N. Indeed, many biological factors can influence N_e to be smaller than N (69), but a likely factor contributing to the observed lack of sensitivity of γ and θ to variation in N arises from the interplay between natural selection and genetic linkage (70, 71). The consequence of selection on genetically linked sites is equivalent to an increase in genetic drift (i.e., a reduction in N_e/N) (54, 70–76). Most models of selection and linkage predict that the relative reduction in N_e/N will increase with N, making N_e (and γ and θ) partially independent of N. Further empirical and theoretical studies are needed to fully understand the selective and genetic processes that cause weak selection to be perceptible in very diverse species.

Materials and Methods

DNA Samples and Analyses.

Synonymous variation was investigated in 264 protein-encoding genes in a sample of 90 chromosomes from European-American and African-American populations. We obtained information on SNPs from the SeattleSNPs web site (part of the National Heart, Lung, and Blood Institute's Programs for Genomics Applications). SNP information is obtained by complete resequencing (77). We studied all mutations with orthologous sequence in chimpanzee that were informative to discern the ancestral and derived synonymous variants in humans. Polymorphic sites with the two variants different from the nucleotide observed in chimpanzee were not used in the analyses. CpG dinucleotides are mutational hot spots with a high mutation rate of C→T and G→A, and their presence might impact the number and frequency of polymorphic and fixed variants; hence, we removed all CpG dinucleotides from the analyses. Homoplasy could result in the incorrect inference of the ancestral and derived variants and influence our estimates of f and H. Nevertheless, the effect of misoriented variants is negligible in studies of human samples when using chimpanzee as an outgroup (78).

We studied a total of 454 informative synonymous polymorphic sites and 13,513 informative noncoding polymorphic sites. To study synonymous evolution in the human lineage after human–chimpanzee separation, we investigated 7,645 human–chimpanzee–mouse orthologous gene alignments (79). We inferred synonymous mutations fixed in the human lineage after the split from chimpanzee by using mouse as an outgroup: Of the 17,511 codons with a single synonymous difference among the three species, 8,610 synonymous changes can be assigned to the human lineage. We group genes into five distinct isochore families according to their GC content (80): L1 (GC < 37%), L2 (37% < GC < 42%), H1 (42% < GC < 47%), H2 (47% < GC < 52%), and H3 (GC > 53%). GC content was obtained based on the study of fixed-length 100-kb windows centered from the midpoint of the gene.

We classified derived synonymous mutations based on the set of codons overrepresented and underrepresented in highly expressed genes in humans after taking into account possible isochore effects (26). Codons with a significant increase in their frequency in highly expressed genes in both GC-poor and GC-rich isochores are defined as favored under a translational selection model. Equivalently, nonfavored codons are those that decrease their frequency with expression in both GC-rich and GC-poor isochores (see ref. 26 for details).

Coalescent Simulations.

We investigated the statistical significance of the observed difference in f and H between two classes of mutations (Δf and ΔH, respectively) by comparing these differences to those obtained by coalescent simulations under the neutral model (59). All simulations were conditional on the number of chromosomes and number of informative mutations analyzed. After 10,000 independent replicates, we obtained the null distribution for Δf and ΔH under the neutral model.

We investigated four different demographic conditions following Wall and Przeworski (60) under the most conservative condition of complete linkage (81, 82). (i) “Growth”: constant ancestral population size at n = 10,000; then, 60,000 years ago, the population grows exponentially to a current size of 10⁵. (ii) “Severe growth”: constant ancestral population size at n = 10,000; then, 60,000 years ago, the population grows exponentially to a current size of 10⁶. (iii) “Bottleneck and growth”: constant ancestral population size at n = 10,000, a 10-fold reduction 60,000 years ago for 10,000 years, and then the population grows exponentially to a current size of 10⁵. (iv) “Bottleneck and severe growth”: constant ancestral population size at n = 10,000, a 10-fold reduction 60,000 years ago for 10,000 years, and then the population grows exponentially to a current size of 10⁶. In all cases, an average generation time of 20 years was assumed. We also investigated a demographic case with constant population size with different degrees of recombination, from complete linkage to independence among loci. Coalescent simulations were performed by using the ms program (83), kindly made available by R. R. Hudson (University of Chicago, Chicago).

Estimates of Selection Intensity (γ) on Synonymous Mutations.

We investigated selection intensity in terms of the product between the diploid effective population size (N_e) and the selection coefficient (s); γ = 2N_es. The relative fitness of genotypes PU and PP over UU is assumed to be 2sh and 2s, respectively, with h indicating the dominance parameter; h = 0.5 designates genic selection (semidominance). To avoid the requirement of using sequences evolving under complete neutrality, we applied methods to estimate γ on synonymous mutations that use P and U mutations simultaneously (40), assuming in all cases the infinitely many sites model under MSD equilibrium (31, 33, 54, 84).

The first method uses the ratio of polymorphism to divergence (rpd) for P and U mutations to estimate γ (γ_rpd). Estimates of γ_rpd and their confidence intervals after 10,000 iterations are obtained by using the mkprf program (85). The second method is based on the relative presence of U and P polymorphic derived mutations (see ref. 39 for details). Estimates of γ based on the ratio (r) of U-to-P polymorphic derived mutations (γ_r) are independent of mutation rates and patterns and allow contemporary estimates of γ to be obtained. Confidence intervals for γ_r are obtained based on binomial sampling of the ratio of U-to-P polymorphic mutations (39). The third method takes advantage of the expected influence of selection on the average frequency of mutations in a sample and uses the difference in frequency (Δf) between P and U mutations (γ_Δf), based on the analytical predictions under MSD equilibrium. Last, we estimated γ based on the complete frequency spectrum of derived mutations [γ_s (58)]. Interestingly, this methodology provides a maximum-likelihood framework for estimating γ and the dominance parameter h simultaneously as well as their sampling variances and covariances. Maximum-likelihood estimates of γ_s and h and sampling variances and covariances were obtained by using programs kindly provided by Scott Williamson (Cornell University, Ithaca, NY).

Abbreviations

BGC

biased gene conversion

MSD

mutation–selection–drift

P

preferred

U

unpreferred

N

neutral