Physically realistic homology models built with rosetta can be more accurate than their templates

Abstract

We have developed a method that combines the rosetta de novo protein folding and refinement protocol with distance constraints derived from homologous structures to build homology models that are frequently more accurate than their templates. We test this method by building complete-chain models for a benchmark set of 22 proteins, each with 1 or 2 candidate templates, for a total of 39 test cases. We use structure-based and sequence-based alignments for each of the test cases. All atoms, including hydrogens, are represented explicitly. The resulting models contain approximately the same number of atomic overlaps as experimentally determined crystal structures and maintain good stereochemistry. The most accurate models can be identified by their energies, and in 22 of 39 cases a model that is more accurate than the template over aligned regions is one of the 10 lowest-energy models.

Building accurate 3D structural models for protein sequences of unknown structure is a challenging, unsolved problem in contemporary biology, and its solution would provide insight into a broad range of biological systems. Large-scale genomic sequencing efforts are providing increasing numbers of sequences, but the number of experimentally determined structures remains small by comparison. The goal of homology modeling methods is to match these query sequences with known template structures and construct accurate 3D models of the proteins.

This task involves four steps: identifying suitable templates, aligning the query sequence to the templates, building the model for the query sequence by using information from the templates, and evaluating the models. Several methods are available to perform these steps and appear to perform similarly when used optimally (see refs. 1 and 2 for a description of several current methods). Although these methods have been useful, in most cases the final model is not more structurally similar to the query structure than the parent template (3, 4). In addition, many homology-modeling methods introduce physically unrealistic properties into the models in efforts to substitute the query sequence onto a nonnative backbone (2). The fixed backbone of the template is not always able to accommodate the side chains of the query sequence, particularly at buried positions, resulting in poor stereochemistry or atomic overlaps. Although the overall topology of the query structure can be derived from its homologs assuming a reasonably confident alignment, the atomic details of a homology model are of equal interest. Accurate modeling of side-chain and loop conformations is necessary in modeling and manipulating small molecule interactions, protein–protein and protein–nucleic acid interactions, and protein function.

A useful homology model is one that can provide more information about a protein of interest than any homologous structures. The positions of the query sequence that are aligned to a template can be modeled by simply copying coordinates for the backbone atoms or by using this information to generate spatial restraints, but modeling unaligned regions requires different tactics. Reliably modeling loops and unaligned regions is a challenge, and many current homology-modeling protocols do not build coordinates for all of the residues in every sequence. To date it has not been demonstrated that homology models can be built that are consistently more accurate over backbone and side-chain atoms than their templates, physically realistic according to a structure validating programs such as procheck (5), whatcheck (6), or molprobity (7), and model all residues in the query sequence with all atoms explicitly represented. Our goal in this research was to meet these challenges.

rosetta builds models of protein structures by inserting small fragments derived from the structures in the Protein Data Bank (PDB) into an initially unstructured chain (8, 9). We modified the rosetta ab initio folding protocol (8–10) to incorporate interatomic distance information from homologous structures and applied the revised protocol to a test set of query sequences. We compared models generated with this method to models generated with a fixed template method, rosetta Structurally Variable Region (rosettasvr) modeling (11, 12). To assess the accuracy of side-chain modeling, we compared the rosetta models folded with constraints to those generated with modeller (13). Our method preserves chain connectivity throughout the simulation, strictly enforces the steric properties of experimentally determined protein structures thereby ensuring physically plausible models, and unaligned regions of any length or conformation can be modeled by using the relatively successful rosetta fragment insertion method.

Results

It is generally accepted that the most important component of homology modeling is the choice of the template structure and initial alignment of the query sequence to that template (4, 14). To decouple the sequence-alignment task from the coordinate modeling process, we used structure–structure alignments derived from 3dpair (15) to first test our methods. We also used standard sequence-based alignments derived from psi-blast (16) to test the sensitivity of our method to incomplete coverage and minor sequence-alignment errors. We chose our test set of query–template pairs to be in a sequence similarity range detectable with psi-blast, so the template and query structure adopt the same topology, and sequence-alignment errors are minor but the structural differences are still significant.

Near-Native Homology Models Can Be Selected by Energy.

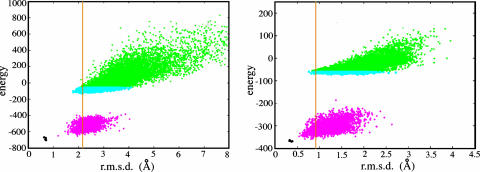
The method we have developed, rosetta folding with constraints, uses a low-resolution search with side chains approximated with centroids followed by a high-resolution search with all atoms, including hydrogens, represented explicitly. Thousands of trajectories are required to adequately sample conformational space, and a diverse population of models is generated that satisfy the constraint set and energy function to varying degrees. In both the low- and high-resolution populations, models with low rms deviation (rmsd) to the native structure can be selected based on their energies (Fig. 1; for additional examples, see Fig. 7, which is published as supporting information on the PNAS web site). In the examples shown in Fig. 1, the low-rmsd models are also low in energy, and the lowest-energy model in the full-atom refined population (magenta points) is the most accurate model (1acf-1awi) or one of the most accurate models (1b07–2sem). In some test cases the lowest-rmsd models have high energies (discussed below); however, a low-rmsd model can be found in the lowest 10 energy models selected from the complete full-atom refined population (referred to as the low-energy* model).

Fig. 1.

Low-rmsd models have low energies. Representative data from the 1acf–1awi (Left) and 1b07–2sem (Right) query–template pair centroid and full-atom searches are shown. Each point represents one trajectory. Green points represent the energies and rmsd values of the low-resolution population. Cyan points are the lowest 15% by energy subset of models that were selected for full-atom refinement. Magenta points represent the energies and rmsd values of the final models after full-atom refinement. For reference, the results of five trajectories of idealized minimized 1acf and 1b07 native structures (described in ref. 17) are shown in black. The orange vertical lines represent the rmsd of the template based model; the energy of the template-based model is out of range of this plot.

The population of full-atom refined models (Fig. 1, magenta points) is shifted toward lower rmsd values than the starting low-resolution population from which they were derived (Fig. 1, cyan points). Both populations contain low-energy models that are more similar to the query structures than the template-based rosettasvr structures (rosettasvr template model rmsd denoted with the vertical orange line). Although the protocol samples conformations close to the native conformation, it does not sample the true native state (black points, idealized minimized native structures; described in ref. 17). The idealized minimized native structures are lower in energy than all of the models we folded with constraints (Fig. 1); this energy gap has been observed previously in our group (17, 18). This finding indicates that the rosetta energy function is reasonably accurate and suggests that if enough sampling were performed, the native structure (or the closest approximation allowed using fixed bond lengths and angles) would be found.

Folding with Constraints Produces Physically Realistic Complete-Chain Models.

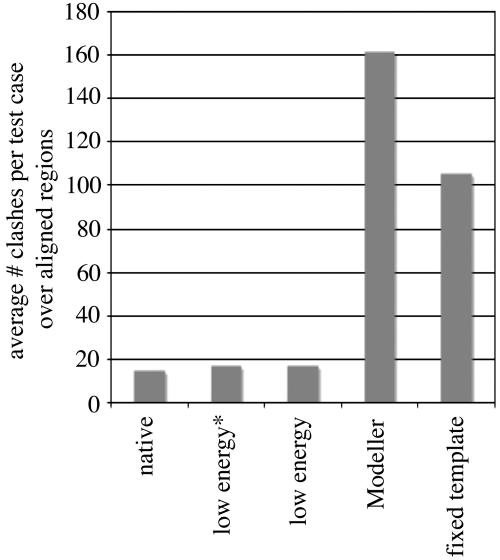
The final all-atom models were analyzed for atomic clashes by using the program molprobity (7), and the results were compared with those obtained for the native query structures, the template-based model generated by using rosettasvr modeling (12), and the model built with modeller (13). Only aligned regions were included in the calculation. The models folded with constraints have considerably fewer numbers of atomic clashes than models generated by using modeller or rosettasvr modeling (≈10% of the total modeller clashes and ≈20% of total fixed-template model clashes) and on average contain approximately the same number as native crystal structures (Fig. 2). We used modeller as one standard of comparison because it is one of the best and most widely used comparative modeling programs available. The models we generate using rosetta with constraints are more accurate in many respects than the models built with modeller; however, the compute time of the method presented here is orders of magnitude longer. The average time required to produce a population of 100 homology models using modeller is ≈1 hour on a single modern processor, compared with 90 days using our method (≈300 h are required to generate the 30,000 low-resolution starting conformations and ≈1,875 h are required to refine the 4,500 all-atom models).

Fig. 2.

Comparison of atomic clashes observed in native structures, models folded using rosetta with constraints, models generated with modeller, and models generated using a fixed template and rosettasvr modeling protocol. The y axis reports the average number of clashes per test case in aligned regions over the 39 test cases in the benchmark set.

Folding with Constraints Produces Homology Models Closer to the Native Structure than Their Parent Templates.

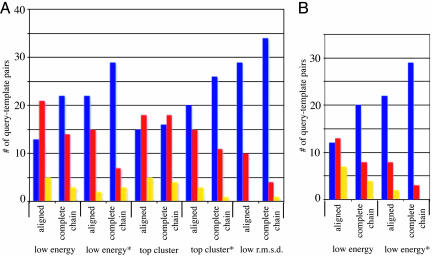
We used structure–structure alignments generated with the program 3dpair for each query–template pair to examine the success of the protocol in the absence of alignment errors. This method is a direct test of our sampling strategy and energy function and provides an upper-limit estimate of how well the method can perform; decreases in the rmsd correspond directly to improvements to the model and cannot be simply due to improving the alignment. We selected the lowest-energy model and the low-energy* model produced by folding with constraints and compared their rmsd values with the rosettasvr template-based model over aligned regions as well as over the complete chain. The low-energy* model was frequently more accurate than the template-based model over the aligned regions as well as over the complete chain. For the aligned regions, the rmsd was lower than the template-based model in 22 cases, unchanged in 2 cases, and worse in 15 cases. For the complete chain, the rmsd was lower than the template-based model in 29 cases, unchanged in 7 cases, and worse in 3 cases (Fig. 3A).

Fig. 3.

The rmsd of refined models selected according to lowest energy, lowest energy*, lowest rmsd, top cluster, and top cluster* compared with the initial fixed template-based model for each protein in the test set. (A) Data were obtained by using 3dpair alignments (structure-based). (B) Data were obtained by using psi-blast alignments (sequence-based). The height of the bars represents the number of cases where the rmsd improved (blue bars), became worse (red bars), or remained unchanged (yellow bars) with respect to the fixed template-based model over aligned regions and over the complete chain. Complete chain models were generated by using rosettasvr modeling.

The results for the low-energy model are similar for the complete chain models, where 22 cases show improvement over the template-based model, 3 are unchanged, and 14 are worse. However, the low-energy models are more frequently worse than the template-based model over the aligned regions; 13 are better, 5 are unchanged, and 21 are worse. To see whether we could detect more accurate models, we clustered the full-atom refined populations and compared the models at the centers of the largest cluster and largest cluster* (defined as the lowest rmsd cluster center model out of the largest 5 clusters) to the template-based model. The cluster center of the largest cluster is more accurate than the template more frequently than the lowest-energy model, but the cluster center of the top cluster* is not more accurate than the lowest-energy* model most of the time (Fig. 3).

The low-rmsd models are significantly more accurate than those selected by energy; in 29 cases the low-rmsd model had a lower rmsd value than the template-based model, and in 10 cases the rmsd was higher. For the complete chain, in 34 cases the low-rmsd model had a lower rmsd value than the template-based model; in 1 case the value was unchanged, and in 4 cases the rmsd was higher. We conclude that folding with constraints can produce more accurate backbone scaffolds but that increased sampling is required to find the precise conformation that will allow for native-like side-chain packing.

We also used alignments generated with psi-blast (16) to examine the more realistic case where the alignment is often incomplete or contains errors. As observed for the structure-based alignments, the final low-energy* model is usually more accurate than the template over aligned regions (22 better, 2 unchanged, and 8 worse) as well as over the entire chain (29 are better and 3 are worse) (Fig. 3B). For the low-energy models, 12 are better, 7 are unchanged, and 13 are worse than the template-based model over aligned regions, and 20 are better, 4 are unchanged, and 8 are worse over the complete chain. These results show that folding with constraints is less sensitive to alignment errors than template-based methods. The rosetta fragment replacement protocol can model long stretches of unaligned query sequence (such as the 1pva-1ahr example; see below), which makes folding with constraints less sensitive to incomplete alignment coverage. It is well suited to problems where no template can be found with confidence over one or several regions of the query sequence.

Models Produced by Folding with Constraints Have Reasonably Accurate Side-Chain Conformations.

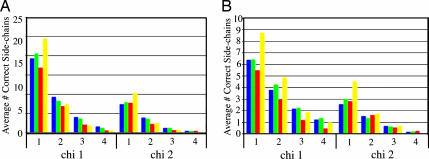
For many applications, accurate prediction of side-chain conformations is important. In addition, the success of our method and the reliability of the energy function to discriminate near-native models depend on accurate side-chain placement, especially in the hydrophobic core. We compared the side-chain conformations over aligned regions of the low-energy and the low-energy* models with the side-chain conformations of models generated by rosettasvr and modeller. First, we computed the absolute difference between the χ1 angle for each residue in the models with the corresponding χ1 angle in the native structures. Then, we classified the side-chain positions as either buried or exposed and grouped the counts into bins of 10°. A side chain was considered buried if >20 C^β atoms were found within a 10-Å radius of its C^β atom. The χ2 angle differences were measured and included in the analysis only if the χ1 value of the same residue differed from the native by an absolute value of <15°. For buried side chains, the models folded with constraints more accurately describe the native side-chain conformations than the modeller models in all angle bins for χ1 and χ2 angles (Fig. 4A). The differences were less pronounced for χ1 angles of exposed side chains and not significant for χ2 angles of exposed positions (Fig. 4B). Surprisingly, the rosettasvr side-chain conformations were the most accurate (Fig. 4). Differences in the energy functions used in the folding with constraints and rosettasvr protocols may account for this result, and clearly there is room for optimization of the rosetta side-chain packing protocol with our method.

Fig. 4.

Comparison of predicted buried side-chain (A) and exposed side-chain (B) conformations over aligned regions between the low energy and low energy* models folded with constraints, models produced by using modeller and models produced with rosettasvr. The height of the bars in bins 1, 2, 3, and 4 represent the average number over the test set of side chains where the χ angle was predicted within 0–10°, 10–20°, 20–30°, and 30–40° of the native value, respectively. Green bars, low-energy models folded with constraints; blue bars, low-energy* models folded with constraints; red bars, models built with modeller; yellow bars, models built with rosettasvr.

Low-Energy Models Disproportionately Violate Incorrect Constraints.

Homology-modeling programs using spatial restraints such as the one presented here rely heavily on the accuracy of the constraints. However, because the query structure is not identical to its homologs, some of the constraints derived from the homologs may be violated in the native structure. Therefore, the most accurate homology models should violate the constraint set to a certain extent. We analyzed the lowest 10 energy models for each query–parent pair in our test set and compared the constraint violations with those found in the native structure. In most cases, the percent of correct constraints (defined as constraints satisfied in the native structure) that were violated in the final models was less than the percent incorrect constraints (defined as constraints violated in the native structure) that were violated in the final models (average values of 16.5% of incorrect constraints violated and 2.5% of correct constraints violated over the test set; see Supporting Text, which is published as supporting information on the PNAS web site). Thus, the stiffness of our physical model, with stringent treatment of sterics, makes it robust to spurious forces arising from incorrect constraints. The considerable added information from the energy function makes the method less sensitive to the choice of template. Although the lowest-energy models are more frequently worse than their templates over the aligned regions, the energy function allows the generation of some models that are better than the starting template.

Successful Examples.

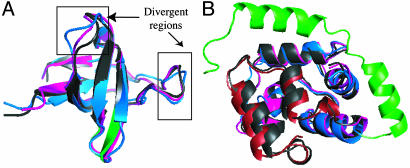
The Crk SH3 domain (PDB ID code 1b07) structure consists of strands and short connecting loops. The backbones of the template-based model and the low-energy* model folded with constraints derived from the homologous 2sem structure overlay closely with the 1b07 structure. However, two aligned regions show differences (Fig. 5A, boxed regions). The model folded with constraints more closely resembles the 1b07 native structure than the template-based model.

Fig. 5.

Examples of successful test cases. (A) 1b07 query, 2sem template. The native 1b07 structure is shown in dark gray with the unaligned regions shown in green, the fixed template model in blue, and the model folded with constraints is shown in magenta. Backbone superposition of the native structure and the two models are shown. (B) 1pva query, 1ahr template. The aligned regions of the native 1pva structure, the fixed template model, and the model folded with constraints are shown in gray, blue, and magenta, respectively. The 38-residue unaligned region is shown in gray, green, and red for the native structure, the template-based model, and the model folded with constraints, respectively. This figure was made with pymol (23).

For the Pike parvalbumin α-component (PDB ID code 1pva) example, the most significant difference between the native structure and the models folded with constraints is the 38-residue unaligned region at the N terminus of the 1pva sequence. Both the model folded with constraints and the fixed template model with loops built with rosetta predict two helices and a short loop for this unaligned region, but the extension closely resembles the native structure in the model folded with constraints, whereas in the rosettasvr template-based model the orientations and locations of the helices are incorrect (Fig. 5B). An additional 50 models were made using rosettasvr, and none modeled the correct conformation of the unaligned region.

Effect of Increased Conformational Space Sampling on the 1pva-1ahr Test Case.

As discussed above, we believe that many independent trajectories are required to finely sample conformational space around the native structure such that the details of the native backbone and the native side-chain packing arrangement can be found. To test this hypothesis, we used the distributed computing software boinc (19) on the 1pva example because it showed a promising correlation of energy with rmsd but was not an easy target because of the long unaligned region and features in the aligned region that differed from the 1ahr template. We were able to run thousands of simulations each day, and the population of 54,267 full-atom models contained 43 models with <1.5 Å rmsd (compared with 6 produced using our in-house computing clusters).

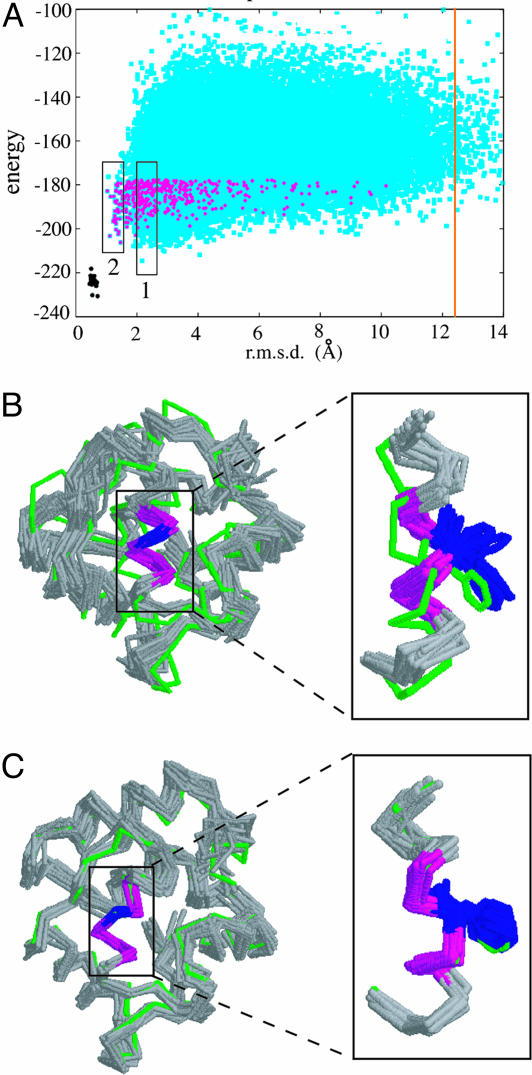
Even with thousands of trajectories, the space near the native is still under-sampled and the lowest energy models do not correspond to the most accurate models (Fig. 6A). However, in clustering the lowest 30% energy models, we found that the second-largest cluster was structurally very similar to the native structure (Fig. 6A, boxed region 2, and Fig. 6C), The region highlighted in green in Fig. 6 A and B is a continuous helix in the 1ahr template structure and is predicted to be a continuous helix with the secondary structure prediction programs used by rosetta to select fragments. The helix is broken in the 1pva native structure at Phe-65, and this unusual feature is rarely incorporated into the models. In the models belonging to the largest cluster (Fig. 6A, boxed region 1) the helix is continuous (Fig. 6B) but adopts the correct conformation in the second-largest cluster (Fig. 6C).

Fig. 6.

The 1pva–1ahr query–template pair full-atom models generated using the boinc distributed computing resource. (A) Cyan points represent the energy and rmsd values of the full-atom models; 54,267 full-atom models are shown. Magenta points represent models that contained nonhelical backbone torsion angles at position 65 and are a subset of the 30% lowest-energy models used for clustering. For reference, the results of 20 trajectories of idealized minimized 1pva native structures (described in ref. 17) are shown in black. The boxes labeled 1 and 2 denote the locations of the models belonging to the largest and second-largest cluster, respectively. The orange vertical line represents the rmsd of the template-based model; the energy of the template-based model is out of range of this plot. (B and C) Models belonging to the largest cluster (B) and second-largest cluster (C) correspond to the lowest-energy and most accurate models in the population, respectively. (B) Average cluster rmsd = 2.5 Å. (C) Average cluster rmsd = 1.4 Å. Models are shown in gray, the native 1pva structure is shown in green, and the irregular helix is shown in magenta. Phe-65, which has nonhelical backbone torsion angles, is shown in blue. The helix in Inset is rotated by 90° to better show the superposition of the backbones and the Phe-65 side chains.

Thus, although the low-rmsd models are not sufficiently similar to the native structure to have as low energies, they can be detected based on their close proximity to one another. This finding is reminiscent of the ability of clustering to select native-like models out of populations of low-resolution models (20), but here the selection is based on finer details such as an irregular helix rather than overall topology. It is at first surprising that several of the models that incorporate the bent helix are found in a tight cluster, because only 3.5% of the population used for clustering contained this feature. However, as shown in Fig. 6A (magenta points), the lowest-energy models containing the bent helix feature are native-like, and hence similar to each other. Many low-energy conformations are possible if Phe-65 and neighboring residues are in a canonical α-helix conformation, but only the native-like conformation is low in energy if the backbone torsion angles at this position are nonhelical.

Discussion

We have developed a method to build homology models of protein sequences of unknown structure using rosetta fragment insertion combined with distance constraints derived from homologous structures. Coordinates are built for all residues in the query sequence, regardless of whether they were aligned to a template or not, or are in regular secondary-structure elements or flexible loops. Although the resulting lowest-energy models are frequently less accurate than their templates over aligned regions, at least 1 of the 10 lowest-energy models is frequently more accurate than the template from which they were derived. In addition, the models are physically reasonable; they contain the same number or fewer atomic overlaps than native crystal structures and by construction have ideal bond lengths and angles. It has been found that models may sometimes be numerically evaluated incorrectly as being more native-like by virtue of overlaps (21), an error we wished to avoid in determining whether our method truly accomplishes structural improvement. As such, we are encouraged by the lack of atomic overlaps demonstrated by our low-rmsd models.

In the course of this study, we used distance constraints derived from a single template applied to a single query sequence. It is possible that incorporating constraints from multiple templates, as modeller (13) does, will improve the results and extend the method to more remote sequence–structure pairs. Constraints derived from experimental information also could be easily incorporated. In addition, it may be possible to refine and discriminate among candidate alignments by generating populations of models for each alignment and comparing their energies.

The method presented here is an improvement over current methods in the range of sequence identity, protein size, and alignment coverage tested here, but it has some limitations. The computational cost is large, especially when compared with other homology modeling programs such as modeller. The method is currently less successful for proteins with high contact order, and the simulations require even more computational time for these cases. Although the method is comparable with fixed-template-based methods for the very largest proteins we tested, a 255-residue TIM barrel (1aw2) and a 245-residue two-domain ATPase (1d2n), these cases will likely require additional sampling because the near-native space was not well populated (see Fig. 7).

The size of the conformational space a polypeptide chain can occupy is vast, even for small proteins when an initial low-resolution model is structurally similar to the native conformation. In addition to the increased degrees of freedom, searching this space becomes more difficult with higher resolution because of increased steric constraints. Slight differences in the backbone conformation may accommodate entirely different combinations of side-chain conformations, leading to a very rough energy landscape. Irregular features such as the 1pva broken helix add to the complexity of the search problem, because they are essential to locating the native minimum but may be rare in model populations. Distributed computing resources provide a powerful tool in which to navigate this space and potentially populate the region near native conformation with enough backbone scaffolds such that the native side-chain conformations can be accommodated.

Methods

The data set, generation of sequence alignments, and the full-atom refinement protocol are described in Supporting Text.

Distance Constraint Generation.

Interatomic distances between β-carbon atoms were calculated for each template structure. For each pair of atoms whose distance d < 10 Å in the template structure a constraint was derived with a lower bound (l) of d − 1.5 Å and an upper bound (u) of d + 2.0 Å. To generate a set of constraints as consistent as possible with the query structure, the initial set of constraints was combined with the rosetta ab initio protocol by penalizing pairwise distances that deviated from the bounds and used to generate 1,000 initial low-resolution models. These initial models were then analyzed to determine how many times each distance constraint was violated. The constraints that were violated more often than (0.5 × max) times, where max equals the maximum number of times any one constraint was violated, were removed, and the low-resolution folding protocol was repeated. This procedure reduced the number of violations of the native query structure with the initial constraint data set by 36.1% on average, compared with 14.0% if the same number of constraints were randomly removed from the complete constraint set (see Table 1, which is published as supporting information on the PNAS web site).

Folding Protocol.

Initial models were folded by using the rosetta fragment insertion protocol (8–10) with side chains represented by centroids. Custom fragment libraries were constructed for each query–template pair by first generating fragments from structures of homologous proteins with sequence identities less than or equal to the test query–template pair. These fragments then were added to a standard set of fragments from a set of nonredundant PDB structures, where the sequences of the structures are <60% identical to any other sequence in the set.

A fragment screening protocol modified from Rohl et al. (8) was used to maximize the satisfaction of the constraints. After a position was randomly selected for insertion, the candidate fragments for that site were evaluated for the effect that they would have on the constraints violation score after insertion. The net rotation and offset of each fragment was determined and applied to one of the atoms for each constrained pair of atoms by using the methods described for wobble moves in ref. 8. A constraint satisfaction score was computed for each candidate fragment, cs = Σ_max(0, ((d_ij²) − (r_ij²))), where d_ij is the distance between the two atoms defining the constraint and u_ij is the upper distance bound, which is taken to be the distance between the same two atoms in the template structure. The sum is over the subset of constraints for which the distance between the constrained atoms would be affected by the insertion (e.g., pairs in which atoms i and j are on opposite sides of the insertion point). A fragment was then randomly selected from among those fragments for which cs ≤ (rs*tolerance), where the reference score rs was calculated as for cs but for the structure before the insertion. The value of tolerance alternates between 2.0 or 5.0. If no fragments meeting these criteria were found, a fragment insertion at the N-terminally adjacent site was tried. If an insertion site was selected that did not affect the distance between any constrained atom pairs, 1 of the top 25 fragments for this site was selected at random from the fragment library, as in the standard rosetta de novo structure prediction protocol (8, 9).

The conformation of the model after each fragment insertion then was evaluated with the rosetta low-resolution energy function (8) in combination with the distance constraint data. A penalty was applied to residues with interatomic distances d_ij that were outside the allowed range described above. Small and large distance violations were penalized by using quadratic and linear functional forms, respectively, according to the following:

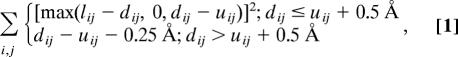where 0.5 Å is the switching distance, d_ij is the distance between C^β atoms i and j, and l and u are the upper and lower bounds, respectively, as described above.

The method described above plus two variations designed to improve and increase the diversity of the low-resolution population were used to generate low-resolution models. The first variation used a fragment library that had been enriched with fragments of high local sequence identity to the query sequence in addition to the homologous fragments described above. For the second variation, an initial population of structures was generated by using the method described above, and the variance in φ and ψ in the population was computed for each residue in the lowest 10% energy models. For residues where the mean square deviation was >40°, the φ–ψ distributions were clustered. The φ–ψ distributions in the cluster centers observed at high frequencies then were preferentially resampled in a large-scale run. At the beginning of each run, for each stretch of five or fewer consecutive “variable” positions, a single residue and a corresponding cluster center were selected at random, and only fragments with deviation < 40° in φ and ψ of the selected cluster center were allowed for insertion. In a number of cases, this procedure produced a population of low-scoring structures with lower rmsds than in the starting population (data not shown). A total of 10,000 models using each method were generated for each query–template pair with 3dpair alignments, but because of limited computer time only 1,000 were made for each query–template pair with psi-blast alignments. Their energies were ranked by using the standard rosetta centroid energy function plus the constraint energy, and the lowest 15% of the population from each of the three methods was subjected to full-atom refinement.

Final Model Selection.

Following the refinement protocol, the refined models from each of the three folding protocols were combined and ranked according to energy. We used the energy function described in ref. 17 combined with the constraint energy described above. We selected three types of models for analysis: the lowest-energy model, the lowest-rmsd model, and the lowest-rmsd model out of the lowest 10 energy models (referred to as lowest-energy*). The rmsd was calculated over all C^α atoms. Cluster analysis was carried out as described in ref. 22, by using a clustering threshold of between 1 and 3 Å.

Generation of Complete Chain Models with modeller and Fixed-Template rosettasvr Modeling.

We generated one model for each query sequence by using the rosettasvr modeling protocol (12). The modeller model used for analysis was the best-scoring model, using the modeller score, out of 100 models produced initially. The same alignments were used as for the folding protocol.

Atomic Clash Score Analysis Calculation.

Atomic clashes for native structures, rosetta models produced by folding with constraints, models produced with the rosettasvr fixed-template method (12), or models produced with modeller (13) were calculated by using molprobity (7). Before calculating clashes, hydrogen atoms were optimized and added according to suggestions from the “Reduce” utility incorporated with molprobity. Clashes were calculated over aligned regions only. An atomic clash was counted if the distance between atoms 1 and 2 is less than [(r₁ + r₂)/2] − 0.4 Å where r₁ and r₂ are the radii in Å of atoms 1 and 2, respectively.

Model Generation Using boinc Distributed Computing.

Each boinc (19) client in the Rosetta@Home project (http://boinc.bakerlab.org) generated 10 low-resolution models with the rosetta fragment insertion protocol and refined the two lowest-energy models by using the full-atom refinement protocol. The community that participated in this project produced 265,000 low-resolution models and 53,000 full-atom models with constraint information for the 1pva-1ahr test case.

Abbreviations

PDB

Protein Data Bank

rmsd

rms deviation.