Simple and accurate estimation of ancestral protein sequences

Abstract

There are a variety of reasons to reconstruct the sequences of ancient proteins, but whatever the reason, the value of the reconstructed protein depends on the accuracy with which the ancient sequence is inferred. This study uses sequences simulated by a sequence-evolution simulation program that compares parsimony, maximum likelihood, and the Bayesian methods of inferring ancestral sequences and concludes that the Bayesian method, as implemented by mrbayes 3.11, is preferred. Estimated ancestral sequences are of necessity the same length as the alignment on which the underlying phylogeny is based. A highly accurate method for correcting the estimated sequences is introduced, and it is shown that the correction permits inferring the sequences of ancient protein sequences with a very high degree of accuracy.

Over the last 15 years, reconstruction of ancestral protein sequences has become an important way to infer information about the past. Reconstruction of the ancestor of the α- and β-chymases showed that the narrow substrate specificity of the α-chymases was the ancestral state (1). Reconstruction also demonstrated that the ancestor of the eosinophil-derived neurotoxin/eosinophil cationic protein RNase possessed weak antiviral activity that was enhanced 13-fold by amino acid substitutions at two interacting sites to produce the eosinophil-derived neurotoxin RNase (2). Because neither substitution alone enhanced RNase activity, Zhang and Rosenberg were able to conclude that the individually neutral substitutions were critical to the complementary advantageous double substitution. Golding and Dean (3) have elegantly reviewed several studies in which ancestral reconstruction, protein structure, and phylogenetics have jointly contributed to understanding the properties of ancestral proteins. Ancestral protein reconstruction has also been used to draw inferences about the physical environment of ancient organisms. Reconstruction of the ancestral Eubacterial elongation factor EF-Tu showed that it had a temperature optimum of 55–65°C, indicating that the eubacterial ancestor was a thermophile not a mesophile or hyperthermophile (4). Similarly, reconstruction of an ancestral archosaur visual pigment indicated that that the archosaur ancestral pigment supported dim-light vision, suggesting that the ancestor may have been nocturnal not diurnal (5).

There are two distinctly different approaches to reconstructing ancestral sequences. The first approach involves identifying sites that are likely to be important to the activity of interest, inferring the ancestral states of those sites, then replacing the corresponding residues of a modern protein with the ancestral residues by site-directed mutagenesis of an existing gene. That approach has the advantage that the investigator needs to infer the ancestral states of only a few residues, but the approach is limited to proteins in which structure–function relationships are well understood. Another disadvantage is that the ancestral residues must function within the context of a protein that is largely modern, and it must be assumed that the modern residues do not significantly affect the function conferred by the ancestral residues. Examples of the site-directed mutagenesis approach can be found in refs. 2 and 6. The alternative involves inferring the entire ancestral sequence then assembling the corresponding gene de novo. That approach has the advantages that structure–function relationships need not be well understood and that not only the critical residues, but all residues, are ancient. Examples of the de novo construction approach are found in refs. 7 and 1.

Benner and his colleagues (8) have combined the best features of the two approaches into an approach that they describe as the “paleobiochemical experiment.” Although they use site-directed mutagenesis to construct the sequences of ancient enzymes, they construct the complete inferred ancient sequences. In studying ancient ribonucleases (9–11), they used parsimony to infer the sequences of ancient RNases of the artiodactyls superfamily and found that most amino acids could be inferred unambiguously. In several cases where amino acid assignments were ambiguous, they reconstructed multiple sequences. By comparing the properties, including substrate specificity and thermal stability, of the ancient enzymes, they were able to identify the key amino acid substitution that was responsible for the changes in catalytic activity and to relate those changes to probable roles of the RNase during artiodactyls evolution. In a recent study of yeast alcohol dehydrogenases (8), they used a maximum likelihood approach to infer the most probable sequences of Adh_A, the ancestor of Adh1 and Adh2. Again, where ancient amino acids could not be assigned with posterior probabilities >80%, they reconstructed multiple sequences. Measurement of the kinetic properties of the reconstructed Adh_A proteins showed that the ancient protein resembled modern Adh1 from which they inferred that “the ancient yeast cell did not have an Adh specialized for the consumption of ethanol, similar to modern Adh2, but rather had an Adh specialized for making ethanol, similar to Adh1.” In both studies, the behaviors of ancient proteins that differed at ambiguous amino acids were sufficiently similar so that the interpretations of that behavior, and the resulting inferences, were quite robust. Those studies were facilitated by the fact that internal gaps were absent from the alignments of the relevant modern proteins.

Whatever the means of physically reconstructing the ancestral protein, the first step is to estimate a robust phylogeny, and the second step is to estimate the sequence of the protein at the node of interest within that phylogeny. The most widely used methods of ancestral state reconstruction have been parsimony (12–14) and maximum likelihood (15–18), although distance-based methods have also been described (19). mrbayes (20) implements the Bayesian method of phylogenetic tree reconstruction, and the most recent version, version 3.1, now implements the reconstruction of ancestral states by the Bayesian method.

The cost, in both money and time, of constructing ancestral proteins is considerable, and the inferences drawn from characterizing such ancient proteins are only as accurate as the sequences of the proteins. It is therefore essential to estimate the sequences of ancestral proteins by the most accurate means available. Several studies have used computer simulations to compare the accuracies with which different methods reconstruct ancestral sequences (17–19); however, the simulated sequences in those studies were not very realistic in that they did not include insertions and deletions. A recently described sequence-evolution simulation program, evolveagene (21), is biologically realistic in that it separates mutation and selection and in that the mutations not only include base substitutions but also insertions and deletions. That program was used to compare the accuracies of several phylogenetic methods (21). This study uses evolveagene to compare the accuracies with which three methods reconstruct ancestral sequences.

Most of the programs that reconstruct ancestral sequences are quite sophisticated, suitable for use only by those with considerable experience in phylogenetics and systematics, and are available only for unix or windows platforms. The widely used programs paup* (14) and mrbayes (20) are available for macintosh, windows, and unix platforms, are relatively easy to use, and their use has been described in detail in a book specifically intended for those with little experience in phylogenetics (22) and in a very well written user manual for mrbayes 3.1. This study therefore focuses on comparing the accuracies of weighted parsimony and maximum likelihood as implemented by paup* 4.0b10 and the Bayesian method as implemented by mrbayes 3.1.

Results

Seven data sets were simulated by using evolveagene as described in Materials and Methods. Mean branch lengths ranged from 0.0058 to 0.189. As branch lengths increased, the percentage of the alignment occupied by gap characters increased, and the Q scores decreased (Table 1). The lowest Q scores were similar to those of an alignment of the class D β-lactamases (23) in which the root of the tree is more than a billion years old.

Table 1.

Details of simulated sequences

Data set	Root gene	Length	Alignment length	Average mutations per branch	Mean branch length in mutations per site (range)	Percent gap characters, %	Protein Q score
D1	Tem1	858	867	5.7	0.0058 (0.00115–0.00153)	0.97	91.71
D2	Tem1	858	858	10.0	0.01167 (0.00117–0.02331)	0	87.61
D3	Tem1	858	858	21.2	0.02466 (0.00233–0.04662)	0.35	77.71
D4	Tem1	858	861	39.7	0.04608 (0.00116–0.09059)	2.0	60.11
D5	Tem1	858	915	87.6	0.09570 (0.00437–0.17486)	8.2	39.82
D6	Tem1	858	900	170.3	0.18918 (0.01667–0.35333)	7.8	24.48
D7	XisC	1554	1593	215.9	0.13555 (0.00126–0.25047)	8.3	26.27

Correction of Estimated Ancestral Sequences by Elimination of Ancestral Gaps.

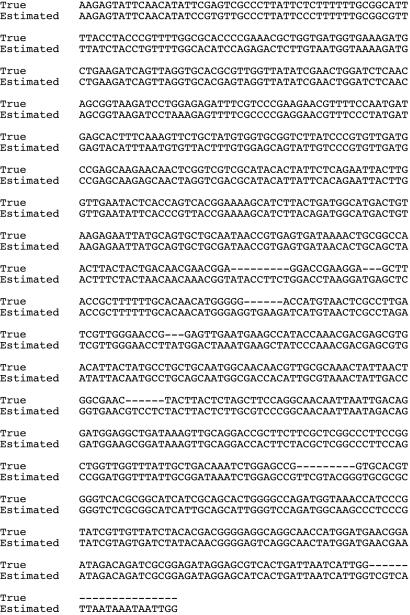
When ancestral sequences are reconstructed by any method, the reconstructed sequence is, of necessity, exactly as long as the alignment. When gaps are present in the alignment as the result of insertions and deletions (indels) that occurred during the evolution of the terminal sequence, it is likely that the ancestral sequence was actually shorter than the alignment. Fig. 1 shows an alignment of the node B ancestral DNA sequence from data set D5 as estimated by the Bayesian method with the true DNA sequence of node B. The true sequence is 858 bases, whereas the estimated sequence is 915 characters. As a result, there are numerous gaps in the true sequence when it is aligned to the estimated sequence. When sequence evolution is simulated and the true sequence is known, the estimated sequence can be corrected by deletion of those characters corresponding to the gaps in the true sequences. In reality, of course, the true sequence is unknown and that correction is not possible. It is possible, however, to estimate the positions of the ancestral gaps by treating the gaps as characters.

Fig. 1.

Alignment of a true ancestral sequence with the estimated ancestral sequence. The sequence is that of node B from data set D5.

To estimate ancestral gaps by parsimony, the nucleotide characters in the DNA alignments were converted to 0 and the gap characters to 1, parsimony trees were estimated from the binary data, as described in Materials and Methods except that there was no transversion penalty, and the ancestral binary sequences were estimated. To estimate ancestral gaps by the Bayesian method, the nucleotide characters in the DNA alignment were converted to “A” and the gap characters to “G.” Bayesian trees were estimated as described in Materials and Methods except that the data were not partitioned according to codon position: nst was set to 1, ratepr was set to fixed, and statefreqpr was set to dirichlet (1), and the ancestral sequences were estimated. The program extractancestralgaps was used to extract the ancestral sequences from the “.p” files in much the same manner as described for extractancestralgaps, except that the “A” characters were converted to “+” and the “G” characters to “−.”

To correct the estimated ancestral DNA sequences, the ancestral gap sequences (consisting of “+” and “−”) were written below the corresponding ancestral DNA and protein sequences, and characters corresponding to the “−” were deleted from the ancestral DNA and protein sequences. The maximum likelihood method as implemented by paup* 4.0b10 is not applicable to binary data. Therefore, ancestral gap sequences estimated by parsimony were used to correct ancestral sequences estimated by maximum likelihood.

Accuracies of Ancestral Sequences.

Tables 2 and 3 show the accuracies of corrected reconstructed DNA and protein sequences respectively for nodes B, D, H, and P and for data set D7 for node FF as reconstructed by weighted parsimony and by maximum likelihood as implemented by paup* 4.0b10. Some general patterns are seen. As branch lengths increase and Q scores decrease, the accuracies of the reconstructed node sequences decrease. Paired t tests show, for both reconstructed DNA sequences and reconstructed protein sequences, that sequences reconstructed by maximum likelihood are more accurate than those reconstructed by weighted parsimony and reconstructed protein sequences are more accurate than reconstructed DNA sequences (in each case P < 0.0001). The higher accuracy of reconstructed protein sequences is because the degeneracy of the genetic code means that often an erroneous base does not result in an erroneous amino acid.

Table 2.

Accuracies of corrected ancestral DNA sequences estimated by weighted parsimony (Pars) and maximum likelihood (ML)

Data set	Node accuracies
	Node B		Node D		Node H		Node P		Node FF
	Pars	ML	Pars	ML	Pars	ML	Pars	ML	Pars	ML
D1	0.991	0.992	0.987	0.991	0.985	0.992	0.991	0.991
D2	0.986	0.999	0.979	0.999	0.993	1.0	0.987	0.994
D3	0.941	0.999	0.987	0.999	0.980	0.995	0.941	0.956
D4	0.900	0.948	0.833	0.981	0.938	0.990	0.920	0.970
D5	0.830	0.894	0.807	0.911	0.805	0.921	0.765	0.934
D6	0.781	0.833	0.692	0.838	0.730	0.840	0.486*	0.814*
D7	0.776†	0.881†	0.747‡	0.866‡	0.729§	0.880§	0.738§	0.895§	0.873*	0.968*

*Corrected sequence is six codons longer than the true sequence.

^†Corrected sequence is seven codons shorter than the true sequence.

^‡Corrected sequence is eight codons shorter than the true sequence.

^§Corrected sequence is three codons longer than the true sequence.

Table 3.

Accuracies of corrected ancestral protein sequences estimated by weighted parsimony (Pars) and maximum likelihood (ML)

Data set	Node accuracies
	Node B		Node D		Node H		Node P		Node FF
	Pars	ML	Pars	ML	Pars	ML	Pars	ML	Pars	ML
D1	0.997	1.0	0.996	1.0	0.993	1.0	1.0	1.0
D2	0.990	1.0	0.997	0.997	0.993	1.0	0.993	1.0
D3	0.951	1.0	1.0	1.0	0.982	0.996	0.943	0.958
D4	0.955	0.997	0.936	1.0	0.986	1.0	0.971	0.986
D5	0.895	0.965	0.886	0.989	0.864	0.982	0.817	0.950
D6	0.790	0.948	0.753	0.947	0.771	0.937	0.693*	0.866*
D7	0.807†	0.934†	0.800‡	0.931‡	0.827§	0.971§	0.778§	0.937§	0.895*	0.994*

*Corrected sequence is six amino acids longer than the true sequence.

^†Corrected sequence is seven amino acids shorter than the true sequence.

^‡Corrected sequence is eight amino acids shorter than the true sequence.

^§Corrected sequence is three amino acids longer than the true sequence.

Tables 4 and 5 show the accuracies of corrected reconstructed DNA and protein sequences respectively for nodes B, D, H, and P and for data set D7 for node FF as reconstructed by the Bayesian method. Again, accuracy decreases as branch lengths increase and Q scores decrease. Paired t tests show that the Bayesian method is more accurate than weighted parsimony (P < 0.0001) and that reconstructed protein sequences are more accurate than reconstructed DNA sequences (P < 0.0001). For DNA sequences, the Bayesian method is better (P = 0.016), but for protein sequences maximum likelihood is better (P = 0.029).

Table 4.

Accuracies of corrected reconstructed ancestral DNA sequences estimated by the Bayesian method

Data set	Node accuracies
	Node B		Node D		Node H		Node P		Node FF
	Est	Accuracy	Est	Accuracy	Est	Accuracy	Est	Accuracy	Est	Accuracy
D1	1.0	1.0	0.999	0.999	1.0	1.0	1.0	0.999
D2	0.997	1.0	0.999	0.999	0.999	1.0	0.999	1.0
D3	0.998	0.997	0.996	0.995	0.992	0.995	0.997	0.999
D4	0.963	0.945	0.985	0.980	0.989	0.993	0.994	0.992
D5	0.922	0.876	0.919	0.908*	0.938	0.922†	0.970	0.974
D6	0.902	0.826	0.877	0.825	0.884	0.835	0.904	0.884
D7	0.916	0.868‡	0.910	0.884*	0.947	0.932	0.983	0.986	0.976	0.967

Est is the mean probability of the most probable base at each site, i.e., the estimated accuracy.

*Corrected sequence was one codon shorter than the true sequence.

^†Corrected sequence was one codon longer than the true sequence.

^‡Corrected sequence was five codons shorter than the true sequence.

Table 5.

Accuracies of corrected reconstructed ancestral protein sequences estimated by the Bayesian method

Data set	Node accuracies
	Node B		Node D		Node H		Node P		Node FF
	Est	Accuracy	Est	Accuracy	Est	Accuracy	Est	Accuracy	Est	Accuracy
D1	0.999	1.0	0.999	1.0	0.999	1.0	0.999	1.0
D2	1.0	1.0	0.999	0.997	1.0	1.0	1.0	1.0
D3	0.999	1.0	0.997	1.0	0.996	0.996	0.999	1.0
D4	0.989	0.993	0.997	1.0	0.998	1.0	0.998	1.0
D5	0.965	0.972	0.972	0.989*	0.973	0.986†	0.994	0.996
D6	0.929	0.923	0.926	0.937	0.923	0.940	0.941	0.960
D7	0.958	0.960‡	0.946	0.962*	0.975	0.980	0.995	0.996	0.990	0.994

Est is the mean probability of the most probable amino acid at each site, i.e., the estimated accuracy.

*Corrected sequence was one amino acid shorter than the true sequence.

^†Corrected sequence was one amino acid longer than the true sequence.

^‡Corrected sequence was five amino acids shorter than the true sequence.

Aside from accuracy, the Bayesian method as implemented by mrbayes 3.1 offers a significant advantage over maximum likelihood as implemented by paup* 4.0b10: mrbayes provides an estimate of the probability of the most probable base or amino acid at each site. The average of those probabilities over all of the sites in the corrected ancestral sequence is an estimate of the accuracy of that sequence. Tables 4 and 5 show both the estimated accuracies and the actual accuracies of the sequences. Paired t tests show that for the DNA sequences mrbayes overestimates the accuracy by ≈1.3% (P = 0.03), but for protein sequences mrbayes underestimates accuracy by ≈0.4% (P = 0.001).

Discussion

Both maximum likelihood and the Bayesian method provide very accurate estimates of ancestral sequences, particularly ancestral protein sequences, even for very deep nodes of trees with long branches. By estimating the positions of gaps in the estimated ancestral sequences, it is possible to correct those sequences very accurately. By using the Bayesian method, the correction was perfect in 25 of the 29 reconstructed sequences.

Because of the uncertainty associated with reconstructing entire ancient proteins, many studies instead use site-directed mutagenesis to introduce ancient amino acids into positions that are believed to be critical for function and specificity. Although valuable, that approach depends not only on the accuracy and completeness with which those critical sites are identified but also on the assumption that ancient amino acids function in the context of a modern protein background identically to the way they functioned in the context of an entire ancient protein. The present study suggests that correcting the estimated sequences of ancient proteins by using the estimated ancient gaps makes it possible, by using the Bayesian method as implemented by mrbayes 3.1, to estimate entire ancient proteins with a high degree of accuracy and, at the same time, to estimate correctly that accuracy. Indeed, because the probability of each individual residue being correct is reported, it is possible to know the accuracies with which the critical amino acids are estimated as well as knowing the overall estimate of the accuracy of the ancient protein.

How well does this approach perform with real data? Barlow and Hall (23) constructed a phylogeny of the highly divergent OXA β-lactamases and estimated the ages of two nodes at which the ancient genes had been mobilized to plasmids. Reconstruction of the protein sequence at node B, estimated to have occurred 43 million years ago, gave an estimated accuracy of 0.964, and that of node C, estimated to have occurred 116 million years ago, gave an estimated accuracy of 0.914. This finding is not to suggest that those accuracies are typical or representative of accuracies associated with nodes that old; it simply illustrates that an investigator can use those estimates to decide whether or not to reconstruct an entire protein.

As pointed out by one reviewer, the uncertainty involved in deciding which phylogenetic method to use is generally small relative to the uncertainty arising from factors such as rapid sequence evolution and other features of the natural history. Whatever methods are used, robust interpretations of reconstructed ancient proteins requires identification of ambiguous amino acid assignments and construction and explorations of multiple sequences to accommodate those ambiguities.

Materials and Methods

Computer Simulations.

evolveagene (21) simulates evolution by introducing random base substitutions, insertions, and deletions into a starting DNA sequence (the root) according to the Escherichia coli mutational spectrum. The evolveagene simulation program is described in detail in ref. 21. Briefly, a bifurcating tree such as that shown in Fig. 2 is constructed. The user specifies the number of terminal taxa, the probability of base substitutions (which is the dN/dS ratio), the probabilities of accepting insertions and deletions, and the average number of mutations per branch. The actual number of mutations on each branch is drawn at random from a uniform distribution from zero to twice the average number of mutations. Given that tree and the sequence of the root node, mutations are introduced at random sites according to the mutational spectrum of E. coli. Base substitutions that result in nonsense mutations and indels that result in frame shifts are not accepted on the grounds that they result in loss of function and would be eliminated by purifying selection. The probabilities of accepting other mutations are those set by the user. The process of random mutagenesis is continued until the number of mutations that have been accepted corresponds to the previously determined length for that branch. The resulting sequence constitutes the sequence at the node that is the immediate descendant of the starting sequence. That process is reiterated to generate the sequences of all internal and external nodes. The sequences of all nodes are saved to a file. The simulation program is unusual in that it does not rely on any formal model of evolution, substitution rates, etc. The evolutionary model is simply that of mutation (according to the spontaneous mutation spectrum of E. coli) and selection according to the probabilities set by the user.

Fig. 2.

Node naming convention for simulated trees. [Reproduced with permission from ref. 21 (Copyright 2005, Oxford Univ. Press).]

The root sequence for data sets D1–D6 was TEM1 (GenBank accession no. AF309824), an 858-bp sequence that encodes the TEM-1 β-lactamase. The root sequences for data set D7 was XisC (GenBank accession no. U08014), a sequence that encodes the HupL site-specific recombinase from an Anabena species (Table 1). For all simulations, the probability of accepting a base substitution was 0.1, the probability of accepting an insertion or deletion was 0.025, and the average number of mutations per branch is shown in Table 1. For data sets D1–D6, there were 32 terminal taxa, and for data set D7, there were 64 terminal taxa. Fig. 2 shows the naming convention for terminal and internal nodes.

Alignment.

An earlier study (21) showed that the most accurate phylogenetic reconstructions of coding sequences were obtained by aligning the corresponding proteins, then by using the program codonalign (24) to introduce triplet gaps into the coding sequences at positions corresponding to the gaps in the protein alignment. Proteins corresponding to the simulated sequences were aligned with clustalx (25) by using pairwise gap penalties of 10.0 and 0.1 for gap opening and gap extension and multiple alignment gap penalties of 3.0 and 1.8. clustalx calculates a quality score for each site in the alignment. The Q score (Table 1), the average quality score over all sites, is a measure of the overall quality of the alignment, and the higher the Q score, the better the alignment (21). codonalign 2.0 (24) was used to align the simulated sequences on the basis of the alignment of the corresponding protein sequences.

Phylogenetic Tree Reconstructions.

Phylogenetic trees were estimated by the weighted parsimony method (26) and maximum likelihood method (27) by using paup* 4.0b10 (14) and by the Bayesian method (28) by using mrbayes 3.1 (20). For weighted parsimony, the transversion weight penalty was set at 2. For maximum likelihood, the data were partitioned by codon position, the number of substitution types was set to 6, and the ratepr was set to variable so that rates were site-specific according to codon position. For the Bayesian method, the data were partitioned by codon position, the number of substitution types was set to 6, the rate matrix and the base frequencies were estimated, and the rates were site-specific according to codon position. Four chains were run for one million generations, trees were estimated every 100 generations, and a consensus tree was estimated by using a burnin of 2,000 trees.

Estimation of Ancestral Sequences.

paup* estimates the sequences of all internal nodes by the command DescribeTrees with the XOut parameter set to internal. The results are printed to a log file. paup* does not print the ancestral sequences in a format that permits them to easily be copied for the purpose of alignment with the true sequences of the internal nodes. A simple text manipulation program, paupextractancseq, was written to extract the sequences from the log file, to translate each sequence to a corresponding protein sequence, and to write each DNA and corresponding protein sequence to a new file in a suitable format.

mrbayes requires that for each internal node a constraint is set to keep all of the descendants of that node together in a clade, and the report command parameter is set to ancstates = yes. mrbayes does not print the ancestral sequences in a format the permits them to easily be copied for the purpose of alignment with the true sequences of the internal nodes. A text manipulation program, extractancseq, extracts the probabilities of each base at each site from the .p file that mrbayes writes, calculates the mean probabilities from the postburnin trees, and writes those probabilities, the most probable base at each site and its probability, and the most probable DNA sequence in a suitable format to an output file. It then translates the most probable DNA sequence, calculates the probability of the most probable amino acid at each site, and writes those probabilities and the most probable protein sequence to the output file. extractancseq for macintosh and windows platforms is available from the author upon request.

Calculation of Ancestral Sequence Accuracy.

The estimated ancestral DNA and protein sequences were aligned with the true ancestral sequences by the blast 2 sequences program (29) as implemented by the National Center for Biotechnology Information blast web site (www.ncbi.nlm.nih.gov/blast/). The accuracy score is the number of identical sequences divided by the length of the true sequence.