The biological lifetime of nitric oxide: Implications for the perivascular dynamics of NO and O₂

Abstract

Endothelial nitric oxide (nitrogen monoxide) is synthesized at the intravascular/extravascular interface. We previously have reported the intravascular half-life of NO, as a result of consumption by erythrocytes, as approximately 2 ms. We report here studies designed to estimate the lifetime of NO in the parenchymal (extravascular) tissue and describe the implications of these results for the distribution of NO and oxygen concentration gradients away from the blood vessel. The rate of consumption of NO by parenchymal cells (hepatocytes) linearly depends on both NO and O₂ concentration. We estimate that the extravascular half-life of NO will range from 0.09 to > 2 s, depending on O₂ concentration and thus distance from the vessel. Computer modeling reveals that this phenomenon, coupled with reversible NO inhibition of cellular mitochondrial oxygen consumption, substantially extends the zone of adequate tissue cellular oxygenation away from the blood vessel, with an especially dramatic effect during conditions of increased tissue work (oxygen consumption). This represents a second action of NO, in addition to vasodilation, in enhancing tissue cellular respiration and provides a possible physiological function for the known reversible inhibition of mitochondrial respiration by low concentrations of NO.

Quite possibly, the two most important properties of nitric oxide (nitrogen monoxide) as a messenger and effector molecule in mammals are its ready diffusibility and its relatively short lifetime (1). With regard to the lifetime of NO, initial measurements using cascade perfusion experiments suggested a disappearance of NO with a lifetime on the order of seconds (2); however, measurements with intact tissue (the coronary circulation) yield a much faster rate, on the order of 0.1 s (3). Although reaction of NO with oxygen (4) is commonly cited as the explanation for this disappearance, this is highly unlikely because it will be too slow with physiologically relevant NO concentrations, even considering the 300-fold acceleration of this process in hydrophobic compartments such as the cell membrane (5). The characteristics of the disappearance of NO by parenchymal cells, which will determine its perivascular diffusion, have not been reported. We have previously characterized the consumption of NO by erythrocytes and estimate that the half-life of NO in the vascular lumen is approximately 2 ms (6). Here we characterize NO consumption by parenchymal cells (isolated rat hepatocytes) and present the implications of these results in terms of the concentration gradients of NO and of O₂ away from a blood vessel.

Materials and Methods

Chemicals.

Chemicals and supplies were from standard sources and were of the highest purity available.

Hepatocyte Isolation.

Rat hepatocytes were isolated as described (7). Cells were finally resuspended in 10 mM phosphate buffer + 20 mM dextrose, pH 7.4 and kept on ice until use. Viability was >90% for all experiments, and exposure to NO did not result in appreciable decreases in this number.

Measurement of NO Reaction with Cells.

NO gas (air liquid) was scrubbed of higher nitrogen oxides by passage first through a U-tube containing NaOH pellets and then through a 1 M deaerated (bubbled with 100% argon) KOH solution, in a custom-designed apparatus using only glass or stainless steel (no plastic) tubing and fittings. The purified NO was collected by saturating a deaerated phosphate buffer solution (0.1 M potassium phosphate, pH 7.4/0.1 M NaCl), contained in a glass sampling flask with septum. The saturated NO solution was routinely assayed to ensure no significant contamination with higher nitrogen oxides and to determine the NO concentration, which was 1.6–1.9 mM. This was performed by comparison of nitrite concentration in two vials into which an aliquot of the NO stock solution was injected: (i) an anaerobic vial that was sparged thoroughly with argon after the aliquot addition to remove the NO, and (ii) an aerobic closed vial with no headspace that was allowed to react completely after NO addition. Comparison of these two values provides a concentration of the NO in the stock solution as well as detection of any contaminating nitrite or higher nitrogen oxides in the stock solution. All electrochemical measurements of NO were carried out at 37°C by using a BAS CV50W Electrochemical Analyzer with a PA-1 preamplifier and C2 cell stand from Bioanalytical Systems (West Lafayette, IN). The potential on the working electrode was held at 0.55 V vs. Ag/AgCl reference. The detection electrode was a Nafion-coated electrode of our own design (6), a platinum disk electrode (200 μm in diameter) was used as the working electrode, and a platinum wire and an Ag/AgCl electrode were used as the auxiliary and reference electrodes, respectively. The response time of the electrode was approximately 0.3 s, and the current was linear with NO concentration from 0.05 to 60 μM. Oxygen uptake by isolated hepatocytes was determined by continuous polarographic measurements using a miniature Clark-style electrode. The potential was held at −0.644 V, and the current was linear with O₂ concentration. The reactions were carried out in a sealed, 4-ml glass water-jacketed vessel containing small holes in the top for inserting the NO electrodes and a port in the side for the oxygen electrode. The temperature of the reaction vessel was maintained at a constant 37°C by circulating water from a temperature-controlled H₂O bath. The headspace in the vessel was negligible compared with the volume to assure that under these conditions the volatilization of NO was insignificant compared with the reaction in the solution. The reaction vessel was filled completely with buffer. The oxygen concentration in the reaction vessel was equilibrated with room air and assumed to be 220 μM. The O₂ concentration was modified by bubbling the solution with 100% argon while monitoring the O₂ concentration with the oxymeter. Any headspace that resulted was replaced with deaerated phosphate buffer. NO reactions were initiated by injection of a 3 μM final concentration of a saturated NO solution with a gas-tight syringe with rapid stirring. The addition of hepatocytes or reactants was accomplished by injection into the vessel with a gas-tight syringe.

Computer Modeling of Perivascular NO and O₂ Distribution.

For the computer simulations, we applied a simple one-dimensional multicompartment finite-differences algorithm, as described (8–10). Briefly, governing equations for the production, disappearance, and intercompartmental diffusion of NO and O₂ are defined, and rate constants for diffusion and disappearance are based on experimentally published data, as described in the text. Only the rates of appearance of NO and O₂ are adjusted, and these values are assigned based on the steady-state levels of NO and O₂ at the vessel surface as depicted in the figures. Initial conditions of very low NO and O₂ are selected and the calculations are allowed to proceed (with incremental very small increases in time to ensure against instabilities) until steady state is reached.

Results

Parenchymal Cell NO Consumption.

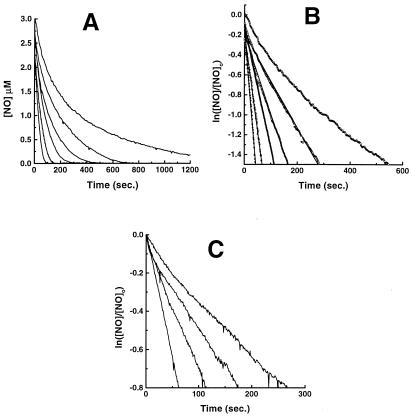
We have measured the cellular (isolated rat hepatocytes) consumption of NO, using an NO-selective electrode. As shown in Fig. 1A, bolus addition of a physiologically relevant concentration of NO (3 μM) to an aerated, rapidly stirred suspension of cells (under conditions where the O₂ concentration does not change, data not shown) is followed by rapid NO disappearance, which is accelerated with increasing concentration of cells (from 2.5 × 10⁴ to 40 × 10⁴ cell/ml). Fig. 1B is a first-order plot for this data for NO concentration, demonstrating that the rate of disappearance in the absence of cells is not first-order in NO, as expected (4), and that the increased rates with cells is first order. The apparent first-order dependence on [NO]‖ rules out autoxidation as a major contributor to the overall consumption of NO. In addition, the consumption rate of NO by cells is many fold greater than the autoxidation rate, even considering the acceleration caused by hydrophobic partitioning in membranes (5). Fig. 1C shows the dependence of this cellular NO consumption on oxygen concentration, and further analysis reveals a linear dependence of the rate of NO disappearance on oxygen concentration, with a minor nonzero intercept that may be caused by oxygen-independent mechanisms of NO consumption (data not shown). Thus, this reaction can be approximated

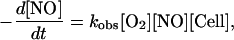1

where [Cell] is the cell concentration. Our data yield a value for k_obs of 5.38 ± 0.3 × 10⁻⁴ M⁻¹⋅s⁻¹(Cell/ml)⁻¹.

Figure 1.

Kinetics and O₂ dependence of NO consumption by isolated rat hepatocytes. NO was added at zero time and its concentration was measured electrochemically as described in Materials and Methods. (A) Effects of increasing cell numbers. Top tracing, buffer alone. Next five tracings, increasing cell density in the measuring chamber (0, 2.5 × 10⁴, 5 × 10⁴, 10 × 10⁴, 20 × 10⁴, 40 × 10⁴ cell/ml). (B) First-order plot of data in A. Note nonlinearity of top tracing (buffer alone), because of the fact that this rate is second order in [NO] (4). The linearity of the tracings with cells indicates first-order dependence. (C) Effects of decreasing O₂ tension. Oxygen concentrations were 220 μM, 100 μM, 50 μM, and 12 μM, with the most rapid disappearance with the highest [O₂]. Cell density was 2 × 10⁵ cell/ml.

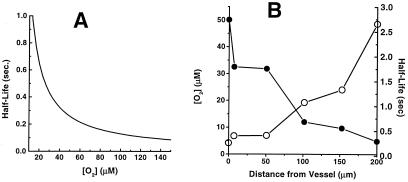
Assuming a hepatocyte density in whole liver of 10⁸ cell/ml (11), Fig. 2A shows a plot of NO half-life** as a function of tissue oxygenation. From these data we estimate that the half-life of NO at a homogeneously normoxic tissue location (pO₂ 100 mm Hg or 140 μM) is 0.092 s. It is important to point out, however, that this does not take into account the important effects on NO lifetime of its diffusion in the spatially heterogeneous tissue environment. We address this in the following section.

Figure 2.

Predicted half-life of NO in tissue as a function of O₂ concentration (A) and distance from the surface of a blood vessel (B). (A) The rate constant for NO disappearance is 5.38 × 10⁻⁴ M⁻¹⋅s⁻¹⋅(cell/ml)⁻¹ and cell density 10⁸ cell/ml was used. (B) The values for O₂ concentration as a function of distance from vessel surface were taken from Filho et al. (16).

Modeling the Perivascular Distribution of NO and O_2.

From the data reported here, we can estimate the half-life of NO in the intervascular tissue volume, which allows us to model the distribution of NO in tissue. Although we (1, 8–10) and others (12–15) have modeled this previously, these two values (the intravascular and extravascular half-life of NO) were not known at the time.

Because the vasculature is a tissue source for both NO and O₂, a gradient for both of these membrane-permeable nonelectrolytes will exist extending outward from a blood vessel. Based on the data reported above, the half-life for NO will increase with distance from the vessel, because of the declining O₂ concentration. Combining our data with results from previous experimental measurements of perivascular oxygen concentrations (16), Fig. 2B shows an estimated apparent half-life for NO as a function of distance from a vessel. This result shows that the diffusional spread for NO (i.e., the “broadness” of the declining NO concentration with distance from the vessel) will be substantially greater than if the NO half-life were independent of O₂, because NO will disappear more slowly as it moves away from the vessel. Thus, the O₂ gradient will extend the diffusion gradient of NO.

Another important factor that will influence the diffusion gradient away from a vessel for both NO and O₂ is the potent inhibition of cellular mitochondrial respiration by NO (17). This inhibition is reversible and appears to involve binding of NO to both oxygen-binding components of cytochrome oxidase (copper center B and heme a₃; refs. 18 and 19). It is thus reasonable to assume that the inhibition can be expressed by the relationship for competitive enzyme inhibition:

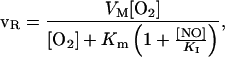2

where ν_R is the respiration rate, V_M is the maximal respiration rate (i.e., at saturating O₂ in the absence of NO), K_m is the half-saturation concentration for O₂ in the absence of NO, and K_I is the inhibition constant for NO.

To examine these effects on NO and O₂ distribution, we applied a simple finite-differences numerical method we have used previously (8, 9). Using this simplified model, sources and sinks for both NO and O₂ can be placed at any specified spatial location(s) or compartment along a one-dimensional axis, with free diffusion of NO and O₂ occurring between adjacent compartments. The simulation is begun with a selected set of initial conditions, and concentration profiles of NO and O₂ are calculated with increasing small time increments until a steady state is achieved. We present here the steady-state results.

It can be shown from first principles that the steady-state concentration of a diffusible solute ([C]) as a function of distance (Δx) away from a source (where the concentration is [C]_o) when the solute disappears homogeneously (i.e., everywhere) with a half-life t_1/2 is given by

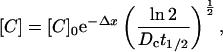3

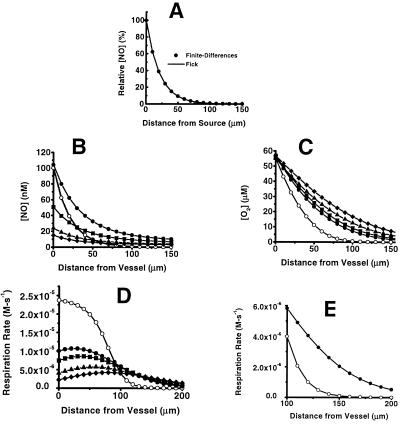
where D_C is the diffusion constant for C (9). It was important to verify that the computer-calculated simulation method used here is fully consistent with this relation, which is derived from the Fick equations for diffusion. Assuming a value of D for NO of 3,300 μm²⋅s⁻¹ (10) and our value for t_1/2 of 92 ms, the solid line in Fig. 3A shows the diffusional spread of NO using Eq. 3. The filled circles show the profile using our numerical method, also assuming D = 3,300 μm²⋅s⁻¹ and t_1/2 = 92 ms at every location. For this calculation, the source for NO is located at the origin (i.e., the vessel surface) and the only adjustable parameter is the rate of NO formation, which was empirically adjusted to yield a steady-state concentration of approximately 100 nM at the source. As is clear from Fig. 3A, the steady-state finite-differences calculation produces a result that is indistinguishable from the analytical solution to Fick's equations for diffusion (Eq. 3), validating the fidelity of the numerical method.

Figure 3.

Simulations of the steady-state concentration profiles of NO and O₂ and of cellular respiration rate away from the surface of a vessel. (A) Comparison of the results from the equation based on Fick's Law (Eq. 3; solid line) with results from the finite-differences simulation (○). (B) NO concentration away from the vessel. ○, The result with a uniform half-life for NO of 0.092 s and no effect of NO on tissue oxygen consumption. The filled symbols denote results that include both the O₂ dependence of cellular NO consumption (Eq. 1) and inhibition of cellular respiration by NO (Eq. 2), with increasing rates of NO formation, which yield steady-state levels at the vessel surface from 15 to 100 nM. (C) O₂ concentration away from the vessel. Open symbols denote no NO/O₂ interactions and a uniform NO half-life of 0.092 s. Filled symbols denote results that include the O₂ dependence of cellular NO consumption and inhibition of cellular respiration by NO. (D) Profile of cellular respiration rate as a function of distance from the surface of a vessel, using Eq. 2. Symbols are as described for B and C. (E) Expansion of the distance scale from D, with no NO/O₂ interaction (○) and with NO/O₂ interactions and [NO] = 100 nM at the vessel surface.

For the simulations of both NO and O₂ dynamics, the rate of tissue O₂ appearance caused by vascular delivery was adjusted to yield a steady-state O₂ concentration of 40 mm Hg or 56 μM at the surface of the vessel (16). This becomes a model for simulating the concentration of NO (and O₂, see below) at increasing distances from a blood vessel. With this tool, it is possible to model the effects on tissue respiration of the coupled diffusion of NO and O₂ away from the surface of a blood vessel and predict these effects with changes in various physiologically important conditions. For our simulations, in addition to the experimental parameters above (D for NO and the rate of NO disappearance), values for O₂ diffusion and O₂ consumption via mitochondrial respiration are required. For the rate of parenchymal cell O₂ consumption (V_R), we use Eq. 2 with V_M = 0.9 μmol O₂ consumed/10⁶ cell per h (20) for 10⁸ cell/ml. We use a value of 1,390 μm²/s for the diffusion constant for O₂ (21). We use values for K_m of 2.86 μM and K_I of 5.22 nM, which were obtained from data measuring inhibition of mitochondrial respiration in synaptosomes (22). The only two parameters we adjust are the rates of NO and O₂ formation at the origin (the vessel), and values are selected solely on the basis of a result that yields the indicated NO and O₂ steady-state concentration at the blood vessel surface ([NO]_S, [O₂]_S).

Fig. 3 B and C presents the steady-state NO and O₂ concentrations at increasing distances from a blood vessel and illustrates a comparison between completely independent NO and O₂ diffusion (open symbols) and when NO and O₂ interact, via reaction (described by Eq. 1) and also considering NO inhibition of respiration (described by Eq. 2; filled symbols, with increasing NO concentration). The presence of the interaction between NO and O₂ substantially increases the concentration of NO away from the vessel surface (Fig. 3B). Fig. 3C shows that this interaction also extends the O₂ concentration away from the vessel, with increasing NO concentration.

Although increased O₂ concentration (Fig. 3C) may seem to increase cell respiration, NO concentration increases also (Fig. 3B) and thus mitochondrial inhibition could offset this effect. Fig. 3D shows that indeed NO does inhibit perivascular cell respiration, but the bulk of this inhibition occurs closer to the vessel. The result is that O₂ “survives” the zone of cells immediately adjacent to the vessel where it would be rapidly consumed were it not for the decreased mitochondrial consumption caused by the NO inhibition. Thus, these NO/O₂ interactions extend the zone of adequate cellular respiration away from the vessel, as illustrated in Fig. 3E, which is an expansion of the results for the range of 100 to 200 μm.

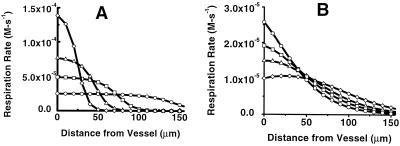
With this approach, it is possible to model the effects of these NO/O₂ interactions on perivascular respiration with changes in the physiological state of the tissue, and Fig. 4 shows the effects of increasing total respiration, which mimics increased tissue work. In the absence of interaction (Fig. 4A), increased V_M for respiration rapidly consumes O₂ near the surface of the vessel, resulting in increasing hypoxic regions distally. When NO/O₂ interactions are included (Fig. 4B), the effects of increased tissue work on the development of hypoxic distal regions are dramatically blunted.

Figure 4.

Effects of increased tissue respiratory demand (work) on steady-state profiles of respiration. (A) Profiles in the absence of coupled NO/O₂ diffusion. ○, The same as for Fig. 3D (V_M = 2.5 × 10⁻⁵ Ms⁻¹ for O₂ consumption, which corresponds to 0.9 μmol O₂ consumed/10⁶ cell per h; ref. 20). □, ▵, and ◊, Results with increasing V_M for oxygen (5 × 10⁻⁵ Ms⁻¹, 8 × 10⁻⁵ Ms⁻¹, 15 × 10⁻⁵ Ms⁻¹, and 20 × 10⁻⁵ Ms⁻¹, respectively). (B) Profiles with coupled NO/O₂ diffusion. Symbols same as A. For both plots, the concentrations of NO and O₂ at the vessel surface are 15 nM and 56 μM, respectively for the baseline condition (V_M = 2.5 × 10⁻⁵ Ms⁻¹).

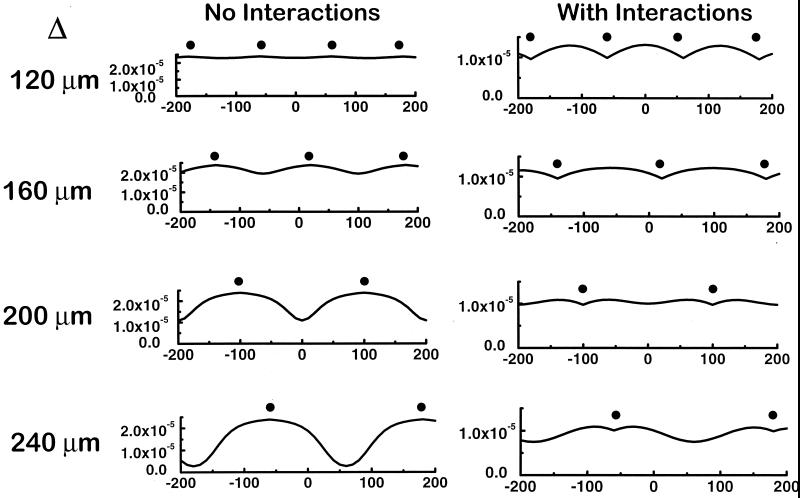
Finally, we examined the effects of NO/O₂ interactions on the overlap of O₂ profiles from multiple adjacent vessels with different intervessel distances (Δ) from 120 μm to 240 μm, within the biologically relevant range (23; Fig. 5). Comparison of the results of increasing intervessel distance without NO/O₂ interactions to those with these interactions reveals that these effects allow adequate tissue respiration with a lower tissue vessel density. Specifically, even with an intervessel separation distance of 240 μm there is only a minor drop in respiration between vessels compared with dramatic hypoxia without NO/O₂ interactions.

Figure 5.

Effects of coupled NO/O₂ diffusion on overlap of tissue oxygenation/respiration with increasing intervessel distances. (Left) Rates of respiration surrounding vessels that are separated by 120 μm, 160 μm, 200 μm, and 240 μm (position of vessels denoted by ●), with independent diffusion of NO and O₂. (Right) Results similar to the plots on the left but including the mutual effects of NO and O₂ on each other's diffusion, as described in the text.

Discussion

We report here that tissue parenchymal cells (isolated rat hepatocytes) rapidly consume NO, as has been reported (24), and that this consumption depends on oxygen. Our results yield a value for apparent rate constant k_app for second-order consumption of NO (rate = k_app[NO][O₂]) of 5.38 × 10⁻⁴ M⁻¹⋅s⁻¹ on a cell per ml basis. The rate of NO disappearance is first order with NO concentration and rapid, thus ruling out simple autoxidation [in either aqueous (4) or hydrophobic (5) phases]. At present, the nature of this consumption is unknown; however, the dependence on oxygen is not what would be expected for consumption of NO by mitochondrial reduction, e.g., at the cytochrome oxidase level (17). In this case, oxygen should be competitive with NO because NO competes with O₂. The first-order dependence on O₂ might be consistent with a first-order dependence on reduction of O₂ to superoxide, which would react rapidly with NO to form peroxynitrite (25). This may occur at the level of the mitochondrion, because it has been shown that NO-inhibited isolated mitochondria produce superoxide (26). Alternatively, NO could react with O₂ to yield nitrosyldioxyl radical, the presumed first step in the autoxidation reaction (27). In simple aqueous solution or in a simple heterogeneous system with a hydrophobic phase, the nitrosyldioxyl radical (ONOO⋅) produced by this reaction (which is rapid but thermodynamically unfavorable) reacts rapidly and irreversibly with NO and proceeds to N₂O₄, NO₂, N₂O₃, and nitrous acid (HNO₂). In the cellular milieu, it is possible that a nucleophilic species may compete with NO for reaction with ONOO⋅, thus producing the overall second-order kinetics. Indeed, kinetic analyses predict such an effect on NO disappearance rate with a scavenger that reacts with ONOO⋅ (27). Finally, it is possible that NO reacts with an oxygen-ligated reduced metal species to produce oxidized metal and nitrate, similar to the reaction of NO with oxyhemoglobin or oxymyoglobin, known to be a very rapid reaction (28).

No matter what the nature of this reaction, it appears to be very robust and active. Repeated addition of NO up to 10 times consecutively shows that the rate of NO consumption after the 10th addition is virtually identical to the first addition (data not shown). Whatever the nature of this rapid cellular consumption of NO, it is probably not simply a result of stoichiometric reaction with a cellular component, in the absence of rapid regeneration of the putative component. We conclude this because if all of the 3 μM NO (Fig. 1) is reacting with such a component, assuming 22-μm cell diameter for a spherical hepatocyte (29) and 2.5 × 10⁴ cells per ml it can be calculated that this component must be present at an intracellular concentration greater than 2 mM (20 mM for 10 consecutive additions).

Historically, literature estimates of the half-life of NO/endothelium-derived relaxing factor (EDRF) have been based mostly on experimentation using cascade perfusion, whereby an NO-producing tissue or cell preparation is perfused with solution, which, downstream, flows past an EDRF(NO)-detecting cell/tissue preparation (2, 30, 31). An early and universally consistent finding was that the actions of EDRF decline as the distance between the source and detector are increased. This result demonstrated the instability of EDRF and laid the groundwork for the conclusion that EDRF is a reactive and thus transient molecular species. When it was postulated that EDRF is nitric oxide, the well-established reactivity of NO with oxygen (which is a hallmark of NO reactivity in other areas such as environmental and atmospheric chemistry; ref. 32) lent further credence to the EDRF/NO postulate of Furchgott (33) and Ignarro et al. (34). However, there are several problems with this picture. First, NO does not spontaneously break down and is stable indefinitely in solution without a reactant (35). Second, measurement of the rate of reaction of NO with O₂ in aerobic aqueous solution (4) reveals that the NO lifetime for physiologically relevant concentrations (nM to low μM range) is very long, on the order of 6 min (1 μM) to nearly 10 h (10 nM). Third, as first reported by Kelm and Schrader (3), the lifetime of NO when exposed to tissue (the coronary circulation with crystalloid perfusate) is very short (0.1 s), showing that tissue does indeed increase the rate of NO disappearance. One possibility for the increased rate of NO disappearance in vessel cascades (and also in tissue) was its rapid reaction with superoxide, which also provided important evidence for the postulate that EDRF is NO (2). Using our data, our estimated half-life for NO disappearance in tissue (under normoxic conditions 0.092 s) is remarkably close to the value reported by Kelm and Schrader (3).

In terms of in vivo NO consumption, an admittedly simplistic view would be that there are two major compartments in the body, the vasculature and the extravascular compartment. We previously have addressed the role of the intravascular reaction of NO with oxyhemoglobin on the extravascular distribution of NO (8). Initially we had suggested that the extremely rapid rate of this reaction poses a serious problem for the postulate that EDRF is free NO. However, we subsequently showed that the rate of the reaction of NO with oxyhemoglobin within erythrocytes is nearly 1,000 times slower than an equivalent concentration of free oxyhemoglobin (6). We suggested that the reaction with intact erythrocytes is limited by the rate at which NO enters the cell, which has been supported by subsequent studies (36). This “packaging” of oxyhemoglobin thus slows NO consumption and, along with the existence of an erythrocyte-free zone in flowing blood, appears to explain how free NO is competent to function as EDRF (14, 36). The work reported here is an examination of the role of extravascular NO consumption on the delivery of O₂ to the tissues.

Consumption of NO by extravascular parenchymal cells (isolated rat hepatocytes) directly depends on oxygen concentration (Fig. 1). Previous studies with animals and tissue are consistent with the dependence of NO disappearance on O₂, including several reports that conditions of lowered oxygenation enhance and prolong the bioactivity of NO (37–39). This result suggests that tissue conditions of relative hypoxia (e.g., vascular coagulation or ischemia) would increase the amount of NO, thus perhaps acting as a negative “feedback” mechanism to induce both vasodilation and also inhibition of leukocyte adhesion and aggregation. Importantly, there is also evidence that there is an obverse relationship between NO and O₂ in tissue, namely, that NO also acts to decrease tissue O₂ consumption. Specifically, numerous studies have shown that NO is a potent competitive inhibitor of mitochondrial O₂ consumption (17), and, perhaps more importantly, tissue NO production decreases respiration in tissue and also whole animals (40). The possible physiological role of this inhibition has not been uncovered but we suggest one possibility based on our experimental results and computer simulations.

Considering the decline in O₂ concentration away from the surface of the blood vessel, the dependence of the rate of NO disappearance on O₂ concentration means that the NO concentration gradient is “flattened” because of this O₂ gradient. That is, NO disappears more slowly with farther distance from the vessel. Thus, the oxygen gradient extends the NO gradient. Likewise, as has been suggested previously (26, 41), the declining NO gradient also extends the O₂ gradient. This is because NO inhibits O₂ consumption by tissue cellular mitochondria, and this inhibition will be higher closer to the vessel because of the higher NO concentration there. Thus, O₂ which has just exited the vessel, will “survive” diffusion through a zone, which would otherwise have consumed it were it not for the inhibition by NO. As illustrated in Fig. 3, the combination of these two phenomena substantially extends the zone of effective tissue respiration away from the surface of the blood vessel. Not only does NO act to increase O₂ delivery to a tissue site by vasodilation, it also extends the effective zone of oxygenation away from the vessel.

We point out that the extension of the O₂ gradient to cells farther away from the vessel comes at the expense of the cells near the vessel, because it is inhibition of O₂ consumption of these proximal cells by NO that “allows” O₂ to reach the more distal cells. A legitimate question therefore is whether there is any net gain? We answer that the “bottom line” for all these effects is tissue work, i.e., whether more total cells are able to perform their energy-dependent functions. As pointed out (42), the activity of energy-requiring processes within a cell (such as transport) will depend on the apparent K_m for ATP. If this K_m is relatively low, than lowering the ATP level (i.e., by inhibition of respiration) will have little effect until the intracellular ATP falls below a value determined by the apparent K_m. Using rat liver slices, when respiration is progressively inhibited with cyanide (which, like NO, acts by competitive inhibition of cytochrome oxidase) it has been shown that neither the rate of net transport nor the total amount of each ion transported is inhibited unless the rate of respiration is decreased below a critical value, which corresponds to approximately 50% of the endogenous rate. Thus, in principle, partial inhibition of respiration by NO‡‡ of cells proximal to the blood vessel may have minimal to moderate effects. However, the effects will be much more dramatic for the distal cells, which in the absence of the NO-induced extension of the O₂ gradient would experience severely hypoxic conditions (Fig. 3E). The net result will be an increase in the number of functioning parenchymal cells. This could explain the apparent increase in work efficiency reported for intact tissue in the presence of endogenous NO synthesis compared with NO synthase inhibition (43). Additional ramifications of this coupling of the perivascular diffusion of NO and O₂ include dramatically increased tissue respiration under conditions of increased parenchymal cell work (Fig. 4) and increased overlap of zones of effective oxygenation with adjacent vessels (Fig. 5), thus further amplifying these effects under in vivo conditions, where vessels are not isolated from each other.

The modeling presented here assumes homogeneous distribution of cells consuming NO, all at a uniform rate. In reality, a heterogeneous distribution of cells in tissue with different rates of NO consumption would influence NO concentration at specific locations in a manner analogous to a heterogeneous distribution of cells producing NO (1).

Finally, we would like to point out that we view the results of simulations presented here as primarily “proof of principle.” Because of the unavoidable simplistic nature of the computer simulation and uncertainties in the values of the parameters used, these results should be considered as qualitative only. Nevertheless, as pointed out above, it is indeed clear that endogenous NO does inhibit cellular respiration, and the concepts presented here suggest a physiological function for this phenomenon and may represent a second function for NO (in addition to vasodilation) in modulating oxygen delivery to tissue.

Abbreviation

EDRF

endothelium-derived relaxing factor