Modeling the Effects of HER/ErbB1-3 Coexpression on Receptor Dimerization and Biological Response

Abstract

The human epidermal growth factor receptor (HER/ErbB) system comprises the epidermal growth factor receptor (EGFR/HER1) and three other homologs, namely HERs 2–4. This receptor system plays a critical role in cell proliferation and differentiation and receptor overexpression has been associated with poor prognosis in cancers of the epithelium. Here, we examine the effect of coexpressing varying levels of HERs 1–3 on the receptor dimerization patterns using a detailed kinetic model for HER/ErbB dimerization and trafficking. Our results indicate that coexpression of EGFR with HER2 or HER3 biases signaling to the cell surface and retards signal downregulation. In addition, simultaneous coexpression of HERs 1–3 leads to an abundance of HER2-HER3 heterodimers, which are known to be potent inducers of cell growth and transformation. Our new approach to use parameter dependence analysis in experimental design reveals that measurements of HER3 phosphorylation and HER2 internalization ratio may prove to be especially useful for the estimation of critical model parameters. Further, we examine the effect of receptor dimerization patterns on biological response using a simple phenomenological model. Results indicate that coexpression of EGFR with HER2 and HER3 at low to moderate levels may enable cells to match the response of a high HER2 expresser.

INTRODUCTION

The HER system of receptor tyrosine kinases plays an important role in growth, proliferation, and differentiation of epithelial cells. This receptor system consists of four members—HER1, which is also known as the epidermal growth factor receptor (EGFR); and HERs 2–4. These receptors are also known as ErbBs 1–4 (1). In addition to the important physiological role of the HER system, these receptors play a key role in transformation and tumor progression. For instance, overexpression of HER2 is associated with poor prognosis in breast cancers with 25–30% of tumors from this tissue displaying significant HER2 overexpression (2). Although the link between HER overexpression and tumorigenesis is well documented, a number of details regarding the molecular mechanisms that are involved in this process remain to be elucidated.

The importance of the HER system in physiology and pathology coupled with the scientific desire to understand the general principles underlying growth factor signaling have led to extensive research in this area (3–9). It is known that all members of this receptor family display significant homology, with each of these receptors having distinct properties such as ligand binding or receptor trafficking (6,10). For example, the EGFR is rapidly internalized and degraded upon binding its ligand EGF (11,12), whereas the other receptors in the family do not display significant ligand-induced internalization and/or recycle rapidly back to the cell surface after endocytosis (10,13–15). Further, ligand binding induces dimerization of HER family receptors where various combinations of homo- and heterodimeric species can be formed (16–18). Dimerized receptors undergo trans-phosphorylation, which activates downstream signaling pathways such as the MAPK, PI3K/Protein Kinase B, and PKC pathways via the binding of signaling adaptors to phosphotyrosine sites on the receptor cytoplasmic tails (19). There is considerable evidence suggesting that the types of receptor heterodimers that are formed and their trafficking properties are important determinants of the cellular response to HER family ligands (17,20–22).

The important role of dimer identity in driving the cellular response is exemplified by the HER2-HER3 heterodimer, which has been reported as being a potent mitogenic and oncogenic unit (22–26). This is despite the fact that HER3 has impaired tyrosine kinase activity (27) and HER2 is devoid of an activating ligand (28). The potency of this dimer is thought to stem from the trafficking properties of this dimer, which tend to prolong signaling (13,15), and from the unique ability of HER3 to efficiently engage the pro-survival PI3K/PKB pathway (29,30).

In general, it is clear that the molecular mechanisms, underlying the manner in which heterodimer identity controls the cellular response, are complex. It has been reported that the specific tyrosine sites on the cytoplasmic tail of a receptor that end up getting trans-phosphorylated depend upon the specific HER member with which the receptor dimerizes (31). This would in turn cause qualitative changes in the signaling properties of the very same HER receptor depending upon its dimerization partner, and each dimer type may be capable of engaging a unique complement of cell-signaling pathways. In addition, since the heterodimers possess distinct trafficking properties, the spatial location (plasma membrane versus internal compartments) and the duration of the phosphorylation signal would also depend upon dimer identity. Therefore, knowledge of the types of heterodimers formed in cells expressing various levels of HER molecules may pave the way toward unraveling the connections between receptor expression levels and cell phenotype. We use the term “cell phenotype” to characterize such eventual biological responses of the cell as cell migration, proliferation, and transformation.

Here, we describe the development of a multitiered predictive model that strives to establish a link between receptor expression levels and cell phenotype for the HER system. The current state of quantitative information available on the HER system provides us with an ability to predict receptor heterodimerization and trafficking in an accurate fashion using detailed kinetic modeling. We construct such a kinetic model to generate predictions about the receptor dimerization patterns in cells expressing varying levels of the receptors EGFR, HER2, and HER3. In addition, we use the model as a guide to identify the types of experiments necessary to accurately parameterize it for any given cell type. These are important and necessary steps in the context of model development and refinement. Fig. 1 A shows our conceptual framework for developing and refining predictive mathematical models. Given a set of system inputs X, a model is expected to generate predictions about a set of variables Y, which are functionally relevant and may be difficult to measure. In our case, X denotes ligand dosages and receptor expression levels and Y denotes the number and location of activated dimers of various types within the cell. This article describes the setting-up and parameterization of a model for EGFR family of receptors using values obtained from literature. Furthermore, we describe how the transition to the parameter estimation and validation phase can be accomplished through the systematic design of experiments using the model predictions.

FIGURE 1.

Steps of kinetic model development for ErbB family of receptors. (A) Schematic representation of the model development process. The central item is a detailed kinetic model of associations among HER receptors that is intended to convert inputs on receptor expression levels and ligand dosages X to receptor dimerization pattern Y. Setting up of the kinetic model is described in detail in text. In addition, the model is used to design experiments for parameter estimation to facilitate the transition to the next phase of model refinement. (B) Schematic of two-tiered modeling approach to relate HER expression levels to cell phenotype. The model for the HER receptor family is used to predict the receptor dimerization patterns in the cell. A phenomenological equation is then used to link model predictions to the cell phenotype estimation.

The kinetic model with multiple receptor types still leaves us short of our stated goal of creating a prediction engine for cell phenotype. The development of a kinetic model linking receptor expression levels to biological outcome is restricted by the paucity of detailed mechanistic information on how the receptor dimerization pattern Y affects the biological outcome. This necessitates a multitiered approach to the problem depicted in Fig. 1 B. Here we advocate the use of a phenomenological equation to establish the link between the dimerization pattern Y for the HER family and the biological outcome Z. We consider a simple linear representation for the above and present results on how the phenotype would vary based on the parameter values of this phenomenological equation. The phenomenological equation used here can be subsequently refined as more data about biological outcomes under different environmental cues becomes available. We note that Hendriks et al. (32) have recently employed a similar approach to dissect the relative contributions of EGFR and HER2 to ERK signaling in human mammary epithelial cells.

Using our kinetic model, we demonstrate how the current literature on rate constants for receptor-ligand binding and dimerization lead naturally to the enhanced formation of HER2-HER3 heterodimers when HERs 1–3 are coexpressed. When combined with the potency of the HER2-HER3 dimer, this dimerization pattern results in a marked effect on the cell phenotype. Thus, coexpression of all three receptors at low to moderate levels may enable a cell to match the phenotype of a cell expressing EGFR and very high levels of HER2. In addition to presenting simulation results using the kinetic model, we employ the model to design experiments aimed at parameter estimation. These exercises reveal that measurements of HER3 phosphorylation in cells coexpressing EGFR and HER3 and the HER2 internalization ratio in cells coexpressing EGFR and HER2 may be especially useful for the estimation of critical model parameters. The model we present here can serve as a platform to design experiments and to gain a deeper insight into the manner in which the HER system functions.

METHODS

Kinetic model for HER dimerization

For given expression levels of HERs and stimulating ligand dosages, our integrated model of receptor dimerization and trafficking is capable of predicting the time-dependent receptor dimerization patterns. Fig. 2 presents the various components of our mathematical model. The model was formulated and solved as a system of ordinary differential equations. Despite the relatively low receptor copy numbers encountered in our model it was found that a deterministic treatment yielded results that were in good agreement with those obtained using dynamic Monte Carlo simulations (33) of the corresponding stochastic problem (results not shown). Further, knowledge of the magnitude of stochastic fluctuations in species concentrations is not critical to our current study. Hence, we have opted to use the computationally less demanding deterministic approach. The governing equations and the solution methodology for the kinetic model are described below. Machine-readable versions of the model and the simulation code can be obtained from the authors upon request.

FIGURE 2.

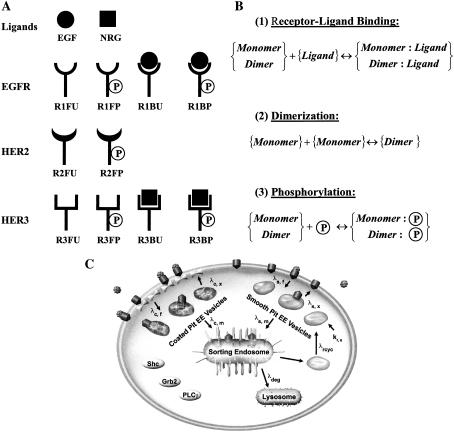
Reactant species and reactions in the mathematical model. (A) Reactants in the mathematical model. The ligands and the possible states of the receptors in our kinetic model are shown. The nomenclature used for each of the reactant species is indicated at the bottom of each cartoon. EGFR and HER3 can exist in one of four states. Since HER2 does not bind any ligands, it has only two possible states. Receptors can either be found in monomeric form as depicted, or can be part of dimers. As an illustration, R1FU·R3BP is one such dimer species formed between an EGFR and a HER3 molecule. (B) Biochemical reaction classes in the model. The reactions of (1) receptor-ligand binding, (2) receptor dimerization, and (3) phosphorylation are depicted in canonical form. (C) Schematic of the trafficking portion of the model. The compartments involved in receptor trafficking are indicated. The biochemical reactions shown in panel B are overlapped with the receptor trafficking model depicted in panel C to arrive at the spatial distribution of the various receptor species within the cell. Panel C is adapted from Resat et al. (42).

Reactants

We constructed our kinetic model of HER receptor activation with the objective of predicting the abundance and types of activated receptor dimers formed when cells expressing various levels of EGFR, HER2, and HER3 are subjected to ligand stimulation. In the model, each individual receptor is assumed to be in one of four possible states: 1), ligand free and unphosphorylated (FU); 2), ligand bound and unphosphorylated (BU); 3), ligand free and phosphorylated (FP); and 4), ligand bound and phosphorylated (BP). Since HER2 does not bind any ligands, it is restricted to two possible states (FU and FP). Receptors can either exist as monomers or be part of dimers. To illustrate the naming convention, R1BP is a ligand-bound and phosphorylated EGFR monomer, while R1BP·R2FP is an EGFR-HER2 heterodimer where EGFR is bound by its ligand and both receptors are phosphorylated. Having four possible states, EGFR and HER3 can form 10 distinct types of homodimers, while HER2 can form three types of homodimers. In all, the model contains 55 distinct dimer species: 10 (EGFR) + 3 (HER2) + 10 (HER3) = 23 types of homodimers; and 8 (EGFR-HER2) + 16 (EGFR-HER3) + 8 (HER2-HER3) = 32 types of heterodimers. Adding the 10 receptor monomers and the two ligand species (epidermal growth factor, EGF, i.e., the EGFR ligand; and neuregulin, NRG, i.e., the HER3 ligand) results in 67 total reactants. Each of these reactants can exist in one of four possible cell compartments (plasma membrane, smooth-pit endosomes, coated-pit endosomes, and sorting-late endosomes).

Reactions

The concentration of a species in a specific compartment can change for two reasons. The species can be 1), generated and destroyed through a biochemical reaction; or 2), can be transported in and out of the compartment due to vesicle trafficking. The following sections present a brief description of the biochemical and trafficking reactions in the model. The detailed mathematical equations governing the model are provided in Appendix A.

Biochemical reactions. The model includes three types of biochemical reactions: 1), receptor-ligand binding; 2), receptor dimerization; and 3), receptor phosphorylation. The process of obtaining a dually phosphorylated receptor dimer is allowed to occur in any order. For instance, a receptor monomer can spontaneously undergo phosphorylation, albeit at a low rate, after which a dimerization reaction can occur, yielding an active dimer. However, the rate constants are such that the kinetically dominant pathway for active dimer formation is one in which receptor-ligand binding leads to dimerization, followed by receptor trans-phosphorylation. The combinatorial nature of the dimerization problem and the fact that we allow for explicit representation of the ligand binding and phosphorylation states of the receptors in a dimer results in a large number of reactant species and reactions in the model. The model contains 308 distinct biochemical reactions for which rate constants need to be assigned. These rate constants in our model are described in terms of a basal rate and an enhancement factor based on phosphorylation state and ligand occupancy (Table 1). The exact manner in which the parameters listed in Table 1 are used to compute the individual rate constants is described in Appendix B. We note that other researchers have used similar notions of reaction classes and rules to parameterize large models of signal transduction (34–38). In these models, as well as in our work, receptors are allowed to have multiple states, each of which is included as a distinct reactant species in the model. This leads to a large number of reactions that need to be parameterized. The problem is alleviated by assigning rate constants for entire classes of reactions and formulating rules for how the rate constants would change based on specific receptor modifications. We follow this well-documented approach in our current work.

TABLE 1.

Parameters used in the model

Parameter No.	Parameter description	Value
Receptor-ligand binding rates
1	BR for EGF binding.	2.38 × 10−6/nM/s
2	BR for NRG binding.	2.38 × 10−6/nM/s
3	Multiplier for EGF binding rate in endosomes.	0.135
4	Multiplier for NRG binding rate in endosomes.	0.135
5	Multiplier for EGF binding to EGFR-HER3.	0.5
Ligand dissociation rates
6	BR for EGF dissociation.	4 × 10−3/s
7	BR for NRG dissociation.	4 × 10−3/s
8	Multiplier for EGF dissociation in endosomes.	4.125
9	Multiplier for NRG dissociation in endosomes.	8.25
10	Multiplier for NRG dissociation from HER2-HER3.	0.1
11	Multiplier for EGF dissociation from EGFR-HER3.	1.5
Receptor dimerization rates
12	Receptor dimerization rate.	1 × 10−2/nM/s
Dimer dissociation rates
13	BR for EGFR homodimers.	1 × 10−2/s
14	BR for HER2 homodimers.	2.5 × 10−1/s
15	BR for EGFR-HER2.	2 × 10−2/s
16	BR for HER3 homodimers.	1 × 10−2/s
17	BR for HER2-HER3.	2 × 10−2/s
18	BR for EGFR-HER3.	1 × 10−2/s
19	Multiplier when phosphate is removed.	2
20	Multiplier when ligand is removed.	5
Receptor phosphorylation rates
21	BR for EGFR monomer.	1 × 10−3/s
22	BR for HER2 monomer.	2 × 10−4/s
23	BR for EGFR homodimers.	1 × 10−2/s
24	BR for HER2 homodimers.	8 × 10−3/s
25	BR. for EGFR-HER2.	8 × 10−3/s
26	BR for HER2-HER3.	8 × 10−3/s
27	BR for EGFR-HER3.	8 × 10−3/s
28	Multiplier when a receptor is phosphorylated.	3
29	Multiplier when a receptor is bound.	2
Receptor dephosphorylation rates
30	BR for EGFR monomer.	5 × 10−2/s
31	BR for HER2 monomer.	5 × 10−2/s
32	BR for HER3 monomer.	5 × 10−2/s
33	BR for EGFR homodimers.	5 × 10−3/s
34	BR for HER2 homodimers.	5 × 10−3/s
35	BR for EGFR-HER2.	5 × 10−3/s
36	BR for HER3 homodimers.	5 × 10−3/s
37	BR for HER2-HER3.	5 × 10−3/s
38	BR for EGFR-HER3.	5 × 10−3/s
39	Multiplier when phosphate is removed.	2
40	Multiplier when ligand is removed.	4
Vesicle trafficking rates
41	CP vesicle formation.	2.1 × 10−1/s
42	SP vesicle formation.	2.1 × 10−1/s
43	SP vesicle recycling.	6.9 × 10−4/s
44	CP vesicle recycling.	2.07 × 10−3/s
45	SP vesicle merging with LE.	1.61 × 10−3/s
46	CP vesicle merging with LE.	2.3 × 10−4/s
47	SP formation from LE.	2.47 × 10−4/s
48	Lysosome formation from LE.	1.3 × 10−5/s
Receptor incorporation factors
49	Factor for EE vesicles.	7.94 × 10−4
50	Multiplier for ligand-bound EGFR.	15.5
51	Multiplier for ligand-bound EGFR-HER2.	5.4
52	Multiplier for ligand-bound EGFR-HER3.	5.4
Degradation multipliers
53	Multiplier for single-ligand-bound EGFR.	3
54	Multiplier for doubly-bound EGFR homodimers.	6

BR stands for the basal rate. Sources of these parameters and the manner in which these parameters are used to obtain rate constants for specific reactions are described in Appendix B.

Some of the key assumptions regarding the biochemical rate constants in the model are as follows:

1. With respect to ligand binding, on- and off-rates for binding are assumed to depend upon the identity of the dimer. The dissociation of neuregulin from HER2-HER3 heterodimers is assumed to be 10-times slower than that from other species involving HER3 (18,39). Further, in EGFR-HER3 heterodimers, the presence of NRG halves the EGF on-rate and increases the EGF off-rate by a factor of 1.5 (40).

2. Receptor dimerization is assumed to be a diffusion-limited process and thus occurs at a constant rate independent of the species participating in the dimerization reaction. Dimer dissociation is assumed to depend upon the species identity and accounts for the greater stability of certain HER dimers compared to others seen in practice (18). We assume a low basal rate for the dissociation of a dimer where both partners are ligand-bound and phosphorylated. Removal of the ligand or the phosphate group is assumed to decrease the dimer stability and hence facilitates dissociation. This is in agreement with the currently held views of HER receptor dimerization wherein ligand binding is thought to stabilize the dimer by inducing a conformational change (7,41).

3. Receptor phosphorylation is assumed to occur at a low basal rate when both receptors are unoccupied by ligand and are unphosphorylated. Ligand binding and the presence of a phosphate group on one of the receptors is assumed to increase the phosphorylation rate. This assumption envisions a molecular model wherein ligand-binding results in a conformational change, which brings the receptor kinase domains in direct opposition to each other, thereby facilitating trans-phosphorylation. In cells, HER receptors are dephosphorylated by phosphatases. Here we assume that dephosphorylation occurs at a low basal rate in dimers which are dually phosphorylated and have both receptors engaged by ligand. Such dimers are expected to have the highest level of conformational stability, thus preventing access to the phosphatase. In addition, we assume that the removal of a phosphate group from one of the receptors and the removal of each ligand molecule enhances the dephosphorylation rate.

Trafficking. The trafficking portion of the model is based on our earlier work on EGFR signaling (42). The parameters for the trafficking portion of our model and the details of how these parameters are employed in the model are described in Table 1 and in Appendix B, respectively. Briefly, receptors in the plasma membrane (PM) are internalized either through a constitutive pathway involving smooth-pit endosomes or a ligand-induced pathway involving coated-pit endosomes. The incorporation rates of receptor species into coated-pit vesicles depend upon the ligand-binding state of the receptors as defined by the receptor incorporation factors in Table 1. Smooth- and coated-pit endosomes that constitute early endosomic (EE) vesicles are either allowed to recycle back to the plasma membrane or merge into the late endosomes (LE). When an EE vesicle merges with either the plasma membrane or the LE, all of its contents are assumed to be transferred to the target compartment. The rates at which EE vesicles are formed, recycled to the PM, and targeted to the LE are assumed to depend upon whether the vesicle is a smooth-pit or a coated-pit compartment. Receptors go through a second stage of sorting in the LE wherein vesicles are formed from the LE and can either be targeted to the lysosome or recycled back to the PM. A vesicle from the LE that fuses with the lysosome ends up having its contents degraded. The enhanced propensity of ligand-bound EGFR to get targeted to lysosomes for degradation is captured by the degradation multipliers in Table 1. The mathematical equations governing the formation and sorting of vesicles and how this affects species concentrations are described in detail in Appendix A.

Parametric sensitivity analysis of the kinetic model

Parametric sensitivity of the receptor dimerization pattern

The results generated by a kinetic model are a function of the rate constants used to define the mathematical model. In our current model, we have a set of 321 rate constants for the individual biochemical and trafficking reactions. Although this is an apparently large parameter set, all the rates are essentially derived from a reduced set of 54 distinct parameters that completely define the model. To facilitate the characterization of the model, it is instructive to examine the effect of varying each of these parameters on the model outputs. The functionally relevant model outputs in this case are the number of phosphorylated dimer species of each type present both in the cell as a whole and at the cell surface. We performed a sensitivity analysis by allowing a 10% increase in each of the parameters one at a time and examining the impact of the parameter variation on the system outputs. Control parameters were identified as those that induced a large change in the number of activated receptor dimers. We note that more robust approaches to sensitivity analysis do exist that enable the determination of the effect of parameter changes on the model over larger regions of the parameter space (43,44). We plan on addressing rigorous sensitivity analysis and parameter estimation issues in future work using real experimental data for model refinement.

Defining the dependence of experimental observables on model parameters

The rate constants in our model have been largely derived from experimental observations in model systems and are known to various degrees of confidence. For the model to be used for a specific experimental system, it is important to determine the applicability of these values to the system in question. This can be done by designing a set of experiments, which can then be used in conjunction with the model for estimation of the model parameters. Parameter estimation involves the fitting of a predefined model to experimental measurements using techniques such as nonlinear least-squares regression. Nonlinear regression is a nontrivial problem if the number of parameters to be estimated is large. The process of parameter estimation could be simplified if the model were used as a guide to design the experiments to be performed. To this end, we attempted to define a systematic methodology to decide which experimental output would yield the best data set for estimating specific model parameters. These measurable quantities can then be chosen as the most relevant observable targets in experimental studies. For our specific case, we considered cell lines expressing various combinations of EGFR, HER2, and HER3 and sought to determine both the cell line and the specific measurement in each cell line that would have the highest information content for parameter estimation. The experimental observables included in this analysis were the total receptor mass of EGFR, HER2, and HER3, the fractional phosphorylation of the three receptors, and the Inside/Surface ratio (In/Sur) of the phosphorylated forms of the three receptors. These outputs are routinely measured by us and by others in cell lines expressing HER molecules using standard biochemical techniques such as ELISAs and/or Western blots (42,45,46).

The kinetic model was run and the values of experimental observables were generated as a function of time using the base parameter set listed in Table 1 (base curve) and a parameter set with a 10% increase in a single model parameter (modified curve). The difference between the base curve and the modified curve was quantified using the relative root-mean-squared difference (RMSD) between the two curves, which is computed using the fractional change between the two curves at specific sampling time points. We chose a uniform sampling scheme with seven time points between 0 s and 2 h of ligand stimulation. The relative RMSD between the two curves was then computed as

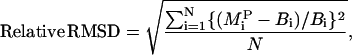(1)

where B_i is the model output generated at the i^th time point using the base parameter values listed in Table 1, 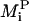is the model output generated at the i^th time point generated using a parameter set with a 10% increase in parameter P, and N is the total number of time points. This relative RMSD is an indicator of how sensitive an experimental output is to the parameter P, which is altered to generate the modified curve. Here, we computed the relative RMSD for the various model parameters using the experimental observables as outputs for each of four cell lines:

1. A cell line expressing 200,000 copies of EGFR alone.

2. A cell line coexpressing 200,000 molecules each of EGFR and HER2.

3. A cell line coexpressing 200,000 molecules each of EGFR and HER3.

4. A cell line expressing 200,000 receptors each of EGFR, HER2, and HER3.

These RMSD values were then used to judge the best possible experiment to perform for estimating a given model parameter.

Application of the results of the kinetic model to the prediction of cell phenotype

To relate the dimerization results to the cellular phenotype we begin with a simple representation wherein the phenotype is a linear function of the activated dimers in the cell. Thus, the phenotype P is expressed as

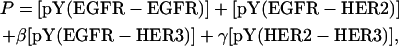(2)

where the quantities within square brackets represent the total number of phosphorylated dimers of the specified type. These quantities are either evaluated at a fixed time-point 1 h after the introduction of the ligand stimulus, or are obtained as an integral over the first two hours after ligand stimulation. In Eq. 2, β represents the relative potency of activated EGFR-HER3 heterodimers compared to EGFR homodimers and EGFR-HER2 heterodimers. Similarly, γ is a potency factor for HER2-HER3 heterodimers. Here, we compute the phenotype value P = P* of a reference cell line expressing 200,000 EGFR and 600,000 HER2 molecules. This cell line is a high HER2 expresser and is assumed to possess the target phenotype. We then determine the relative potencies β and γ that would be necessary to obtain a phenotype value of P* in cells expressing varying levels of HER2 and HER3. This approach implicitly assumes that the overall biological response of the cell, i.e., cell migration, proliferation, and transformation, can be represented with a phenomenological expression that uses the number of activated receptors as parameters.

RESULTS AND DISCUSSION

The ordinary differential equations comprising the kinetic model were solved using the parameter values listed in Table 1 to obtain the dimerization and receptor phosphorylation profiles as a function of time for cells expressing varying levels of EGFR, HER2, and HER3. For all the simulations, a saturating ligand dose of 100 nM was employed for both EGF and NRG. A receptor expression level of 200,000 receptors was employed unless stated otherwise. After the characterization of model behavior for the base parameter set, sensitivity of the system outputs and experimental observables to the variations in the parameters was examined. The dependence of the receptor dimerization pattern (which we defined as the system output) upon the parameter values enables us to identify the key control parameters in the model. The dependence of experimental observables on the parameters provides us with information about the types of experiments to perform to estimate system parameters. After the characterization of the kinetic model, the phenomenological equation (Eq. 2) was used to relate the predictions of the kinetic model to cell phenotype. Results are presented for the manner in which the phenotype varies as a function of receptor expression levels for various parameter inputs to the phenomenological equation.

Behavior of the HER family for the base parameter set

Dimerization pattern when EGFR, HER2, and HER3 are coexpressed

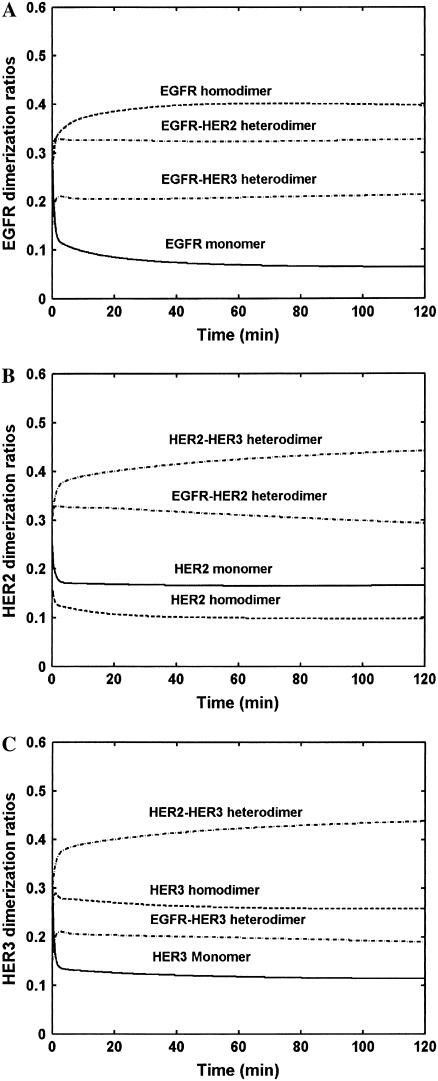
The pattern of dimerization when HER family receptors are coexpressed is important since each of the dimer species might be capable of activating a unique complement of downstream signaling pathways (47,48). We employed our model to determine the dimerization patterns when HERs 1–3 are equally coexpressed (Fig. 3). For these simulations, cells coexpressing 200,000 molecules each of EGFR, HER2, and HER3 were subjected to saturating concentrations of EGF and NRG and the dimerization fractions were determined. The dimerization ratio for each HER family member is computed as the fraction of the receptor that is present as part of a specified dimer type. It should be noted that the actual number of receptor homodimers would be one-half the dimerization ratio value computed for the homodimer. As an illustration, a ratio of 0.4 for EGFR homodimers would imply that 40% of the total cellular EGFR is present in the form of EGFR-EGFR dimers. Thus, the number of EGFR homodimer moieties expressed as a fraction of the total number of EGFR molecules would be only 0.2.

FIGURE 3.

Receptor dimerization hierarchy. The response of cell lines expressing 200,000 molecules each of EGFR, HER2, and HER3, exposed to saturating concentrations of both EGF and NRG, was simulated. The figure presents the fraction of the total receptor population of each type present as part of the specified type of monomer/dimer. The dimer type is indicated on top of each curve, while the receptor whose distribution is being analyzed is noted on the Y axis. The dimerization ratios were computed based on total receptor numbers present in the entire cell and therefore include receptors both at the plasma membrane and in the internal compartments. Dimerization patterns for (A) EGFR, (B) HER2, and (C) HER3 are presented.

As seen in Fig. 3, after a brief transient lasting for ∼2 min, species concentrations achieve relative stability. In the case of the EGFR (Fig. 3 A), the EGFR-HER2 heterodimer is the most abundant species accounting for ∼35% of the total receptor population. Approximately 40% of the EGFR molecules are part of EGFR homodimers. Hence, EGFR homodimers account for 20% of all EGFR-containing moieties. The number of EGFR-HER3 heterodimers is approximately the same as the number of EGFR homodimers. Monomers account for <10% of total EGFR. Overall EGFR-HER2 heterodimers are the most abundant EGFR containing species. Using a similar analysis it is clear from Fig. 3, B and C, that HER2-HER3 heterodimers are more abundant than any other species bearing either HER2 or HER3. HER2-HER3 heterodimers account for nearly 45% of the total HER2 and HER3 receptor numbers. The increased formation of HER2-HER3 heterodimers in comparison to the other dimer types has also been seen in experiments (18). In our model, the rate constants for dimerization are not strong functions of the receptor type to which the monomers belong. However, the rates are strong functions of ligand occupancy. Thus, the increased formation of HER2-HER3 heterodimers occurs in part due to the increased NRG affinity of this dimer.

It should be noted that the abundance of a particular dimer type is a function both of the dimerization affinity and of the relative local species concentrations. In our model, the dimerization affinities of the different species are in the same order of magnitude (Table 1). The local species concentrations are thus critical determinants of the dimerization pattern seen in the cell. In this regard, our model is in agreement with that of Hendriks et al. (45) for cells coexpressing EGFR and HER2.

HER2 has a more pronounced effect on EGFR trafficking than HER3

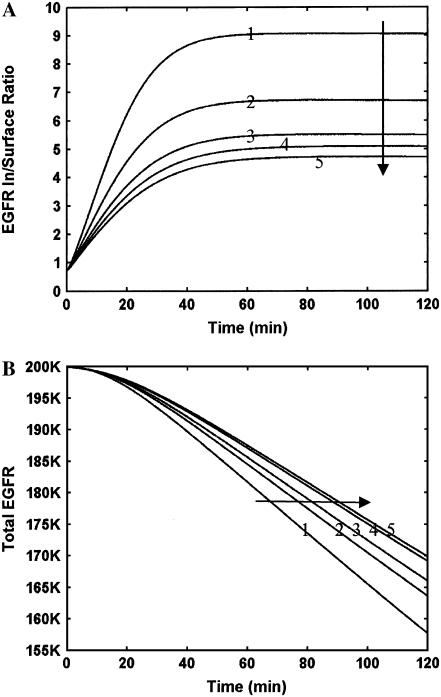
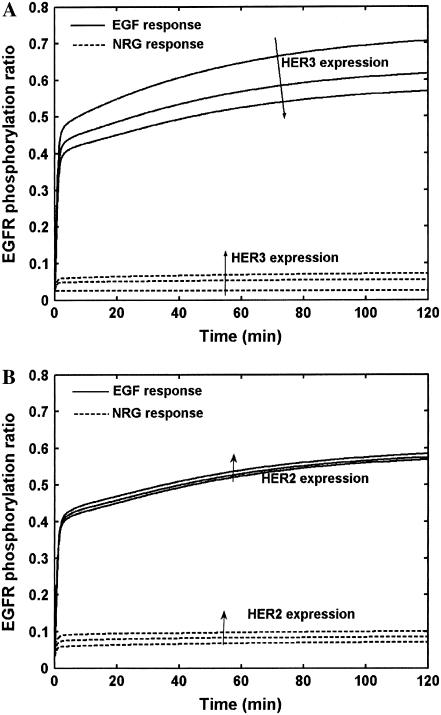
An important consequence of heterodimerization is that HER receptors are expected to exert an influence on the localization of their receptor partners. For instance, while EGFR is expected to internalize and commit to the lysosomal pathway, HER2 and HER3 have a much higher tendency to recycle back to the plasma membrane (PM) upon ligand binding (6). In contrast, an EGFR-HER2 heterodimer is expected to have an intermediate trafficking behavior. To investigate the effect of heterodimerization on receptor localization, we quantified the inside-to-surface (In/Sur) ratio for the HER molecules in our model. As seen in Fig. 4 A, the In/Sur ratio of EGFR increases immediately after ligand stimulation and takes ∼40 min to reach a steady-state value. Comparison of this 40-min lag for achieving receptor localization steady state with the ∼2 min transient for receptor dimerization (see Fig. 3) reveals the fact that the trafficking and biochemical reactions in the model occur on significantly different timescales. When a cell expresses EGFR alone, after the initial transient the In/Sur ratio of EGFR reaches a constant value of 9. In other words, 90% of EGFR gets internalized, and only 10% of the receptor population can be found on the cell surface. This reflects the propensity for ligand-induced EGFR downregulation. Coexpression of EGFR with HER3 alone results in 14% of the EGFR at the cell surface even when EGF alone is used as the stimulating ligand. This increased surface retention is a consequence of the conflicting trafficking properties of these two receptors discussed above. When both EGF and NRG are used as agonists, we get an EGFR surface expression of 15.6%. In comparison to HER3, HER2 has a slightly more pronounced effect on EGFR localization with a ratio of ∼4.5, i.e., 18% EGFR surface expression. Coexpression of equal amounts of all three receptors results in only a marginal increase in EGFR surface expression compared with coexpression of EGFR and HER3 alone. Overall, both HER2 and HER3 impede the internalization of EGFR, thereby resulting in a prolonged surface-localized EGFR phosphorylation signal. However, it is difficult to predict the importance of this change because, although the number of surface EGFR molecules roughly doubles between a cell line expressing EGFR alone and that coexpressing equal amounts of EGFR and HER2, the absolute change is only 8% and this modest change may not be enough to alter the biological response.

FIGURE 4.

Effects of HER2 and HER3 on EGFR internalization and degradation. Simulations were performed where EGFR was expressed at 200,000 molecules either alone or in conjunction with HER2 and HER3. Results are presented in both panels for five simulated cases, and the curves are numbered in the following order: 1, EGFR alone + EGF; 2, EGFR+HER3+EGF; 3, EGFR+HER3+EGF+NRG; 4, EGFR+HER2+EGF; and 5, EGFR+HER2+HER3+EGF+NRG. (A) EGFR internalization quantified using the inside/surface ratio of receptors. (B) EGFR degradation seen as a drop in the total number of receptors with time after addition of ligand stimulus. Arrows in the plots indicate the directions along which the curve labels increase.

Next, we examined the effect of receptor coexpression on EGFR degradation. It is known that EGFR degradation mediated by receptor ubiquitination in the internal compartments is a mechanism for signal termination. Our results (Fig. 4 B) indicate that coexpression of EGFR with HER2 and HER3 reduces the EGFR degradation rate, thereby prolonging the signal. This is a consequence of the effect of heterodimerization on EGFR trafficking and could be an additional mechanism by which HER2 and HER3 modulate EGFR signaling.

To summarize, coexpression of EGFR with HER2 and HER3 causes 1), increased EGFR surface localization; and 2), reduced receptor degradation. With respect to cell transformation, both of these factors may play an important role. It is still a matter of debate as to whether receptors continue to signal as effectively once they are inside the cell and are part of either early or late endosomes (49). It is conceivable that signaling is accomplished most effectively when the receptors are at the PM for various reasons, such as having a better chance to interact with the readily available membrane-associated proteins involved in the receptor signaling pathway (50). Hence increased PM localization could enhance EGFR signaling via pathways such as the MAPK and PLC-γ pathways. The dynamics of MAPK signaling is known to have an effect on the type of phenotypic changes induced in cells. For instance, studies have shown that while sustained MAPK activation induces cell proliferation, MAPK transients induces differentiation in mammalian PC12 cells (51). Thus, reduced degradation of EGFR, when coexpressed with HER2 and HER3, could have a bearing on downstream signaling transients, thereby altering the eventual cellular response.

HER2-mediated lateral information transfer between EGFR and HER3

It is of interest to determine the mechanism by which EGFR and HER3 interact with each other in cells coexpressing HER1–3. One possibility is that HER2 is the lateral information carrier between EGFR and HER3/4 receptors by virtue of its ability to form a large number of heterodimers with HER family receptors (18). In other words, the dominant mechanism by which EGFR and HER3/4 modify each other's behavior could be through the involvement of HER2. We examined whether our model yielded such behavior using simulations where the EGFR expression was kept fixed at 200,000 receptors and the expression levels of HER2 and HER3 were varied (Fig. 5). Firstly, we performed simulations of cells coexpressing EGFR and HER3 alone and examined the extent of EGFR phosphorylation (Fig. 5 A). It should be noted that the EGFR binds EGF, and is not known to have a significant binding affinity for NRG (39). Hence, cells expressing EGFR and HER3 when stimulated with neuregulin alone can undergo EGFR phosphorylation only through the involvement of HER3. As seen in Fig. 5 A, <10% of the total cellular EGFR gets phosphorylated when stimulated with NRG (dashed lines). This suggests a low EGFR-HER3 heterodimerization propensity in the presence of the HER3 ligand. Increase in the HER3 expression only slightly increases the EGFR phosphorylation. In contrast, when EGF is used as the ligand, ∼70% of EGFR gets phosphorylated via homodimerization in the absence of HER3. Upon increasing HER3 expression in these EGF-stimulated cells, EGFR-HER3 heterodimers begin to out-compete some of the EGFR homodimers. EGFR-HER3 heterodimers in this scenario can only have single ligand occupancy, due to the lack of the HER3 ligand in these simulations. Hence, these heterodimers are not as effective at yielding EGFR phosphorylation as EGFR homodimers would be. The net result is a reduction in EGFR phosphorylation when HER3 expression is increased. Overall, HER3 expression does not contribute significantly to EGFR phosphorylation in this system.

FIGURE 5.

The EGFR-HER3 interaction. The extent of EGFR phosphorylation in response to EGF and NRG are plotted for cases when EGFR is coexpressed with (A) HER3 alone in the absence of HER2 and (B) varying amounts of HER2 in the presence of a constant amount of HER3. Varying the levels of HER2 and HER3 has a minimal effect on the extent of EGFR phosphorylation. Whereas increasing HER2 causes a slight increase in EGFR phosphorylation, increasing HER3 slightly decreases EGFR phosphorylation in response to EGF. The NRG response is evidence of cross-activation of EGFR either by ligand-bound HER3 (A) or by HER2 activated by ligand-bound HER3 (panel B).

Next we examined the case where cells were made to express 200,000 each of EGFR and HER3, while the level of HER2 was varied (Fig. 5 B). These simulations were performed to explore whether HER2 enhances EGFR-HER3 communication via lateral information transfer. As seen, when neuregulin alone is used as the ligand, ∼7% of EGFR gets phosphorylated even in the absence of HER2. Increasing HER2 expression to 200,000 receptors enhances EGFR phosphorylation to ∼10%. This suggests the existence of modest levels of lateral information transfer. In this scenario, the effect of HER2 on EGFR in the absence of HER3 is expected to be modest since there is no EGF in the system. The presence of HER3 and its ligand would result in HER2 phosphorylation through the formation of HER2-HER3 heterodimers. In the model, these heterodimers can dissociate yielding phosphorylated HER2 monomers, albeit at a low rate. If these activated HER2 monomers complex with an EGFR before getting dephosphorylated, the EGFR in the resultant dimer can get efficiently trans-phosphorylated. When the stimulating ligand is EGF (Fig. 5 B, solid lines), HER2 again has only a modest effect on EGFR phosphorylation. Overall, our model exhibits elements of HER2-mediated lateral information transfer, which can be interpreted as arising due to the dynamic formation and breakup of receptor dimers. Specifically, the lateral transformation transfer occurs due to the initial phosphorylation of HER2 in HER2-HER3 heterodimers. These dimers then dissociate, yielding phosphorylated HER2 monomers, which then engage with and phosphorylate EGFR molecules.

It would be of interest to examine the extent of lateral information transfer using experiments mimicking these simulation conditions. By knocking down the expression of HER2 and by using antibodies to block HER2 from forming heterodimers with other receptors, it would be possible to investigate the role of HER2 as the mediator of interaction between EGFR and HER3 receptors. It is reasonable to suggest that real cells could display increased HER2-mediated transfer beyond what is predicted by our model. It has been suggested that HER family receptors are capable of forming higher order oligomer complexes (8,52). That being the case, the diffusion-mediated collision of a free EGFR with a HER2-HER3 heterodimer could activate EGFR in such a trimeric complex. This is one possible means of obtaining increased lateral transfer other than that predicted by our model, which is restricted to dimer species.

Parametric sensitivity of system outputs and experimental observables

Dimerization affinities play a major role in controlling the dimer distribution within the cell

In our mathematical model, the formation of dimers of a given type is dictated by a complex interplay among the reversible reactions of ligand binding, dimerization, phosphorylation, and trafficking. We sought to identify the key reactions among these that serve as controlling entities in determining the model output by performing parametric sensitivity analysis. Simulations were performed for cells coexpressing 200,000 receptors each of EGFR, HER2, and HER3. Each of the 54 parameters in our model was increased by 10%, one at a time, and the effect of these changes on the dimer distribution was analyzed. Table 2 lists the parameter changes that result in a >2% change in the number of activated dimer species. Results are presented for both the total number of dimers in the cell and the number of dimers at the plasma membrane. As seen from Column 1 of Table 2, the EGFR-EGF binding and dissociation rates (parameters 1 and 6) affect the number of homo- and heterodimers involving EGFR. Similarly, the HER3-NRG affinity (parameters 2 and 7) has a bearing on the number of EGFR-HER3 heterodimers. When receptor dimerization affinities (Column 2) are examined, the competitive nature of the dimerization process becomes apparent. For instance, an increase in the dissociation rate of EGFR homodimers (parameter 13) not only has the direct effect of reducing the number of EGFR homodimers but also results in an increase in the number of EGFR-HER2 and EGFR-HER3 dimers. The relationship between receptor phosphorylation and dephosphorylation rates (Column 3) on the number of active dimers is relatively simpler. Increasing the rate of receptor phosphorylation for a given dimer increases the number of activated molecules of that dimer, and increasing the corresponding dephosphorylation rate has the opposite effect. Analysis of the effect of trafficking rates on dimer distribution (Column 4) yields intuitively apparent results. The number of molecules of a given dimer species increases when receptor recycling rates (parameters 43 and 47) are increased. Increasing the coated-pit vesicle formation rate (parameter 41) and the fraction of receptors incorporated into these vesicles (parameters 49–52) results in a decrease in the number of dimer species at the plasma membrane. It is interesting to note that the number of HER2-HER3 heterodimers (Row 4) does not display a marked dependence either on the HER2-HER3 affinity or on the dimerization affinities of the competing species (Row 4; Columns 1 and 2). This follows from the increased NRG binding affinity of these dimers. The 10-fold-lower dissociation rate of NRG from the HER2-HER3 heterodimer thus makes the number of HER2-HER3 dimers a robust quantity.

TABLE 2.

Critical parameters determining model output

		Ligand binding		Receptor dimerization		Receptor phosphorylation		Trafficking
Output variable		+	−	+	−	+	−	+	−
EGFR-EGFR	Total	1	6	15,18	13,17	23,29		47
	Surface			15,18	13,17	23,29		43,47	41,45,49–52
EGFR-HER2	Total		6	13,17		25,28,29	35,39,40
	Surface			12,17	15	25,28,29	35	43,47	41,49–51
EGFR-HER3	Total	2	6,7,11	13	18	27,28,29	38	47	41,49
	Surface		7,11	13	18	27,28,29		43,47	41,49–52
HER2-HER3	Total				17	26,28,29	37
	Surface					26,28,29	37	47	41,49

Parametric sensitivity analysis was performed by increasing each of the 54 model parameters (listed in Table 1) by 10%, one at a time, and studying the effect of this increase on the levels of activated dimers both at the whole-cell level and at the plasma membrane. Parameters that elicit a >2% change in the concentrations of the specific dimer species are listed. Parameter changes that result in an increase in the output, are listed in the plus (+) column; parameters whose increase results in a decrease in the output, are listed in the minus (−) column.

For the model to be able to reliably predict the dimerization pattern in a given cell type it is critical to quantify the parameters listed in Table 2 to a greater degree of accuracy than what would be acceptable for the other model parameters. Of these critical parameters, the dimerization affinities are unique in that altering a single affinity has wide-ranging consequences on the overall dimer distribution within the cell. These affinities can be estimated using techniques such as fluorescence resonance energy-transfer imaging of labeled dimers (32,53–55) or through protein coimmunoprecipitation experiments (18). However, accurate quantification of dimerization affinities from these experimental results is still a nontrivial task. In the following section we describe how the kinetic model can be used to address the problem of parameter estimation by enabling the design of relatively facile experiments from which parameters such as the dimerization affinities can be extracted.

Using the model to define measurement strategies for dimerization affinities

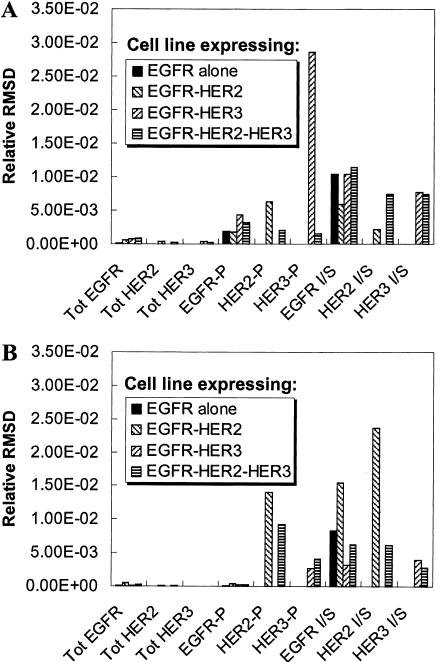
Before a model can be used in a predictive fashion for a specific cell type it is necessary to establish the validity of the parameter values in the chosen experimental system. Although some parameters, such as receptor-ligand affinities, may be independent of cell type, other parameters may be dependent upon the cell type and on the experimental conditions used for the measurement. A way of effectively addressing this issue is to perform experiments in the chosen cell type and to use this experimental data in conjunction with the mathematical model to estimate model parameters. A corollary conjuncture to this would be to use the model itself to choose the types of experimental measurements that need to be made to estimate a specific set of parameters. As an illustration of this approach we sought to identify experimental measurements that could be used to estimate the dimerization affinities in our kinetic model. As described in Methods, we considered a set of nine possible experimental measurements and four possible cell lines. The experimental observables considered were the total receptor mass of EGFR, HER2 and HER3, the fractional phosphorylation of the three receptors and the In/Sur ratio of the phosphorylated forms of the three receptors. The cell lines chosen expressed various combinations of EGFR, HER2, and HER3 receptors. Each of the dimerization parameters (parameters 13–20) was varied and the RMSD was used to identify the measurement that would be most sensitive to the variation of each of the parameters (see Methods). Fig. 6 presents the RMSD values for various choices of experiments for two of the dimerization parameters—the basal rate for dissociation of EGFR homodimers (parameter 13) and the enhancement in dimer dissociation rate when a receptor is dephosphorylated (parameter 19). The HER3 phosphorylation ratio in a cell line coexpressing EGFR and HER3 is the observation that displays the highest sensitivity to parameter 13 (Fig. 6 A). Therefore, if the aim is to better define the value of parameter 13 (the EGFR homodimer dissociation rate), measurement of HER2 phosphorylation ratio would be the most informative experiment to perform. Similarly Fig. 6 B shows that a good experiment to estimate parameter 19 would be the measurement of the inside/surface ratio of HER2 in a cell line coexpressing EGFR and HER2. The results also indicate that measurements of EGFR In/Sur ratio and the HER2 phosphorylation fraction in the same cell line could provide adequate data sets for estimation of parameter 19. In such a scenario the actual choice of experiments can be guided by the availability of antibodies and other such operational concerns regarding the experiment.

FIGURE 6.

Experimental design for parameter estimation. The model was run and the values of experimental observables were generated as a function of time using the base parameter set (base curves) and a parameter set with a 10% increase in a single model parameter (modified curves). The difference between the base curve and the modified curve was quantified using the relative root-mean-squared difference (RMSD) between the two curves (see the text). The experimental observables considered are the total receptor mass, the phosphorylation ratio, and the inside/surface ratio (denoted I/S in the figure) for the three receptors. The relative RMSD is plotted for these experimental outputs measured in four different cell lines for (A) a 10% change in parameter 13, the basal rate for the dissociation of EGFR homodimers; and (B) a 10% change in parameter 19, which is the enhancement in dimer dissociation rate when a receptor in a dimer becomes unphosphorylated. As seen, the fractional HER3 phosphorylation in a cell line expressing EGFR and HER3 would be the best output if one is interested in estimating parameter 13. Similarly, measurement of the HER2 In/Sur ratio in an EGFR-HER2 cell line provides the best estimate for parameter 19.

Table 3 lists the measurement variable and the cell line that would provide the best data set for the estimation of the various dimerization parameters in the model. Two experiments stand out in their ability to simultaneously provide information about a number of parameters. The first such measurement is that of the HER3 phosphorylation ratio in a cell line coexpressing EGFR and HER3. It is known that HER3 is kinase-deficient and can only be phosphorylated when it forms heterodimers with EGFR in this cell line. Hence, it should not be surprising that this measurement is effective in providing information about homo- and heterodimerization rates for EGFR and HER3. The second measurement providing the best data set for the estimation of multiple parameters is the measurement of HER2 In/Sur ratio in a cell line coexpressing EGFR and HER2. The internalization of HER2 is contingent upon its dimerization with ligand-bound EGFR. Hence, the extent of HER2 internalization serves as a good readout for HER2 homo- and heterodimerization affinities. It is clear from these results that the choice of the appropriate measurement for a given model parameter is not always intuitively obvious due to the complexity of the system. We believe that our approach to choose the most appropriate experimental measurement for estimation of model parameters may prove to be valuable in systematically constructing well-parameterized predictive models and in designing new sets of experiments.

TABLE 3.

Experiments to be performed for estimation of dimerization parameters

Parameter No.	Parameter description	Output to be measured	Cell line
13	BR for EGFR homodimer dissociation.	HER3 phosphorylation	EGFR/HER3
14	BR for HER2 homodimer dissociation.	HER2 In/Sur ratio	EGFR/HER2
15	BR for EGFR-HER2 dissociation.	EGFR In/Sur ratio	EGFR/HER2
16	BR for HER3 homodimer dissociation.	HER3 phosphorylation	EGFR/HER3
17	BR for HER2-HER3 dissociation.	HER3 phosphorylation	EGFR/HER2/HER3
18	BR for EGFR-HER3 dissociation.	HER3 phosphorylation	EGFR/HER3
19	Dissociation rate enhancement upon dephosphorylation.	HER2 In/Sur ratio	EGFR/HER2
20	Dissociation rate enhancement upon ligand removal.	HER3 phosphorylation	EGFR/HER3
50	Enhanced incorporation factor for ligand-bound EGFR.	EGFR In/Sur ratio	EGFR
51	Enhanced incorporation factor for ligand-bound EGFR-HER2.	HER2 In/Sur ratio	EGFR/HER2
52	Enhanced incorporation factor for ligand-bound EGFR-HER3.	HER3 In/Sur ratio	EGFR/HER3

BR stands for the basal rate. The relative RMSD between experimental observables generated using the base parameter set and a parameter set with a 10% change in a single model parameter was computed for all the dimerization parameters for four possible HER-expressing cell lines. These RMSD values were used to determine the experimental output that would serve to provide the best data set for estimation of each of the parameters listed. Experiments that turn out to be the best ones for the estimation of multiple parameters are italicized.

Phenotypic consequences of HER2 and HER3 overexpression

As mentioned earlier, the objective of this work is to provide computational tools for the establishment of a mechanistic link between HER overexpression and cellular transformation. Although it is possible to develop a detailed kinetic model for HER dimerization and activation, the complex nature of downstream signal transduction and its effects on cell phenotype impede the development of kinetic models for these stages of the process. However, it is possible to construct intuitive mathematical expressions describing the link between receptor activation and cell phenotype, which may facilitate the interpretation of experimental data. Equation 2 for the cell phenotype is one such expression. Explicitly stated, this equation suggests that the change in phenotype elicited in a cell stimulated by EGF and NRG depends upon the number of heterodimers of each type formed in the cell and on the potencies of each of these heterodimers. Introduction of this equation enables us to place the mechanisms behind transformation on a quantitative footing wherein the details of the process are captured by the β- and γ-parameters, the potencies of EGFR-HER3 and HER2-HER3 heterodimers relative to that of the EGFR homodimers, respectively. Using this equation, we examined the potential consequences of the receptor dimerization hierarchy on cell phenotype (Fig. 7). Specifically we attempted to address the question of whether coexpression of EGFR with both HER2 and HER3 at low-to-moderate levels would enable a cell to match the phenotype of a cell expressing EGFR along with extremely high levels of HER2 (600,000 receptors).

FIGURE 7.

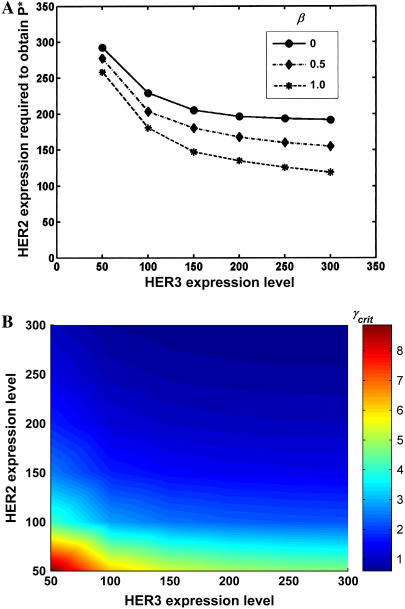
Effect of receptor expression levels on phenotype. Computations were performed for cells coexpressing 200,000 EGFR molecules and varying levels of HER2 and HER3 molecules. In both plots the receptor expression levels have units of thousands of molecules. (A) Critical HER2 required to match the phenotype P* of the reference cell line as a function of HER3 expression at three different β-values (EGFR-HER3 potencies). For all cases, HER2-HER3 potency is set at γ = 1. (B) Critical HER2-HER3 potency γ required to match P* for cell lines expressing varying levels of HER2 and HER3. For all cases, EGFR-HER3 potency is set at β = 0. Results indicate that coexpression of all three receptor subtypes at low-to-moderate levels may enable a cell to match the phenotype of a high HER2 expresser.

For the computations in Fig. 7, all cells were assumed to express 200,000 EGFR molecules while the expression levels of HER2 and HER3 were varied. The kinetic model was solved to obtain the number of dually phosphorylated dimers of various types required by Eq. 2 for the computation of the phenotype. For the results presented here, receptor activation levels 1 h after ligand stimulation were used to determine the phenotype. Employing the time-integral of receptor activation to determine the phenotype yielded qualitatively similar results (results not shown). In Fig. 7 A we present results for the scenario where HER2-HER3 heterodimers are only as potent as EGFR homodimers, i.e., γ is set to equal 1, and the critical levels of HER2 and HER3 required to match the phenotype value P* of the reference cell line (expressing 600,000 HER2 molecules) were determined. As seen, for the case where EGFR-HER3 dimers do not make any phenotypic contribution (β = 0), cells expressing 200,000 EGFR and 200,000 HER3 molecules need ∼200,000 HER2 molecules to display the phenotype P*. Setting β = 1 reduces the HER2 requirement to <100,000 molecules. In other words, cells expressing a combined HER2 and HER3 receptor number of <300,000 are capable of mimicking the phenotype of a cell line expressing 600,000 HER2 receptors. As noted earlier, the HER2-HER3 heterodimer is believed to be the most potent signaling entity in the HER-receptor family. Thus, in reality, γ-values are expected to be ≫1. In Fig. 7 B, we examine the critical potency γ_crit required to match the reference phenotype P* in cells expressing various combinations of HER2 and HER3 receptor numbers. For these computations, the EGFR-HER3 heterodimer was assumed to have no potency (β = 0). As seen, cells expressing a mere 50,000 each of HER2 and HER3 receptors are enabled to match the phenotype of a 600,000 HER2 expresser if the HER2-HER3 heterodimer is approximately nine times more potent than the EGFR homodimer. In addition, the figure nicely illustrates the nonlinear response characteristics of the model system.

Overall, our results indicate that HER3 can have a profound impact on cell phenotype through the enhanced recruitment of HER2 receptors into a potent signaling moiety. We are currently setting up experiments in cell lines expressing varying amounts of EGFR, HER2, and HER3 to test these predictions. In addition, the experiments will enable us to refine Eq. 2 into a more comprehensive definition of the physico-chemical factors that govern cellular responses mediated by the HER family of receptors.

SUMMARY AND CONCLUSIONS

The utility of mathematical modeling as a tool to understand cell biology is increasingly being recognized. Models can serve the dual role of providing 1), predictive capability obviating the need for repeated experiments; and 2), mechanistic information about how a cell converts environmental cues to an eventual phenotypic outcome. Furthermore, mathematical models can be used as powerful tools to organize knowledge in the era of systems biology. The necessity for quantitative precision in the definition of a model motivates one to critically examine relevant experimental data, formalize the assumptions regarding mechanisms, and enables one to uncover gaps in knowledge. Extant information on molecular interactions, concentrations, and reaction rates within the cell serve to restrict the scope and the detail of models in cell biology. Toward one end of the spectrum processes such as receptor-ligand binding, receptor phosphorylation and vesicle trafficking are sufficiently well quantified to warrant the use of detailed kinetic representations. Toward the other end, information about processes such as transcription and translation and the manner in which a second messenger concentration dictates a biological outcome is currently not amenable to kinetic modeling. Hence, the development of predictive models that can establish a link between a stimulus and a biological response requires the integration of mathematical descriptions of cellular processes, which may vary vastly in their degree of detail. We describe the development of a predictive model that strives to establish a link between receptor expression levels and cell phenotype for the human epidermal growth factor receptor (HER) system.

We have demonstrated how detailed kinetic models of receptor dimerization and trafficking that are permissible by virtue of the quantitative information available can be combined with crude curve-fitting type approaches to establish a link between HER overexpression and cellular transformation. The major results of our analysis and their implications are highlighted below:

1. Our kinetic model brings together the available quantitative information about receptor-ligand binding, dimerization, phosphorylation, and trafficking properties of the EGFR family of receptors, and presents it in the form of a concise mathematical model. Using the model, we demonstrated how the current literature on rate constants for receptor-ligand binding and dimerization lead naturally to the enhanced formation of HER2-HER3 heterodimers in cells coexpressing HER1-3 receptors. It has been previously shown that coexpression of HER2 and HER3 has a synergistic effect on cell transformation (56,57). Our results indicate that this effect can be explained in part due to the enhanced formation of HER2-HER3 dimers.

2. We found that coexpression of EGFR with HER2 and HER3 retards EGFR internalization and degradation, thereby prolonging signaling through the EGFR while decreasing the bias toward endosomal compartments. This could be an additional reason for the synergistic effect of receptor coexpression on cell transformation.

3. We have utilized the developed model to design experiments aimed at estimating the dimerization affinities of different receptor types. Parameter sensitivity analysis revealed that measurements of HER3 phosphorylation in cells coexpressing EGFR and HER3 and the HER2 internalization ratio in cells coexpressing EGFR and HER2 would be especially useful for the estimation of critical model parameters. We plan to incorporate these findings into the design of our planned experiments to validate and to better parameterize our model.

4. The reaction network presented here can be easily adapted to develop models for other receptor signaling systems where receptor dimerization and trafficking play a similarly important role.

5. We have used a simple intuitive expression grounded in our qualitative understanding of the biological system to explore the possible effects of our model predictions on biological response. This analysis indicates that coexpression of HER1–3 at low-to-moderate levels may enable a cell to match the phenotype of a cell expressing very high levels of EGFR and HER2. This result is both due to the enhanced formation of HER2-HER3 heterodimers and to the enhanced potency of this dimer species when it comes to transformation. Such approaches borrowed from engineering and statistical sciences could prove to be valuable in designing experiments aimed at dissecting the mechanistic link between molecular level events and biological endpoints.

APPENDIX A: EQUATIONS GOVERNING THE KINETIC MODEL

The concentration of a species in a specific type of compartment can change due to one of two reasons. The species can be 1), generated and destroyed through a biochemical reaction; or 2), transported in and out of the compartment due to vesicle trafficking. The flux for species i in compartment C can be written as the linear combination of the flux contributions due to these processes as

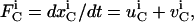(A1)

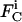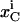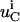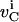where is the net flux for species i in compartment C, is the concentration of species i in compartment C, and and are the net biochemical reaction and trafficking fluxes for species i in compartment C. For a given set of rate constants, flux 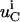can be computed based on the reactions that species i participate in. The trafficking flux for species i in the various compartments depends upon the abundance of various types of vesicles in the cell. These vesicle concentrations in turn evolve according to the equations

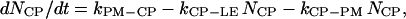(A2a)

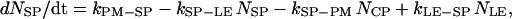(A2b)

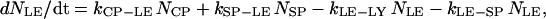(A2c)

where N_CP, N_SP, and N_LE are the number of coated-pit (CP), smooth pit (SP), and late endosomic (LE) vesicles, respectively. These variables have units of unit-vesicle size. In Eq. A2, k_xx-yy are the rate constants encoded such that xx is the two-letter code for the source compartment, whereas yy is that for the target compartment. Thus k_PM-CP is the zero-order rate constant for the formation of coated-pit vesicles from the plasma membrane, while k_LE-LY is the first-order rate constant for the merging of a vesicle from the late endosome into the lysosome.

The trafficking flux for species i in the various compartments can be written in terms of the vesicle abundances and the rate constants for vesicle trafficking as

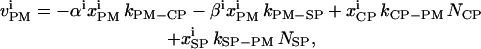(A3a)

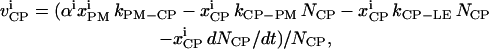(A3b)

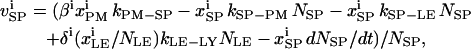(A3c)

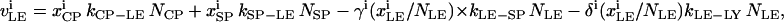(A3d)

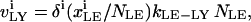(A3e)

where 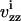is the trafficking flux for species i in compartment zz in units of molecules per unit time. The values αⁱ and βⁱ are incorporation coefficients for species i into coated-pit and smooth-pit vesicles forming from the PM, respectively. The values γⁱ and δⁱ are multiplication factors that account for the increased propensity of a species to get recycled from the LE or targeted from the LE to the lysosome, respectively. 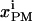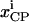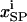The value is the total number of molecules in the plasma membrane, and and are the number of molecules in a single coated-pit vesicle and a single smooth-pit vesicle, respectively. The total number of molecules of species Xⁱ in the EE is thus 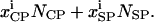Similarly, 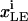is the total number of molecules in the LE compartment. The differential trafficking properties of the various receptor monomers and dimers of the HER family are captured in our model by specifying different incorporation coefficients (αⁱ and βⁱ) for the various receptor species. A species that tends to internalize more rapidly is given a higher early endosome incorporation coefficient, while a species that gets degraded more rapidly would have a higher value of δⁱ.

Solution of the model entails simultaneous solution of the system of ordinary differential equations obtained by combining Eqs. A1–A3. For a given receptor expression level, the receptors are initially assigned to the plasma membrane in the form of ligand-free, unphosphorylated monomers. Thus, at time t = 0, the concentrations of all species except R1FU, R2FU, and R3FU are set to equal zero. In addition, the simulation is started with a coated-pit, smooth-pit and sorting endosome number of one each. Equations A1 and A3 are then solved in the absence of ligand until t = 5 h to generate a steady-state distribution of vesicles and receptors in the cell, and this configuration is used as the initial starting point for later simulations investigating the response to ligand stimuli. Subsequently ligand is added to the system and the time-evolution of species concentrations is computed by solving the system of differential equations. The raw-species concentration profiles resulting from solution of the mathematical model were analyzed to extract relevant information such as the fraction of phosphorylated receptors, the In/Sur ratio of the receptors, and the dimerization fractions for the various receptors.

APPENDIX B: RATE CONSTANTS FOR THE KINETIC MODEL

The combinatorial nature of the dimerization model necessitates the specification of rate constants for 308 biochemical reactions for each of the cellular compartments. We tackle this problem by specifying reaction rates in terms of a representative or basal rate for a specific species that serves as a reference complex for an entire class of reactions. In addition, we specify how the rate constants would change if the phosphorylation or ligand-binding state of this reference species were to change. A rate constant value for a reaction involving any given species is obtained as the product of the basal rate for the class to which the reaction belongs and the multiplier for the species. We consider each of the reaction types one by one and describe how actual rate constants are derived from the parameter list presented in Table 1. For the sake of brevity, the parameter number n from Table 1 is written as pn.

Receptor-ligand binding and dissociation

The parameters for the binding of EGF to EGFR and NRG to HER3 are based on Jones et al. (39) and French et al. (58). The basal rates for ligand binding and dissociation represent the rate constants for reactions at the plasma membrane (p1, p2, p6, p7). These rates are assumed to be independent of receptor dimerization and phosphorylation state. However, they are adjusted to correct for the effect of pH in intracellular compartments. Specifically the association and dissociation rates are multiplied by 0.135 (p3) and 4.125 (p8), respectively, to obtain the corresponding intracellular rates for EGF-EGFR complexes (58). NRG–HER3 complexes are assumed to display a pH-dependent enhancement in ligand dissociation similar to that of TGFα-EGFR complexes, i.e., the plasma membrane association rate is multiplied by 0.l35 (p4) and the dissociation rate is multiplied by a value of 8.25 (p9) to obtain the endosomal rates for these complexes (42). This assumption has the effect of inducing enhanced recycling of HER3 receptors, similar to that observed for TGFα-EGFR complexes. The dissociation of neuregulin from HER2-HER3 heterodimers is assumed to be 10-times slower than the basal rate indicated (p10) (18,39). Further, In EGFR-HER3 heterodimers the presence of NRG halves the EGF on-rate (p5) and increases the EGF off- rate by a factor of 1.5 (p11) (40).

Receptor dimerization and dimer dissociation

The dimerization rates have been adapted from Resat et al. (42) and Kholodenko et al. (46). Dimerization is assumed to be diffusion-limited. A constant value is used for all receptor types. Dimer dissociation is assumed to occur at the basal rate when both receptors are ligand-bound and phosphorylated. Thus, p13 represents the rate constant for the reaction R1BP·R1BP→R1BP + R1BP. Dephosphorylation of each receptor is assumed to double the rate of dimer dissociation. Removal of each ligand is assumed to further induce a fivefold increase in the dissociation rate. For example, the reaction R1BP·R1FU→R1BP + R1BP would have a rate constant equal to 10-times (2 × 5) the value specified for p13. This is because this dimer is obtained after dephosphorylation and ligand dissociation from one of the receptors in the reference species R1BP·R1BP. In dimers involving HER2, HER2 is assumed to behave as if it were ligand-bound, for the purpose of determining the dimer dissociation rate. This is in agreement with models based on crystallographic data (59,60), which indicate that HER2 may constitutively present a conformation that is conducive to receptor dimerization (41). In dimers involving HER3, the receptor is assumed to behave similar to EGFR in terms of its dissociation properties.

Receptor phosphorylation and dephosphorylation

The receptor phosphorylation and dephosphorylation rates have also been adapted from Resat et al. (42) and Kholodenko et al. (46). The phosphorylation rates of free (no-ligand) EGFR, HER2, and HER3 receptor monomers are set to 0. Phosphorylation of EGFR homodimers is assumed to occur at the basal rate when both receptors are free and unphosphorylated. Thus, p23 represents the rate constant for the reaction R1FU·R1FU→R1FU·R1FP. Each ligand bound to the complex is assumed to double the phosphorylation rate (p29). If one of the receptors is already phosphorylated, phosphorylation is assumed to proceed at three times the basal rate (p28). EGFR-HER3, HER2-HER3, and EGFR-HER2 dimers are assumed to have 80% of the basal phosphorylation rate of the corresponding EGFR homodimers. Dephosphorylation of EGFR homodimers is assumed to occur at the basal rate when both receptors are ligand-bound and phosphorylated. Thus, p33 represents the rate constant for the reaction R1BP·R1BP→ R1BU·R1BP. Whereas removal of each ligand causes a fourfold increase (p40) in the dephosphorylation rate, the presence of one unphosphorylated receptor further doubles the rate (p39). HER2 is assumed to behave as if it were a ligand-bound receptor, for the purpose of determining phosphorylation and dephosphorylation rates.

Vesicle trafficking rates

Parameters 41–48 were taken from Resat et al. (42). These parameters were determined by making the following assumptions:

1. The half-life of early endosomal vesicles is 5 min.

2. Ninety-percent of smooth pit endosomes recycle to the plasma membrane (the rest merge into sorting endosomes).

3. Thirty-percent of coated-pit vesicles recycle to the plasma membrane.

4. The lifetime of a sorting endosome is 45 min.

5. Five-percent of sorting endosomes get degraded.

These parameters specify the rates k_xx-yy in Eqs. A2 and A3 of Appendix A.

Receptor incorporation factors

Parameter 49 represents the value for the incorporation coefficients (denoted as αⁱ and βⁱ in Eq. A3 in Appendix A) for the case of receptor species, which have no bound ligand. The incorporation coefficient β of ligand-bound EGFR in coated-pit endosomes is 15.5 times (p50) higher than this value. Similarly, the β-values of ligand-bound EGFR-HER2 and EGFR-HER3 heterodimers is 5.4 times higher than the basal incorporation coefficient. These multiplier values are given by p51 and p52, respectively.

Receptor recycling and degradation factors

All γⁱ values are set to equal 1 in the model, i.e., all of the receptors are assigned the same propensity for getting incorporated into a vesicle recycling from the LE to the plasma membrane. The degradation of molecules in the late endosome occurs at a basal rate dictated by a uniform concentration-dependent incorporation into pseudo-vesicles targeted for lysosomal degradation. The presence of one EGF molecule on a receptor complex causes a threefold increase (p53) in its incorporation rate, whereas the presence of two EGF molecules causes a sixfold increase (p54) in the rate. These parameters provide values for the variable δⁱ in Eq. A3 of Appendix A.