Abstract
During mitosis, ensembles of dynamic MTs and motors exert forces that coordinate chromosome segregation. Typically, chromosomes align at the metaphase spindle equator where they oscillate along the pole-pole axis before disjoining and moving poleward during anaphase A, but spindles in different cell types display differences in MT dynamicity, in the amplitude of chromosome oscillations and in rates of chromatid-to-pole motion. Drosophila embryonic mitotic spindles, for example, display remarkably dynamic MTs, barely detectable metaphase chromosome oscillations, and a rapid rate of “flux-pacman-dependent” anaphase chromatid-to-pole motility. Here we develop a force-balance model that describes Drosophila embryo chromosome motility in terms of a balance of forces acting on kinetochores and kMTs that is generated by multiple polymer ratchets and mitotic motors coupled to tension-dependent kMT dynamics. The model shows that i), multiple MTs displaying high dynamic instability can drive steady and rapid chromosome motion; ii), chromosome motility during metaphase and anaphase A can be described by a single mechanism; iii), high kinetochore dynein activity is deployed to dampen metaphase oscillations, to augment the basic flux-pacman mechanism, and to drive rapid anaphase A; iv), modulation of the MT rescue frequency by the kinetochore-associated kinesin-13 depolymerase promotes metaphase chromosome oscillations; and v), this basic mechanism can be adapted to a broad range of spindles.
INTRODUCTION
Chromosome segregation depends upon the action of the mitotic spindle, a protein machine that uses ensembles of mitotic motors and MT dynamics to capture chromosomes consisting of duplicated sister chromatids and align them at the metaphase spindle equator and then to move sister chromatids to opposite spindle poles during anaphase (1–3). The sister chromatids are attached to the spindle by kts, protein complexes assembled on centromeric DNA that consist of several distinct layers as observed by EM (4,5), and which bind to the plus ends of a subset of spindle MTs called kMTs whose minus ends are also linked to the poles (6).
KMTs play important roles in chromatid motility, and in many systems they are very dynamic. For example, during metaphase, kMTs display dynamic instability (7) at their plus ends and they also exhibit motor-dependent poleward flux, in which the MT polymer lattice persistently translocates poleward as tubulin subunits undergo net addition onto the dynamic MT plus ends and net dissociation from their pole-associated minus ends (8,9). This dynamic behavior contributes to the oscillations of congressed metaphase chromosomes along the pole-pole axis, a process called “directional instability” (10). During anaphase A, kMTs continue to undergo poleward flux as tubulin subunits dissociate at their pole-associated minus ends, and, if subunit addition at the kt ceases or slows down, the kMTs can then shorten and drag the disjoined chromatids poleward (11–13). In many systems, this “flux mechanism” for anaphase A is supplemented or replaced by a “pacman” mechanism, in which the kinetochores actively “chew” their way to the poles by depolymerizing kMTs at their plus ends, dragging the attached chromatids poleward (14–18). While kMTs exert the forces that underlie both metaphase chromosome oscillations and anaphase A chromatid-to-pole motility, a second subset of MTs, the ipMTs, drive spindle elongation during anaphase B. Modifications of these basic events occur in many cell-types and there exists significant variability in the rates of chromosome motility, in the magnitude of the oscillations associated with directional instability, in the relative contributions of the flux and pacman components of anaphase A, and in the relative contributions of anaphase A and B to chromosome segregation, within different systems (11–15,18,19).
The Drosophila syncytial blastoderm stage embryo (cycles 10–13) is a veritable mitotic factory packed with mitotic spindles whose hallmark is rapid mitosis (14,15,18,20,21). The syncytium contains the order of a thousand spindles lying just under the cortex that are derived from the single nucleus of the fertilized egg through a stereotypical series of mitoses and nuclear migrations. Each spindle assembles as the nuclear envelope fenestrates during prometaphase when eight pairs of sister chromatids are captured and maneuvered onto the equator of the ∼10 μm long metaphase spindle, where they are held in a relatively static state, displaying no obvious directional instability (Fig. 1 A) (3,13). Anaphase A chromatid-to-pole motility depends on a combined “flux-pacman mechanism” and is remarkably fast (0.1 μm s−1) (14,18). Once chromatid-to-pole motion is essentially complete, anaphase B onset is triggered by the suppression of poleward flux within ipMTs, which allows persistently sliding ipMTs to exert forces that drive spindle pole separation at a similar fast rate (14,21). The spindle MTs are highly dynamic, displaying a turnover half-time of ∼5 s in FRAP experiments, independent of the position or phase of photobleaching ((21) and D. Cheerambathur and J. M. Scholey, unpublished results) and fluxing poleward at 0.05 μm s−1 before anaphase B onset (14). This rapid turnover rate is plausibly due to dynamic instability of all subsets of spindle MTs, leading to the question “how can MTs that display rapid turnover and switch frequently between fast growth and shrinkage, drive steady and rapid motility?” Computational modeling using systems of force-balance and rate equations suggests that highly dynamic ipMTs can drive steady, linear pole-pole separation during anaphase B (21), and below we use similar modeling approaches to determine the feasibility of driving rapid, steady chromatid-to-pole movements using highly dynamic kMT tracks.
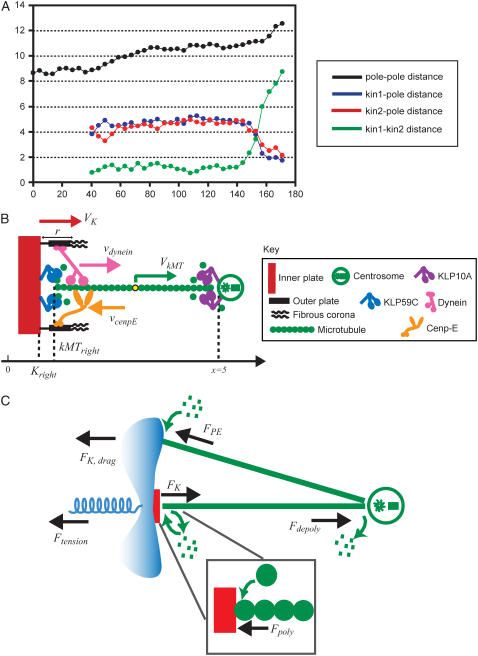
FIGURE 1.
Metaphase and anaphase A chromatid motility in Drosophila embryos; qualitative and force-balance model. (A) Dynamics of spindle poles and chromatids in Drosophila embryos. During metaphase (∼80–135 s), the chromatids remain at the spindle equator, and do not exhibit oscillations between the spindle poles as observed in some other organisms. During anaphase A (∼135–175 s), chromatids move steadily and rapidly toward the spindle poles, which are held at constant spacing at ∼10 μm (14,18). (B) Kinetochore-MT interface in Drosophila embryos, adapted from Maiato (5) and Rogers et al. (18). A kinetochore inner (red) and outer plate (black) along with the fibrous corona (black), a dynein (pink), and a cenpE (orange) motor generating antagonistic forces at the kinetochore, the KLP59C motors (blue) depolymerizing MT's (green) plus end inserted into the kinetochore, a centrosome (green circle), and the KLP10A motors (purple) depolymerizing the minus end of the MT at the spindle pole are shown. The direction of the velocities of motors, kinetochore and MT, and the position of the spindle equator (x = 0), the kinetochore plate, the plus end of the kMT, and the right spindle pole (x = 5) are indicated. (C) Force-balance model. Forces acting on the kinetochore and the kMT are shown. For simplicity, only a single kMT is shown bound to the kinetochore, and only a single spindle MT impinging on the chromosome arm generating polar ejection forces is shown.
Several mitotic motors have been implicated in chromosome motility during metaphase-anaphase A in Drosophila embryo spindles. For example, dynein and members of the kinesin-7 (cenpE), kinesin-3 (KLP38B), and kinesin-13 (KLP59C) families (22) appear to act on kts or chromosome arms to contribute to chromosome positioning at the metaphase equator, whereas the rapid, flux-pacman-driven chromatid-to-pole motion during anaphase A is thought to be driven by a kinesin-13-dependent mechanism in which KLP10A depolymerizes kMTs at the spindle poles to drive poleward flux, whereas KLP59C depolymerizes kMTs at the kinetochore to drive “pacman” motility (18,20,23,24). In this mechanism, dynein located at the kinetochores is thought to assist KLP59C by inserting the plus ends of kMTs into the kinetochore structure to facilitate KLP59C-mediated depolymerization (5,18,20,25).
Although some aspects of chromatid motility that are used in Drosophila embryos are likely to be widely employed among different cell types, other features may represent adaptations for rapid motility. For example, evidence is accumulating from a number of systems in support of the hypothesis that a kinesin-13 depolymerase located at the spindle poles plays a significant role in driving poleward flux (26–28). In contrast, most studies on the role of kinesin-13 and dynein on kinetochores has focused on the role of these motors in error-correction mechanisms and in the spindle assembly checkpoint, rather than in chromatid motility per se (29–33). Thus, it is possible that the KLP59C and dynein-based “pacman” mechanism used in Drosophila embryos is a functional adaptation that facilitates rapid motility concordant with the rapid rates of mitosis observed, a possibility that can be explored using modeling.
Two pioneering quantitative models have recently been proposed to describe chromosome motility (34–36). In the first, a force-balance model of the kinetochore was successfully used to describe the forces that drive metaphase chromosome oscillations and directional instability, based on a “Hill-sleeve” structure in which the kinetochore contains “sleeves” that bind kMTs on their inner surface (34,37,38). However, in this study, the identity and mechanism of action of the relevant kinetochore motors were not examined. A different theoretical approach was used to describe the positioning of metaphase kinetochores in the budding yeast spindle (35,36), but in that study the mechanism by which kinetochores attach to spindle MTs and remain attached under varying force regimes was not addressed.
Here, we develop a mathematical force-balance model of chromosome motility that describes the dynamics of a pair of sister kinetochores and their associated kMTs during metaphase and anaphase A in Drosophila syncytial blastoderm embryos. The model is based on a kinetochore-MT interface as drawn in Rogers et al. (18), Maiato et al. (5), Maddox et al. (13), and Rieder and Salmon (25), and incorporates the concerted action of force generators coupled to MT-dynamics. The model includes the dynamics of kMT and its modulation by enzymes and forces; the forces generated by antagonistic and complementary enzymes and polymers at the kinetochores and poles; a simplified mechanistic description of the centromeric cohesin bonds between sister chromatids; polar ejection forces; and a force-balance between the forces acting on kts and viscous drag forces (34–36). By varying the model parameters, we provide a good description of metaphase-anaphase A kt behavior in Drosophila embryos and also in various other cell-types based on the action of mitotic motors and MT dynamics, without the need to invoke additional poorly characterized structures such as “Hill sleeves”. The model demonstrates: 1), that multiple highly dynamic and transiently attached kMTs can drive steady, accurate chromosome movements; 2), that kts can maintain persistent attachment to a spindle pole despite the high dynamicity of the kMT plus ends and the presence of several force generators; 3), that the low amplitude and frequency of metaphase chromosome oscillations in Drosophila embryonic spindles may be due to high dynein activity at the kinetochores, 4), that the action of the kinesin-13 depolymerase KLP59C promotes metaphase oscillations; and finally 5), explores the generality of the proposed mode of action of the Drosophila pacman motor in other organisms.
MODEL
In this section, we first describe the model variables and equations in a simplified configuration as shown in Fig. 1, B and C, where only a single kMT is shown bound to the kinetochore. In the final subsection, we generalize the model to account for a realistic configuration of the kinetochore-MT interface in Drosophila embryos and other organisms where multiple MTs are bound to kinetochores. In formulating the model, the relevant properties of mitosis in Drosophila embryos are: i), a combined flux-pacman mechanism for anaphase A; ii), spindle MTs that display high levels of dynamic instability; and iii), the presence of plus and minus end-directed MT-based motors on the kinetochores (cenpE and dynein) and the presence of kinesin-13 family depolymerases (KLP59C and KLP10A) on the kinetochores and spindle poles, respectively (see Introduction).
Definitions and assumptions
During metaphase/anaphase A, the spindle poles in the Drosophila mitotic spindle are maintained at ∼10 μm spacing (cycle 12) (14). In all descriptions below, the positions of the kinetochores, and microtubule plus and minus ends, correspond to distances from the spindle equator, located at the origin (x = 0), and the left and right spindle poles are located at x = −5 and x = 5, respectively, mimicking the metaphase/anaphase A steady-state pole separation of ∼10 μm in the Drosophila embryo. All forces and velocities associated with the right and left kinetochores and kMTs are assumed to be positive in the poleward direction (toward the right pole for the kinetochore tethered to the right pole, and toward the left pole for the kinetochore tethered to the left pole) unless otherwise specified. 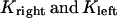 denote the current position of the right and left sister kinetochores' plates with respect to the spindle equator (Fig. 1 B).
denote the current position of the right and left sister kinetochores' plates with respect to the spindle equator (Fig. 1 B). 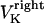 and
and 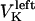 denote the time-dependent velocities of the right and left sister kinetochores, respectively (Fig. 1 B).
denote the time-dependent velocities of the right and left sister kinetochores, respectively (Fig. 1 B). 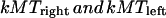 denote the current position of the plus ends of kMTs with respect to the spindle equator, and
denote the current position of the plus ends of kMTs with respect to the spindle equator, and 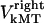 and
and 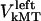 are the time-dependent poleward sliding rates of the right and left kMTs, mediated by motors sliding them against ipMTs, or by motors located near the spindle poles and “reeling in” the kMTs toward the poles, respectively (Fig. 1 B).
are the time-dependent poleward sliding rates of the right and left kMTs, mediated by motors sliding them against ipMTs, or by motors located near the spindle poles and “reeling in” the kMTs toward the poles, respectively (Fig. 1 B).
In our model, we make the following explicit assumptions: i), We assume that the motility events examined here are driven by an intrinsic balance of forces generated in the spindle, and we do not consider the possibility of morphogens or other external factors such as the dynamics of a hypothetical spindle matrix driving the motility events we investigate. ii), We assume that throughout the metaphase/anaphase A isometric state, pole-pole distance is maintained by a balance of antagonistic forces generated at antiparallel overlaps between ipMTs and astral MTs, and in this model, as in previous considerations of kinetochore positioning, we do not address how changes in spindle pole positions can/may affect kinetochore positions and vice versa (34-36). iii), We assume that all motor-generated forces are additive, i.e., the total motor generated force depends linearly on the total number of active force generators. We further assume that all motor enzymes considered have linear force-velocity relationships (see Appendix) similarly to conventional kinesin and as proposed recently for dynein (39–41). iv), We assume that in the MT-motor-kinetochore interactions, the length of the MT tip interacting with the kinetochore structure is the force limiting factor.
Force-balance equations
In this analysis we consider separately the forces acting on the kinetochore and the kMT.
Force-balance on the kinetochore
The direction of movement and the velocity of a chromosome during metaphase/anaphase A are determined by a balance of forces acting on its kinetochore (Fig. 1 C). These forces include: 1), forces resulting from the antagonistic effect of plus and minus end-directed motors, cenpE and dynein, bound to the kinetochore and moving along their kMT tracks that flux poleward by being “reeled in” toward the poles or slid poleward and depolymerized, 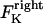 and
and 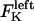 for the right and left kinetochores; 2), forces generated by polymerizing plus ends of kMTs impinging on the kinetochore plate,
for the right and left kinetochores; 2), forces generated by polymerizing plus ends of kMTs impinging on the kinetochore plate, 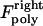 and
and 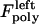 ; 3), elastic tension forces due to flexible cohesin bonds between sister kinetochores during metaphase, pulling the kinetochores toward one another,
; 3), elastic tension forces due to flexible cohesin bonds between sister kinetochores during metaphase, pulling the kinetochores toward one another, 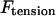 ; and 4), polar ejection forces pushing the chromosome arms toward the spindle equator during metaphase, thereby exerting forces to push the kinetochores toward the spindle equator,
; and 4), polar ejection forces pushing the chromosome arms toward the spindle equator during metaphase, thereby exerting forces to push the kinetochores toward the spindle equator, 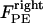 and
and  . The sum of these forces is, at any time, balanced by the viscous drag forces on the kinetchores,
. The sum of these forces is, at any time, balanced by the viscous drag forces on the kinetchores, 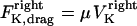 , and
, and 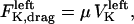 where μ is the effective drag coefficient associated with the Drosophila chromosome (42). Thus, for the right and the left kinetochore, we have the following force-balance equations coupled to one another via the tension force:
where μ is the effective drag coefficient associated with the Drosophila chromosome (42). Thus, for the right and the left kinetochore, we have the following force-balance equations coupled to one another via the tension force:
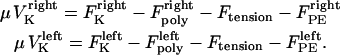 |
(1) |
In the coupled force-balance equations (Eq. 1), the magnitude of 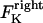 (similarly
(similarly 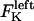 ) depends upon: i), the total number of kMTs bound to the kinetochore (for simplicity a single kMT is shown in Figs. 1, B and C, and equations here describe the situation shown); ii), the number of active motors at the kinetochore that are bound to the MT and exert forces, i.e., the average number of cenpE and dynein motors per unit length of MT embedded in the kinetochore structure (
) depends upon: i), the total number of kMTs bound to the kinetochore (for simplicity a single kMT is shown in Figs. 1, B and C, and equations here describe the situation shown); ii), the number of active motors at the kinetochore that are bound to the MT and exert forces, i.e., the average number of cenpE and dynein motors per unit length of MT embedded in the kinetochore structure (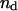 and
and 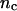 for dynein and cenpE motors, respectively), and the length of the MT tip inserted into the kinetochore structure
for dynein and cenpE motors, respectively), and the length of the MT tip inserted into the kinetochore structure 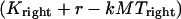 , where r is the distance between the tip of the fibrous corona and the kinetochore plate in the three layer kinetochore structure (Fig. 1 B) (4,5,25); and finally iii), the force generated by each plus and minus end-directed motor,
, where r is the distance between the tip of the fibrous corona and the kinetochore plate in the three layer kinetochore structure (Fig. 1 B) (4,5,25); and finally iii), the force generated by each plus and minus end-directed motor, 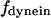 and
and 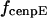 . That is,
. That is,
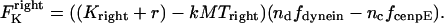 |
(2) |
Assuming that motors obey linear force-velocity relationships (see Appendix), the forces  and
and 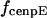 in Eq. 2 can be written as
in Eq. 2 can be written as  and
and 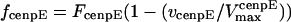 , where
, where  ,
,  ,
,  , and
, and  ,
, 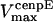 , and
, and 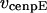 are the stall force, unloaded velocity, and the current time-dependent velocity of the dynein and cenpE motors, respectively. Furthermore, the velocities of the motors can be written in terms of the velocities of the kinetochore and that of the kMT along which they are moving, in the following kinematic equations:
are the stall force, unloaded velocity, and the current time-dependent velocity of the dynein and cenpE motors, respectively. Furthermore, the velocities of the motors can be written in terms of the velocities of the kinetochore and that of the kMT along which they are moving, in the following kinematic equations:
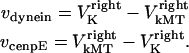 |
(3) |
Thus, Eq. 2 can be written as
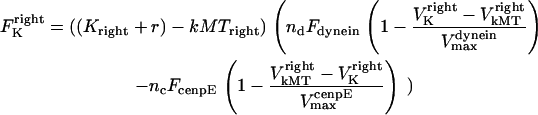 |
(4) |
The magnitude of 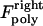 (similarly
(similarly 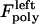 ) depends upon the position of the plus ends of kMTs impinging on the kinetochore plate. Specifically, the polymerization force is equal to zero when the kMT tip is not impinging on the kinetochore plate and increases linearly in proportion to the length of kMT tip embedded in, and impinging on the kinetochore plate, at rate ɛ. Here, ɛ is a parameter representing the elastic modulus of the kinetochore plate:
) depends upon the position of the plus ends of kMTs impinging on the kinetochore plate. Specifically, the polymerization force is equal to zero when the kMT tip is not impinging on the kinetochore plate and increases linearly in proportion to the length of kMT tip embedded in, and impinging on the kinetochore plate, at rate ɛ. Here, ɛ is a parameter representing the elastic modulus of the kinetochore plate:
 |
(5) |
Similarly to previous quantitative models proposed to explain the dynamics of metaphase chromosomes, we represent the tension force between the kinetochores by a linear spring (34–36). The magnitude of the force Ftension thus depends only on the distance between the sister kinetochores, i.e., the relative position between the kinetochores: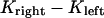 , the rest length and the stiffness of the spring-like cohesin bonds, d0 and κ, respectively:
, the rest length and the stiffness of the spring-like cohesin bonds, d0 and κ, respectively:
 |
(6) |
Finally, the polar ejection forces, 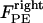 (or
(or 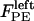 ), are directed toward the spindle equator and are positive in the right-half spindle and negative in the left-half spindle for the chromosome associated with the right pole, and respectively positive in the left-half spindle and negative in the right-half spindle for the left pole-associated chromosome. The polar ejection forces are assumed to be due to interactions between the chromosome arms and the spindle MTs' plus ends, and thus are proportional to the density of MTs emanating from each pole. Therefore, the magnitude of this force depends on the position of the kinetochore in the spindle and is represented by the square of the distance between the kinetochore and the spindle equator, and an adjustable parameter, ρ, depicting the steepness of this relationship similarly to previous models (34–36). For example, in the right-half spindle, the polar ejection forces exerted on the right kinetochore are
), are directed toward the spindle equator and are positive in the right-half spindle and negative in the left-half spindle for the chromosome associated with the right pole, and respectively positive in the left-half spindle and negative in the right-half spindle for the left pole-associated chromosome. The polar ejection forces are assumed to be due to interactions between the chromosome arms and the spindle MTs' plus ends, and thus are proportional to the density of MTs emanating from each pole. Therefore, the magnitude of this force depends on the position of the kinetochore in the spindle and is represented by the square of the distance between the kinetochore and the spindle equator, and an adjustable parameter, ρ, depicting the steepness of this relationship similarly to previous models (34–36). For example, in the right-half spindle, the polar ejection forces exerted on the right kinetochore are
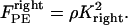 |
(7) |
Substituting the force terms in Eqs. 4–7 into Eq. 1 yields
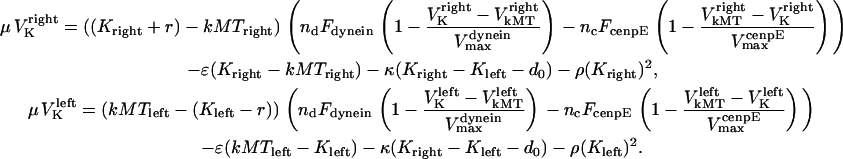 |
(8) |
Force-balance on kMT and kMT minus end dynamics
Similarly to the kinetochore, we also consider the forces on the kMTs that link the kinetochores to the spindle poles. As mentioned above, we assume that kMTs are being “reeled in” or slid toward the spindle poles at rates 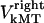 and
and 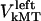 by motors. We do not specify or distinguish whether these motors are located at the spindle poles and reeling the kMTs into the poles, or are located along the kMTs themselves and sliding them poleward against the ipMTs in the vicinity of an unknown spindle structure. We further assume that the minus ends of kMTs are being depolymerized at the rate they are being pushed into the poles during the metaphase/anaphase A steady state, i.e., the depolymerization/flux rate of the minus ends of kMTs equals their sliding rate,
by motors. We do not specify or distinguish whether these motors are located at the spindle poles and reeling the kMTs into the poles, or are located along the kMTs themselves and sliding them poleward against the ipMTs in the vicinity of an unknown spindle structure. We further assume that the minus ends of kMTs are being depolymerized at the rate they are being pushed into the poles during the metaphase/anaphase A steady state, i.e., the depolymerization/flux rate of the minus ends of kMTs equals their sliding rate, 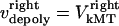 and
and 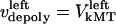 , and hereafter this velocity will be referred to simply as the depolymerization velocity, and the associated force generator and force as the depolymerization motor and depolymerization force, respectively. The forces due to the depolymerization motors, reeling the kMTs into the poles, are antagonized by motors at the kinetochores pulling the kMTs toward the kinetochore, and assisted by polymerization ratchet forces if the kMT tip impinges on the kinetochore plate, pushing the kMT away from the kinetochore. The sum of these forces is, at any time, balanced by viscous drag forces on the kMTs:
, and hereafter this velocity will be referred to simply as the depolymerization velocity, and the associated force generator and force as the depolymerization motor and depolymerization force, respectively. The forces due to the depolymerization motors, reeling the kMTs into the poles, are antagonized by motors at the kinetochores pulling the kMTs toward the kinetochore, and assisted by polymerization ratchet forces if the kMT tip impinges on the kinetochore plate, pushing the kMT away from the kinetochore. The sum of these forces is, at any time, balanced by viscous drag forces on the kMTs:
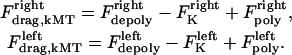 |
(9) |
The viscous drag forces on a 5–10 μm long MT, moving at a speed ∼0.1 μm s−1, are in the order of femtoNewtons (43) (note that the highest known poleward flux rate or equivalently the depolymerization rate of kMTs minus ends in Drosophila are ∼0.05 μm s−1 (14,15)), and are negligible in comparison with picoNewton-range motor forces. Also, assuming a linear-force velocity relationship for the depolymerization motors, Eq. 9 can be recast as:
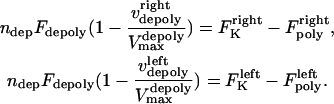 |
(10) |
Here, 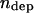 is the number of active depolymerization motors per kMT,
is the number of active depolymerization motors per kMT, 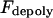 is the stall force, and
is the stall force, and 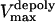 is the maximal velocity of the depolymerization motors. Note that the depolymerization or equivalently the flux rate of the kMTs' minus ends,
is the maximal velocity of the depolymerization motors. Note that the depolymerization or equivalently the flux rate of the kMTs' minus ends, 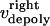 and
and 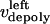 , are coupled to the kinetochore dynamics through Eq. 10.
, are coupled to the kinetochore dynamics through Eq. 10.
kMT plus end dynamics
We assume that the plus ends of kMTs undergo dynamic instability, a phenomenon characterized by stochastic switching of microtubules between the growing and shrinking states referred to as catastrophe and rescue events, respectively, whereas they flux poleward as they are reeled into the poles and depolymerize at their minus ends (7,8). Both the growth and shrinkage events of the plus ends and that of the minus end-associated poleward flux modify the position of the plus ends of kMTs with respect to the kinetochores and within the spindle. We assume that the four parameters of dynamic instability, namely the growth and shrinkage rates and the catastrophe and rescue frequencies, that determine the dynamics of kMTs' plus ends are affected by forces acting on the kinetochore, the kinetochore structure, and motor enzymes bound to the kinetochore as described below, and all the parameters introduced in what follows are essential in the model to account for the chromosome behavior in the Drosophila embryo:
The growth and shrinkage velocities of MTs are constants vg and vs for MT plus ends that are not bound to the kinetochore structure, and these rates are scaled down by a factor of φ due to steric hindrance for MT tips that interact with the kinetochore; i.e., the growth and shrinkage velocities of MT plus ends that are attached to the kinetochore are vg/φ and vs/φ.
Similarly to the diagram of the kinetochore-MT interface in Maiato et al. (5), we assume that the effect of the depolymerase enzymes that are located at the kinetochore alter the dynamic instability parameters of kMTs. This depends upon the sum of tension forces on the kinetochore resulting from cohesin stretching, polar ejection forces, and polymerization ratchet forces. Namely, when tension per kMT is low, the MT-depolymerase at the kinetochore can freely act on the plus ends of kMTs and alters their dynamics by suppressing the rescue frequency, fres, by a factor γKLP59C > 1, down to fres/γKLP59C, thereby prolonging the duration of shrinkage events (44). When tension per kMT is high, on the other hand, the MT-depolymerase cannot act on the plus ends of kMTs, thus the rescue frequency recovers proportionally to the tension force per kMT resulting in succinct shrinkage events (see Appendix).
When the MT plus end contacts, and begins impinging on the kinetochore plate, it stops growing (adding tubulin subunits to its plus end), its catastrophe frequency is increased by a factor of ϕ, and its rescue frequency, fres, returns to the low tension state (fres/γKLP59C) irrespective of the current tension on the kinetochore, while it continues to impinge on the kinetochore plate (45).
A similar tension-dependent rescue mechanism for MTs was used to model the metaphase kinetochore positioning of the budding yeast, where each kinetochore is linked to its pole by a single MT (35). However, in that model, the single kMT is assumed to maintain attachment with the kinetochore under all tension forces and the authors do not address the dynamics of this attachment. Indeed, the dependence of the MT dynamic transition frequencies on tension forces exerted on the kinetochore provides a mechanism for the kinetochore to regulate the number of kMTs (33,46). When kMT number is high, tension force per kMT is low (even when the total tension on the kinetochore is high), thus kMTs that undergo catastrophe do not rescue frequently/quickly enough, resulting in loss of kMTs. This loss continues until tension force per kMT is elevated to or above a value that causes a significant increase in the rescue frequency, which not only prevents further loss of existing kMTs from the kinetochore, but enables it to gain new MTs until the tension force per kMT decreases sufficiently to cause a significant drop in the rescue frequency, and the cycle continues. Thus, here, we propose a tension-dependent regulation mechanism for kMT plus end dynamics (and therefore the number of kMTs) along the lines of the slip-clutch model for kinetochores proposed by Salmon and co-workers (13,47) based on a tension-dependent regulation of MT rescue frequency at the kinetochore-MT interface of a kinetochore fiber, the subset of spindle MTs that link a kinetochore to its pole, composed of multiple MTs.
Realistic kinetochore-MT interface in the Drosophila embryo: multiple kMTs per kinetochore
Equations 8 and 10 describe the dynamics of a pair of sister kinetochores with only a single kMT attached to each kinetochore, similar to the kinetochores in budding yeast mitosis or at best, can only describe the dynamics of kinetochores with, say, N identical kMTs with synchronized dynamics. In the Drosophila embryo spindles, even though the exact number of kMTs per kinetochores has not yet been determined, it is thought to be between 5 and 15, similar to but fewer than that of the PtK cell kinetochores (2,6) but unlike the Saccharomyces cerevisiae, which has a single kMT per kinetochore (48), and no mechanism that would lead to the synchronization of kMTs dynamics is currently known. We describe the dynamics of kinetochores bound to multiple MTs by assuming that forces are additive and by considering forces generated by each MT attached to the kinetochore as described above, and considering the dynamics of each MT separately (see Appendix). This yields a large system of coupled algebraic equations that is solved numerically (See Appendix).
RESULTS
The system of equations was repeatedly solved numerically to calculate the dynamic evolution of kinetochores and kMTs for a realistic kinetochore-MT interface with multiple kMT attachment sites (typically for 7, 15, and 30 MT attachment sites). We explored a range of model parameter values (Table 1) to evaluate, first, how well the model describes the dynamics of the kinetochores in the Drosophila embryo, and second, how general is the model. Some of the model parameters listed in Table 1 are known from experiments, and others, for example the scaling factors, are estimated through simulations. In the case of Drosophila embryos, the relevant properties of the spindle to be borne in mind are i), fast MT dynamics (FRAP turnover half-time ∼5 s); ii), fast KLP59C and dynein-driven pacman mechanism (∼0.06 μm s−1); iii), fast KLP10A-driven poleward flux (∼0.04 μm s−1); and iv), an assumed 5–10 kMTs per kinetochore. Solutions of the model are displayed as computer animations (Supplemental Material movies 1–4), and graphs and histograms (Figs. 2–4).
TABLE 1.
Model variables and parameters
| Symbol | Meaning | Value used in shown figures | Values tested in model | Reference |
|---|---|---|---|---|
| Model variables | ||||
 , , 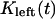
|
Position of the right and left kinetochore | Variable | ||
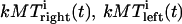 |
Position of the plus end of the ith right and left kMT | Variable | ||
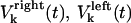 |
Velocity of the right and left kinetochore | Variable | ||
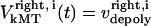 |
Velocity of the ith right kMT | Variable | ||
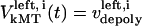 |
Velocity of the ith left kMT | Variable | ||
| Model parameters | ||||
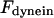 |
Maximal motor force for dynein, cenpE, and depolymerization motors, respectively. | 1.2 pN | ||
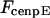 |
2 pN | 0.1–10 pN | (40,69) | |
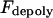 |
5 pN | |||
| nd | Number of dynein, cenpE motors per micron, and depolymerization motors per MT minus end, respectively. | 15 | ||
| nc | 5 | 1–50 | Assumed in this article. | |
| ndep | 20 | |||
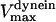 |
Unloaded rate for dynein, cepnE, and depolymerization motors, respectively. | 0.5 μm/s | ||
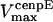 |
0.12 μm/s | 0.01–1 μm/s | (40,70) | |
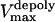 |
0.05 μm/s | |||
| μ | Effective viscous drag coefficient of Drosophila chromosome | 5 pN·s/μm | 1–10 | (42) |
| N | Maximum number of MT binding sites at the kt. | 7–30 | 1–50 | (2,6) |
| ɛ | Elastic modulus of the kt plate. | 25–100 pN/μm | 10–200 pN/μm | Assumed in this article. |
| κ | The spring constant and the rest length of cohesin bonds between sister kts. | 50–100 pN/μm | 10–200 pN/μm | (34) |
| d0 | 0.5 μm | 0.5–2 μm | ||
| r | Distance between the corona tip and the kt plate. | 0.5 μm | 0.1–1 μm | (25) |
| ρ | Coefficient of polar ejection force intensity. | 4 pN/μm2 | 1–10 pN/μm2 | (34,36) |
| vg and vs | Growth and shrinkage rate of MTs. | 0.25 μm/s | 0.05–0.3 μm/s | (71) |
| fres | Rescue and catastrophe frequencies of MTs. | 0.05–0.1/s | 0.2–0.005/s | (58,71) |
| fcat | 0.08–0.01/s | |||
| φ | Scaling factor for growth and shrinkage rate of MT tips in the kt. | 2 | 1–5 | Assumed in this article. |
| γKLP59C | Scaling factor for decrease in rescue frequency by KLP59C. | 10 | 1–50 | (44) |
| ϕ | Scaling factor for increase in catastrophe frequency for MT tip impinging on kt plate. | 2 | 1–5 | (45) |
| α | Factor for rescue frequency dependence on tension between kts. | 0.45/pN | 0.1–2 | Assumed in this article. |
| β | Factor for rescue frequency dependence on polar ejection forces. | 0.3/pN | 0.1–2 | Assumed in this article. |
| ζ | Factor for rescue frequency dependence on polymerization ratchet forces. | 0.2–0.1/pN | 0.01–1 | Assumed in this article. |
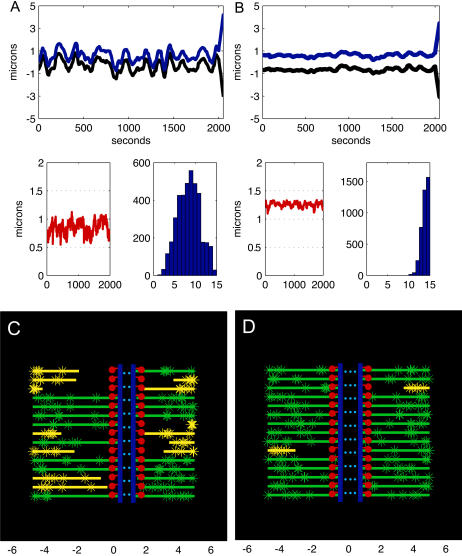
FIGURE 2.
Metaphase and anaphase A chromatid dynamics is sensitive to MT turnover. (A) (Upper plot) Positions of sister kinetochores versus time during metaphase (initial 2000 s) and anaphase A (from 2000 to 2050 s) in a spindle where MTs turn over very rapidly. The left kinetochore (black) is tethered to the left spindle pole located at −5 μm from spindle equator and its sister kinetochore (blue) is tethered to the right spindle pole (located at 5 μm from spindle equator) throughout the duration of the metaphase and anaphase A. The initial conditions are as described in the Appendix, and simulations are run for 2000 s to stabilize before the recording. The MT dynamic parameters are vg = vs = 0.25 μm s−1; fres = 0.1 s−1; fcat = 0.06 s−1; nd = 15 μm−1; the kinetochores have 15 MT binding sites, and all other parameters are as shown in Table 1. During metaphase (initial 2000 s), the sister chromatids oscillate around the spindle equator, the mean duration of poleward or antipoleward oscillations is ∼50–100 s, and the distance traveled during a poleward or anti-poleward excursion is ∼0.5–2 μm, whereas the MTs flux toward the spindle poles at rate vflux = 0.048 ± 0.015 μm s−1 and polymerize/depolymerize at their plus ends near the kinetochores (see movie 1 in the Supplementary Material for the dynamics of MTs). After the dissolution of the cohesin links between the sisters (at 2000th s), during anaphase A (from 2000 to 2050 s), the chromatids move along the kt-fibers steadily at a rate vA ∼ 0.065 μm s−1 toward their respective poles, despite the highly dynamic nature of the MTs they are attached to. Note that the MTs continue to flux toward the poles (vflux = 0.049 ± 0.016 μm s−1) and polymerize/depolymerize at their plus ends during anaphase A, according to the same rules as in metaphase; however, the sister kinetochore tension and polar ejection forces being set to zero no longer contribute to the force on the kinetochore, which alters the transition frequencies. (Lower left plot) Distance between the sister kinetochores during metaphase, the rest length of the cohesin link between the sisters is 0.5 μm; kinetochores thus remain almost always under tension, at ∼0.9 μm average distance from one another. (Lower right plot) Histogram of number of MTs attached to kinetochores during metaphase, value 8 ± 3 (data from left and right kinetochores were pooled together since there was no significant difference in the separately calculated mean values and standard deviations). (B) (Upper plot) Positions of sister kinetochores versus time during metaphase (initial 2000 s) and anaphase A (from 2000 to 2050 s) in a spindle where MTs turn over slowly. The left (black) and right (blue) kinetochore and spindle poles, and the initial conditions and parameters are as described in A, except fres = 0.02 s−1; fcat = 0.0012 s−1. During metaphase (initial 2000 s), the sister chromatids remain stably around the spindle equator, jiggle only very little, whereas the MTs flux toward the spindle poles at rate vflux = 0.047 ± 0.0061 μm s−1 and polymerize/depolymerize at their plus ends near the kinetochores (see movie 2 for the dynamics of MTs). During anaphase A (from 2000 to 2050 s), the chromatids move along the kt-fibers steadily at a rate vA ∼ 0.055 μm s−1 toward their respective poles, whereas MTs continue to flux toward the poles at the rate vflux = 0.05 ± 0.008 μm s−1. (Lower left plot) Distance between the sister kinetochores during metaphase, the rest length of the cohesin link between the sisters is 0.5 μm; kinetochores thus remain always under tension, at ∼1.3 μm average distance from one another. (Lower right plot) Histogram of number of MTs attached to kinetochores during metaphase, value 14 ± 1 (a higher value than in A). (C) A snapshot from the simulation (movie 1) of kinetochore motility in a spindle, where MTs turn over rapidly as in A, is shown. The left and right kinetochore plates are shown in blue, the cohesin bonds are blue dotted lines between the kinetochores, and 15 MTs that transiently bind to the kinetochores (green and yellow lines) are shown. The left and the right spindle poles are located at −5 and 5, respectively, along the horizontal axis. All MT minus ends terminate near the spindle poles, whereas MTs undergo poleward flux and MT plus ends undergo dynamic instability. The MTs whose plus ends are currently interacting with the kinetochore are shown in green; others are shown in yellow. The green/yellow stars on MTs are fiduciary marks, representing the tubulin speckles on the MTs. The red lines and dots represent the fibrous corona and the outer kinetochore structure where the MT plus ends are inserted in and attach to the kinetochore. (D) A snapshot from the simulation (movie 2) of kinetochore motility in a spindle, where MTs turn over slowly as in B, is shown. Definitions of the lines and colors are as in C. Note that more MTs are bound to the kinetochores compared with C, and the kinetochores are positioned at the spindle equator.
FIGURE 3.
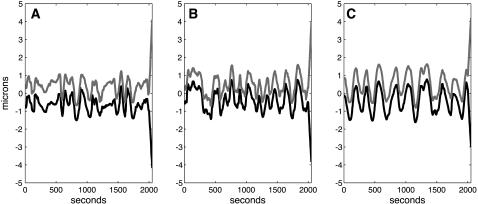
Kinetochore size does not affect metaphase oscillations but affects anaphase A rates. Positions of the sister chromatids versus time during metaphase (initial 2000 s) and anaphase A (from 2000 to 2050 s) in spindles, where MTs turn over rapidly and the kinetochores have 7 (A), 15 (B), and 30 (C) MT binding sites, are shown. In all three figures, positions of the left and right kinetochore are shown in black and gray, respectively. The positions of the spindle poles, and the initial conditions and all parameters except the number of MT binding sites at the kinetochores, are as described in Fig. 2A. In all three cases, during metaphase (initial 2000s) kinetochores switch between poleward and antipoleward movements and thus exhibit directional instability, although the excursions become smoother and more regular as kinetochore-MT binding site increases. During Anaphase A (2000–2050 s), the kt to pole rate increases slightly with decreasing number of kinetochore MT binding sites: vA ∼ 0.075, 0.07, and 0.065 μm s−1, for A, B, and C, respectively. The average number of MTs bound to the kinetochore is 5 ± 1, 8 ± 3, and 20 ± 5 for the kinetochores in A–C, respectively.
FIGURE 4.
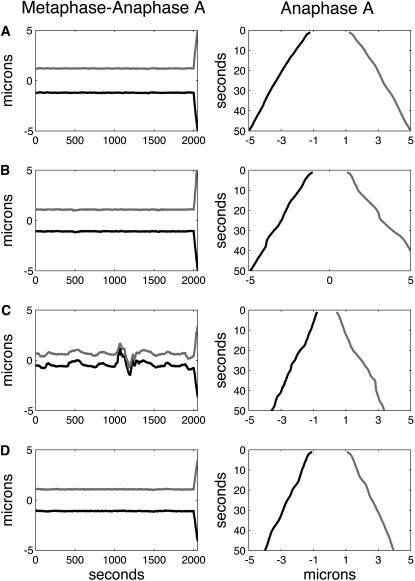
Dynamics of kinetochores during metaphase and anaphase A is sensitive to dynein and KLP59C activity at the kinetochores. In all the figures, the positions of the left and right kinetochores are shown in black and gray, and the left and right spindle poles are at −5 and 5, respectively. (A) High dynein activity level at the kinetochores damps the metaphase oscillations and increases anaphase A rates. Positions of sister chromatids versus time during metaphase (initial 2000 s in the left panel) and anaphase A (in the right panel, the last 50 s are blown up from the left panel) in a spindle where MTs turn over rapidly is shown in spindles with high levels of dynein activity at the kinetochores with 15 MT binding sites. In both panels, the initial conditions and all parameters, except for nd = 30 and ɛ = 50 pN μm−1, are as in Fig. 2 A. Oscillations of sister chromatids around the spindle equator during metaphase (initial 2000 s) are absent, and anaphase A (from 2000 to 2050 s, shown blown up on the right) chromatid-to pole-rate is increased to vA ∼ 0.08 μm s−1 (compare with Fig. 2 A). (B) Metaphase-anaphase A chromatid motility in wild-type Drosophila embryo. Positions of sister chromatids versus time where the kinetochores have seven MT binding sites, and spindle MTs turn over rapidly is shown during metaphase (initial 2000 s in the left panel) and anaphase A (right panel, the last 50 s are blown up from the left panel), for kinetochores with high levels of dynein activity (nd = 30). The initial conditions and all parameters, are as in Fig. 3 A except for nd = 30, ɛ = 50 pN μm−1 and 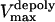 = 0.04 μm s−1. During metaphase (left panel, initial 2000 s), the kinetochores remain at the spindle equator, do not exhibit oscillations, and maintain attachment with highly dynamic kMTs, and during anaphase A (right panel) the kinetochores move rapidly and steadily toward the spindle poles (vA ∼ 0.09 μm s−1). Note that the left kinetochore is slightly slower than the right one. (C) Metaphase-anaphase A chromatid motility in dynein inhibited Drosophila embryo. Positions of sister chromatids versus time where the kinetochores have seven MT binding sites, and spindle MTs turn over rapidly is shown during metaphase (initial 2000 s in the left panel) and anaphase A (right panel, the last 50 s are shown blown up from the left panel); for kinetochores with lowered levels of dynein activity (nd = 16), all other parameters are as in B. During metaphase (left panel, initial 2000 s), the kinetochores oscillate between the spindle poles and occasionally detach from the pole (see the ∼1000th and 1200th s), and anaphase A (right panel) rates are attenuated by ∼30% (vA ∼ 0.06 μm s−1). (D) Metaphase-anaphase A chromatid motility in KLP59C-inhibited Drosophila embryo. Positions of sister chromatids versus time where the kinetochores have seven MT binding sites, have high levels of dynein activity (nd = 30), and spindle MTs turn over rapidly but the pacman motor activity is inhibited (γKLP59C = 1) is shown during metaphase (initial 2000 s in left panel) and anaphase A (right panel, the last 50 s are shown blown up from the left panel). All other parameters are as in B. During metaphase, the kinetochores remain around the spindle equator and maintain attachment with all kMTs (mean value of occupied MT binding sites at kinetochores ∼7), but the anaphase A rates are severely attenuated (vA ∼ 0.055 μm s−1) by ∼40%.
= 0.04 μm s−1. During metaphase (left panel, initial 2000 s), the kinetochores remain at the spindle equator, do not exhibit oscillations, and maintain attachment with highly dynamic kMTs, and during anaphase A (right panel) the kinetochores move rapidly and steadily toward the spindle poles (vA ∼ 0.09 μm s−1). Note that the left kinetochore is slightly slower than the right one. (C) Metaphase-anaphase A chromatid motility in dynein inhibited Drosophila embryo. Positions of sister chromatids versus time where the kinetochores have seven MT binding sites, and spindle MTs turn over rapidly is shown during metaphase (initial 2000 s in the left panel) and anaphase A (right panel, the last 50 s are shown blown up from the left panel); for kinetochores with lowered levels of dynein activity (nd = 16), all other parameters are as in B. During metaphase (left panel, initial 2000 s), the kinetochores oscillate between the spindle poles and occasionally detach from the pole (see the ∼1000th and 1200th s), and anaphase A (right panel) rates are attenuated by ∼30% (vA ∼ 0.06 μm s−1). (D) Metaphase-anaphase A chromatid motility in KLP59C-inhibited Drosophila embryo. Positions of sister chromatids versus time where the kinetochores have seven MT binding sites, have high levels of dynein activity (nd = 30), and spindle MTs turn over rapidly but the pacman motor activity is inhibited (γKLP59C = 1) is shown during metaphase (initial 2000 s in left panel) and anaphase A (right panel, the last 50 s are shown blown up from the left panel). All other parameters are as in B. During metaphase, the kinetochores remain around the spindle equator and maintain attachment with all kMTs (mean value of occupied MT binding sites at kinetochores ∼7), but the anaphase A rates are severely attenuated (vA ∼ 0.055 μm s−1) by ∼40%.
Effect of MT dynamics on metaphase positioning and anaphase A rates
The animations (Supplemental Material, movies 1–2) vividly display the dynamic relationship between kMTs sliding poleward and depolymerizing at their minus ends at the spindle poles while at the same time undergoing dynamic instability at their plus ends, i.e., they attach, pull, push, and detach from kinetochores as a result of the tug-of-war between the kinetochore associated and poleward sliding motors, and the plus end dynamics. Movie 1 shows the dynamics of kinetochores in a spindle where MTs are turning over rapidly, corresponding to high frescue and fcat rates as in Drosophila embryo spindles, where t1/2 ∼ 5 s by FRAP (21). Movie 2 shows the dynamics of kinetochores in a spindle where MTs are turning over slowly, corresponding to low frescue and fcat rates as in some mammalian cells, where t1/2 > 100 s by FRAP (49). In spindles where MT plus ends are highly dynamic and turn over rapidly (movie 1), sister kinetochores oscillate between spindle poles during metaphase, and anaphase A rates are driven by a combined flux-pacman mechanism in which kMTs shorten at both their kinetochore-bound plus ends and their pole-proximal minus ends, and the anaphase A rate is faster than that of poleward flux. In spindles where MT plus ends are less dynamic and turn over slowly (movie 2), the kinetochores remain stably positioned at the spindle equator during metaphase, and the anaphase A rate is governed by the flux mechanism and here the pacman based mechanism of chromosome segregation is less effective.
The solutions to the model equations are displayed as plots of positions of a pair of sister kinetochores over time in Fig. 2, A and B. Even though the duration of metaphase is ∼60–80 s in the Drosophila embryo, in the figures, the duration of metaphase was artificially extended, typically to 2000 s, to better illustrate the characteristics of the sister kinetochores' behavior under various metaphase conditions. Plots of the metaphase/anaphase A kinetochore positions over time where kinetochores can bind to a maximum of 15 MTs (Fig. 2, A and B, upper panels) show that, in the spindle where MTs are highly dynamic and transiently attach to the kinetochores, the combined action of motor enzymes, polymer ratchets, and MT dynamics leads to metaphase oscillations of chromatids around the spindle equator (Fig. 2 A, upper panel, initial 2000 s and the simulation snapshot shown in Fig. 2 C). Alternatively, in spindles where MTs are less dynamic, a stable metaphase positioning of chromatids around the spindle equator is produced (Fig. 2 B, upper panel, initial 2000 s and the simulation snapshot shown in Fig. 2 D). In the spindle where MTs are highly dynamic (Fig. 2 A), the average distance traveled during each poleward or antipoleward excursion is ∼1–2 μm and of average duration ∼50–100 s, similar to rates observed in newt lung cells (10).
It is also seen that the tension-dependent regulation of kMT dynamics is sufficient to account for the coupling between sister chromosomes: while a kinetochore moves poleward, its sister moves antipoleward. Also, in Fig. 2, A and B (lower left panels), the distance between the sister kinetochores is shown: in both spindles, the kinetochores are mostly under tension, since the distance between sisters is greater than the rest length of the cohesin bonds, r, in good agreement with experimental observations (50). In the right lower panels in Fig. 2, A and B, the histograms of the number MTs attached to the kinetochores are shown, and in the spindle where MTs are very dynamic, the kinetochores only maintain attachment with half of the MTs, ∼8 out of the 15 MTs on average (Fig. 2 A and the simulation snapshot shown in Fig. 2 C), indicating that kinetochore-MT attachments are transient. In contrast, in spindles where MTs are less dynamic, the kinetochores maintain attachment with more MTs, ∼14 out of the 15 MTs, on average (Fig. 2 B and the simulation snapshot shown in Fig. 2 D), indicating that kinetochore-MT attachments are longer lasting (note that there can be a maximum of 15 MTs attached to kinetochores in this instance).
The movement of a kinetochore toward its pole requires that most (if not all) of the MTs that are bound to the kinetochore throughout this movement remain in a depolymerization state, whereas those of its sisters may depolymerize and detach or polymerize and attach. These results indicate that, when MTs are highly dynamic and turn over rapidly, the MT-kinetochore attachments are transient (duration of kt-MT attachment is 43 ± 45 s in Fig. 2 A) and depolymerization events are frequent. This allows the kinetochore module, consisting of the motors and forces at the kinetochore that regulate kMT dynamics (specifically, prolong the catastrophe events by suppressing the rescue frequency of kMT), to synchronize the shrinkage/depolymerization events of multiple kMTs, leading to the excursions of the kinetochores toward and away from their poles. In contrast, when MTs turn over slowly, the MTs' attachment to the kinetochores persist for longer times (duration of kt-MT attachment is 450 ± 412 s in Fig. 2 B) and shrinkage events are rare. In this case, the kinetochore module cannot synchronize the depolymerization of multiple kMTs even when the MT rescue is suppressed by the KLP59C motors, and catastrophe events are prolonged, which leads to stable positioning of the kinetochores at the spindle equator. In spindles in which the MTs are highly dynamic and the kinetochores undergo excursions between the spindle poles, the leading kt's MTs are mostly in a depolymerization state as it moves poleward, and the kt switches direction when the forces acting on the kinetochore increase to a level that inhibits the suppression of rescue (due to the action of KLP59C motors) and when a sufficient number of MTs have switched to a polymerization phase.
Finally, in Fig. 2, A and B (upper panels), it is also seen that the dissolution of the cohesin bonds and inactivation of polar ejection forces alone (at time = 2000 s) is sufficient to mediate the metaphase to anaphase A switch in kinetochore behavior. The rates of anaphase A kinetochore to pole movement in the spindle with highly dynamic MTs (Fig. 2 A, last 50 s) is vA ∼ 0.065 μm s−1, and it is faster than the flux rate vflux ∼0.05 ± 0.01 μm s−1. In the spindle with less dynamic MTs (Fig. 2 B, last 50 s), the anaphase A rate is only slightly above the mean flux rate vA ∼ 0.055 μm s−1, thus the pacman rate is attenuated regardless of the pacman machinery being present and active. This result also indicates that the extent of the regulation of kMT dynamics by the kinetochore module is limited by the turnover rate of MTs, i.e., when MTs turnover is fast, the kinetochore module contributes to the chromosome-to-pole motility rate through a pacman mechanism, and when MT turnover is slow, the effect of motors and forces becomes ineffective in synchronizing the shrinkage events of kMTs, leading to an attenuation of the pacman component of anaphase A.
Role of the number of MT binding sites on the kinetochore on metaphase positioning and anaphase A rates
The maximal number of kMTs that make up a kinetochore fiber, or equivalently the number of MT attachment sites on the kinetochore, i.e., the size of the kinetochore, is species-specific: at the lower end of the scale, S. cerevisiae kinetochores attach to a single MT (48), whereas mammalian cell kinetochores attach to 20 or more MTs (6) compared to the assumed number in Drosophila of between 5 and 15 (2). Differences in kinetochore size and kinetochore fiber composition might, in addition to MT dynamics, affect the metaphase oscillations and the efficiency of the pacman mechanism investigated here, which is based on the properties of the KLP59C motor that works by suppressing MT rescue frequency as in Drosophila embryo (44). We thus modeled kinetochores that can accommodate up to 7, 15, or 30 MTs, mimicking various kinetochore sizes, to examine whether and how the metaphase oscillations or the anaphase A rates depend on the average number of MTs in the k-fiber. In Fig. 3, A–C, the positions of metaphase chromatids with a maximum of 7, 15, and 30 MT attachment sites are shown for spindles with highly dynamic MTs (note that only in spindles with highly dynamic MTs, metaphase chromatid oscillations occur (Fig. 2 A)). In all three different sized kinetochores, the chromosomes exhibit long poleward and antipoleward excursions with rapid reversals in direction, the signature of directional instability (10). However, there are some subtle differences, for example, the excursions become smoother and regular as the kinetochore size (maximal number of MT attachment sites) increases (compare Fig. 3, A and C), and a predicted disadvantage of having small kinetochores with fewer MT binding sites is the occasional detachment of kinetochores from all its MTs (data not shown). Also, there is a slight decrease in the anaphase A rates with an increase in the kinetochore size (vA ∼ 0.075–0.065 μm s−1).
The parameters for MT dynamics used in Fig. 2 A or Fig. 3, A–C, mimic the rapid MT turnover rates observed in the Drosophila embryo (21); however, such excursions of chromosomes are not observed in the embryos (13,15). Also, the anaphase A rates found under these conditions (vA ∼ 0.065–0.075 μm s−1, in Fig. 2 A and Fig. 3, A–C) are below the experimentally observed rates of 0.1 μm s−1; however the anaphase A rates of smaller kinetochores with up to 7 kMTs (Fig. 3 A) are in better agreement with the observed rates (0.075 μm s−1), therefore the Drosophila kinetochore may have fewer than 15 MT binding sites, possibly somewhere between 5 and 10. We reasoned that an additional cause for the discrepancy between the observations and the results shown in Fig. 2 A and Fig. 3, A–C, i.e., the lack of metaphase oscillations in the embryo and the faster anaphase A rates, could be a small number of working dynein motors. The effect of dynein in Drosophila embryos, particularly its localization at the kinetochores during metaphase and anaphase A and its role in chromosome segregation, has been a controversial one (20). However, as a minus end-directed MT motor, dynein is thought to “feed” kMTs' plus ends into the kinetochore and thereby facilitate the pacman mechanism (5,18,20). Therefore, we wanted to examine if increased dynein activity at the kinetochores affects metaphase behavior and anaphase A rates.
Role of active dynein at kinetochores on metaphase positioning and anaphase A rates
First, in Fig. 4 A (left and right panels), the model was solved for the conditions and parameter values as in Fig. 2 A, except for a high number of working dynein motors and a corresponding increase in the stiffness of the kinetochore plate to prevent unrealistic elastic deformations of the kinetochore due to dynein pushing the kMTs toward the kinetochore plate (corresponding to nd = 30 and ɛ = 50 in Eqs. 4, 5, and 8, in contrast with nd = 15 and ɛ = 25, which were the values used in Fig. 2 A). We find that this increase in dynein activity at the kinetochores i), dampens the metaphase oscillations (compare the behavior of kinetochores in Fig. 4 A (left panel), with those in Fig. 2 A), and ii), accelerates the rate of kinetochore to pole motility to vA ∼ 0.08 μm s−1 by ∼25% (compare the last 50 s of Fig. 4 A, left panel, or Fig. 4 A, right panel, and Fig. 2 A). The cessation of metaphase oscillations in response to increased dynein motors working at the kinetochores is due to an increased poleward force acting at the kinetochore to oppose a higher tension force between the sister kinetochores. This not only suppresses the activity of the depolymerase (i.e., inhibits the suppression of rescue) but also promotes a higher rescue rate during metaphase, both of which slow down the turnover rate of kMTs and stabilize MTs. Under these conditions, MT-kinetochore attachments therefore become less transient during metaphase, and at anaphase A onset, the kinetochore begins its excursion toward the spindle pole with the advantage of holding onto almost all its MTs. Now the KLP59C depolymerase motors effectively suppress kMT rescue events of kMTs that are inserted into the kinetochore plate by dynein motors and catastrophe at a higher rate, leading to an increase in the pacman rate.
Metaphase positioning and anaphase A rates in Drosophila embryos: wild-type and dynein inhibition
Indeed, an excellent agreement with both metaphase and anaphase A chromatid motility rates in Drosophila embryos was obtained (vA ∼ 0.09 μm s−1) for spindles with highly dynamic MTs, high dynein activity, and 7 MT binding sites per kinetochore (Fig. 4 B, left and right panels, and Supplemental Material movie 3). Since the flux rate is vflux ∼ 0.035 μm s−1, this augmented anaphase A rate requires that pacman accounts for ∼60% of the anaphase A rates (18). In movie 3, it can be seen that the kinetochores overtake the tubulin speckles, typical of the combined flux-pacman anaphase A mechanisms in Drosophila embryo. Furthermore, reducing dynein activity by 50% alone under these conditions (nd = 15) to simulate dynein inhibition resulted in 30–40% attenuation of anaphase chromatid to pole rates, and occasional chromosome detachment, which is in very good agreement with earlier experimental observations in some dynein inhibited embryos (in which a gradient of phenotypes including detached kinetochores and reduced anaphase A rates were observed) (20) (Fig. 4 C, left and right panels). The poleward flux rates of the kMTs in these spindles with lowered dynein activity levels (Fig. 4 C) were not significantly different than those with higher dynein activity (vflux ∼ 0.04 μm s−1). This indicates that this change in dynein activity is not sufficient to alter the flux rate nor interfere with the flux mechanism, i.e., the flux motors continue to operate near unloaded regime regardless of the 50% change in dynein activity at kinetochores that antagonizes the flux motors, but elevated dynein activity at kinetochores increases anaphase A rates by engaging the pacman mechanism (18,20). This result, together with the results in Fig. 2 B, suggest that the efficiency of the specific pacman mechanism investigated here depends on the level of dynein activity at the kinetochores and is limited by the dynamics of MTs: increasing the dynein activity enhances the extent of engagement of the pacman mechanism, and the pacman mechanism investigated here is ineffective if the MTs turn over very slowly.
Role of KLP59C depolymerase on anaphase A rates in Drosophila
To further investigate the contribution of the KLP59C motors to the rapid chromatid to pole rates (Fig. 4 B, right panel), we tested our model under conditions that mimic the inhibition of KLP59C motors (corresponds to setting γKLP59C =1). The KLP59C motors are suggested to function by suppressing the rescue frequency of MT plus ends in Drosophila, which is the only effect these motors have on kMT dynamics in our model (18,44). The plots of sister kinetochores' positions shown in Fig. 4 D (left and right panels) or movie 4 (Supplemental Material) thus pertain to a KLP59C–inhibited Drosophila embryonic spindle with highly dynamic MTs, kinetochores with 7 MT binding sites, and high dynein activity at kinetochores (2,20,21). In contrast with the motility of the sister chromatids in a wild-type Drosophila embryo (Fig. 4 B), where the anaphase A rate is vA ∼ 0.09 μm s−1, in the KLP59C-inhibited spindle (Fig. 4 D, last 50 s in left panel or Fig. 4 D, right panel) the anaphase A rate is attenuated by ∼40%, vA ∼ 0.055 μm s−1, in reasonable agreement with experimental results (18). It can also be seen in movie 4 that, in this spindle, the kinetochores rarely overtake the speckles.
Role of KLP59C depolymerase on metaphase positioning and anaphase A rates in other species
We also wanted to study the efficiency of the KLP59C-based pacman mechanism in an organism with larger kinetochores and a correspondingly higher number of MT binding sites, such as in PtK cells (6). Can this mechanism work as fast in spindles with larger kinetochores if dynein activity is high and MTs are highly dynamic as in Drosophila embryos? We find that, in spindles where kinetochores can accommodate up to 30 MTs, where MTs are highly dynamic, and where dynein activity is high, the anaphase A rates are only ∼10–20% higher than the mean flux rate (vflux ∼ 0.05 μm s−1) despite the presence of active pacman motors. This indicates that the Drosophila pacman mechanism loses efficiency (maximal pacman rate ∼0.01 μm s−1 for the value of γKLP59C, the factor for the suppression of rescue frequency used for the Drosophila spindle) in spindles with large-sized kinetochores (or equivalently kinetochore fibers composed of more than 15 kMTs) even if dynein activity and MT dynamics are sufficiently high to effectively engage the KLP59C pacman motors (results not shown). Further, we find that in spindles with dynamic microtubules such as in Fig. 3, A–C, where dynein activity is low, when we inhibit the KLP59C activity, the oscillations cease (results not shown). This suggests that a KLP59C-like depolymerase, which suppresses rescue frequency, promotes metaphase oscillations, possibly by helping kMT plus ends synchronize their depolymerization dynamics during metaphase through prolonging the shrinkage events that are otherwise short lived when kinetochores are under tension.
DISCUSSION
Here we developed a model that provides a quantitative description of the experimentally observed behavior and rates of metaphase/anaphase A kinetochore and kMT dynamics in Drosophila embryos (Fig. 1 and Fig. 4 B, left and right panels). The model was built to account for the rapid, highly dynamic properties of Drosophila embryo mitotic spindle (14,15,18,21), but it is a basic model that, with suitable parameter adjustments, accounts for kinetochore motility in a range of distinct cell types (see subsections below). The model explains kt dynamics in terms of plausible molecular events in which the antagonistic and complementary actions of motor enzymes, polymer ratchets, and MT dynamics produce a balance of forces that reels kMTs steadily into the spindle poles to drive poleward flux. The model shows that kts can remain attached to the poles, whereas individual kMTs are transiently attached and undergo persistent dynamic instability and describes plausible conditions that allow such dynamic kt fibers to support significant chromosome oscillations during metaphase and to drive steady chromatid-to-pole motility during anaphase A (Fig. 2 A, movie 1). Thus, although we cannot rule out a role for additional spindle components such as the “Hill-sleeve” or a “spindle matrix” in driving chromatid motility, the model shows that the behavior of metaphase and anaphase A chromosomes can be adequately described in the absence of such components (37,51).
Chromosome motility in Drosophila embryos
Chromosome motility in Drosophila embryos is well characterized (Fig. 1 A) and proceeds in spindles that contain highly dynamic MTs (turnover half-life ∼5 s) with each kt having ∼5–15 maximum MT attachment sites (2,14,15,18,21). The dynamics of chromosome motility in this system can be reproduced very well by our model, so long as dynein and KLP59C remain active at the kinetochore (Fig. 4 B, left and right panels) in good agreement with experimental data (18,20). Our model shows that, in this system, where MTs are highly dynamic and flux rates are high, to ensure the observed fast and steady rates of chromatid-to-pole motility, i), high dynein activity at kinetochores must be maintained throughout metaphase/anaphase A to prevent detachment of the kinetochores from poles, and ii), KLP59C motors are required to prevent high rescue during anaphase A. Thus, the combined action of these two motors dampens the metaphase chromosome oscillations, a model prediction supported by previous experimental work in Drosophila embryos (13,15,20), and produces a fast pacman mechanism.
The model also predicts that kt dynein activity is necessary for KLP59C to work effectively as a pacman motor (Fig. 4 C, left and right panels) (20). Our analysis is consistent with the idea that the use of KLP59C and a high number of dynein motors on kts in the Drosophila embryo spindles represent the adaptation of a general mechanism, governing the behavior of metaphase and anaphase A chromosomes in many systems, for fast motility, which is a characteristic feature of the fly embryos. A significant result of the model is that highly dynamic kMTs are capable of driving chromatid-to-pole motility at a fast, steady rate, as is observed (14,15,18,21). Thus the model complements a recent model for anaphase B in this system, which also describes steady linear pole-pole separation by motors that are working on tracks that are constantly growing and shrinking (21).
Forces on kinetochores, kMTs, and motors
The model results suggest that both the plus and minus end-directed motors at the kinetochore (dynein and cenpE) work near their stall regime throughout metaphase and anaphase A (data not shown). During anaphase A, the action of the minus end-directed motor dynein, in particular, is antagonized mainly by the MT ends impinging on the kinetochore plate, in addition to the plus end-directed motors at the kinetochore and the flux motors at the spindle pole. This implies that the anaphase A kinetochore must be compressed. The available EM data on kinetochore structure in some systems supports this idea: the anaphase A kinetochore is very deformed and ragged compared with an early metaphase kinetochore (6). Also, at least a subset of kMT tips must be compressed at the kinetochore interface by the action of the minus end-directed MT motors, e.g., dynein in the case of Drosophila, pushing them into the kinetochore plate.
Mechanism of coupling kMT dynamics
To produce coordinated behavior of the sister kinetochores, the dynamics of the sister kMTs as well as the dynamics of the kMTs of each kinetochore must be coordinated and coupled. For example, during metaphase, when a kinetochore moves poleward by net depolymerization of its kMTs, its sister's kMTs must, on average, polymerize. Similarly, during anaphase A, the dynamics of the kMTs of a kinetochore must be coordinated to ensure the kinetochore's attachment to its pole throughout anaphase A. The presence of tension forces across the kt appears to be sufficient to coordinate the dynamics of the kMTs of the sister kinetochores. However, coordination of the dynamics of a kinetochore's MTs is more complex: in this case, i), the kinetochore plate provides a barrier beyond which individual kMTs cannot grow, therefore couples the dynamics of growing plus ends of kMTs to one another; ii), when the kinetochore is not under tension, the KLP59C pacman motors couple the shrinkage/depolymerization dynamics; and iii), when the kinetochore is under tension, kMTs remain, on average, in either a growth or neutral state (impinging on the kinetochore plate, without being able to undergo net growth).
Predictions and generality of the model
Our model makes several predictions about the role of MT dynamics and the utilization of kinetochore motors that can be evaluated in the context of previous or future experiments. In Table 2, we summarize known and predicted spindle properties that influence the chromosome dynamics observed in different systems (see below). Our model predicts that the action of KLP59C on the kt facilitates metaphase chromosome oscillations, whereas dynein activity suppresses oscillations and both KLP59C and dynein enhance the rate of anaphase A. In addition, the model predicts that the proposed mechanism of KLP59C (44) can account for a rapid pacman rate as observed during Drosophila embryo mitosis only under circumstances where the number of MT binding sites on the kt is low, and MTs are highly dynamic. However, in most systems where anaphase A is driven mostly by a pacman mechanism, the kts bind to many MTs and these MTs are not as dynamic as in the Drosophila embryo. Nevertheless, the chromatid-to-pole rates are typically order(s) of magnitude slower than that in the Drosophila embryo (11,19,52); therefore, the slow pacman rates observed in these organisms can still be attained via a KLP59C homologue, which suppresses the rescue frequency more effectively (higher value of γKLP59C than in Drosophila).
TABLE 2.
Chromatid motility in various organisms: model predictions
| Organism properties | Characteristic MT turnover half-time
|
Poleward flux rate
|
Anaphase A rate
|
Metaphase kt oscillations
|
No. of kMTs per ktc
|
Model prediction
|
|---|---|---|---|---|---|---|
| Organism | ||||||
| Drosophila blastoderm embryo | 5 s (21) | 0.05 μm/sec (14) | 0.1 μm/s (15,18,21) | None (15,18,21) | 5–15 suggested in Maiato and Sunkel (2) | High dynein activity and 5–10 kMTs per kt |
| Crane fly spermatocyte | ? | 0.7–0.9 μm/min (12) | 0.5 μm/min (12) | None (12) | 34–56 (12) | No oscillations since no pacman activity |
| Xenopus eggs | ? | 2 ± 0.5 μm/min (13) | 2.4 μm/min (13,54) | None (13,54) | ? | No oscillations since no pacman activity |
| Grasshopper spermatocyte | ? | Severed MT ends flux at 0.5 μm/min (53) | 0.58 ± 0.16 μm/min (53) | ? | 40 between 27 and 55 (46,72) | No oscillations since no pacman activity |
| Budding yeast | 52 ± 23 s (55) | 0 μm/s (55) | 0.33 ± 0.16 μm/min (52) | Yes (16) | 1 (48) | Low dynein activity and pacman motor |
| Newt lung cells | 75 s (73) stated as unpublished observations | 0.4–05 μm/min (19) | 1.7–1.8 μm/min (19) | Yes (10) | 20 (74,75) | Low dynein activity and strong pacman motor |
| PtK1 cells | 50–300 s (49) and 77 s (75) | 0.5 μm/min (8,49) | 1–2 μm/min (11,57) | Yes (57) | 20–25 (6) | Low dynein activity and strong pacman motor |
In summary, our model predicts that, in a given organism: i), If there is no pacman activity at the kinetochores, metaphase oscillations should not be observed; ii), If MTs are highly dynamic, the flux rate is high and the kinetochore size (and the number of MT binding sites) is small, there should be a high number of working dynein motors at the kinetochores to prevent kinetochore detachment, and as a consequence, there should be no metaphase oscillations. iii), If the flux rate is slow and kinetochore size is large, there is no need for high dynein activity at the kinetochore to ensure kinetochore attachment, so the MT depolymerase pacman motor should be more efficient than the KLP59C motors to ensure chromosome segregation. Moreover, in case the MTs are sufficiently dynamic, metaphase oscillations will occur. iv), If the kinetochores can accommodate a high number of MTs, kinetochore movements should be smooth (Fig. 3 C).
We assessed the generality of the model by determining how well different spindles conform to the aforementioned model predictions and obtained clues about how different spindles may selectively utilize components of the available spindle machinery to produce distinct mechanical outputs (Table 2). At one end of the scale, in organisms where anaphase A rates are driven entirely by flux and there is no pacman, for example in crane fly spermatocytes (12), grasshopper spermatocytes (53), and Xenopus extracts (13,54), our model predicts that the chromosomes should not exhibit oscillations, and this is supported by previous experimental observations (12,13) (Table 2). At the other end of the scale is the budding yeast, where anaphase A is fully driven by a pacman mechanism and spindle MTs do not flux (52,55). Here, our model predicts that the high activity of a minus end-directed MT-based motor (e.g., the kinesin-14, kar 3) at kinetochores is not necessary and thus the MT depolymerase pacman motors can promote oscillations if MTs are sufficiently dynamic, a prediction that is also supported by previous experimental observations (16,56) (Table 2).
In other systems, where anaphase A is driven by a combined flux-pacman mechanism but the flux rate is slow, such as in the newt lung cells (19) or the PtK cells (8,11,49,57), our model predicts that high dynein activity at the kinetochores is not needed to ensure kts attachment to the poles, and thus a MT depolymerase, pacman motor, can promote oscillations if MTs are sufficiently dynamic. In both of these systems, metaphase oscillations are observed (10,57) (Table 2). Moreover, since the kMT number is high in both cell types, smooth metaphase oscillations and anaphase movements are predicted by the model, in agreement with experimental observations (Table 2). However, it is important to note that the anaphase A pacman rates observed in both newt lung cells and PtK cells are higher than the pacman rate that can be attained using the KLP59C rate (γKLP59C) used for the Drosophila embryo, given the high number of kMTs in these systems (see Results). Therefore, it is highly plausible that in these systems, particularly in PtK cells, the pacman motor is either able to alter MT dynamics more effectively (i.e., γKLP59C ≫ 1) or the pacman mechanism is driven by another type of depolymerase that functions differently, for example, one like KLP10A, which functions by increasing the catastrophe frequency of MT plus ends. Moreover, the spindle MTs in PtK cells are reported to conform to a considerably slow turnover half time, t1/2 ∼ 300 s in Zhai et al. (49). Our model, in its current form, cannot explain the existence of chromosome oscillations in this system if the latter pertains to the dynamics of kMT plus ends; however, the existence of a different depolymerase, which works by increasing the catastrophe frequency of kMTs, may account for both metaphase oscillations and high pacman rates observed despite very slow MTs turnover.
Relationship of the model to previous theoretical models
Our model was stimulated by previous theoretical studies that successfully recapitulate the dynamics or positioning of kinetochores in newt lung cells based on a Hill-sleeve model (34), or in budding yeast based on spatial- and tension-dependent kMT dynamics (35,36).
In Sprague et al. (36) and Gardner et al. (35), the authors describe the positioning of the kinetochores in the budding yeast, where only a single MT is bound to each kinetochore (48), and spindle MTs do not exhibit dynamics at their pole-proximal minus ends, and thus they do not flux. This study, however, does not focus on understanding if and how the kinetochores maintain attachment with their kMT and how forces generated by motors or by a polymerization ratchet mechanisms at the kinetochore MT interface affect tension between the sister kinetochores and thus the positioning of the kinetochores.
In Joglekar and Hunt (34), as in our model, the authors employ a force balance approach and address the attachment of metaphase kinetochores to spindle MTs by considering a Hill-sleeve structure. The Hill-sleeve structure, in principle, can be viewed as a protein motor or an ensemble of protein motors working cooperatively. However, in this model, the forces on the kinetochores, e.g., the tension between the sister kinetochores, alters the motor's behavior, i.e., the motor obeys a nonlinear force-velocity relationship, or in case of multiple motors, the forces on the kinetochore alter the cooperativity of the motors. Thus, their approach is different from ours since tension forces on the kinetochore do not affect the dynamics of the kMTs in their model. Furthermore, in this study (34), neither the poleward flux of kMTs nor the anaphase A chromosome motility was considered, and the authors assumed very slow MT growth and shrinkage rates for kMTs. Finally, an important difference between their model and ours is that their model is mainly deterministic and comprises an inherent limit cycle oscillator, whereas stochastic effects have minor consequences on the metaphase oscillations of the chromosomes. In contrast, our model does not yield oscillations if it is reduced to a purely deterministic form and results in stable positioning of the chromosomes at the spindle equator (as can be seen in Fig. 2 B, where MTs are not very dynamic, and stochastic effects are minimal), and thus, in our model, the stochastic nature of the MT dynamics underlies the oscillatory behavior of chromosomes.
Limitations of the model
Our model does not address how the spindle poles are maintained at constant spacing throughout metaphase and anaphase A. In particular, as in previous theoretical considerations of kinetochore positioning (34,35), our model does not address the role of kinetochore dynamics on forces affecting pole-pole spacing and vice versa. That is, we assume that changes in the forces imposed on the poles due to kinetochore dynamics are of negligible magnitude compared to frictional drag forces acting on the spindle poles in wild-type conditions, but this is an assumption of the model that may have to be revised in the future as new data become available. We favor the idea that antagonistic forces generated by ipMTs and astral MTs can maintain pole-pole spacing during metaphase and anaphase A, but whether other factors, such as a spindle matrix, play a role in this process will require further analysis. Our model does not address the important roles of several kinetochore associated proteins such Rod and ZW-10, which are likely to work with dynein in the spindle assembly checkpoint or the role of MT plus tip trackers such as EB-1 and APC in chromosome dynamics (31,58,59). Also, in our model, we only consider the centrosome-directed pathway of kinetochore fiber formation, and ignore other pathways, for example, the chromosome-directed pathway where MTs are nucleated near the kinetochore to form the kt-fiber as observed in other systems (60). Recently, the existence of spatial catastrophe/rescue gradients in the budding yeast and the HeLa cells mitotic spindles were proposed to account for kinetochore behavior during metaphase and prometaphase, respectively (35,61). In our model, we do not consider the effect of such a spatial gradient, which may potentially be able to augment or substitute for the effect of the depolymerase at the kinetochore, or the polar ejection forces. Nevertheless, this model provides a significant step toward developing a description of chromosome dynamics in terms of the underlying molecular machinery in Drosophila embryos and other organisms.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank members of the Scholey Lab, especially Dr. I. Brust-Mascher, for insightful discussions, and Dr. I Brust-Mascher for Fig. 1 A.
This work was supported by National Institutes of Health grants GM-55507 to J.M.S and GM-068952 to A.M. and J.M.S.
APPENDIX
Force-velocity relationships of the motor proteins
We assume that all motor proteins considered in this work obey a linear force velocity relationship similar to conventional kinesin (39), and as recently proposed in a theoretical framework for cytoplasmic dynein (41). In addition, these linear force-velocity relationships are assumed to be unbounded, and thus they carry over into negative velocities. We do not consider nonlinear force velocity relationships for these motors for several reasons: First, under such a consideration, the model is not amenable to analysis. Second, in its current form, the model results show that some motors work in their unloaded regime (e.g., the depolymerase KLP10A at the spindle pole) and others near their stall regime (e.g., dynein and cenpE at the kinetochore), but motors do not shift their working regime. Therefore, we do not anticipate that such a consideration would affect the results of the model.
Rationale for the alteration of the rescue frequency of kMTs by forces acting on the kinetochore
Structural changes associated with the dynamic instability of MT ends probably determine the switching of MTs between growth and shortening phases: growing ends are typically blunt and protofilaments are straight as they add GTP tubulin. In contrast, protofilaments are highly curved in rapidly depolymerizing MT ends that have lost their GTP caps (62). Based on earlier models proposed for the regulation of kMT dynamics (2,13,25,38, 47,63), we assume that forces exerted on the kinetochore affect the dynamics of kMT plus ends embedded in the kinetochore structure in any one of the following ways: i), Similar to the depolymerase activity of the kinesin-13 MCAK (64), we assume that the depolymerase activity of KLP59C is activated by a kinase located at the inner centromere, such that when the kinetochores are under tension, KLP59C moves away from the inner centromere and can not suppresses the rescue frequency of kMTs, whereas when the kinetochores are not under tension, KLP59C becomes closely associated with its activator kinase and therefore suppresses the rescue frequency of kMTs. ii), In an alternative scenario along the lines of the conformation wave model, we assume that a ring-like protein structure similar to the recently discovered Dam1 complex in the budding yeast kt (47,65–67) is associated with kMT plus ends, and when the kinetochore is under tension pulling the ring toward the spindle equator, the rings induce forces resisting the outward curving of the protofilaments for depolymerization and promote rescue, whereas when the kinetochore is not under tension, the elastic forces released by the outward curving of the protofilaments easily dislocate the rings.
Force-balance equations generalized to account for multiple kMTs per kinetochore
To account for the realistic situation in which multiple kMTs with autonomous dynamics are bound to the kinetochores, we consider independent dynamics for each kMT and modify the first and the last terms on the right-hand sides of Eq. 1, or equivalently Eq. 8, by writing the motor-generated forces at the kinetochores as the sum of forces generated by each one of the kMTs: for example, at a given moment, if there were M number of kMTs bound to the left kinetochore, the total motor generated force at the right kinetochore would be 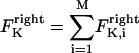 . Similarly to the motor-generated force, the total polymerizing ratchet force can also be written as the sum of all polymerization ratchet forces due to all kMTs impinging on the inner kinetochore plate. Also, an additional force-balance equation for each kMT bound to the kinetochore can be formulated similarly to Eq. 9, and in this situation, each MT would be slid and depolymerized at the spindle poles at an autonomous rate
. Similarly to the motor-generated force, the total polymerizing ratchet force can also be written as the sum of all polymerization ratchet forces due to all kMTs impinging on the inner kinetochore plate. Also, an additional force-balance equation for each kMT bound to the kinetochore can be formulated similarly to Eq. 9, and in this situation, each MT would be slid and depolymerized at the spindle poles at an autonomous rate 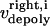 and
and 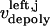 (or equivalently
(or equivalently 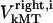 and
and 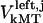 ) depending on its interaction with the kinetochore structure. However, the velocities and the dynamics of MTs that are bound to the kinetochore remain coupled to one another through the Eqs. 10 and 1, and the velocity of the kinetochores,
) depending on its interaction with the kinetochore structure. However, the velocities and the dynamics of MTs that are bound to the kinetochore remain coupled to one another through the Eqs. 10 and 1, and the velocity of the kinetochores, 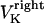 and
and 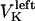 .
.
Calculation of the transition frequencies of MT plus ends
For each MT tip, the probability of a catastrophe or rescue occurring during a single time step, τ, is calculated by the equation Pswitch = 1 − exp (−fswitchτ), where a switch is either a rescue or a catastrophe event (36,68). If a MT plus end is bound to the kinetochore structure but not impinging on the kinetochore plate, its rescue frequency is calculated as fswitch,res = fres exp(Ftotal)/γKLP59C; here, fres is the rescue frequency in the absence of any force, γKLP59C is the scaling factor due to the action of KLP59C motors, and Ftotal is the current dimensionless tension force on the MT, i.e., Ftotal = (α Ftension + β FPE + ζ Fpoly)/M, where M is the current number of MTs bound to the kinetochore but not impinging on it, and α, β, and ζ are scaling factors for the effect of the tension force, the polar ejection force, and the polymerization ratcheting force on the rescue frequency of the MT tip, respectively, with units pN−1 (35,36). If a MT is not bound to the kinetochore, the rescue frequency of its plus end is simply fres, and if it is impinging on the kinetochore plate it is fres/γKLP59C. The catastrophe frequency of all MTs is fcat, except for those impinging on the kt plate, which is assumed to be fcat/ϕ . If a MT shrinks all the way back to its pole, its rescue probability is set to 1, and if it is grown to the opposite pole, its catastrophe probability is set to 1. Once the transition frequencies are calculated, the growth and shrinkage rates of the plus ends of MTs are determined based on the current position of the MT ends: for MTs bound to the kinetochore, the growth and shrinkage velocities are vg/φ and vs/φ, and for those that are not, it is simply vg and vs. The growth rate of MTs impinging on the kinetochore plate is set to vg = 0, regardless of the actual value of the parameter vg.
Computation of velocities and positions of kinetochores and MTs
The model was solved numerically using MATLAB (version 7.0.1, The MathWorks, Natick, MA) to simulate the dynamics of sister kinetochores and kMTs. A computer program was written to solve the system of algebraic equations in successive time steps. The initial condition is such that the kinetochores are positioned at the spindle equator with the spring-like cohesin bond at its rest length, and both kinetochores are attached to the maximal number of MTs (typically 5, 15, and 30), while each MT tip is inserted into the kinetochore structure by a randomly chosen distance from 0 to r (random number generator function, MATLAB). At each moment, based on the current position of the right and left kinetochores and the MT plus ends, the tension, polar ejection, and polymerization ratchet forces are determined from Eqs. 5–7, and then Eqs. 8 and 10 are solved to determine the velocities of the right and left kinetochores, 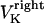 and
and 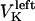 , and that of the right and left kMTs,
, and that of the right and left kMTs, 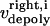 and
and 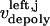 . Then, for each MT, first, the probability that a rescue or catastrophe event occurs, and the growth/shrinkage rates are calculated as above, and then a random number using the built-in random number generator function (MATLAB) is assigned to each MT plus end. For each MT plus end, based on whether the switch probability is greater than the random number, a switch event is or is not assumed to take place, and either the growth or the shrinkage rate calculated above is assigned to the MT tip. Then, the new positions of all MT plus ends are calculated using the computed transition frequencies and growth/shrinkage rates, and the depolymerization rates
. Then, for each MT, first, the probability that a rescue or catastrophe event occurs, and the growth/shrinkage rates are calculated as above, and then a random number using the built-in random number generator function (MATLAB) is assigned to each MT plus end. For each MT plus end, based on whether the switch probability is greater than the random number, a switch event is or is not assumed to take place, and either the growth or the shrinkage rate calculated above is assigned to the MT tip. Then, the new positions of all MT plus ends are calculated using the computed transition frequencies and growth/shrinkage rates, and the depolymerization rates 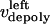 and
and 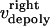 obtained by solving the force-balance equations as explained above, and the kinetochore positions, and MTs' plus and minus ends positions, are calculated using the velocities of the kinetochores, the MTs flux/depolymerization rates, and the growth/shrinkage rates that were determined for each MT plus end. The time is then increased by one step (Δt = 0.1 corresponding to 1 s in real time) and the above scheme is repeated to calculate, first, the velocities of kts and MTs, and then the MT plus ends' dynamic rates, and finally the new positions of all MT ends and kts in the new time step. The system is therefore iteratively solved for typically up to 5000 time steps, corresponding to 5000 s in real time. For the simulations, the model was nondimensionalized using the characteristic size of kinetochore motility, 1 μm, as the unit of length, and the ratio of this length to characteristic velocity of chromosomes in Drosophila embryo 0.1 μm s−1, 1 μm/0.1 μm s−1 = 10 s, as the unit of time. The simulation time step is equal to 0.1 unit of time = 1 s of real time. Random number-generated stochastic variations are added to the growth and shrinkage rates of the MT ends, and to the number of working motors at the kinetochores and poles in the simulations.
obtained by solving the force-balance equations as explained above, and the kinetochore positions, and MTs' plus and minus ends positions, are calculated using the velocities of the kinetochores, the MTs flux/depolymerization rates, and the growth/shrinkage rates that were determined for each MT plus end. The time is then increased by one step (Δt = 0.1 corresponding to 1 s in real time) and the above scheme is repeated to calculate, first, the velocities of kts and MTs, and then the MT plus ends' dynamic rates, and finally the new positions of all MT ends and kts in the new time step. The system is therefore iteratively solved for typically up to 5000 time steps, corresponding to 5000 s in real time. For the simulations, the model was nondimensionalized using the characteristic size of kinetochore motility, 1 μm, as the unit of length, and the ratio of this length to characteristic velocity of chromosomes in Drosophila embryo 0.1 μm s−1, 1 μm/0.1 μm s−1 = 10 s, as the unit of time. The simulation time step is equal to 0.1 unit of time = 1 s of real time. Random number-generated stochastic variations are added to the growth and shrinkage rates of the MT ends, and to the number of working motors at the kinetochores and poles in the simulations.
Abbreviations used: MT, microtubule; kt, kinetochore; kMT, kinetochore microtubule; ipMT, interpolar microtubule; EM, electron microscopy; FRAP, fluorescence recovery after photobleaching.
A. Mogilner and J. M. Scholey contributed equally to this work.
References
- 1.McIntosh, J. R., E. L. Grishchuk, and R. R. West. 2002. Chromosome-microtubule interactions during mitosis. Annu. Rev. Cell Dev. Biol. 18:193–219. [DOI] [PubMed] [Google Scholar]
- 2.Maiato, H., and C. E. Sunkel. 2004. Kinetochore-microtubule interactions during cell division. Chromosome Res. 12:585–597. [DOI] [PubMed] [Google Scholar]
- 3.Kwon, M., and J. M. Scholey. 2004. Spindle mechanics and dynamics during mitosis in Drosophila. Trends Cell Biol. 14:194–205. [DOI] [PubMed] [Google Scholar]
- 4.Rieder, C. L. 1982. The formation, structure, and composition of the mammalian kinetochore and kinetochore fiber. Int. Rev. Cytol. 79:1–58. [DOI] [PubMed] [Google Scholar]
- 5.Maiato, H., J. DeLuca, E. D. Salmon, and W. C. Earnshaw. 2004. The dynamic kinetochore-microtubule interface. J. Cell Sci. 117:5461–5477. [DOI] [PubMed] [Google Scholar]
- 6.McDonald, K. L., E. T. O'Toole, D. N. Mastronarde, and J. R. McIntosh. 1992. Kinetochore microtubules in PTK cells. J. Cell Biol. 118:369–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mitchison, T., and M. Kirschner. 1984. Dynamic instability of microtubule growth. Nature. 312:237–242. [DOI] [PubMed] [Google Scholar]
- 8.Mitchison, T. J. 1989. Polewards microtubule flux in the mitotic spindle: evidence from photoactivation of fluorescence. J. Cell Biol. 109:637–652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Margolis, R. L., and L. Wilson. 1978. Opposite end assembly and disassembly of microtubules at steady state in vitro. Cell. 13:1–8. [DOI] [PubMed] [Google Scholar]
- 10.Skibbens, R. V., V. P. Skeen, and E. D. Salmon. 1993. Directional instability of kinetochore motility during chromosome congression and segregation in mitotic newt lung cells: a push-pull mechanism. J. Cell Biol. 122:859–875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mitchison, T. J., and E. D. Salmon. 2001. Mitosis: a history of division. Nat. Cell Biol. 3:E17–E21. [DOI] [PubMed] [Google Scholar]
- 12.LaFountain, J. R., Jr., C. S. Cohan, A. J. Siegel, and D. J. LaFountain. 2004. Direct visualization of microtubule flux during metaphase and anaphase in crane-fly spermatocytes. Mol. Biol. Cell. 15:5724–5732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Maddox, P., A. Straight, P. Coughlin, T. J. Mitchison, and E. D. Salmon. 2003. Direct observation of microtubule dynamics at kinetochores in Xenopus extract spindles: implications for spindle mechanics. J. Cell Biol. 162:377–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Brust-Mascher, I., and J. M. Scholey. 2002. Microtubule flux and sliding in mitotic spindles of Drosophila embryos. Mol. Biol. Cell. 13:3967–3975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maddox, P., A. Desai, K. Oegema, T. J. Mitchison, and E. D. Salmon. 2002. Poleward microtubule flux is a major component of spindle dynamics and anaphase a in mitotic Drosophila embryos. Curr. Biol. 12:1670–1674. [DOI] [PubMed] [Google Scholar]
- 16.Pearson, C. G., P. S. Maddox, E. D. Salmon, and K. Bloom. 2001. Budding yeast chromosome structure and dynamics during mitosis. J. Cell Biol. 152:1255–1266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.He, X., D. R. Rines, C. W. Espelin, and P. K. Sorger. 2001. Molecular analysis of kinetochore-microtubule attachment in budding yeast. Cell. 106:195–206. [DOI] [PubMed] [Google Scholar]
- 18.Rogers, G. C., S. L. Rogers, T. A. Schwimmer, S. C. Ems-McClung, C. E. Walczak, R. D. Vale, J. M. Scholey, and D. J. Sharp. 2004. Two mitotic kinesins cooperate to drive sister chromatid separation during anaphase. Nature. 427:364–370. [DOI] [PubMed] [Google Scholar]
- 19.Mitchison, T. J., and E. D. Salmon. 1992. Poleward kinetochore fiber movement occurs during both metaphase and anaphase-A in newt lung cell mitosis. J. Cell Biol. 119:569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sharp, D. J., G. C. Rogers, and J. M. Scholey. 2000. Cytoplasmic dynein is required for poleward chromosome movement during mitosis in Drosophila embryos. Nat. Cell Biol. 2:922–930. [DOI] [PubMed] [Google Scholar]
- 21.Brust-Mascher, I., G. Civelekoglu-Scholey, M. Kwon, A. Mogilner, and J. M. Scholey. 2004. Model for anaphase B: role of three mitotic motors in a switch from poleward flux to spindle elongation. Proc. Natl. Acad. Sci. USA. 101:15938–15943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lawrence, C. J., R. K. Dawe, K. R. Christie, D. W. Cleveland, S. C. Dawson, S. A. Endow, L. S. Goldstein, H. V. Goodson, N. Hirokawa, J. Howard, R. L. Malmberg, J. R. McIntosh, H. Miki, T. J. Mitchison, Y. Okada, A. S. Reddy, W. M. Saxton, M. Schliwa, J. M. Scholey, R. D. Vale, C. E. Walczak, and L. Wordeman. 2004. A standardized kinesin nomenclature. J. Cell Biol. 167:19–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yucel, J. K., J. D. Marszalek, J. R. McIntosh, L. S. Goldstein, D. W. Cleveland, and A. V. Philp. 2000. CENP-meta, an essential kinetochore kinesin required for the maintenance of metaphase chromosome alignment in Drosophila. J. Cell Biol. 150:1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Molina, I., S. Baars, J. A. Brill, K. G. Hales, M. T. Fuller, and P. Ripoll. 1997. A chromatin-associated kinesin-related protein required for normal mitotic chromosome segregation in Drosophila. J. Cell Biol. 139:1361–1371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rieder, C. L., and E. D. Salmon. 1998. The vertebrate cell kinetochore and its roles during mitosis. Trends Cell Biol. 8:310–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mitchison, T. J., P. Maddox, J. Gaetz, A. Groen, M. Shirasu, A. Desai, E. D. Salmon, and T. M. Kapoor. 2005. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol. Biol. Cell. 16:3064–3076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ganem, N. J., K. Upton, and D. A. Compton. 2005. Efficient mitosis in human cells lacking poleward microtubule flux. Curr. Biol. 15:1827–1832. [DOI] [PubMed] [Google Scholar]
- 28.Zhu, C., J. Zhao, M. Bibikova, J. D. Leverson, E. Bossy-Wetzel, J. B. Fan, R. T. Abraham, and W. Jiang. 2005. Functional analysis of human microtubule-based motor proteins, the kinesins and dyneins, in mitosis/cytokinesis using RNA interference. Mol. Biol. Cell. 16:3187–3199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sproul, L. R., D. J. Anderson, A. T. Mackey, W. S. Saunders, and S. P. Gilbert. 2005. Cik1 targets the minus-end kinesin depolymerase kar3 to microtubule plus ends. Curr. Biol. 15:1420–1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Encalada, S. E., J. Willis, R. Lyczak, and B. Bowerman. 2005. A spindle checkpoint functions during mitosis in the early Caenorhabditis elegans embryo. Mol. Biol. Cell. 16:1056–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Karess, R. 2005. Rod-Zw10-Zwilch: a key player in the spindle checkpoint. Trends Cell Biol. 15:386–392. [DOI] [PubMed] [Google Scholar]
- 32.Howell, B. J., B. F. McEwen, J. C. Canman, D. B. Hoffman, E. M. Farrar, C. L. Rieder, and E. D. Salmon. 2001. Cytoplasmic dynein/dynactin drives kinetochore protein transport to the spindle poles and has a role in mitotic spindle checkpoint inactivation. J. Cell Biol. 155:1159–1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cimini, D., L. A. Cameron, and E. D. Salmon. 2004. Anaphase spindle mechanics prevent mis-segregation of merotelically oriented chromosomes. Curr. Biol. 14:2149–2155. [DOI] [PubMed] [Google Scholar]
- 34.Joglekar, A. P., and A. J. Hunt. 2002. A simple, mechanistic model for directional instability during mitotic chromosome movements. Biophys. J. 83:42–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gardner, M. K., C. G. Pearson, B. L. Sprague, T. R. Zarzar, K. Bloom, E. D. Salmon, and D. J. Odde. 2005. Tension-dependent regulation of microtubule dynamics at kinetochores can explain metaphase congression in yeast. Mol. Biol. Cell. 16:3764–3775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sprague, B. L., C. G. Pearson, P. S. Maddox, K. S. Bloom, E. D. Salmon, and D. J. Odde. 2003. Mechanisms of microtubule-based kinetochore positioning in the yeast metaphase spindle. Biophys. J. 84:3529–3546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hill, T. L. 1985. Theoretical problems related to the attachment of microtubules to kinetochores. Proc. Natl. Acad. Sci. USA. 82:4404–4408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Inoue, S., and E. D. Salmon. 1995. Force generation by microtubule assembly/disassembly in mitosis and related movements. Mol. Biol. Cell. 6:1619–1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Svoboda, K., and S. M. Block. 1994. Force and velocity measured for single kinesin molecules. Cell. 77:773–784. [DOI] [PubMed] [Google Scholar]
- 40.Mallik, R., B. C. Carter, S. A. Lex, S. J. King, and S. P. Gross. 2004. Cytoplasmic dynein functions as a gear in response to load. Nature. 427:649–652. [DOI] [PubMed] [Google Scholar]
- 41.Singh, M. P., R. Mallik, S. P. Gross, and C. C. Yu. 2005. Monte Carlo modeling of single-molecule cytoplasmic dynein. Proc. Natl. Acad. Sci. USA. 102:12059–12064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Marshall, W. F., J. F. Marko, D. A. Agard, and J. W. Sedat. 2001. Chromosome elasticity and mitotic polar ejection force measured in living Drosophila embryos by four-dimensional microscopy-based motion analysis. Curr. Biol. 11:569–578. [DOI] [PubMed] [Google Scholar]
- 43.Howard, J. 2001. Mechanics of Motor Proteins and the Cytoskeleton. Sinauer Associates, Sunderland, MA.
- 44.Mennella, V., G. C. Rogers, S. L. Rogers, D. W. Buster, R. D. Vale, and D. J. Sharp. 2005. Functionally distinct kinesin-13 family members cooperate to regulate microtubule dynamics during interphase. Nat. Cell Biol. 7:235–245. [DOI] [PubMed] [Google Scholar]
- 45.Janson, M. E., M. E. de Dood, and M. Dogterom. 2003. Dynamic instability of microtubules is regulated by force. J. Cell Biol. 161:1029–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.King, J. M., and R. B. Nicklas. 2000. Tension on chromosomes increases the number of kinetochore microtubules but only within limits. J. Cell Sci. 113:3815–3823. [DOI] [PubMed] [Google Scholar]
- 47.Salmon, E. D. 2005. Microtubules: a ring for the depolymerization motor. Curr. Biol. 15:R299–R302. [DOI] [PubMed] [Google Scholar]
- 48.Winey, M., C. L. Mamay, E. T. O'Toole, D. N. Mastronarde, T. H. Giddings Jr., K. L. McDonald, and J. R. McIntosh. 1995. Three-dimensional ultrastructural analysis of the Saccharomyces cerevisiae mitotic spindle. J. Cell Biol. 129:1601–1615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zhai, Y., P. J. Kronebusch, and G. G. Borisy. 1995. Kinetochore microtubule dynamics and the metaphase-anaphase transition. J. Cell Biol. 131:721–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Waters, J. C., R. V. Skibbens, and E. D. Salmon. 1996. Oscillating mitotic newt lung cell kinetochores are, on average, under tension and rarely push. J. Cell Sci. 109:2823–2831. [DOI] [PubMed] [Google Scholar]
- 51.Scholey, J. M., G. C. Rogers, and D. J. Sharp. 2001. Mitosis, microtubules, and the matrix. J. Cell Biol. 154:261–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Palmer, R. E., M. Koval, and D. Koshland. 1989. The dynamics of chromosome movement in the budding yeast Saccharomyces cerevisiae. J. Cell Biol. 109:3355–3366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chen, W., and D. Zhang. 2004. Kinetochore fibre dynamics outside the context of the spindle during anaphase. Nat. Cell Biol. 6:227–231. [DOI] [PubMed] [Google Scholar]
- 54.Desai, A., P. S. Maddox, T. J. Mitchison, and E. D. Salmon. 1998. Anaphase A chromosome movement and poleward spindle microtubule flux occur at similar rates in Xenopus extract spindles. J. Cell Biol. 141:703–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Maddox, P. S., K. S. Bloom, and E. D. Salmon. 2000. The polarity and dynamics of microtubule assembly in the budding yeast Saccharomyces cerevisiae. Nat. Cell Biol. 2:36–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Maddox, P. S., J. K. Stemple, L. Satterwhite, E. D. Salmon, and K. Bloom. 2003. The minus end-directed motor Kar3 is required for coupling dynamic microtubule plus ends to the cortical shmoo tip in budding yeast. Curr. Biol. 13:1423–1428. [DOI] [PubMed] [Google Scholar]
- 57.Kline-Smith, S. L., A. Khodjakov, P. Hergert, and C. E. Walczak. 2004. Depletion of centromeric MCAK leads to chromosome congression and segregation defects due to improper kinetochore attachments. Mol. Biol. Cell. 15:1146–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Rogers, S. L., G. C. Rogers, D. J. Sharp, and R. D. Vale. 2002. Drosophila EB1 is important for proper assembly, dynamics, and positioning of the mitotic spindle. J. Cell Biol. 158:873–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kaplan, K. B., A. A. Burds, J. R. Swedlow, S. S. Bekir, P. K. Sorger, and I. S. Nathke. 2001. A role for the Adenomatous polyposis coli protein in chromosome segregation. Nat. Cell Biol. 3:429–432. [DOI] [PubMed] [Google Scholar]
- 60.Rieder, C. L. 2005. Kinetochore fiber formation in animal somatic cells: dueling mechanisms come to a draw. Chromosoma. 114:310–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wollman, R., E. N. Cytrynbaum, J. T. Jones, T. Meyer, J. M. Scholey, and A. Mogilner. 2005. Efficient chromosome capture requires a bias in the ‘search-and-capture’ process during mitotic-spindle assembly. Curr. Biol. 15:828–832. [DOI] [PubMed] [Google Scholar]
- 62.Howard, J., and A. A. Hyman. 2003. Dynamics and mechanics of the microtubule plus end. Nature. 422:753–758. [DOI] [PubMed] [Google Scholar]
- 63.Koshland, D. E., T. J. Mitchison, and M. W. Kirschner. 1988. Polewards chromosome movement driven by microtubule depolymerization in vitro. Nature. 331:499–504. [DOI] [PubMed] [Google Scholar]
- 64.Andrews, P. D., Y. Ovechkina, N. Morrice, M. Wagenbach, K. Duncan, L. Wordeman, and J. R. Swedlow. 2004. Aurora B regulates MCAK at the mitotic centromere. Dev. Cell. 6:253–268. [DOI] [PubMed] [Google Scholar]
- 65.Westermann, S., A. Avila-Sakar, H. W. Wang, H. Niederstrasser, J. Wong, D. G. Drubin, E. Nogales, and G. Barnes. 2005. Formation of a dynamic kinetochore- microtubule interface through assembly of the Dam1 ring complex. Mol. Cell. 17:277–290. [DOI] [PubMed] [Google Scholar]
- 66.Molodtsov, M. I., E. L. Grishchuk, A. K. Efremov, J. R. McIntosh, and F. I. Ataullakhanov. 2005. Force production by depolymerizing microtubules: a theoretical study. Proc. Natl. Acad. Sci. USA. 102:4353–4358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.McIntosh, J. R. 2005. Rings around kinetochore microtubules in yeast. Nat. Struct. Mol. Biol. 12:210–212. [DOI] [PubMed] [Google Scholar]
- 68.Fall, C. P., E. Marland, J. Tyson, and J. Wagner, editors. 2002. Computational Cell Biology. Springer, New York.
- 69.Schnitzer, M. J., K. Visscher, and S. M. Block. 2000. Force production by single kinesin motors. Nat. Cell Biol. 2:718–723. [DOI] [PubMed] [Google Scholar]
- 70.Wood, K. W., R. Sakowicz, L. S. Goldstein, and D. W. Cleveland. 1997. CENP-E is a plus end-directed kinetochore motor required for metaphase chromosome alignment. Cell. 91:357–366. [DOI] [PubMed] [Google Scholar]
- 71.Rusan, N. M., U. S. Tulu, C. Fagerstrom, and P. Wadsworth. 2002. Reorganization of the microtubule array in prophase/prometaphase requires cytoplasmic dynein-dependent microtubule transport. J. Cell Biol. 158:997–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Nicklas, R. B., and D. F. Kubai. 1985. Microtubules, chromosome movement, and reorientation after chromosomes are detached from the spindle by micromanipulation. Chromosoma. 92:313–324. [DOI] [PubMed] [Google Scholar]
- 73.Wadsworth, P., and E. D. Salmon. 1986. Microtubule dynamics in mitotic spindles of living cells. Ann. N. Y. Acad. Sci. 466:580–592. [DOI] [PubMed] [Google Scholar]
- 74.Rieder, C. L., and R. Hard. 1990. Newt lung epithelial cells: cultivation, use, and advantages for biomedical research. Int. Rev. Cytol. 122:153–220. [DOI] [PubMed] [Google Scholar]
- 75.Cassimeris, L., S. Inoue, and E. D. Salmon. 1988. Microtubule dynamics in the chromosomal spindle fiber: analysis by fluorescence and high-resolution polarization microscopy. Cell Motil. Cytoskeleton. 10:185–196. [DOI] [PubMed] [Google Scholar]