Abstract
We show that the standard theoretical framework in single-molecule force spectroscopy has to be extended to consistently describe the experimental findings. The basic amendment is to take into account heterogeneity of the chemical bonds via random variations of the force-dependent dissociation rates. This results in a very good agreement between theory and rupture data from several different experiments.
INTRODUCTION
Dynamic force spectroscopy is a widely used tool for investigating binding properties of biomolecular complexes at the atomic scale by means of the dissociation of single chemical bonds under an external force (1,2). Since the first reported ligand-receptor experiments (3–5) the technique has rapidly evolved into a quantitative single molecule binding assay technology giving access to binding forces, molecular elasticities, reaction off-rates, and binding energy landscapes with a sensitivity of single point mutations for single molecule affinity ranking. Essentially, the molecular complex of interest is connected via suitable linkers (spacer molecules) to an atomic force microscope (AFM) (see Fig. 1), or a micropipette-based force probe and pulled apart at a constant speed v while monitoring the acting forces until the chemical bond ruptures.
FIGURE 1.
Schematic illustration of dynamic AFM force spectroscopy: a single chemical bond, e.g., in a ligand-receptor complex, is connected via two flexible linker molecules with the tip of an AFM cantilever and a piezoelectric element. The latter pulls down the attached linker molecule at some constant velocity υ. The resulting elastic reaction force of the cantilever can be determined from the deflection of a laser beam. The main quantity of interest is the force value at the moment when the bond dissociates.
Since the molecular dissociation process is of stochastic nature, the theoretical interpretation of the observed rupture forces is a nontrivial task: upon repeating the same experiment at the same pulling velocity υ several times, the rupture forces are found to be distributed over a wide range (see Fig. 2). Furthermore, for different pulling velocities υ different such distributions are obtained. Hence, neither a single rupture event nor the average rupture force at any fixed pulling velocity can serve as a meaningful characteristic quantity of a given chemical bond strength.
FIGURE 2.
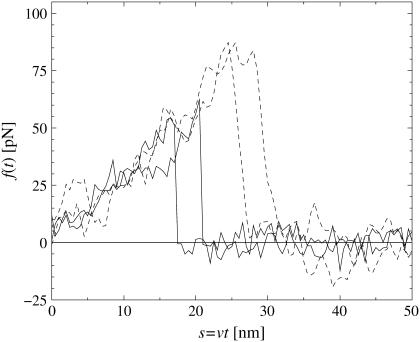
Force-extension curves of four representative single-molecule pulling experiments, two with pulling velocity υ = 100 nm/s (solid) and two with υ = 5000 nm/s (dashed), obtained by dynamic AFM force spectroscopy for the DNA fragment expE1/E5 and the regulatory protein ExpG (23). The abrupt drop of f(t) indicates dissociation of the chemical bond between expE1/E5 and ExpG. Apart from noise effects, the forces f(t) before dissociation (relevant in Eq. 1) collapse quite well to a single force-extension master-curve F(s); see Eq. 2. It can be noted that for a given pulling velocity, the rupture forces are distributed over a considerable range and that larger pulling velocities result in larger average dissociation forces.
On the other hand, direct molecular dynamics simulations of the forced dissociation process are still very far from reaching experimentally realistic conditions due to the limited accessible timescale (6–9). Hence, nontrivial theoretical modeling steps are unavoidable.
The main breakthrough in solving the puzzle came with the hallmark articles by Bell in 1978 (10) and by Evans and Ritchie in 1997 (11), recognizing that a forced bond rupture event is a thermally activated decay of a metastable state that can be described within the general framework of reaction rate theory (12).
While Evans and Ritchie's original theoretical approach has been extended and refined in several important directions (1,2,13–19), the essential physical picture—henceforth called “standard theory”—has remained unchanged and has been the basis for evaluating the observed rupture data of all experimental investigations ever since (1,2). In the next section, we present this so-called standard theory and its underlying assumptions in more detail. Then we evaluate rupture data from several different experiments and we show that all of them are incompatible with the basic assumptions of the standard theory. In the central section, we propose an extension of the standard theory which leads to a very good agreement with the experiments. The basic new idea is to take into account heterogeneity of the chemical bonds by means of a simple and natural phenomenological ansatz to quantify the proposed randomness of the dissociation rates. We show that our theory is largely independent of the details of this phenomenological ansatz. Next, the previously established standard data analysis procedure is reconsidered from the viewpoint of the new theory. The final section contains our Summary and Conclusions.
THE STANDARD THEORY
Assumptions
The standard theory, which is at the heart of all recent experimental and theoretical studies in the field of single-molecule force spectroscopy (1,2), is mainly due to Evans and Ritchie (11). Adopting the common concepts and notions of equilibrium (static) reaction rate theory (12), a rupture event is viewed as a thermally activated decay of a metastable state, governed by a reaction kinetics
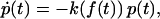 |
(1) |
where p(t) is the probability of bond survival up to time t and k(f) the dissociation rate in the presence of a pulling force f.
A first assumption implicit in Eq. 1 is that the applied force f(t) changes slowly compared to the molecular relaxation into the accompanying equilibrium of the metastable bound state and also compared to the typical duration of thermally activated transition and decay processes. Second, rebinding after dissociation is neglected because of an immediate separation of the two molecules after their dissociation (see section Unsuccessful Explanations).
Another main ingredient of the standard theory regards the dependence of the force f(t) in Eq. 1 on the pulling velocity υ. Namely, it is assumed that
 |
(2) |
where the function F(s) is independent of υ. In other words, the instantaneous force f(t) only depends on the externally imposed total extension s = υt of all elastic components of the setup (molecules, linkers, AFM-cantilever, etc.), but not on the velocity υ at which this extension increases. The theoretical justification is that under realistic conditions all elastic components remain close to their accompanying/instantaneous equilibrium states and hence their previous history does not matter. An experimental verification is provided by Fig. 2; see also Raible et al. (20).
Supplementing the standard theory—consisting in the basic assumptions Eq. 1 and Eq. 2—by certain additional approximations gives rise to the so-called standard method for analyzing rupture force distributions. A more detailed discussion of this method is given in the section Comparison with the Standard Method.
Implications
Combining Eqs. 1 and 2, a straightforward calculation yields for the probability pυ(f) of bond survival up to a force f (defined via pυ(f(t)) = p(t)) the result
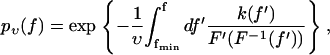 |
(3) |
where fmin denotes the threshold below which rupture events cannot be distinguished from fluctuations in the experiment (e.g., fmin ≈ 20 pN in Fig. 2). Accordingly, f ≥ fmin is henceforth tacitly understood in relations like Eqs. 1 and 3. Furthermore, we assumed F(s) to be monotonically increasing so that its inverse F−1 exists. (If F(s) were decreasing within a certain interval of s-values, this would imply a mechanical instability and hence the coexistence of yet at least two further stable branches of F(s). These two stable branches would furthermore imply hysteresis and hence an incompatibility with the assumption discussed below Eq. 2.) For the rest, the force-extension characteristic F(s) may be completely arbitrary and the rate k(f) may describe a completely general activated decay of a metastable state in a high-dimensional potential energy landscape (19,21). The only prerequisite for Eq. 3 is the validity of Eqs. 1 and 2. The latter, in turn, is basically tantamount to the requirement of quasi-equilibrium of the entire setup in Fig. 1 (bound complex, linkers, AFM) for all times before bond dissociation.
Eq. 3 implies that the function −υ ln pυ(f) is independent of the pulling velocity v, resulting in a single master curve, onto which the data points should collapse for all pulling velocities (22). Next, this conclusion will be used to check the consistency of the standard theory Eqs. 1 and 2 with the experimental data.
INCONSISTENCY WITH EXPERIMENTAL FINDINGS
Evaluation of experimental data
Given a set of Nυ experimentally observed rupture forces fn at a fixed pulling velocity υ (n = 1, …, Nυ, fn > fmin for all n), we can infer the following estimate 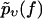 for the true bond survival probability pυ(f):
for the true bond survival probability pυ(f):
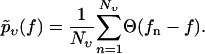 |
(4) |
Here,  is the Heaviside step function with the convention
is the Heaviside step function with the convention
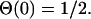 |
(5) |
By definition, 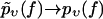 for Nυ → ∞ (with probability 1), and for any finite Nv, Eq. 4 is in fact the best estimate for pυ(f) that can be inferred from the given data without additional a priori assumptions about the system.
for Nυ → ∞ (with probability 1), and for any finite Nv, Eq. 4 is in fact the best estimate for pυ(f) that can be inferred from the given data without additional a priori assumptions about the system.
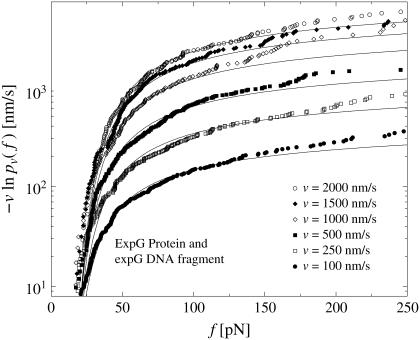
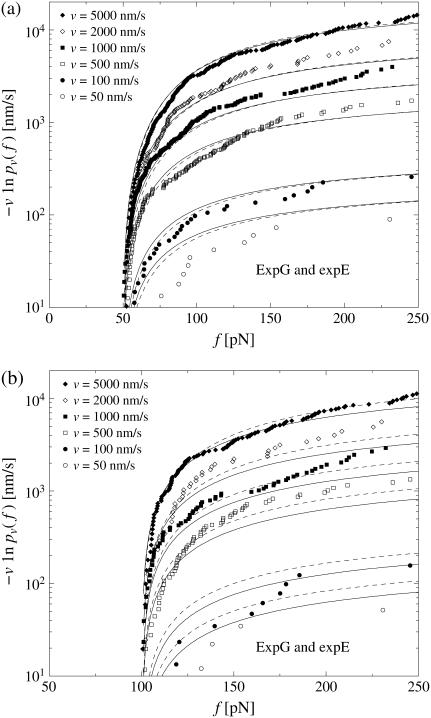
In Fig. 3 we have evaluated 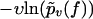 for different pulling velocities υ according to Eq. 4 for the same experimental system as in Fig. 2 (rupture data obtained by dynamic AFM force spectroscopy for the DNA fragment expE1/E5 and the regulatory protein ExpG (23)).
for different pulling velocities υ according to Eq. 4 for the same experimental system as in Fig. 2 (rupture data obtained by dynamic AFM force spectroscopy for the DNA fragment expE1/E5 and the regulatory protein ExpG (23)).
FIGURE 3.
(Symbols) The functions 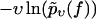 for different pulling velocities υ, obtained according to Eq. 4 from the same experiment (23) as in Fig. 2. Each depicted point corresponds to one rupture event at f = fn and hence a step of the piecewise constant function Eq. 4. Only fn above fmin = 20 pN have been taken into account; see discussion below Eq. 3. The number Nυ of experimental data points for the six different velocities υ in Eq. 4 are N50nm/s = 20; N100nm/s = 44; N500nm/s = 179; N1000nm/s = 208; N2000nm/s = 108; and N5000nm/s = 253. A few very small or large fn are omitted in this plot for the sake of better visibility of the remaining symbols. (Solid lines) Theoretical functions
for different pulling velocities υ, obtained according to Eq. 4 from the same experiment (23) as in Fig. 2. Each depicted point corresponds to one rupture event at f = fn and hence a step of the piecewise constant function Eq. 4. Only fn above fmin = 20 pN have been taken into account; see discussion below Eq. 3. The number Nυ of experimental data points for the six different velocities υ in Eq. 4 are N50nm/s = 20; N100nm/s = 44; N500nm/s = 179; N1000nm/s = 208; N2000nm/s = 108; and N5000nm/s = 253. A few very small or large fn are omitted in this plot for the sake of better visibility of the remaining symbols. (Solid lines) Theoretical functions 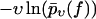 for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 21. For more details, see section Heterogeneity of Chemical Bonds.
for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 21. For more details, see section Heterogeneity of Chemical Bonds.
In contrast to Eq. 3, the functions 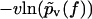 evaluated from the experimental data using Eq. 4 at different values of υ do not collapse onto a single master curve. Rather, increasing the velocity results in an increased value of this function for sufficiently high forces. In view of the very strong dependence of the experimental curves
evaluated from the experimental data using Eq. 4 at different values of υ do not collapse onto a single master curve. Rather, increasing the velocity results in an increased value of this function for sufficiently high forces. In view of the very strong dependence of the experimental curves 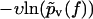 on the pulling velocities υ, we conclude that the experimental findings are incompatible with Eq. 3 and hence with the basic assumptions from Eqs. 1 and 2 of the standard theory (20).
on the pulling velocities υ, we conclude that the experimental findings are incompatible with Eq. 3 and hence with the basic assumptions from Eqs. 1 and 2 of the standard theory (20).
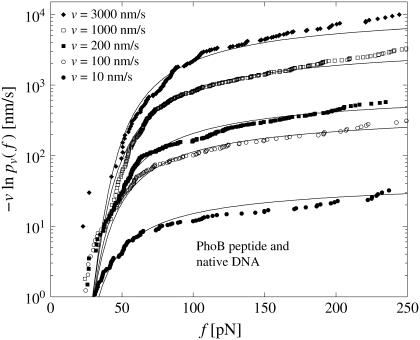
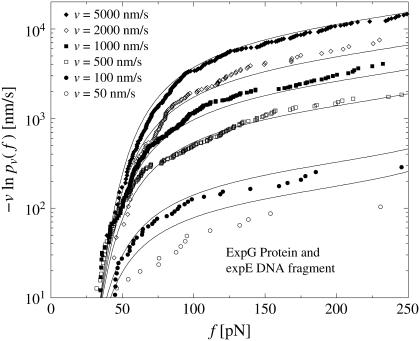
To check if this finding depends on the chosen experimental system, we have also evaluated dynamic AFM force spectroscopy data for the dissociation of another DNA fragment from the regulatory protein ExpG (see Fig. 4), a PhoB peptide (wild-type) from the corresponding DNA target sequence (see Fig. 5), and a cationic guest molecule from a supramolecular calixaren host molecule (see Fig. 6). Since essentially the same linkers have been used in all those AFM-experiments, the force-extension curves always look similar to those in Fig. 2. For more experimental details we refer to Bartels et al. (23), Eckel et al. (24), and Eckel et al. (25).
FIGURE 4.
Same symbols as in Fig. 3 but for dynamic AFM force spectroscopy data by Bartels et al. (23) for the dissociation of the DNA fragment expG1/G4 from the regulatory protein ExpG. (Symbols) The functions 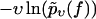 for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 10 pN. (Solid lines) Theoretical functions
for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 10 pN. (Solid lines) Theoretical functions 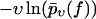 for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 20.
for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 20.
FIGURE 5.
Same as in Fig. 3 but for dynamic AFM force spectroscopy data by Eckel et al. (24) for the dissociation of the PhoB peptide (wild-type) of E. coli from the DNA target sequence. (Symbols) The functions 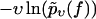 for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 20 pN. (Solid lines) Theoretical functions
for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 20 pN. (Solid lines) Theoretical functions  for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 21.
for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 21.
FIGURE 6.
Same as in Fig. 3 but for dynamic AFM force spectroscopy data by Eckel et al. (25) for the dissociation of a calixaren host molecule (resorc[4]arene) from a cationic guest (ammonium). (Symbols) The functions 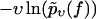 for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 25 pN. (Solid lines) Theoretical functions
for different pulling velocities υ, obtained according to Eq. 4 and taking into account only fn above fmin = 25 pN. (Solid lines) Theoretical functions 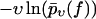 for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 22.
for the same pulling velocities υ as the symbols, using Eqs. 9, 11–16, and 22.
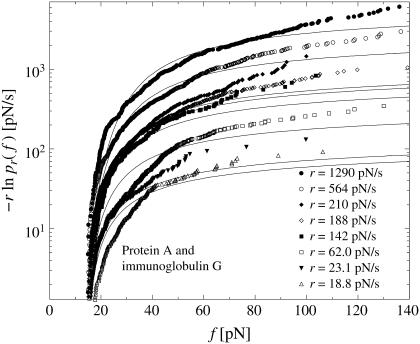
Furthermore, we have evaluated in Fig. 7 rupture data observed by means of a micropipette-based force probe for the dissociation of a rabbit immunoglobulin of type G from protein A (see (19) for the experimental details). In doing so, we have employed as an additional assumption a linear force-extension characteristic
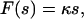 |
(6) |
where κ is the effective elastic spring constant of the entire setup (bound complex, red blood cell, microbeads, etc.). Moreover, instead of different pulling velocities υ, we considered different loading rates
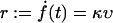 |
(7) |
of the force f(t) in Eq. 2. The reason for this modification is that in the experiment from Nguyen-Duong (19), rupture data both for different υ and different κ are available and can be simultaneously evaluated in this way. Namely, by exploiting that F′(s) ≡ κ (independent of s) and renaming pυ(f) as pr(f) we can again conclude from Eq. 3 that 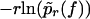 should be independent of r.
should be independent of r.
FIGURE 7.
Same as in Fig. 3 but for micropipette-based force probe data by Nguyen-Duong et al. (19) for the dissociation of immunoglobulin of type G from protein A. (Symbols) The functions 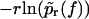 for different loading rates r; see below Eq. 6, taking into account only fn above fmin = 15 pN. (Solid lines) Theoretical functions
for different loading rates r; see below Eq. 6, taking into account only fn above fmin = 15 pN. (Solid lines) Theoretical functions 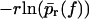 for the same loading rates r as the symbols, using Eqs. 7, 9, 11–16, and 23.
for the same loading rates r as the symbols, using Eqs. 7, 9, 11–16, and 23.
In all the different experimental systems in Figs. 3–7 we thus recover the same kind of incompatibility with Eq. 3 and hence with the basic assumptions Eq. 1 and Eq. 2 of the standard theory.
Unsuccessful explanations
Since the incompatibility between experimental findings and the standard theory is essentially of the same character in all the different cases evaluated in Figs. 3–7, we concentrate on one of them, namely, the system from Fig. 3. Moreover, since Eq. 2 is verified experimentally by Fig. 2, we can focus on Eq. 1 to pinpoint the leakage of the standard theory and possibly repair it.
We first note that only f(t)-curves surpassing fmin = 20 pN in Fig. 2 have been taken into account in Fig. 3. Hence, rebinding after dissociation would require a huge and hence extremely unlikely random fluctuation (1,2) and has indeed never been observed in the experiment at hand. Moreover, upon increasing fmin we did not observe any clear tendency toward a better data collapse than in Fig. 3 (see Fig. 8). In other words, rebinding events are indeed negligible.
FIGURE 8.
Same as in Fig. 3 except that in panel a, only fn above fmin = 50 pN and in panel b, only fn above fmin = 100 pN have been taken into account. The solid lines are the corresponding theoretical functions 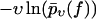 using Eqs. 9, and 11–19. (Dashed lines) Same as solid lines but after refitting the parameters k0, αm, and σ to the given data subset, resulting in k0 = 0.000020 s−1, αm = 0.19 pN−1, σ = 0.095 pN−1 for panel a, and in k0 = 0.017 s−1, αm = 0.091 pN−1, σ = 0.040 pN−1 for panel b.
using Eqs. 9, and 11–19. (Dashed lines) Same as solid lines but after refitting the parameters k0, αm, and σ to the given data subset, resulting in k0 = 0.000020 s−1, αm = 0.19 pN−1, σ = 0.095 pN−1 for panel a, and in k0 = 0.017 s−1, αm = 0.091 pN−1, σ = 0.040 pN−1 for panel b.
Concerning the accompanying equilibrium assumption implicit in Eq. 1, the most convincing possibility leading to its failure is the existence of several metastable (sub-) states of the bound complex with relatively slow transitions between them (11,15,16,26) and possibly several different dissociation pathways (27); this possibility will be considered below. As discussed in detail in Raible et al. (20), one indeed gets a spreading of −υ ln(pυ(f)) for different υ in this way. This spreading is, however, qualitatively quite different from that in Fig. 3 for a generic model with a few internal states. With more complex networks of internal states—and a concomitant flurry of fit parameters in the form of transition rates between them—a satisfactory fit to the data in Figs. 3–7 may well be possible, but their actual existence in all the different experimental systems seems quite difficult to justify.
For further unsuccessful attempts to quantitatively explain the noncollapse of the data to a single master curve in Figs. 3–7, see Raible et al. (20).
HETEROGENEITY OF CHEMICAL BONDS
Basic idea
We now come to the central point of our article. Namely, we propose heterogeneity of the chemical bonds as an explanation of the experimental findings in Figs. 3–7. Basically, this means that Eqs. 1 and 2 remain valid except that the force-dependent dissociation rate k(f) is subjected to random variations upon repeating the pulling experiment. As a consequence, the experimentally determined 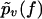 from Eq. 4 should not be compared with the function pυ(f) from Eq. 3, but instead, with its average with respect to the probability distribution of the rates k(f), henceforth denoted as
from Eq. 4 should not be compared with the function pυ(f) from Eq. 3, but instead, with its average with respect to the probability distribution of the rates k(f), henceforth denoted as 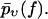
At a first glance, such an intrinsic randomness of the dissociation rate k(f) might appear unlikely in view of the fact that, after all, it is always the same species of molecules dissociating. Yet, possible physical reasons for such random variations of the dissociation rate k(f) might be:
Random variations and fluctuations of the local molecular environment by ions, water, and solvent molecules locally modulating ionic strength, pH, and electric fields, which may influence the dissociation process of the molecular complex (28).
Structural fluctuations due to thermal activation may lead to different conformations of a (macro-) molecule.
Orientational fluctuations of the molecular complex relative to the direction of the applied pulling force may amount to different dependences of the rate k on f. In addition, the linker molecules may be attached to the complex at different positions, but also many other random geometrical variations may be possible (see Fig. 1 and (29,30)).
Even more importantly, in a number of dissociation events one is actually not pulling apart the specific molecular complex of interest but rather some different, unspecific chemical bond. In a small but not necessarily negligible number of such unspecific events, the force-extension-curve may still look exactly like in Fig. 2 and hence it is impossible to eliminate those events from the experimental data set.
We remark that not all those general reasons may be pertinent to the specific experimental data in Figs. 3–7 and that there may well exist additional sources of randomness that we overlooked so far. Their detailed quantitative modeling is a daunting task beyond the scope of our present work and also beyond the present possibilities of experimental verification. Rather, we will resort to the ad hoc ansatz that all those different sources of randomness approximately sum up to an effective Gaussian distribution with two fit parameters (see Eq. 16 below). Furthermore, we will verify that moderate variations of this Gaussian ansatz indeed leave our main conclusions practically unchanged (see the next section).
Formalization
To quantify the basic qualitative ideas from the discussion above, the usual starting point will be some parametric ansatz for the functional form of the rate, 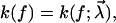 with a set of parameters
with a set of parameters  These parameters are randomly distributed according to a certain (conditional) probability density
These parameters are randomly distributed according to a certain (conditional) probability density 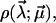 which itself depends on some fit parameters
which itself depends on some fit parameters 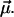 In such a case, the parametric
In such a case, the parametric 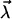 -dependence of
-dependence of 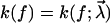 is inherited by
is inherited by 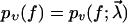 via Eq. 3, yielding
via Eq. 3, yielding
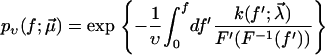 |
(8) |
The relevant 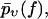 to which the experimentally determined
to which the experimentally determined 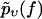 from Eq. 4 should be compared (see beginning of this section), follows by averaging with respect to the probability distribution of the rates, i.e.,
from Eq. 4 should be compared (see beginning of this section), follows by averaging with respect to the probability distribution of the rates, i.e.,
 |
(9) |
The denominator accounts for the fact that rupture forces below fmin cannot be distinguished from thermal fluctuations and other artifacts (see Fig. 2) and therefore are missing in the experimental data set. Hence 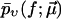 is restricted to f ≥ fmin and must be normalized to unity for f = fmin. (Note that rupture events at f < fmin, though not detectable by the specific experiment at hand, do occur in actual reality and hence fmin does not play any role regarding the validity range or functional form of Eq. 8 (in contrast to Eq. 3).)
is restricted to f ≥ fmin and must be normalized to unity for f = fmin. (Note that rupture events at f < fmin, though not detectable by the specific experiment at hand, do occur in actual reality and hence fmin does not play any role regarding the validity range or functional form of Eq. 8 (in contrast to Eq. 3).)
Finally, the fit parameters 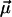 are determined so that
are determined so that 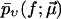 reproduces the experimentally observed
reproduces the experimentally observed 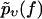 as closely as possible. The resulting optimal parameters
as closely as possible. The resulting optimal parameters 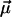 yield an estimate for the heterogeneity of the chemical bonds in the form of the probability distribution
yield an estimate for the heterogeneity of the chemical bonds in the form of the probability distribution  of the rates
of the rates 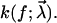
In practice, one has to choose a cost function to quantify the fitness or quality of a given 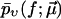 with respect to the experimental data
with respect to the experimental data 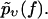 A natural choice, which we will use in the following, is
A natural choice, which we will use in the following, is
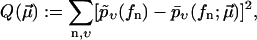 |
(10) |
where the sum runs over all experimentally observed rupture forces fn and all pulling velocities υ. The main argument in favor of the cost function Eq. 10 is that it attributes the same importance to each rupture event, independent of the velocity υ at which it has been observed. Its main shortcoming is that if one artificially partitions the data for one pulling velocity υ into two subsets, then the resulting minimizing parameters 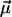 will not remain the same for these subsets in general. A more detailed discussion of this issue will be given elsewhere.
will not remain the same for these subsets in general. A more detailed discussion of this issue will be given elsewhere.
Model functions
To further substantiate these ideas, assumptions about the functional form of the force-extension characteristic F(s), the dissociation rate 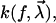 and the probability density
and the probability density 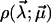 are unavoidable.
are unavoidable.
According to Fig. 2, the force-extension characteristic is approximately linear,
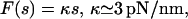 |
(11) |
see Eq. 6.
Further, we adopt the standard approximation (Eqs. 1, 2, 10, and 11) of
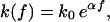 |
(12) |
where k0 is the force-free dissociation rate and eαf is supposed to capture the dominating Arrhenius-type dependence of the decay rate on the applied force (12). In doing so, the parameter α can be identified with the dissociation length, that is, the distance Δx between the potential minimum and the (unstable) transition state, projected along the force direction and measured in units of the thermal energy,
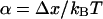 |
(13) |
(see also section Intermediate Energy Barriers below).
Introducing Eq. 11 and Eq. 12 into Eq. 8 yields the simplified expression
 |
(14) |
The above proposed heterogeneity of the chemical bonds in general amounts to a randomization of the two parameters k0 and α in Eq. 12, i.e., 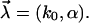 In view of the exponential function in Eq. 12 we can expect that the randomness of α has a much stronger effect than that of k0. Hence, we first consider k0 as fixed and only α as random parameter, i.e.,
In view of the exponential function in Eq. 12 we can expect that the randomness of α has a much stronger effect than that of k0. Hence, we first consider k0 as fixed and only α as random parameter, i.e.,
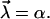 |
(15) |
The corresponding probability distribution is thus of the form 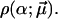 A particularly simple and natural choice is the truncated Gaussian
A particularly simple and natural choice is the truncated Gaussian
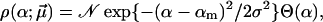 |
(16) |
with  Negative α-values in Eq. 12 appear quite unphysical and hence are suppressed by the factor Θ(α), while 𝒩 is a normalization constant, whose explicit value is actually not needed in Eq. 9. The remaining truncated Gaussian may be viewed as a poor man's guess to effectively take into account the many different possible sources of bond randomness mentioned above. The parameters αm and σ approximate the mean and the dispersion of α, provided the relative dispersion σ/αm is sufficiently small. Otherwise, the actual mean value
Negative α-values in Eq. 12 appear quite unphysical and hence are suppressed by the factor Θ(α), while 𝒩 is a normalization constant, whose explicit value is actually not needed in Eq. 9. The remaining truncated Gaussian may be viewed as a poor man's guess to effectively take into account the many different possible sources of bond randomness mentioned above. The parameters αm and σ approximate the mean and the dispersion of α, provided the relative dispersion σ/αm is sufficiently small. Otherwise, the actual mean value
 |
(17) |
may exceed the most probable value αm of the density in Eq. 16 quite notably.
Since k0 is considered fixed (see Eq. 15), this parameter effectively moves from the set 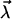 into the set
into the set 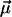 ; i.e., we are left with three fit parameters
; i.e., we are left with three fit parameters
 |
(18) |
The standard theory Eqs. 1 and 2 with Eqs. 11 and 12 are recovered from Eq. 16 for σ → 0, thus leaving only two fit parameters 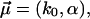 and hence
and hence  with α = αm.
with α = αm.
Application to experimental data
The fit to the five experimental data sets in Figs. 3–7 along the lines described in the previous section is very good in the first three cases and still satisfactory in the two remaining cases.
For the corresponding fit parameters in Eq. 18 we have obtained the following results.
For expE1/E5 and ExpG (Figs. 2 and 3):
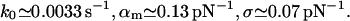 |
(19) |
For expG1/G4 and ExpG (Fig. 4):
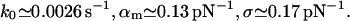 |
(20) |
For PhoB peptide and DNA (Fig. 5):
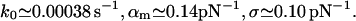 |
(21) |
For resorc[4]arene and ammonium (Fig. 6):
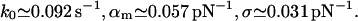 |
(22) |
For immunoglobulin G and protein A (Fig. 7):
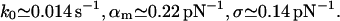 |
(23) |
As already mentioned, essentially the same linkers have been used for all the AFM experiments in Figs. 3–6, hence the force-extension curves always look similar to those in Fig. 2. Accordingly, Eq. 11 has been employed throughout Eqs. 19–22.
In all cases, the relative dispersion σ/αm is comparable to or smaller than unity. Hence the mean α-value, given by 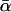 in Eq. 17, is always close to the most probable α-value, given by αm in Eq. 16.
in Eq. 17, is always close to the most probable α-value, given by αm in Eq. 16.
Since the experiments are conducted at room temperature, the typical dissociation lengths 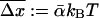 (see Eq. 13) resulting from Eqs. 19–23 with
(see Eq. 13) resulting from Eqs. 19–23 with 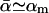 are:
are:
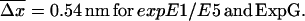 |
 |
 |
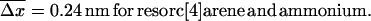 |
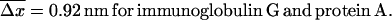 |
Synthetic data, fluctuations, systematic deviations
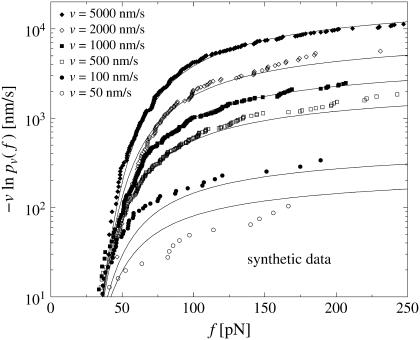
By means of a random number generator, synthetic rupture data can be easily produced numerically, which satisfy Eqs. 1, 2, and 11–19 exactly. The resulting Fig. 9 is indeed strikingly similar to Fig. 3.
FIGURE 9.
Same symbols as in Fig. 3 but for synthetic rupture data, sampled numerically according to Eqs. 9, and 11–19. The velocities υ and the number of rupture events Nυ for each υ are identical to those in Fig. 3.
Fig. 9 also provides a feeling for the typical statistical fluctuations due to the finite numbers Nυ of rupture events at a given pulling speed υ.
It seems plausible that all deviations between experiment and theory in Fig. 3 can be attributed to such purely statistical uncertainties with the exception of the small but systematic deviations at large forces f. Note that the same type of systematic deviations at large f are also apparent in Figs. 4–7.
We come back to those systematic deviations in section Generalized Dissociation Rates, while the statistical fluctuations will be addressed in more detail elsewhere.
OTHER RATE DISTRIBUTIONS
In this section, we discuss variations and generalizations of our model function ansatz Eq. 16 for the probability density quantifying the bond heterogeneity, while modifications of the ansatz for the dissociation rate Eq. 12 itself are postponed to the subsequent section. We focus on one experimental system, namely the data for expE1/E5 and ExpG from Fig. 3. Throughout this section, 𝒩 denotes normalization constants.
Distribution of α
In the following, we discuss modifications of the probability distribution Eq. 16 for α in several paradigmatic ways, while keeping k0 fixed and the ansatz for the dissociation rate Eq. 12 unchanged.
Gaussian distribution
Gaussian distribution, but in contrast to Eq. 16 without suppressing negative α-values, has the form
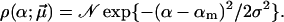 |
(24) |
The fit to the experimental data (not shown) is practically identical to that in Fig. 3, and also the corresponding fit parameters,
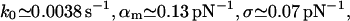 |
(25) |
are essentially the same as in Eq. 19. The obvious reason for the good agreement is the smallness of the Gaussian tail with negative α-values. In other words, the suppression of negative α-values in Eq. 16 is not an essential point for small-to-moderate relative dispersions σ/αm.
Parabolic distribution
Parabolic distribution of α between the limiting values αl and αr has the form
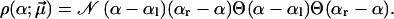 |
(26) |
The resulting fit to the experimental data (not shown) is of the same quality as in Fig. 3, except for small forces ∼40 pN, where the numerically predicted functions 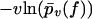 are closer to each other than in Fig. 3. For the corresponding fit parameters
are closer to each other than in Fig. 3. For the corresponding fit parameters 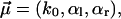 we obtained
we obtained
 |
(27) |
Thus, k0 is comparable to the result in Eq. 19 and also mean and dispersion of the parabolic distribution Eq. 26 are close to those of the truncated Gaussian Eq. 16.
Box distribution
Box distribution of α has the form
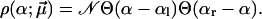 |
(28) |
The fit to the experimental data (not shown) is slightly worse than in Fig. 3, due to a steeper increase of the functions 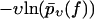 for υ ≤ 100 nm/s and f ≥ 200 pN. For the corresponding fit parameters
for υ ≤ 100 nm/s and f ≥ 200 pN. For the corresponding fit parameters 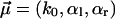 we obtained
we obtained
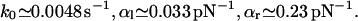 |
(29) |
Again, k0 is comparable to the result in Eq. 19 and also mean and dispersion of the box distribution Eq. 28 are close to those of the truncated Gaussian Eq. 16.
All in all, for the above modifications and several further variations of the distribution equation (Eq. 16) and of the dissociation rates equation (Eq. 12) that we tried out, the resulting fit parameters were always comparable to those in Eq. 19 and the agreement with the experimental data was comparable to or worse than that in Fig. 3, but never significantly better.
Randomization of k0
In a first step, we keep α in Eq. 12 fixed and instead randomize k0 according to a truncated Gaussian distribution of the form (see Eq. 16)
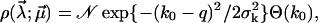 |
(30) |
with random parameters 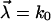 and fit parameters
and fit parameters 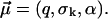 The fit to the experimental data (not shown) is considerably worse than in Fig. 3. For the corresponding fit parameters
The fit to the experimental data (not shown) is considerably worse than in Fig. 3. For the corresponding fit parameters 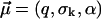 we obtained the result
we obtained the result
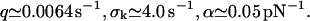 |
(31) |
Although the most probable dissociation rate q and the parameter α are still comparable to k0 and αm in Eq. 19, the relative dispersion σk/q of the dissociation rate distribution takes the quite unlikely value of ∼1000. The latter is in accordance with our above guess (see Eq. 15) that randomizing α has a much stronger effect than randomizing k0 in Eq. 12 due to the exponentiation.
In view of the aforementioned bad agreement between theory and experiment and the prediction that the dissociation rate k0 will vary by factors of 1000 between different realizations of the same chemical bond, we conclude that varying k0 instead of α does not admit a satisfactory theoretical description of the experimental reality.
We remark that under the assumptions Eq. 11 and Eq. 12, the quantities k0 and κ appear in the combination k0/κ in Eq. 14. Hence, a randomization of the linker stiffness, as considered in Friedsam et al. (31) and Kühner et al. (32), is basically equivalent to a randomization of k0 and does not satisfactorily explain our present experimental findings.
As a next step, we consider a simultaneous randomization of k0 and α. Specifically, we employed a distribution function of the form (see Eqs. 16 and 28)
 |
(32) |
with random parameters  (see Eq. 15) and fit parameters
(see Eq. 15) and fit parameters 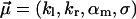 (see Eq. 18). The resulting fit to the experimental data (not shown) is practically indistinguishable from that in Fig. 3. For the corresponding fit parameters we obtained the result
(see Eq. 18). The resulting fit to the experimental data (not shown) is practically indistinguishable from that in Fig. 3. For the corresponding fit parameters we obtained the result
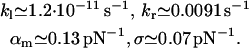 |
(33) |
These parameters are also very similar to those in Eq. 19.
In other words, the agreement with the experimental data and the quantitative numbers hardly change despite the two extra fit parameters.
The main conclusion of this subsection is that randomizing k0 is of no use.
A second basic observation of this section is that variations of the rate k0 in Eq. 12, or equivalently of κ in Eq. 11, have a much weaker effect than variations of α. The same conclusion is corroborated by comparison of the solid and dashed lines in Fig. 8 and by the huge variations of the linker stiffness in the works (31,32), and is naturally explained by the discussion preceding Eq. 15.
Conversely, this implies that estimating k0 from experimental data is much more critical, i.e., accompanied by much larger uncertainties, than estimating α.
GENERALIZED DISSOCIATION RATES
Complementary to the previous section, in this section we address modifications of the dissociation rate, Eq. 12, while keeping the ansatz for the probability density, Eq. 16, unchanged. In doing so, the main motivation is the observation from section Synthetic Data, Fluctuations, Systematic Deviations that Figs. 3–7 exhibit a small but still significant systematic underestimation of the experimental data by the theoretical lines for large forces f. Accordingly, the basic criterion for the subsequent variations of the dissociation rate will be to further reduce those small deviations between theory and experiment. As usual, we focus on one experimental data for expE1/E5 and ExpG from Fig. 3.
Throughout this section, the following simple argument plays a crucial role. If one modifies the force-dependent dissociation rate k(f) of a given chemical bond such that it becomes larger than before for all f-values, then the survival probability pυ(f) up to the force f will obviously become smaller than before for any f-value. The same property is inherited by 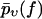 after averaging over the random variations of the dissociation rate k(f); see Eq. 9. Since
after averaging over the random variations of the dissociation rate k(f); see Eq. 9. Since 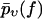 is decreasing from 1 toward 0 as f increases from fmin toward ∞, the resulting property of the function
is decreasing from 1 toward 0 as f increases from fmin toward ∞, the resulting property of the function 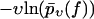 is to become larger than before. The opposite behavior results if the rate k(f) is modified so that it becomes smaller than before for all f-values.
is to become larger than before. The opposite behavior results if the rate k(f) is modified so that it becomes smaller than before for all f-values.
Hence, to reduce the above-mentioned deviations between experiment and theory, we are seeking for physical mechanisms which systematically increase the dissociation rates k(f), especially for large forces f.
Nonlinear generalization of Bell's rate
First, we generalize Bell's ansatz Eq. 12 for the dissociation rate (10) according to
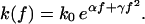 |
(34) |
A straightforward calculation shows that a negative contribution to γ arises from the nonlinear corrections to the so-far adopted leading-order approximation ΔU(f) = ΔU0 – Δx f for the effective potential barrier that has to be surmounted by thermal activation in the presence of an external pulling force f ≥ 0; see also the discussion above Eq. 13 and in the sequel. According to the general argument at the beginning of this section, it follows that including nonlinear corrections of the potential barrier ΔU(f) does not improve the agreement between theory and experiment but rather worsens it.
So, to further improve our theory, a mechanism that generates positive γ-values is required. For instance, such a positive value of γ may be caused by deformations of the polymer linkers attached to the ligand-receptor complex (see Fig. 1), such that an increasing force f leads to an alignment of the reaction coordinate with the force direction. Since the supposed rotation of the reaction coordinate is caused by the component of the force perpendicular to it and larger values of α correspond to a close alignment of the reaction coordinate and the force direction from the beginning of the pulling process (see item 3 in section Basic Idea), γ is a decreasing function of α.
In the absence of a quantitative model for the mechanisms of bond heterogeneities mentioned in section Basic Idea, we quantify the above mentioned decreasing behavior of γ as a function of α, together with further possibly existing mechanisms contributing to γ in Eq. 34, by the heuristic ad hoc ansatz,
 |
(35) |
where β0 is an additional fit parameter and α is randomly distributed according to Eq. 16.
In other words, our generalized model involves still the usual single random parameter Eq. 15, while the original fit parameters Eq. 18 are now extended to 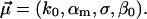 The fit to the experimental data along these lines in Fig. 10 is of the same quality as in Fig. 3, except that the agreement for large forces f is now indeed slightly better. For the corresponding fit parameters, we obtained the result
The fit to the experimental data along these lines in Fig. 10 is of the same quality as in Fig. 3, except that the agreement for large forces f is now indeed slightly better. For the corresponding fit parameters, we obtained the result
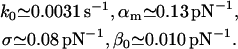 |
(36) |
FIGURE 10.
(Symbols) Same experimental data as in Fig. 3. (Solid lines) Theoretical functions 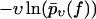 for the same pulling velocities υ as the symbols, using Eqs. 8, 9, 11, 16, 34, and 36.
for the same pulling velocities υ as the symbols, using Eqs. 8, 9, 11, 16, 34, and 36.
Again, these results for k0, αm, and σ are close to those in Eq. 19.
In conclusion, the slight systematic deviations between theory and experiment in Figs. 3–7 can be reduced by means of a physically meaningful generalization of the force-dependent dissociation rate Eq. 34 (nonlinear corrections in the exponent) with a single additional fit parameter.
Intermediate energy barriers
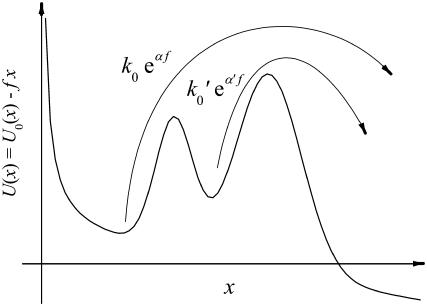
Although the chemical reaction path, in the simplest case, proceeds from a bound metastable state across an energy barrier (activated state) toward a dissociated product state, in more general cases there may exist additional intermediate metastable states separated by additional intermediate energy barriers (11,15,16,26).
The simplest example of such a situation with one intermediate state is sketched in Fig. 11. At small forces f the population of this state is small and the dissociation is effectively governed by a decay rate of the form k(f) = k0eαf, where α is the distance between the first and the last extremum of the potential U0(x) divided by the thermal energy kBT; see Eqs. 12 and 13. On the other hand, the decay is always limited by the escape rate across the outer energy barrier k′0eα′f with k0 < k′0 and α > α′. At larger forces this becomes the effective decay rate, because most of the population is now in the intermediate metastable state. Altogether, we thus have k(f) = k0eαf for small forces and k(f) = k′0eα′f < k0eαf for larger forces.
FIGURE 11.
Sketch of the relevant dissociation rates of a chemical bond whose reaction coordinate x experiences a reaction potential U(x) with an intermediate energy barrier.
According to the general argument at the beginning of this section it follows that such a modification of k(f) due to the presence of an additional intermediate energy barrier cannot lead to an improved agreement between experiment and theory. It only can lead to an increased curvature of the theoretical lines in Figs. 3–7, while a better agreement would require that the curvatures decrease.
In Fig. 11 we have tacitly assumed that upon increasing the tilt f, the two minima exchange their roles (local versus global minima) before the two barriers exchange their roles (local versus global maxima). One can easily see that our final conclusions remain valid also in the opposite situation. Moreover, the conclusions persist also in the case of more than one intermediate state.
The same conclusion is once more confirmed by Fig. 8. If there were an intermediate state present along the dissociation pathway, then the rate law k(f) = k0eαf, which governs the small–f regime, would become less and less relevant with increasing fmin, whereas the large-f law k(f) = k′0eα′f would become more and more dominant. Hence one should see a systematic increase of the fit parameter k0 with increasing fmin, while αm should systematically decrease. Comparing the fit parameters Eq. 19 for fmin = 20 pN (Fig. 3) with those for fmin = 50 pN and fmin = 100 pN in Fig. 8, such a systematic tendency is not observed.
In conclusion, the experimental data in Figs. 3–7 do not imply the existence of intermediate states within the framework of our present theoretical description.
Note the difference between this conclusion and the one from Raible et al. (20), mentioned also as one of the unsuccessful explanations. There, it has been shown that within the framework of the standard theory, it is not possible to explain the very strong disagreement of the experimental curves  for different pulling velocities υ in Figs. 3–7 by taking into account intermediate states.
for different pulling velocities υ in Figs. 3–7 by taking into account intermediate states.
COMPARISON WITH THE STANDARD METHOD
In this section we discuss some practical aspects of experimental data evaluation in the light of our extension of the standard theory, thereby also providing a further strong argument in favor of our new theory.
Although our main quantity of interest so far was 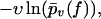 traditionally one mostly considers rupture force distributions
traditionally one mostly considers rupture force distributions 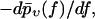 and similarly for
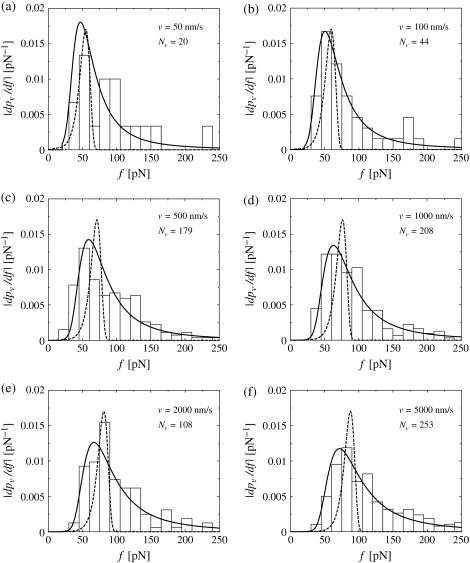
and similarly for 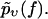 Fig. 12 illustrates a well-known problem of the standard theory Eqs. 1 and 2 supplemented by Eqs. 11 and 12 in this context (see e.g., (29,30)): the dotted theoretical curves and the experimental rupture force histograms have opposite skewness and agree very badly after fitting k0 and α = αm according to the so-called standard method, as described in more detail in the next paragraph. On the other hand, our generalized theory has the correct skewness and agrees very well with the experimental histograms in Fig. 12, thus quantitatively confirming the qualitative arguments in Simson et al. (29) and Strigl et al. (30).
Fig. 12 illustrates a well-known problem of the standard theory Eqs. 1 and 2 supplemented by Eqs. 11 and 12 in this context (see e.g., (29,30)): the dotted theoretical curves and the experimental rupture force histograms have opposite skewness and agree very badly after fitting k0 and α = αm according to the so-called standard method, as described in more detail in the next paragraph. On the other hand, our generalized theory has the correct skewness and agrees very well with the experimental histograms in Fig. 12, thus quantitatively confirming the qualitative arguments in Simson et al. (29) and Strigl et al. (30).
FIGURE 12.
(Histograms) Same experimental rupture data as in Fig. 3 but represented as rupture force distributions. (Solid lines) Theoretical curves 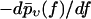 according to Eqs. 9 and 11–19. (Dotted lines) Same but for k0 = 0.011 s−1, αm = 0.14 pN−1, σ = 0 pN−1, fmin = 0 (see main text), and with
according to Eqs. 9 and 11–19. (Dotted lines) Same but for k0 = 0.011 s−1, αm = 0.14 pN−1, σ = 0 pN−1, fmin = 0 (see main text), and with 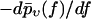 divided by a factor 3 for better visibility of the other curves.
divided by a factor 3 for better visibility of the other curves.
The most probable rupture force f* by definition maximizes the rupture force distribution 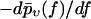 within the regime f ≥ fmin, implying
within the regime f ≥ fmin, implying
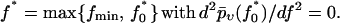 |
(37) |
For the standard theory Eqs. 1 and 2 with Eqs. 11 and 12, it readily follows that
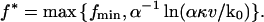 |
(38) |
Accordingly, in many experimental studies one traditionally plots f* versus ln v and determines k0 and α according to Eq. 38, by means of a (piecewise) linear fit, where f*(υ) is estimated for each pulling velocity v by way of fitting a Gaussian with four parameters c1, …, c4 of the form
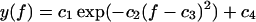 |
(39) |
to the experimentally observed rupture force histogram. This procedure is commonly referred to as the standard method. Along these lines we determined the fit parameters k0 and αm = α used for the dotted curves in Fig. 12.
Note the difference between our present notions of standard method and standard theory. The standard theory consists in the assumptions from Eqs. 1 and 2 about the rupture process (often supplemented by the assumptions from Eqs. 11 and 12). The standard method consists in fitting Gaussians Eq. 39 to the experimental histograms of rupture force distributions and using the resulting most probable rupture forces f* to determine α and k0 according to formula Eq. 38.
The standard theory, together with the common ansatz Eqs. 11 and 12, implies formula Eq. 38. We will now demonstrate that the standard method may still be a satisfactory approximation although the standard theory is not.
Within our generalized theory, Eq. 37 is no longer tractable analytically but easily solved numerically (see Fig. 13).
FIGURE 13.
Most probable rupture force f* versus pulling velocity υ (logarithmic scale) by solving Eq. 37 numerically with Eq. 9, fmin = 0, Eqs. 11–16, k0 and αm from Eq. 19, and five different values of σ. For fmin > 0, the maximum of the plotted curves and fmin yield f*.
Although the mean α-value, given by 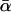 in Eq. 17, and the most probable α-value, given by αm in Eq. 16, are quite similar if the relative dispersion σ/αm is comparable to or smaller than unity, they may notably differ for larger dispersions. In Fig. 13 we have kept αm fixed and compared the resulting curves for different ratios σ/αm and thus different dispersions σ, hence implicitly varying
in Eq. 17, and the most probable α-value, given by αm in Eq. 16, are quite similar if the relative dispersion σ/αm is comparable to or smaller than unity, they may notably differ for larger dispersions. In Fig. 13 we have kept αm fixed and compared the resulting curves for different ratios σ/αm and thus different dispersions σ, hence implicitly varying 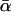 as well. Complementarily, in Fig. 14 we have kept
as well. Complementarily, in Fig. 14 we have kept 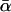 fixed while varying σ and hence also αm in such a way that their ratio σ/αm was still the same as in Fig. 13.
fixed while varying σ and hence also αm in such a way that their ratio σ/αm was still the same as in Fig. 13.
FIGURE 14.
Same as Fig. 13, except that 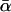 in Eq. 17 rather than αm in Eq. 16 has been kept fixed to the value 0.135 pN−1.
in Eq. 17 rather than αm in Eq. 16 has been kept fixed to the value 0.135 pN−1.
Finally, in Fig. 15 we again kept 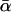 fixed like in Fig. 14, but now we did not determine f* by numerically solving Eq. 37 but rather by fitting Gaussians of the form Eq. 39 to the actual rupture force distributions
fixed like in Fig. 14, but now we did not determine f* by numerically solving Eq. 37 but rather by fitting Gaussians of the form Eq. 39 to the actual rupture force distributions 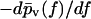 in the spirit of the standard method.
in the spirit of the standard method.
FIGURE 15.
Same as Fig. 14, except that f* was not determined according to Eq. 37 but rather by fitting the rupture force distributions 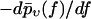 by Gaussian Eq. 39. (The fit was performed on the interval 0 ≤ f ≤ 250 pN.)
by Gaussian Eq. 39. (The fit was performed on the interval 0 ≤ f ≤ 250 pN.)
In all three Figs. 13–15, the curves for σ = 0 (solid lines) are almost identical and represent the prediction Eq. 38 of the standard theory (see discussion below Eq. 18)). Surprisingly, even for σ > 0, in all three figures f* still remains in very good approximation (but not rigorously) a (piecewise) linear function of ln υ. However, in general the dependence of these curves on the parameters k0, αm, or 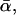 and σ, is much more complex than for the standard theory in Eq. 38.
and σ, is much more complex than for the standard theory in Eq. 38.
Curiously enough, the increasing agreement of the different curves when proceeding from Fig. 13 to Fig. 15 implies that if one estimates f* in the traditional spirit by fitting Gaussian Eq. 39 to the rupture force distributions then the dependence of this fit on the dispersion σ is approximately negligible. Hence one still can approximately determine k0 and  by means of the standard method, since the error of the underlying standard theory and of the Gaussian fitting procedure almost compensate each other!
by means of the standard method, since the error of the underlying standard theory and of the Gaussian fitting procedure almost compensate each other!
E.g., the parameters k0, 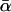 which can be inferred from the five functions in Fig. 15 via Eq. 38, remain between k0 = 0.0046 s−1,
which can be inferred from the five functions in Fig. 15 via Eq. 38, remain between k0 = 0.0046 s−1, 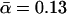 pN−1, and k0 = 0.0033 s−1,
pN−1, and k0 = 0.0033 s−1,  pN−1—i.e., quite close to their actual values k0 = 0.0033 s−1,
pN−1—i.e., quite close to their actual values k0 = 0.0033 s−1, 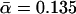 pN−1.
pN−1.
In other words, the inconsistency of the standard theory as unraveled in our present work could not be discovered in the traditional f* versus ln υ plots. Conversely, such plots still remain admissible from the viewpoint of our present generalized theory to approximately determine k0 and 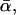 while σ (and hence αm) can only be estimated by means of a more elaborate data analysis.
while σ (and hence αm) can only be estimated by means of a more elaborate data analysis.
SUMMARY AND CONCLUSIONS
The theory by Evans and Ritchie (11) plays a key role in the field of single-molecule force spectroscopy. While extended in several important directions, their basic assumptions from Eqs. 1 and 2 have been taken over in all subsequent theoretical and experimental works in this field, reflected also by the almost 450 citations of that article.
We demonstrated that the incompatibility of this standard theory with experimental findings—originally unraveled in Raible et al. (20)—is a general feature of many different experimental systems. The qualitative similarity of Figs. 3–7 suggests that this incompatibility is, in fact, universal.
The central part of our present work is represented by section Heterogeneity of Chemical Bonds, where we show how the problem can be cured. Namely, we explain and remedy the discrepancy between experiment and theory by postulating heterogeneities of the chemical bonds in extension of the standard theory. In the simplest case, the single new fit parameter of the generalized theory is the dispersion of the effective dissociation lengths. The resulting very good agreement with the experimental data corroborates that the proposed heterogeneity of the chemical bonds is ubiquitous in dynamic force spectroscopy experiments and that our model equations (Eqs. 9, 11–16) constitute a faithful model for the interpretation of these experimental data.
At the same time, another long-known problem of the standard data analysis procedure is resolved in Comparison with the Standard Method, namely the notoriously bad agreement between experimentally observed and theoretically calculated rupture force distributions (Fig. 12). Since this procedure builds on the standard theory and since the rupture force distribution from Comparison with the Standard Method is basically the derivative of the survival probability from Heterogeneity of Chemical Bonds, it seems possible that the two problems of the standard theory treated in those two sections are essentially two sides of the same coin, though we have not been able to explicitly demonstrate such a connection.
A main open problem is a more detailed understanding and quantitative modeling of the bond heterogeneities instead of the rather qualitative arguments in section Basic Idea and an ad hoc ansatz like in Eq. 16. On the other hand, by assuming a distribution of α we could demonstrate that the specific quantitative form of those ansatzes does not matter very much. Moreover, such a detailed modeling of the many different potential sources of bond randomness would probably go beyond the present possibilities of experimental verification.
In view of our numerous unsuccessful previous attempts to explain the experimental findings, we believe that our present explanation indeed captures an important real effect in such experiments. In particular, the fact that the experimental curves in Figs. 3–7 are typically increasing with increasing pulling velocity v, seems difficult or even impossible to explain quantitatively in a different way. Although the standard theory predicts no such υ-dependence at all, most physically meaningful alternative explanations lead just to the opposite υ-dependence that is observed experimentally (20). That an explanation is both physically meaningful and in quantitative agreement with the experiment seems to be an important requirement to us. E.g., it may be easily possible to fit the curves in Fig. 3–7 by some ad hoc mathematical ansatz with a few fit parameters but without a physical basis. An example of such an ansatz is a scaling function with certain scaling exponents. The fragility of such a satisfactory quantitative agreement between theory and experiment is once more illustrated when we assumed a random distribution of the parameter.
Since our central theoretical quantity, 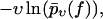 is very different from the traditional observables considered in the context of dynamic force spectroscopy (see section Comparison with the Standard Method), it may be worthwhile to summarize the effects of our three basic fit parameters k0, αm, and σ (see Eq. 18) on the shape of this function. The qualitative effect of the force free dissociation rate k0 and of the most probable dissociation length αm in units of kT can still be inferred from Eq. 14, yielding
is very different from the traditional observables considered in the context of dynamic force spectroscopy (see section Comparison with the Standard Method), it may be worthwhile to summarize the effects of our three basic fit parameters k0, αm, and σ (see Eq. 18) on the shape of this function. The qualitative effect of the force free dissociation rate k0 and of the most probable dissociation length αm in units of kT can still be inferred from Eq. 14, yielding
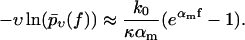 |
(40) |
Plotted on a logarithmic scale, like in Figs. 3–10, the small-f regime is thus dominated by a logarithmic asymptotic of the form ln(f k0/κ), crossing over for large f toward a linear asymptotics of the form αm f. The remaining parameter σ, representing the random dispersion of the dissociation lengths α in units of kT, mainly determines the spreading of the functions 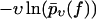 upon variation of the pulling speed υ. In particular, for σ → 0 this spreading disappears and our new theory reduces to the standard theory (with α = αm).
upon variation of the pulling speed υ. In particular, for σ → 0 this spreading disappears and our new theory reduces to the standard theory (with α = αm).
The remaining small systematic differences between theory and experiment at large forces f in Figs. 3–7 have been explained with the help of nonlinear generalization of Bell's rate by means of a simple physical mechanism, giving rise to one further fit parameter. This mechanism would support the physical reason 3 to explain bond heterogeneities in section Basic Idea, namely geometrical variations of the entire setup in Fig. 1, which are changing upon increasing the external load f on the bound complex.
According to the conclusions of section Randomization of k0, variations of k0, or equivalently, of κ in Eq. 12, have a much weaker effect than variations of α. Further closely related conclusions are:
Randomization of the linker stiffness (31,32) is of no help to explain the experimental observations in Figs. 3–7.
Small-to-moderate variations of the force-extension curves are of little importance in Figs. 3–7. Except for the rigorous arguments in Assumptions (see The Standard Theory), no such variations are admissible (see also Fig. 2).
Estimating k0 from experimental data is accompanied by a much larger uncertainty than estimating the mean value αm and the dispersion σ of the random distribution governing α. In fact, Eq. 12 suggests that not k0 itself, but rather ln k0, should be considered as the natural fit parameter complementing αm and σ.
Acknowledgments
We thank Ralf Eichhorn for providing Fig. 1.
This work was supported by the Deutsche Forschungsgemeinschaft under grant No. SFB 613, grant No. ME 1458/3, grant No. RE 1344/3-1, the Alexander von Humboldt-Stiftung, and the European Science Foundation program STOCHDYN.
References
- 1.Merkel, R. 2001. Force spectroscopy on single passive biomolecules and single biomolecular bonds. Phys. Rep. 346:343–385. [Google Scholar]
- 2.Evans, E. 2001. Probing the relation between force, lifetime, and chemistry in single biomolecular bonds. Annu. Rev. Biomol. Struct. 30:105–128. [DOI] [PubMed] [Google Scholar]
- 3.Florin, E.-L., V. T. Moy, and H. E. Gaub. 1994. Adhesion forces between individual ligand-receptor pairs. Science. 264:415–417. [DOI] [PubMed] [Google Scholar]
- 4.Lee, G., L. A. Chrisey, and R. J. Colton. 1994. Direct measurement of the interaction forces between complementary strands of DNA with atomic force microscopy. Science. 266:771–775. [DOI] [PubMed] [Google Scholar]
- 5.Dammer, U., O. Popescu, P. Wagner, D. Anselmetti, H.-J. Güntherodt, and G. N. Misevic. 1995. Binding strength between cell adhesion proteoglycans measured by atomic force microscopy. Science. 267:1173–1175. [DOI] [PubMed] [Google Scholar]
- 6.Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gullingsrud, J. R., R. Braun, and K. Schulten. 1999. Reconstructing potentials of mean force through time series analysis of steered molecular dynamics simulations. J. Comput. Phys. 151:190–211. [Google Scholar]
- 8.Paci, E., A. Caflisch, A. Plückthun, and M. Karplus. 2001. Forces and energetics of hapten-antibody dissociation: a biased molecular dynamics study. J. Mol. Biol. 314:589–605. [DOI] [PubMed] [Google Scholar]
- 9.Heymann, B., and H. Grubmüller. 2001. Molecular dynamics force probe simulations of antibody/antigen unbinding. Entropic control and nonadditivity of unbinding forces. Biophys. J. 81:1295–1313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bell, G. I. 1978. Models for the specific adhesion of cells to cells. Science. 200:618–627. [DOI] [PubMed] [Google Scholar]
- 11.Evans, E., and K. Ritchie. 1997. Dynamic strength of molecular adhesion bonds. Biophys. J. 72:1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hänggi, P., P. Talkner, and M. Borkovec. 1990. Reaction rate theory: fifty years after Kramers. Rev. Mod. Phys. 62:251–341. [Google Scholar]
- 13.Rief, M., J. M. Fernandez, and H. E. Gaub. 1998. Elastically coupled two-level systems as a model for biopolymer extensibility. Phys. Rev. Lett. 81:4764–4767. [Google Scholar]
- 14.Shillcock, J., and U. Seifert. 1998. Escape from a metastable well under a time-ramped force. Phys. Rev. E. 57:7301–7304. [Google Scholar]
- 15.Merkel, R., P. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
- 16.Strunz, T., K. Oroszlan, I. Schumakovitch, H.-J. Güntherodt, and M. Hegner. 2000. Model energy landscapes and the force-induced dissociation of ligand-receptor bonds. Biophys. J. 79:1206–1212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heymann, B., and H. Grubmüller. 2000. Dynamic force spectroscopy of molecular adhesion bonds. Phys. Rev. Lett. 84:6126–6129. [DOI] [PubMed] [Google Scholar]
- 18.Seifert, U. 2000. Rupture of multiple parallel molecular bonds under dynamic loading. Phys. Rev. Lett. 84:2750–2753. [DOI] [PubMed] [Google Scholar]
- 19.Nguyen-Duong, N., K. W. Koch, and R. Merkel. 2003. Surface anchoring reduces the lifetime of single specific bonds. Europhys. Lett. 61:845–851. [Google Scholar]
- 20.Raible, M., M. Evstigneev, P. Reimann, F. W. Bartels, and R. Ros. 2004. Theoretical analysis of dynamic force spectroscopy experiments on ligand-receptor complexes. J. Biotechnol. 112:13–23. [DOI] [PubMed] [Google Scholar]
- 21.Sain, A., and M. Wortis. 2004. Influence of tether dynamics on forced Kramers escape from a kinetic trap. Phys. Rev. E. 70:031102. [DOI] [PubMed] [Google Scholar]
- 22.Evstigneev, M., and P. Reimann. 2003. Dynamic force spectroscopy: optimized data analysis. Phys. Rev. E. 68:045103. [DOI] [PubMed] [Google Scholar]
- 23.Bartels, F. W., B. Baumgarth, D. Anselmetti, R. Ros, and A. Becker. 2003. Specific binding of the regulatory protein ExpG to promoter regions of the galactoglucan biosynthesis gene cluster of Sinorhizobium meliloti—a combined molecular biology and force spectroscopy investigation. J. Struct. Biol. 143:145–152. [DOI] [PubMed] [Google Scholar]
- 24.Eckel, R., S.-D. Wilking, A. Becker, N. Sewald, R. Ros, and D. Anselmetti. 2005. Single molecule experiments in synthetic biology—a new approach to the affinity ranking of DNA-binding peptides. Angew. Chem. Int. Ed. Engl. 44:3921–3924. [DOI] [PubMed] [Google Scholar]
- 25.Eckel, R., R. Ros, B. Decker, J. Mattay, and D. Anselmetti. 2005. Supramolecular chemistry at the single molecule level. Angew. Chem. Int. Ed. Engl. 44:484–488. [DOI] [PubMed] [Google Scholar]
- 26.Derényi, I., D. Bartolo, and A. Ajdari. 2004. Effects of intermediate bound states in dynamic force spectroscopy. Biophys. J. 86:1263–1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bartolo, D., I. Derényi, and A. Ajdari. 2002. Dynamic response of adhesion complexes: beyond the single path picture. Phys. Rev. E. 65:051910. [DOI] [PubMed] [Google Scholar]
- 28.Vijayendran, R. A., and D. E. Leckband. 2001. A quantitative assessment of heterogeneity for surface-immobilized proteins. Anal. Chem. 73:471–480. [DOI] [PubMed] [Google Scholar]
- 29.Simson, D. A., M. Strigl, M. Hohenadl, and R. Merkel. 1999. Statistical breakage of single protein A-IgG bonds reveals crossover from spontaneous to force-induced bond dissociation. Phys. Rev. Lett. 83:652–655. [Google Scholar]
- 30.Strigl, M., D. A. Simson, C. M. Kacher, and R. Merkel. 1999. Force-induced dissociation of single protein A-IgG bonds. Langmuir. 15:7316–7324. [Google Scholar]
- 31.Friedsam, C., A. K. Wehle, F. Kühner, and H. E. Gaub. 2003. Dynamic single-molecule force spectroscopy: bond rupture analysis with variable spacer length. J. Phys. Condens. Matter. 15:S1709–S1723. [Google Scholar]
- 32.Kühner, F., L. T. Costa, P. M. Bisch, S. Thalhammer, W. M. Heckl, and H. E. Gaub. 2004. LexA-DNA bond strength by single molecule force spectroscopy. Biophys. J. 87:2683–2690. [DOI] [PMC free article] [PubMed] [Google Scholar]